Winter Wheat Yield Estimation with Color Index Fusion Texture Feature
Abstract
1. Introduction
2. Materials and Methods
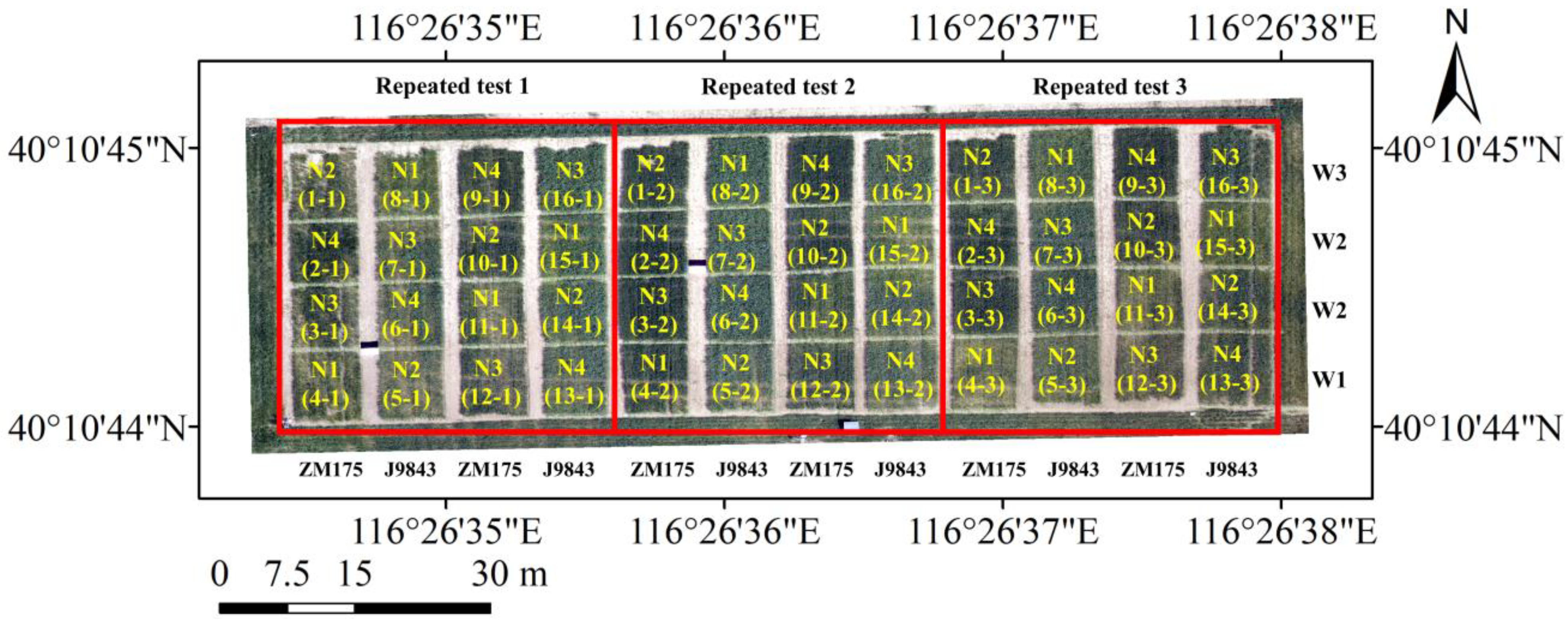
2.1. Experimental Design
2.2. Data Acquisition
2.2.1. Yield Acquisition
2.2.2. Acquisition of Digital Images by UAV
2.3. Color Indexes Selection
2.4. Texture Feature Acquisition
2.5. Data Analysis and Accuracy Evaluation
2.6. Precision Evaluation
3. Results and Discussion
3.1. Correlation between Color Indexes and Yield
3.2. Correlation between Texture Feature Indexes and Yield
3.3. Inversion of Winter Wheat Yield Model
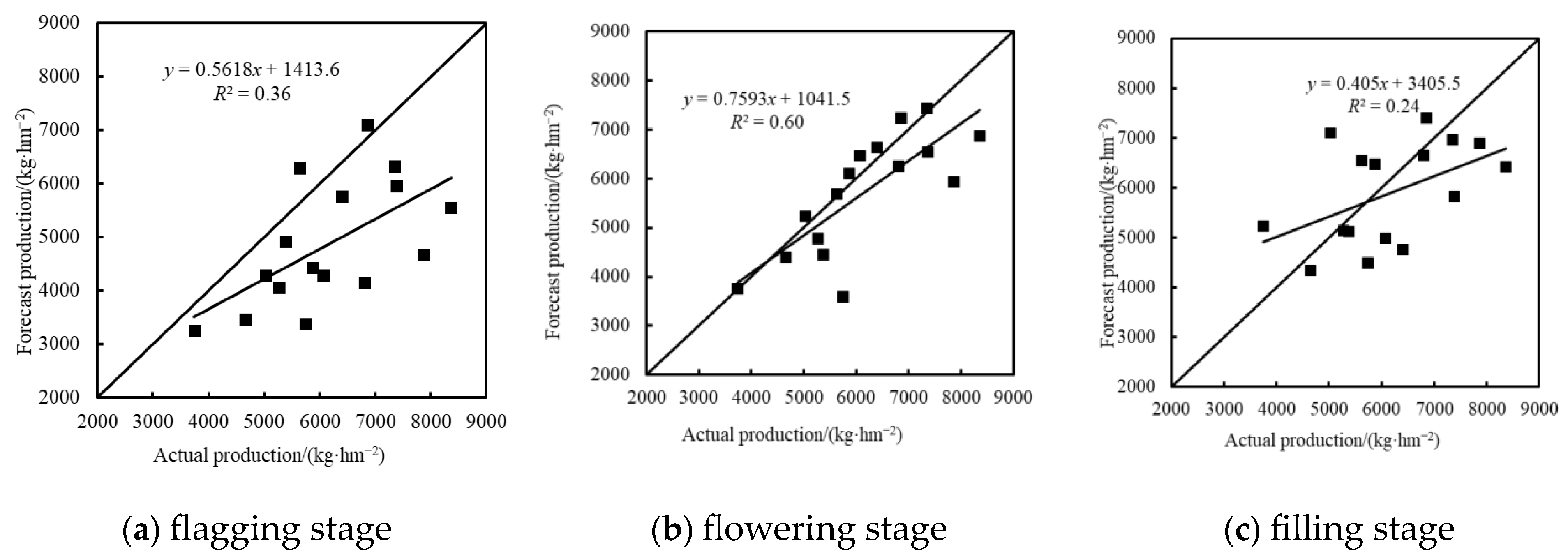
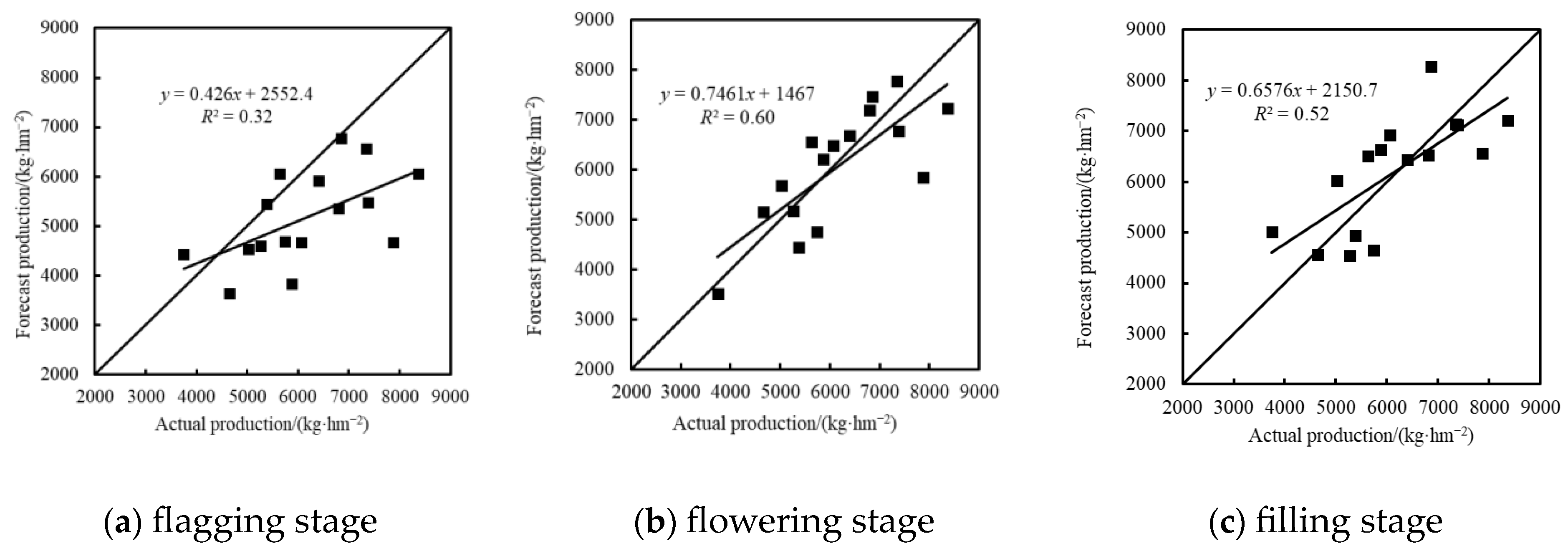
3.3.1. Yield Inversion Based on Color Indexes
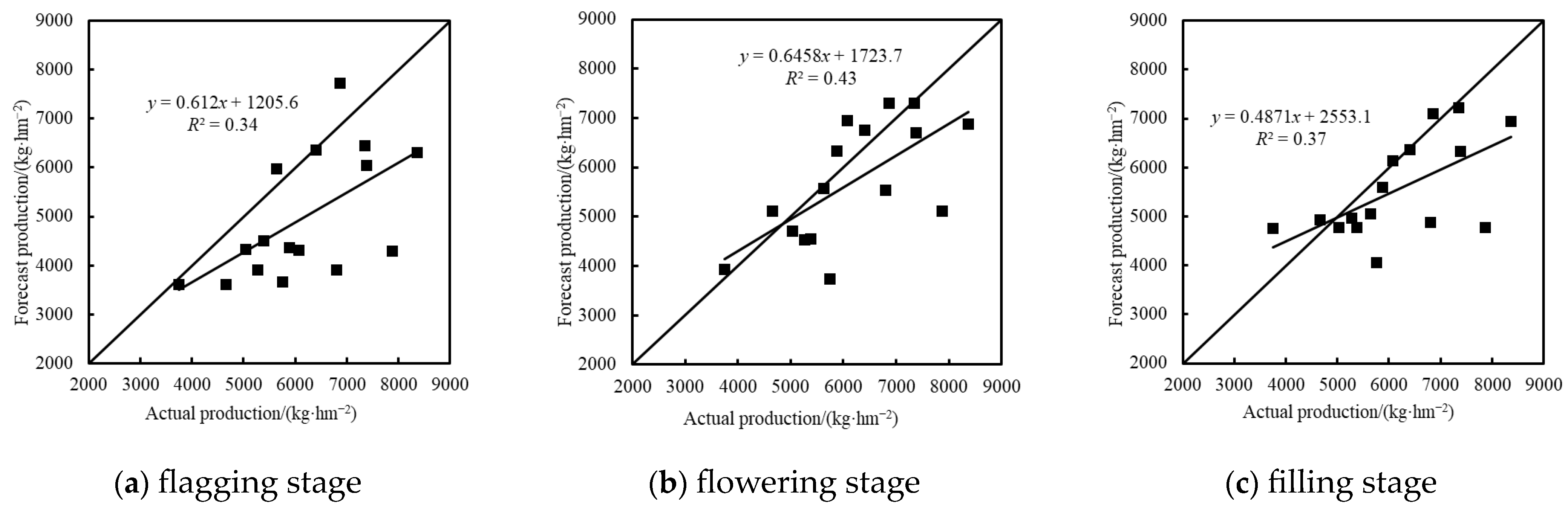
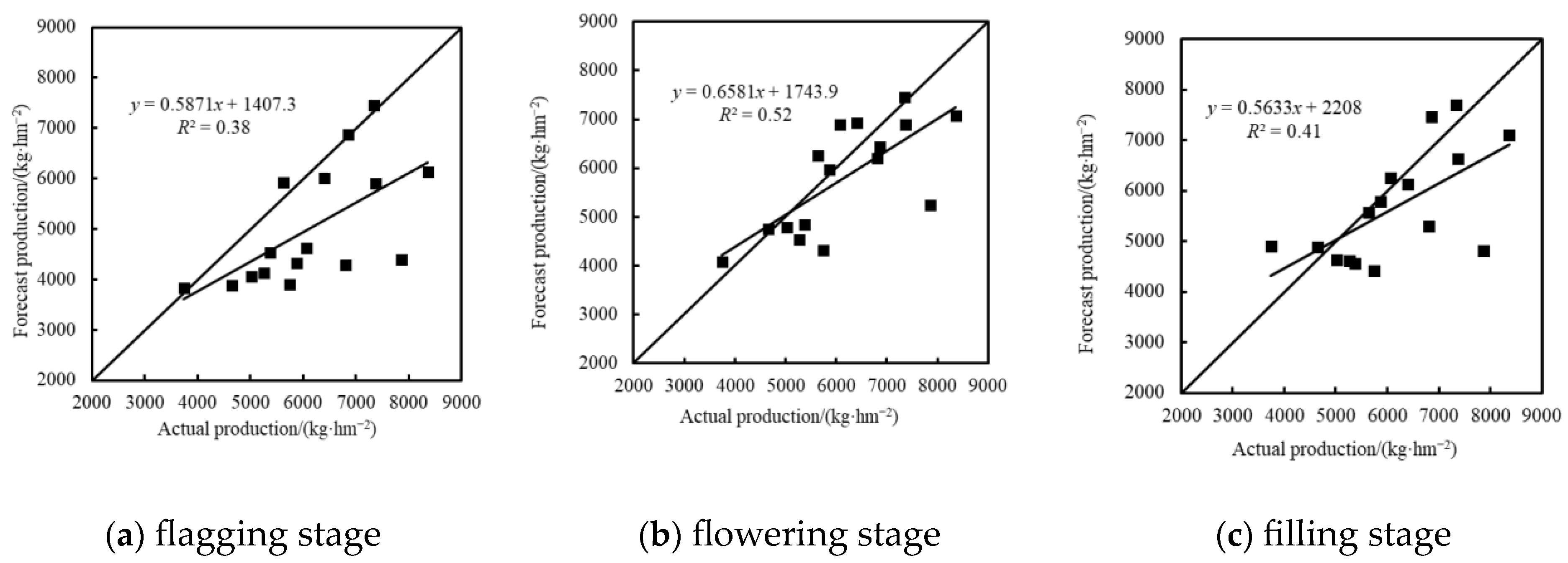
3.3.2. Yield Inversion Based on Texture Feature Indexes
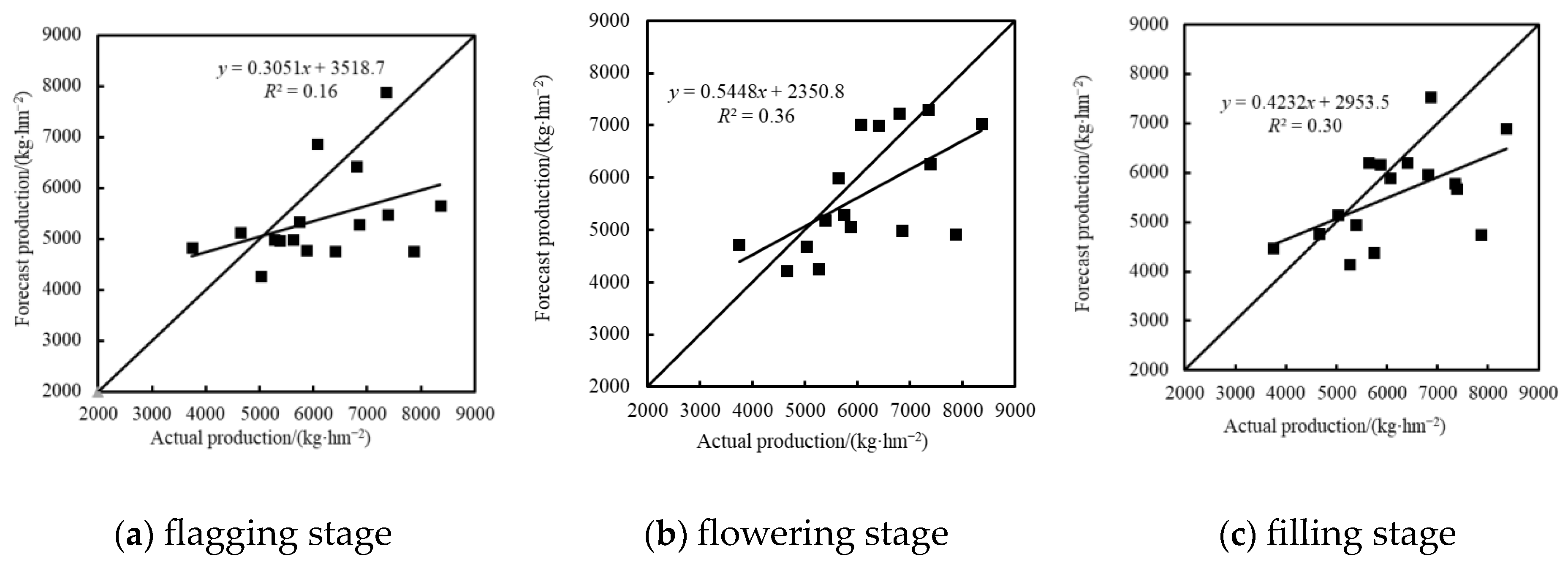
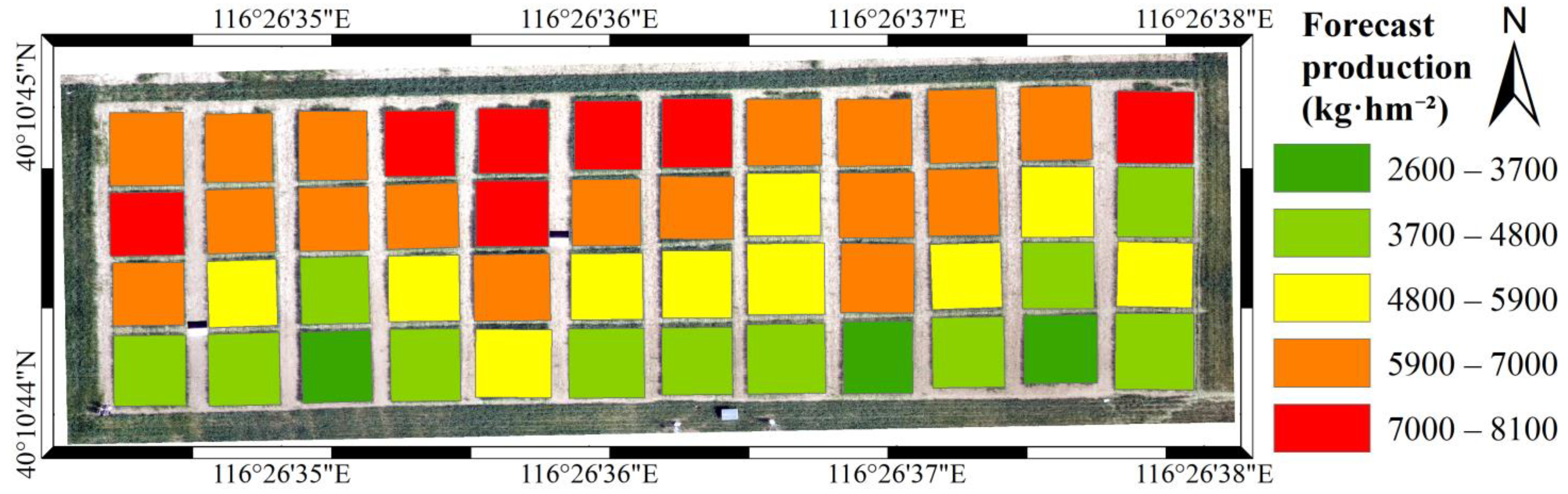
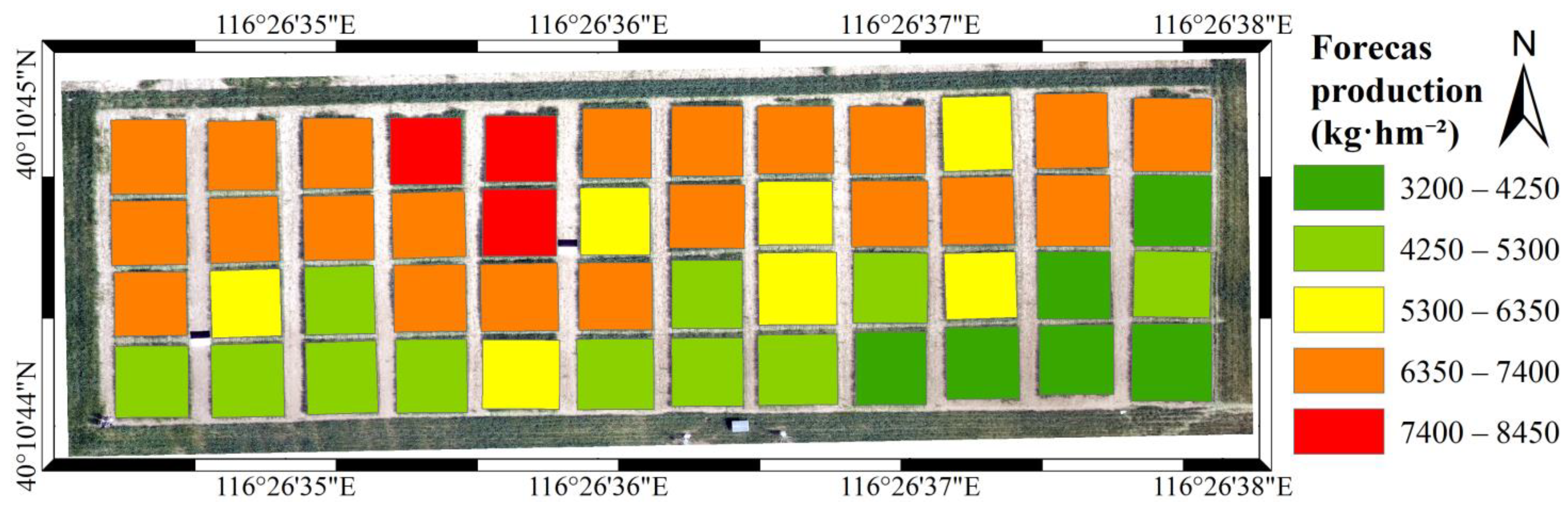
3.3.3. Yield Inversion Based on Fusion of Color Indexes and Texture Feature
4. Discussion
4.1. The Impact of Growth Period on Yield
4.2. The Impact of Different Algorithms on Yield Estimation
5. Conclusions
- (1)
- A model for estimating winter wheat yield using color indexes fused with texture feature indexes outperforms wheat yield models constructed using color indexes or texture feature indexes;
- (2)
- The wheat yield model constructed by PLSR was superior to the yield model constructed by RF for the flagging stage, flowering stage, and filling stage. The R2 and RMSE values of the optimal yield model modeled with PLSR were 0.75, 0.71 and 0.76 and 738.48 kg/hm2, 794.77 kg/hm2 and 728.85 kg/hm2 when using color indexes, texture indexes and color indexes fused with texture indexes, respectively, as the independent variable in the filling stage;
- (3)
- A winter wheat yield distribution map can be used to more effectively monitor winter wheat yield distribution and provide a more scientific method for guiding fertilization and irrigation, and increasing yield.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Feng, H.K.; Yue, J.B.; Li, Z.H.; Yang, G.J.; Song, X.Y.; Yang, X.D.; Zhao, Y. Remote-sensing estimation of potato above-ground biomass based on spectral and spatial features extracted from high-definition digital camera images. Comput. Electron. Agr. 2022, 198, 107089. [Google Scholar] [CrossRef]
- Geipel, J.; Link, J.; Claupein, W. Combined spectral and spatial modeling of corn yield based on aerial images and crop surface models acquired with an unmanned aircraft system. Remote Sens. 2014, 6, 10335–10355. [Google Scholar] [CrossRef]
- Wang, L.; Tian, Y.; Yao, X.; Zhu, Y.; Cao, W.X. Predicting grain yield and protein content in wheat by fusing multi-sensor and multi-temporal remote-sensing images. Field Crop. Res. 2014, 164, 178–188. [Google Scholar] [CrossRef]
- Noureldin, N.; Aboelghar, M.; Saudy, H.; Ali, A. Rice yield forecasting models using satellite imagery in Egypt. Egypt. J. Remote Sens. Space Sci. 2013, 16, 125–131. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhao, C.J.; Huang, W.J. Fundamentals and Applications of Quantitative Remote Sensing in Agriculture; Science Press: Beijing, China, 2008. [Google Scholar]
- Zhu, W.X.; Li, S.J.; Zhang, X.B.; Li, Y.; Sun, Z.G. Estimation of winter wheat yield using optimal vegetation indices from unmanned aerial vehicle remote sensing. Trans. Chin. Soc. Agric. Eng. 2018, 34, 78–86. [Google Scholar]
- Liu, J.M.; Zhou, Z.; He, X.X.; Wang, P.X.; Huang, J.X. Winter Wheat Yield Estimation Method Based on NDWI and Convolutional Neural Network. Trans. Chin. Soc. Agric. Mach. 2021, 52, 273–280. [Google Scholar]
- Zhou, X.; Zheng, H.B.; Xu, X.Q.; He, J.Y.; Ge, X.K.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Predicting grain yield in rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogramm. 2017, 130, 246–255. [Google Scholar] [CrossRef]
- Tao, H.L.; Xu, L.J.; Feng, H.K.; Yang, G.J.; Yang, X.D.; Niu, Y.C. Winter Wheat Yield Estimation Based on UAV Hyperspectral Remote Sensing Data. Trans. Chin. Soc. Agric. Mach. 2020, 51, 146–155. [Google Scholar]
- Zhang, M.N.; Feng, A.J.; Zhou, J.F.; Lv, X.L. Cotton yield prediction using remote visual and spectral images captured by UAV system. Trans. Chin. Soc. Agric. Eng. 2019, 35, 91–98. [Google Scholar]
- Fei, S.; Chen, Z.; Li, L.; Ma, Y.; Xiao, W. Bayesian model averaging to improve the yield prediction in wheat breeding trials. Agric. For. Meteorol. 2023, 328, 109237. [Google Scholar] [CrossRef]
- Tao, H.L.; Feng, H.K.; Xu, L.J.; Miao, M.K.; Yang, G.J.; Yang, X.D.; Fan, L. Estimation of the yield and plant height of winter wheat using UAV-based hyperspectral images. Sensors 2020, 20, 1231. [Google Scholar] [CrossRef]
- Huang, J.X.; Huang, H.; Ma, H.Y.; Zhuo, W.; Huang, R.; Gao, X.R.; Liu, J.M.; Su, W.; Li, L.; Zhang, X.D.; et al. Review on data assimilation of remote sensing and crop growth models. Trans. Chin. Soc. Agric. Eng. 2018, 34, 144–156. [Google Scholar]
- Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.L.; Mouazen, A.M. Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.B.; Su, W.; Zhang, X.D.; Zhu, D.H.; Wu, W.B. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- Wang, L.G.; Zheng, G.Q.; Guo, Y.; He, J.; Cheng, Y.Z. Prediction of Winter Wheat Yield Based on Fusing Multi-source Spatio-temporal Data. Trans. Chin. Soc. Agric. Mach. 2022, 53, 198–204. [Google Scholar]
- Zhang, N.; Liu, X.; Ren, J.; Wu, S.; Li, F. Estimating the winter wheat harvest index with canopy hyperspectral remote sensing data based on the dynamic fraction of post-anthesis phase biomass accumulation. Int. J. Remote Sens. 2022, 43, 2029–2058. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Sedano, F.; Lewis, P.; Liang, S.; Wu, Q.L.; Su, W.; Zhang, X.D.; Zhu, D.H. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST–PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.K.; Yue, J.B.; Fan, Y.G.; Bian, M.B.; Ma, Y.P.; Jin, X.L.; Song, X.Y.; Yang, G.J. Estimating potato above-ground biomass by using integrated unmanned aerial system-based optical, structural, and textural canopy measurements. Comput. Electron. Agr. 2023, 213, 108229. [Google Scholar] [CrossRef]
- Schwalbert, R.A.; Amado, T.; Corassa, G.; Pott, L.P.; Prasad, P.V.; Ciampitti, I.A. Satellite-based soybean yield forecast: Integrating machine learning and weather data for improving crop yield prediction in southern Brazil. Agric. For. Meteorol. 2020, 284, 107886. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.K.; Yue, J.B.; Jin, X.L.; Li, Z.H.; Yang, G.J. Estimation of potato above-ground biomass based on unmanned aerial vehicle red-green-blue images with different texture features and crop height. Front. Plant Sci. 2022, 13, 938216. [Google Scholar] [CrossRef]
- Ma, Y.R.; Ma, L.L.; Zhang, Q.; Huang, C.P.; Yi, X.; Chen, X.Y.; Hou, T.Y.; Lv, X.; Zhang, Z. Cotton yield estimation based on vegetation indices and texture features derived from RGB image. Front. Plant Sci. 2022, 13, 925986. [Google Scholar] [CrossRef] [PubMed]
- Qu, H.C.; Zheng, C.F.; Ji, H.; Barai, K.; Zhang, Y.J. A fast and efficient approach to estimate wild blueberry yield using machine learning with drone photography: Flight altitude, sampling method and model effects. Comput. Electron. Agric. 2024, 216, 108543. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Wang, Y.M.; Zhang, Z.; Feng, L.W.; Du, Q.Y.; Runge, T. Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sens. 2020, 12, 1232. [Google Scholar] [CrossRef]
- Feng, L.W.; Zhang, Z.; Ma, Y.C.; Du, Q.Y.; Williams, P.; Drewry, J.; Luck, B. Alfalfa yield prediction using UAV-based hyperspectral imagery and ensemble learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Fei, S.P.; Hassan, M.A.; He, Z.H.; Chen, Z.; Shu, M.Y.; Wang, J.K.; Li, C.C.; Xiao, Y.G. Assessment of ensemble learning to predict wheat grain yield based on UAV-multispectral reflectance. Remote Sens. 2021, 13, 2338. [Google Scholar] [CrossRef]
- Cui, Y.X.; Ji, Y.S.; Liu, R.; Li, W.Y.; Liu, Y.J.; Liu, Z.H.; Zong, X.; Yang, T. Faba bean (Vicia faba L.) yield estimation based on dual-sensor data. Drones 2023, 7, 378. [Google Scholar] [CrossRef]
- Alabi, T.R.; Abebe, A.T.; Chigeza, G.; Fowobaje, K.R. Estimation of soybean grain yield from multispectral high-resolution UAV data with machine learning models in West Africa. Remote Sens. Appl. Soc. Environ. 2022, 27, 100782. [Google Scholar] [CrossRef]
- Cheng, Q.; Xu, H.; Cao, Y.; Duan, F.; Chen, Z. Grain yield prediction of Winter Wheat using Multi-temporal UAV base on multispectral vegetation index. Trans. Chin. Soc. Agric. Mach. 2021, 52, 160–167. [Google Scholar]
- Fan, J.H.; Zhou, J.; Wang, B.W.; Kaeppler, S.M.; Lima, D.C.; Zhang, Z. Estimation of maize yield and flowering time using multi-temporal UAV-based hyperspectral data. Remote Sens. 2022, 14, 3052. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.K.; Yue, J.B.; Jin, X.L.; Fan, Y.G.; Chen, R.Q.; Bian, M.B.; Ma, Y.P.; Song, X.Y.; Yang, G.J. Improved potato AGB estimates based on UAV RGB and hyperspectral images. Comput. Electron. Agr. 2023, 214, 108260. [Google Scholar] [CrossRef]
- Dai, J.G.; Jiang, N.; Xue, J.L.; Zhang, G.S.; He, X.L. Method for predicting cotton yield based on CNN-BiLSTM. Trans. Chin. Soc. Agric. Eng. 2021, 37, 152–159. [Google Scholar]
- Zhang, J.; Qiu, X.; Wu, Y.; Zhu, Y.; Cao, Q.; Liu, X.; Cao, W. Combining texture, color, and vegetation indices from fixed-wing UAS imagery to estimate wheat growth parameters using multivariate regression methods. Comput. Electron. Agric. 2021, 185, 106138. [Google Scholar] [CrossRef]
- He, C.L.; Zheng, S.L.; Wan, N.X.; Zhao, T.; Yuan, J.C.; He, W.; Hu, J. Potato spectrum and the digital image feature parameters on the response of the nitrogen level and its application. Spectrosc. Spect. Anal. 2016, 36, 2930–2936. [Google Scholar]
- Som-ard, J.; Hossain, M.D.; Ninsawat, S.; Veerachitt, V. Pre-harvest sugarcane yield estimation using UAV-based RGB images and ground observation. Sugar Tech 2018, 20, 645–657. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Pei, H.J.; Feng, H.K.; Li, C.C.; Jin, X.L.; Li, Z.H.; Yang, G.J. Remote sensing monitoring of winter wheat growth with UAV based on comprehensive index. Trans. Chin. Soc. Agric. Eng. 2017, 33, 74–82. [Google Scholar]
- Vol, N. Color indices for weed identification under various soil, residue, and lighting conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar]
- Gao, C.F.; Ji, X.J.; He, Q.; Gong, Z.; Sun, H.G.; Wen, T.; Guo, W. Monitoring of wheat fusarium head blight on spectral and textural analysis of UAV multispectral imagery. Agriculture 2023, 13, 293. [Google Scholar] [CrossRef]
- Gitelson, A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Meyer, G.E.; Neto, J.C. Verification of color vegetation indices for automated crop imaging applications. Comput. Electron. Agr. 2008, 63, 282–293. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, J.; Si, H.; Gao, Z.; Shi, L. Winter wheat yield prediction using an LSTM model from MODIS LAI products. Agriculture 2022, 12, 1707. [Google Scholar] [CrossRef]
- Zhao, Y.S. Principles and Methods of Remote Sensing Applications; Science Press: Beijing, China, 2013. [Google Scholar]
- Liu, X.Y.; Zhong, X.C.; Chen, C.; Liu, T.; Sun, C.M.; Li, D.S.; Liu, E.P.; Wang, J.J.; Ding, D.W.; Huo, Z.Y. Prediction of Wheat Yield Using Color and Texture Feature Data of UAV Image at Early Growth Stage. J. Triticeae Crops 2020, 40, 1002–1007. [Google Scholar]


| Dataset | Min | Mean | Max | Standard Deviation | Coefficient of Variation (%) |
|---|---|---|---|---|---|
| Calibration | 3345 | 5669 | 8792 | 1484 | 26.60 |
| Validation | 3744 | 6149 | 8362 | 1198 | 20.12 |
| Color Feature Index | Formula | References |
|---|---|---|
| R | R = R | Red band |
| G | G = G | Green band |
| B | B = B | Blue band |
| r | r = R/(R + G + B) | Normalized red band |
| g | g = G/(R + G + B) | Normalized green band |
| b | b = B/(R + G + B) | Normalized blue band |
| r/b | r/b | [33] |
| g/b | g/b | [33] |
| r − b | r − b | [33] |
| r + b | r + b | [33] |
| g − b | g − b | [33] |
| (r − b)/(r + b) | (r − b)/(r + b) | [33] |
| (r − g − b)/(r + g) | (r − g − b)/(r + g) | [21] |
| EXG | EXG = 2g − b − r | [34] |
| GRVI | GRVI = (g − r)/(g + r) | [35] |
| MGRVI | MGRVI = (g2 − r2)/(g2 + r2) | [25] |
| RGBVI | RGBVI = (g2 − br)/(g2 + br) | [35] |
| WI | WI = (g − b)/(r − g) | [35] |
| EXR | EXR = 1.4r − g | [35] |
| NDI | NDI = (r − g)/(r + g + 0.01) | [36] |
| VARI | VARI = (g − r)/(g + r −b) | [37] |
| EXGR | EXGR = 3g −2.4r − b | [38] |
| Color Feature Index | Flagging Stage | Flowering Stage | Filling Stage |
|---|---|---|---|
| r | −0.6763 ** | −0.7635 ** | −0.7521 ** |
| VARI | 0.6806 ** | 0.7609 ** | 0.7327 ** |
| EXR | −0.6813 ** | −0.7604 ** | −0.7395 ** |
| GRVI | 0.6798 ** | 0.7579 ** | 0.7336 ** |
| NDI | −0.6797 ** | −0.7579 ** | −0.7336 ** |
| MGRVI | 0.6796 ** | 0.7568 ** | 0.7335 ** |
| (r − g – b)/(r + g) | −0.6696 ** | −0.7552 ** | −0.7484 ** |
| EXGR | 0.6485 ** | 0.7315 ** | 0.7100 ** |
| r − b | −0.6495 ** | −0.7161 ** | −0.7187 ** |
| r/b | −0.6436 ** | −0.7092 ** | −0.7034 ** |
| (r-b)/(r + b) | −0.6442 ** | −0.7082 ** | −0.6938 ** |
| g | 0.5325 ** | 0.6841 ** | 0.6721 ** |
| EXG | 0.5325 ** | 0.6841 ** | 0.6721 ** |
| r + b | −0.5325 ** | −0.6841 ** | −0.6721 ** |
| RGBVI | 0.4580 ** | 0.6642 ** | 0.6454 ** |
| b | 0.5832 ** | 0.4528 ** | 0.3710 ** |
| g − b | −0.2965 * | 0.3410 * | 0.4420 ** |
| g/b | −0.3921 ** | 0.2056 NS | 0.3212 NS |
| WI | 0.4178 ** | 0.0698 NS | 0.0811 NS |
| Texture Features | Flagging Stage | Flowering Stage | Filling Stage |
|---|---|---|---|
| MEAN_R | −0.5296 ** | −0.5052 ** | −0.6263 ** |
| VAR_R | −0.2586 * | −0.0513 NS | 0.2215 NS |
| HOM_R | 0.4229 ** | 0.0778 NS | −0.2890 * |
| CON_R | −0.0325 NS | −0.0808 NS | 0.0694 NS |
| DIS_R | −0.3215 * | −0.0759 NS | 0.2374 NS |
| ENT_R | −0.4844 ** | −0.0404 NS | 0.3418 * |
| SEC_R | 0.4950 ** | 0.0228 NS | −0.3488 * |
| COR_R | −0.0650 NS | −0.3299 * | 0.1795 NS |
| MEAN_G | −0.5001 ** | −0.5136 ** | −0.5169 ** |
| VAR_G | −0.2943 * | −0.0517 NS | 0.2152 NS |
| HOM_G | 0.4404 ** | 0.0541 NS | −0.3058 * |
| CON_G | −0.0525 NS | −0.0760 NS | 0.0702 NS |
| DIS_G | −0.3520 * | −0.0645 NS | 0.2417 NS |
| ENT_G | −0.4878 ** | 0.0050 NS | 0.3595 ** |
| SEC_G | 0.4966 ** | −0.0270 NS | −0.3676 ** |
| COR_G | −0.0602 NS | −0.3814 ** | 0.2121 NS |
| MEAN_B | −0.4145 ** | −0.4318 ** | −0.5373 ** |
| VARE_B | −0.2831 * | −0.0493 NS | 0.1471 NS |
| HOM_B | 0.4265 ** | 0.0639 NS | −0.2477 NS |
| CON_B | −0.0500 NS | −0.0764 NS | 0.0530 NS |
| DIS_B | −0.3405 * | −0.0659 NS | 0.1776 NS |
| ENT_B | −0.4718 ** | −0.0126 NS | 0.3010 * |
| SEC_B | 0.4798 ** | −0.0081 NS | −0.3072 * |
| COR_B | −0.0495 NS | −0.3905 ** | 0.1893 NS |
| Flagging Stage | Flowering Stage | Filling Stage | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Modeling | Testing | Modeling | Testing | Modeling | Testing | |||||||
| R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | |
| PLSR | 0.68 | 848.68 | 0.36 | 1654.29 | 0.70 | 808.95 | 0.60 | 905.40 | 0.75 | 738.48 | 0.24 | 1145.22 |
| RF | 0.52 | 1052.53 | 0.34 | 1626.26 | 0.67 | 857.28 | 0.43 | 1079.48 | 0.66 | 936.62 | 0.37 | 1150.43 |
| Flagging Stage | Flowering Stage | Filling Stage | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Modeling | Testing | Modeling | Testing | Modeling | Testing | |||||||
| R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | |
| PLSR | 0.49 | 1056.4 | 0.27 | 1765.35 | 0.49 | 1056.20 | 0.25 | 1133.59 | 0.71 | 794.77 | 0.40 | 1241.21 |
| RF | 0.16 | 1396.38 | 0.16 | 1390.63 | 0.43 | 1125.97 | 0.36 | 1115.12 | 0.45 | 1110.89 | 0.30 | 1192.71 |
| Flagging Stage | Flowering Stage | Filling Stage | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Modeling | Testing | Modeling | Testing | Modeling | Testing | |||||||
| R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | R2 | RMSE (kg·hm−2) | |
| PLSR | 0.73 | 775.75 | 0.32 | 1406.08 | 0.72 | 780.21 | 0.60 | 801.95 | 0.76 | 728.85 | 0. 52 | 859.94 |
| RF | 0.57 | 975.47 | 0.38 | 1523.90 | 0.70 | 804.74 | 0.52 | 928.46 | 0.70 | 1163.96 | 0.41 | 1081.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Liu, Y.; Yan, J.; Guo, L.; Tan, J.; Meng, X.; Xiao, Y.; Feng, H. Winter Wheat Yield Estimation with Color Index Fusion Texture Feature. Agriculture 2024, 14, 581. https://doi.org/10.3390/agriculture14040581
Yang F, Liu Y, Yan J, Guo L, Tan J, Meng X, Xiao Y, Feng H. Winter Wheat Yield Estimation with Color Index Fusion Texture Feature. Agriculture. 2024; 14(4):581. https://doi.org/10.3390/agriculture14040581
Chicago/Turabian StyleYang, Fuqin, Yang Liu, Jiayu Yan, Lixiao Guo, Jianxin Tan, Xiangfei Meng, Yibo Xiao, and Haikuan Feng. 2024. "Winter Wheat Yield Estimation with Color Index Fusion Texture Feature" Agriculture 14, no. 4: 581. https://doi.org/10.3390/agriculture14040581
APA StyleYang, F., Liu, Y., Yan, J., Guo, L., Tan, J., Meng, X., Xiao, Y., & Feng, H. (2024). Winter Wheat Yield Estimation with Color Index Fusion Texture Feature. Agriculture, 14(4), 581. https://doi.org/10.3390/agriculture14040581








