Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters
Abstract
1. Introduction
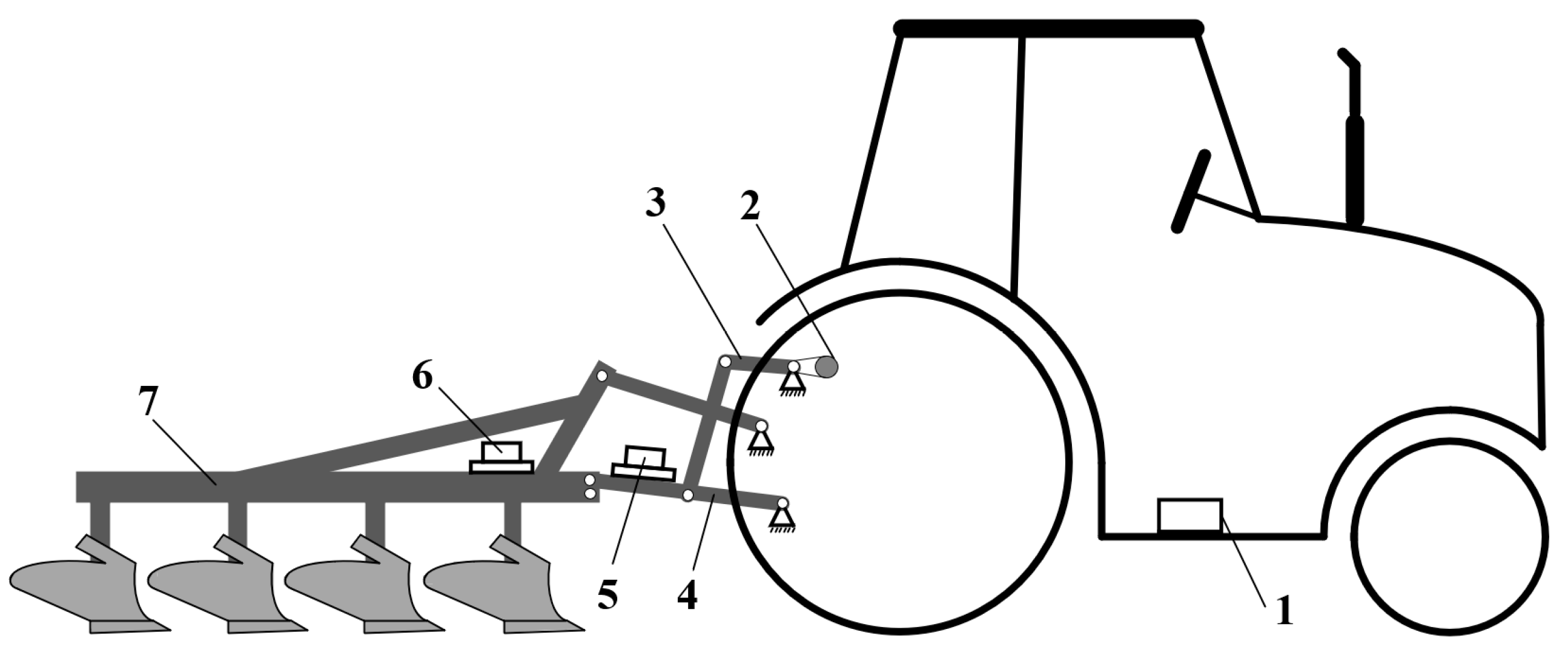
2. Tillage Depth Detection Scheme
2.1. Tillage Depth Detection Model
2.2. Attitude Estimation Method
- (1)
- b-frame: SINS body frame, IMU-centered orthogonal reference frame aligned with Right–Forth–Up (RFU) axes. In this paper, the IMU is placed above the share plow. Therefore, the origin of the b-frame is the IMU, and the directions of the b-frame are rightward, forward, and upward of the tractor–plow, respectively.
- (2)
- n-frame: navigation frame, equivalent to geographic frame, carrier-centered orthogonal reference frame aligned with East–North–Up (ENU) geodetic axes. In this paper, the origin of the n-frame is the IMU, and the directions of the n-frame are eastward, northward, and upward of the tractor–plow, respectively.
- (3)
- e-frame: earth frame, Earth-centered Earth-fixed (ECEF) orthogonal reference frame. In this paper, the origin of the e-frame is the geocentric. The x-axis of the e-frame points to the intersection of the tractor–plow’s meridian and the equator. The z-axis points to the North Pole. The y-axis, along with the x-axis and z-axis, forms a right-handed coordinate system.
- (4)
- b0-frame: inertially non-rotating frame aligned with the b-frame at t0.
- (5)
- n0-frame: inertially non-rotating frame aligned with the n-frame at t0.
- (6)
- e0-frame: inertially non-rotating frame aligned with the e-frame at t0.
2.3. The Calibration Model
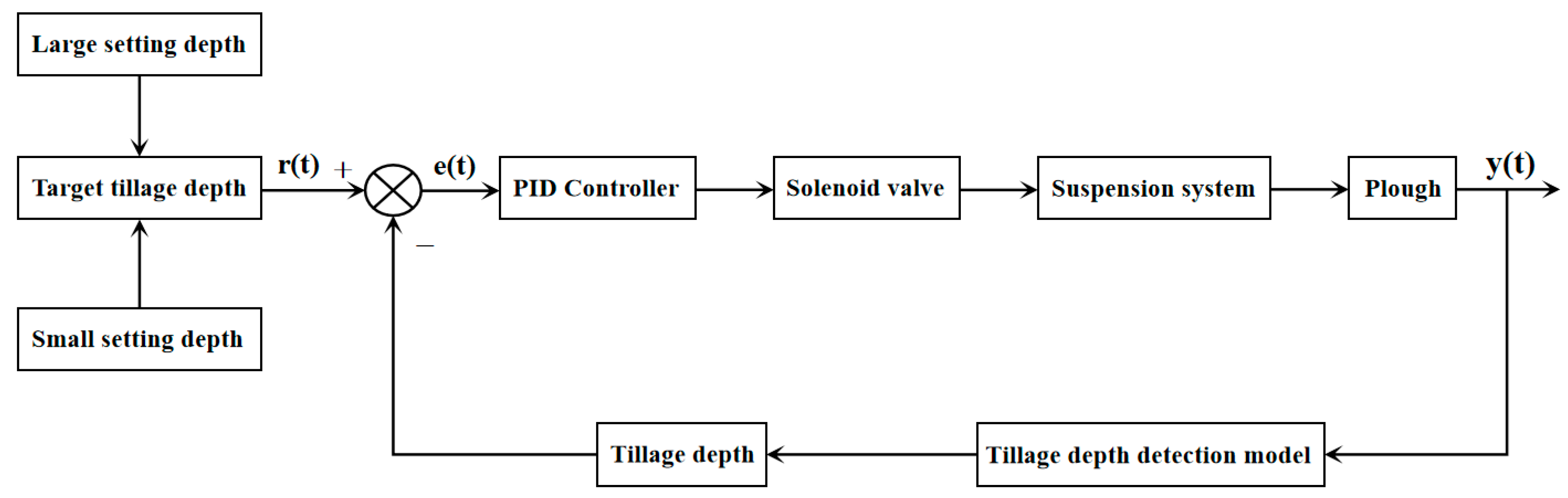
3. Tillage Depth Control Scheme
3.1. The PID Control Algorithm
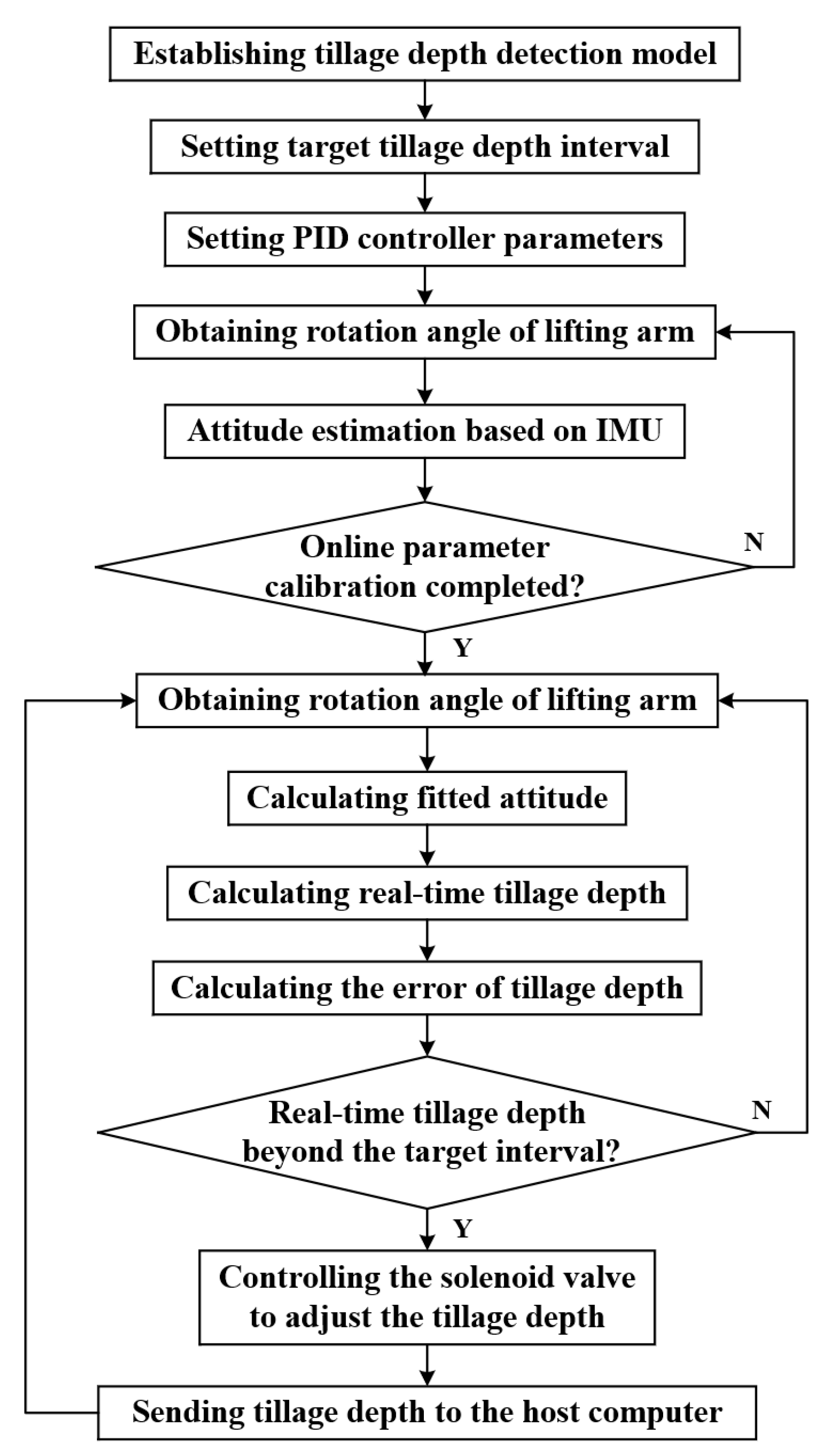
3.2. The Tillage Depth Control Process
- (1)
- Initialization: The tractor tillage depth detection model is first established. Then the target tillage depth interval during the plowing operation and the parameters of the PID controller are set.
- (2)
- Parameter calibration: The model parameters between the rotation angle of the lifting arm and the pitch angle of the plow implement are calibrated. First, the rotation angle of the lifting arm is obtained. Second, the attitude estimation method proposed in Section 2.2 is used to solve the horizontal attitude of the lower link and the plow implement. Finally, the model parameters are estimated online using the adaptive Kalman filter algorithm.
- (3)
- Tillage depth detection: The real-time tillage depth detection during the tractor plowing operation is achieved. The fitted pitch angles of the lower link and the plow implement are calculated using the rotation angle of the lifting arm and the calibration model. The real-time tillage depth is solved by substituting the fitted pitch angle into the tillage depth detection model.
- (4)
- Tillage depth control: The autonomous control of the tillage depth during the tractor plowing operation is completed. The tillage depth error is calculated using the real-time tillage depth detection results. The PID controller outputs the control parameters to the solenoid valve according to the tillage depth error. By controlling the tractor suspension system to drive the plow, the tillage depth control system accomplishes the autonomous regulation and control of tillage depth.
4. Simulation and Field Tests
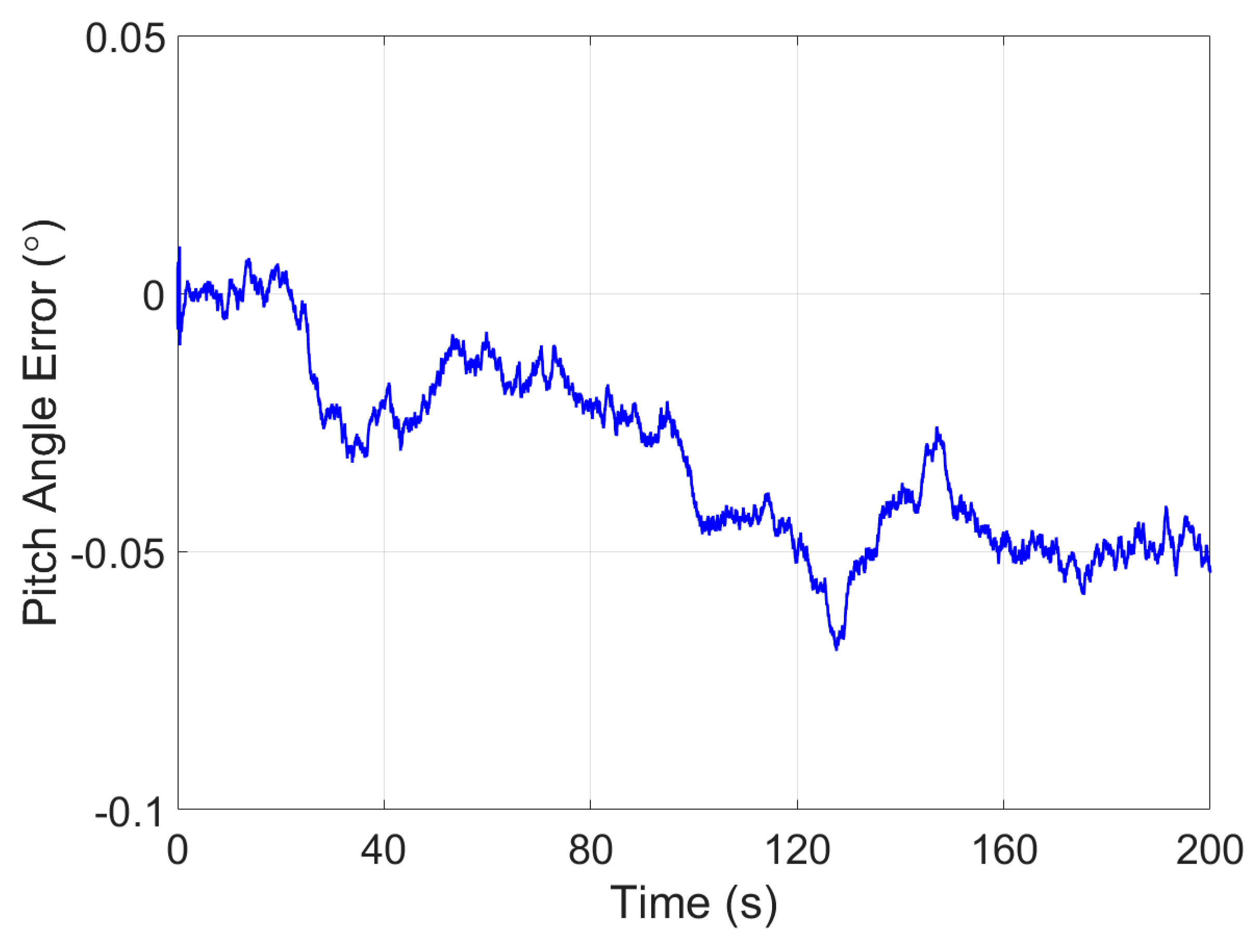
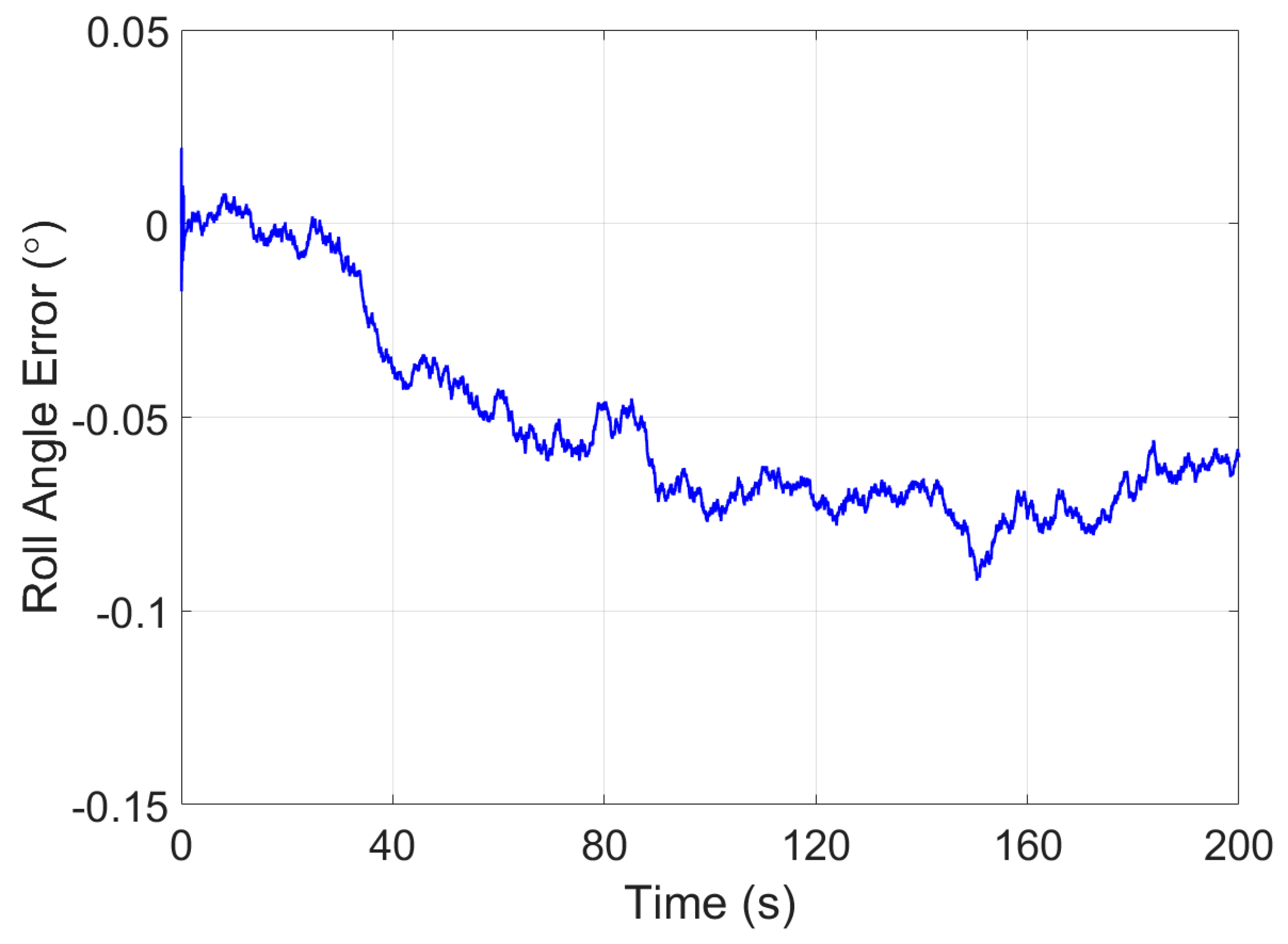
4.1. Simulation Test of Attitude Estimation
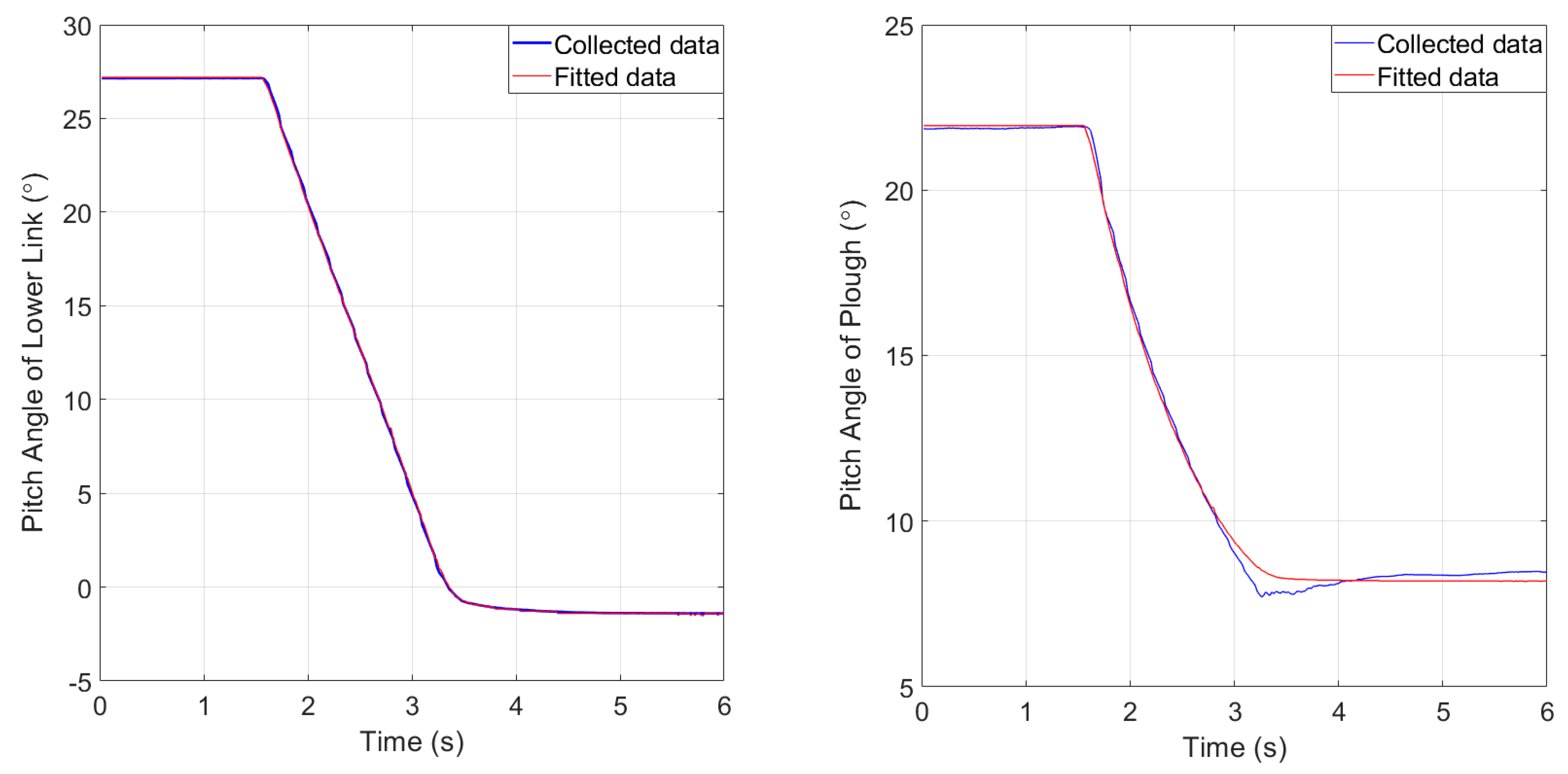
4.2. Online Calibration Test of Model Parameters
- (1)
- The plow implement is lifted to the highest place by the tractor suspension system. Pressing and holding the “Calibration” button on the microcontroller panel for more than 5S is utilized as the opening signal for initiating the calibration process. The microcontroller uses the received data to start the parameter identification process of the calibration model, including the rotation angle of the lifting arm and the horizontal attitude of the lower link and the plow.
- (2)
- The plow implement is lowered slowly by the tractor suspension system. The microcontroller records in real time the rotation angle of the lifting arm, as well as the horizontal attitude of the lower link and the plow and continues the parameter identification.
- (3)
- The plow implement is lowered to the lowest position by the tractor suspension system. Pressing and holding the “Calibration” button on the microcontroller panel for more than 5S is utilized as the end signal of the calibration process. The microcontroller stops the parameter identification process and saves the results.
- (4)
- The microcontroller starts to use the calibration parameters and the rotation angle of the lifting arm to calculate the pitch angle of the lower link and the plow when the tractor is plowing. Finally, the dynamic measurement of tillage depth can be completed according to the tillage depth detection model.
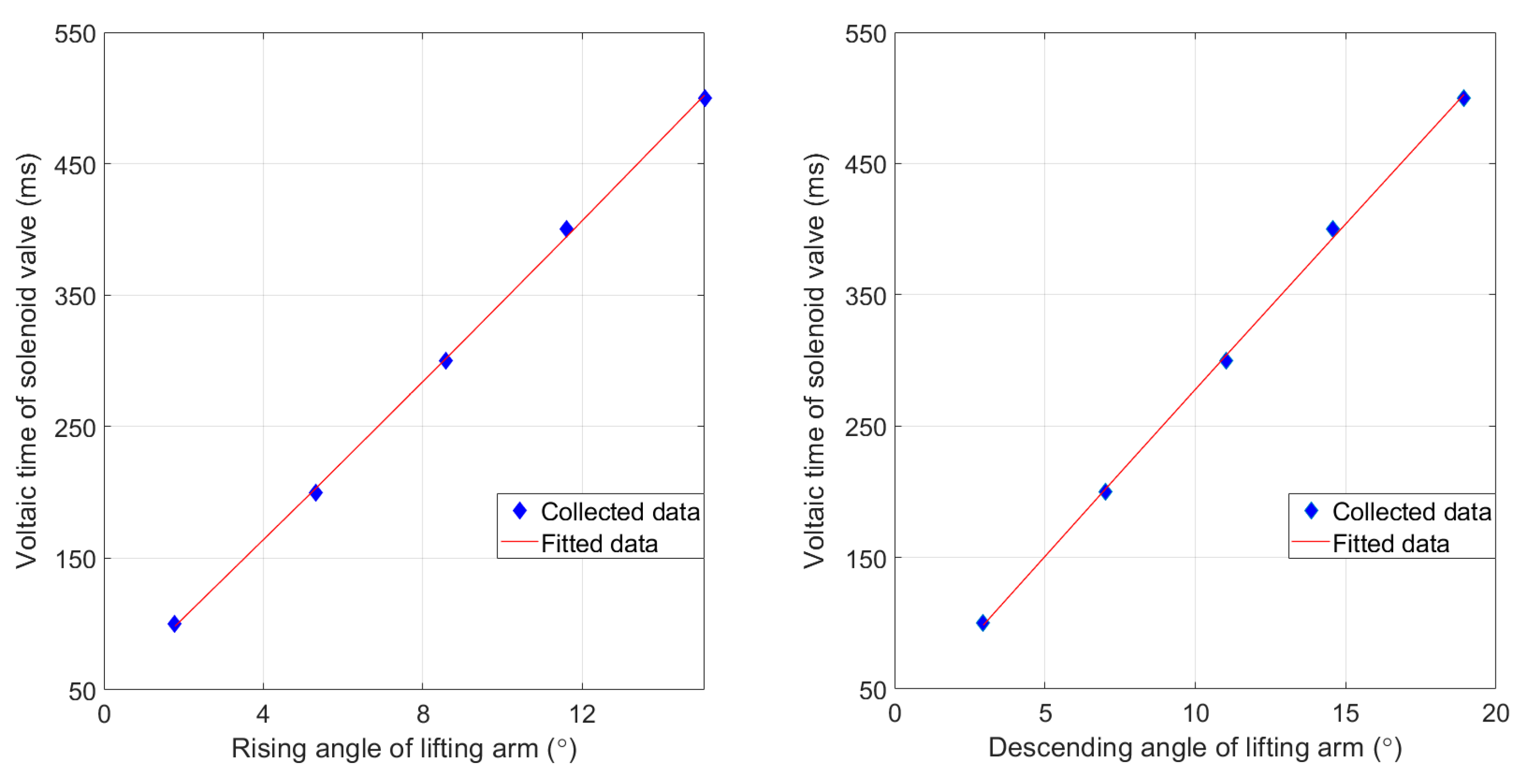
4.3. Parameter Test of Solenoid Valve
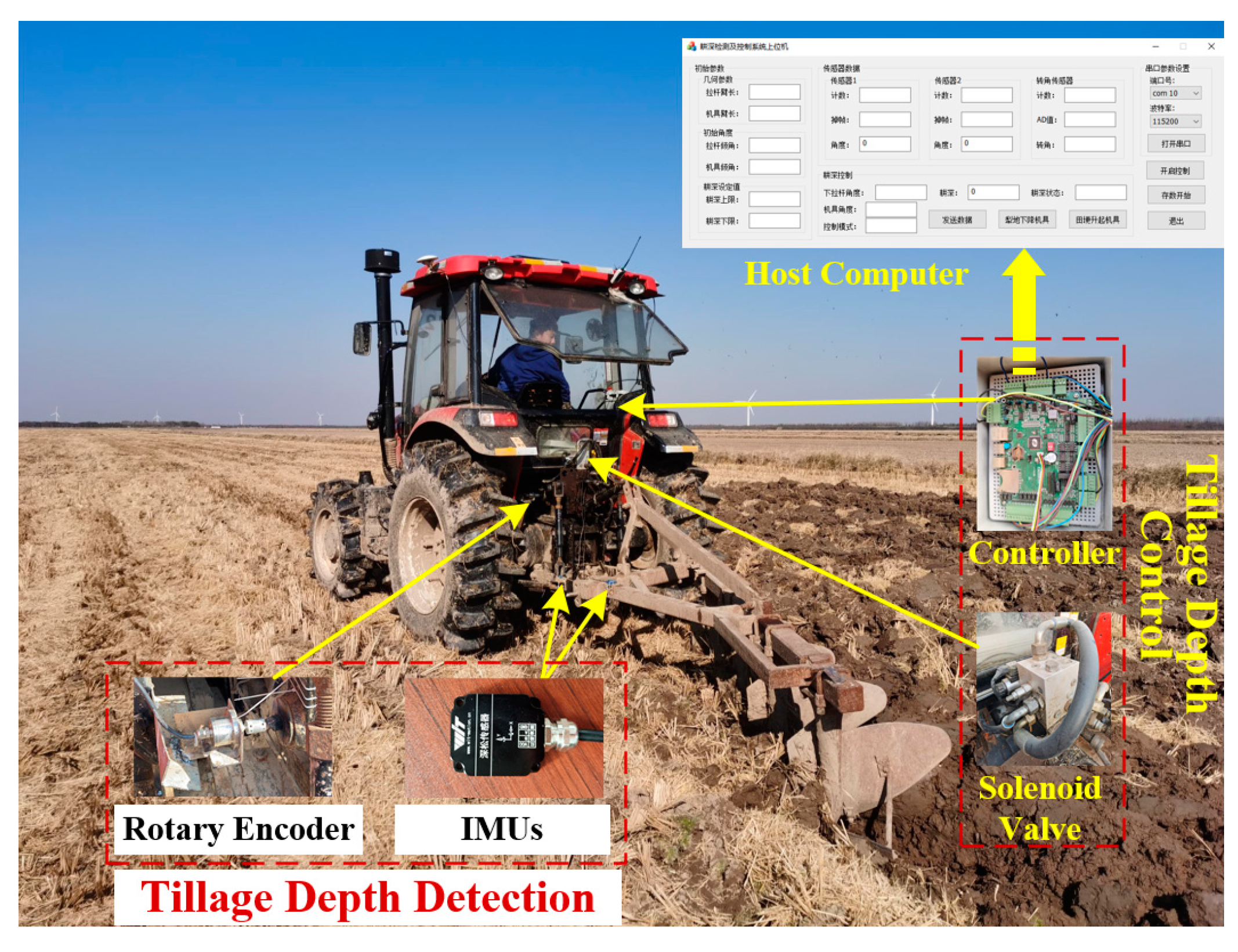
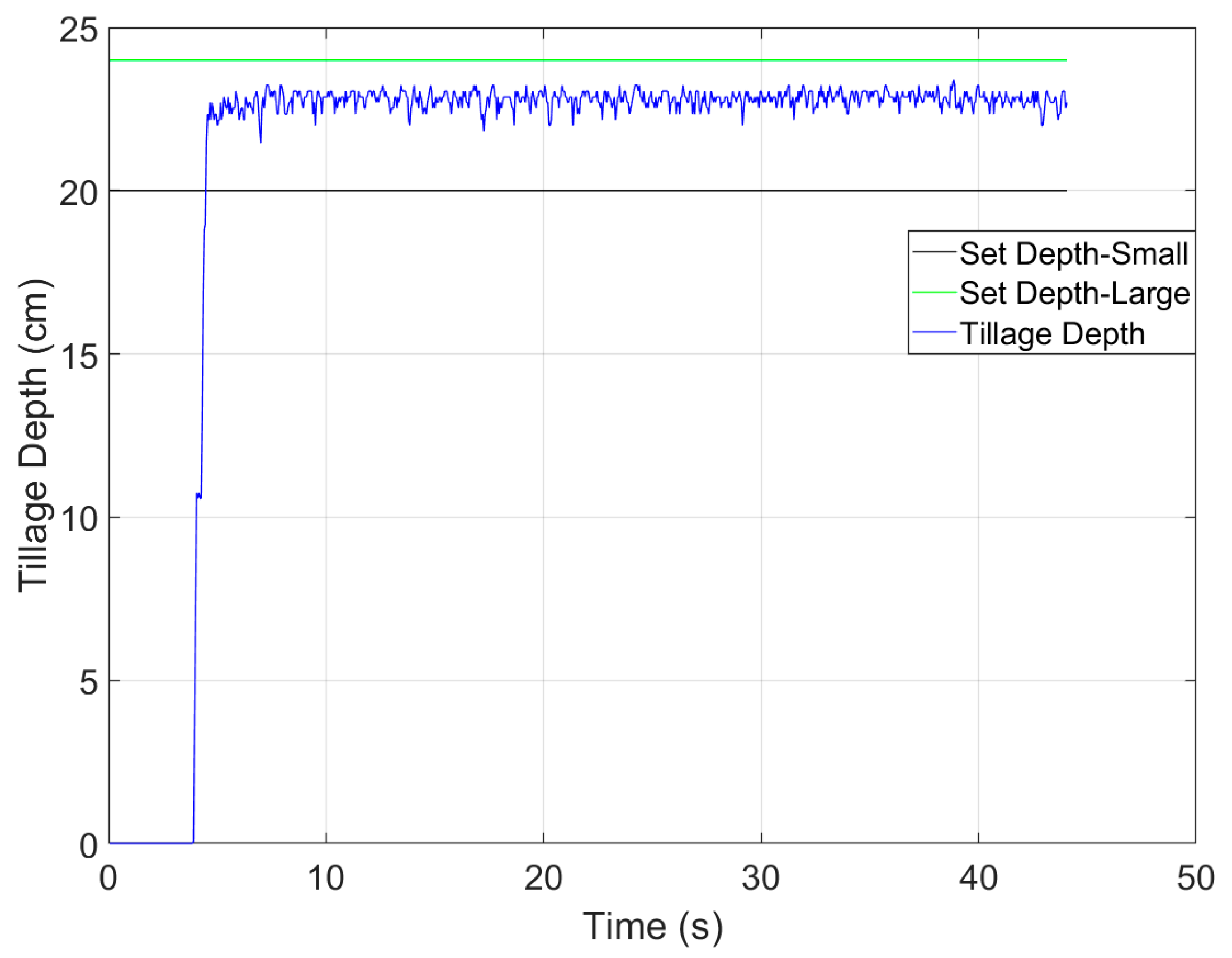
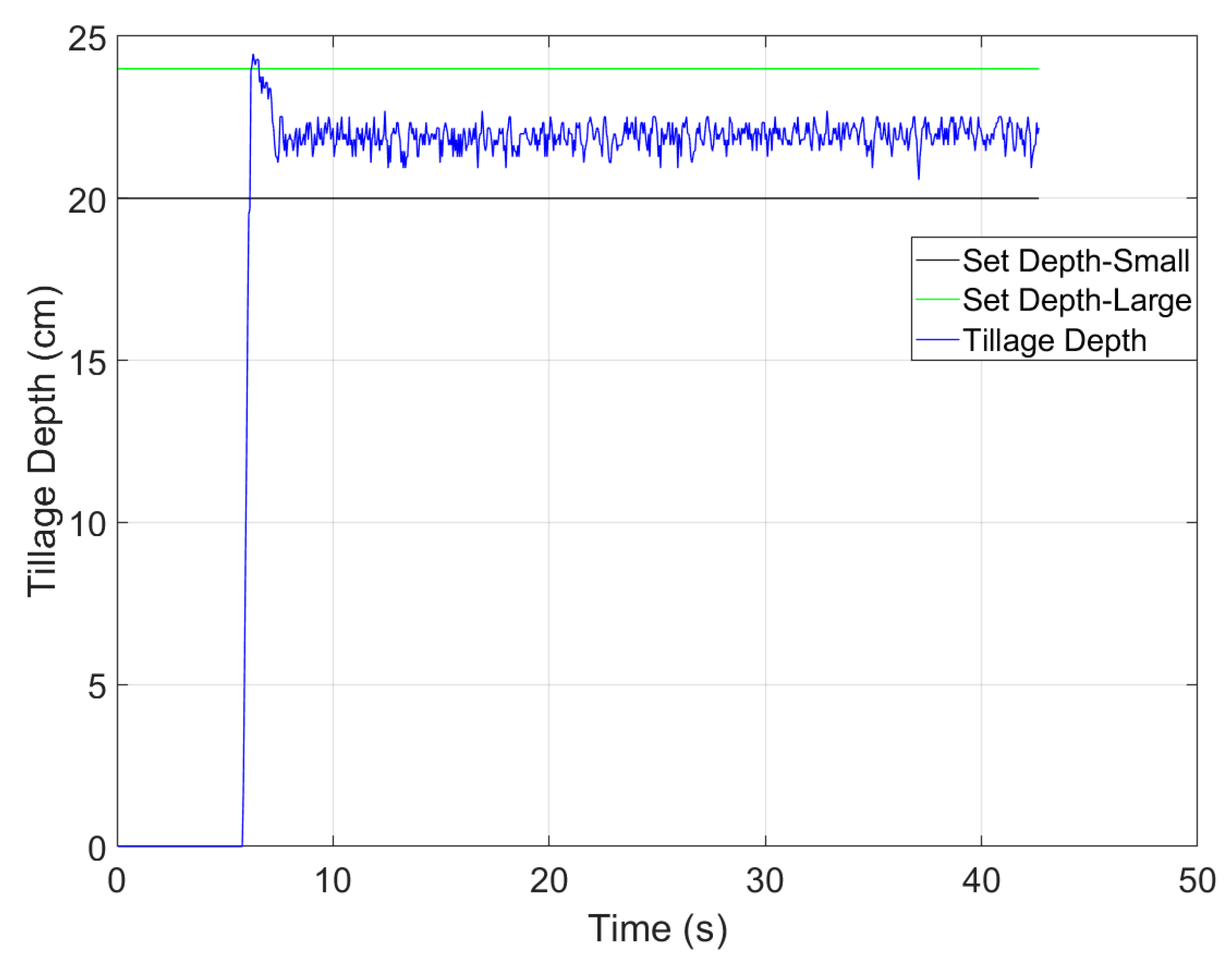
4.4. Field Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, N.K.; Dogra, B.; Manes, G.S.; Parihar, D.S.; Salem, A.; Elbeltagi, A. Effect of the Spading Machine on Various Soil Parameters at Different Tillage Depths. Sustainability 2024, 16, 4334. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, S.H.; Guo, S.B.; Tang, Z.; Chen, S.R. Motor Torque Distribution Strategy for Different Tillage Modes of Agricultural Electric Tractors. Agriculture 2022, 12, 1373. [Google Scholar] [CrossRef]
- Morugán-Coronado, A.; Linares, C.; Gómez-López, M.D.; Faz, A.; Zornoza, R. The impact of intercropping, tillage and fertilizer type on soil and crop yield in fruit orchards under Mediterranean conditions: A meta-analysis of field studies. Agric. Syst. 2020, 178, 102736. [Google Scholar] [CrossRef]
- Guo, Y.; Cui, M.L.; Xu, Z.G. Spatial characteristics of transfer plots and conservation tillage technology adoption: Evidence from a survey of four provinces in China. Agriculture 2023, 13, 1601. [Google Scholar] [CrossRef]
- Gao, Y.Y.; Yang, Y.F.; Fu, S.; Feng, K.Y.; Han, X.; Hu, Y.Y.; Zhu, Q.Z.; Wei, X.H. Analysis of vibration characteristics of tractor–rotary cultivator combination based on time domain and frequency domain. Agriculture 2024, 14, 1139. [Google Scholar] [CrossRef]
- Chen, X.X.; Xu, G.M.; Zhang, X.Y.; Tan, W.C.; Ding, Q.S.; Tagar, A.A. Performance Evaluation of Biomimetic-Designed Rotary Blades for Straw Incorporation in an Intensive Tillage System. Agriculture 2024, 14, 1426. [Google Scholar] [CrossRef]
- Hu, R.W.; Liu, Y.J.; Chen, T.; Zheng, Z.Y.; Peng, G.J.; Zou, Y.D.; Tang, C.G.; Shan, X.H.; Zhou, Q.M.; Li, J. Responses of soil aggregates, organic carbon, and crop yield to short-term intermittent deep tillage in Southern China. J. Clean. Prod. 2021, 298, 126767. [Google Scholar] [CrossRef]
- Schneider, F.; Don, A.; Hennings, I.; Schmittmann, O.; Seidel, S.J. The effect of deep tillage on crop yield–What do we really know? Soil Tillage Res. 2017, 174, 193–204. [Google Scholar] [CrossRef]
- Han, J.Y.; Yan, X.X.; Tang, H. Method of controlling tillage depth for agricultural tractors considering engine load characteristics. Biosyst. Eng. 2023, 227, 95–106. [Google Scholar] [CrossRef]
- Huang, S.S.; Ul Islam, M.; Jiang, F.H. The effect of deep-tillage depths on crop yield: A global meta-analysis. Plant Soil Environ. 2023, 69, 105–117. [Google Scholar] [CrossRef]
- Pang, J.; Zhang, X.W.; Lin, X.J.; Liu, J.H.; Du, X.W.; Han, J.A. Tillage-Depth Verification Based on Machine Learning Algorithms. Agriculture 2023, 13, 130. [Google Scholar] [CrossRef]
- Sun, X.X.; Song, Y.; Wang, Y.F.; Qian, J.; Lu, Z.X.; Wang, T. Design and test of a tractor electro-hydraulic-suspension tillage-depth and loading-control system test bench. Agriculture 2023, 13, 1884. [Google Scholar] [CrossRef]
- Luo, C.H.; Wen, C.K.; Meng, Z.J.; Liu, H.Y.; Li, G.Q.; Fu, W.Q.; Zhao, C.J. Research on the slip rate control of a power shift tractor based on wheel speed and tillage depth adjustment. Agronomy 2023, 13, 281. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, T.J.; Kim, Y.J.; Lee, S.D.; Park, S.U.; Kim, W.S. Development of a real-time tillage depth measurement system for agricultural tractors: Application to the effect analysis of tillage depth on draft force during plow tillage. Sensors 2020, 20, 912. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Zhang, W.Y.; Qi, B.; Ji, Y. Tillage depth dynamic monitoring and precise control system. Meas. Control-UK 2024. [Google Scholar] [CrossRef]
- Jia, H.L.; Guo, M.Z.; Yu, H.B.; Li, Y.; Feng, X.Z.; Zhao, J.L.; Qi, J.T. An adaptable tillage depth monitoring system for tillage machine. Biosyst. Eng. 2016, 151, 187–199. [Google Scholar] [CrossRef]
- Jiang, X.H.; Tong, J.; Ma, Y.H.; Li, J.G.; Wu, B.G.; Sun, J.Y. Study of tillage depth detecting device based on Kalman filter and fusion algorithm. Trans. Chin. Soc. Agric. Mach. 2020, 51, 53–60. [Google Scholar]
- Lou, S.Y.; He, J.; Lu, C.Y.; Liu, P.; Li, H.; Zhang, Z.G. A tillage depth monitoring and control system for the independent adjustment of each subsoiling shovel. Actuators 2021, 10, 250. [Google Scholar] [CrossRef]
- Kim, Y.S.; Siddique, M.A.; Kim, W.S.; Kim, Y.J.; Lee, S.D.; Lee, D.K.; Hwang, S.J.; Nam, J.S.; Park, S.U.; Lim, R.G. DEM simulation for draft force prediction of moldboard plow according to the tillage depth in cohesive soil. Comput. Electron. Agric. 2021, 189, 106368. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, W.S.; Siddique, M.A.; Baek, S.Y.; Baek, S.M.; Cheon, S.H.; Lee, S.D.; Lee, K.H.; Hong, D.H.; Park, S.U.; et al. Power transmission efficiency analysis of 42 kW power agricultural tractor according to tillage depth during moldboard plowing. Agronomy 2020, 10, 1263. [Google Scholar] [CrossRef]
- Wang, A.Z.; Ji, X.; Zhu, Y.Y.; Wang, Q.Z.; Wei, X.H.; Zhang, S.C. Tillage depth regulation system via depth measurement feedback and composite sliding mode control: A field comparison validation study. Meas. Control-UK 2024, 57, 685–702. [Google Scholar] [CrossRef]
- Zhou, M.K.; Xia, J.F.; Zhang, S.; Hu, M.J.; Liu, Z.Y.; Liu, G.Y.; Luo, C.M. Development of a depth control system based on variable-gain single-neuron PID for rotary burying of stubbles. Agriculture 2021, 12, 30. [Google Scholar] [CrossRef]
- Wang, Y.X.; Jing, H.R.; Zhang, D.X.; Cui, T.; Zhong, X.J.; Yang, L. Development and performance evaluation of an electric-hydraulic control system for subsoiler with flexible tines. Comput. Electron. Agric. 2018, 151, 249–257. [Google Scholar] [CrossRef]
- Candan, B.; Soken, H.E. Robust attitude estimation using IMU-only measurements. IEEE Trans. Instrum. Meas. 2021, 70, 9512309. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Zeng, C.W.; Tian, X.R.; Zeng, Q.X.; Yao, R. A Discrete Quaternion Particle Filter Based on Deterministic Sampling for IMU Attitude Estimation. IEEE Sens. J. 2021, 21, 23266–23277. [Google Scholar] [CrossRef]
- Huang, P.K.; Zhang, Z.G.; Luo, X.W.; Liu, Z.P.; Wang, H.; Yue, B.B.; Gao, W.W. Development of external acceleration identification and attitude estimation system of field working vehicle. Trans. Chin. Soc. Agric. Eng. 2019, 35, 9–15. [Google Scholar]
- Vieira, D.; Orjuela, R.; Spisser, M.; Basset, M. Positioning and attitude determination for precision agriculture robots based on IMU and two RTK GPSs sensor fusion. In Proceedings of the 7th IFAC Conference on Sensing, Control and Automation Technologies for Agriculture, Munich, Germany, 14–16 September 2022. [Google Scholar]



| Sensors | Parameters | Value |
|---|---|---|
| Gyroscopes | Constant Bias | 8.5°/h |
| Random Noise | 0.25°/√h | |
| Frequency | 200 Hz | |
| Accelerometers | Constant Bias | 200 μg |
| Random Noise | 50 μg/√Hz | |
| Frequency | 200 Hz |
| Sensors | Parameters | Value |
|---|---|---|
| Gyroscopes | Measurement Range | ±250°/s |
| Constant Bias | 8.5°/h | |
| Random Noise | 0.45°/√h | |
| Accelerometers | Measurement Range | ±8 g |
| Constant Bias | 200μg | |
| Random Noise | 50 μg/√Hz | |
| Rotary Encoder | Measurement Range | ±45° |
| Accuracy | 0.05° |
| Error | Test 1 | Test 2 |
|---|---|---|
| MN (cm) | 0.8115 | −0.0840 |
| STD (cm) | 0.2429 | 0.3551 |
| RMS (cm) | 0.8470 | 0.3646 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Cui, B.; Yu, Z.; Gao, Y.; Wei, X. Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters. Agriculture 2024, 14, 2130. https://doi.org/10.3390/agriculture14122130
Zhu Y, Cui B, Yu Z, Gao Y, Wei X. Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters. Agriculture. 2024; 14(12):2130. https://doi.org/10.3390/agriculture14122130
Chicago/Turabian StyleZhu, Yongyun, Bingbo Cui, Zelong Yu, Yuanyuan Gao, and Xinhua Wei. 2024. "Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters" Agriculture 14, no. 12: 2130. https://doi.org/10.3390/agriculture14122130
APA StyleZhu, Y., Cui, B., Yu, Z., Gao, Y., & Wei, X. (2024). Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters. Agriculture, 14(12), 2130. https://doi.org/10.3390/agriculture14122130







