Research on the Tensile and Impact Mechanical Properties of Millet Ear Petals
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Equipment
2.2. Experimental Methods
2.2.1. Tensile Test
2.2.2. Impact Test
2.3. Test Indicators
2.3.1. Tensile Fracture Strength
2.3.2. Grain Drop Rate
2.3.3. Grain Breakage Rate
3. Results and Analysis
3.1. Effect of Millet Ear Petal Tensile Fracture Strength
3.1.1. Effect of Tensile Angle on Millet Ear Petal Tensile Fracture Strength
3.1.2. Effect of Growth Part on Millet Ear Petal Tensile Fracture Strength
3.2. Effect of Millet Petal Impact Drop Rate
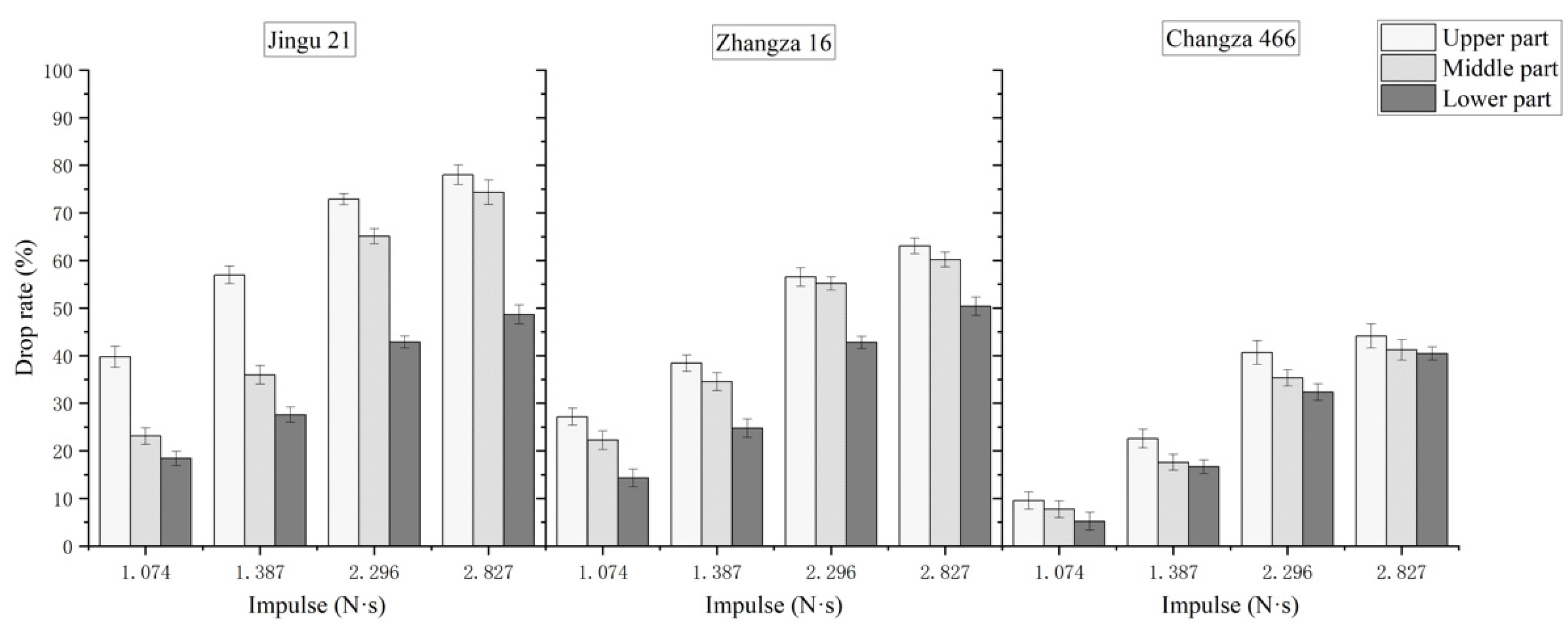
3.2.1. Effect of Impulse on Millet Petal Impact Drop Rate
3.2.2. Effect of Variety on Millet Petal Impact Drop Rate
3.3. Effect of Millet Petal Impact Breakage Rate
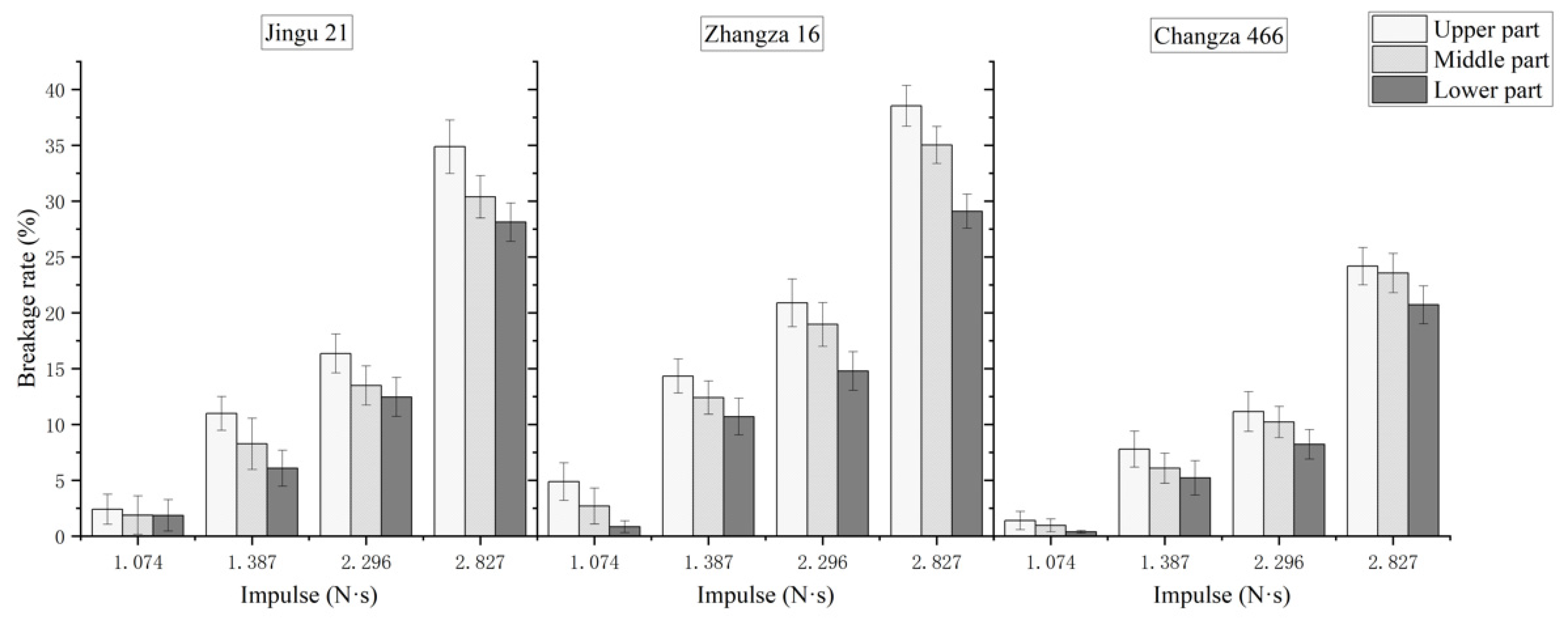
3.3.1. Effect of Impulse on Millet Petal Impact Breakage Rate
3.3.2. Effect of Variety on Millet Petal Impact Breakage Rate
4. Discussion
5. Conclusions
- (1)
- The variety, tensile angle, and growth part all have a highly significant effect on tensile fracture strength. The tensile fracture strength of the millet petals’ pedicel decreases as the tensile angle increases, with the highest fracture strength corresponding to a tensile angle of 0°, ranging from 19.013 MPa to 28.357 MPa. At a tensile angle of 90°, the fracture strength is lower, with a range of 6.409 MPa to 12.249 MPa; the lowest fracture strength corresponds to a tensile angle of 180°, with a range of 2.534 MPa to 6.395 MPa. The lower part of the millet petals’ pedicel has the highest tensile fracture strength, followed by the middle part, and the upper part has the lowest. When designing the threshing structure, it can be considered that the millet petals are subjected to forces in different directions in the drum, thereby improving the threshing efficiency.
- (2)
- The impulse and variety significantly affect the drop rate of millet petals due to impact, with the drop rate increasing as the impulse increases. When the impulse increases from 1.074 N·s to 2.296 N·s, the drop rate increases more rapidly; when the impulse increases from 2.296 N·s to 2.827 N·s, the drop rate increases more slowly. Jingu 21 has the highest drop rate, followed by Zhangza 16, while Changza 466 has the lowest drop rate.
- (3)
- Impulse and variety are the main factors affecting the impact breakage rate of millet petals. The breakage rate increases with the increase in impulse, growing more slowly when the impulse increases from 1.074 N·s to 2.296 N·s, and more rapidly when the impulse increases from 2.296 N·s to 2.827 N·s. Zhangza 16 has the highest breakage rate, followed by Jingu 21, while Changza 466 has the lowest breakage rate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, H.; Zhang, J.; Liu, K.; Wu, N.; Li, Y.; Zhou, K.; Ye, M.; Zhang, T.; Zhang, H.; Yang, X.; et al. Earliest Domestication of Common Millet (Panicum Miliaceum) in East Asia Extended to 10,000 Years Ago. Proc. Natl. Acad. Sci. USA 2009, 106, 7367–7372. [Google Scholar] [CrossRef] [PubMed]
- Saleem, S.; Mushtaq, N.U.; Shah, W.H.; Rasool, A.; Hakeem, K.R.; Seth, C.S.; Tahir, I.; Rehman, R.U. Millets as Smart Future Food with Essential Phytonutrients for Promoting Health. J. Food Compos. Anal. 2023, 124, 105669. [Google Scholar] [CrossRef]
- Li, S.; Liu, F.; Liu, M.; Cheng, R.; Xia, E. Current Status and Future Prospective of Foxtail Millet Production and Seed Industry in China. Chin. Acad. Agric. Sci. 2021, 54, 459–470. [Google Scholar]
- Li, X.; Ma, L.; Geng, L.; Wang, S.; Pang, J.; Ji, J. Performance Test and Parameter Optimization of Corn Seed Bionic Thresher. Trans. Chin. Soc. Agric. Eng. 2017, 33, 62–69. [Google Scholar]
- Wang, Q.; Mao, H.; Li, Q. Modelling and Simulation of the Grain Threshing Process Based on the Discrete Element Method. Comput. Electron. Agric. 2020, 178, 105790. [Google Scholar] [CrossRef]
- Yang, L.; Wang, W.; Zhang, H.; Li, L.; Wang, M.; Hou, M. Improved Design and Bench Test Based on Tangential Flow Transverse Axial Flow Maize Threshing System. Trans. Chin. Soc. Agric. Eng. 2018, 34, 35–43. [Google Scholar]
- Zhu, X.; Xu, Y.; Han, C.; You, J.; Zhang, X.; Mao, H.; Ma, X. Design and Experiment of In-Situ Bionic Harvesting Device for Edible Sunflower. Agriculture 2024, 14, 1169. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, P.; Sun, J.; Zheng, D. Oat Threshing Damage and Its Effect on Nutritional Components. Agriculture 2024, 14, 842. [Google Scholar] [CrossRef]
- Que, K.; Tang, Z.; Wang, T.; Su, Z.; Ding, Z. Effects of Unbalanced Incentives on Threshing Drum Stability during Rice Threshing. Agriculture 2024, 14, 777. [Google Scholar] [CrossRef]
- Delprete, C.; Giacosa, S.; Raviolo, E.; Rolle, L.; Sesana, R. Experimental Characterization and Numerical Modeling of the Compressive Mechanical Behavior of Hazelnut Kernels. J. Food Eng. 2015, 166, 364–369. [Google Scholar] [CrossRef]
- Hernández-Estrada, Z.J.; Figueroa, J.D.C.; Rayas-Duarte, P.; Peña, R.J. Viscoelastic Characterization of Glutenins in Wheat Kernels Measured by Creep Tests. J. Food Eng. 2012, 113, 19–26. [Google Scholar] [CrossRef]
- Huang, J.; Liu, W.; Zhou, F.; Peng, Y. Effect of Multiscale Structural Parameters on the Mechanical Properties of Rice Stems. J. Mech. Behav. Biomed. Mater. 2018, 82, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Yang, Y.; Zhou, F.; Deng, X. Biomechanical Stability Variation of Rice Stem during Maturation and Wilting. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 74. [Google Scholar] [CrossRef]
- Su, Y.; Cui, T.; Xia, G.; Gao, X.; Li, Y.; Qiao, M.; Xu, Y. Effects of Different Moisture Content and Varieties on Physico-Mechanical Properties of Maize Kernel and Pedicel. J. Food Process Eng. 2021, 44, e13778. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Fang, Z.; Zheng, F. Analysis of Mechanical Characteristic of Maize Based on the FEM. Comput. Simul. 2018, 35, 194–197+276. [Google Scholar]
- Shi, Y.; Jiang, Y.; Wang, X.; Thuy, N.T.D.; Yu, H. A Mechanical Model of Single Wheat Straw with Failure Characteristics Based on Discrete Element Method. Biosyst. Eng. 2023, 230, 1–15. [Google Scholar] [CrossRef]
- Kakade, A.; Khodke, S.; Jadhav, S.; Gajabe, M.; Othzes, N. Effect of Moisture Content on Physical Properties of Soybean. Int. J. Curr. Microbiol. App. Sci. 2019, 8, 1770–1782. [Google Scholar] [CrossRef]
- Chandio, F.A.; Li, Y.; Ma, Z.; Ahmad, F.; Syed, T.N.; Shaikh, S.A.; Tunio, M.H. Influences of Moisture Content and Compressive Loading Speed on the Mechanical Properties of Maize Grain Orientations. Int. J. Agric. Biol. Eng. 2021, 14, 41–49. [Google Scholar] [CrossRef]
- Gupta, R.K.; Das, S.K. Fracture Resistance of Sunflower Seed and Kernel to Compressive Loading. J. Food Eng. 2000, 46, 1–8. [Google Scholar] [CrossRef]
- Babić, L.; Radojèin, M.; Pavkov, I.; Babić, M.; Turan, J.; Zoranović, M.; Stanišić, S. Physical Properties and Compression Loading Behaviour of Corn Seed. Int. Agrophys. 2013, 27, 119–126. [Google Scholar] [CrossRef]
- Li, Y.; Chandio, F.A.; Ma, Z.; Lakhiar, I.A.; Sahito, A.R.; Ahmad, F.; Mari, I.A.; Farooq, U.; Suleman, M. Mechanical Strength of Wheat Grain Varieties Influenced by Moisture Content and Loading Rate. Biol. Eng. 2018, 11, 52–57. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Hao, Y.; Zheng, C.; Du, D. Effects on Relaxation Properties of Chinese Cabbage (Brassica campestris L.) Subjected to Different Compression Directions. Biosyst. Eng. 2021, 207, 81–91. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Chen, J. Construction of Visco-Elasto-Plasticity Contact Model of Vibratory Screening and Its Parameters Calibration for Wheat. Trans. Chin. Soc. Agric. Eng. 2018, 34, 37–43. [Google Scholar]
- Xu, L.; Li, Y. Critical Speed of Impact Damage on a Rice Kernel. Trans. Chin. Soc. Agric. Mach. 2009, 40, 54–57. [Google Scholar]
- Qiu, S.; Yuan, X.; Guo, Y.; Cui, Q.; Wu, X.; Zhang, Z. Effects of Variety and Moisture Content on Mechanical Properties of Millet. Trans. Chin. Soc. Agric. Eng. 2019, 35, 322–326. [Google Scholar]
- Wang, W.; Wang, Z.; Pan, B.; Cui, Q.; Zhang, L.; Qiu, S.; Zhang, Y. Study on the Shear and Bending Mechanical Properties of Millet Stem. Agriculture 2024, 14, 923. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, J.; Guo, Y. Effect of Moisture Content on Compression Mechanical Properties and Frictional Characteristics of Millet Grain. Trans. Chin. Soc. Agric. Eng. 2015, 31, 253–260. [Google Scholar]
- Zhang, Y.; Cui, Q.; Guo, Y.; Li, H. Experiment and Analysis of Cutting Mechanical Properties of Millet Stem. Trans. Chin. Soc. Agric. Mach. 2019, 50, 146–155+162. [Google Scholar]
- Sun, J.; Yang, Z.; Guo, Y.; Cui, Q.; Wu, X.; Zhang, Y. Compression Mechanical Properties and Crack Formation Law of Millet Grain. Trans. Chin. Soc. Agric. Eng. 2017, 33, 306–314. [Google Scholar]
- Yang, Z.; Guo, Y.; Cui, Q.; Li, H. Test and Influence Factors Analysis of Friction Characteristics of Millet. Trans. Chin. Soc. Agric. Eng. 2016, 32, 258–264. [Google Scholar]
- GB/T 5262-2008; Agricultural Machinery Testing Conditions-General Rules for Measuring Methods. China National Agricultural Machinery Standardization Technical Committee: Beijing, China, 2008.
- Fang, W.; Wu, Z.; Li, W.; Sun, X.; Mao, W.; Li, R.; Majeed, Y.; Fu, L. Fruit Detachment Force of Multiple Varieties Kiwifruit with Different Fruit-Stem Angles for Designing Universal Robotic Picking End-Effector. Comput. Electron. Agric. 2023, 213, 108225. [Google Scholar] [CrossRef]
- Li, H.; Xue, J.; Wang, B.; Zhang, Y.; Wu, X.; Li, X.; Cui, Q.; Yang, Z. Tensile Properties of Foxtail Millet Leaf Sheath, Leaf and Leaf Collar. Trans. Chin. Soc. Agric. Eng. 2020, 36, 11–17. [Google Scholar]
- Zhang, D.; Ji, J.; Zhang, F.; Yi, S.; Yang, L. Fracture Characteristics and Tensile Test of Millet Branches and Stems. J. Agric. Mech. Res. 2022, 44, 156–161. [Google Scholar] [CrossRef]
- Al-Dairi, M.; Pathare, P.B.; Al-Yahyai, R.; Al-Mahdouri, A. Effect on Physiological Properties of Banana Fruit Based on Pendulum Impact Test and Storage. Curr. Res. Food Sci. 2023, 7, 100640. [Google Scholar] [CrossRef]
- Fu, H.; Du, W.; Yang, J.; Wang, W.; Wu, Z.; Yang, Z. Bruise Measurement of Fresh Market Apples Caused by Repeated Impacts Using a Pendulum Method. Postharvest Biol. Technol. 2023, 195, 112143. [Google Scholar] [CrossRef]
- Yin, Y.; Guo, Y.; Wang, J.; Wu, C. Experimental Research of Millet Grain at the Impacting Load. J. Agric. Mech. Res. 2022, 44, 203–207. [Google Scholar] [CrossRef]
- Li, X.; Gao, L.; Ma, F.; Yu, Y.; Zhang, Y. Experimental Research of Corn Seed Kernel on the Impacting Damage. J. Shenyang Agric. Univ. 2007, 38, 89–93. [Google Scholar]


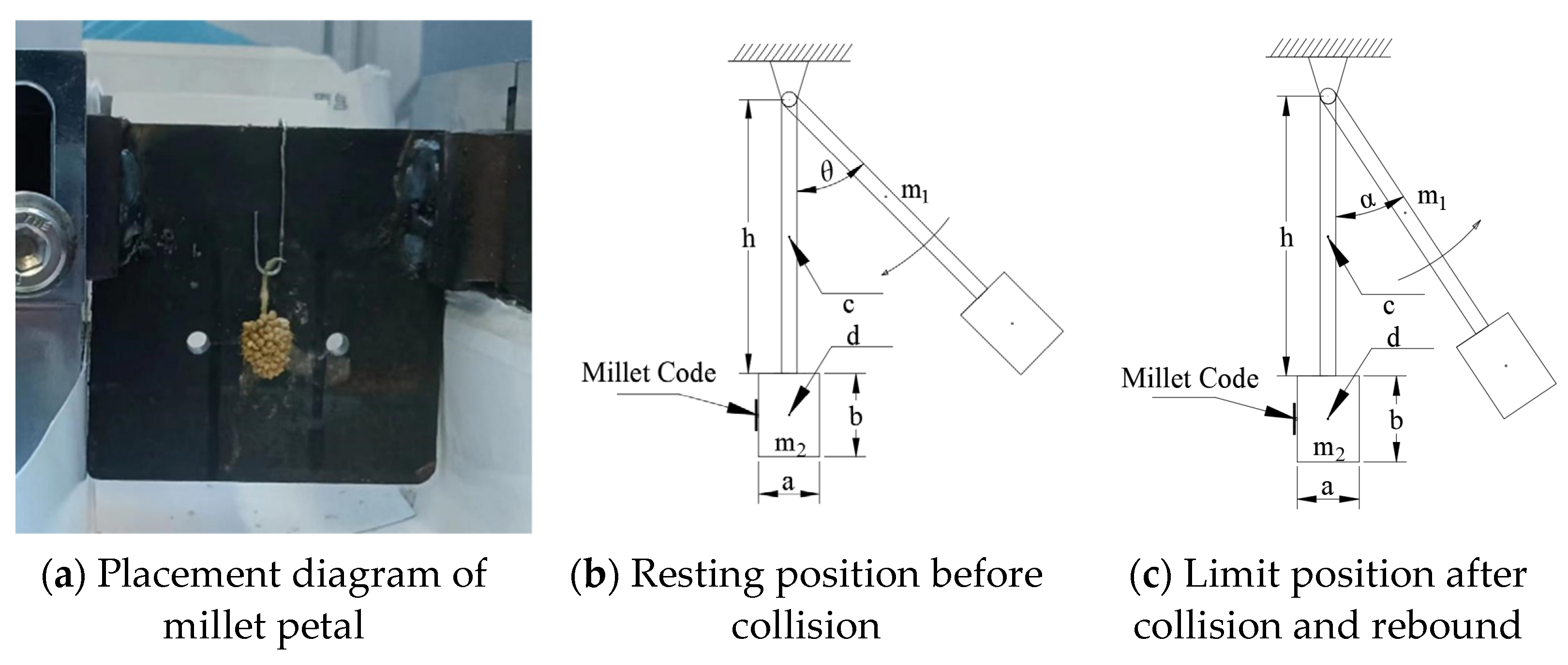



| Variety | Angle (°) | Tensile Fracture Strength (MPa) | ||
|---|---|---|---|---|
| Upper Part | Middle Part | Lower Part | ||
| Jingu21 | 0 | 19.013 ± 0.426 b | 21.315 ± 0.913 b | 23.71 ± 0.721 ab |
| 90 | 6.409 ± 0.647 d | 7.281 ± 0.832 d | 8.299 ± 0.705 d | |
| 180 | 2.534 ± 0.205 f | 3.518 ± 0.303 f | 4.11 ± 0.264 e | |
| Zhangza16 | 0 | 23.814 ± 1.039 b | 26.012 ± 1.008 a | 28.357 ± 1.048 a |
| 90 | 8.148 ± 1.08 cd | 10.188 ± 0.992 c | 12.249 ± 0.903 c | |
| 180 | 4.173 ± 0.673 e | 5.179 ± 0.433 e | 6.395 ± 0.956 de | |
| Changza466 | 0 | 19.557 ± 0.822 b | 23.487 ± 0.51 a | 25.992 ± 0.931 a |
| 90 | 7.473 ± 0.559 d | 8.339 ± 0.633 c | 9.155 ± 0.744 c | |
| 180 | 2.834 ± 0.366 f | 3.805 ± 0.64 f | 4.909 ± 0.757 e | |
| Source of Variation | DF | Tensile Fracture | Strength |
|---|---|---|---|
| F-Value | p-Value | ||
| Variety | 2 | 5.04 | 0.0261 |
| Growth Part | 2 | 59.19 | <0.0001 |
| Tensile Angle | 2 | 524.22 | <0.0001 |
| R2 = 0.9195 | |||
| Variety | Angle θ (°) | Impulse (N·s) | Drop Rate (%) | ||
|---|---|---|---|---|---|
| Upper Part | Middle Part | Lower Part | |||
| Jingu21 | 20° | 1.074 | 39.744 ± 2.216 d | 23.108 ± 1.721 f | 18.406 ± 1.516 fg |
| 30° | 1.387 | 56.954 ± 1.841 b | 35.972 ± 1.943 e | 27.611 ± 1.612 f | |
| 40° | 2.296 | 72.887 ± 1.162 a | 65.091 ± 1.574 a | 42.873 ± 1.241 c | |
| 50° | 2.827 | 78.007 ± 2.055 a | 74.319 ± 2.575 a | 48.638 ± 2.003 bc | |
| Zhangza16 | 20° | 1.074 | 27.136 ± 1.782 e | 22.253 ± 1.968 fg | 14.295 ± 1.859 gh |
| 30° | 1.387 | 38.439 ± 1.727 d | 34.568 ± 1.863 de | 24.777 ± 1.917 f | |
| 40° | 2.296 | 56.521 ± 1.961 b | 55.164 ± 1.399 b | 42.782 ± 1.258 c | |
| 50° | 2.827 | 63.039 ± 1.627 ab | 60.186 ± 1.57 b | 50.386 ± 1.93 bc | |
| Changza466 | 20° | 1.074 | 9.55 ± 1.794 gh | 7.738 ± 1.778 h | 5.203 ± 1.902 h |
| 30° | 1.387 | 22.58 ± 1.94 f | 17.593 ± 1.674 g | 16.648 ± 1.438 g | |
| 40° | 2.296 | 40.65 ± 2.502 d | 35.352 ± 1.691 cd | 32.333 ± 1.755 e | |
| 50° | 2.827 | 44.126 ± 2.501 c | 41.226 ± 2.144 cd | 40.442 ± 1.392 d | |
| Source of Variation | DF | Drop Rate | |
|---|---|---|---|
| F-Value | p-Value | ||
| Variety | 2 | 302.05 | <0.0001 |
| Growth Part | 2 | 115.28 | <0.0001 |
| Impulse | 3 | 797.83 | <0.0001 |
| Variety × Growth Part | 4 | 25.04 | <0.0001 |
| Variety × Impulse | 6 | 2.87 | 0.0215 |
| Growth Part × Impulse | 6 | 7.99 | 0.0148 |
| R2 = 0.9648 | |||
| Variety | Angle (°) | Impulse (N·s) | Breakage Rate (%) | ||
|---|---|---|---|---|---|
| Upper Part | Middle Part | Lower Part | |||
| Jingu21 | 20° | 1.074 | 2.409 ± 1.346 gh | 1.876 ± 1.718 gh | 1.855 ± 1.412 h |
| 30° | 1.387 | 10.981 ± 1.517 e | 8.256 ± 2.294 f | 6.077 ± 1.603 g | |
| 40° | 2.296 | 16.352 ± 1.754 c | 13.487 ± 1.751 d | 12.451 ± 1.742 d | |
| 50° | 2.827 | 34.864 ± 2.387 a | 30.377 ± 1.892 a | 28.115 ± 1.719 b | |
| Zhangza16 | 20° | 1.074 | 4.871 ± 1.683 g | 2.687 ± 1.609 g | 0.835 ± 0.522 h |
| 30° | 1.387 | 14.33 ± 1.533 d | 12.403 ± 1.492 d | 10.703 ± 1.652 e | |
| 40° | 2.296 | 20.884 ± 2.146 b | 18.954 ± 1.963 c | 14.784 ± 1.727 c | |
| 50° | 2.827 | 38.52 ± 1.829 a | 35.012 ± 1.655 a | 29.089 ± 1.52 ab | |
| Changza466 | 20° | 1.074 | 1.396 ± 0.816 h | 0.963 ± 0.579 h | 0.377 ± 0.127 q |
| 30° | 1.387 | 7.787 ± 1.615 f | 6.085 ± 1.344 f | 5.21 ± 1.544 g | |
| 40° | 2.296 | 11.149 ± 1.778 e | 10.212 ± 1.384 e | 8.216 ± 1.312 f | |
| 50° | 2.827 | 24.165 ± 1.669 b | 23.547 ± 1.761 b | 20.704 ± 1.688 c | |
| Source of Variation | DF | Breakage Rate | |
|---|---|---|---|
| F-Value | p-Value | ||
| Variety | 2 | 294.18 | <0.0001 |
| Growth Part | 2 | 132.20 | <0.0001 |
| Impulse | 3 | 741.16 | <0.0001 |
| Variety × Growth Part | 4 | 9.01 | 0.0084 |
| Variety × Impulse | 6 | 28.77 | <0.0001 |
| Growth Part × Impulse | 6 | 4.82 | 0.0153 |
| R2 = 0. 9542 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, S.; Pan, B.; Wang, Z.; Fang, S.; Hu, J.; Yang, S.; Wang, W.; Cui, Q.; Yuan, X. Research on the Tensile and Impact Mechanical Properties of Millet Ear Petals. Agriculture 2024, 14, 1925. https://doi.org/10.3390/agriculture14111925
Qiu S, Pan B, Wang Z, Fang S, Hu J, Yang S, Wang W, Cui Q, Yuan X. Research on the Tensile and Impact Mechanical Properties of Millet Ear Petals. Agriculture. 2024; 14(11):1925. https://doi.org/10.3390/agriculture14111925
Chicago/Turabian StyleQiu, Shujin, Ben Pan, Zeze Wang, Shige Fang, Jiangfan Hu, Shubo Yang, Wei Wang, Qingliang Cui, and Xiangyang Yuan. 2024. "Research on the Tensile and Impact Mechanical Properties of Millet Ear Petals" Agriculture 14, no. 11: 1925. https://doi.org/10.3390/agriculture14111925
APA StyleQiu, S., Pan, B., Wang, Z., Fang, S., Hu, J., Yang, S., Wang, W., Cui, Q., & Yuan, X. (2024). Research on the Tensile and Impact Mechanical Properties of Millet Ear Petals. Agriculture, 14(11), 1925. https://doi.org/10.3390/agriculture14111925






