Abstract
The New Zealand Emissions Trading Scheme allows landowners to be remunerated for the carbon sequestration capabilities of eligible forests established post 1990. For afforested areas of 100 hectares or fewer, carbon sequestration is estimated with the use of default carbon look-up tables administered by the Ministry for Primary Industries. However, a disparity exists between exotic pines (Pinus radiata), where carbon sequestration predictions are regionally differentiated, and native species, where carbon sequestration estimations are neither distinguished by species or locality. This paper aims to highlight this inequality by comparing the calculated carbon storage of endemic tree species with the ‘Indigenous Forest’ category in the carbon look-up tables. The carbon storage of 12-year-old naturally regenerated tea trees (Leptospermum scoparium and Kunzea ericoides) was calculated using allometric measurements and compared to the look-up tables. The results suggest that carbon look-up tables underestimate the carbon sequestration of native tea trees by 81.8%. A bimodal data distribution suggests that carbon sequestration is heavily dependent on light interception levels. It is recommended that carbon sequestration data for specific native species in different environments are collected and integrated into such tables.
1. Introduction
The Paris Agreement, with a commitment period of 2021 through to 2030, aims to limit global warming to less than 2 °C (preferably < 1.5 °C) above preindustrial levels [1,2,3]. Unlike previous international climate change agreements, it is signed by nearly all countries of the world, with reduction commitments from all the major polluters. New Zealand’s greenhouse gas reduction target under the Paris Agreement is 30% below 2005 levels; its first nationally determined contribution (NDC) [1].
New Zealand has a ‘Zero Carbon Bill’, which is a 2019 amendment to the ‘Climate Change Response Act 2002′ [4]. It puts a legal framework in place to help New Zealand meet its international commitments set out in the Paris Agreement. This includes the setting of national targets for the reduction of net greenhouse gas emissions, of which there are two. Firstly, all net emissions of greenhouse gases, excluding biogenic methane, should be zero by 2050. Secondly, the biogenic methane emissions should be reduced by 24–47% below 2017 levels by 2050, with a 10% reduction by 2030 [5]. The bill also formed the Climate Change Commission [6], whose purpose it is to monitor and give advice to the government on how to reach these targets [7,8], as well as the Emissions Trading Scheme (ETS) [9], New Zealand’s tool for imposing an economic tax on emissions [4].
The ETS is a government-led initiative that effectively taxes industries for the greenhouse gases they emit, passing ‘carbon credits’ (NZUs) on to forestry owners, whose trees sequester carbon [9,10]. Having to pay for their emissions in the form of carbon credits (1 NZU = 1 tCO2-e) [11,12], the emitters are economically incentivized to reduce their emissions [13]. In turn, NZUs are earned from the government by the owners of greenhouse-gas-sequestering activities such as forestry. NZUs are traded for profit [11], creating a supply and demand dynamic between the greenhouse gas emitters and those sequestering carbon. A rising ‘carbon price’ increasingly creates a large incentive for ‘carbon farmers’ to blanket plant fast-growing exotic tree species, mainly Pinus radiata. As the ETS reimburses landowners for the carbon sequestration capability of their land, exotic species are comparatively more profitable than their native counterparts [14].
The economic returns for carbon sequestration through the NZ ETS are based on the mass of carbon dioxide subsequently stored within woody biomass. Afforested areas under 100 hectares in area are subject to carbon storage estimation through the use of default ‘carbon look-up tables’, which may be downloaded from [15]. A disparity exists within these tables, attributed to the quantity of data that carbon sequestration models of various species have been developed. Where many studies have investigated the carbon sequestration capabilities of pine trees in a range of environments, few studies have documented similar growth rates of naturally regenerated bush, let alone tea trees, specifically [14,15]. Due to the amount of data associated with pines (Pinus radiata), these look-up tables can differentiate the expected carbon stocks depending on the region they are located in [15]. In contrast, the likes of the indigenous tea trees (mainly Leptospermum scoparium, Kunzea ericoides) are broadly grouped into an Indigenous Forest category with no regional differentiation. It has previously been reported that these tables are conservative by nature for the Indigenous Forest category [16].
This disparity signifies a major knowledge gap, which is important as it is these data that drive the profitability of naturally regenerated land. To address this, the carbon storage of tea trees on a case study property was calculated, based on allometric measurements. The objective of this was to highlight the difference in carbon storage between tea trees and default carbon look-up tables for naturally regenerating land. It is hypothesized that a significant difference occurs between the carbon storage of naturally regenerated tea trees and the Indigenous Forest category in the carbon look-up tables [16]. It is important to note that this study formed the exploratory work of a master’s thesis that had a more limited data collection than desirable due to COVID-19 travel restrictions that were in place during the scholarship-funding period. The initial goal was to provide an average carbon sequestration rate for the subsequent economic modelling of regenerating tea trees. It was not designed to disprove the existing datasets, nor has the scale to do so. However, some discrepancies between the measured data and the table values are raised, which may warrant further work.
2. Materials and Methods
The Above-Ground Biomass (AGB) data were collected of naturally regenerated tea trees at a property in South Taranaki using the method shown in [17]. Nukuhau Carbon Limited operate a 151-hectare carbon farming business at 1326 Okahutiria Rd, Waverley, New Zealand. Previously a pastoral farm, the property was planted primarily in pines and eucalyptus c. 2009/2010 (pers. comm.: Neil Walker 2022, the property owner), providing a shaded environment for the natural regeneration of the native bush [18]. Being a primary colonizer, tea trees are typically the first species to establish within gaps in the canopy where the light levels are sufficient [19,20]. In this case, natural regeneration meant the tea trees established almost immediately with the removal of ruminant grazing. Therefore, an establishment year of 2010 is used for the purposes of the study, with plants being approximately 12 years old at the time of measurement. This is carried out as tea tree establishment on pastoral hill country is usually achieved by the retirement of land [19,21], possibly aided by the spreading of seed capsules [22]. Being unpalatable to stock, the seedlings are left relatively undisturbed by grazing ruminants [20]. Planting individual Leptospermum scoparium (manuka) trees sourced from nurseries is usually reserved for higher input systems such as dedicated honey production. This is because a high concentration of Leptospermum scoparium compared to other species needs to be maintained, to obtain a premium from manuka honey production. High concentrations of methylglyoxal, leptosperin (only found in Leptospermum sp. flowers), dihydroxyacetone and hydromethyliforfural mean the manuka honey factors can provide a price premium up to 300 times that of nonmanuka honeys [23]. Without financial assistance (from the likes of national or regional afforestation support schemes) or a likely return on investment (e.g., honey or production forestry), sourcing the seedlings from nurseries can be an expensive task, especially with volatile carbon prices. Collecting the AGB data of naturally regenerated tea trees would benefit the study, as Leptospermum scoparium seedlings transplanted from a nursery environment may display different growth characteristics. Leptospermum scoparium planted for honey is also planted at lower densities of 1100–1600 stems per hectare compared with that recommended for erosion control (>10,000 stems/ha), due to the differences in tree allometry (axial rather than apical dominance) to promote flower development for honey production [20]. However, honey produced from Kunzea ericoides (kanuka), the tea tree that regenerates in association with Leptospermum scoparium when grazing ceases on steep hill country, pays no premium and reduces the concentration of manuka honey factors in honey produced from the regenerating bush, reducing the price premium.
A shapefile of the property boundary allowed the existing areas of indigenous bush to be identified before the establishment of the carbon farming operation. Imagery dated 5 September 2007 was used in Google Earth™ to manually identify these areas as well as the existing infrastructure and waterways. With these areas removed from the analysis, a sampling grid of 5 m by 5 m was overlayed to the area using ArcGIS Pro v2.5.0™ (ESRI, Redlands, CA, USA) using the ‘Create Fishnet’ tool on the newly formed polygon. A random number was assigned to each grid section, using a random number generator. The lowest 16 random numbers and their associated grid squares were selected, representing the randomly selected samples. Selected samples are subject to a quality control operation to ensure accessibility and the presence of tea trees. Figure 1 illustrates the quality control procedure, displaying the status and location of sample sites. A corresponding centroid point file generated with the same ArcGIS Pro™ process where then selected and transferred to a handheld GPS [24,25].

Figure 1.
The location of sample sites utilized by the study.
A method developed by Beets et al. [17] was used to measure the AGB of the tea trees and subsequently, the total carbon sequestered. As per Figure 2, a 5 m by 5 m square was measured with an industrial 30 m measuring tape; the GPS centroid point located in the center of each plot. A Juno T41 GPS (Trimble, Sunnyvale, CA, USA) device was used to locate each point in the field. The plot orientation was aligned with magnetic North on each occasion.

Figure 2.
An example of the 5 m by 5 m plots used to quantify tea tree AGB.
Within each plot, every tea tree over 1 m in height was measured. Those under this height were deemed to be insignificant. Two measurements were taken: the basal diameter and height. The basal diameter was measured 100 mm above the lowest point where the trunk intercepts the soil [17]. This was carried out as the basal diameter was shown to provide better estimates of the stem volume of smaller shrubs compared to the Diameter at Breast Height (DBH) [26]. Where the trunk partitioned into two or more stems below 100 mm, each was measured separately. The cumulative diameter was then used. For stems with a diameter above 25 mm, it was easiest to measure the circumference with measuring tape (Figure 3), with the diameter calculated after field measurement. A caliper accurately measured the diameter of the smaller stems (Figure 3). Both had an accuracy of ±0.5 mm. It was assumed that stems were nearly circular.

Figure 3.
A measuring tape was used to measure the circumference of stems >25 mm in diameter (a). A caliper was used to measure the diameter of stems <25 mm in diameter (b). The measurements are taken 100 mm above the ground.
Under the current NZ ETS, the carbon stocks of forestry of 100 hectares or more was measured per the Field Measurement Approach (FMA) [27]. This was carried out using the DBH method. This measured the trunk diameter at 1.4 m above the ground. Smaller trees (such as Leptospermum scoparium, usually slower growing than Kunzea ericoides) over 300 mm in height that have a DBH under 25 mm, were subject to basal diameter measurements [27]. For simplicity’s sake, the basal diameter method was used to estimate the carbon stocks of all tea trees, regardless of height and DBH within plots. This aligns with the methodology employed by Beets et al. [17] and the inclusion of younger stems allowed for a more complete picture of the carbon sequestration to be calculated [28].
The height of the tallest stem on each tree was also measured. This was achieved with a Trupulse 200L™ (Laser Technology Inc., Centennial, CO, USA) laser rangefinder. The steep topography and density of vegetation made the use of a measuring stick unsafe. The measurement accuracy, due to the topography (the tea tree height varied with observer position), was limited to ±0.5 m. This could introduce some variation to the study. However, when height data were utilized in the allometric equations, the accuracy of prediction was shown to increase [29].
Beets et al. [17] devised a nonintrusive AGB measurement method. A SAS V2.0 GLIMMIX (SAS Institute, Cary, NC, USA) procedure was used to calculate species-specific coefficients to ensure the accuracy of using Equation (1) in predicting the AGB of different arboreal shrubs. This process assumed a gamma distribution, and the model was built by fitting the Dry Weight to the log function of (Basal Area (BA) × Height). The result was a coefficient of 234 + −29 for Leptospermum scoparium, which is utilized as aspecies in Equation (1). Dry Weight is the oven dry weight of the plant in kg. BA is the Basal Area (m2) of the stems and is calculated using either the circumference or diameter data measured 100 mm above the ground. The Height (m) is the height of the tallest stem. This calculation was used to estimate the AGB of tea tree plots. Other potentially significant inputs of carbon to the system, including leaf litter, microalgae and soil carbon fluxes, are not measured [30].
The Dry Weight of all tea trees within the plot was combined and subsequently scaled to an area of 1 hectare. The carbon content was assumed to be 50% of the total dry matter [14,17], citing a lack of verified data specific to the species in question. Recent studies have shown that this value can differ slightly between species [31,32]. From this, the total quantity of carbon sequestered per unit area was extrapolated.
The economic returns for carbon sequestration through the NZ ETS were based upon the mass of carbon dioxide subsequently stored within woody biomass. The molar mass of carbon (12.01 gmol−1) and carbon dioxide (44.01 gmol−1) were used to convert between the mass of carbon and carbon dioxide. This assumes that 100% of sequestered carbon is transferred into woody biomass. The measured carbon dioxide sequestered was compared to that of 12-year-old ‘Indigenous Forest’ in the MPI’s look-up tables, which estimates carbon storage to be 60.3 tCO2/ha (or 16.5 tC/ha). The MPI’s carbon sequestration estimates for the Indigenous Forest category are based on primary colonizers such as tea trees [15], therefore, the results should be comparable.
3. Results
The dataset consists of measurements of 422 individual tea trees, with a mean carbon storage of 2.84 kgC/tree. A large interquartile range of 2.41 kgC/tree shows that although tea tree stands were in their 12th year of regeneration, not all trees would have been that old. With a confidence interval of 95%, we can predict that the true population mean for 12-year-old naturally regenerated tea trees sits between 2.12 kgC/tree and 3.55 kgC/tree.
The mean tree height was 3.91 m when averaged amongst all individuals in the sample population. It is within 95% certainty that the population mean sits between the values of 3.77 m and 4.06 m. An interquartile range of 2.00 m indicates that the majority of sample sites were located in similar environments (under the canopy of exotic species of similar densities). The range is larger at 6.00 m due to two factors. At the lower end of this range, young trees filling the previously uninhabited areas were measured. A small number of sample sites where light is not blocked by an exotic canopy appear to have relatively fast vertical growth rates. The mean height infers a vertical growth of 326 mm/yr. This is lower than estimates provided by Saunders [20] of 410 mm/yr and is likely due to the increased shade levels from relatively fast-growing exotic trees. The same source states that a healthy Leptospermum scoparium tree will be 4 m high at year 10, suggesting that vertical growth is stunted by the overarching exotic canopy. As a result, we can assume that the measured carbon sequestration of tea trees in this study is conservative.
For the same reasons as the variation in the mean heights of trees, the basal circumference had a relatively small interquartile range of 164.75 mm and a large overall range of 1171 mm. The mean circumference was 186.42 mm, with the population mean likely falling between 169.45 mm and 203.39 mm (CI = 95%). Marden et al. [33] explained 92% to 99% of the variability within the measured AGB with a root collar diameter (RCD). However, that study was in a plantation where the nursery seedlings were transplanted in an orderly spatial pattern (3 m × 3 m spacing). This eliminated any influence that plant density (constant 1111 trees/ha) and age had upon such a relationship, in stark contrast to regenerated bush where the density and age of vegetation is largely dependent on environmental factors.
Plotting the calculated carbon storage of each tree on a histogram returns a gamma distribution as displayed in Figure 4 [17]. Applying a log(10) function to the raw data transforms it to an approximate normal distribution, inferring the original held a Chi-squared distribution (a subclass of gamma distribution). A normal QQ plot is shown in Figure 5 to demonstrate the approximate normality of the transformed data. The authors hypothesize that if data from ample sample sites are collected, the distribution would reflect that shown amongst the individual trees (gamma; Chi-squared distribution).
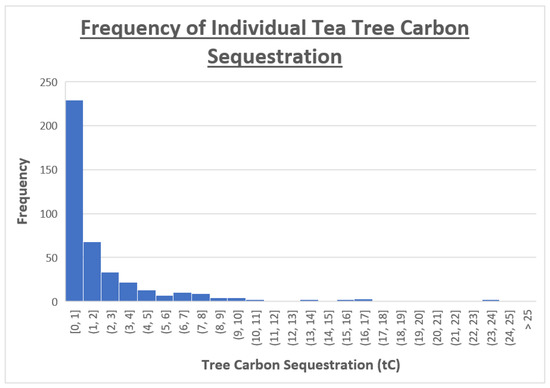
Figure 4.
The gamma distribution of individual tree carbon storage (n = 422).

Figure 5.
A QQ plot of individual tree carbon storage (n = 422) after applying a log(10) function. This illustrates approximate normality.
The mean tree density across the sample sites is 10,750 trees/ha. Saunders [20] suggests that self-seeded tea trees grow in densities of over 10,000 stems/ha, from comparing collected datasets. Natural thinning occurs within the stand over time as trees compete for light and other resources [18]. After several decades, as the primary colonizers are about to be outcompeted by under-story species, the stem density is likely to find an equilibrium as low as 1600 stems/ha [20,26].
The mean tea tree carbon storage of 12-year-old naturally regenerated tea trees is 29.92 tC/ha. This value is 81.80% more than the MPI estimates from the regenerating bush of the same age [27]. The median carbon storage is 22.50 tC/ha (82.45 tCO2/ha), indicating that the data are right skewed (Figure 4 and Figure 6). The range of calculated tea tree carbon storage values is large; 59.74 tC/ha between the minimum of 11.11 tC/ha and maximum of 70.85 tC/ha. This large range is due to the bimodal nature of the data, as shown in Figure 6. This means that regression models or confidence intervals cannot be effectively applied to the data. Pedersen and Skovsgaard [34] state that due to the nature of the data, ‘nonlinearity is often addressed, but rarely quantified’ in the discipline of forestry science. Being a biological system, relationships between variables are often complex, resulting in data that do not follow a recognized distribution pattern [35].
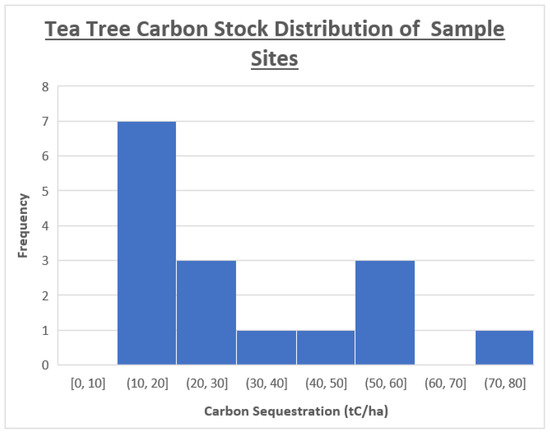
Figure 6.
The distribution of calculated carbon storage among the sample sites.
4. Discussion
4.1. Inclusion of Unvegetated Land
The collected tea tree carbon storage data greatly differ from that described by the MPI (+81.80%). This is somewhat aligned with the findings of Dodd et al. [14], who predict that default look-up tables underrepresent carbon storage by 24%, for established indigenous forest (over 50 years old) and by up to 270% for planted indigenous species. This could be due to varying establishment rates of woody vegetation. The initial establishment issues could be due to a variety of factors, such as a lack of viable seed, competition amongst species, animal grazing, the soil environment, climate, or a mixture of factors [20,22,36,37].
An argument is made that farmers wishing to maximize profitability will not leave hill country land unforested or ungrazed. This provides an explanation as to why estimated carbon storage is higher than that reported in the MPI look-up tables, where unvegetated space is accounted for in the carbon storage estimates [15]. If sample sites found not to contain regenerating tea trees (Figure 1) are considered to have no carbon storage capacity (before the quality control procedure), the mean carbon storage becomes 20.82 tC/ha (76.28 tCO2/ha). This is still 26.50% more than estimated with the MPI look-up tables for regenerating native bush of the same age [27]. This further brings results into line with [14].
Funk et al. [38] suggest that the age of naturally regenerated forestry in any one study area has a sigmoidal relationship from year 0 through to year 10, when a total canopy cover is expected. This is similar to estimates provided by Marden et al. [33], who estimates total canopy cover to be achieved between years 6.5 and 9. This suggests that carbon storage estimates from look-up tables are not viable in the longer term, when a complete canopy cover is achieved [27]. The continued establishment of primary colonizers will eventually vegetate the entire land available, whether by tea trees or other species.
4.2. Bimodal Distribution
A bimodal distribution in total carbon storage amongst the sample sites was found, the cause of which is likely attributable to the study design [34]; in this case, the sampling of two populations. Under a recently closed canopy of exotic species, tea tree growth rates are stunted. This is in contrast with tea tree stands of a comparable age growing in high densities exhibiting similar vertical growth rates [20]. As tea tree seedlings do not tolerate shade, it can be assumed that all measured trees growing within an exotic canopy are of similar age to the exotic tree crop. In contrast, the areas with full light interception would likely be composed of trees of different ages. This is a function of the sigmoidal relationship of tree age over the time it takes to achieve a full canopy cover [38].
Historic imagery reveals that all tea tree sample sites that had measured carbon stocks of over 40 tC/ha were subject to increased light levels at some point in their life. Therefore, the vertical and horizontal (trunk expansion) growth were not limited, leading to increased carbon storage. The two sample sites with the largest measured carbon stock did not compete with any exotic species from establishment until measurement. As a result, the data show two peaks (Figure 5). One from tea trees grown under the canopy of exotic species and one from tea trees grown with partial/full access to sunlight. The former appears to have a gamma distribution, while too few sample sites exist of the latter to determine if it is normally distributed [17]. As the available light levels were not measured, the subgroups cannot be extrapolated for linear regression modelling.
The measuring of naturally regenerated tea tree carbon storage was conducted under an exotic canopy because a physical date could be assigned to the land retirement, and subsequently, an approximate age of regenerated bush could be inferred. In this case, the planting of an exotic canopy provided this information. The alternative method to determine age is stem analysis [17]; however, the landowner did not want destructive techniques used. Most regenerated tea trees on retired farmland would not be under an exotic canopy. Although sufficient data were not collected to make inferences, it is likely that the mean carbon sequestration of tea trees in full light conditions is significantly larger than the MPI predicts. This supports the notion that the MPI look-up tables underestimate the carbon sequestration of tea trees. This warrants longer-term studies that may include the quantification of light interception by tea trees. As the regeneration of native bush under an exotic canopy is currently being considered as a form of managed succession, such a dataset could have real impact on future carbon accounting policy.
4.3. Potential Sources of Bias
The TruPulse 200L™ (Laser Technology Inc., Centennial, CO, USA) rangefinder calculated tree height to ±0.5 m. Considering the basal diameter is measured to the nearest millimetre, this could have introduced an experimental error in the modelled carbon storage. The value and range of this potential bias is unknown [29]. For the purposes of the study, the ability to nondestructively measure the biomass was essential. With the equipment available to the authors at the time, the rangefinder provided the best combination of accuracy, cost and time efficiency. The use of rangefinders to measure tree height is common within forestry science; however, their application is usually reserved for taller species [29]. The use of a measuring stick could provide a greater detail of accuracy in the future; however, this is not practical on such steep terrain.
Bias may have been introduced because of the inaccessible sample site locations. As displayed in Figure 1, the areas unable to be accessed are largely concentrated on a North-facing hill face. As light interception levels are generally higher for North-facing slopes in the Southern hemisphere, it is thought that the mean carbon storage would be increased if these sites were measured. Areas were inaccessible due to (a) higher densities of tea trees and undergrowth and (b) the steepness of terrain.
Tea trees over a height of 1 m have equal statistical weighting. This was carried out to better understand the overall carbon storage capabilities of the regenerated native bush [28]. However, this could impact the statistical relationship between the three variables and carbon storage when comparing individual trees within a stand, with younger trees decreasing the mean from each sample location. It is for this reason that studies comparing the carbon storage of individual trees know the age of the individual, as opposed to the age of the stand.
4.4. Review of Indigenous Forestry Category on the MPI Look-Up Tables
A limited number of sample sites coupled with bimodal data distribution prevents any meaningful statistical relationships between the tree measurements and carbon storage being found. However, results do suggest a substantial difference to those reported in the MPI look-up tables [14]. West et al. [16] state that these reference tables are conservative in nature, where many species fall under the ‘Indigenous Forest’ category. This is significant as it is these tables that predetermine the earnings from retired land under 100 hectares, which is allowed to either naturally regenerate or is planted with seedlings [27]. By underpredicting the carbon storage capacity of the primary colonizers of the retired land, the resultant profitability gap between pines and tea trees grows larger [30]. As the opportunity cost of planting natives grows, property owners will revert to the planting of exotic species [39].
This means that the establishment of long-term trials in a variety of environments is required [14]. Region, topographical features, local climate, light interception, soil fertility and plant cultivar are all variables that should be considered due to their impact on plant growth rates. Due to the amount of data associated with pines, the same look-up tables can differentiate the expected carbon stocks depending on the region they are located in [27]. This should be the overall goal; to form a similar database for different native tree species detailing regional differences in carbon sequestration over time [18,37]. Such a dataset would allow the landowners to be renumerated for the actual carbon sequestration of naturally regenerated land, which is essential if natives are to be encouraged over exotic species.
5. Conclusions
This work provides evidence in support of the hypothesis that a disparity exists between the carbon sequestration of regenerating tea trees and default carbon look-up tables. Although gaps in regenerating bush are not accounted for, the author argues that landowners would want to maximize the value from the land, filling any spaces with nursed seedlings. Although the study lacked the range and scale to categorically refute the use of default carbon look-up tables, it does support initiating further investigative work. A comprehensive dataset pertaining to the carbon sequestration rates of primary colonizers in different regions and/or environments is required.
Future work that takes into account the carbon fluxes from leaf litter, microalgae and soil would help build a more complete picture of the changes in carbon storage in regenerating land and would be beneficial. It is key that landowners are remunerated fairly, according to the carbon sequestration capabilities of their forests, especially if natives are to be incentivized to landowners for biodiversity over exotic species.
Author Contributions
Conceptualization, T.W. and M.G.; methodology, T.W.; software, T.W. and M.I.; validation, T.W., M.I. and M.G.; formal analysis, T.W. and M.G.; investigation, T.W.; resources, M.I. and M.G.; data curation, T.W.; writing—original draft preparation, T.W.; writing—review and editing, M.G.; visualization, T.W. and M.I.; supervision, M.G. and M.I.; project administration, M.G.; funding acquisition, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ravensdown Limited.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge Neil Walker of Nukuhau Carbon Limited for site access and informative and engaging conversations regarding carbon farming. The lead author is thankful for the financial assistance of the following scholarships, which supported the postgraduate study this work is derived from: Millar Massey Buchanan Scholarship, George Terry Memorial Scholarship, Pukehou Poutū Scholarship, Sinclair Cummings Veterinary and Animal Sciences Scholarship, Taranaki Tree Crops Scholarship and the Tilt Renewables Tararua Wind Farm Research Bursary.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fernandez, M.A.; Daigneault, A. The Paris Agreement and its impact on cattle and food sectors of New Zealand. N. Z. J. Agric. Res. 2016, 59, 436–443. [Google Scholar] [CrossRef]
- Fernandez, M.A.; Daigneault, A.J. Money does Grow on Trees: Impacts of the Paris Agreement on the New Zealand Economy. Clim. Chang. Econ. 2018, 9, 23. [Google Scholar] [CrossRef]
- Leahy, S.; Clark, H.; Reisinger, A. Challenges and Prospects for Agricultural Greenhouse Gas Mitigation Pathways Consistent with the Paris Agreement. Front. Sustain. Food Syst. 2020, 4, 8. [Google Scholar] [CrossRef]
- New Zealand Government. Climate Change Response Act 2002. 2919, Wellington. pp. 571p. Available online: https://faolex.fao.org/docs/pdf/nze80299.pdf (accessed on 22 February 2023).
- Wang, Y.; Sharp, B.; Poletti, S.; Nam, K.-M. Economic and land use impacts of net zero-emission target in New Zealand. Int. J. Urban Sci. 2022, 26, 291–308. [Google Scholar] [CrossRef]
- Leining, C.; Kerr, S.; Bruce-Brand, B. The New Zealand Emissions Trading Scheme: Critical review and future outlook for three design innovations. Clim. Policy 2020, 20, 246–264. [Google Scholar] [CrossRef]
- Climate Change Commission. Ināia Tonu Nei: A Low Emissions Future for AOTEAROA. 2021; Wellington; pp. 418p. Available online: https://www.climatecommission.govt.nz/public/Inaia-tonu-nei-a-low-emissions-future-for-Aotearoa/Inaia-tonu-nei-a-low-emissions-future-for-Aotearoa.pdf (accessed on 16 February 2023).
- Climate Change Commission. Progress Towards Agricultural Emissions Pricing. 2022; Wellington; pp. 25p. Available online: https://environment.govt.nz/assets/publications/Pricing-agricultural-emissions-report-under-section-215-of-the-CCRA.pdf (accessed on 16 February 2023).
- Evison, D. The New Zealand forestry sector’s experience in providing carbon sequestration services under the New Zealand Emissions Trading Scheme, 2008 to 2012. For. Policy Econ. 2017, 75, 89–94. [Google Scholar] [CrossRef]
- Kerr, S.; Anastasiadis, S.; Olssen, A.; Power, W.; Timar, L.; Zhang, W. Spatial and Temporal Responses to an Emissions Trading Scheme Covering Agriculture and Forestry: Simulation Results from New Zealand. Forests 2012, 3, 1133–1156. [Google Scholar] [CrossRef]
- Manley, B.; Maclaren, P. Potential impact of carbon trading on forest management in New Zealand. For. Policy Econ. 2012, 24, 35–40. [Google Scholar] [CrossRef]
- Kerr, S.; Ormsby, J.; White, D. Delinking the New Zealand Emissions Trading Scheme from the Kyoto Protocol: Comparing theory with practice. Clim. Policy 2021, 21, 792–803. [Google Scholar] [CrossRef]
- Diaz-Rainey, I.; Tulloch, D.J. Carbon pricing and system linking: Lessons from the New Zealand Emissions Trading Scheme. Energy Econ. 2018, 73, 66–79. [Google Scholar] [CrossRef]
- Dodd, M.B.; Rennie, G.; Kirschbaum, M.U.F.; Giltrap, D.L.; Smiley, D.; van der Weerden, T.J. Improving the economic and environmental performance of a New Zealand hill country farm catchment: 4. Greenhouse gas and carbon stock implications of land management change. N. Z. J. Agric. Res. 2021, 64, 540–564. [Google Scholar] [CrossRef]
- Ministry for Primary Industries. Carbon Look-Up Tables for Forestry in the Emissions Trading Scheme. 2017. Wellington. pp. 44p. Available online: https://www.bioenergy.org.nz/documents/resource/Carbon-look-up-tables-2017-ETS-guide.pdf (accessed on 17 February 2023).
- West, T.A.P.; Monge, J.J.; Dowling, L.J.; Wakelin, S.J.; Gibbs, H.K. Promotion of afforestation in New Zealand’s marginal agricultural lands through payments for environmental services. Ecosyst. Serv. 2020, 46, 10. [Google Scholar] [CrossRef]
- Beets, P.N.; Kimberley, M.O.; Oliver, G.R.; Pearce, S.H. The Application of Stem Analysis Methods to Estimate Carbon Sequestration in Arboreal Shrubs from a Single Measurement of Field Plots. Forests 2014, 5, 919–935. [Google Scholar] [CrossRef]
- Lambie, S.M.; Awatere, S.; Daigneault, A.; Kirschbaum, M.U.F.; Marden, M.; Soliman, T.; Spiekermann, R.I.; Walsh, P.J. Trade-offs between environmental and economic factors in conversion from exotic pine production to natural regeneration on erosion prone land. N. Z. J. For. Sci. 2021, 51, 19. [Google Scholar] [CrossRef] [PubMed]
- Beets, P.N.; Brandon, A.M.; Goulding, C.J.; Kimberley, M.O.; Paul, T.S.H.; Searles, N. The inventory of carbon stock in New Zealand’s post-1989 planted forest for reporting under the Kyoto protocol. For. Ecol. Manag. 2011, 262, 1119–1130. [Google Scholar] [CrossRef]
- Saunders, L.; Boffa Miskell Ltd. The Manuka and Kanuka Plantation Guide. 2017; pp. 86p. Available online: https://www.trc.govt.nz/assets/Documents/Guidelines/Land-infosheets/Manuka-plantation-guide-landcare-April2017.pdf (accessed on 13 February 2023).
- Morales, N.S.; Perry, G.L.W.; Burns, B.R. Fencing is not enough to reinstate regeneration: Evidence from a large fruited canopy tree Beilschmiedia tawa. For. Ecol. Manag. 2016, 376, 36–44. [Google Scholar] [CrossRef]
- Douglas, G.B.; Dodd, M.B.; Power, I.L. Potential of direct seeding for establishing native plants into pastoral land in New Zealand. N. Z. J. Ecol. 2007, 31, 143–153. Available online: http://www.newzealandecology.org/nzje/ (accessed on 25 March 2022).
- UMF Ltd. Quality Factors that Matter in Manuka Honey. 2023. Available online: https://www.umf.org.nz/unique-manuka-factor/umf-four-factor-quality-testing/on (accessed on 20 February 2023).
- Gordon, A.D.; Pont, D. Inventory estimates of stem volume using nine sampling methods in thinned Pinus radiata stands, New Zealand. N. Z. J. For. Sci. 2015, 45, 8. [Google Scholar] [CrossRef]
- Ucar, Z.; Bettinger, P.; Merry, K.; Siry, J.; Bowker, J.M.; Akbulut, R. A comparison of two sampling approaches for assessing the urban forest canopy cover from aerial photography. Urban For. Urban Green. 2016, 16, 221–230. [Google Scholar] [CrossRef]
- Scott, N.A.; White, J.D.; Townsend, J.A.; Whitehead, D.; Leathwick, J.R.; Hall, G.M.J.; Marden, M.; Rogers, G.N.D.; Watson, A.J.; Whaley, P.T. Carbon and nitrogen distribution and accumulation in a New Zealand scrubland ecosystem. Can. J. For. Res. 2000, 30, 1246–1255. [Google Scholar] [CrossRef]
- Ministry for Primary Industries. A Guide to the Field Measurement Approach for Forestry in the Emissions Trading Scheme. 2023; Wellington; pp. 94p. Available online: https://www.mpi.govt.nz/dmsdocument/3666-A-Guide-to-the-Field-Measurement-Approach-for-Forestry-in-the-Emissions-Trading-Scheme (accessed on 21 February 2023).
- Searle, E.B.; Chen, H.Y.H. Tree size thresholds produce biased estimates of forest biomass dynamics. For. Ecol. Manag. 2017, 400, 468–474. [Google Scholar] [CrossRef]
- Sullivan, M.J.P.; Lewis, S.L.; Hubau, W.; Qie, L.; Baker, T.R.; Banin, L.F.; Chave, J.; Cuni-Sanchez, A.; Feldpausch, T.R.; Lopez-Gonzalez, G.; et al. Field methods for sampling tree height for tropical forest biomass estimation. Methods Ecol. Evol. 2018, 9, 1179–1189. [Google Scholar] [CrossRef]
- Lambie, S.M.; Dando, J. Seasonal litterfall composition and carbon and nitrogen returns in New Zealand shrubland. Aust. J. Bot. 2019, 67, 610–616. [Google Scholar] [CrossRef]
- New Zealand Institute of Forestry Inc. Forestry Handbook, 4th ed.; Colley, M., Ed.; Design & Print Management Ltd.: Tauranga, New Zealand, 2005; 382p, Available online: https://nzif.org.nz/assets/NZIF-Handbook-HiRes.pdf (accessed on 20 February 2023).
- Beets, P.N.; Garrett, L.G. Carbon fraction of Pinus radiata biomass components within New Zealand. N. Z. J. For. Sci. 2018, 48, 14. [Google Scholar] [CrossRef]
- Marden, M.; Lambie, S.; Phillips, C. Potential effectiveness of low-density plantings of manuka (Leptospermum scoparium) as an erosion mitigation strategy in steeplands, northern Hawke’s Bay, New Zealand. N. Z. J. For. Sci. 2020, 50, 20. [Google Scholar] [CrossRef]
- Pedersen, R.O.; Skovsgaard, J.P. Impact of bias in predicted height on tree volume estimation: A case-study of intrinsic nonlinearity. Ecol. Model. 2009, 220, 2656–2664. [Google Scholar] [CrossRef]
- Tozer, K.; Douglas, G.; Dodd, M.; Muller, K. Vegetation Options for Increasing Resilience in Pastoral Hill Country. Front. Sustain. Food Syst. 2021, 5, 22. [Google Scholar] [CrossRef]
- Burns, B.R.; Floyd, C.G.; Smale, M.C.; Arnold, G.C. Effects of forest fragment management on vegetation condition and maintenance of canopy composition in a New Zealand pastoral landscape. Austral. Ecol. 2011, 36, 153–166. [Google Scholar] [CrossRef]
- Carver, T.; Kerr, S. Facilitating Carbon Offsets from Native Forests. 2017, pp. 6p. Available online: https://www.motu.org.nz/assets/Documents/our-work/environment-and-resources/climate-change-mitigation/emissions-trading/Native-Forest-Offset-Options-Exec-Summary.pdf (accessed on 22 February 2023).
- Funk, J.M.; Field, C.B.; Kerr, S.; Daigneault, A. Modeling the impact of carbon farming on land use in a New Zealand landscape. Environ. Sci. Policy 2014, 37, 1–10. [Google Scholar] [CrossRef]
- Norton, D.A.; Suryaningrum, F.; Buckley, H.L.; Case, B.S.; Cochrane, C.H.; Forbes, A.S.; Harcombe, M. Achieving win-win outcomes for pastoral farming and biodiversity conservation in New Zealand. N. Z. J. Ecol. 2020, 44, 9. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).