Predicting Ventilation Rate in a Naturally Ventilated Dairy Barn in Wind-Forced Conditions Using Machine Learning Techniques
Abstract
1. Introduction
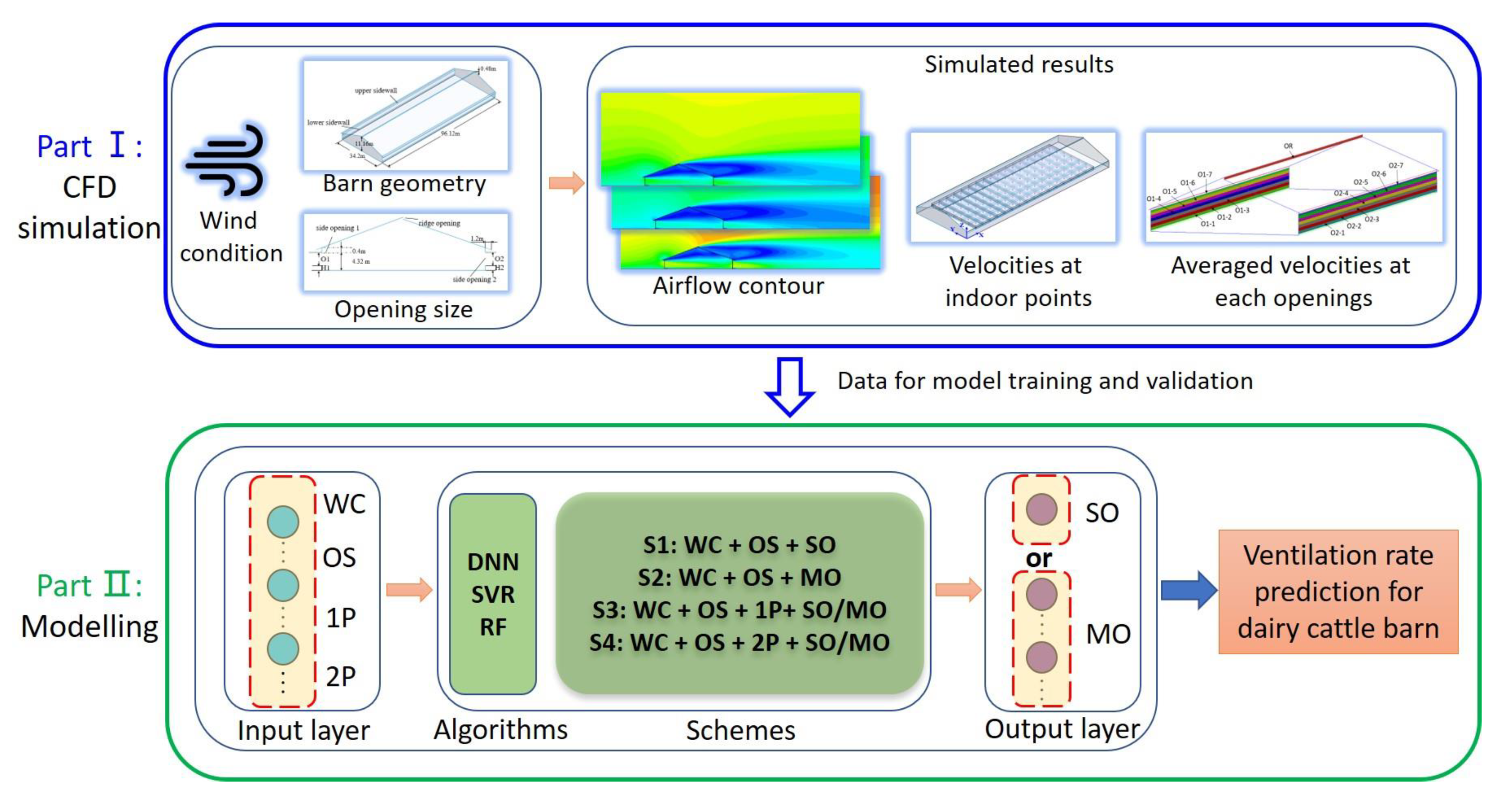
2. Materials and Methods
2.1. CFD Simulation
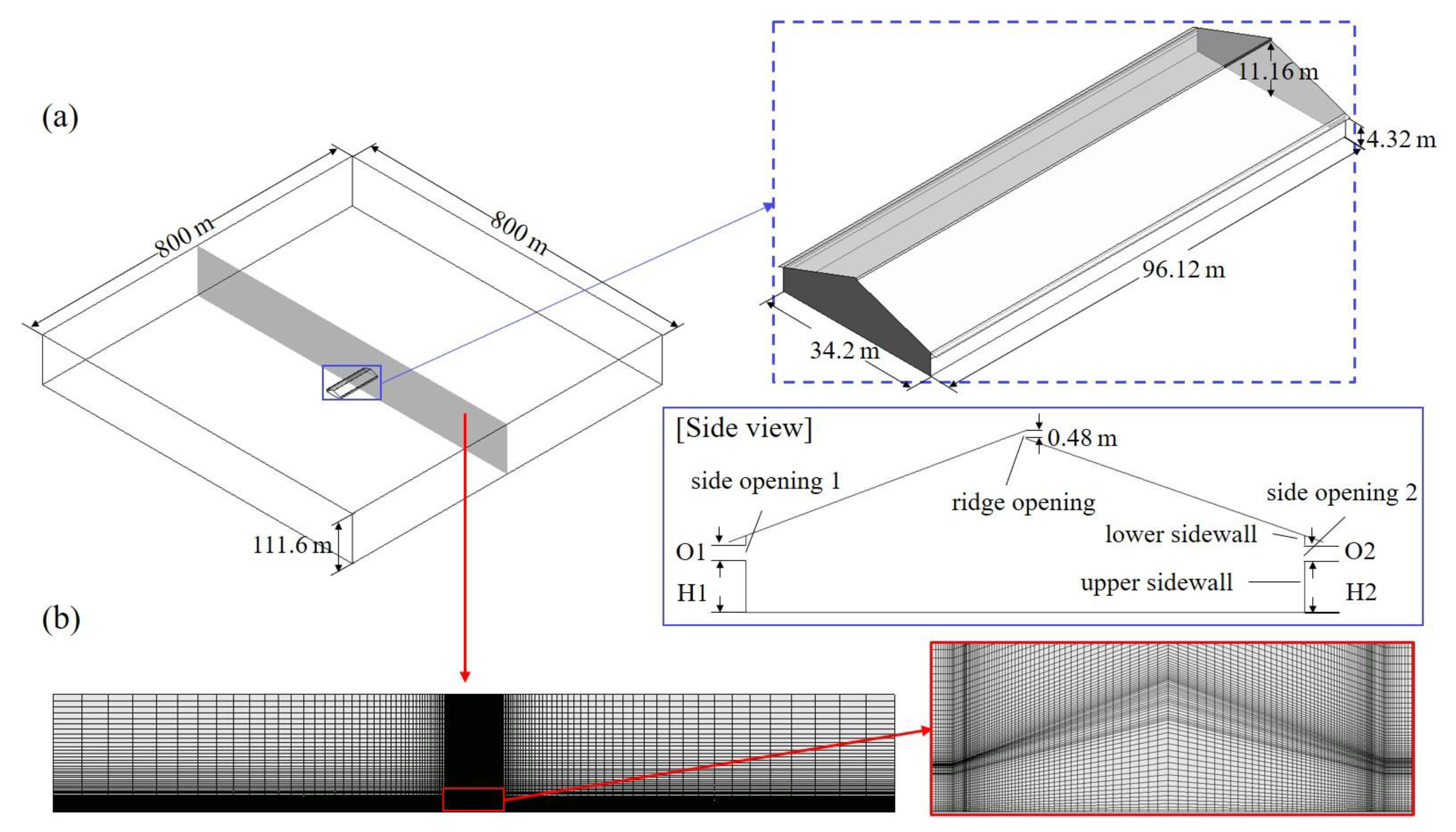
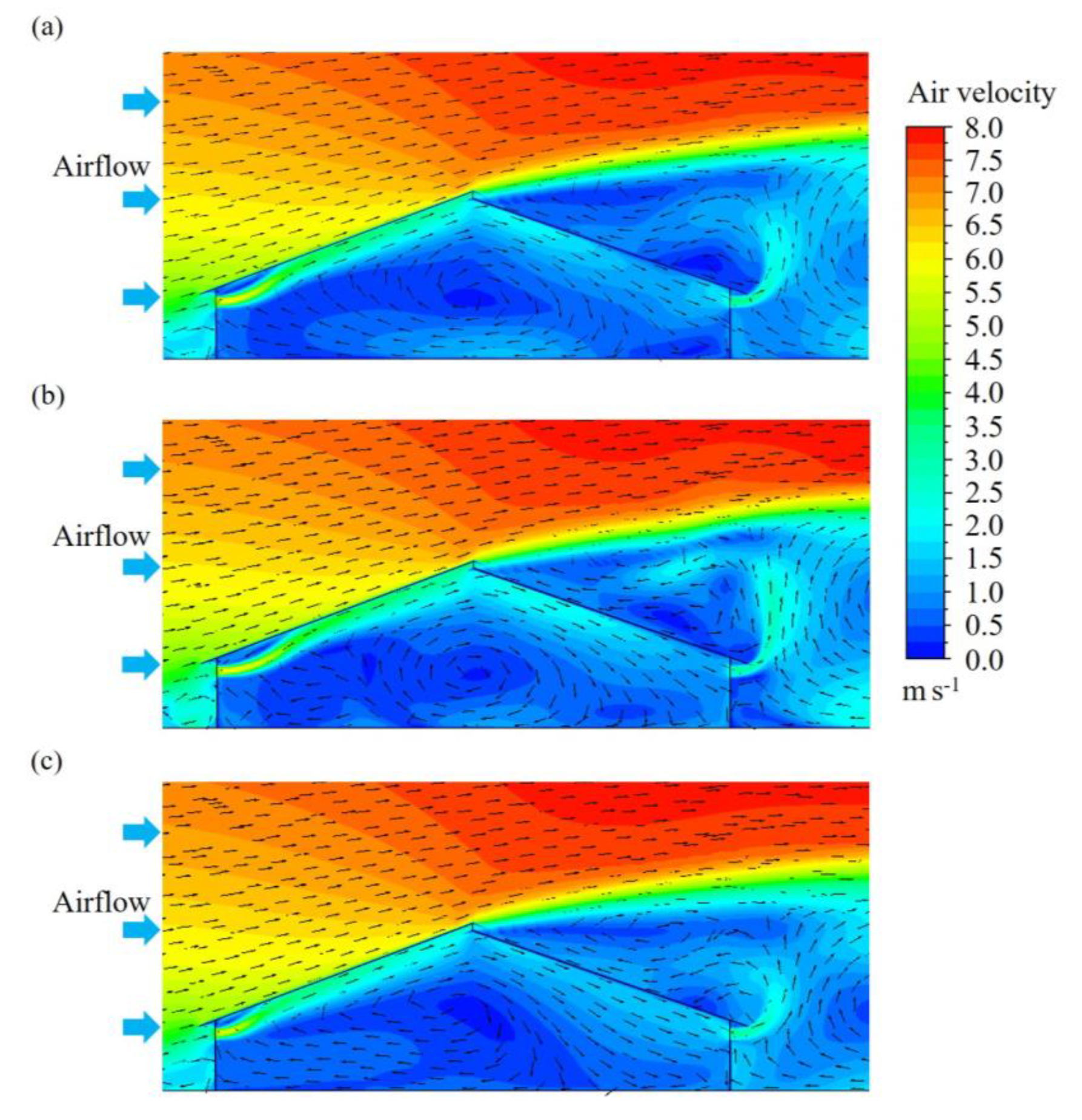
2.1.1. Computational Domain, Mesh Distribution, and Boundary Condition
2.1.2. Governing Equation, Turbulence Models, and Simulation Scheme
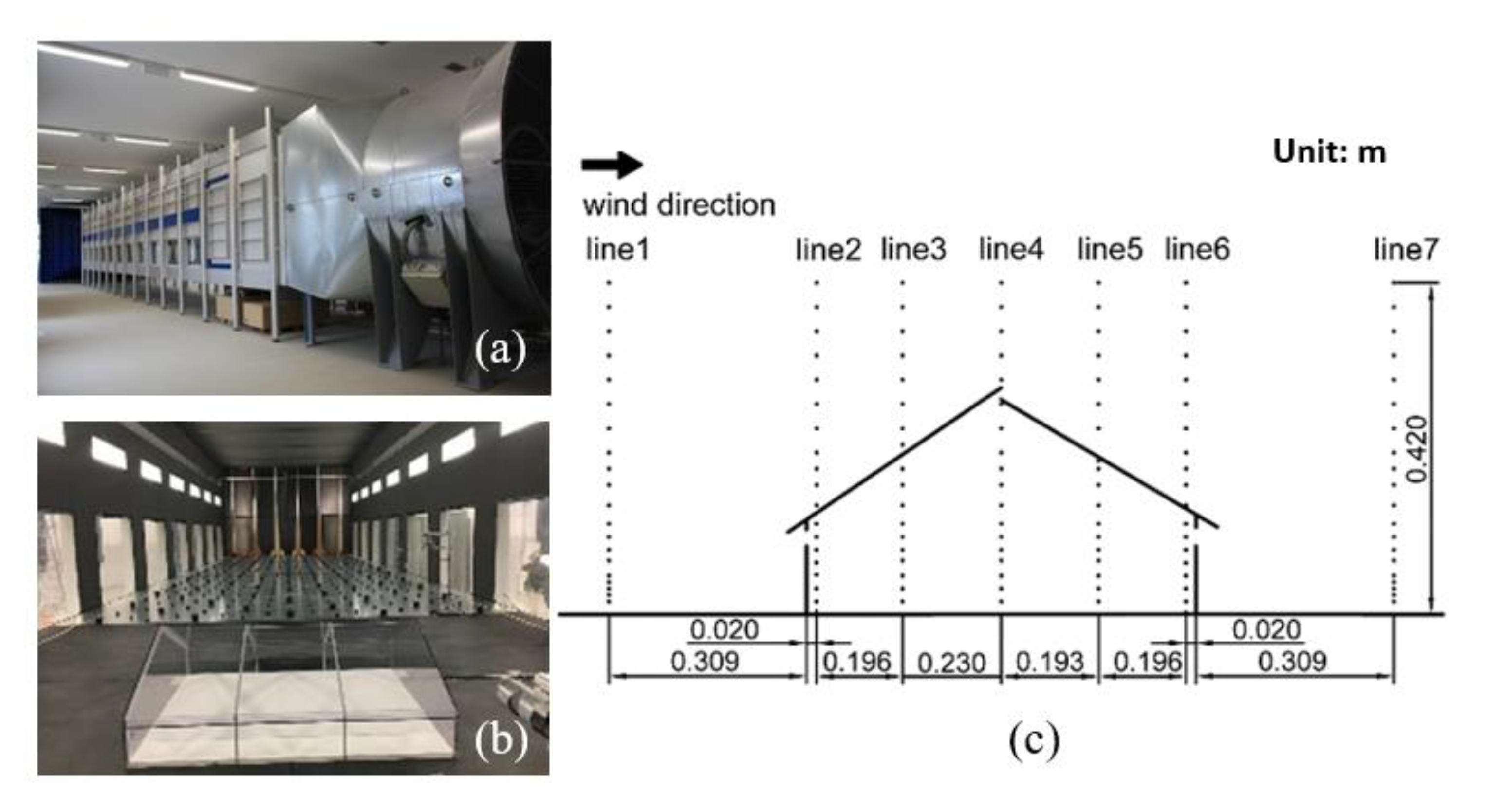
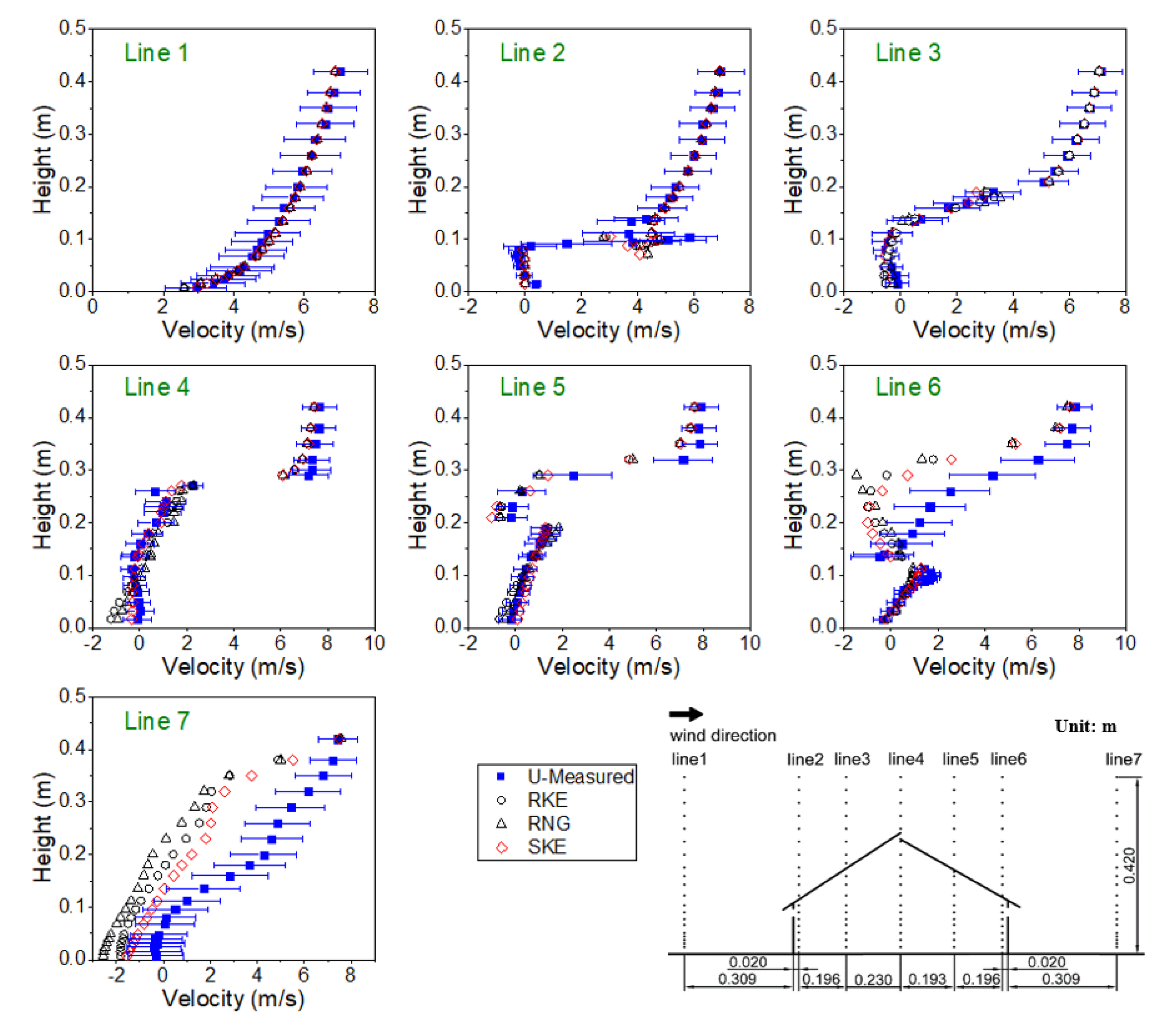
2.1.3. Experimental Data for CFD Model Validation
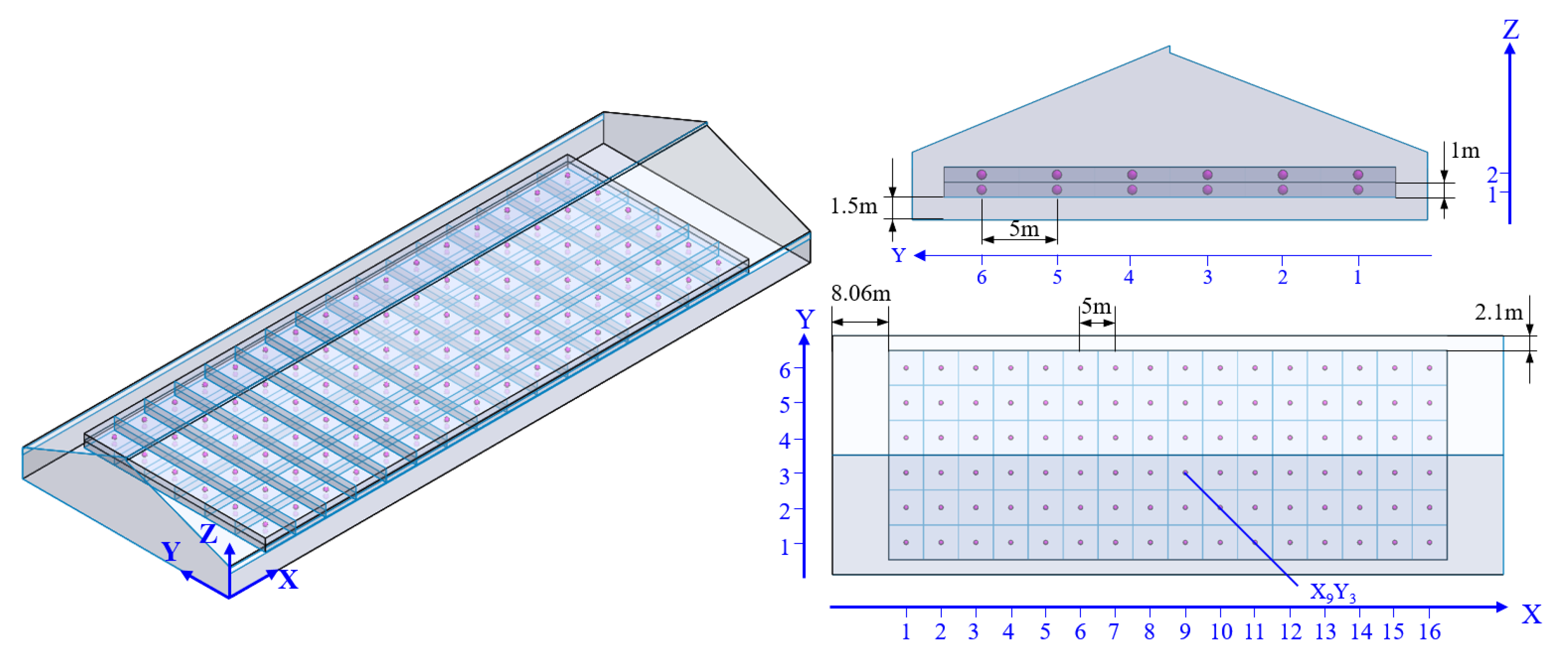
2.1.4. Determination of Independent and Response Variables
2.1.5. Simulated Data Acquisition
2.2. Development of Ventilation Predictive Models
2.2.1. Dataset Construction
2.2.2. Determination of Modeling Scheme
2.2.3. Algorithm for Machine Learning
- (1)
- Deep Neural Networks (DNN)
- (2)
- Support Vector Regression (SVR)
- (3)
- Random forest (RF)
2.2.4. Evaluation Metrics
3. Results and Discussion
3.1. CFD Model Validation
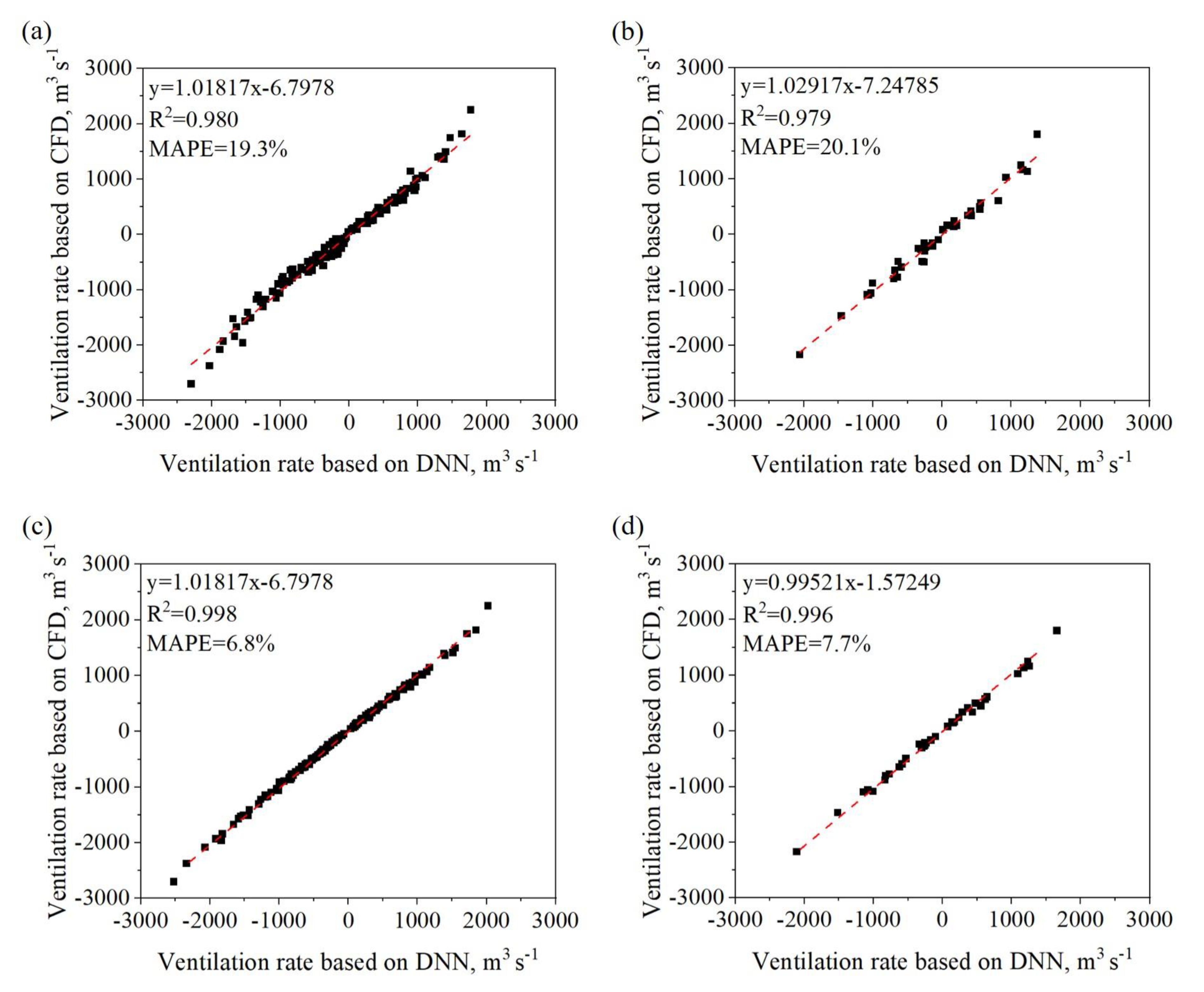
3.2. Evaluation of Different Machine Learning Algorithms
3.3. Comparison of Single and Multiple Outputs
3.4. The Impact of Real-Time In-Barn Air Velocity Measurement
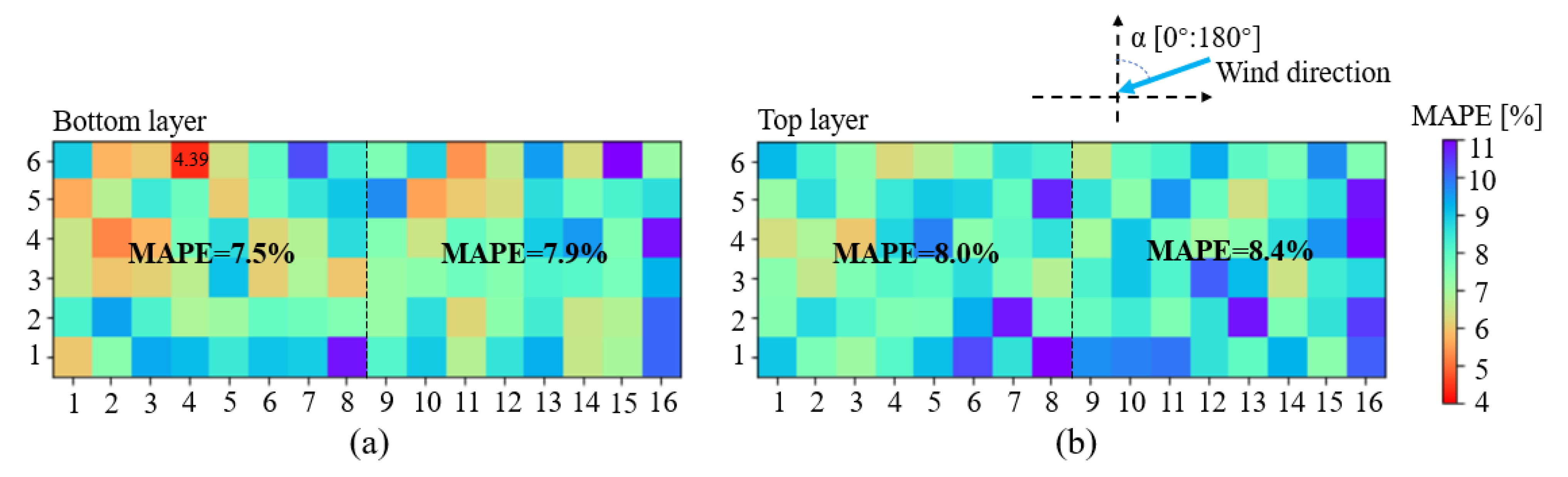
3.5. Effect of Anemometer Placement
3.6. Limitations and Perspectives
4. Conclusions
- (1)
- The R2 value of the DNN algorithm was greater than those of the SVR and RF algorithms. The MAPE value of the DNN algorithm was greater than those of the SVR and RF algorithms. The DNN algorithm was more suitable for the ventilation rate prediction of a dairy barn.
- (2)
- The R2 value of Scheme 2 was greater than that of Scheme 1 and the MAPE value of Scheme 2 was smaller than that of Scheme 1. Using the air velocities at the openings as the modeling outputs was more suitable for the ventilation rate prediction of the dairy barn than using the ventilation rate directly as the model output.
- (3)
- Among the three modeling schemes, the MAPE of the prediction decreased from 7.7% for Scheme 2 to 4.4% for Scheme 3 and 3.1% for Scheme 4. Adding indoor monitoring points as the model inputs could improve the predictive accuracy. The predictive accuracy increased as the number of indoor monitoring points increased. However, adding two indoor air velocities improved the accuracy of the scheme with one indoor air velocity by 1.3%.
- (4)
- Due to the height and the operating strategies of the sidewall openings, selecting the velocities of the monitoring points at the lower layer as the model inputs performed generally better than selecting those at the top layer.
- (5)
- Scheme 3 with the velocities at one point added in the model inputs was recommended. The velocities at the monitoring point X4Y6Z1 were recommended for the model inputs when the wind direction is 0–180°.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seedorf, J.; Hartung, J.; Schröder, M.; Linkert, K.H.; Pedersen, S.; Takai, H.; Johnsen, J.O.; Metz, J.H.M.; Groot Koerkamp, P.W.G.; Uenk, G.H.; et al. A Survey of Ventilation Rates in Livestock Buildings in Northern Europe. J. Agric. Eng. Res. 1998, 70, 39–47. [Google Scholar] [CrossRef]
- Tomasello, N.; Valenti, F.; Cascone, G.; Porto, S.M.C. Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows. Buildings 2019, 9, 183. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Investigation of response surface methodology for modelling ventilation rate of a naturally ventilated building. Build. Environ. 2012, 54, 174–185. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Assessments of experimental designs in response surface modelling process: Estimating ventilation rate in naturally ventilated livestock buildings. Energy Build. 2013, 62, 570–580. [Google Scholar] [CrossRef]
- Fagundes, B.; Damasceno, F.A.; Andrade, R.R.; Saraz, J.A.O.; Barbari, M.; Vega, F.A.O.; Nascimento, J.A.C. Comparison of airflow homogeneity in Compost Dairy Barns with different ventilation systems using the CFD model. Agron. Res. 2020, 18, 788–796. [Google Scholar] [CrossRef]
- Pakari, A.; Ghani, S. Comparison of different mechanical ventilation systems for dairy cow barns: CFD simulations and field measurements. Comput. Electron. Agric. 2021, 186, 106207. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Comparison of different methods for estimating ventilation rates through wind driven ventilated buildings. Energy Build. 2012, 54, 297–306. [Google Scholar] [CrossRef]
- Yi, Q.; Wang, X.; Zhang, G.; Li, H.; Janke, D.; Amon, T. Assessing effects of wind speed and wind direction on discharge coefficient of sidewall opening in a dairy building model—A numerical study. Comput. Electron. Agric. 2019, 162, 235–245. [Google Scholar] [CrossRef]
- Yi, Q.; Zhang, G.; Li, H.; Wang, X.; Janke, D.; Amon, B.; Hempel, S.; Amon, T. Estimation of opening discharge coefficient of naturally ventilated dairy buildings by response surface methodology. Comput. Electron. Agric. 2020, 169, 105224. [Google Scholar] [CrossRef]
- Ayata, T.; Arcaklıoğlu, E.; Yıldız, O. Application of ANN to explore the potential use of natural ventilation in buildings in Turkey. Appl. Therm. Eng. 2007, 27, 12–20. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Faria, E.A.; Ruano, A.E. Neural network models in greenhouse air temperature prediction. Neurocomputing 2002, 43, 51–75. [Google Scholar] [CrossRef]
- Becker, C.A.; Aghalari, A.; Marufuzzaman, M.; Stone, A.E. Predicting dairy cattle heat stress using machine learning techniques. J. Dairy Sci. 2021, 104, 501–524. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuang, Y.; Ji, B.; Zhang, G.; Rong, L.; Teng, G.; Wang, C. Prediction of laying hen house odor concentrations using machine learning models based on small sample data. Comput. Electron. Agric. 2022, 195, 106849. [Google Scholar] [CrossRef]
- Arulmozhi, E.; Basak, J.K.; Sihalath, T.; Park, J.; Kim, H.T.; Moon, B.E. Machine Learning-Based Microclimate Model for Indoor Air Temperature and Relative Humidity Prediction in a Swine Building. Animals 2021, 11, 222. [Google Scholar] [CrossRef]
- Chen, Y.; Tong, Z.; Zheng, Y.; Samuelson, H.; Norford, L. Transfer learning with deep neural networks for model predictive control of HVAC and natural ventilation in smart buildings. J. Clean. Prod. 2020, 254, 119866. [Google Scholar] [CrossRef]
- Gan, V.J.L.; Wang, B.; Chan, C.M.; Weerasuriya, A.U.; Cheng, J.C.P. Physics-based, data-driven approach for predicting natural ventilation of residential high-rise buildings. Build. Simul. 2022, 15, 129–148. [Google Scholar] [CrossRef]
- Jing, G.; Cai, W.; Chen, H.; Zhai, D.; Cui, C.; Yin, X. An air balancing method using support vector machine for a ventilation system. Build. Environ. 2018, 143, 487–495. [Google Scholar] [CrossRef]
- Li, Q.Y.; Han, J.; Lu, L. A Random Forest Classification Algorithm Based Personal Thermal Sensation Model for Personalized Conditioning System in Office Buildings. Comput. J. 2021, 64, 500–508. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlunzen, K.H.; Carissimo, B. The COST 732 Best Practice Guideline for CFD simulation of flows in the urban environment: A summary. Int. J. Environ. Pollut. 2011, 44, 419. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Wu, W.; Zhai, J.; Zhang, G.; Nielsen, P.V. Evaluation of methods for determining air exchange rate in a naturally ventilated dairy cattle building with large openings using computational fluid dynamics (CFD). Atmos. Environ. 2012, 63, 179–188. [Google Scholar] [CrossRef]
- Wieringa, J. Updating the Davenport roughness classification. J. Wind Eng. Ind. Aerodyn. 1992, 41, 357–368. [Google Scholar] [CrossRef]
- Rong, L.; Nielsen, P.V.; Bjerg, B.; Zhang, G. Summary of best guidelines and validation of CFD modeling in livestock buildings to ensure prediction quality. Comput. Electron. Agric. 2016, 121, 180–190. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Washington, DC, USA; Hemisphere Publishing Corp.: London, UK, 1980; p. 210. [Google Scholar]
- Yi, Q.; König, M.; Janke, D.; Hempel, S.; Zhang, G.; Amon, B.; Amon, T. Wind tunnel investigations of sidewall opening effects on indoor airflows of a cross-ventilated dairy building. Energy Build. 2018, 175, 163–172. [Google Scholar] [CrossRef]
- Yi, Q.; Zhang, G.; König, M.; Janke, D.; Hempel, S.; Amon, T. Investigation of discharge coefficient for wind-driven naturally ventilated dairy barns. Energy Build. 2018, 165, 132–140. [Google Scholar] [CrossRef]
- Yi, Q.; Li, H.; Wang, X.; Zong, C.; Zhang, G. Numerical investigation on the effects of building configuration on discharge coefficient for a cross-ventilated dairy building model. Biosyst. Eng. 2019, 182, 107–122. [Google Scholar] [CrossRef]
- Maharani, D.; Murfi, H. Deep Neural Network For Structured Data—A Case Study Of Mortality Rate Prediction Caused By Air Quality. In Proceedings of the 2nd International Conference on Data and Information Science (ICoDIS), Bandung, Indonesia, 15–16 November 2018. [Google Scholar]
- Shen, Z.; Pan, P.; Zhang, D.; Huang, S. Rapid Structural Safety Assessment Using a Deep Neural Network. J. Earthq. Eng. 2022, 26, 2625–2641. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Vens, C.; Van Assche, A.; Blockeel, H.; Dzeroski, S. First order random forests with complex aggregates. In Inductive Logic Programming, Proceedings; Camacho, R., King, R., Srinivasan, A.S., Eds.; Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3194, pp. 323–340. [Google Scholar]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M. Mining data with random forests: A survey and results of new tests. Pattern Recognit. 2011, 44, 330–349. [Google Scholar] [CrossRef]
- Morsing, S.; Ikeguchi, A.; Bennetsen, J.C.; Strom, J.S.; Ravn, P.; Okushima, L. Wind induced isothermal airflow patterns in a scale model of a naturally ventilated swine barn with cathedral ceiling. Appl. Eng. Agric. 2002, 18, 97–101. [Google Scholar] [CrossRef]
- Nosek, S.; Klukova, Z.; Jakubcova, M.; Yi, Q.; Janke, D.; Demeyer, P.; Janour, Z. The impact of atmospheric boundary layer, opening configuration and presence of animals on the ventilation of a cattle barn. J. Wind. Eng. Ind. Aerodyn. 2020, 201, 104185. [Google Scholar] [CrossRef]
- Evola, G.; Popov, V. Computational analysis of wind driven natural ventilation in buildings. Energy Build. 2006, 38, 491–501. [Google Scholar] [CrossRef]
- Ntinas, G.K.; Shen, X.; Wang, Y.; Zhang, G. Evaluation of CFD turbulence models for simulating external airflow around varied building roof with wind tunnel experiment. Build. Simul. 2018, 11, 115–123. [Google Scholar] [CrossRef]
- Gorczyca, M.T.; Milan, H.F.M.; Campos Maia, A.S.; Gebremedhin, K.G. Machine learning algorithms to predict core, skin, and hair-coat temperatures of piglets. Comput. Electron. Agric. 2018, 151, 286–294. [Google Scholar] [CrossRef]
- Huang, J.-C.; Tsai, Y.-C.; Wu, P.-Y.; Lien, Y.-H.; Chien, C.-Y.; Kuo, C.-F.; Hung, J.-F.; Chen, S.-C.; Kuo, C.-H. Predictive modeling of blood pressure during hemodialysis: A comparison of linear model, random forest, support vector regression, XGBoost, LASSO regression and ensemble method. Comput. Methods Programs Biomed. 2020, 195, 105536. [Google Scholar] [CrossRef] [PubMed]
- Dayal, B.S.; MacGregor, J.F. Multi-output process identification. J. Process Control 1997, 7, 269–282. [Google Scholar] [CrossRef]

| Item | Total Number of Meshes in Each Case | ||
|---|---|---|---|
| ~6.3 Million | ~3.1 Million | ~1.5 Million | |
| , m s−1 | 2.313 | 2.310 | 2.291 |
| Relative difference, % | 0 | 0.1 | 1.0 |
| Item | Line1 | Line2 | Line3 | Line4 | Line5 | Line6 | Line7 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y, m | v, m s−1 | Y, m | v, m s−1 | Y, m | v, m s−1 | Y, m | v, m s−1 | Y, m | v, m s−1 | Y, m | v, m s−1 | Y, m | v, m s−1 | |
| P1 | 0.008 | 2.93 ± 0.87 | 0.016 | 0.35 ± 0.19 | 0.016 | −0.12 ± 0.43 | 0.016 | −0.11 ± 0.59 | 0.016 | −0.22 ± 0.47 | 0.016 | −0.36 ± 0.41 | 0.008 | −0.32 ± 1.16 |
| P2 | 0.016 | 3.41 ± 0.90 | 0.032 | −0.02 ± 0.28 | 0.032 | −0.17 ± 0.46 | 0.032 | −0.01 ± 0.59 | 0.032 | −0.10 ± 0.46 | 0.032 | −0.04 ± 0.38 | 0.016 | −0.36 ± 1.18 |
| P3 | 0.024 | 3.70 ± 0.92 | 0.05 | −0.17 ± 0.24 | 0.048 | −0.31 ± 0.40 | 0.048 | −0.07 ± 0.53 | 0.048 | 0.07 ± 0.47 | 0.05 | 0.22 ± 0.38 | 0.024 | −0.41 ± 1.16 |
| P4 | 0.032 | 3.84 ± 0.90 | 0.064 | −0.22 ± 0.23 | 0.068 | −0.46 ± 0.42 | 0.068 | −0.11 ± 0.49 | 0.068 | 0.15 ± 0.47 | 0.064 | 0.49 ± 0.37 | 0.032 | −0.27 ± 1.19 |
| P5 | 0.04 | 4.16 ± 0.93 | 0.072 | −0.27 ± 0.22 | 0.08 | −0.54 ± 0.42 | 0.08 | −0.22 ± 0.49 | 0.08 | 0.21 ± 0.45 | 0.072 | 0.55 ± 0.43 | 0.04 | −0.34 ± 1.14 |
| P6 | 0.048 | 4.25 ± 0.92 | 0.08 | −0.25 ± 0.33 | 0.096 | −0.47 ± 0.52 | 0.096 | −0.25 ± 0.47 | 0.096 | 0.31 ± 0.47 | 0.08 | 0.93 ± 0.38 | 0.048 | −0.20 ± 1.19 |
| P7 | 0.068 | 4.51 ± 0.93 | 0.088 | 0.19 ± 0.95 | 0.112 | −0.30 ± 0.72 | 0.112 | −0.33 ± 0.48 | 0.112 | 0.43 ± 0.48 | 0.088 | 1.42 ± 0.40 | 0.068 | 0.07 ± 1.25 |
| P8 | 0.08 | 4.64 ± 0.87 | 0.092 | 1.48 ± 1.60 | 0.135 | 0.51 ± 0.99 | 0.135 | −0.23 ± 0.56 | 0.135 | 0.66 ± 0.53 | 0.092 | 1.58 ± 0.40 | 0.08 | 0.10 ± 1.30 |
| P9 | 0.096 | 4.80 ± 0.88 | 0.096 | 3.80 ± 1.72 | 0.14 | 0.70 ± 0.99 | 0.14 | −0.20 ± 0.53 | 0.14 | 0.77 ± 0.49 | 0.096 | 1.67 ± 0.39 | 0.096 | 0.50 ± 1.39 |
| P10 | 0.112 | 4.96 ± 0.93 | 0.099 | 5.05 ± 1.37 | 0.16 | 1.68 ± 1.16 | 0.16 | 0.01 ± 0.59 | 0.16 | 0.99 ± 0.57 | 0.099 | 1.75 ± 0.39 | 0.112 | 1.01 ± 1.43 |
| P11 | 0.135 | 5.28 ± 0.89 | 0.105 | 5.84 ± 1.00 | 0.17 | 2.33 ± 1.17 | 0.18 | 0.31 ± 0.67 | 0.17 | 1.16 ± 0.58 | 0.105 | 1.68 ± 0.37 | 0.135 | 1.70 ± 1.57 |
| P12 | 0.16 | 5.43 ± 0.88 | 0.112 | 3.69 ± 1.63 | 0.18 | 2.95 ± 1.08 | 0.2 | 0.69 ± 0.77 | 0.18 | 1.29 ± 0.63 | 0.112 | 1.41 ± 0.39 | 0.16 | 2.84 ± 1.6 |
| P13 | 0.18 | 5.68 ± 0.87 | 0.135 | 3.76 ± 1.21 | 0.19 | 3.29 ± 0.99 | 0.22 | 0.97 ± 0.79 | 0.19 | 1.28 ± 0.62 | 0.135 | −0.49 ± 1.23 | 0.18 | 3.67 ± 1.52 |
| P14 | 0.2 | 5.79 ± 0.87 | 0.14 | 4.31 ± 1.13 | 0.21 | 5.07 ± 0.89 | 0.23 | 1.03 ± 0.84 | 0.21 | −0.19 ± 0.66 | 0.14 | −0.31 ± 1.30 | 0.2 | 4.27 ± 1.41 |
| P15 | 0.23 | 5.95 ± 0.84 | 0.16 | 4.87 ± 0.87 | 0.23 | 5.46 ± 0.87 | 0.24 | 1.10 ± 0.86 | 0.23 | −0.14 ± 0.67 | 0.16 | 0.45 ± 1.32 | 0.23 | 4.62 ± 1.33 |
| P16 | 0.26 | 6.19 ± 0.86 | 0.18 | 5.14 ± 0.82 | 0.26 | 5.93 ± 0.82 | 0.26 | 0.65 ± 0.84 | 0.26 | 0.26 ± 1.02 | 0.18 | 0.90 ± 1.38 | 0.26 | 4.85 ± 1.38 |
| P17 | 0.29 | 6.30 ± 0.86 | 0.2 | 5.33 ± 0.84 | 0.29 | 6.23 ± 0.83 | 0.27 | 2.27 ± 0.44 | 0.29 | 2.45 ± 1.68 | 0.2 | 1.19 ± 1.39 | 0.29 | 5.43 ± 1.47 |
| P18 | 0.32 | 6.59 ± 0.82 | 0.23 | 5.78 ± 0.83 | 0.32 | 6.47 ± 0.82 | 0.29 | 7.18 ± 0.84 | 0.32 | 7.15 ± 1.24 | 0.23 | 1.65 ± 1.50 | 0.32 | 6.18 ± 1.4 |
| P19 | 0.35 | 6.68 ± 0.81 | 0.26 | 5.99 ± 0.81 | 0.35 | 6.71 ± 0.80 | 0.3 | 7.32 ± 0.81 | 0.35 | 7.85 ± 0.74 | 0.26 | 2.51 ± 1.68 | 0.35 | 6.82 ± 1.19 |
| P20 | 0.38 | 6.85 ± 0.76 | 0.29 | 6.29 ± 0.80 | 0.38 | 6.87 ± 0.79 | 0.32 | 7.32 ± 0.77 | 0.38 | 7.82 ± 0.73 | 0.29 | 4.32 ± 1.83 | 0.38 | 7.22 ± 1.00 |
| P21 | 0.42 | 7.03 ± 0.77 | 0.32 | 6.32 ± 0.81 | 0.42 | 7.11 ± 0.77 | 0.35 | 7.46 ± 0.78 | 0.42 | 7.92 ± 0.72 | 0.32 | 6.26 ± 1.57 | 0.42 | 7.43 ± 0.84 |
| P22 | 0.35 | 6.67 ± 0.79 | 0.38 | 7.61 ± 0.74 | 0.35 | 7.49 ± 0.95 | ||||||||
| P23 | 0.38 | 6.84 ± 0.77 | 0.42 | 7.66 ± 0.74 | 0.38 | 7.71 ± 0.79 | ||||||||
| P24 | 0.42 | 6.97 ± 0.81 | 0.42 | 7.83 ± 0.75 | ||||||||||
| Variables (Unit) | Value |
|---|---|
| WS 1 (m s−1) | 3, 5, 7, 9 |
| WD 2 (°) | 0, 30, 45, 60, 120, 135, 150 |
| O1 3 (m) | 0.6, 1.2, 1.8, 2.4, 3, 3.6, 4 |
| O2 3 (m) | 0.6, 1.2, 1.8, 2.4, 3, 3.6, 4 |
| Modeling Scheme | Number of Inputs | Number of Outputs | Number of Cases |
|---|---|---|---|
| Scheme 1 | 4 | 1 | 196 1 × 1 |
| Scheme 2 | 4 | 15 | 196 × 1 |
| Scheme 3 | 7 | 1 or 15 2 | 196 × 192 |
| Scheme 4 | 10 | 1 or 15 | 196 × 36,672 |
| Scheme No. | Item | Training Set (80%) | Test Set (20%) | ||||
|---|---|---|---|---|---|---|---|
| DNN | SVR | RF | DNN | SVR | RF | ||
| Scheme 1 | R2 | 0.980 | 0.908 | 0.986 | 0.979 | 0.885 | 0.975 |
| MAPE (%) | 19.3 | 23.8 | 13.5 | 20.1 | 23.2 | 21.0 | |
| Scheme 2 | R2 | 0.998 | 0.993 | 0.978 | 0.996 | 0.992 | 0.965 |
| MAPE (%) | 6.8 | 9.6 | 16.5 | 7.7 | 10.5l | 21.6 | |
| Item | Scheme 2 | Scheme 3 | Scheme 4 |
|---|---|---|---|
| R2 | 0.996 | 0.998 | 0.999 |
| MAPE (%) | 7.7 | 4.4 | 3.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Yi, Q.; Wang, K.; Li, J.; Wang, X. Predicting Ventilation Rate in a Naturally Ventilated Dairy Barn in Wind-Forced Conditions Using Machine Learning Techniques. Agriculture 2023, 13, 837. https://doi.org/10.3390/agriculture13040837
Cao M, Yi Q, Wang K, Li J, Wang X. Predicting Ventilation Rate in a Naturally Ventilated Dairy Barn in Wind-Forced Conditions Using Machine Learning Techniques. Agriculture. 2023; 13(4):837. https://doi.org/10.3390/agriculture13040837
Chicago/Turabian StyleCao, Mengbing, Qianying Yi, Kaiying Wang, Jiangong Li, and Xiaoshuai Wang. 2023. "Predicting Ventilation Rate in a Naturally Ventilated Dairy Barn in Wind-Forced Conditions Using Machine Learning Techniques" Agriculture 13, no. 4: 837. https://doi.org/10.3390/agriculture13040837
APA StyleCao, M., Yi, Q., Wang, K., Li, J., & Wang, X. (2023). Predicting Ventilation Rate in a Naturally Ventilated Dairy Barn in Wind-Forced Conditions Using Machine Learning Techniques. Agriculture, 13(4), 837. https://doi.org/10.3390/agriculture13040837









