Identification of Box Scale and Root Placement for Paddy–Wheat Root System Architecture Using the Box Counting Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of Experimental Location and Design
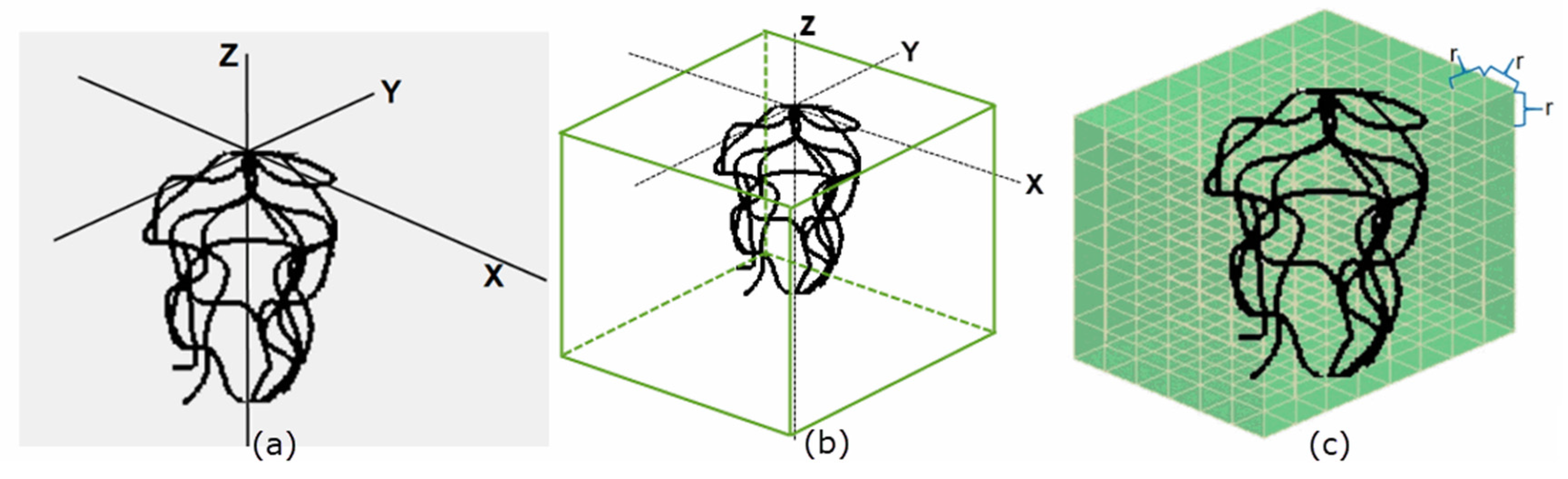
2.2. Visualization of the Paddy–Wheat Root System
2.3. Fractal Quantification of the Paddy–Wheat Root System
3. Results
3.1. Axile Root Growth Dynamics in Paddy–Wheat Seedings
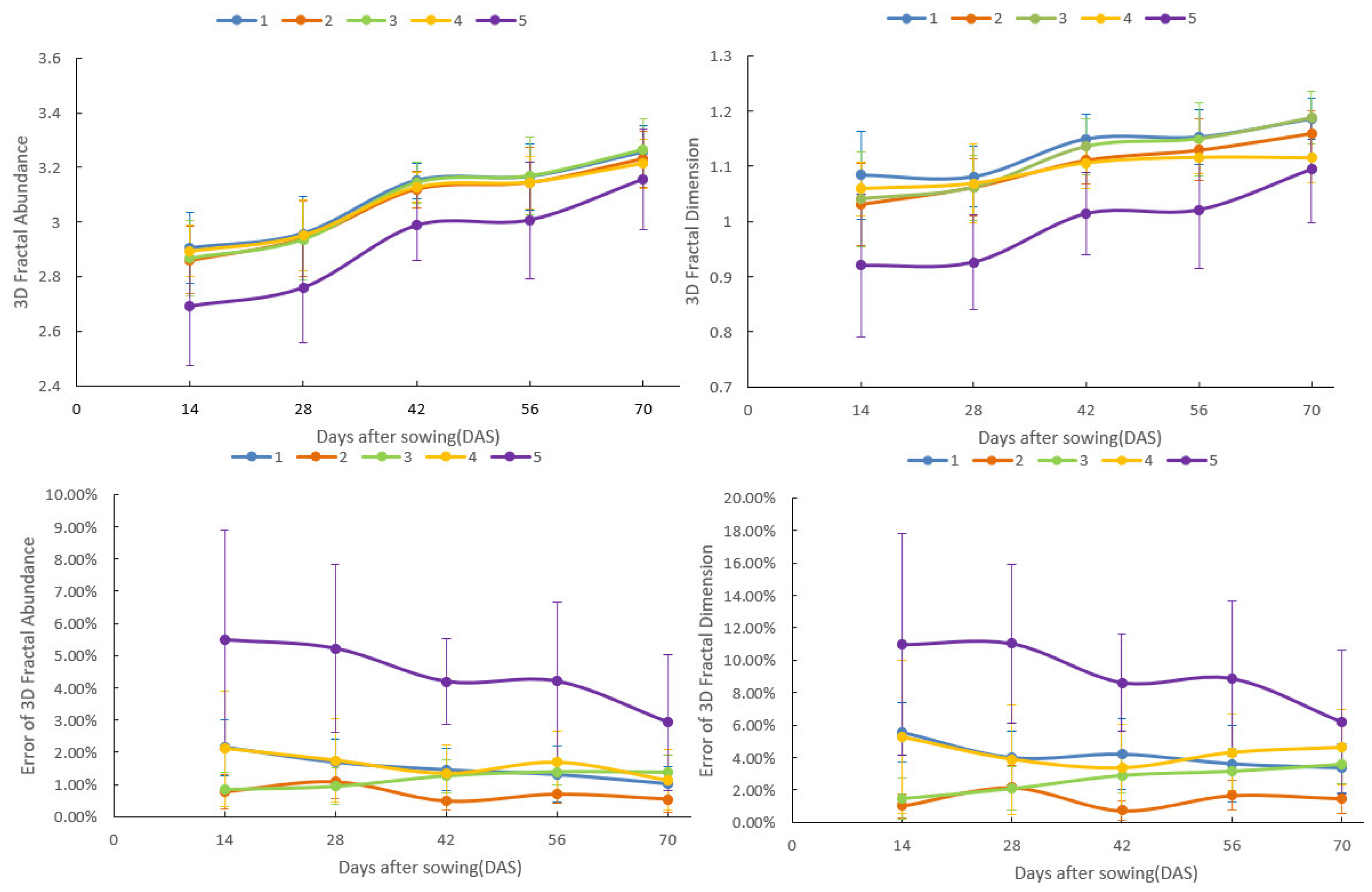
3.2. The 3D Fractal Dynamics of Paddy–Wheat RSAs at Different Box Dimension Scales during Seedling Stage
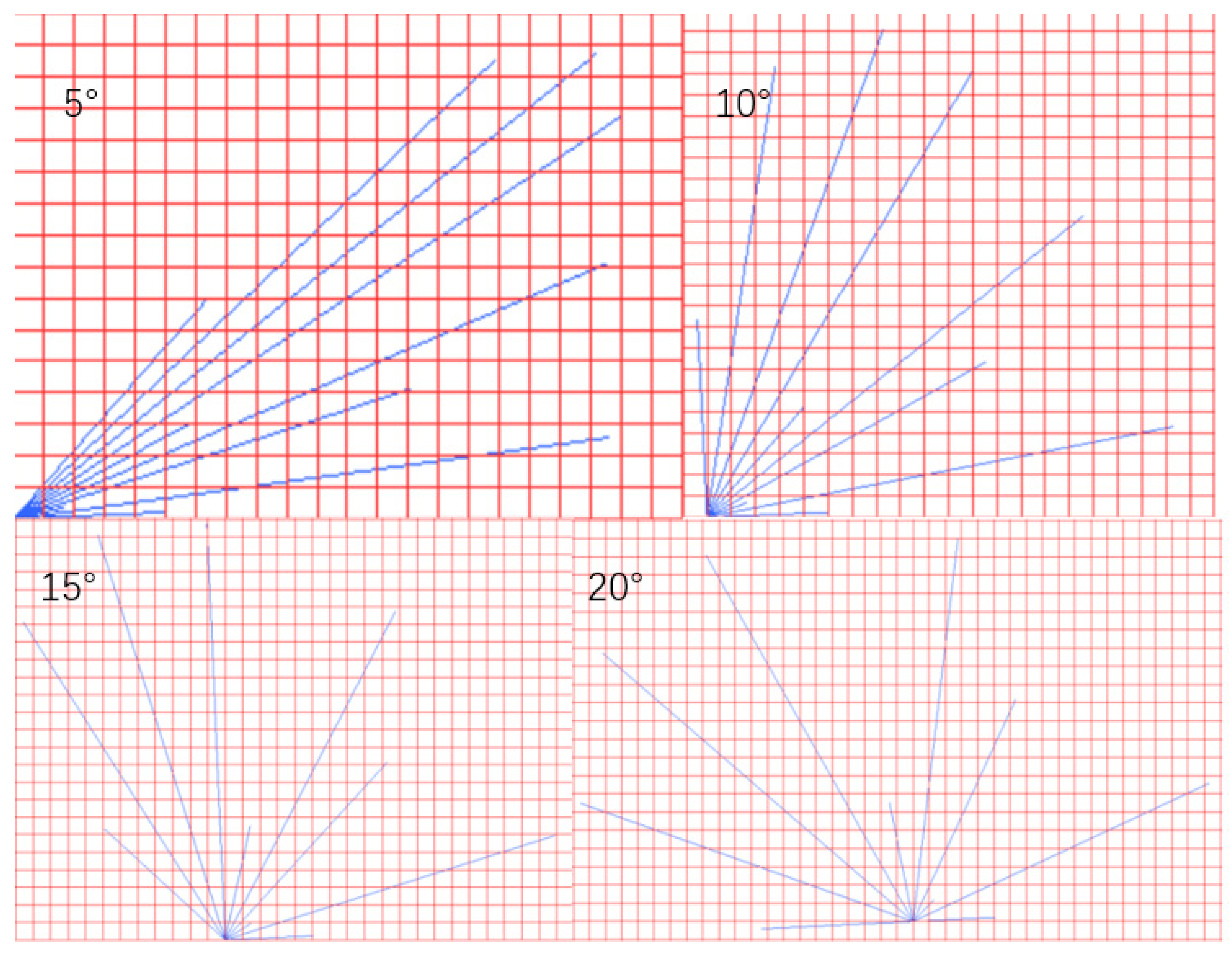
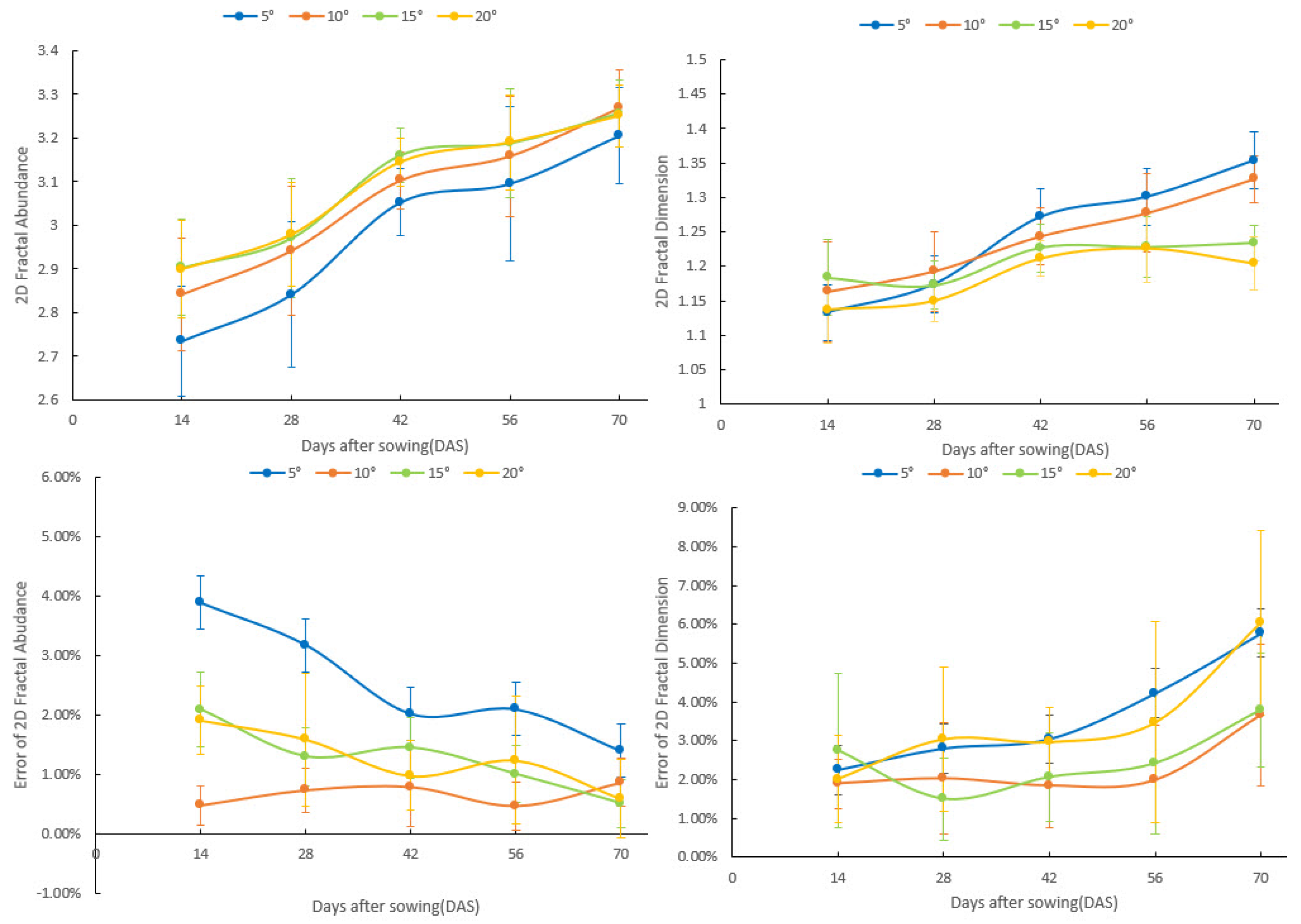
3.3. The Fractal Dynamics of Paddy–Wheat RSAs at Different Placement Angles during the Seedling Stage
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Postma, J.A.; Lynch, J.P. Complementarity in root architecture for nutrient uptake in ancient maize/bean and maize/bean/squash polycultures. Ann. Bot. 2012, 110, 521–534. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Inukai, Y.; Yamauchi, A. Root development and nutrient uptake. Crit. Rev. Plant Sci. 2006, 25, 279–301. [Google Scholar] [CrossRef]
- Ennos, A.R. The mechanics of root anchorage. Adv. Bot. Res. 2000, 33, 133–157. [Google Scholar]
- Stubbs, C.J.; Cook, D.D.; Niklas, K.J. A general review of the biomechanics of root anchorage. J. Exp. Bot. 2019, 70, 3439–3451. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Tilman, D. Soil and root carbon storage is key to climate benefits of bioenergy crops. Biofuel Res. J. 2020, 7, 1143–1148. [Google Scholar] [CrossRef]
- Barea, J.M.; Azcón, R.; Azcón-Aguilar, C. Mycorrhizosphere interactions to improve plant fitness and soil quality. Antonie Van Leeuwenhoek 2002, 81, 343–351. [Google Scholar] [CrossRef]
- Hao, H.X.; Qin, J.H.; Sun, Z.X.; Guo, Z.L.; Wang, J.G. Erosion-reducing effects of plant roots during concentrated flow under contrasting textured soils. Catena 2021, 203, 105378. [Google Scholar] [CrossRef]
- Wang, N.Q.; Kong, C.H.; Wang, P.; Meiners, S.J. Root exudate signals in plant–plant interactions. Plant Cell Environ. 2021, 44, 1044–1058. [Google Scholar] [CrossRef]
- Xiong, Q.; Hu, J.; Wei, H.; Zhang, H.; Zhu, J. Relationship between plant roots, rhizosphere microorganisms, and nitrogen and its special focus on rice. Agriculture 2021, 11, 234. [Google Scholar] [CrossRef]
- Galindo-Castañeda, T.; Lynch, J.P.; Six, J.; Hartmann, M. Improving soil resource uptake by plants through capitalizing on synergies between root architecture and anatomy and root-associated microorganisms. Front. Plant Sci. 2022, 13, 577. [Google Scholar] [CrossRef]
- Borden, K.A.; Anglaaere, L.C.; Owusu, S.; Martin, A.R.; Buchanan, S.W.; Addo-Danso, S.D.; Isaac, M.E. Soil texture moderates root functional traits in agroforestry systems across a climatic gradient. Agric. Ecosyst. Environ. 2020, 295, 106915. [Google Scholar] [CrossRef]
- Lynch, J.P. Harnessing root architecture to address global challenges. Plant J. 2022, 109, 415–431. [Google Scholar] [CrossRef] [PubMed]
- Rangarajan, H.; Lynch, J.P. A comparative analysis of quantitative metrics of root architecture. Plant Phenomics 2021, 2021, 6953197. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Tang, Y.; Duan, Q.; Hu, J. Phenotypic quantification of root spatial distribution along circumferential direction for field paddy-wheat. PLoS ONE 2023, 18, e0279353. [Google Scholar] [CrossRef]
- Chen, X.; Ding, Q.; Błaszkiewicz, Z.; Sun, J.; Sun, Q.; He, R.; Li, Y. Phenotyping for the dynamics of field wheat root system architecture. Sci. Rep. 2017, 7, 37649. [Google Scholar] [CrossRef]
- Lynch, J.P. Root phenes for enhanced soil exploration and phosphorus acquisition: Tools for future crops. Plant Physiol. 2019, 179, 1042–1049. [Google Scholar] [CrossRef]
- Pagliai, M.; Vignozzi, N. The soil structure and the plant roots: The rhizosphere. J. Plant Nutr. Soil Sci. 2002, 165, 382–396. [Google Scholar]
- Smith, S.; Smet, I. Root system architecture: insights from Arabidopsis and cereal crops. Philos. Trans. R. Soc. B 2012, 367, 1441–1452. [Google Scholar]
- Bardgett, R.D.; Mommer, L.; De Vries, F.T. Going underground: Root traits as drivers of ecosystem processes. Trends Ecol. Evol. 2014, 29, 692–699. [Google Scholar] [CrossRef]
- Mickelbart, M.V.; Hasegawa, P.M.; Bailey-Serres, J. Genetic mechanisms of abiotic stress tolerance that translate to crop yield stability. Nat. Rev. Genet. 2015, 16, 237–251. [Google Scholar] [CrossRef]
- Rellán-Álvarez, R.; Lobet, G.; Lindner, H.; Pradier, P.L.; Sebastian, J. GLO-Roots: An imaging platform enabling multidimensional characterization of soil-grown root systems. eLife 2015, 4, e07597. [Google Scholar] [CrossRef] [PubMed]
- Ghezzehei, T.A.; Or, D.; Irmak, A.; Moldrup, P.; Tuller, M. Soil structure and plant growth: Impact of bulk density and biopores. Plant Soil 2006, 280, 173–183. [Google Scholar]
- Wang, Y.; Zhang, H.; Bai, K.; Sun, Y. The Application of Fractal Geometry in the Study of Plant Roots. Chin. J. Nat. 1999, 3, 143–146. (In Chinese) [Google Scholar]
- Tatsumi, J.; Yamauchi, A.; Kono, Y. Fractal Analysis of Plant Root Systems. Ann. Bot. 1989, 64, 499–503. [Google Scholar] [CrossRef]
- Eghball, B.; Settimi, J.R.; Maranville, J.W.; Parkhurst, A.M. Fractal analysis for morphological description of corn roots under nitrogen stress. Agron. J. 1993, 85, 287–289. [Google Scholar] [CrossRef]
- Nielsen, K.L.; Lynch, J.P.; Weiss, H.N. Fractal geometry of bean root systems: Correlations between spatial and fractal dimension. Am. J. Bot. 1997, 84, 26–33. [Google Scholar] [CrossRef]
- Wang, H.; Siopongco, J.; Wade, L.J.; Yamauchi, A. Fractal analysis on root systems of rice plants in response to drought stress. Environ. Exp. Bot. 2009, 65, 338–344. [Google Scholar] [CrossRef]
- Dannowski, M.; Block, A. Fractal geometry and root system structures of heterogeneous plant communities. Plant Soil 2005, 272, 61–76. [Google Scholar] [CrossRef]
- Eamus, D.; Chen, X.; Kelley, G.; Hutley, L.B. Root biomass and root fractal analyses of an open Eucalyptus forest in a savanna of north Australia. Aust. J. Bot. 2002, 50, 31–41. [Google Scholar] [CrossRef]
- Chen, X.; Ding, Q.; Li, Y.; Xue, J.; He, R. Three Dimensional Fractal Characteristics of Wheat Root System for Rice-Wheat Rotation in Southern China. Sci. Agric. Sin. 2017, 50, 451–460. (In Chinese) [Google Scholar]
- Persson, H. Methods of Studying Root Dynamics in Relation to Nutrient Cycling. In Nutrient Cycling in Terrestrial Ecosystems: Field Methods, Application and Interpretation; Elsevier Applied Science: London, UK, 1990; pp. 198–217. [Google Scholar]
- Lobet, G.; Pages, L.; Draye, X. A novel image-analysis toolbox enabling quantitative analysis of root system architecture. Plant Physiol. 2011, 157, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.T.; MacCurdy, R.B.; Jung, J.K.; Shaff, J.E.; McCouch, S.R.; Aneshansley, D.J.; Kochian, L.V. Three-dimensional root phenotyping with a novel imaging and software platform. Plant Physiol. 2011, 156, 455–465. [Google Scholar] [CrossRef] [PubMed]
- Pound, M.P.; Atkinson, J.A.; Townsend, A.J.; Wilson, M.H.; Griffiths, M.; Jackson, A.S.; French, A.P. Deep machine learning provides state-of-the-art performance in image-based plant phenotyping. GigaScience 2017, 6, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Trachsel, S.; Kaeppler, S.M.; Brown, K.M.; Lynch, J.P. Shovelomics: High throughput phenotyping of maize (Zea mays L.) root architecture in the field. Plant Soil 2011, 341, 75–87. [Google Scholar] [CrossRef]
- Postma, J.A.; Lynch, J.P. Theoretical evidence for the functional benefit of root cortical aerenchyma in soils with low phosphorus availability. Ann. Bot. 2011, 107, 829–841. [Google Scholar] [CrossRef] [PubMed]
- Bouda, M.; Caplan, J.S.; Saiers, J.E. Box-counting dimension revisited: Presenting an efficient method of minimizing quantization error and an assessment of the self-similarity of structural root systems. Front. Plant Sci. 2016, 7, 149. [Google Scholar] [CrossRef]
- Araki, H.; Morita, S.; Tatsumi, J.; Iijima, M. Physiol-morphological analysis on axile root growth in upland rice. Plant Prod. Sci. 2002, 5, 286–293. [Google Scholar] [CrossRef]
- Fiscus, E.L. Analysis of the components of area growth of bean root systems. Crop Sci. 1981, 21, 909–913. [Google Scholar] [CrossRef]
- Chen, X.; He, R.; Ding, Q.; Sun, Q. A Digitization and visualization procedure for 3D wheat root system architecture in rice–wheat rotation. J. Inst. Eng. Ser. A 2019, 100, 1–8. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Z. MATLAB (R2018a); Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Hendriks, M.; Ravenek, J.; Smit-Tiekstra, A.E.; van der Paauw, J.W.; de Caluwe, H.; van der Putten, W.H.; Mommer, L. Spatial heterogeneity of plant–soil feedback affects root interactions and interspecific competition. New Phytol. 2015, 207, 830–840. [Google Scholar] [CrossRef]
- Tian, H.; De Smet, I.; Ding, Z. Shaping a root system: Regulating lateral versus primary root growth. Trends Plant Sci. 2014, 19, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Linkohr, B.I.; Williamson, L.C.; Fitter, A.H.; Leyser, H.O. Nitrate and phosphate availability and distribution have different effects on root system architecture of Arabidopsis. Plant J. 2002, 29, 751–760. [Google Scholar] [CrossRef] [PubMed]
- Lynch, J.P. Root architecture and plant productivity. Plant Physiol. 1995, 109, 7–13. [Google Scholar] [CrossRef]
- Fitter, A.H.; Stickland, T.R. Architectural analysis of plant root systems 1. Architectural correlates of exploitation efficiency. New Phytol. 1991, 118, 375–382. [Google Scholar] [CrossRef]
- Pregitzer, K.S.; King, J.S. Effects of Soil Temperature on Nutrient Uptake. In Nutrient Acquisition by Plants; Springer: Berlin/Heidelberg, Germany, 2005; pp. 155–173. [Google Scholar]
- Stokes, A.; Douglas, G.B. Effect of tree species and root reinforcing method on soil slope stability in New Zealand. Plant Soil 2010, 327, 397–409. [Google Scholar]
- Grover, M.; Bodhankar, S.; Sharma, A.; Sharma, P.; Singh, J.; Nain, L. PGPR mediated alterations in root traits: Way toward sustainable crop production. Front. Sustain. Food Syst. 2021, 4, 618230. [Google Scholar] [CrossRef]
- Brown, G.; Welsch, D. Box-Counting fractal dimension estimates of triazine-resistant and -susceptible biotypes of Solanum ptychanthum (Eastern Black Nightshade). Am. J. Bot. 2002, 89, 924–931. [Google Scholar]
- Yang, Q.; Cheng, W.; Hao, Z.; Zhang, Q.; Yang, D.; Teng, D.; Lei, S. Study on the fractal characteristics of the plant root system and its relationship with soil strength in tailing ponds. Wirel. Commun. Mob. Comput. 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, C.Z.; Wen, J.; Kang, M.; Li, X. Fractal analysis of root architecture responses of Saussurea salsa to a gradient of flooding intensity and salinity. Plant Soil 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Dupuy, L.X.; Bengough, A.G. Image analysis of root systems: Quantifying architectural traits at the whole root system level. Plant Soil 2012, 372, 165–184. [Google Scholar]
- Walk, T.C.; Van Erp, E.; Lynch, J.P. Modelling applicability of fractal analysis to efficiency of soil exploration by roots. Ann. Bot. 2004, 94, 119–128. [Google Scholar] [CrossRef] [PubMed]

| Fractal Traits | Fractal Abundance | Fractal Dimension | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sampling Time | Scale | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| 14 | 1 | 1 | 1 | ||||||||
| 2 | 0.991 | 1 | 0.969 | 1 | |||||||
| 3 | 0.983 | 0.996 | 1 | 0.959 | 0.996 | 1 | |||||
| 4 | 0.951 | 0.972 | 0.967 | 1 | 0.652 | 0.726 | 0.711 | 1 | |||
| 5 | 0.945 * | 0.95 * | 0.955 * | 0.897 * | 1 | 0.884 ** | 0.871 * | 0.882 * | 0.446 ** | 1 | |
| 28 | 1 | 1 | 1 | ||||||||
| 2 | 0.991 | 1 | 0.906 | 1 | |||||||
| 3 | 0.989 | 0.991 | 1 | 0.934 | 0.944 | 1 | |||||
| 4 | 0.957 | 0.95 | 0.96 | 1 | 0.789 | 0.689 | 0.738 | 1 | |||
| 5 | 0.955 | 0.968 * | 0.948 * | 0.859 * | 1 | 0.735 ** | 0.859 ** | 0.785 ** | 0.311 ** | 1 | |
| 42 | 1 | 1 | 1 | ||||||||
| 2 | 0.954 | 1 | 0.811 * | 1 | |||||||
| 3 | 0.921 | 0.975 | 1 | 0.778 | 0.989 | 1 | |||||
| 4 | 0.705 | 0.823 | 0.825 | 1 | 0.127 * | 0.443 | 0.453 | 1 | |||
| 5 | 0.9 ** | 0.888 ** | 0.862 ** | 0.516 ** | 1 | 0.758 ** | 0.817 ** | 0.799 ** | −0.038 ** | 1 | |
| 56 | 1 | 1 | 1 | ||||||||
| 2 | 0.983 | 1 | 0.795 | 1 | |||||||
| 3 | 0.977 | 0.993 | 1 | 0.792 | 0.979 | 1 | |||||
| 4 | 0.95 | 0.943 | 0.942 | 1 | 0.375 * | 0.11 | 0.162 | 1 | |||
| 5 | 0.927 * | 0.955 | 0.961 * | 0.847 | 1 | 0.742 ** | 0.921 ** | 0.948 ** | 0.018 ** | 1 | |
| 70 | 1 | 1 | 1 | ||||||||
| 2 | 0.986 | 1 | 0.812 | 1 | |||||||
| 3 | 0.984 | 0.993 | 1 | 0.816 | 0.987 | 1 | |||||
| 4 | 0.897 | 0.931 | 0.935 | 1 | 0.072 ** | 0.366 * | 0.407 ** | 1 | |||
| 5 | 0.905 | 0.858 | 0.846 | 0.737 | 1 | 0.785 ** | 0.638 | 0.588 ** | −0.059 | 1 | |
| Scale | Sampling Time | Regression Function | R2 | Regression Function | R2 | Regression Function | R2 |
|---|---|---|---|---|---|---|---|
| 2.5~80 | 14 | L = 654.35X2 − 1371.61 | 0.85 | X2 = 1.37X1 + 1.42 | 0.71 | L = 703.64X1 − 234.37 | 0.37 |
| 28 | L = 1010.35X2 − 2355.94 | 0.91 | X2 = 1.74X1 + 1.08 | 0.5 | L = 1462.56X1 − 949.68 | 0.32 | |
| 42 | L = 1420.79X2 − 3592.24 | 0.72 | X2 = 1.11X1 + 1.87 | 0.58 | L = 1018.59X1 − 286.46 | 0.17 | |
| 56 | L = 1986.39X2 − 5032.77 | 0.83 | X2 = 1.95X1 + 0.91 | 0.63 | L = 2986.83X1 − 2472.94 | 0.34 | |
| 70 | L = 1868.64X2 − 4940.65 | 0.82 | X2 = 2.07X1 + 0.8 | 0.64 | L = 3128X1 − 2567.83 | 0.34 | |
| 2~100 | 14 | L = 696.74X2 − 1463.96 | 0.88 | X2 = 1.33X1 + 1.48 | 0.65 | L = 735.2X1 − 229.48 | 0.36 |
| 28 | L = 1001.8X2 − 2313.35 | 0.93 | X2 = 2.18X1 + 0.62 | 0.68 | L = 2043.63X1 − 1538.68 | 0.55 | |
| 42 | L = 1458.58X2 − 3664.9 | 0.85 | X2 = 1.4X1 + 1.57 | 0.76 | L = 1824.11X1 − 1142.56 | 0.52 | |
| 56 | L = 1813.11X2 − 4728.63 | 0.85 | X2 = 2.09X1 + 0.79 | 0.83 | L = 3383.06X1 − 2850.99 | 0.56 | |
| 70 | L = 1825.1X2 − 4753.67 | 0.88 | X2 = 2.01X1 + 0.85 | 0.53 | L = 3839.45X1 − 3312.05 | 0.61 | |
| 3~96 | 14 | L = 616.87X2 − 1240.37 | 0.84 | X2 = 1.36X1 + 1.45 | 0.71 | L = 667.57X1 − 166.41 | 0.38 |
| 28 | L = 941.88X2 − 2133.62 | 0.93 | X2 = 2.01X1 + 0.8 | 0.66 | L = 1735.37X1 − 1210.92 | 0.51 | |
| 42 | L = 1239.29X2 − 3013.08 | 0.76 | X2 = 1.37X1 + 1.59 | 0.84 | L = 1432.76X1 − 742.68 | 0.45 | |
| 56 | L = 1663.29X2 − 4301.39 | 0.87 | X2 = 1.98X1 + 0.89 | 0.85 | L = 2952.93X1 − 2423.72 | 0.6 | |
| 70 | L = 1685.73X2 − 4363.49 | 0.86 | X2 = 2.02X1 + 0.87 | 0.76 | L = 3065.62X1 − 2498.86 | 0.53 | |
| 4~16 | 14 | L = 894.93X2 − 2060.9 | 0.83 | X2 = 0.9X1 + 1.94 | 0.21 | L = 207.82X1 + 308.22 | 0.01 |
| 28 | L = 1005.26X2 − 2334.72 | 0.82 | X2 = 1.03X1 + 1.85 | 0.32 | L = 454.25X1 + 145.99 | 0.05 | |
| 42 | L = 1692.95X2 − 4408.71 | 0.76 | X2 = 0.85X1 + 2.18 | 0.51 | L = 746.94X1 + 58.32 | 0.1 | |
| 56 | L = 2493.05X2 − 6870.5 | 0.9 | X2 = 1.59X1 + 1.37 | 0.23 | L = 3174.81X1 − 2572.91 | 0.13 | |
| 70 | L = 2072.75X2 − 5519.67 | 0.86 | X2 = 1.11X1 + 1.97 | 0.3 | L = 1509.84X1 − 541.19 | 0.1 | |
| 10~160 | 14 | L = 366.28X2 − 457.79 | 0.75 | X2 = 1.61X1 + 1.21 | 0.9 | L = 518.31X1 + 51.27 | 0.53 |
| 28 | L = 651.81X2 − 1167.24 | 0.86 | X2 = 2.23X1 + 0.7 | 0.89 | L = 1383.77X1 − 650.53 | 0.7 | |
| 42 | L = 587.12X2 − 868.92 | 0.48 | X2 = 1.62X1 + 1.34 | 0.91 | L = 821.18X1 + 51.71 | 0.32 | |
| 56 | L = 1000.53X2 − 2037.08 | 0.7 | X2 = 1.93X1 + 1.03 | 0.93 | L = 1964.48X1 − 759.36 | 0.51 | |
| 70 | L = 749X2 − 1220.5 | 0.47 | X2 = 1.82X1 + 1.16 | 0.93 | L = 1055.23X1 − 12.82 | 0.26 |
| Planar Fractal Abundance (Planar FA) | Planar Fractal Dimension (Planar FD) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5° | 10° | 15° | 20° | 5° | 10° | 15° | 20° | ||
| 14 | 5° | 1 | 1 | ||||||
| 10° | 0.983 | 1 | 0.954 | 1 | |||||
| 15° | 0.969 ** | 0.98 | 1 | 0.816 | 0.818 | 1 | |||
| 20° | 0.967 ** | 0.986 | 0.991 | 1 | 0.861 | 0.881 | 0.909 * | 1 | |
| 28 | 5° | 1 | 1 | ||||||
| 10° | 0.976 | 1 | 0.89 | 1 | |||||
| 15° | 0.981 | 0.981 | 1 | 0.78 | 0.852 | 1 | |||
| 20° | 0.964 * | 0.956 | 0.984 | 1 | 0.478 | 0.412 * | 0.457 | 1 | |
| 42 | 5° | 1 | 1 | ||||||
| 10° | 0.764 | 1 | 0.645 | 1 | |||||
| 15° | 0.917 ** | 0.827 * | 1 | 0.508 * | 0.365 | 1 | |||
| 20° | 0.922 ** | 0.803 | 0.907 | 1 | 0.447 ** | 0.144 * | −0.045 | 1 | |
| 56 | 5° | 1 | 1 | ||||||
| 10° | 0.971 | 1 | 0.773 | 1 | |||||
| 15° | 0.984 | 0.98 | 1 | 0.689 * | 0.703 * | 1 | |||
| 20° | 0.95 | 0.967 | 0.969 | 1 | 0.154 * | 0.444 * | 0.513 | 1 | |
| 70 | 5° | 1 | 1 | ||||||
| 10° | 0.959 | 1 | 0.497 | 1 | |||||
| 15° | 0.979 | 0.937 | 1 | 0.132 ** | 0.253 ** | 1 | |||
| 20° | 0.929 | 0.891 | 0.913 | 1 | −0.123 ** | −0.008 ** | 0.011 | 1 | |
| Angle | Sampling Time | Regression Function | R² | Regression Function | R² | Regression Function | R² |
|---|---|---|---|---|---|---|---|
| 5° | 14 | L = 709.84X2 − 1413.09 | 0.93 | X2 = 1.54X1 + 0.99 | 0.84 | L = 1028.21X1 − 636.47 | 0.69 |
| 28 | L = 839X2 − 1752.35 | 0.94 | X2 = 1.73X1 + 0.82 | 0.68 | L = 1361.57X1 − 996.75 | 0.56 | |
| 42 | L = 1369.97X2 − 3297.28 | 0.95 | X2 = 0.95X1 + 1.85 | 0.34 | L = 1046.26X1 − 445.77 | 0.21 | |
| 56 | L = 1408.22X2 − 3387.74 | 0.96 | X2 = 1.78X1 + 0.78 | 0.73 | L = 2452.41X1 − 2219.03 | 0.67 | |
| 70 | L = 1783.74X2 − 4574.13 | 0.95 | X2 = 2.04X1 + 0.45 | 0.72 | L = 3284.58X1 − 3303.27 | 0.56 | |
| 10° | 14 | L = 690.6X2 − 1434.65 | 0.93 | X2 = 1.61X1 + 0.97 | 0.83 | L = 994.65X1 − 628.59 | 0.62 |
| 28 | L = 929.09X2 − 2101.8 | 0.91 | X2 = 1.8X1 + 0.79 | 0.51 | L = 1383.04X1 − 1018.05 | 0.32 | |
| 42 | L = 1322.32X2 − 3218.15 | 0.62 | X2 = 0.91X1 + 1.97 | 0.35 | L = 63.5X1 + 805.8 | 0 | |
| 56 | L = 1780.47X2 − 4651.27 | 0.92 | X2 = 1.49X1 + 1.26 | 0.38 | L = 1894.91X1 − 1448.97 | 0.18 | |
| 70 | L = 2135.3X2 − 5835.29 | 0.87 | X2 = 0.96X1 + 1.99 | 0.14 | L = 304.23X1 + 739.23 | 0 | |
| 15° | 14 | L = 774.13X2 − 1719.64 | 0.87 | X2 = 1.47X1 + 1.16 | 0.53 | L = 746.85X1 − 355.55 | 0.2 |
| 28 | L = 1044.5X2 − 2471.23 | 0.97 | X2 = 2.3X1 + 0.28 | 0.34 | L = 2287.51X1 − 2051.09 | 0.3 | |
| 42 | L = 1641.4X2 − 4302.38 | 0.89 | X2 = 1.02X1 + 1.91 | 0.32 | L = 923.35X1 − 247.88 | 0.09 | |
| 56 | L = 1967.36X2 − 5300.07 | 0.94 | X2 = 1.21X1 + 1.7 | 0.18 | L = 1445.05X1 − 802.23 | 0.06 | |
| 70 | L = 2556.62X2 − 7180.9 | 0.93 | X2 = −0.06X1 + 3.33 | 0 | L = 1992.31X1 − 3600.25 | 0.07 | |
| 20° | 14 | L = 784.01X2 − 1744.37 | 0.9 | X2 = 1.88X1 + 0.76 | 0.65 | L = 1148.11X1 − 776.74 | 0.35 |
| 28 | L = 1178.29X2 − 2877.63 | 0.95 | X2 = 0.82X1 + 2.04 | 0.04 | L = 707.76X1 − 182.18 | 0.02 | |
| 42 | L = 1581.86X2 − 4940.05 | 0.91 | X2 = 0.55X1 + 2.48 | 0.06 | L = 153.55X1 + 698.69 | 0 | |
| 56 | L = 2255.52X2 − 6224.38 | 0.92 | X2 = 0.05X1 + 3.13 | 0 | L = −1146.58X1 + 2733.69 | 0.05 | |
| 70 | L = 2666.38X2 − 7525.43 | 0.9 | X2 = −0.2X1 + 3.49 | 0.01 | L = −2110.5X1 + 3684.59 | 0.16 |
| Angle | Sampling Time | Regression Function | R² | Regression Function | |
|---|---|---|---|---|---|
| 5° | 14 | Y2 = 0.93Y1 + 0.35 | 0.81 ** | X2 = 0.68X1 + 0.32 | 0.4 |
| 28 | Y2 = 0.78Y1 + 0.74 | 0.92 | X2 = 0.42X1 + 0.58 | 0.37 ** | |
| 42 | Y2 = 0.73Y1 + 0.91 | 0.76 ** | X2 = 0.68X1 + 0.28 | 0.53 ** | |
| 56 | Y2 = 0.66Y1 + 1.13 | 0.91 | X2 = 0.44X1 + 0.58 | 0.57 ** | |
| 70 | Y2 = 0.77Y1 + 0.78 | 0.77 | X2 = 0.52X1 + 0.48 | 0.41 ** | |
| 10° | 14 | Y2 = 0.94Y1 + 0.24 | 0.86 | X2 = 0.72X1 + 0.24 | 0.43 * |
| 28 | Y2 = 0.86Y1 + 0.42 | 0.88 | X2 = 0.34X1 + 0.67 | 0.13 ** | |
| 42 | Y2 = 0.88Y1 + 0.43 | 0.77 | X2 = 0.74X1 + 0.24 | 0.48 ** | |
| 56 | Y2 = 0.82Y1 + 0.58 | 0.85 | X2 = 0.58X1 + 0.41 | 0.45 ** | |
| 70 | Y2 = 0.92Y1 + 0.26 | 0.69 | X2 = 0.32X1 + 0.77 | 0.08 ** | |
| 15° | 14 | Y2 = 1.03Y1 − 0.09 | 0.77 | X2 = 0.53X1 + 0.46 | 0.13 ** |
| 28 | Y2 = 0.97Y1 + 0.09 | 0.93 | X2 = 0.62X1 + 0.35 | 0.15 ** | |
| 42 | Y2 = 0.87Y1 + 0.39 | 0.71 | X2 = 0.65X1 + 0.35 | 0.26 ** | |
| 56 | Y2 = 0.92Y1 + 0.23 | 0.89 | X2 = 0.66X1 + 0.34 | 0.35 ** | |
| 70 | Y2 = 1.14Y1 − 0.46 | 0.79 | X2 = 0.01X1 + 1.17 | 0 * | |
| 20° | 14 | Y2 = 1.08Y1 − 0.22 | 0.86 | X2 = 1.03X1 − 0.08 | 0.37 |
| 28 | Y2 = 1.11Y1 − 0.36 | 0.96 | X2 = 1.06X1 − 0.13 | 0.32 ** | |
| 42 | Y2 = 1.04Y1 − 0.12 | 0.8 | X2 = 0.41X1 + 0.66 | 0.05 ** | |
| 56 | Y2 = 0.98Y1 + 0.05 | 0.75 | X2 = -0.04X1 + 1.2 | 0 ** | |
| 70 | Y2 = 1.21Y1 − 0.67 | 0.79 | X2 = 0.08X1 + 1.09 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Chen, X.; Hu, J.; Ding, Q.; He, R. Identification of Box Scale and Root Placement for Paddy–Wheat Root System Architecture Using the Box Counting Method. Agriculture 2023, 13, 2184. https://doi.org/10.3390/agriculture13122184
Liu S, Chen X, Hu J, Ding Q, He R. Identification of Box Scale and Root Placement for Paddy–Wheat Root System Architecture Using the Box Counting Method. Agriculture. 2023; 13(12):2184. https://doi.org/10.3390/agriculture13122184
Chicago/Turabian StyleLiu, Shulin, Xinxin Chen, Jianping Hu, Qishuo Ding, and Ruiyin He. 2023. "Identification of Box Scale and Root Placement for Paddy–Wheat Root System Architecture Using the Box Counting Method" Agriculture 13, no. 12: 2184. https://doi.org/10.3390/agriculture13122184
APA StyleLiu, S., Chen, X., Hu, J., Ding, Q., & He, R. (2023). Identification of Box Scale and Root Placement for Paddy–Wheat Root System Architecture Using the Box Counting Method. Agriculture, 13(12), 2184. https://doi.org/10.3390/agriculture13122184







