Next Article in Journal
Cutting Mechanical Properties of Pumpkin Grafted Seedling Investigated by Finite Element Simulation and Experiment
Previous Article in Journal
Enhancing Smallholder Wheat Yield Prediction through Sensor Fusion and Phenology with Machine Learning and Deep Learning Methods
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agriculture
Volume 12
Issue 9
10.3390/agriculture12091353
agriculture-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparing Different Methods for Wheat LAI Inversion Based on Hyperspectral Data

by
Junwei Ma
1,2,
Lijuan Wang
2 and
Pengfei Chen
1,3,*
1
State Key Laboratory of Resource and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
2
School of Geography, Geomatics and Planning, Jiangsu Normal University, Xuzhou 221116, China
3
Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
*
Author to whom correspondence should be addressed.
Agriculture 2022, 12(9), 1353; https://doi.org/10.3390/agriculture12091353
Submission received: 21 July 2022 / Revised: 28 August 2022 / Accepted: 29 August 2022 / Published: 1 September 2022
(This article belongs to the Section Digital Agriculture)
Browse Figures
Versions Notes

Abstract

:
Gaussian process regression (GPR) can effectively solve the problem of high-dimensional modeling with a small sample size. However, there is a lack of studies comparing GPR with other methods for leaf area index (LAI) inversion using hyperspectral data. In this study, winter wheat was used as the research material to evaluate performance of different methods for LAI inversion, i.e., GPR, an artificial neural network (ANN), partial least squares regression (PLSR) and the spectral index (SI). To this end, a 2-year water and nitrogen coupled experiment was conducted, and canopy hyperspectral and LAI data were measured at the critical growth stages of wheat. Based on these data, calibration and validation datasets were obtained, and the LAI prediction model was constructed using the above four methods and validated. The results showed that the LAI inversion models of the SI were the least effective compared with other methods, with R2 and RMSE ranging from 0.42–0.76 and 0.80–1.04 during calibration and R2 and RMSE ranging from 0.37–0.55 and 0.94–1.09 during validation. The ANN and GPR had the best results, with R2 of 0.89 and 0.85 and RMSE of 0.46 and 0.53 during calibration and R2 of 0.74 and 0.71 and RMSE of both 0.74 during validation. The PLSR had intermediate LAI inversion results, with R2 and RMSE values of 0.80 and 0.61 during calibration and R2 and RMSE values of 0.67 and 0.80 during validation. Thus, the ANN and GPR methods were recommended for LAI inversion of winter wheat.

1. Introduction

Wheat is the raw material for bread, cakes, and pasta and is an important food crop that provides 30% of the energy consumed by humans worldwide [1]. The leaf area index (LAI) is defined as the sum of the leaf area on one side of a plant per unit of land area [2]. It is a good indicator of plant population size, is closely related to plant growth status [3] and is widely used in crop growth assessment. Therefore, rapid and nondestructive detection of wheat LAI is important for its growth monitoring and yield prediction.
The traditional method of LAI measurement uses destructive sampling, which is time-consuming and labor-intensive [4]. Numerous studies have shown that remote sensing technology can achieve rapid and nondestructive detection of crop physiological and biochemical parameters [5,6,7,8]. In terms of LAI estimation using remote sensing technology, there are mainly two types of methods: empirical and physical modeling methods. The empirical methods are directly based on statistics to establish a quantitative relationship between measured spectral information and LAI. The established model was used to predict LAI in the target area [9], which is easy to implement but also suffers from the problem that the model is location specific [10]. The physical model has a clear mechanistic explanation and can simulate crop canopy spectra using a set of input variables, such as leaf physiological and biochemical parameters, leaf and canopy structure parameters, the solar zenith angle, solar azimuth angle, and observed zenith angle [11]. As one of the input parameters, LAI can be estimated by inverting the physical model. The advantage of the method is that it has universal applicability. However, it has the problems of requiring many input parameters that are not easy to obtain in practice. When the input parameters are uncertain, it is easy to encounter problems during model inversion [12]. In general, empirical modeling methods are still the current mainstream methods in practical applications for LAI prediction.
The empirical modeling method includes both traditional statistical analysis methods [e.g., spectral index (SI), partial least squares regression (PLSR), principal component regression (PCR)] and machine learning methods [e.g., artificial neural network (ANN), support vector machine (SVM)]. Based on UAV-acquired hyperspectral data, Tian et al. [13] constructed an LAI prediction model using the spectral indices and obtained a coefficient of determination (R2) of 0.85 and a root mean square error (RMSE) value of 0.02 during validation. Yang et al. [14] used the stepwise multiple regression method and SVM method to design rice LAI prediction models using original, first-order derivative, and second-order derivative spectra and found that the LAI prediction model designed using the SVM and original spectra had the best result. Using hyperspectral data, Kiala et al. [15] used the SVM and PLSR methods to construct LAI prediction models for tropical grassland in early and late summer, and the results showed that the PLSR model had better LAI prediction ability. To predict LAI in a single soybean growth stage, Yuan et al. [16] compared the ANN, SVM, PLSR, and random forest (RF) methods, and the results showed that the ANN method had the highest accuracy. In addition to the above methods, the kernel function-based machine learning method has developed rapidly in recent years, as it can perform nonlinear modeling but still relies on linear algebraic operations and can effectively solve the problem of modeling high-dimensional spaces with small data sizes [17]. In addition, for field prediction by remote sensing, people are interested not only in the accuracy of the model but also in the uncertainty generated by the prediction. The Gaussian process regression (GPR) model is based on a kernel function using Bayesian theory to construct prediction models, which has the advantages of a simple structure, few parameters and fast training [18,19]. It can better deal with nonlinear problems and can give the uncertainty of prediction, which is considered to have greater potential for application in remote sensing [20]. However, few studies have been conducted on its application in wheat LAI prediction. Therefore, it is necessary to conduct a comprehensive comparative analysis between the GPR method and other methods for wheat LAI prediction to identify the optimal method for users.
In this study, a field experiment was conducted to obtain LAI and canopy hyperspectral data of winter wheat under different growth conditions. Based on these data, LAI prediction models were designed by the SI, PLSR, ANN and GPR methods and compared, to recommend the best method for high-precision LAI prediction.

2. Materials and Methods

2.1. Field Experiment

The study was conducted at the Yucheng Integrated Experiment Station (116°34′13″ E, 36°50′00″ N) of the Chinese Academy of Sciences in 2018–2019 and 2020–2021. The winter wheat cultivar “Jimai 22” was sown with 20 cm row spacing. The experiment had two irrigation treatments and five nitrogen (N) treatments in 32 plots. Each plot had an area of 10 m × 5 m. The two irrigation levels were 60 and 80% field water capacity and arranged with split plot design. The five N levels were 0 kg N/ha−1 (N1), 70 kg N/ha−1 (N2), 140 kg N/ha−1 (N3), 210 kg N/ha−1 (N4), and 280 kg N/ha−1 (N5) and arranged with randomized block design; N1–N4 had three replications and N5 had four replications. Except for N fertilizer, the other management measures were the same in each plot, and the experimental design is shown in Figure 1.

2.2. Data Acquisition

Field data were collected at the critical growth stages of wheat. Canopy hyperspectral data and LAI were measured. The measurements were made at the Feekes 7 and Feekes 10.51 growth stages in 2019 and at the Feekes 4–5, Feekes 10.2, and Feekes 10.54 growth stages in 2021 [21]. For the field data in each growth stage, a representative area was first selected as the sampling site in each plot, and then the wheat canopy hyperspectral data, LAI and chlorophyll were measured successively. The detailed procedure is described below.

2.2.1. Wheat Canopy Hyperspectral Data

FieldSpec HandHeld (Analytical Spectral Devices Inc., Boulder, CO, USA) was used to measure wheat canopy hyperspectral data. The spectrometer had a wavelength range of 325 nm to 1075 nm, with a sampling interval of 1.6 nm and a resolution of 3.5 nm. To minimize illumination variations, data measurements were conducted during a cloud-free period from 10:00 to 14:00. Measurements were made at each sampling site with the sensor probe placed 1.8 m above the wheat canopy to obtain a field view of exactly four wheat rows. Firstly, the spectrum of a reference white panel was measured, which was used to convert data from digital number (DN) values to reflection values subsequently. Then, at each sampling site, ten scans were made and the averaged value was used.

2.2.2. LAI and Chlorophyll Data

An LAI 2200 Plant Canopy Analyzer (LI-COR Inc., Lincoln, NE, USA) was used for the LAI measurements. During this process, the distance between two adjacent rows was divided into four equal parts, and the LAI was measured at each position and averaged [22]. In addition, chlorophyll was measured by a handheld chlorophyll meter (SPAD-502, Minola Ltd., Osaka, Japan). During this process, five representative plants were firstly selected. Then, the SPAD values of their first fully expanded leaf were measured and averaged to represent SPAD value in each sampling point.

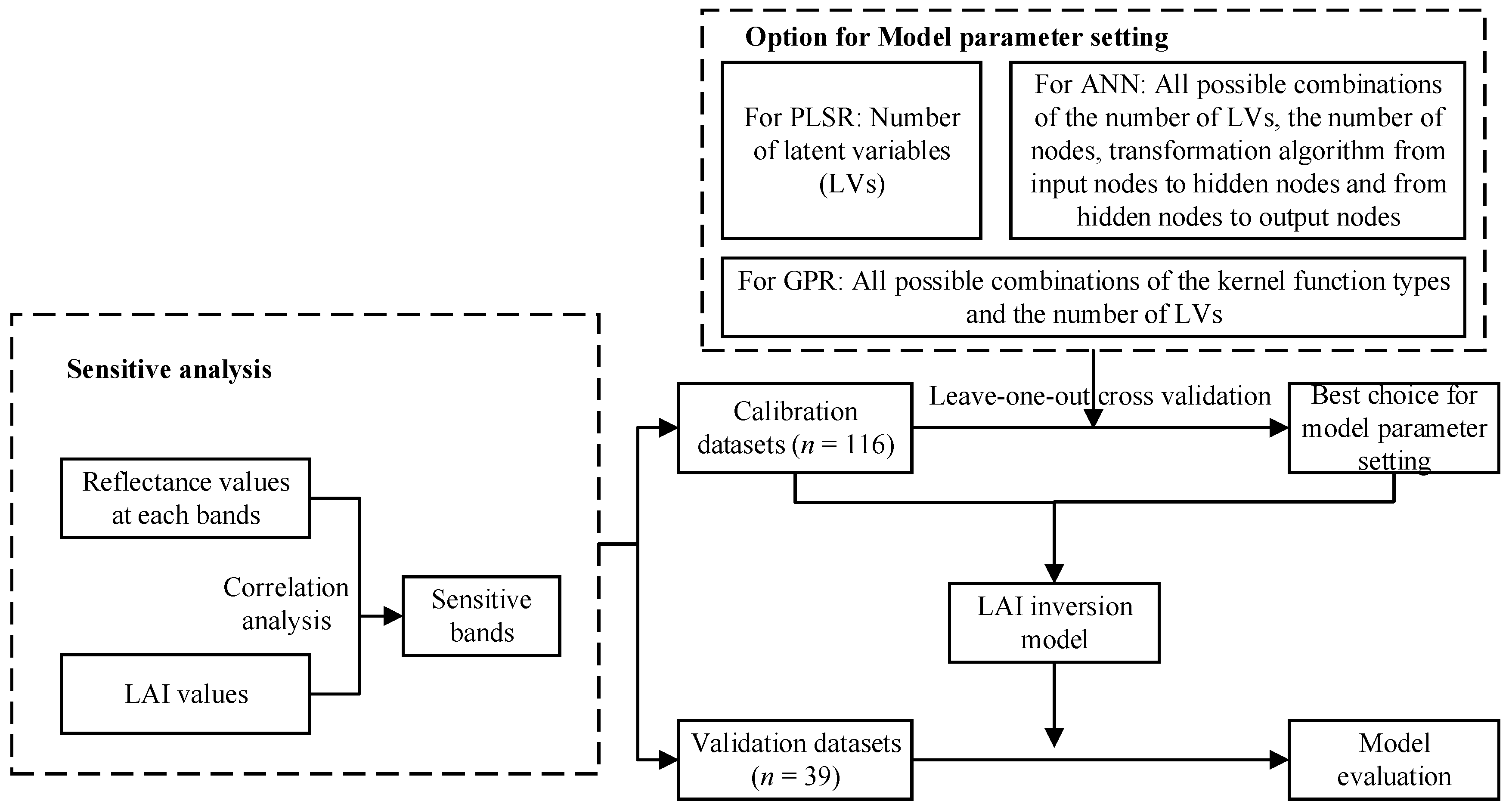
2.3. Data Analysis Method

In this study, the SI, PLSR, ANN, and GPR methods were used to design LAI prediction models. The performance of the four methods were compared. Notably, a total of 159 sampling points were acquired in the two years of this study due to the omission of measured spectral data in a plot during Feekes 4–5 in 2021. During data checking at later stages, four sampling points were found to have errors that were discarded. Thus, a total of 155 sampling points were finally retained. To divide the calibration and validation datasets and eliminate errors caused by uneven samples between years, the sampling points of each year were arranged from smallest to largest LAI; then, one-third of the points were selected at equal intervals and used as validation data, and the remaining points were used as calibration data. Finally, the calibration dataset had 116 sampling points, and the validation dataset had 39 sampling points. The calibration coefficient of determination (Rcal2) and root mean square error (RMSEcal) and the validation coefficient of determination (Rval2) and root mean square error (RMSEval) were used to evaluate the model performance.

2.3.1. SI Method

Spectral indices that were commonly used for LAI prediction were selected and are shown in Table 1 [23]. First, based on the calibration dataset, four types of models, i.e., linear, exponential, power, and logarithmic models, were used for each SI to design the LAI prediction model. Among them, the best model type was selected using the leave-one-out cross validation method, with the largest coefficient of determination (Rcv2) and smallest root mean square error (RMSEcv). Then, the coefficients of selected model types were obtained using calibration samples. Finally, the model was validated using validation samples.

2.3.2. PLSR Method

The PLSR method is one of the commonly used methods to solve the problem of collinearity of variables [32]. The process for designing the LAI prediction model based on the PLSR method was as follows: (1) correlation analysis between LAI and spectral reflectance in each band was carried out to select the bands sensitive to LAI; (2) the reflectance in sensitive bands and LAI were normalized between [−1, 1] to eliminate errors resulting from differences in the magnitudes of the variables; (3) the normalized reflectance data were used as the input of the PLSR method, and the leave-one-out cross validation method was used to select the optimal number of latent variables (LVs); (4) the PLSR model of LAI was designed based on all calibration samples using the optimal number of LVs; and (5) the model was validated based on the validation samples (Figure 2). In this study, a code to perform the above procedure was written in MATLAB 2020a.

2.3.3. ANN Method

Compared with other ANN models, backpropagation (BP) ANN is one of the most widely used neural network models due to its good performance and ability to handle any linear or nonlinear relationship between input and output variables [33]. In addition, it has been documented that a three-layer BP network performed better than other networks [34]. Therefore, a three-layer BP neural network containing an input layer, a hidden layer and an output layer was used in this study.
The process of designing the LAI prediction model based on the BP ANN method was as follows (Figure 2). (1) The same method used in designing the PLSR LAI model was also used to select the bands sensitive to LAI. (2) The sensitive bands were normalized between [−1, 1] to eliminate errors resulting from differences in the magnitudes of the variables. (3) The LVs of PLSR were obtained and used as input variables, as many studies had documented that this approach performed better than using principal components from principal component analysis (PCA) [35,36]. (4) To design the BP ANN model, the input layer was vectors of the LVs, and the output layer was vectors of the LAI. Referring to Chen and Jing [37], the number of nodes in the hidden layer was set between 1 and 5 to avoid overfitting, and the transformation function can be chosen as a tan-sigmoid function, log-sigmoid function and linear function. From all their combinations, leave-one-out cross validation method was used to select the best number of LVs, the number of hidden nodes and the types of transformation function for converting from input nodes to hidden nodes and from hidden nodes to output nodes. (5) The final ANN model was established based on the selected number of LVs, the number of hidden nodes, and the types of transformation function, using all calibration samples. (6) The ANN model was tested using the validation samples. A code to perform the above procedure was written in MATLAB 2020a.

2.3.4. GPR Method

GPR is a nonparametric regression model proposed by Rasmussen and William [38]. By assuming that the training data are sampled from Gaussian processes, the GPR method uses the mean and covariance functions to describe the distribution of the object parameter. During model calibration, the mean and covariance functions were obtained, and then Bayesian theory was used to make predictions.
Considering the GPR model design, when the input variables are normalized between [–1, 1], the mean function is usually set to 0. Therefore, the covariance function determines the accuracy of the GPR model. The process of designing the GPR LAI prediction model is described as follows (Figure 2). (1) Similar to the ANN method, the bands sensitive to LAI variations were first selected and normalized to [–1, 1], and then LVs of PLSR were obtained and used as input variables. (2) The leave-one-out cross validation method was used to determine the number of LVs and kernel function types of the covariance function. During this process, the kernel functions of the covariance function can be chosen as squared exponential, Automatic Relevance Determination (ARD) squared exponential, rational quadratic, ARD rational quadratic, exponential, ARD exponential, Matern 3/2, ARD Matern 3/2, Matern 5/2 or ARD Matern 5/2. (3) The final GPR model was established using the selected number of LVs and the kernel function type of the covariance function, using all calibration samples. (4) The designed GPR model was tested using validation samples. A code to perform the above procedure was written in MATLAB 2020a (MathWorks Inc., Natick, MA, USA).

3. Results

3.1. LAI and SPAD in the Field

ANOVA and Duncan analysis were performed on the LAI and SPAD values of wheat raised under different irrigation and N treatment levels at different growth stages in different years and are shown in Table 2 and Table 3, respectively. It can be noticed that there were significant differences (p < 0.05) in LAI and SPAD among the different N levels in almost all wheat growth stages. The LAI values in the two experimental years varied between 0.34 and 5.56, covering a wide LAI range. This can be considered to be a good dataset for LAI model design.

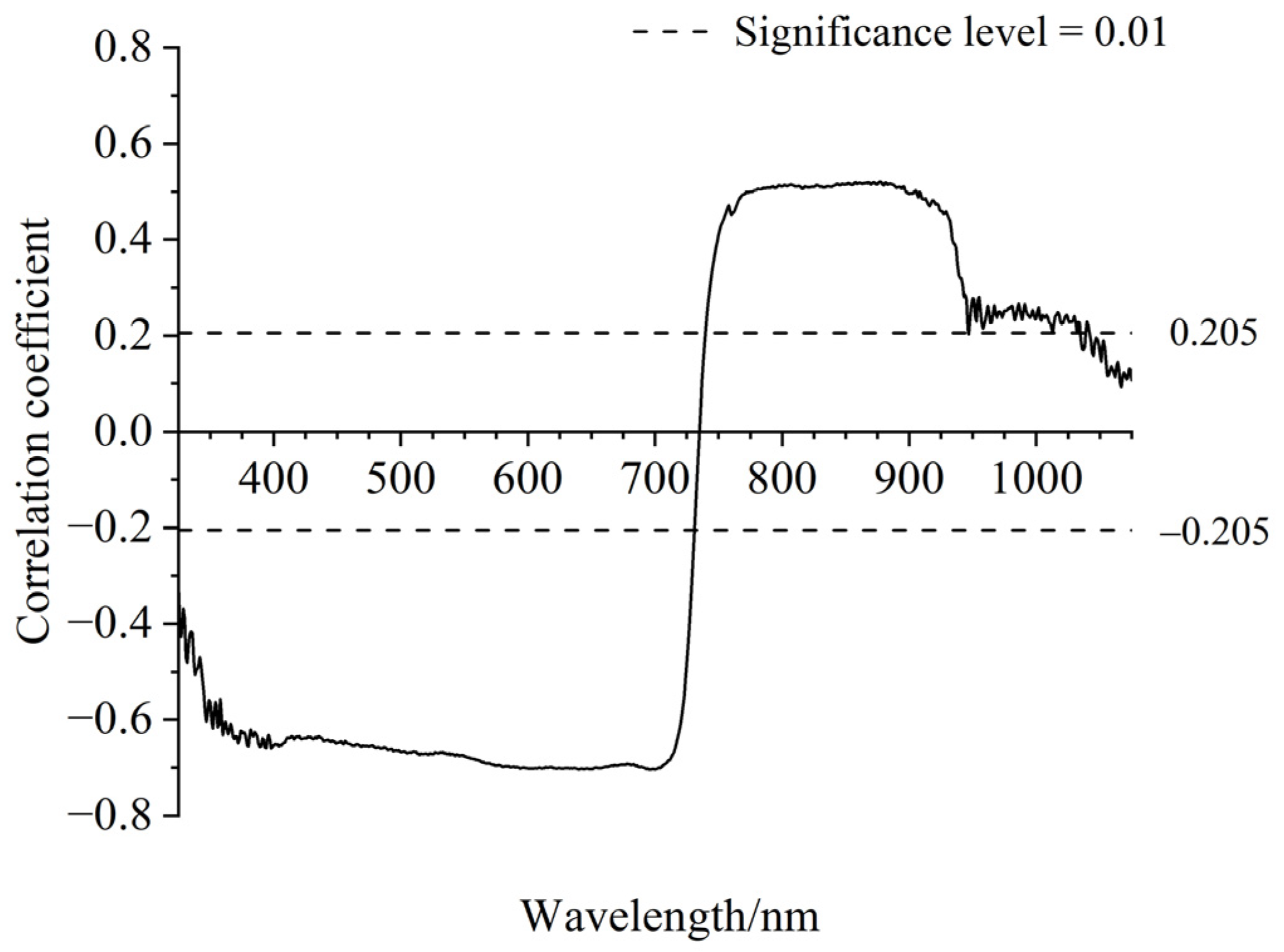
3.2. Feature Bands for LAI Prediction

The correlation coefficients between the spectral reflectance in each band and the LAI are shown in Figure 3. In the 325–730 nm spectral region, there was a significant negative correlation (p < 0.01) between the reflectance and the LAI. This is mainly because N fertilization leads to better wheat growth with higher chlorophyll content and LAI. This spectral region is mainly affected by chlorophyll absorption, so it presents a negative correlation between the reflectance of the bands and the LAI [39]. The 325–400 nm spectral region suffers from noise due to atmospheric interference. In addition, the 740–930 nm spectral region showed a significant positive correlation between the reflectance in each band and the LAI (p < 0.01). This is mainly because the spectrum in this region is mainly influenced by the LAI, and the higher the LAI, the higher the reflectance [40]. Although the reflectance in the 931–1075 nm bands also correlated with the LAI, the results were noisy due to atmospheric water absorption [41]. Therefore, in this study, only 401–730 nm and 740–930 nm spectral regions were selected as sensitive bands for LAI prediction and were used in designing the PLSR, ANN, and GPR models.

3.3. Results of Different Models for LAI Prediction

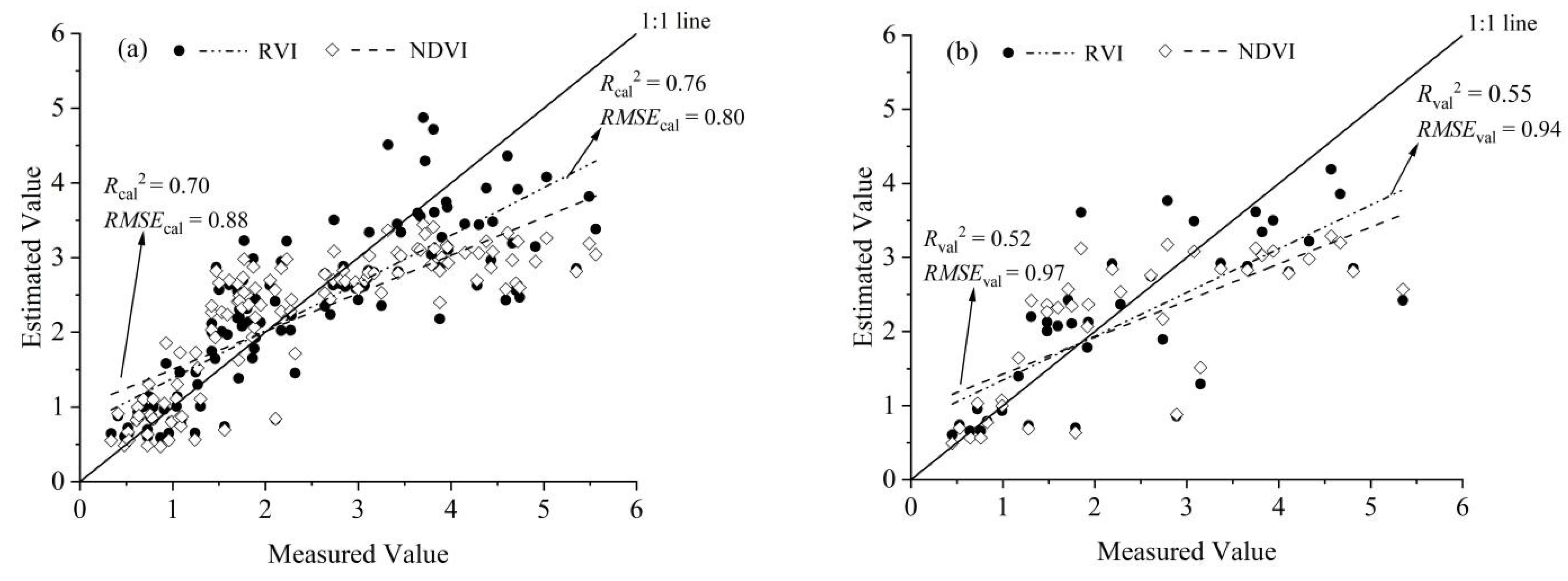
3.3.1. SI Method

The LAI prediction results for the models designed using different spectral indices are shown in Table 4 and ranked from best to worst performance according to the calibration and validation results. The RVI and NDVI had the best results, with Rcal2 values of 0.76 and 0.70 and RMSEcal values of 0.80 and 0.88 during calibration, Rcv2 values of 0.66 and 0.62 and RMSEcv values of 0.81 and 0.89 during cross validation, and Rval2 values of 0.55 and 0.52 and RMSEval values of 0.94 and 0.97 during validation (Figure 4). The GNDVI, OSAVI and RTVI had intermediate LAI estimation results. The LAI prediction model had Rcal2 values between 0.54 and 0.69 and RMSEcal values between 0.89 and 0.93 during calibration, Rcv2 values between 0.53 and 0.60 and RMSEcv values between 0.90 and 0.94 during cross validation, and Rval2 values between 0.47 and 0.49 and RMSEval values between 1.00 and 1.04 during validation. The EVI, MSAVI and DVI had the worst results for LAI prediction. The LAI prediction model had Rcal2 values between 0.42 and 0.50 and RMSEcal values between 0.98 and 1.04 during calibration, Rcv2 values between 0.41 and 0.48 and RMSEcv values between 0.99 and 1.06 during cross validation, and Rval2 values between 0.37 and 0.43 and RMSEval values between 1.04 and 1.09 during validation.

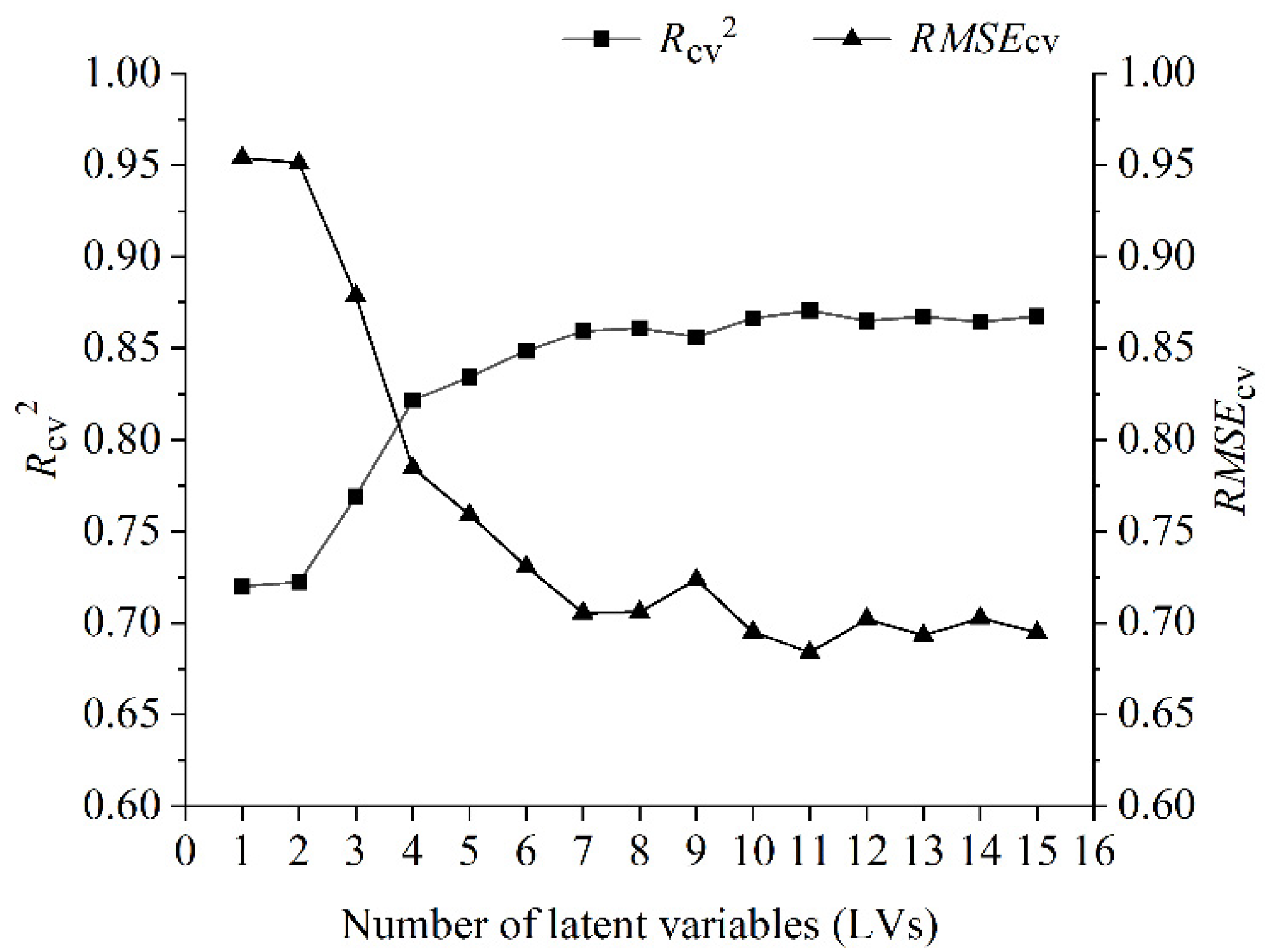
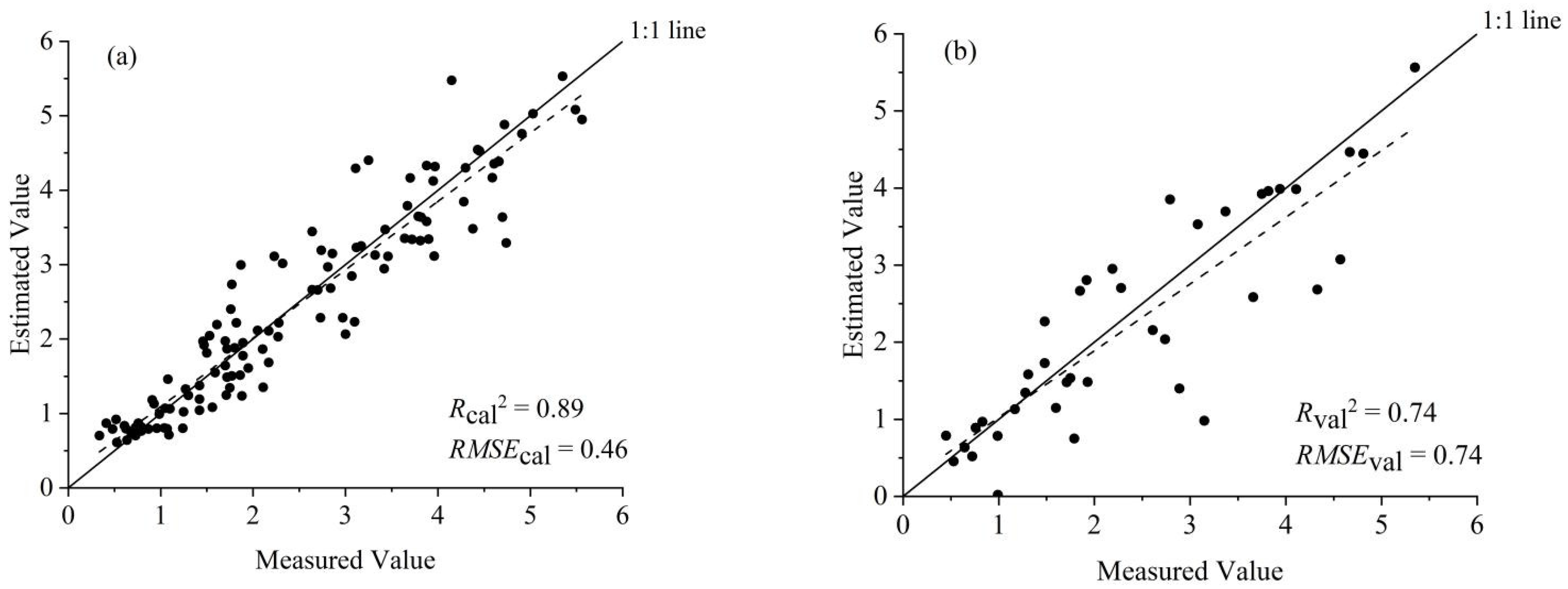
3.3.2. PLSR Method

The leave-one-out cross validation results of the PLSR model under different numbers of LVs are shown in Figure 5. When seven LVs were used, the model had the highest Rcv2 value and lowest RMSEcv value. Thus, seven LVs were used to design the final PLSR model. Considering LAI prediction, the PLSR model had an Rcal2 value of 0.80 and RMSEcal value of 0.61 during calibration (Figure 6a) and an Rval2 value of 0.67 and RMSEval value of 0.80 during validation (Figure 6b).

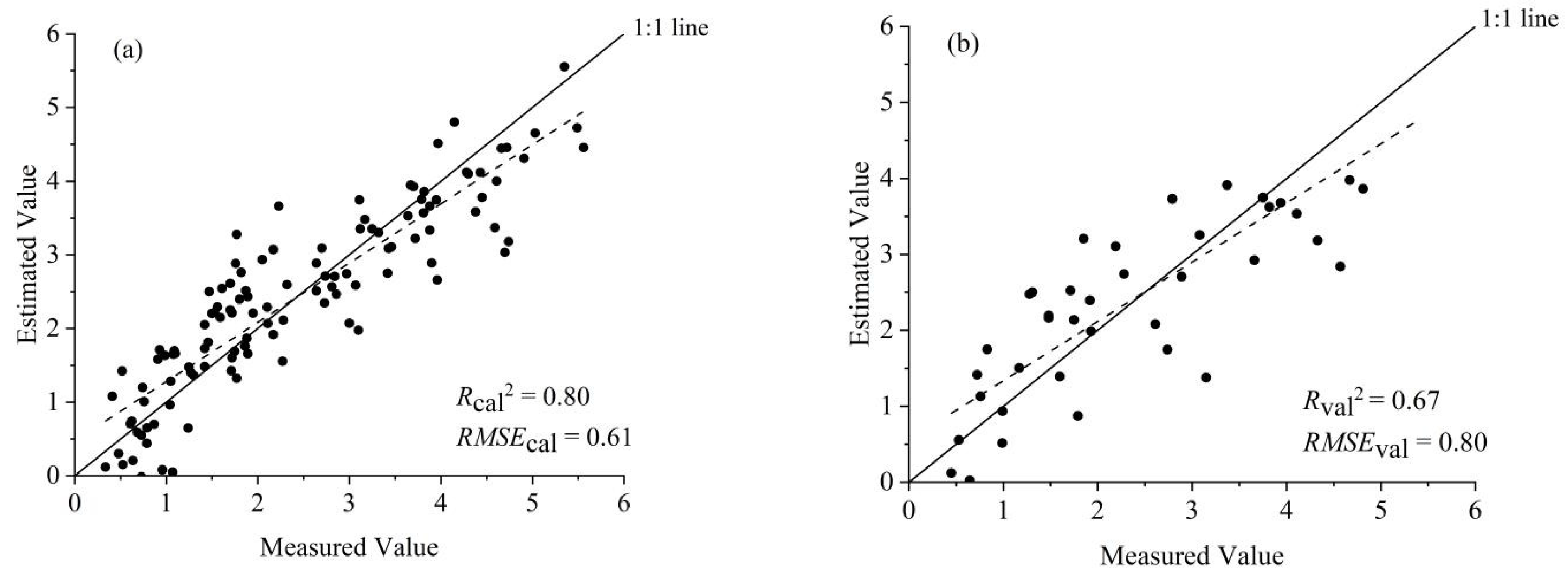
3.3.3. ANN Method

For the ANN model, the highest Rcv2 value and lowest RMSEcv value were obtained by the combination of seven LVs, two hidden nodes, the tan-sigmoid function used as the transformation algorithm from the input nodes to the hidden nodes and the linear function used as the transformation algorithm from the hidden nodes to the output layer. Based on the calibration samples, the model had an Rcal2 value of 0.89 and RMSEcal value of 0.46 (Figure 7a). The cross validation had an Rcv2 value of 0.80 and RMSEcv value of 0.62. When the ANN model was validated using the validation samples, the result was also good, having an Rval2 of 0.74 and RMSEval of 0.74 (Figure 7b).

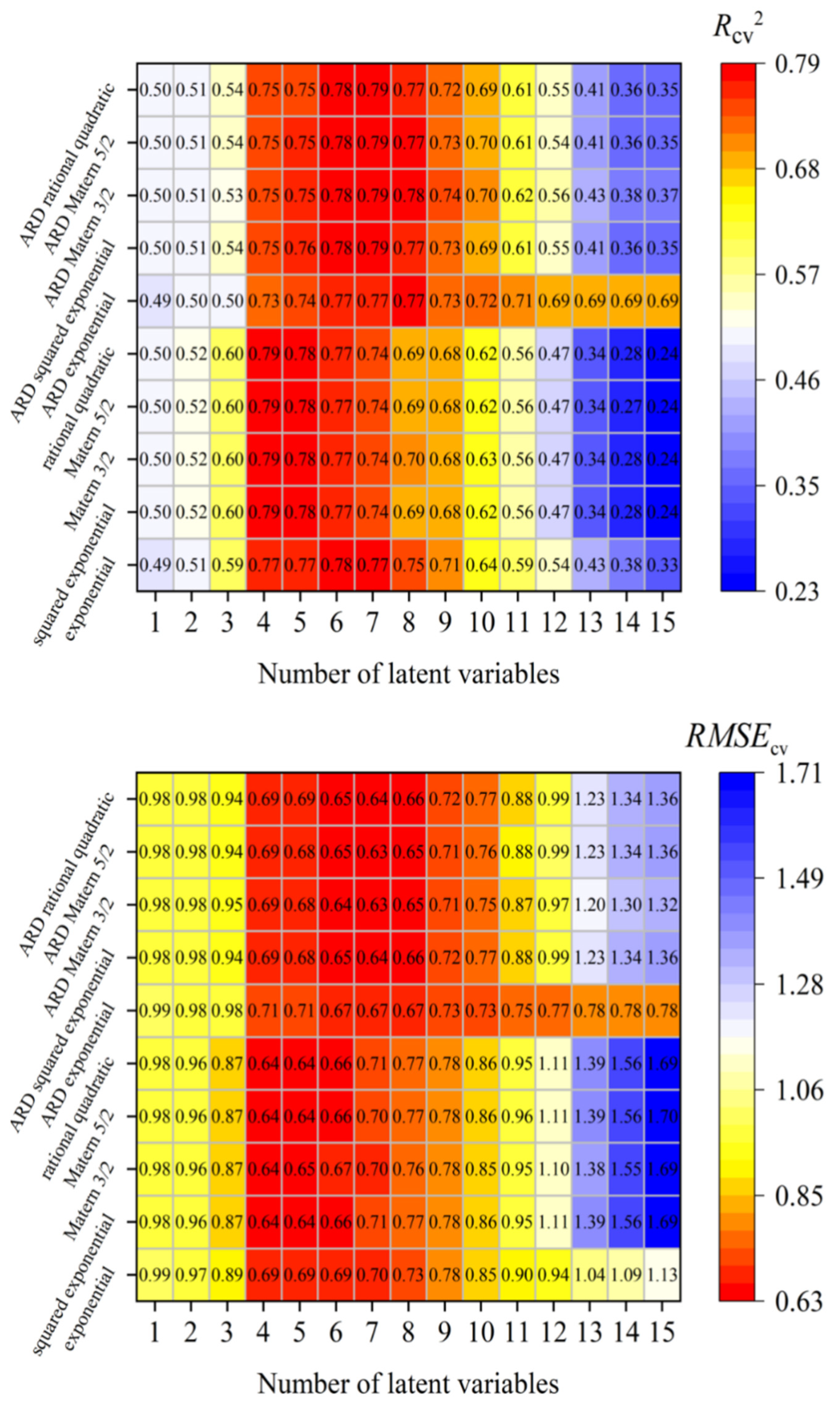
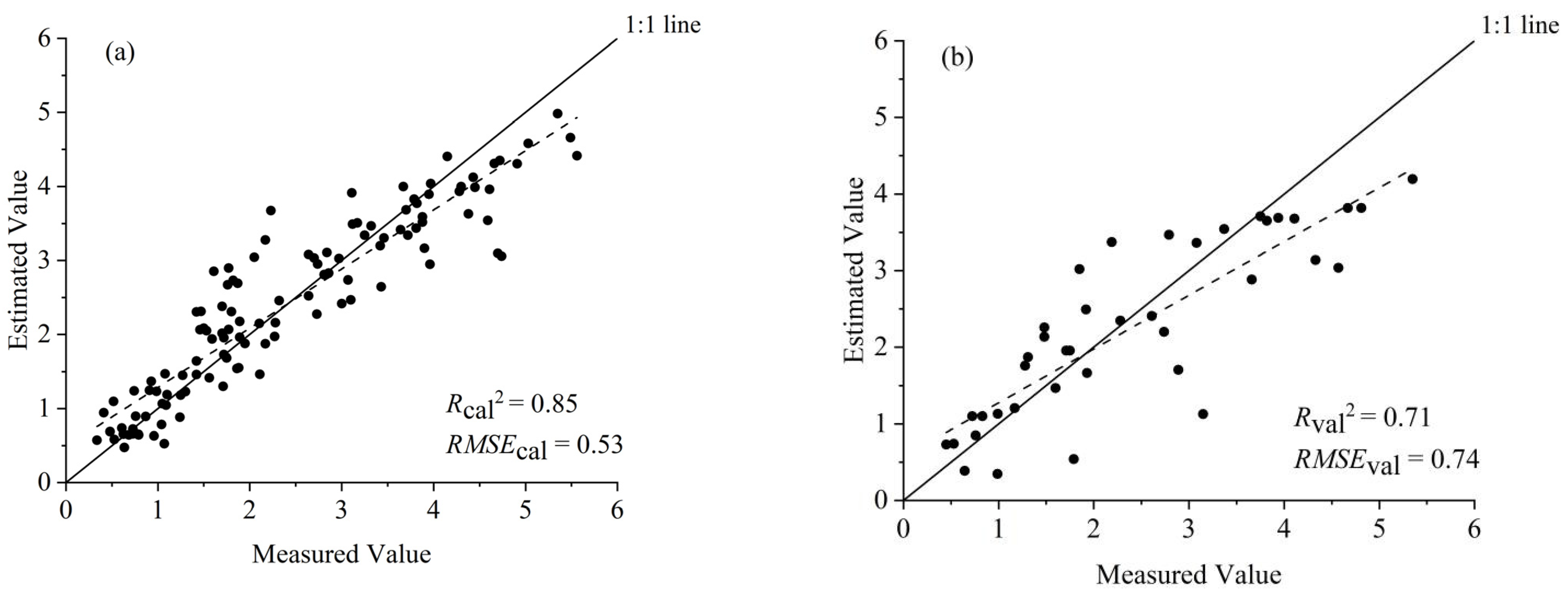
3.3.4. GPR Method

For the GPR model, the cross validation results for all combinations of the number of LVs and kernel functions are shown in Figure 8. The highest Rcv2 value and lowest RMSEcv value were obtained when the number of LVs was seven and the kernel function type was the ARD Matern 3/2, with values of 0.79 and 0.63, respectively. Based on the selected combination and all data in the calibration dataset, the GPR model had an Rcal2 of 0.85 and RMSEcal of 0.53 (Figure 9a). When the GPR model was validated using the validation samples, the result was satisfactory, with a validation Rval2 of 0.71 and an RMSEval of 0.74 (Figure 9b).

4. Discussion

4.1. Comparison with Previous Results

Considering wheat LAI prediction, Xie et al. [42] took formulation as NDVI, MSR, and MSAVI, and used different methods to select bands into the formula to design spectral indices. The spectral indices had R2 values between 0.48 and 0.87 during calibration and R2 values between 0.50 and 0.76 during validation. Liang et al. [43] used the OSAVI to design a wheat LAI prediction model, and the model had R2 values of 0.82 during both calibration and validation. Li et al. [44] selected the sensitive bands of LAI and then used the PLSR method to design a wheat LAI prediction model using these bands. The model had an R2 value of 0.84 during calibration and 0.88 during validation. Based on UAV hyperspectral data, Tao et al. [45] used PLSR to design an LAI prediction model for wheat at different growth stages, and the prediction model had R2 values between 0.64 and 0.76 during calibration and 0.62 and 0.84 during validation. Siegmann et al. [46] also designed PLSR LAI prediction models for wheat in different years, and they had R2 values between 0.90 and 0.92 during validation. In this study, wheat LAI prediction models were designed using the SI, PLSR, ANN and GPR methods, and the models had R2 values between 0.42 and 0.89 during calibration and between 0.37 and 0.74 during validation (Table 5). Compared with existing studies, the results of this study are within a reasonable range.

4.2. Optimal LAI Prediction Method

Considering the LAI prediction accuracy during calibration and validation, the results showed that the ANN achieved the best results. GPR followed, with validation results closely to that of ANN. PLSR displayed intermediate results for LAI prediction, and SI had the worst results. This may be due to the following reasons: (1) SI is based on multispectral information, which only utilizes limited spectral features. The ANN, GPR and PLSR can use more diagnosis features in the spectra. Considering LAI estimation, Neinavaz et al. [47] and He et al. [48] also stated ANN and PLSR performed better than SI respectively. (2) Multiple factors (e.g., LAI, chlorophyll, leaf mesophyll structure, leaf water content, leaf angle distribution function, background) influence canopy reflectance and the combined influence of these factors on the reflectance spectrum is not purely linear [37]. Thus, many studies have reported that the relationships between LAI and spectral information are non-linear [16,23]. The PLSR method is a linear regression method that cannot effectively solve the nonlinear relationship between the spectral reflectance and the LAI. Thus, the accuracy of the PLSR method for estimating LAI is lower than that of the ANN and GPR method.

4.3. Application Potential of This Study

As mentioned earlier, the Gaussian regression method is a new machine learning method that has emerged in recent years. In this study, it was applied to wheat LAI prediction and was compared with other commonly used methods to provide useful information for users selecting methods. The results showed that, though LAI prediction results from GPR were slightly worse than those of ANN, the GPR method also can solve the nonlinear problem well, resulting in accurate LAI prediction. In the future, for “robust” wheat LAI prediction model design, samples covering different climatic areas and different cropping management types should be collected and used to calibrate and validate the ANN or GPR models to apply the models in different scenarios.

5. Conclusions

In this study, a wheat field experiment under different irrigation and N treatments was conducted for two years, and LAI and canopy hyperspectral data were collected during the critical growth stages. Based on these data, different methods, such as the SI, PLSR, ANN and GPR methods, were compared for LAI prediction. The results showed that both ANN and GPR can solve the nonlinear problem well, resulting in better LAI prediction results than PLSR and SI methods. They were recommended for designing LAI prediction models based on hyperspectral data.

Author Contributions

Data analysis, writing original draft, J.M.; Review and editing, L.W.; Conceptualization, data analysis, review and editing, supervision, P.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by “The National Natural Science Foundation of China, grant number 41871344” and “The Strategic Priority Research Program of the Chinese Academy of Sciences, grant number XDA28040500”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to their use in subsequent studies.

Acknowledgments

We thank the Yucheng Integrated Experiment Station of the Chinese Academy of Sciences and Jing Li for providing the experimental field for this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Li, S.; Zhang, C.; Li, J.; Yan, L.; Wang, N.; Xia, L. Present and future prospects for wheat improvement through genome editing and advanced technologies. Plant Commun. 2021, 2, 100211. [Google Scholar] [CrossRef] [PubMed]
  2. Chen, J.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
  3. Inoue, Y. Synergy of remote sensing and modeling for estimating ecophysiological processes in plant production. Plant Prod. Sci. 2003, 6, 3–16. [Google Scholar] [CrossRef]
  4. Yue, J.; Feng, H.; Jin, X.; Yuan, H.; Li, Z.; Zhou, C.; Yang, G.; Tian, Q. A Comparison of Crop Parameters Estimation Using Images from UAV-Mounted Snapshot Hyperspectral Sensor and High-Definition Digital Camera. Remote Sens. 2018, 10, 1138. [Google Scholar] [CrossRef]
  5. Zha, H.; Miao, Y.; Wang, T.; Li, Y.; Zhang, J.; Sun, W.; Feng, Z.; Kusnierek, K. Improving Unmanned Aerial Vehicle Remote Sensing-Based Rice Nitrogen Nutrition Index Prediction with Machine Learning. Remote Sens. 2020, 12, 215. [Google Scholar] [CrossRef]
  6. Chrysafis, I.; Korakis, G.; Kyriazopoulos, A.P.; Mallinis, G. Retrieval of Leaf Area Index Using Sentinel-2 Imagery in A Mixed Mediterranean Forest Area. ISPRS Int. J. Geoinf. 2020, 9, 622. [Google Scholar] [CrossRef]
  7. Fu, Y.; Yang, G.; Li, Z.; Song, X.; Li, Z.; Xu, X.; Wang, P.; Zhao, C. Winter Wheat Nitrogen Status Estimation Using UAV-Based RGB Imagery and Gaussian Processes Regression. Remote Sens. 2020, 12, 3778. [Google Scholar] [CrossRef]
  8. Das, B.; Sahoo, R.N.; Pargal, S.; Krishna, G.; Verma, R.; Chinnusamy, V.; Sehgal, V.K.; Gupta, V.K. Comparative analysis of index and chemometric techniques-based assessment of leaf area index (LAI) in wheat through field spectroradiometer, Landsat-8, Sentinel-2 and Hyperion bands. Geocarto Int. 2020, 35, 1415–1432. [Google Scholar] [CrossRef]
  9. Liu, K.; Zhou, Q.; Wu, W.; Xia, T.; Tang, H. Estimating the crop leaf area index using hyperspectral remote sensing. J. Integr. Agric. 2016, 15, 475–491. [Google Scholar] [CrossRef]
  10. Shi, Y.; Wang, J.; Wang, J.; Qu, Y. A Prior Knowledge-Based Method to Derivate High-Resolution Leaf Area Index Maps with Limited Field Measurements. Remote Sens. 2016, 9, 13. [Google Scholar] [CrossRef] [Green Version]
  11. Chen, P.; Sun, J.; Wang, J.H.; Zhao, C. Remote sensing-based crop nitrogen nutrition diagnosis technology: Status and trends. Sci. China Inf. Sci. 2010, 40, 21–37. (In Chinese) [Google Scholar]
  12. Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
  13. Tian, M.; Ban, S.; Chang, Q.; You, M.; Luo, D.; Wang, L.; Wang, L. Estimation of cotton leaf area index based on low-altitude UAV imaging spectrometer images. J. Agric. Eng. 2016, 32, 102–108. (In Chinese) [Google Scholar]
  14. Yang, X.; Huang, J.; Wu, Y.; Wang, J.; Wang, P.; Wang, X.; Huete, A.R. Estimating biophysical parameters of rice with remote sensing data using support vector machines. Sci. China Life Sci. 2011, 54, 272–281. [Google Scholar] [CrossRef] [PubMed]
  15. Kiala, Z.; Odindi, J.; Mutanga, O.; Peerbhay, K. Comparison of partial least squares and support vector regressions for predicting leaf area index on a tropical grassland using hyperspectral data. J. Appl. Remote Sens. 2016, 10, 036015. [Google Scholar] [CrossRef]
  16. Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
  17. Verrelst, J.; Rivera, J.P.; Moreno, J.; Camps-Valls, G. Gaussian processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. ISPRS J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
  18. Svendsen, D.H.; Martino, L.; Campos-Taberner, M.; Garcia-Haro, F.J.; Camps-Valls, G. Joint Gaussian Processes for Biophysical Parameter Retrieval. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1718–1727. [Google Scholar] [CrossRef]
  19. Zhang, Y.; Yang, J.; Liu, X.; Du, L.; Shi, S.; Sun, J.; Chen, B. Estimation of Multi-Species Leaf Area Index Based on Chinese GF-1 Satellite Data Using Look-Up Table and Gaussian Process Regression Methods. Sensors 2020, 20, 2460. [Google Scholar] [CrossRef]
  20. Berger, K.; Verrelst, J.; Feret, J.B.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef]
  21. Miller, T.D. Growth stages of wheat: Identification and understanding improve crop management. Better Crops 1992, 76, 12–17. [Google Scholar]
  22. Weiss, M.; Baret, F.; Simth, G.J.; Jonckheere, J.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination Part II. estimation of LAI, errors and sampling. Agric. Forest Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
  23. Jin, X.; Yang, G.; Xu, X.; Yang, H.; Feng, H.; Li, Z.; Shen, J.; Zhao, C.; Lan, Y. Combined multi-temporal optical and radar parameters for estimating LAI and biomass in winter wheat using HJ and RADARSAR-2 Data. Remote Sens. 2015, 7, 13251–13272. [Google Scholar] [CrossRef] [Green Version]
  24. Serrano, L.; Penuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in Mediterranean vegetation from AVIRIS data. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
  25. Adams, M.L.; Philpot, W.D.; Norvell, W.A. Yellowness index: An application of spectral second derivatives to estimate chlorosis of leaves in stressed vegetation. Int. J. Remote Sens. 1999, 20, 3663–3675. [Google Scholar] [CrossRef]
  26. Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
  27. Huete, A.; Justice, C.; Liu, H. Development of Vegetation and Soil Indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
  28. Gitelson, A.A.; Kaufma, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
  29. Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Envrion. 1994, 48, 119–126. [Google Scholar] [CrossRef]
  30. Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Envrion. 1996, 55, 95–107. [Google Scholar] [CrossRef]
  31. Chen, P.; Nicolas, T.; Wang, J.; Philippe, V. Study of a new vegetation index for estimating crop canopy biomass. Spectrosc. Spect. Anal. 2010, 30, 512–517. (In Chinese) [Google Scholar]
  32. Yang, B.; Wang, M.; Sha, Z.; Wang, B.; Chen, J.; Yao, X.; Cheng, T.; Cao, W. Evaluation of Aboveground Nitrogen Content of Winter Wheat Using Digital Imagery of Unmanned Aerial Vehicles. Sensors 2019, 19, 4416. [Google Scholar] [CrossRef] [PubMed]
  33. Chen, P.; Wang, J.; Huang, W.; Tremblay, N.; Ou, Y.; Zhang, Q. Critical Nitrogen Curve and Remote Detection of Nitrogen Nutrition Index for Corn in the Northwestern Plain of Shandong Province, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 682–689. [Google Scholar] [CrossRef]
  34. Hornik, K.; Stinchcombe, M.; White, H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Netw. 1990, 3, 551–560. [Google Scholar] [CrossRef]
  35. Mahajan, G.R.; Das, B.; Murgaokar, D.; Herrmann, I.; Berger, K.; Sahoo, R.N.; Patel, K.; Desai, A.; Morajkar, S.; Kulkarni, R.M. Monitoring the Foliar Nutrients Status of Mango Using Spectroscopy-Based Spectral Indices and PLSR-Combined Machine Learning Models. Remote Sens. 2021, 13, 641. [Google Scholar] [CrossRef]
  36. Xu, G.; Li, F.; Luo, Y.; Xie, J.; Guo, X. Soil total nitrogen estimation of alpine grassland using visible/near-infrared spectra: A comparison of multivariate techniques with different spectral transformations. J. Appl. Remote Sens. 2020, 14, 1. [Google Scholar] [CrossRef]
  37. Chen, P.; Jing, Q. A comparison of two adaptive multivariate analysis methods (PLSR and ANN) for winter wheat yield forecasting using Landsat-8 OLI images. Adv. Space Res. 2017, 59, 987–995. [Google Scholar] [CrossRef]
  38. Rasumssen, C.E.; Williams, C.K.I. Gaussian Process for Machine Learning; The MIT Press: New York, NY, USA, 2006; p. 7. [Google Scholar]
  39. Deepak, M.; Keski-Saari, S.; Fauch, L.; Granlund, L.; Oksanen, E.; Keinanen, M. Leaf Canopy Layers Affect Spectral Reflectance in Silver Birch. Remote Sens. 2019, 11, 2884. [Google Scholar] [CrossRef]
  40. Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef]
  41. Zhang, C.; Pattey, E.; Liu, J.; Cai, H.; Shang, J.; Dong, T. Retrieving Leaf and Canopy Water Content of Winter Wheat Using Vegetation Water Indices. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 112–126. [Google Scholar] [CrossRef]
  42. Xie, Q.; Huang, W.; Zhang, B.; Chen, P.; Song, X.; Pascucci, S.; Pignatti, S.; Laneve, G.; Dong, Y. Estimating Winter Wheat Leaf Area Index From Ground and Hyperspectral Observations Using Vegetation Indices. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 771–780. [Google Scholar] [CrossRef]
  43. Liang, L.; Yang, M.; Zhang, L. Wheat leaf area index inversion using hyperspectral remote sensing technology. Spectrosc. Spect. Anal. 2011, 31, 1658–1662. [Google Scholar]
  44. Li, X.; Zhang, Y.; Bao, Y.; Luo, J.; Jin, X.; Xu, X.; Song, X.; Yang, G. Exploring the Best Hyperspectral Features for LAI Estimation Using Partial Least Squares Regression. Remote Sens. 2014, 6, 6221–6241. [Google Scholar] [CrossRef]
  45. Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of Crop Growth Parameters Using UAV-Based Hyperspectral Remote Sensing Data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef]
  46. Siegmann, B.; Jarmer, T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Remote Sens. 2015, 36, 4519–4534. [Google Scholar] [CrossRef]
  47. Neinavaz, E.; Skidmore, A.K.; Darvishzadeh, R.; Groen, T. Retrieval of leaf area index in different plant species using thermal hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2016, 119, 390–401. [Google Scholar] [CrossRef]
  48. He, L.; Ren, X.; Wang, Y.; Liu, B.; Zhang, H.; Liu, W.; Feng, W.; Guo, T. Comparing methods for estimating leaf area index by multi-angular remote sensing in winter wheat. Sci. Rep. 2020, 10, 13943. [Google Scholar] [CrossRef]
Agriculture 12 01353 g001 550
Figure 1. Field trial design (W1: 80% field capacity; W2: 60% field capacity; N1: 0 kg N/ha−1; N2: 70 kg N/ha−1; N3: 140 kg N/ha−1; N4: 210 kg N/ha−1; N5: 280 kg N/ha−1).
Figure 1. Field trial design (W1: 80% field capacity; W2: 60% field capacity; N1: 0 kg N/ha−1; N2: 70 kg N/ha−1; N3: 140 kg N/ha−1; N4: 210 kg N/ha−1; N5: 280 kg N/ha−1).
Agriculture 12 01353 g001
Agriculture 12 01353 g002 550
Figure 2. Flow chart of the LAI prediction models design based on PLSR, ANN and GPR methods.
Figure 2. Flow chart of the LAI prediction models design based on PLSR, ANN and GPR methods.
Agriculture 12 01353 g002
Agriculture 12 01353 g003 550
Figure 3. Correlation coefficients between reflectance and LAI (min/max, 0.34/5.56).
Figure 3. Correlation coefficients between reflectance and LAI (min/max, 0.34/5.56).
Agriculture 12 01353 g003
Agriculture 12 01353 g004 550
Figure 4. Results for LAI prediction model of RVI and NDVI. (a) Calibration; (b) Validation.
Figure 4. Results for LAI prediction model of RVI and NDVI. (a) Calibration; (b) Validation.
Agriculture 12 01353 g004
Agriculture 12 01353 g005 550
Figure 5. Cross-validation result for PLSR.
Figure 5. Cross-validation result for PLSR.
Agriculture 12 01353 g005
Agriculture 12 01353 g006 550
Figure 6. Results for the PLSR model. (a) Calibration; (b) Validation.
Figure 6. Results for the PLSR model. (a) Calibration; (b) Validation.
Agriculture 12 01353 g006
Agriculture 12 01353 g007 550
Figure 7. Results for the ANN model. (a) Calibration; (b) Validation.
Figure 7. Results for the ANN model. (a) Calibration; (b) Validation.
Agriculture 12 01353 g007
Agriculture 12 01353 g008 550
Figure 8. Cross validation results for the GPR method [R2cv (top) and RMSEcv (bottom)].
Figure 8. Cross validation results for the GPR method [R2cv (top) and RMSEcv (bottom)].
Agriculture 12 01353 g008
Agriculture 12 01353 g009 550
Figure 9. Results for the GPR model. (a) Calibration; (b) validation.
Figure 9. Results for the GPR model. (a) Calibration; (b) validation.
Agriculture 12 01353 g009
Table
Table 1. Spectral indices used in this study.
Table 1. Spectral indices used in this study.
IndexNameFormulaSource
RVIRatio Vegetation Index R 800 / R 670 [24]
NDVINormalized Difference Vegetation Index ( R 800 − R 670 ) / ( R 800 + R 670 ) [25]
DVIDifference Vegetation Index R 800 − R 670 [26]
EVIEnhanced Vegetation Index 2.5 ( R 800 − R 670 ) / ( R 800 + 6 R 670 − 7.5 R 470 + 1 ) [27]
GNDVIGreen Normalized Difference Vegetation Index ( R 800 − R 550 ) / ( R 800 + R 550 ) [28]
MSAVIModified Soil-Adjusted Vegetation Index { 2 R 800 + 1 − s q r t [ ( 2 R 800 + 1 ) 2 − 8 ( R 800 − R 670 ) ] } / 2 [29]
OSAVIOptimization of Soil-Adjusted Vegetation Index 1.16 ( R 800 − R 670 ) / ( R 800 + R 670 + 0.16 ) [30]
RTVIRed-edge Triangle Vegetation Index [ 100 ( R 750 − R 730 ) − 10 ( R 750 − R 550 ) ] s q r t ( R 700 / R 670 ) [31]
Note: R470, R550, R670, R700, R730, R750, and R800 indicate the reflectance of the band at 470 nm, 550 nm, 670 nm, 700 nm, 730 nm, 750 nm, and 800 nm, respectively.
Table
Table 2. Results of significance tests for LAI under different irrigation and N treatments at different winter wheat growth stages in different years.
Table 2. Results of significance tests for LAI under different irrigation and N treatments at different winter wheat growth stages in different years.
YearGrowth StageIrrigation TreatmentN Fertilizer Treatment *
N1N2N3N4N5
2019Feekes 7W10.92 a1.57 ab1.32 ab1.35 ab2.25 b
W20.70 a0.99 a1.24 a1.67 a1.97 a
Feekes 10.51W10.57 a0.88 a1.49 b1.67 b1.74 b
W20.53 a0.71 a1.50 b1.53 b2.06 b
2021Feekes 4–5W11.10 a1.91 ab2.52 ab2.80 b2.80 b
W20.85 a2.53 b3.28 b3.78 b3.25 b
Feekes 10.2W12.34 a3.87 ab4.53 b3.83 ab4.88 b
W22.10 a2.68 ab4.44 abc4.22 bc4.95 c
Feekes 10.54W11.42 a2.52 ab3.76 b3.25 b3.39 b
W21.10 a2.54 b3.87 c3.78 c4.13 c
*: Numbers mean averaged LAI in the corresponding N and irrigation treatment. Within each row, the different letters indicate significant differences at the 0.05 level (p < 0.05); W1: 80% field capacity; W2: 60% field capacity; N1: 0 kg N/ha−1; N2: 70 kg N/ha−1; N3: 140 kg N/ha−1; N4: 210 kg N/ha−1; N5: 280 kg N/ha−1.
Table
Table 3. Results of significance tests for SPAD under different irrigation and N treatments at different winter wheat growth stages in different years.
Table 3. Results of significance tests for SPAD under different irrigation and N treatments at different winter wheat growth stages in different years.
YearGrowth StageIrrigation TreatmentN Fertilizer Treatment *
N1N2N3N4N5
2019Feekes 7W131.0 a40.5 b49.5 c45.1 bc47.4 bc
W233.7 a42.2 b46.2 b47.2 b48.0 b
Feekes 10.51W136.2 a53.4 b53.4 b54.4 b53.8 b
W237.3 a51.3 b54.0 b55.0 b52.7 b
2021Feekes 4–5W139.2 a50.2 b51.8 b50.4 b50.9 b
W235.3 a50.2 b51.8 b50.1 b51.1 b
Feekes 10.2W136.0 a42.5 ab51.4 b51.6 b52.3 b
W229.5 a46.4 b52.1 c52.0 c52.9 c
Feekes 10.54W136.5 a44.7 ab52.3 b55.4 b55.2 b
W229.3 a42.2 b50.3 c53.2 cd55.7 d
*: Numbers mean averaged SPAD in the corresponding N and irrigation treatment. Within each row, the different letters indicate significant differences at the 0.05 level (p < 0.05); W1: 80% field capacity; W2: 60% field capacity; N1: 0 kg N/ha−1; N2: 70 kg N/ha−1; N3: 140 kg N/ha−1; N4: 210 kg N/ha−1; N5: 280 kg N/ha−1.
Table
Table 4. LAI prediction results for the models designed using different spectral indices. Linear, logarithmic, exponential, and power models were used for fitting each index. The model type with the highest Rcv2 and lowest RMSEcv was used, and the calibration and validation results are expressed in the table.
Table 4. LAI prediction results for the models designed using different spectral indices. Linear, logarithmic, exponential, and power models were used for fitting each index. The model type with the highest Rcv2 and lowest RMSEcv was used, and the calibration and validation results are expressed in the table.
SICross ValidationCalibrationValidation
Rcv2RMSEcvModelRcal2RMSEcalRval2RMSEval
RVI0.660.81 y = 0.38 x 0.77 0.760.800.550.94
NDVI0.620.89 y = 0.2 e 3.06 x 0.700.880.520.97
GNDVI0.600.90 y = 0.13 e 3.98 x 0.690.890.491.00
OSAVI0.550.95 y = 0.25 e 3.46 x 0.670.930.471.04
RTVI0.530.94 y = 0.18 x + 0.67 0.540.930.471.01
EVI0.471.00 y = 5.93 x − 0.59 0.490.990.431.04
MSAVI0.480.99 y = 6.01 x − 0.47 0.500.980.421.05
DVI0.411.06 y = 10.15 x − 0.38 0.421.040.371.09
Table
Table 5. Summary of results from different LAI prediction methods used in this study.
Table 5. Summary of results from different LAI prediction methods used in this study.
MethodsCalibrationValidation
Rcal2RMSEcalRval2RMSEval
SI0.42–0.760.80–1.040.37–0.550.94–1.09
PLSR0.800.610.670.80
ANN0.890.460.740.74
GPR0.850.530.710.74
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Ma, J.; Wang, L.; Chen, P. Comparing Different Methods for Wheat LAI Inversion Based on Hyperspectral Data. Agriculture 2022, 12, 1353. https://doi.org/10.3390/agriculture12091353

AMA Style

Ma J, Wang L, Chen P. Comparing Different Methods for Wheat LAI Inversion Based on Hyperspectral Data. Agriculture. 2022; 12(9):1353. https://doi.org/10.3390/agriculture12091353

Chicago/Turabian Style

Ma, Junwei, Lijuan Wang, and Pengfei Chen. 2022. "Comparing Different Methods for Wheat LAI Inversion Based on Hyperspectral Data" Agriculture 12, no. 9: 1353. https://doi.org/10.3390/agriculture12091353

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop