Establishment and Validation of a Structural Dynamics Model with Power Take-Off Driveline for Agricultural Tractors
Abstract
:1. Introduction
- (1)
- The load transfer path of the power take-off driveline in agricultural tractors cannot be accurately described.
- (2)
- The lack of a dynamics model for the power take-off driveline of agricultural tractors.
- (3)
- The relationship between the excitation and the response of the power take-off driveline is unclear.
- (4)
- The key dynamic forces that the sensor cannot measure in the transmission process cannot be accurately obtained by dynamic analysis.
2. Materials and Methods
2.1. Coupled Spatial Dynamics Model of the Power Take-off Driveline
2.1.1. Structure Description
2.1.2. Physical Model
- (1)
- The interaction between the driveline and the connection structure is not considered, so the resonance of the gearbox body is ignored.
- (2)
- The mass of the driving shafts and bearings are concentrated in the gears.
- (3)
- The transmission error of gear teeth is ignored in the process of gear transmission.
- (4)
- The gear pairs in idle position are subjected to very little resistance.
2.1.3. Mathematical Model
- The motion equations of the engine and load:
- The motion equations of the driving and driven gears:
2.2. Dynamic Simulations and Experimental Validation
2.2.1. Numerical Simulation
2.2.2. Bench Experimental
3. Results and Discussion
3.1. Comparisons of Simulated and Tested Results
3.1.1. Time Domain Response Analysis
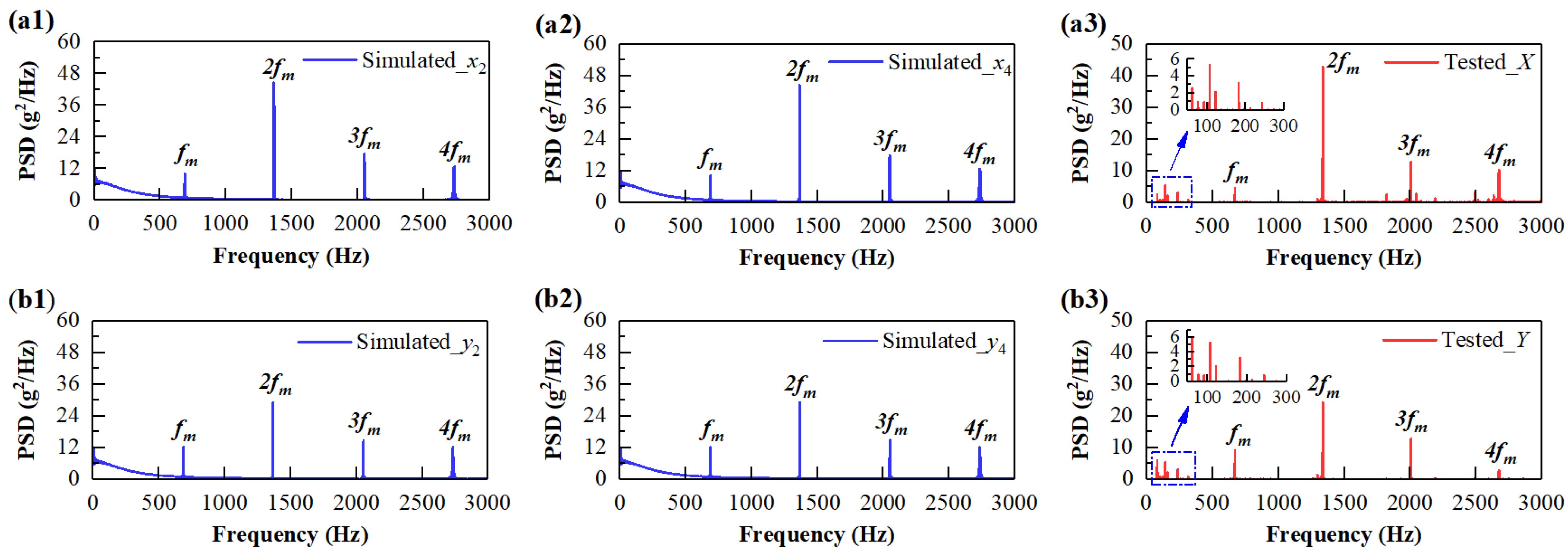
3.1.2. Frequency Domain Response Analysis
3.2. Dynamic Responses of Gear Transmission System
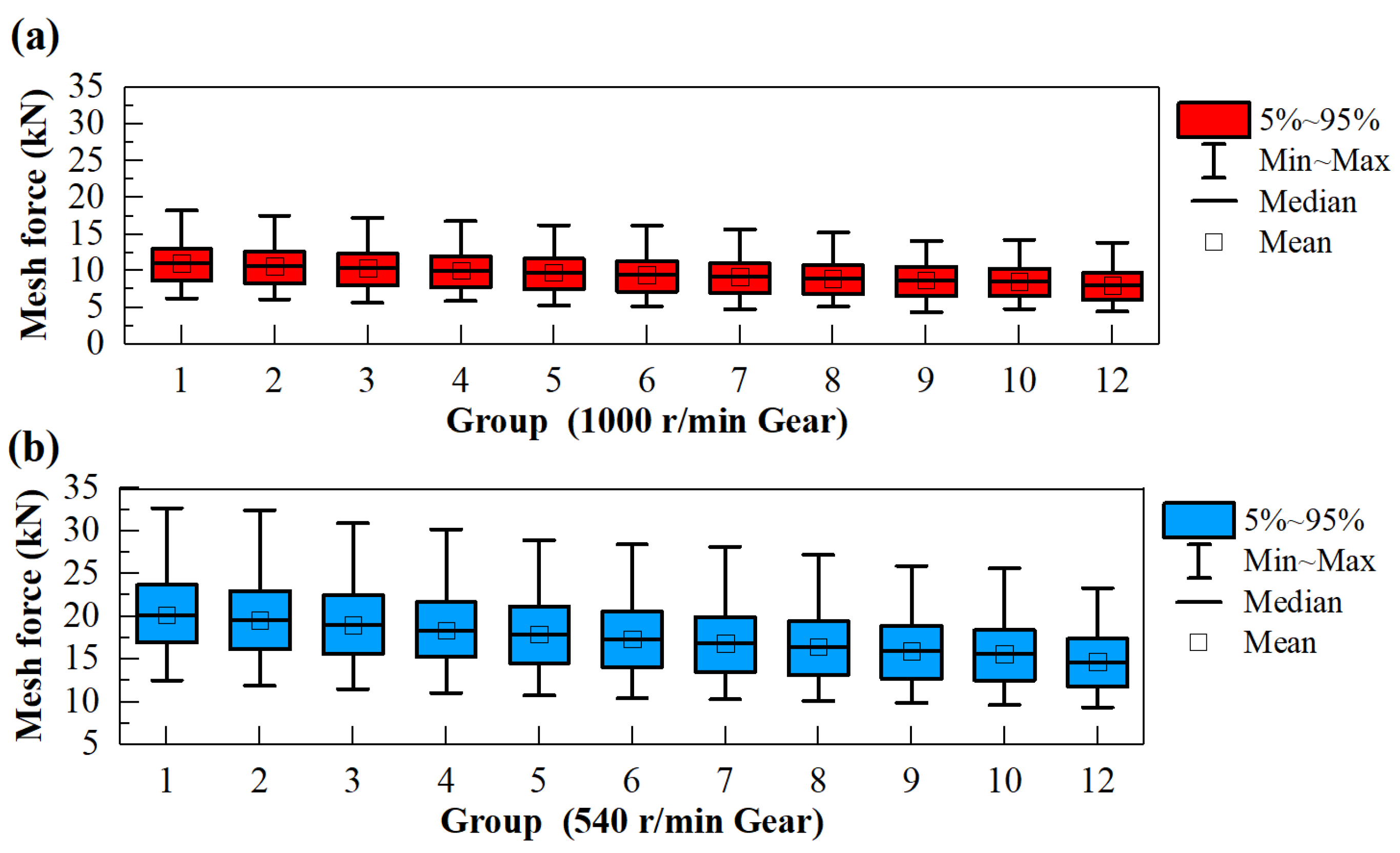
3.2.1. Mesh Forces under Different Drive Modes
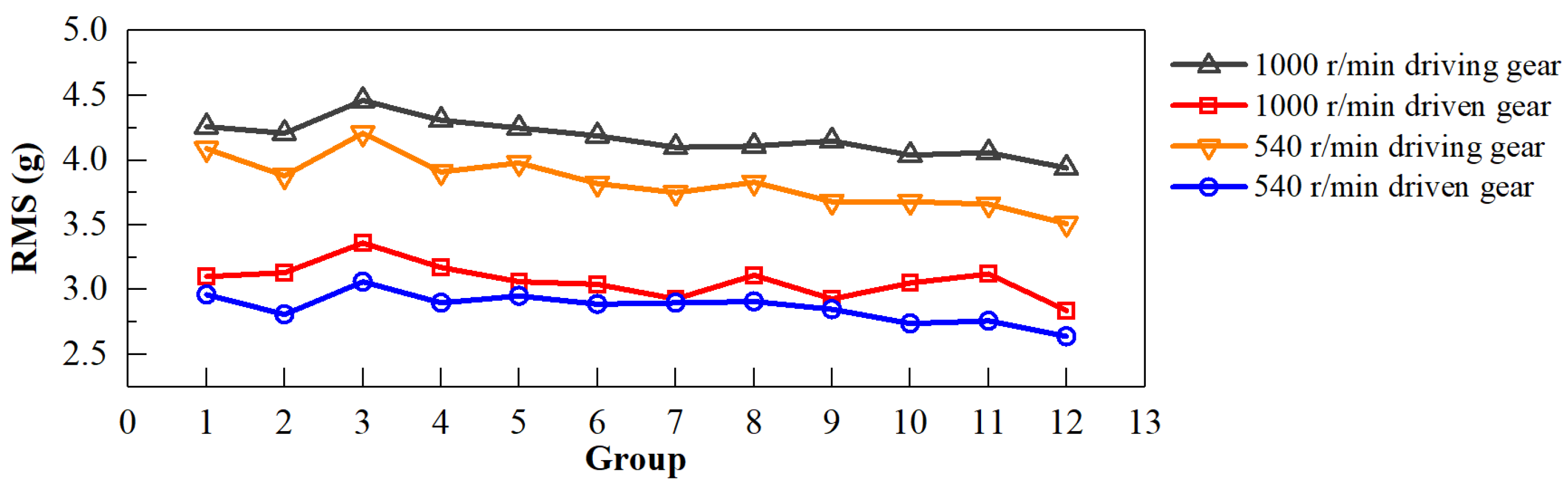
3.2.2. Vibration Responses under Different Drive Modes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, W.-S.; Kim, Y.-J.; Kim, Y.-S.; Park, S.-U.; Lee, K.-H.; Hong, D.-H.; Choi, C.-H. Evaluation of the fatigue life of a tractor’s transmission spiral bevel gear. J. Terramechanics 2021, 94, 13–22. [Google Scholar] [CrossRef]
- Shao, X.; Song, Z.; Yin, Y.; Xie, B.; Liao, P. Statistical distribution modelling and parameter identification of the dynamic stress spectrum of a tractor front driven axle. Biosyst. Eng. 2021, 205, 152–163. [Google Scholar] [CrossRef]
- Wen, C.; Xie, B.; Li, Z.; Yin, Y.; Zhao, X.; Song, Z. Power density based fatigue load spectrum editing for accelerated durability testing for tractor front axles. Biosyst. Eng. 2020, 200, 73–88. [Google Scholar] [CrossRef]
- Wen, C.; Xie, B.; Song, Z.; Yang, Z.; Dong, N.; Han, J.; Yang, Q.; Liu, J. Methodology for designing tractor accelerated structure tests for an indoor drum-type test bench. Biosyst. Eng. 2021, 205, 1–26. [Google Scholar] [CrossRef]
- Tang, X.; Yang, W.; Hu, X.; Zhang, D. A novel simplified model for torsional vibration analysis of a series-parallel hybrid electric vehicle. Mech. Syst. Signal Process. 2017, 85, 329–338. [Google Scholar] [CrossRef]
- Oh, J.J.; Choi, S.B.; Kim, J. Driveline modeling and estimation of individual clutch torque during gear shifts for dual clutch transmission. Mechatronics 2014, 24, 449–463. [Google Scholar] [CrossRef]
- Crowther, A.; Zhang, N. Torsional finite elements and nonlinear numerical modelling in vehicle powertrain dynamics. J. Sound Vib. 2005, 284, 825–849. [Google Scholar] [CrossRef]
- Chen, Z.; Zhai, W.; Wang, K. Dynamic investigation of a locomotive with effect of gear transmissions under tractive conditions. J. Sound Vib. 2018, 408, 220–233. [Google Scholar] [CrossRef]
- Chen, Z.; Zhai, W.; Wang, K. Locomotive dynamic performance under traction/braking conditions considering effect of gear transmissions. Veh. Syst. Dyn. 2017, 56, 1097–1117. [Google Scholar] [CrossRef]
- Wang, Z.; Mei, G.; Xiong, Q.; Yin, Z.; Zhang, W. Motor car–track spatial coupled dynamics model of a high-speed train with traction transmission systems. Mech. Mach. Theory 2019, 137, 386–403. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, Y.; Cheng, H.; Zhou, Y.; Lv, H. Research on dynamic behavior of multistage gears-bearings and box coupling system. Meas. J. Int. Meas. Confed. 2020, 150, 107096. [Google Scholar] [CrossRef]
- Bartelmus, W. Mathematical modelling and computer simulations as an aid to gearbox diagnostics. Mech. Syst. Signal Process. 2001, 15, 855–871. [Google Scholar] [CrossRef]
- Howard, I.; Jia, S.; Wang, J. The dynamic modelling of a spur gear in mesh including friction and a crack. Mech. Syst. Signal Process. 2001, 15, 831–853. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, M.J.; Parey, A. Simulation of spur gear dynamics and estimation of fault growth. J. Sound Vib. 2008, 317, 608–624. [Google Scholar] [CrossRef]
- Tian, Z.; Zuo, M.J.; Wu, S. Crack propagation assessment for spur gears using model-based analysis and simulation. J. Intell. Manuf. 2012, 23, 239–253. [Google Scholar] [CrossRef]
- Liang, X.H.; Liu, Z.L.; Pan, J.; Zuo, M.J. Spur Gear Tooth Pitting Propagation Assessment Using Model-based Analysis. Chin. J. Mech. Eng. 2017, 30, 1369–1382. [Google Scholar] [CrossRef] [Green Version]
- Lundvall, O.; Strömberg, N.; Klarbring, A. A flexible multi-body approach for frictional contact in spur gears. J. Sound Vib. 2004, 278, 479–499. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, Y. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth. Eng. Fail. Anal. 2011, 18, 2149–2164. [Google Scholar] [CrossRef]
- Chen, Z.; Zhai, W.; Shao, Y.; Wang, K.; Sun, G. Analytical model for mesh stiffness calculation of spur gear pair with non-uniformly distributed tooth root crack. Eng. Fail. Anal. 2016, 66, 502–514. [Google Scholar] [CrossRef]
- Ryali, L.; Talbot, D. A dynamic load distribution model of planetary gear sets. Mech. Mach. Theory 2021, 158, 104229. [Google Scholar] [CrossRef]
- Liu, C.; Yin, X.; Liao, Y.; Yi, Y.; Qin, D. Hybrid dynamic modeling and analysis of the electric vehicle planetary gear system. Mech. Mach. Theory 2020, 150, 103860. [Google Scholar] [CrossRef]
- Amabili, M.; Rivola, A. Dynamic analysis of spur gear pairs: Steady-state response and stability of the SDOF model with time-varying meshing damping. Mech. Syst. Signal Process. 1997, 11, 375–390. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, H.; Liu, L.; Zuo, M.J. The influence of tooth pitting on the mesh stiffness of a pair of external spur gears. Mech. Mach. Theory 2016, 106, 1–15. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]
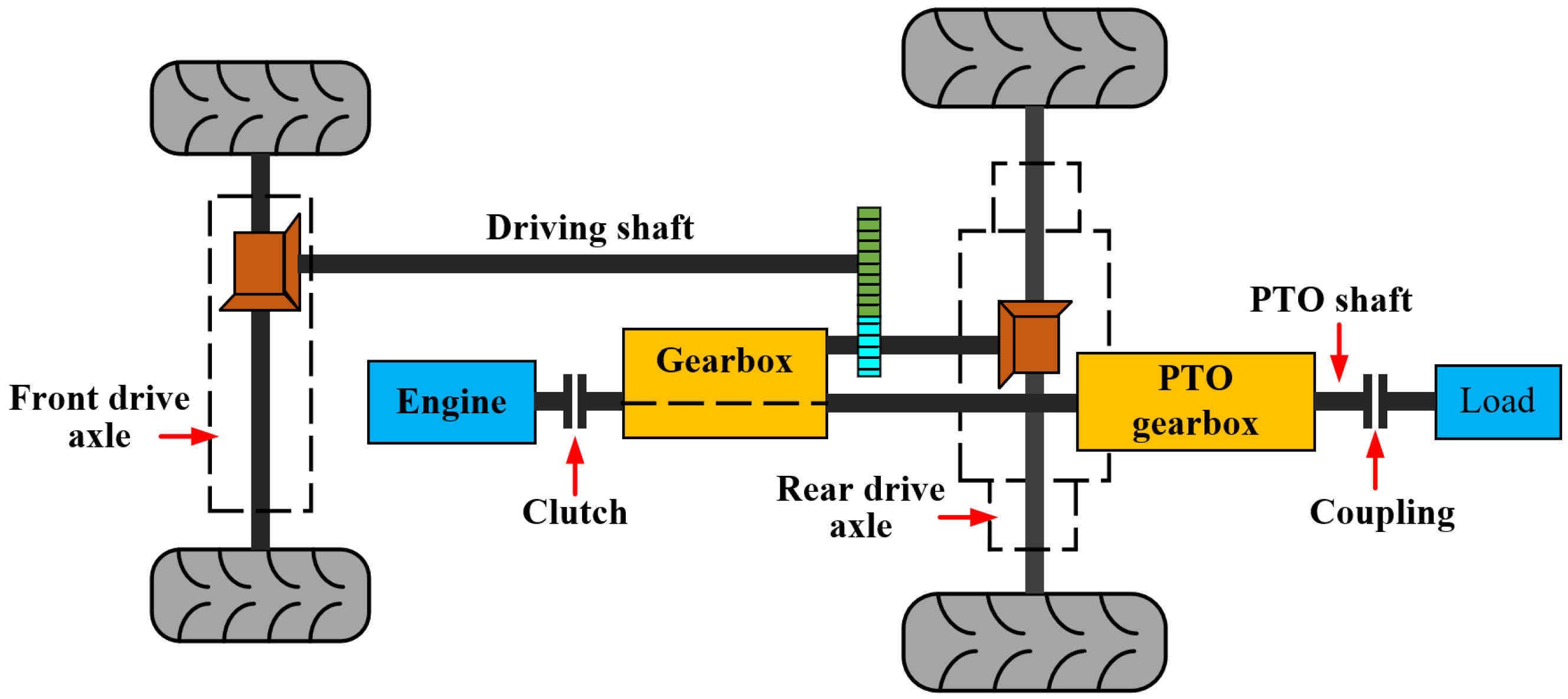
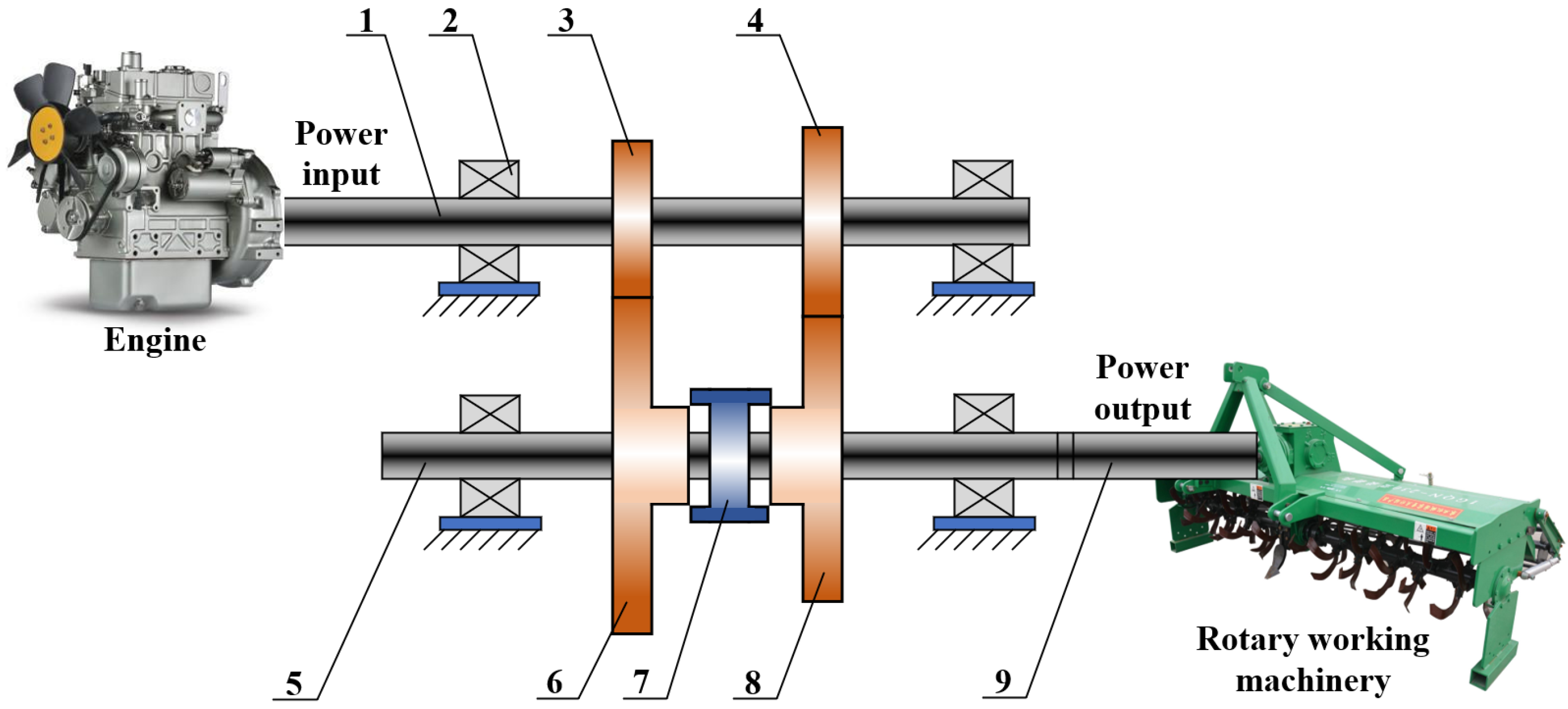


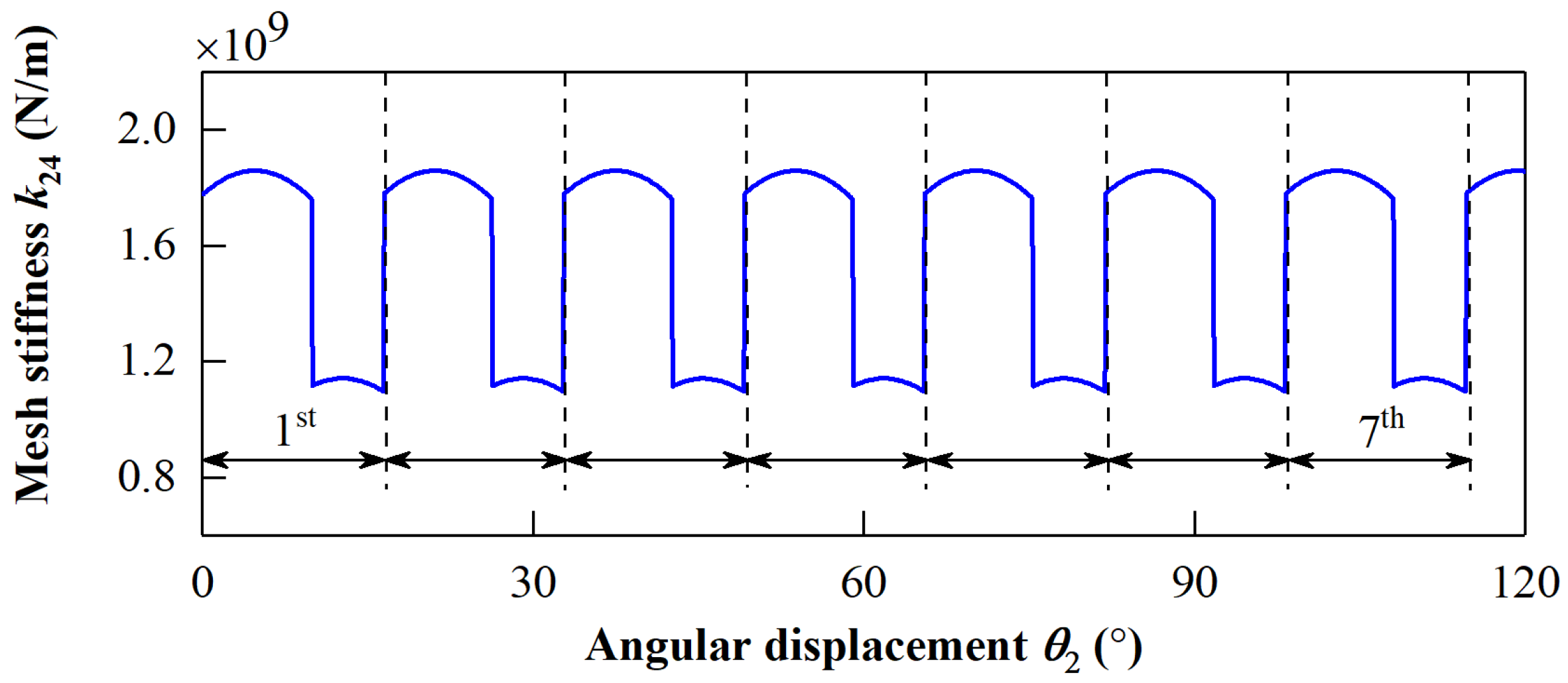

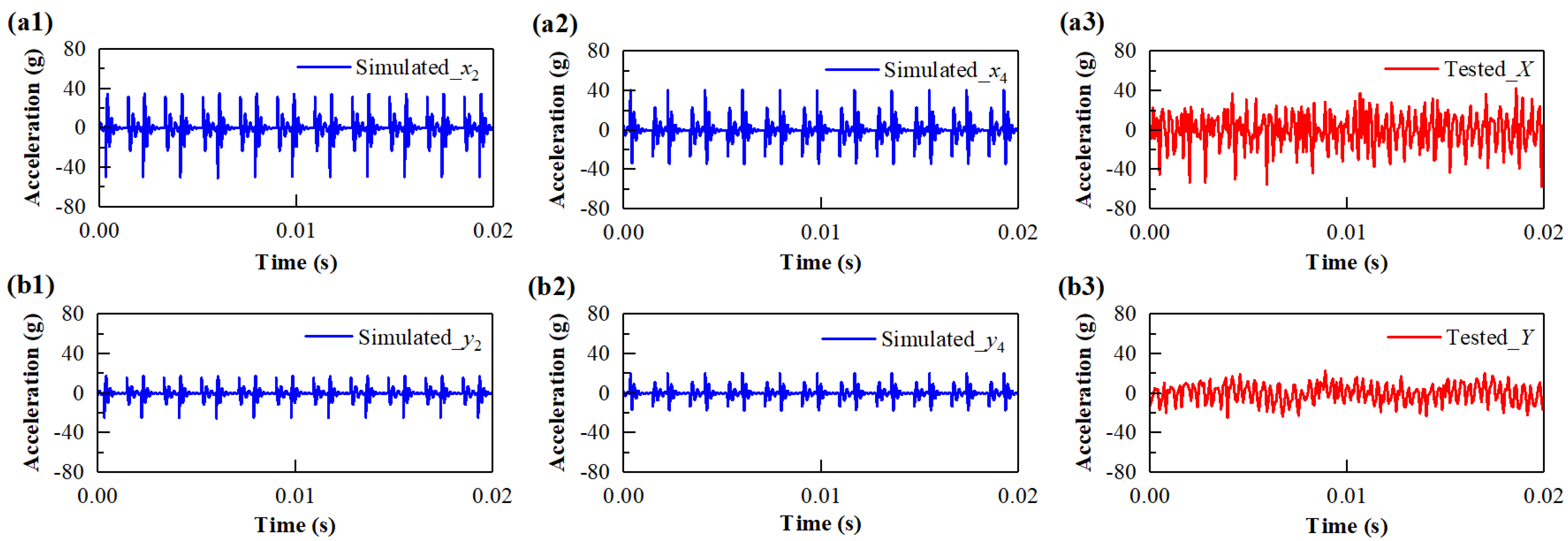

| Component | Vertical | Lateral | Roll |
|---|---|---|---|
| Engine | - | - | θe |
| Gear (i = 1–5) | yi | xi | θi |
| Load | - | - | θL |
| Parameter | Gear 2 | Gear 4 | Gear 5 |
|---|---|---|---|
| Number of teeth | 22 | 41 | 24 |
| Tooth width/mm | 28 | 28 | 22 |
| Module | 6 | 6 | 3.5 |
| Base circle radius/mm | 62 | 116 | 40 |
| Pressure angle/° | 20 | 20 | 20 |
| Lateral support stiffness/(N∙m−1) | 5.0 × 108 | 5.0 × 108 | 5.0 × 108 |
| Vertical support stiffness/(N∙m−1) | 5.0 × 108 | 5.0 × 108 | 5.0 × 108 |
| Lateral support damping/(N∙m−1∙s) | 4.0 × 105 | 4.0 × 105 | 4.0 × 105 |
| Vertical support damping/(N∙m−1∙s) | 4.0 × 105 | 4.0 × 105 | 4.0 × 105 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 |
| Young’s modulus/GPa | 206.8 | 206.8 | 206.8 |
| Index for the Lateral (Vertical) Direction | ||||
|---|---|---|---|---|
| Maximum Amplitude | Stds | |||
| Tested/g | Simulated/g | Tested/g | Simulated/g | |
| Gear 2 | 54.98 (24.14) | 49.18 (24.66) | 10.42 (7.06) | 4.55 (2.73) |
| Gear 4 | 40.33 (20.20) | 5.76 (3.45) | ||
| Frequency Component | Simulated (X)/Hz | Tested (X)/Hz | Error | Simulated (Y)/Hz | Tested (Y)/Hz | Error |
|---|---|---|---|---|---|---|
| fm | 683 | 668 | 2.20% | 683 | 663 | 2.93% |
| 2 fm | 1367 | 1316 | 3.73% | 1367 | 1297 | 5.12% |
| 3 fm | 2050 | 2024 | 1.27% | 2050 | 2014 | 1.76% |
| 4 fm | 2733 | 2617 | 4.24% | 2733 | 2629 | 3.81% |
| Frequency Component | 540 r/min | 1000 r/min | ||
|---|---|---|---|---|
| PTO Rotation Speed/(r/min) | PTO Torque/(N∙m) | PTO Rotation Speed/(r/min) | PTO Torque/(N∙m) | |
| 1 | 490 | 2980 | 950 | 1537 |
| 2 | 500 | 2920 | 960 | 1521 |
| 3 | 510 | 2863 | 970 | 1505 |
| 4 | 520 | 2808 | 980 | 1490 |
| 5 | 530 | 2755 | 990 | 1475 |
| 6 | 540 | 2704 | 1000 | 1460 |
| 7 | 550 | 2655 | 1100 | 1327 |
| 8 | 560 | 2607 | 1200 | 1217 |
| 9 | 570 | 2561 | 1300 | 1123 |
| 10 | 580 | 2517 | 1400 | 1043 |
| 11 | 590 | 2475 | 1500 | 973 |
| 12 | 600 | 2433 | 1600 | 913 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, X.; Zheng, B.; Luo, Z.; Song, Z. Establishment and Validation of a Structural Dynamics Model with Power Take-Off Driveline for Agricultural Tractors. Agriculture 2022, 12, 1297. https://doi.org/10.3390/agriculture12091297
Shao X, Zheng B, Luo Z, Song Z. Establishment and Validation of a Structural Dynamics Model with Power Take-Off Driveline for Agricultural Tractors. Agriculture. 2022; 12(9):1297. https://doi.org/10.3390/agriculture12091297
Chicago/Turabian StyleShao, Xuedong, Bowen Zheng, Zhenhao Luo, and Zhenghe Song. 2022. "Establishment and Validation of a Structural Dynamics Model with Power Take-Off Driveline for Agricultural Tractors" Agriculture 12, no. 9: 1297. https://doi.org/10.3390/agriculture12091297
APA StyleShao, X., Zheng, B., Luo, Z., & Song, Z. (2022). Establishment and Validation of a Structural Dynamics Model with Power Take-Off Driveline for Agricultural Tractors. Agriculture, 12(9), 1297. https://doi.org/10.3390/agriculture12091297






