Task Space Model Predictive Control for Vineyard Spraying with a Mobile Manipulator
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
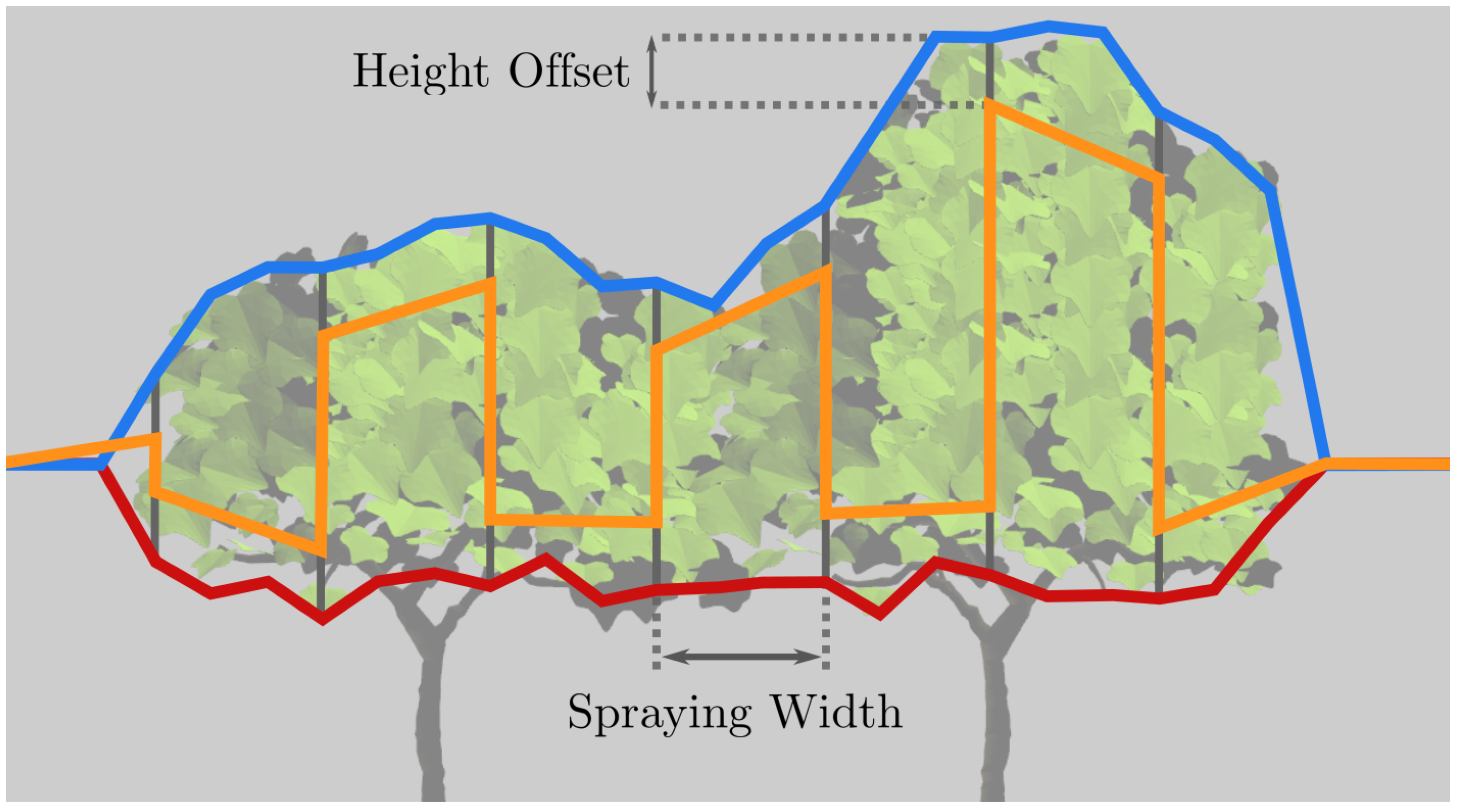
- Row-specific reference trajectory generation based on grapevine canopy description;
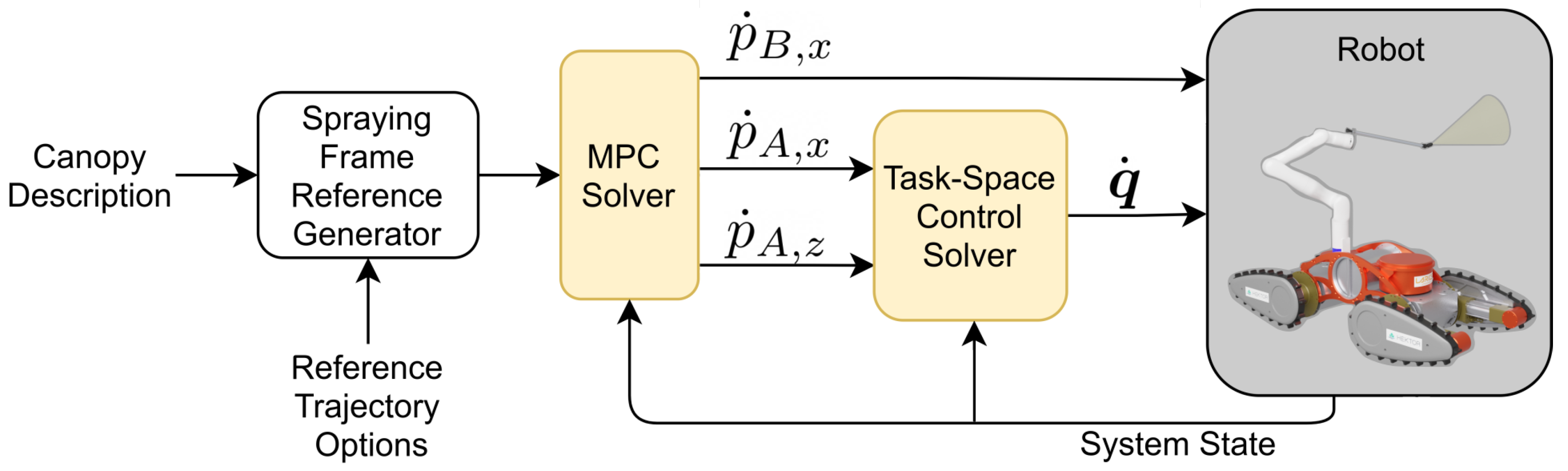
- Forward mobile base and two-dimensional task space manipulator command generation using linear reference tracking MPC;
- Manipulator joint space velocity command selection using task space control.
- A novel method for vineyard spraying with mobile manipulators able to adapt to a specific grapevine row description;
- Reference trajectory generation based on grapevine row description;
- Control design based on computationally efficient task space trajectory tracking MPC that exploits the insight into the motion constraints imposed by the specific task of vineyard spraying.
2. Task Space Model Predictive Control Approach
2.1. Reference Spray Frame Trajectory
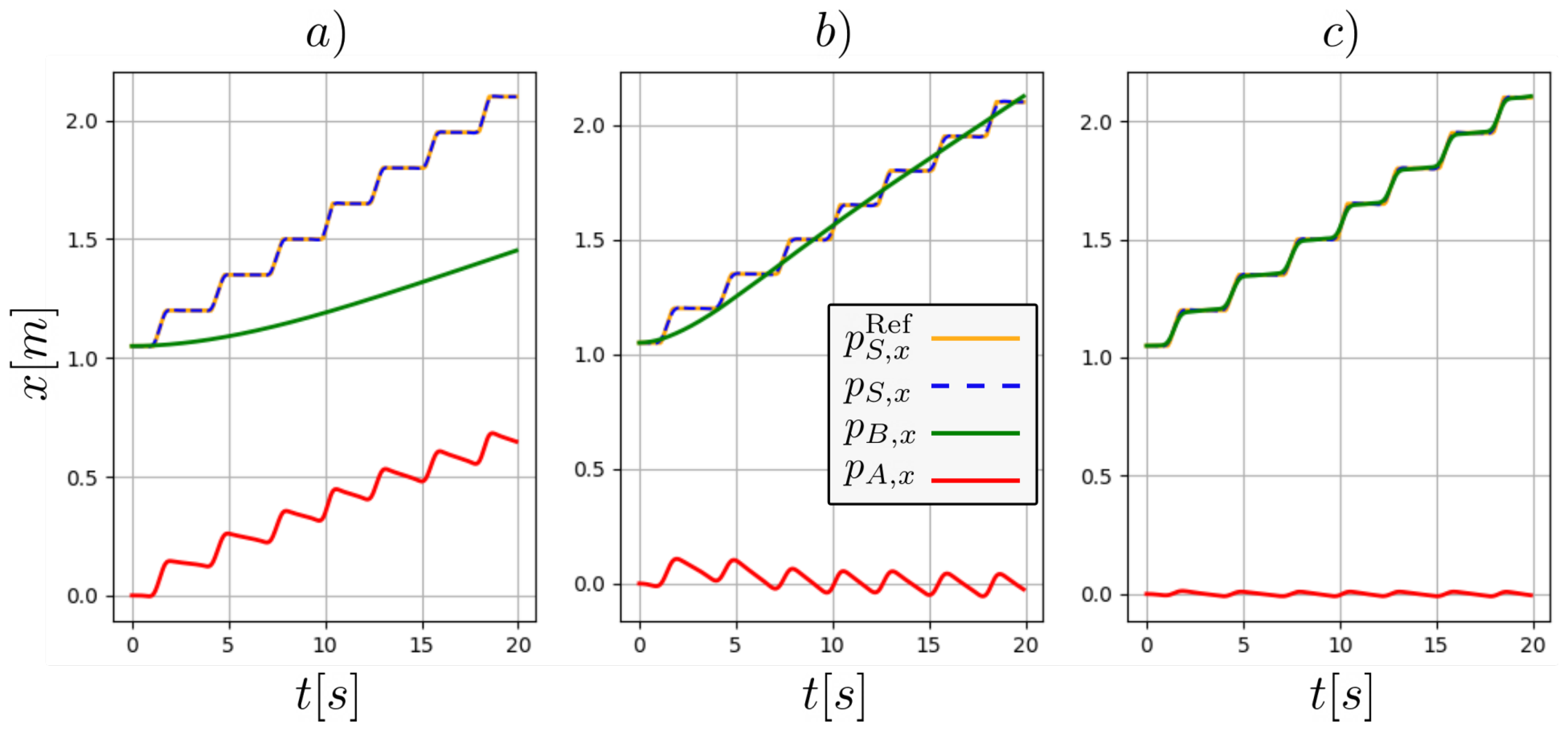
2.2. MPC Algorithm
2.2.1. MPC Parameter Tuning
2.2.2. MPC Constraints
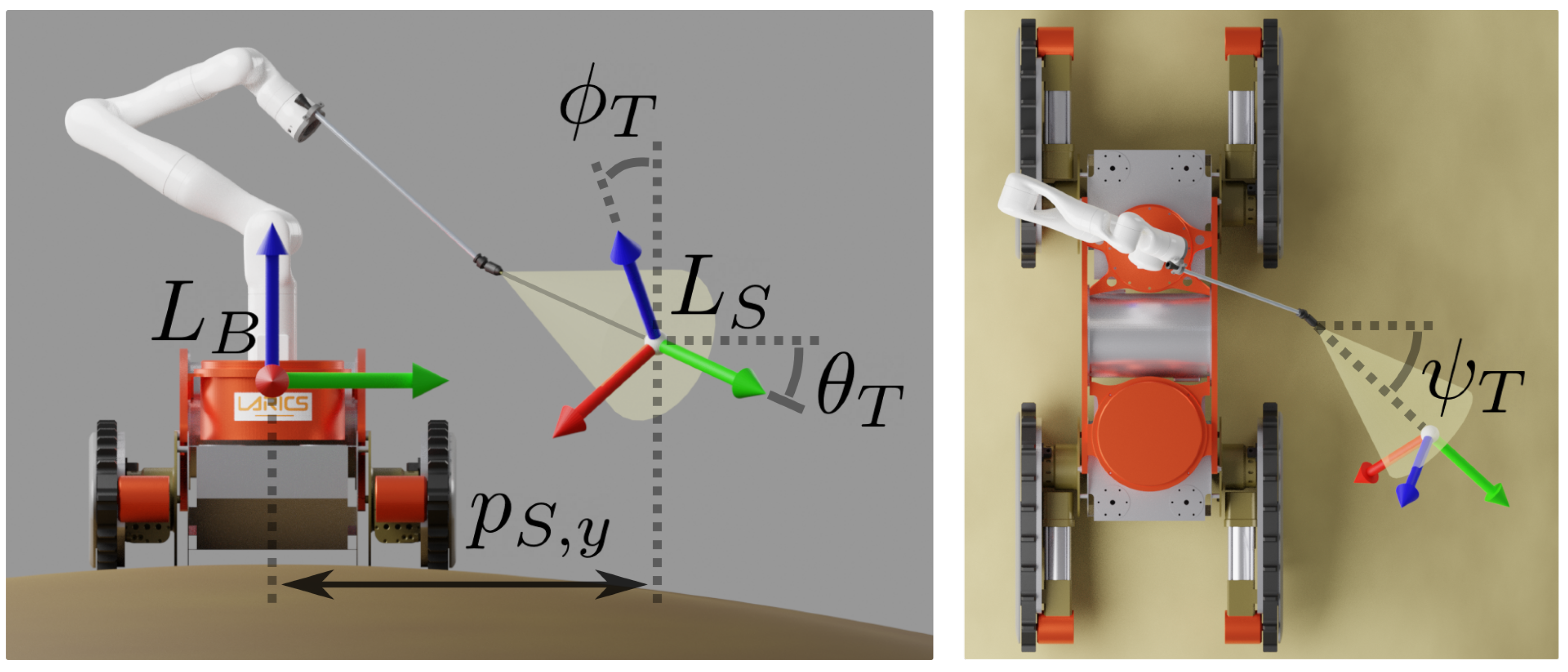
2.3. Manipulator Task Space Control
3. Results
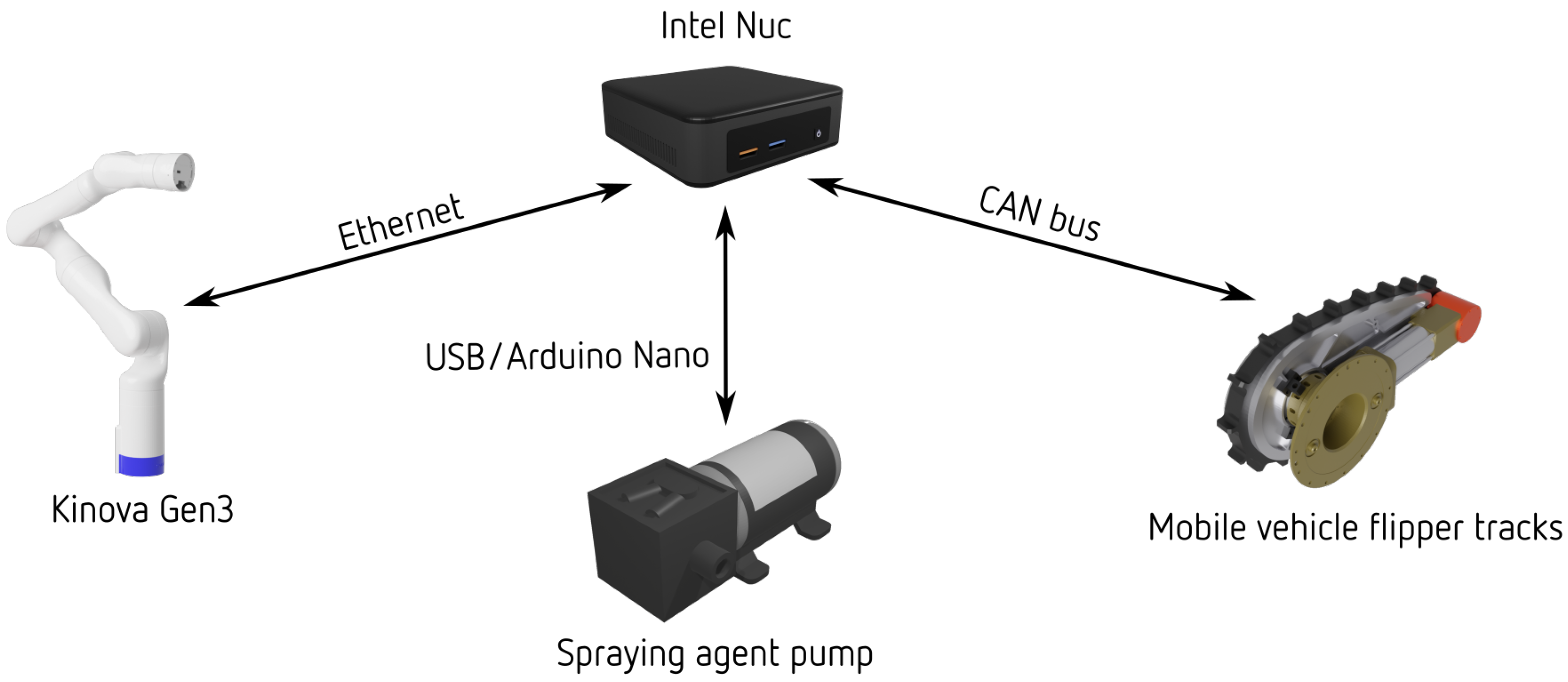
3.1. Equipment
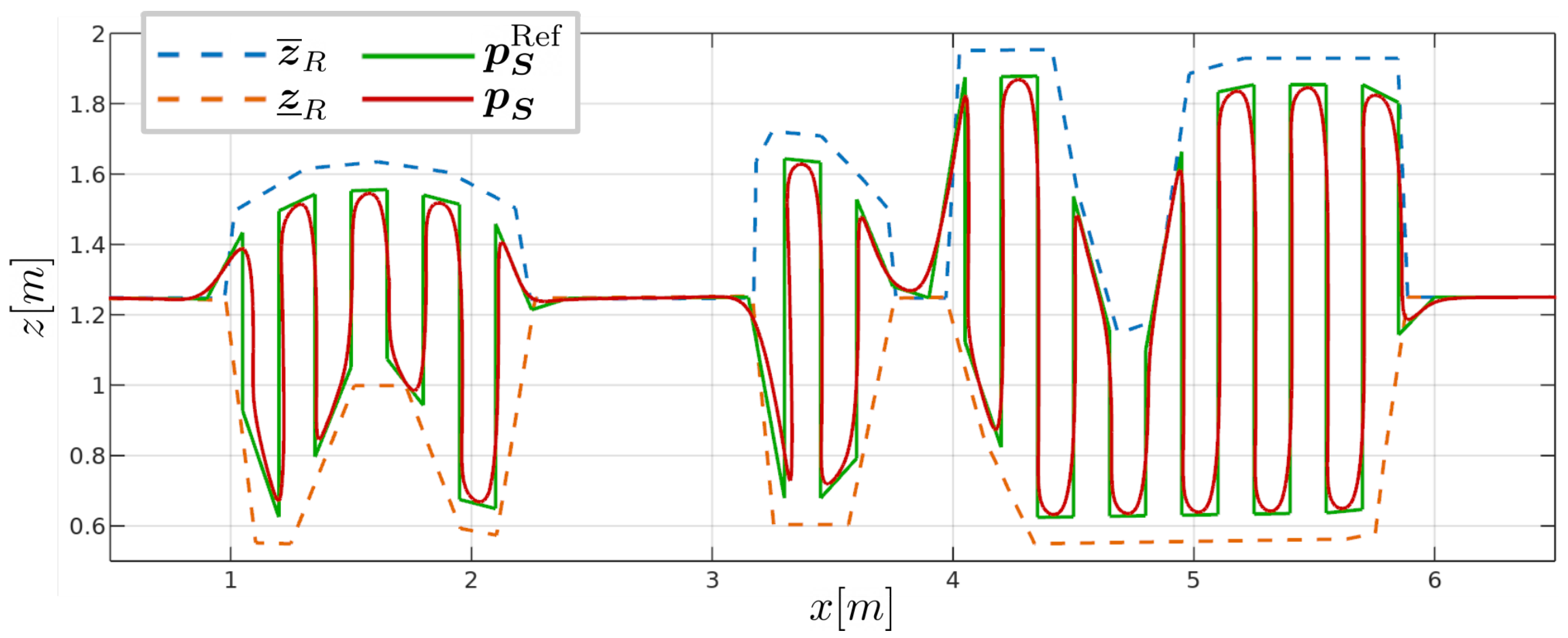
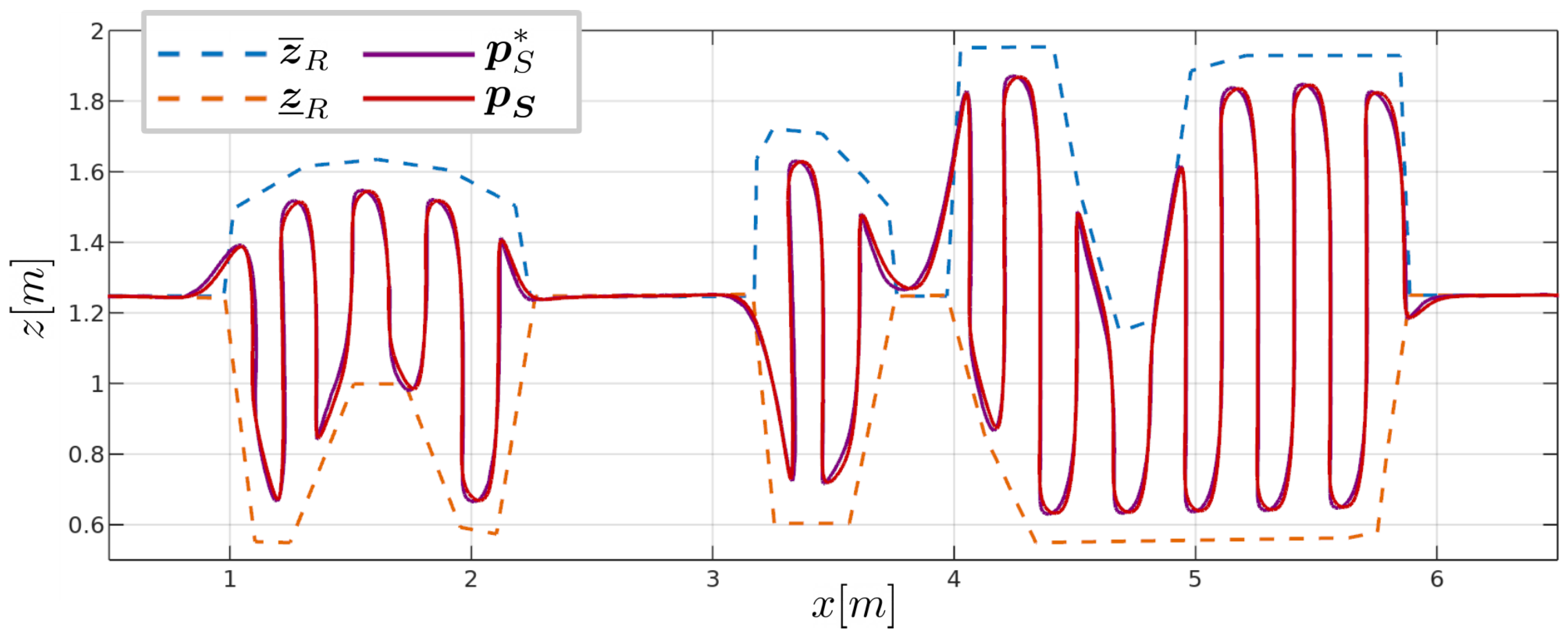
3.2. Vineyard Spraying Demonstration
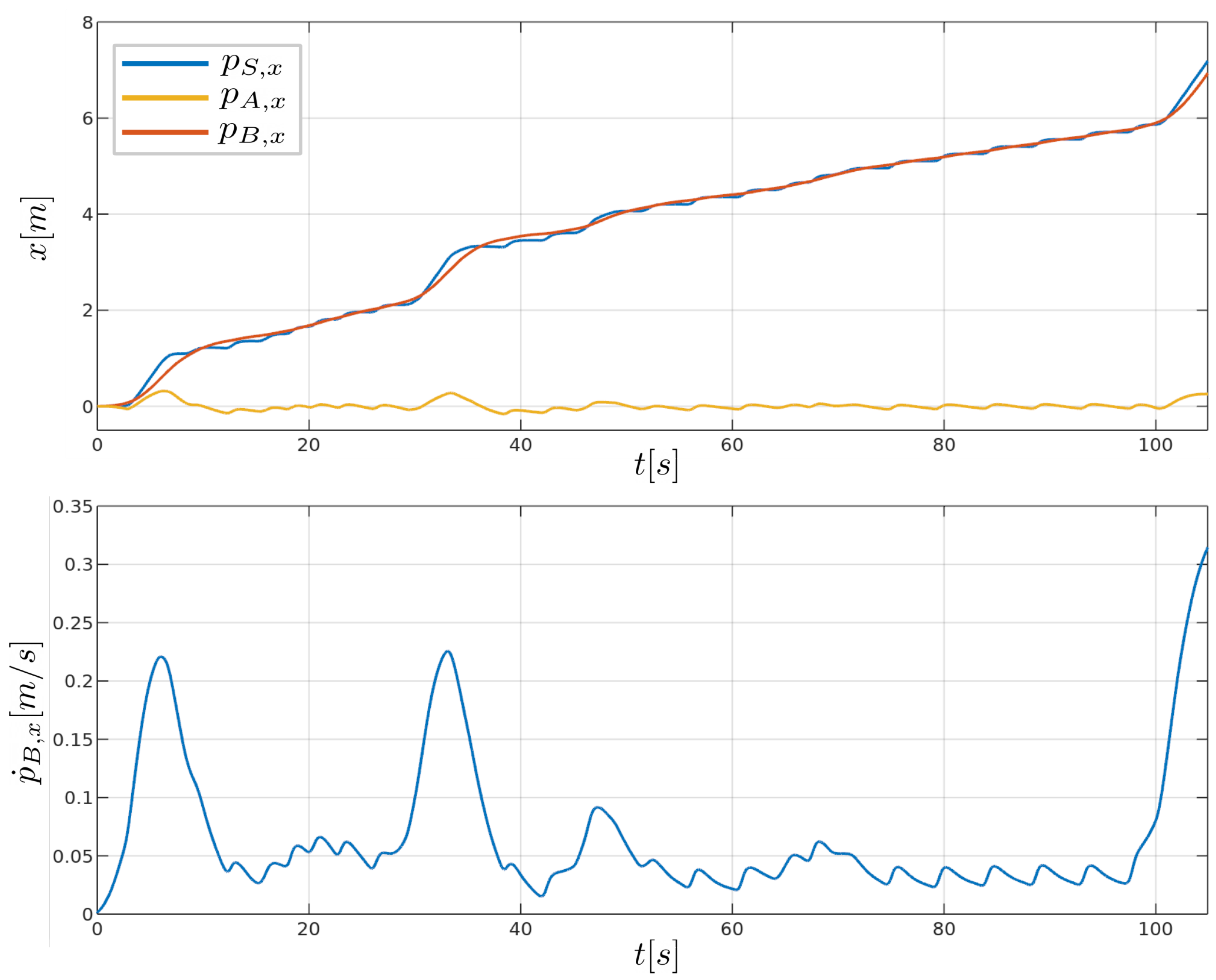
3.3. Optitrack Validation
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MPC | Model Predictive Control |
| QP | Quadratic Programming |
| CPU | Central Processing Unit |
| GUI | Graphical User Interface |
| RMS | Root Mean Square |
| ROS | Robot Operating System |
References
- Oliveira, L.F.P.; Moreira, A.P.; Silva, M.F. Advances in Agriculture Robotics: A State-of-the-Art Review and Challenges Ahead. Robotics 2021, 10, 52. [Google Scholar] [CrossRef]
- Adamides, G. Agricultural Robots in Targeted Spraying: A mini State-of-the-Art review. Robot. Autom. Eng. J. 2017, 2, 5581. [Google Scholar] [CrossRef]
- Hektor Project Website. Available online: hektor.fer.hr (accessed on 8 March 2022).
- Goričanec, J.; Kapetanović, N.; Vatavuk, I.; Hrabar, I.; Vasiljević, G.; Gledec, G.; Stuhne, D.; Bogdan, S.; Orsag, M.; Petrović, T.; et al. Heterogeneous autonomous robotic system in viticulture and mariculture-project overview. In Proceedings of the 2021 16th International Conference on Telecommunications (ConTEL), Zagreb, Croatia, 30 June–2 July 2021; pp. 181–188. [Google Scholar] [CrossRef]
- Monta, M.; Kondo, N.; Shibano, Y. Agricultural robot in grape production system. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 3, pp. 2504–2509. [Google Scholar] [CrossRef]
- Berenstein, R.; Shahar, O.B.; Shapiro, A.; Edan, Y. Grape clusters and foliage detection algorithms for autonomous selective vineyard sprayer. Intell. Serv. Robot. 2010, 3, 233–243. [Google Scholar] [CrossRef]
- Oberti, R.; Marchi, M.; Tirelli, P.; Calcante, A.; Iriti, M.; Hočevar, M.; Baur, J.; Pfaff, J.; Schütz, C.; Ulbrich, H. Selective spraying of grapevine’s diseases by a modular agricultural robot. J. Agric. Eng. 2013, 44, 149–153. [Google Scholar] [CrossRef]
- Oberti, R.; Marchi, M.; Tirelli, P.; Calcante, A.; Iriti, M.; Tona, E.; Hočevar, M.; Baur, J.; Pfaff, J.; Schütz, C.; et al. Selective spraying of grapevines for disease control using a modular agricultural robot. Biosyst. Eng. 2016, 146, 203–215. [Google Scholar] [CrossRef]
- de Soto, M.G.; Emmi, L.; Perez-Ruiz, M.; Aguera, J.; de Santos, P.G. Autonomous systems for precise spraying—Evaluation of a robotised patch sprayer. Biosyst. Eng. 2016, 146, 165–182. [Google Scholar] [CrossRef]
- Botterill, T.; Paulin, S.; Green, R.; Williams, S.; Lin, J.; Saxton, V.; Mills, S.; Chen, X.; Corbett-Davies, S. A Robot System for Pruning Grape Vines. J. Field Robot. 2016, 34, 1100–1122. [Google Scholar] [CrossRef]
- Berenstein, R. The use of agricultural robots in crop spraying/fertilizer applications. In Robotics and Automation for Improving Agriculture; Burleigh Dodds Science Publishing: Cambridge, UK, 2019; pp. 109–136. [Google Scholar] [CrossRef]
- Santos, L.; Santos, F.; Mendes, J.; Costa, P.; Lima, J.; Reis, R.; Shinde, P. Path Planning Aware of Robot’s Center of Mass for Steep Slope Vineyards. Robotica 2019, 38, 684–698. [Google Scholar] [CrossRef]
- Cantelli, L.; Bonaccorso, F.; Longo, D.; Melita, C.D.; Schillaci, G.; Muscato, G. A Small Versatile Electrical Robot for Autonomous Spraying in Agriculture. AgriEngineering 2019, 1, 391–402. [Google Scholar] [CrossRef]
- Santos, L.C.; Aguiar, A.S.; Santos, F.N.; Valente, A.; Ventura, J.B.; Sousa, A.J. Navigation Stack for Robots Working in Steep Slope Vineyard. In Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2020; pp. 264–285. [Google Scholar] [CrossRef]
- Santos, L.C.; Aguiar, A.S.; Santos, F.N.; Valente, A.; Petry, M. Occupancy Grid and Topological Maps Extraction from Satellite Images for Path Planning in Agricultural Robots. Robotics 2020, 9, 77. [Google Scholar] [CrossRef]
- de Aguiar, A.S.P.; dos Santos, F.B.N.; dos Santos, L.C.F.; de Jesus Filipe, V.M.; de Sousa, A.J.M. Vineyard trunk detection using deep learning—An experimental device benchmark. Comput. Electron. Agric. 2020, 175, 105535. [Google Scholar] [CrossRef]
- Sarri, D.; Lombardo, S.; Lisci, R.; Pascale, V.D.; Vieri, M. AgroBot Smash a Robotic Platform for the Sustainable Precision Agriculture. In Lecture Notes in Civil Engineering; Springer International Publishing: Cham, Switzerland, 2020; pp. 793–801. [Google Scholar] [CrossRef]
- Roure, F.; Moreno, G.; Soler, M.; Faconti, D.; Serrano, D.; Astolfi, P.; Bardaro, G.; Gabrielli, A.; Bascetta, L.; Matteucci, M. GRAPE: Ground Robot for vineyArd Monitoring and ProtEction. In ROBOT 2017: Third Iberian Robotics Conference; Springer International Publishing: Cham, Switzerland, 2017; pp. 249–260. [Google Scholar] [CrossRef]
- Astolfi, P.; Gabrielli, A.; Bascetta, L.; Matteucci, M. Vineyard Autonomous Navigation in the Echord++ GRAPE Experiment. IFAC-PapersOnLine 2018, 51, 704–709. [Google Scholar] [CrossRef]
- Kerkech, M.; Hafiane, A.; Canals, R. Vine disease detection in UAV multispectral images using optimized image registration and deep learning segmentation approach. Comput. Electron. Agric. 2020, 174, 105446. [Google Scholar] [CrossRef]
- Bouloumpasi, E.; Theocharis, S.; Karampatea, A.; Pavlidis, S.; Mamalis, S.; Koundouras, S.; Merou, T.; Vrochidou, E.; Pachidis, T.; Manios, M.; et al. Exploration of viticultural tasks to be performed by an autonomous robot: Possibilities and limitations. In Proceedings of the 11th International Scientific Agriculture Symposium (AGROSYM 2020), Jahorina, Bosnia and Herzegovina, 8–9 October 2020; pp. 56–61. [Google Scholar]
- Vrochidou, E.; Tziridis, K.; Nikolaou, A.; Kalampokas, T.; Papakostas, G.A.; Pachidis, T.P.; Mamalis, S.; Koundouras, S.; Kaburlasos, V.G. An Autonomous Grape-Harvester Robot: Integrated System Architecture. Electronics 2021, 10, 1056. [Google Scholar] [CrossRef]
- Adamides, G.; Katsanos, C.; Constantinou, I.; Christou, G.; Xenos, M.; Hadzilacos, T.; Edan, Y. Design and development of a semi-autonomous agricultural vineyard sprayer: Human-robot interaction aspects. J. Field Robot. 2017, 34, 1407–1426. [Google Scholar] [CrossRef]
- Ren, S.; Xie, Y.; Yang, X.; Xu, J.; Wang, G.; Chen, K. A Method for Optimizing the Base Position of Mobile Painting Manipulators. IEEE Trans. Autom. Sci. Eng. 2017, 14, 370–375. [Google Scholar] [CrossRef]
- Liu, G.; Sun, X.; Liu, Y.; Liu, T.; Li, C.; Zhang, X. Automatic spraying motion planning of a shotcrete manipulator. Intell. Serv. Robot. 2021. [Google Scholar] [CrossRef]
- Wang, G.; Yu, Q.; Ren, T.; Hua, X.; Chen, K. Task planning for mobile painting manipulators based on manipulating space. Assem. Autom. 2018, 38, 57–66. [Google Scholar] [CrossRef]
- Wieber, P.B. Trajectory Free Linear Model Predictive Control for Stable Walking in the Presence of Strong Perturbations. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006. [Google Scholar] [CrossRef]
- Pankert, J.; Hutter, M. Perceptive Model Predictive Control for Continuous Mobile Manipulation. IEEE Robot. Autom. Lett. 2020, 5, 6177–6184. [Google Scholar] [CrossRef]
- Elsisi, M. Optimal design of nonlinear model predictive controller based on new modified multitracker optimization algorithm. Int. J. Intell. Syst. 2020, 35, 1857–1878. [Google Scholar] [CrossRef]
- Elsisi, M.; Ebrahim, M.A. Optimal design of low computational burden model predictive control based on SSDA towards autonomous vehicle under vision dynamics. Int. J. Intell. Syst. 2021, 36, 6968–6987. [Google Scholar] [CrossRef]
- Elsisi, M. Improved grey wolf optimizer based on opposition and quasi learning approaches for optimization: Case study autonomous vehicle including vision system. Artif. Intell. Rev. 2022. [Google Scholar] [CrossRef]
- Furuno, S.; Yamamoto, M.; Mohri, A. Trajectory planning of mobile manipulator with stability considerations. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Newport Beach, CA, USA, 14–19 September 2003. [Google Scholar] [CrossRef]
- Avanzini, G.B.; Zanchettin, A.M.; Rocco, P. Constrained model predictive control for mobile robotic manipulators. Robotica 2017, 36, 19–38. [Google Scholar] [CrossRef]
- Minniti, M.V.; Farshidian, F.; Grandia, R.; Hutter, M. Whole-Body MPC for a Dynamically Stable Mobile Manipulator. IEEE Robot. Autom. Lett. 2019, 4, 3687–3694. [Google Scholar] [CrossRef]
- Korayem, M.; Nazemizadeh, M.; Azimirad, V. Optimal trajectory planning of wheeled mobile manipulators in cluttered environments using potential functions. Sci. Iran. 2011, 18, 1138–1147. [Google Scholar] [CrossRef][Green Version]
- Mészáros, C. The BPMPD interior point solver for convex quadratic problems. Optim. Methods Softw. 1999, 11, 431–449. [Google Scholar] [CrossRef]






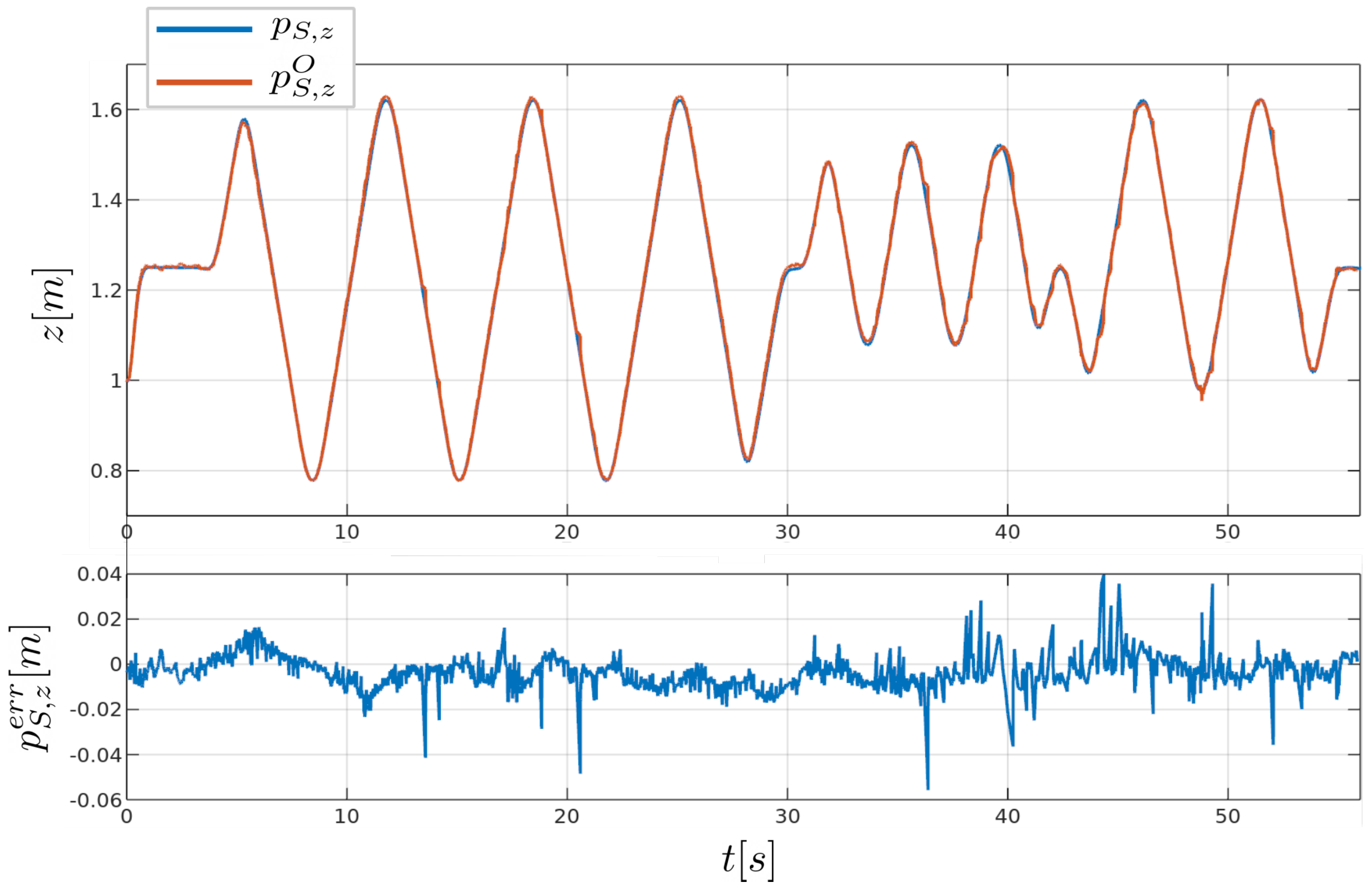
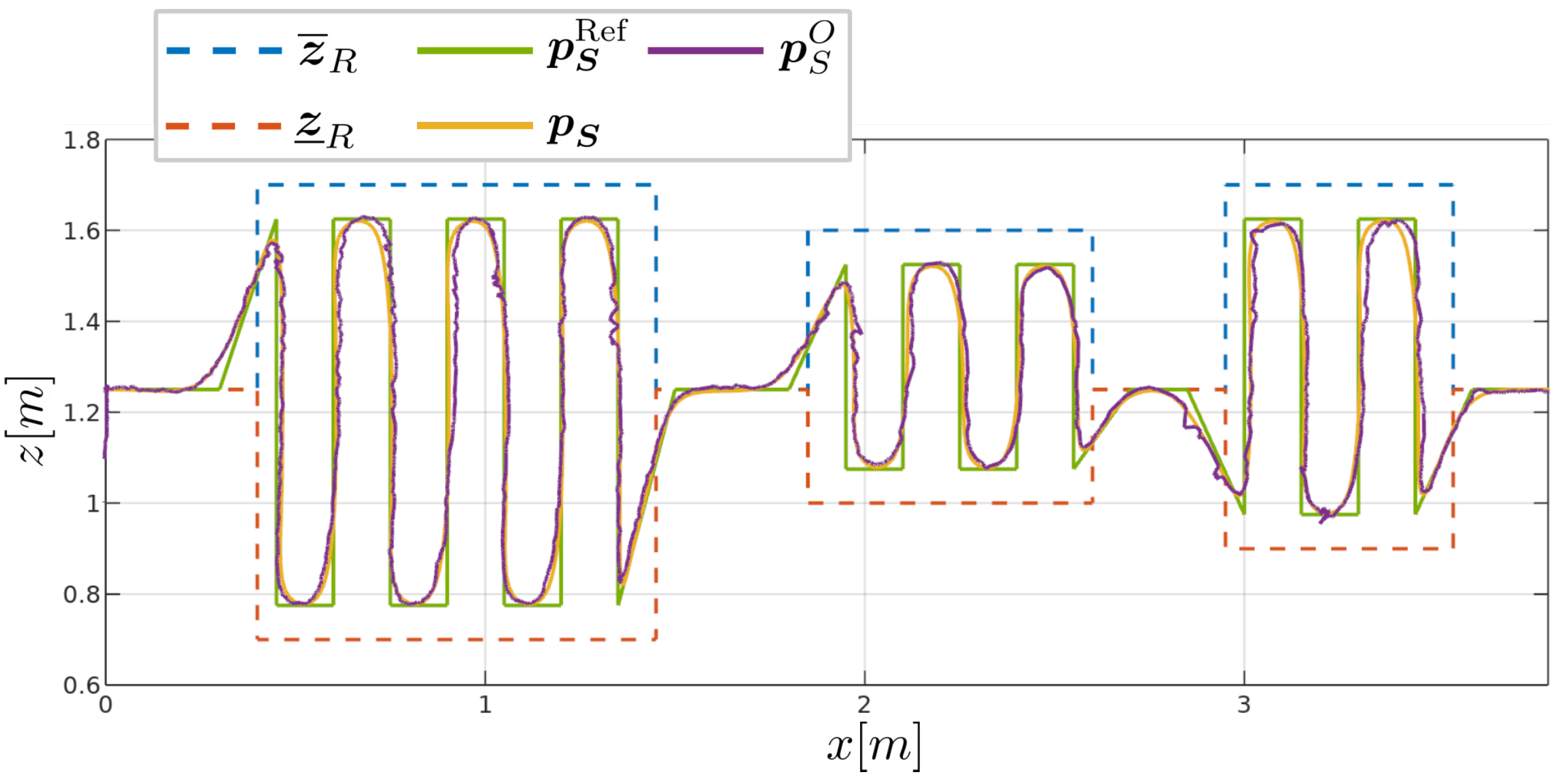
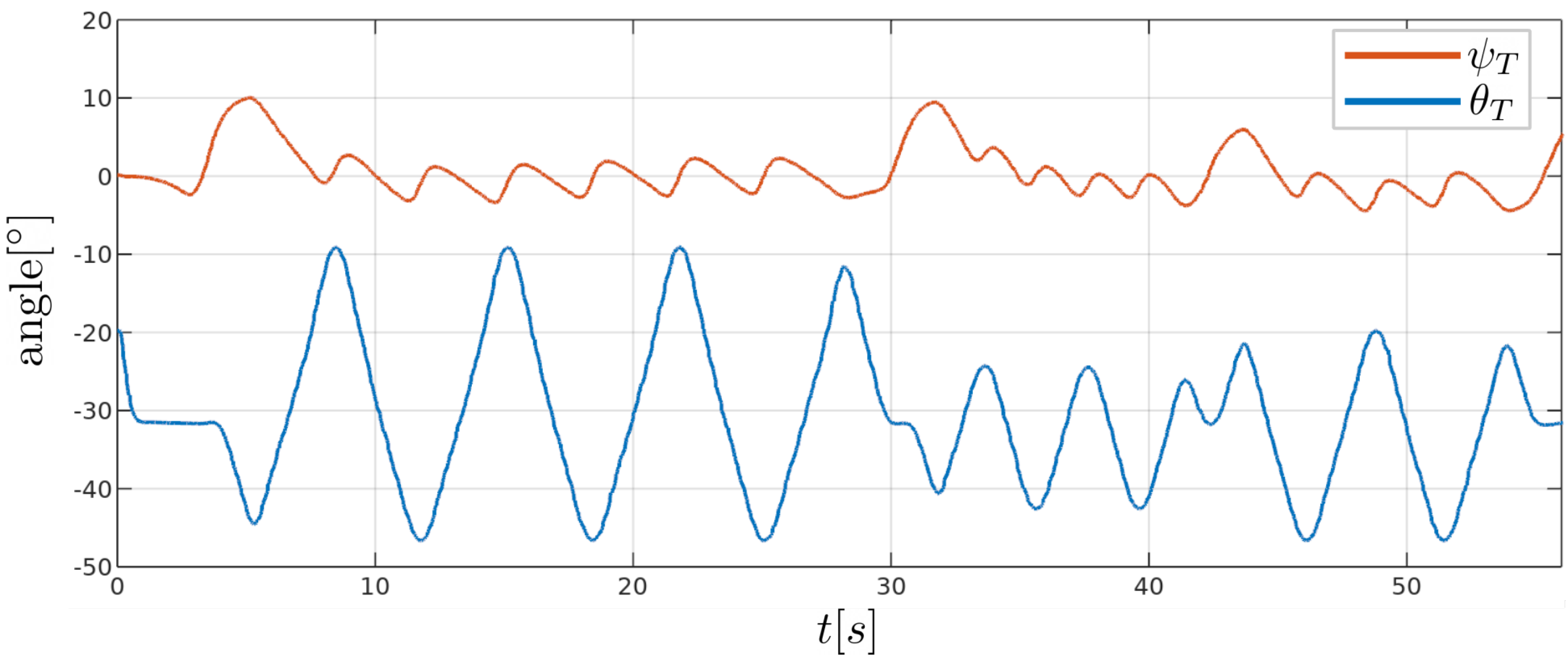
| RMS error [mm] | 4.32 | 0.90 | 3.60 | 2.20 |
| max error [mm] | 22.16 | 3.92 | 22.16 | 18.93 |
| RMS error [mm] | 9.76 | 7.86 | 5.79 |
| max error [mm] | 52.81 | 36.59 | 52.779 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vatavuk, I.; Vasiljević, G.; Kovačić, Z. Task Space Model Predictive Control for Vineyard Spraying with a Mobile Manipulator. Agriculture 2022, 12, 381. https://doi.org/10.3390/agriculture12030381
Vatavuk I, Vasiljević G, Kovačić Z. Task Space Model Predictive Control for Vineyard Spraying with a Mobile Manipulator. Agriculture. 2022; 12(3):381. https://doi.org/10.3390/agriculture12030381
Chicago/Turabian StyleVatavuk, Ivo, Goran Vasiljević, and Zdenko Kovačić. 2022. "Task Space Model Predictive Control for Vineyard Spraying with a Mobile Manipulator" Agriculture 12, no. 3: 381. https://doi.org/10.3390/agriculture12030381
APA StyleVatavuk, I., Vasiljević, G., & Kovačić, Z. (2022). Task Space Model Predictive Control for Vineyard Spraying with a Mobile Manipulator. Agriculture, 12(3), 381. https://doi.org/10.3390/agriculture12030381







