Design and Working Parameter Optimization of Pneumatic Reciprocating Seedling-Picking Device of Automatic Transplanter
Abstract
1. Introduction
2. Device Structure and Working Principle
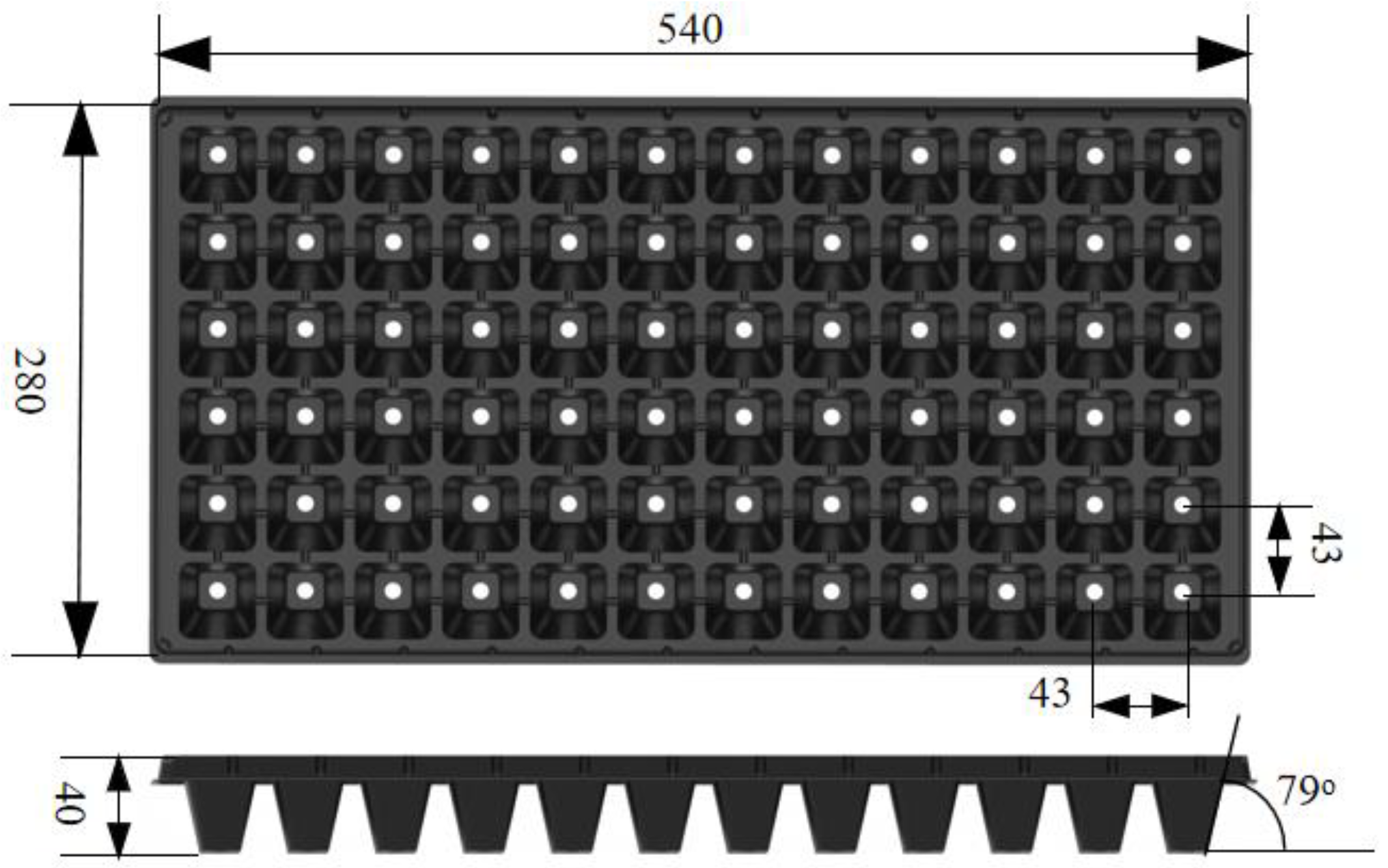
2.1. Seedling Tray Specifications
2.2. Structure of the Device
2.3. Working Principle
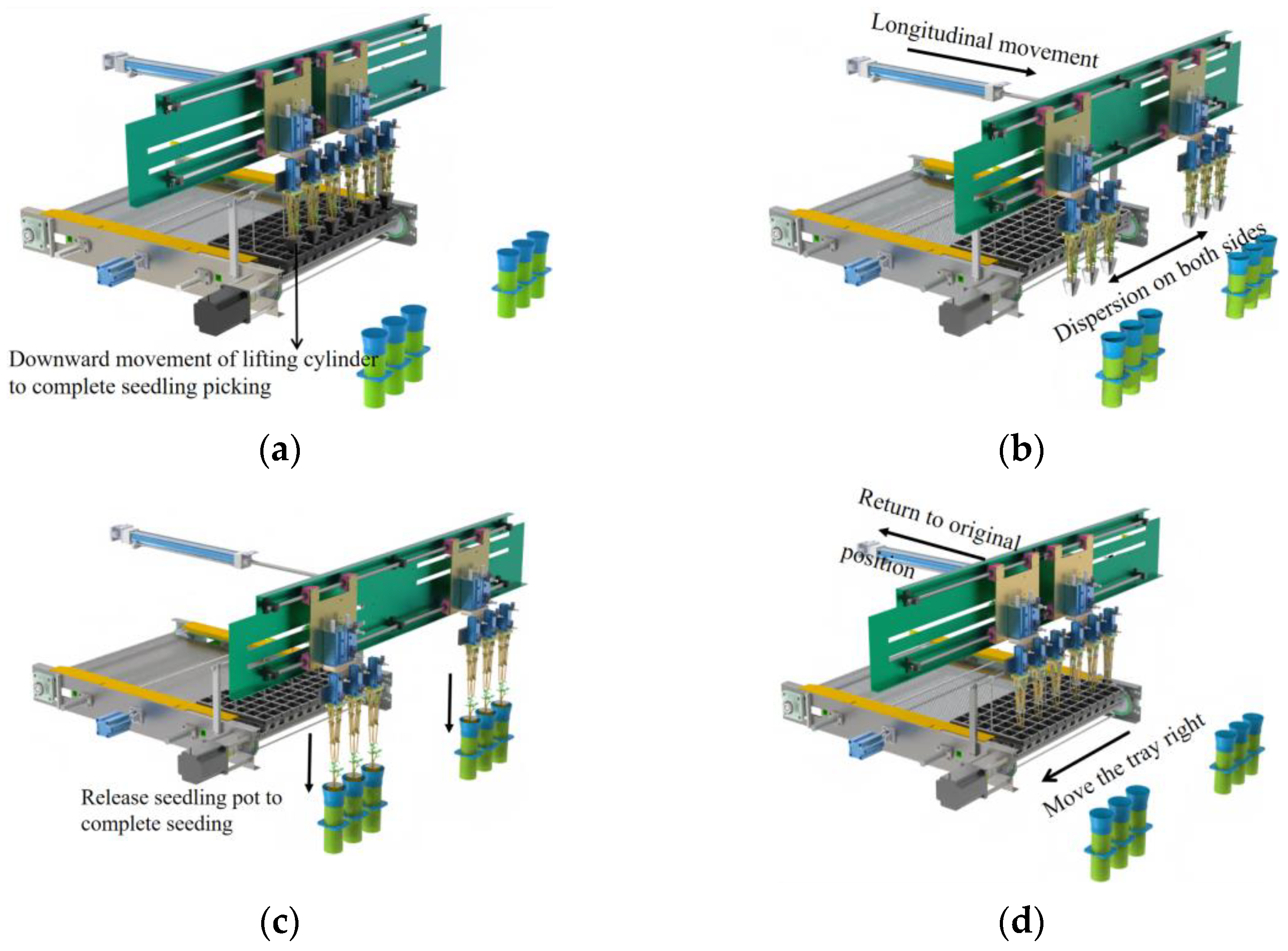
- The seedling tray is placed on the conveying device and the stepping motor rotates and drives the chain stopper forward to push the tray for longitudinal conveying. When the sensor recognizes the seedling tray, the stepping motor stops, and the stopping position is the position point for picking seedlings.
- As shown in Figure 3a, when the seedling tray reaches the seedling-picking position, the seedling-picking execution component installed on the seedling-picking mounting plate will pick up the seedlings. The air cylinder drives the seedling-fetching claws to grip the pot body. When the lifting cylinder triggers the magnetic switch at the lower limit of the cylinder, it starts to move upward. At this time, the seedling pot is driven from the seedling tray by the seedling fetching claws, and the seedling removal is completed.
- The two sides of the seedling-picking plate are connected to the linear slide rails installed on the seedling-picking frame, which can achieve straightforward sliding of the seedling-picking mechanism. The horizontal cylinder drives the end execution components of the seedlings to complete the dispersing action and transports the seedling pots to the seedling-throwing position and waits for the seedlings to be thrown, as shown in Figure 3b.
- When the seedling-throwing command is triggered, the lifting cylinder moves downwards, and at the same time, the clamping cylinder moves in the opposite direction to release the seedling pot, and the seedling pot falls into the seedling guide tube by its own weight to complete the seedling throwing action.
- As shown in Figure 3d, the seedling tray conveying device is moved to the right by a distance of one hole spacing (43 mm), and the combined action of the longitudinal driving cylinder and the horizontal driving cylinder returns to the position of picking seedlings, ready to complete the next cycle of seedling picking and throwing.
3. Design and Analysis of Key Components
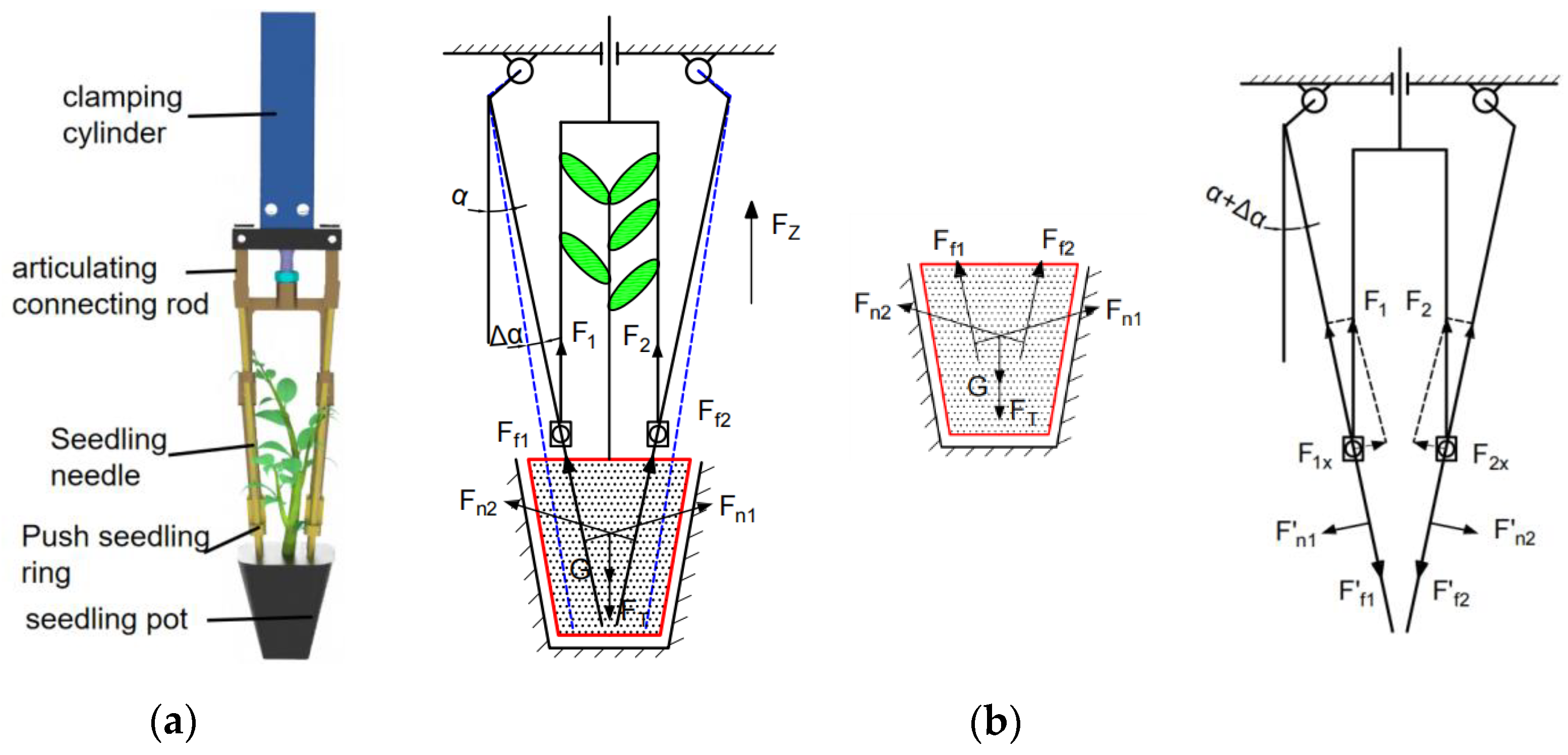
3.1. Design of Seedling-Picking Claw
3.1.1. Principle of Clamping Seedling
3.1.2. Mechanical Analysis of Seedling Claws and Seedling Pot
3.2. Selection and Calculation of Pneumatic Components of Seedling-Picking Mechanism
3.3. Design of Pneumatic System
4. Optimization of Cylinder Working Parameters
4.1. Analysis of Optimization Goals
4.2. AMESim Simulation Analysis of Longitudinal Cylinder Pneumatic Control Circuit
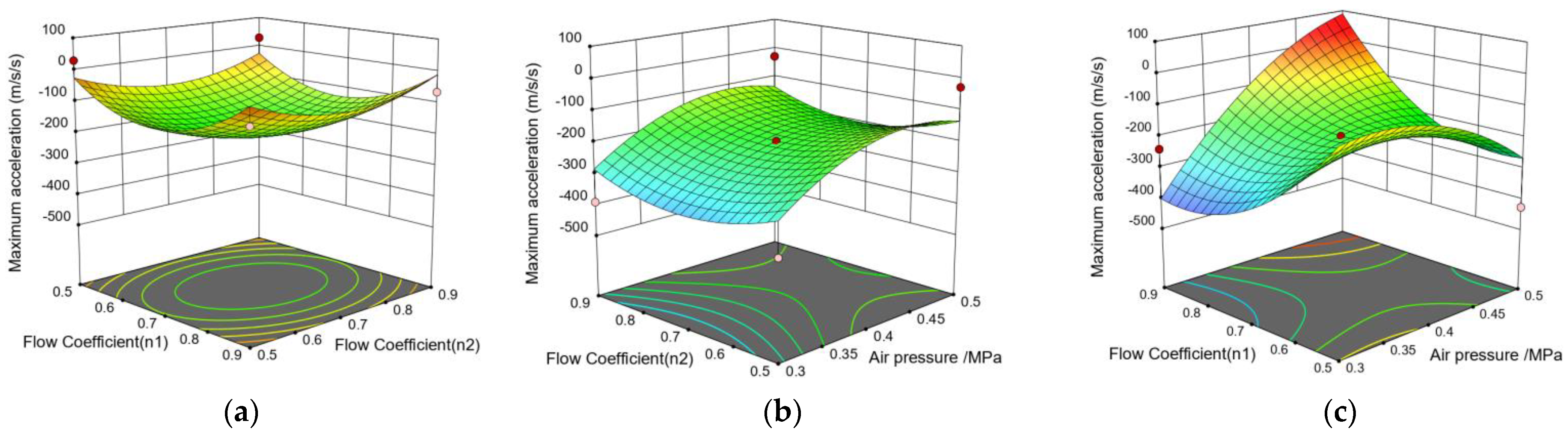
4.3. Optimization of Aerodynamic Parameters Based on Response Surface Method
4.4. Comparative Analysis of Cylinder Parameter Optimization Results
5. Test of the Seedling-Picking Mechanism
5.1. Test Conditions
5.2. Test Design and Evaluation Index
5.3. Test Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Syed, T.N.; Jizhan, L.; Xin, Z.; Shengyi, Z.; Yan, Y.; Mohamed, S.H.A.; Lakhiar, I.A. Seedling-lump integrated non-destructive monitoring for automatic transplanting with Intel RealSense depth camera. Artif. Intell. Agric. 2019, 3, 18–32. [Google Scholar] [CrossRef]
- Hu, J.; Chang, H.; Yang, L. Design and experiment of control system for automatic transplanter picking up and spacing casting whole row of seedlings [J/OL]. Trans. Chin. Soc. Agric. Mach. 2018, 49, 78–84. [Google Scholar]
- Imran, M.; Manan, M.A.; Khalil, A.; MdNaim, M.; Ahmad, R. Design of transplanting mechanism for system of rice intensification (SRI) transplanter in Kedah, Malaysia. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Melaka, Malaysia, 6–7 May 2017; p. 012036. [Google Scholar]
- Han, C.; Xu, Y.; You, J.; Zhang, J.; Yuan, P. Parameter optimization of opener of semi-automatic transplanter for watermelon seedlings raised on compression substrate. Trans. CSAE 2019, 35, 48–56. [Google Scholar]
- Ji, J.; Cheng, Q.; Jin, X.; Zhang, Z.; Xie, X.; Li, M. Design and test of 2ZLX-2 transplanting machine for oil peony. Int. J. Agric. Biol. Eng. 2020, 13, 61–69. [Google Scholar] [CrossRef]
- Kumar, G.P.; Raheman, H. Development of a walk-behind type hand tractor powered vegetable transplanter for paper pot seedlings. Biosyst. Eng. 2011, 110, 189–197. [Google Scholar] [CrossRef]
- Paradkar, V.; Raheman, H.; Rahul, K. Development of a metering mechanism with serial robotic arm for handling paper pot seedlings in a vegetable transplanter. Artif. Intell. Agric. 2021, 5, 52–63. [Google Scholar] [CrossRef]
- Xie, S.; Yang, S.; Liu, J.; Song, L.; Xie, Q.; Duan, T. Development of the seedling taking and throwing device with oblique insertion and plug clipping for vegetable transplanters. Trans. CSAE 2020, 36, 1–10. [Google Scholar]
- Tsuga, K. Development of fully automatic vegetable transplanter. Jpn. Agric. Res. Q. 2000, 34, 21–28. [Google Scholar]
- Choi, W.C.; Kim, D.C.; Ryu, I.H.; Kim, K.U. Development of a seedling pick–up device for vegetable transplanters. Trans. ASAE 2002, 45, 13. [Google Scholar]
- Gaohong, Y.; Lei, W.; Liang, S.; Xiong, Z.; Bingliang, Y. Advancement of Mechanized Transplanting Technology and Equipments for Field Crops. Trans. Chin. Soc. Agric. Mach. 2022, 53, 1–20. [Google Scholar]
- Cui, W.; Fang, X.; Zhao, L.; Song, J.; Lin, J.; Dong, X. Structural optimization and experimental verification of geared five-bar linkage seedling pick-up device. Trans. Chin. Soc. Agric. Mach. 2013, 44, 74–77. [Google Scholar]
- Jin, X.; Li, D.; Ma, H.; Ji, J.; Zhao, K.; Pang, J. Development of single row automatic transplanting device for potted vegetable seedlings. Int. J. Agric. Biol. Eng. 2018, 11, 67–75. [Google Scholar] [CrossRef]
- Sun, L.; Shen, J.; Zhou, Y.; Ye, Z.; Yu, G.; Wu, C. Design of non-circular gear linkage combination driving type vegetable pot seedling transplanting mechanism. Trans. CSAE 2019, 35, 26–33. [Google Scholar]
- Li, H.; Cao, W.; Li, S.; Liu, J.; Chen, B.; Ma, X. Development of 2ZXM-2 automatic plastic film mulching plug seedling transplanter for vegetable. Trans. Chin. Soc. Agric. Eng. 2017, 33, 23–33. [Google Scholar]
- Ye, B.; Yu, G.; Chen, Z.; Zhao, Y. Kinematics modeling and parameters optimization of seedling pick-up mechanism of planetary gear train with eccentric gear andnon-circular gear. Trans. Chin. Soc. Agric. Eng. 2011, 27, 7–12. [Google Scholar]
- Gaohong, Y.; Tengfei, Y.; Bingliang, Y. Design of a rotary plug seedling pick-up mechanism. J. Mech. Eng. 2015, 51, 67–76. [Google Scholar]
- Dang, Y.; Jin, X.; Li, H.; Wang, J.; Lu, Y.; Ding, B. Design of single-degree-of-freedom four-bar seedling-taking and throwing manipulator. Trans. CSAE 2019, 35, 39–47. [Google Scholar]
- Wei, G.; Liang, Z.; Lijing, L.; Zhongjun, L.; Jinhu, Z.; Zhenghin, Z. Kinematic Analysis and Experiment of Rotary Pick-up Mechanism on Seedling Pick-up Device. Trans. Chin. Soc. Agric. Mach. 2020, 51, 79–84+98. [Google Scholar]
- Liu, J.; Cao, W.; Tian, D.; Ouyang, Y.; Zhao, H. Optimization experiment of transplanting actuator parameters based on mechanical property of seedling pot. Trans. Chin. Soc. Agric. Eng. 2016, 32, 32–39. [Google Scholar]
- Yang, Q.; Huang, G.; Shi, X.; He, M.; Ahmad, I.; Zhao, X.; Addy, M. Design of a control system for a mini-automatic transplanting machine of plug seedling. Comput. Electron. Agric. 2020, 169, 105226. [Google Scholar] [CrossRef]
- Bingliang, Y.; Tao, T.; Gaohong, Y.; Weiming, Y.; Guofeng, Z. Dynamic analysis of rotary seedling pick-up mechanism of vegetable transplanting machine with counterweight. Trans. Chin. Soc. Agric. Mach. 2019, 50, 117–122. [Google Scholar]
- Ye, B.; Li, L.; Yu, G.; Liu, A.; Zhao, Y. Dynamics analysis and test of rotary pick-up mechanism for vegetable pot-seedling. Trans. Chin. Soc. Agric. Mach. 2014, 45, 70–78. [Google Scholar]
- Wang, Y.; Yu, H. Experiment and analysis of impact factors for soil matrix intact rate of manipulator for picking-up plug seedlings. Trans. Chin. Soc. Agric. Eng. 2015, 31, 65–71. [Google Scholar]
- Jin, X.; Li, S.; Yang, X. Analysis and parameter optimization for vegetable plug seedling pick-up mechanism [J/OL]. Trans. Chin. Soc. Agric. Mach. 2013, 44, 1–6. [Google Scholar]
- Han, C.; Yang, W.; Zhang, X.; Guo, H.; Yin, W. Design and test of automatic feed system for tray seedlings transplanter. Trans. Chin. Soc. Agric. Eng. 2013, 29, 51–61. [Google Scholar]
- Ryu, K.H.; Kim, G.; Han, J. Development of a robotic transplanter for bedding plants. J. Agric. Eng. Res. 2001, 78, 141–146. [Google Scholar] [CrossRef]
- Feng, Q.; Zhao, C.; Jiang, K.; Fan, P.; Wang, X. Design and test of tray-seedling sorting transplanter. Int. J. Agric. Biol. Eng. 2015, 8, 14–20. [Google Scholar]
- Han, L.; Mao, H.; Miao, X.; Hu, J.; Yang, X. Design of automatic picking up seedling end-effector based on mechanical properties of plug seedlings. Trans. Chin. Soc. Agric. Mach. 2013, 44, 260–265. [Google Scholar]
- Cheng, D. Mechanical Design Manual Booklet—Pneumatic Transmission; Chemistry Industry Press: Beijing, China, 2016. [Google Scholar]
- Qiu, Z.-C.; Shi, M.-L.; Wang, B.; Xie, Z.-W. Genetic algorithm based active vibration control for a moving flexible smart beam driven by a pneumatic rod cylinder. J. Sound Vib. 2012, 331, 2233–2256. [Google Scholar] [CrossRef]
- Song, C.; He, M. Research on cylinder buffer control based on AMESim. In Proceedings of the 21st International Conference on Industrial Engineering and Engineering Management 2014, Selangor Darul Ehsan, Malaysia, 9–12 December 2014; Atlantis Press: Paris, France, 2015; pp. 331–333. [Google Scholar]
- Ministry of Industry and Information Technology of the People’s Republic of China. JB/T10291-2013 Industry Standard for Dry Land Planting Machinery; Machinery Industry Press: Beijing, China, 2013.






| Cylinder Name | Working Air Pressure/MPa | Stroke/mm | Load/kg | Cylinder Inner Diameter/mm |
|---|---|---|---|---|
| Horizontal cylinder | 0.4 | 200 | 6.5 | ≥12.9 |
| Longitudinal cylinder | 0.4 | 400 | 28.66 | ≥28.6 |
| Cylinder Name | Type | Frequency | Diameter/cm | Stroke/cm | Number | Air Consumption/(L·min−1) |
|---|---|---|---|---|---|---|
| Clamping cylinder | MD 16 × 40 | 24 | 1.6 | 4 | 6 | 11.58 |
| Lifting cylinder | TCL 25 × 50-S | 24 | 2.5 | 5 | 2 | 11.78 |
| Horizontal cylinder | MA 16 × 200-S | 24 | 1.6 | 20 | 2 | 19.30 |
| Longitudinal cylinder | SC 32 × 400-S | 24 | 3.2 | 40 | 1 | 77.20 |
| Sum | 119.86 |
| Cylinder Name | Operating Time/s | Stroke/mm | Velocity/(m·s−1) | Load/kg | Kinetic Energy/J |
|---|---|---|---|---|---|
| Clamping cylinder | 0.5 | 40 | 80 | 0.2 | 0.00 |
| Lifting cylinder | 0.5 | 50 | 100 | 4.2 | 0.02 |
| Horizontal cylinder | 1 | 200 | 200 | 6.5 | 0.13 |
| Longitudinal cylinder | 1 | 400 | 400 | 28.66 | 2.29 |
| Parameter | Name | Value | Units |
|---|---|---|---|
| K | Air insulation parameters | 1.4 | —— |
| Ps | Air pressure | 0.3–0.5 | MPa |
| M | Load (Seedling execution component) | 28.66 | kg |
| Fs | Load static friction | 10 | N |
| Ff | Load sliding friction | 12 | N |
| D | Cylinder piston diameter | 32 | mm |
| d | Diameter of cylinder piston rod | 12 | mm |
| Ln | Cylinder buffer stroke | 21 | mm |
| k | Cylinder cushion material stiffness | 2855 | N/mm |
| c | Cylinder cushion material damping | 12 | N/(mm/s) |
| Serial Number | Air Source Pressure (p1/MPa) | Flow Coefficient of Speed-Control Valve (n1) | Flow Coefficient of Safety Valve (n2) |
Maximum Speed of Cylinder (vmax/m·s−1) | Time to Stabilize (tst/s) | Maximum Acceleration (amax/m·s−2) |
|---|---|---|---|---|---|---|
| 1 | 0.40 | 0.70 | 0.70 | 1.53814 | 0.92 | −196.265 |
| 2 | 0.50 | 0.70 | 0.50 | 1.60269 | 0.87 | −28.6913 |
| 3 | 0.30 | 0.70 | 0.50 | 1.42448 | 1.00 | −391.005 |
| 4 | 0.40 | 0.70 | 0.70 | 1.53814 | 0.92 | −196.265 |
| 5 | 0.30 | 0.70 | 0.90 | 1.42447 | 1.00 | −391.09 |
| 6 | 0.40 | 0.90 | 0.50 | 1.51998 | 0.92 | −65.5597 |
| 7 | 0.40 | 0.90 | 0.90 | 1.52002 | 0.92 | −65.6388 |
| 8 | 0.50 | 0.70 | 0.90 | 1.60272 | 0.87 | −28.692 |
| 9 | 0.40 | 0.50 | 0.90 | 1.52029 | 0.93 | 28.8986 |
| 10 | 0.40 | 0.70 | 0.70 | 1.53814 | 0.92 | −196.265 |
| 11 | 0.30 | 0.90 | 0.70 | 1.42971 | 1.00 | −240.411 |
| 12 | 0.50 | 0.50 | 0.70 | 1.62299 | 0.87 | −426.561 |
| 13 | 0.40 | 0.70 | 0.70 | 1.53814 | 0.92 | −196.265 |
| 14 | 0.30 | 0.50 | 0.70 | 1.41166 | 1.00 | −24.2564 |
| 15 | 0.40 | 0.50 | 0.50 | 1.52029 | 0.93 | 28.9134 |
| 16 | 0.40 | 0.70 | 0.70 | 1.53814 | 0.92 | −196.265 |
| 17 | 0.50 | 0.90 | 0.70 | 1.60886 | 0.86 | 37.4641 |
| Name | Optimization Goal | Upper Limit | Lower Limit |
|---|---|---|---|
| Cylinder stabilization time (s) | minimum | 1.000 | 0.860 |
| Maximum acceleration of cylinder operation (m·s−2) | minimum | 37.464 | −426.561 |
| Cylinder running maximum speed (m·s−1) | maximum | 1.623 | 1.412 |
| Name | Goal | Lower Limit | Upper Limit | Lower Weight | Upper Weight | Importance |
|---|---|---|---|---|---|---|
| Air Source Pressure () | within rang | 0.300 | 0.500 | 1 | 1 | 3 |
| Flow Coefficient () | within rang | 0.500 | 0.900 | 1 | 1 | 3 |
| Flow Coefficient () | within rang | 0.500 | 0.900 | 1 | 1 | 3 |
| Serial Number | Air Source Pressure (p1/MPa) | Flow Coefficient (n1) | Flow Coefficient (n2) |
Maximum Speed (vmax/m·s−1) | Time to Stabilize (tst/s) | Maximum Acceleration (amax/m·s−2) | Desirability |
|---|---|---|---|---|---|---|---|
| 1 | 0.50 | 0.87 | 0.70 | 1.60382 | 0.867559 | 37.4551 | 0.946 |
| 2 | 0.50 | 0.87 | 0.71 | 1.60382 | 0.867559 | 37.4612 | 0.946 |
| 3 | 0.50 | 0.87 | 0.71 | 1.60382 | 0.86756 | 37.4589 | 0.946 |
| Seedling Frequency | The Total Number of Pot Seedlings (N) | The Number of Missing Seedlings (q) | The Number of Damaged Seedlings (n) | The Number of Damaged Pots (m) | Damage Rate of Pot Body (%) | Average Damage Rate of Pot Body (%) | The Success Rate of Taking Seedlings (%) | Average Seedling Success Rate (%) |
|---|---|---|---|---|---|---|---|---|
| 120 plants·min−1 (Before optimization) | 216 | 2 | 2 | 4 | 1.9 | 1.7 | 96.3 | 96.4 |
| 216 | 1 | 2 | 3 | 1.4 | 97.2 | |||
| 216 | 3 | 2 | 4 | 1.9 | 95.8 | |||
| 120 plants·min−1 (optimized) | 216 | 2 | 1 | 1 | 0.5 | 0.7 | 98.1 | 97.9 |
| 216 | 2 | 1 | 2 | 0.9 | 97.6 | |||
| 216 | 1 | 1 | 2 | 0.9 | 98.1 | |||
| 144 plants·min−1 (Before optimization) | 216 | 3 | 4 | 10 | 4.6 | 4.3 | 92.1 | 92.4 |
| 216 | 3 | 3 | 8 | 3.7 | 93.5 | |||
| 216 | 4 | 4 | 10 | 4.6 | 91.6 | |||
| 144 plants·min−1 (optimized) | 216 | 3 | 3 | 3 | 1.4 | 1.6 | 95.8 | 95.3 |
| 216 | 4 | 3 | 3 | 1.4 | 95.3 | |||
| 216 | 3 | 4 | 4 | 1.9 | 94.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, R.; Hu, J.; Liu, Y.; Yao, M.; Zhang, T.; Shi, J. Design and Working Parameter Optimization of Pneumatic Reciprocating Seedling-Picking Device of Automatic Transplanter. Agriculture 2022, 12, 1989. https://doi.org/10.3390/agriculture12121989
Yue R, Hu J, Liu Y, Yao M, Zhang T, Shi J. Design and Working Parameter Optimization of Pneumatic Reciprocating Seedling-Picking Device of Automatic Transplanter. Agriculture. 2022; 12(12):1989. https://doi.org/10.3390/agriculture12121989
Chicago/Turabian StyleYue, Rencai, Jianping Hu, Yijun Liu, Mengjiao Yao, Tengfei Zhang, and Jiawei Shi. 2022. "Design and Working Parameter Optimization of Pneumatic Reciprocating Seedling-Picking Device of Automatic Transplanter" Agriculture 12, no. 12: 1989. https://doi.org/10.3390/agriculture12121989
APA StyleYue, R., Hu, J., Liu, Y., Yao, M., Zhang, T., & Shi, J. (2022). Design and Working Parameter Optimization of Pneumatic Reciprocating Seedling-Picking Device of Automatic Transplanter. Agriculture, 12(12), 1989. https://doi.org/10.3390/agriculture12121989








