Bale Collection Path Planning Using an Autonomous Vehicle with Neighborhood Collection Capabilities

Abstract

This research was mainly focused on the evaluation of path planning approaches as a prerequisite for the automation of bale collection operations. A comparison between a traditional bale collection path planning approach using traditional vehicles such as tractors, and loaders with an optimized path planning approach using a new autonomous articulated concept vehicle with neighborhood reach capabilities (AVN) was carried out. Furthermore, the effects of carrying capacity on reduction in the working distance of the bale collection operation was also studied. It was concluded that the optimized path planning approach using AVN with increased carrying capacity significantly reduced the working distance for the bale collection operation and can thus improve agricultural sustainability, particularly within forage handling.

1. Introduction

Up until present, the application of scientific and technological developments through increased mechanization and precision farming have provided several opportunities in agricultural production and within forage handling operations. Some promising engineering developments in the 20th century with regard to forage handling include forage harvesters, balers, and the automated wrapping equipment of balers using stretch films 25 µm thick to reduce the risks of dust, molds, spores, and mycotoxin respiratory allergenic disorders in livestock and humans. Baler machines have made it possible to trade silage (harvest and storage of moist grass using fermentation) in portable packages between farms, which typically weigh 600–800 kg freshly cut per bales and are more popular on smaller farms with limited labor and financial resources to construct silos [1,2].

Bales made up of hay or silage formed by hay are usually too heavy to be picked up by humans alone. Thus, they are picked up from fields using conventional utility vehicles such as tractors or loaders operated by a human. These kinds of operations are labor intensive and associated with health and accident risks [3]. There is also a potential to further improve the efficiency and environmental impact since most decisions are made by humans and thus limited to human capacities in terms of sensing, multitasking, planning, consequence analysis, etc.

Therefore, in this study, the possibility of using a new autonomous agricultural vehicle with the neighborhood pick-up capabilities concept (AVN) was investigated. The research focused on off-board path planning, which is a critical task within the complete automation process of the bale pick-up operation.

Research in the route or path planning of agricultural field tasks can be broadly categorized into two groups based on the similarity of operations: coverage path planning (CCP) and point-to-point path planning (P2P). It has been observed by [4] that agricultural operations that required coverage path planning have been slightly more investigated. Most solutions for the path planning of agricultural field operations are based on optimization methods utilizing heuristic approaches or metaheuristic approaches depending upon the size and context of the problem [5]. In situations where vehicle routes must be planned over large areas with high economical risk, methods such as metaheuristics perform an extensive search for a solution and should thus be preferred [6].

Route planning for agricultural field operations (AFOs) involving the use of vehicles is referred to as vehicle route planning (VRP), which is a well-studied problem in the field of operational planning. Recently, VRP solutions have been applied to the planning and execution of various agricultural field tasks by researchers for the scheduling of the transportation of livestock [7,8] mission planning for coverage operation such as grass mowing and seedling [9], biomass operation scheduling [10], farm-to-farm path determination for scheduling crop harvesting [11], and route planning for fertilizer application [12]. Recently, a decision tool to support farmers in the operational planning of field operations was proposed by [13] to assist in field partitioning, route generation, and evaluation.

Significant improvements have been shown for AFOs in research by the automation of the AFOs. A study [14] on field coverage operations for an autonomous tractor using a mission planner showed a 50% reduction in non-working distance. Coverage operations were then further studied for irregular shaped fields with obstacles [15,16]. In another implementation by [17], the optimal covering route and feasible positions for grain transfer between the combine harvesters and tractors were generated using VRP and the minimum cost network flow.

The application and comparability of metaheuristics for AFOs have been widely studied and is still ongoing. Recently, a hybrid genetic algorithm (GA) was tested by [18] for a capacitive vehicle route problem (CVRP) by utilizing Gillett and Miller, Downhill, and nearest neighbor heuristics to generate the initial population and refine solutions of GA. Experimental results showed that the hybrid approach generated good solutions for CVRP with low computational cost. In another research by [19] with regard to capacitated coverage path planning problem for arable field, two popular metaheuristics—simulated annealing optimization (SAO) and ant colony optimization (ACO) techniques—were evaluated and it was found that SAO performed better than ACO. Aside from AFOs, a multi-objective optimal solution to priority-based waste collection and transportation was proposed by [20] using particle swarm optimization, local search, and simulated annealing (SAO). The optimized solution resulted in a 42.3% reduction in the negative effects of greenhouse gas emissions compared to traditional waste management.

So far, few studies have investigated the bale management in fields. There exists few published studies on the sequence optimization of the bale collection operation using wagons or loaders. The intended bale field operation was described as a bale collection problem (BCP) and was solved as a traveling salesman problem using GA by [21]. While in another study on BCP in [22], a heuristic-based approach based on K-mean clustering and nearest neighbor techniques to optimize the bale collection route were tested in simulation. Comparative results from both studies showed significant improvement in the final generated route. However, no other research studies were found on the route optimization of bale collection and no single study was found on the bale collection on fields, especially with the prerequisite of neighborhood pick-up possibilities.

1.1. Objective

The objective of the research presented in this paper was to optimize the bale collection operation by means of travelled distance using notion of an autonomous articulated vehicle with neighborhood collection capability (AVN) and compare that with traditional collection methods.

1.2. Scope

The research focused on the development of a global route plan for bale collection operations in simulation for notion of using AVN. For a global route plan, a static and known environment was considered since bale positions and fields are static entities. Bale positions were assumed to been known from a previous baling operation.

The following additional general assumptions were made:

-

Only bale collection operation was studied;

-

A notion of new type of agricultural vehicle (AVN) was considered for the application;

-

The AVN was considered to be a nonholonomic point like robot for the path generation;

-

Kinetic constraints of the vehicle were excluded;

-

Feasibility is measured only by total travelled distance.

2. Research Methodology

To investigate the effects of different bale collection strategies, a simulation approach was chosen. Path planning is typically performed in computer environments, which further makes feasibility evaluation easy compared to real life experimental strategies (i.e., to measure the feasibility on path suggestions on an actual field).

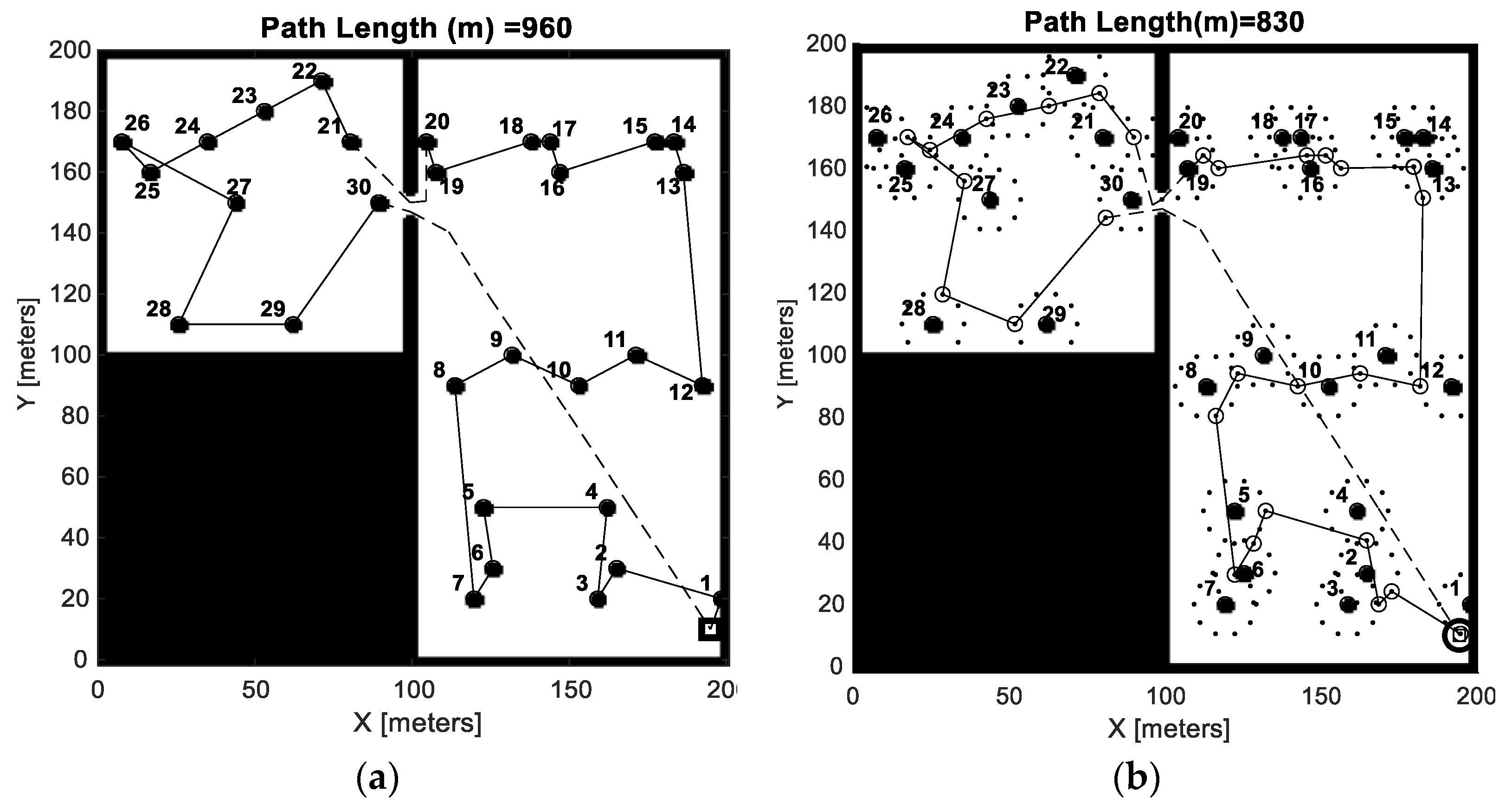
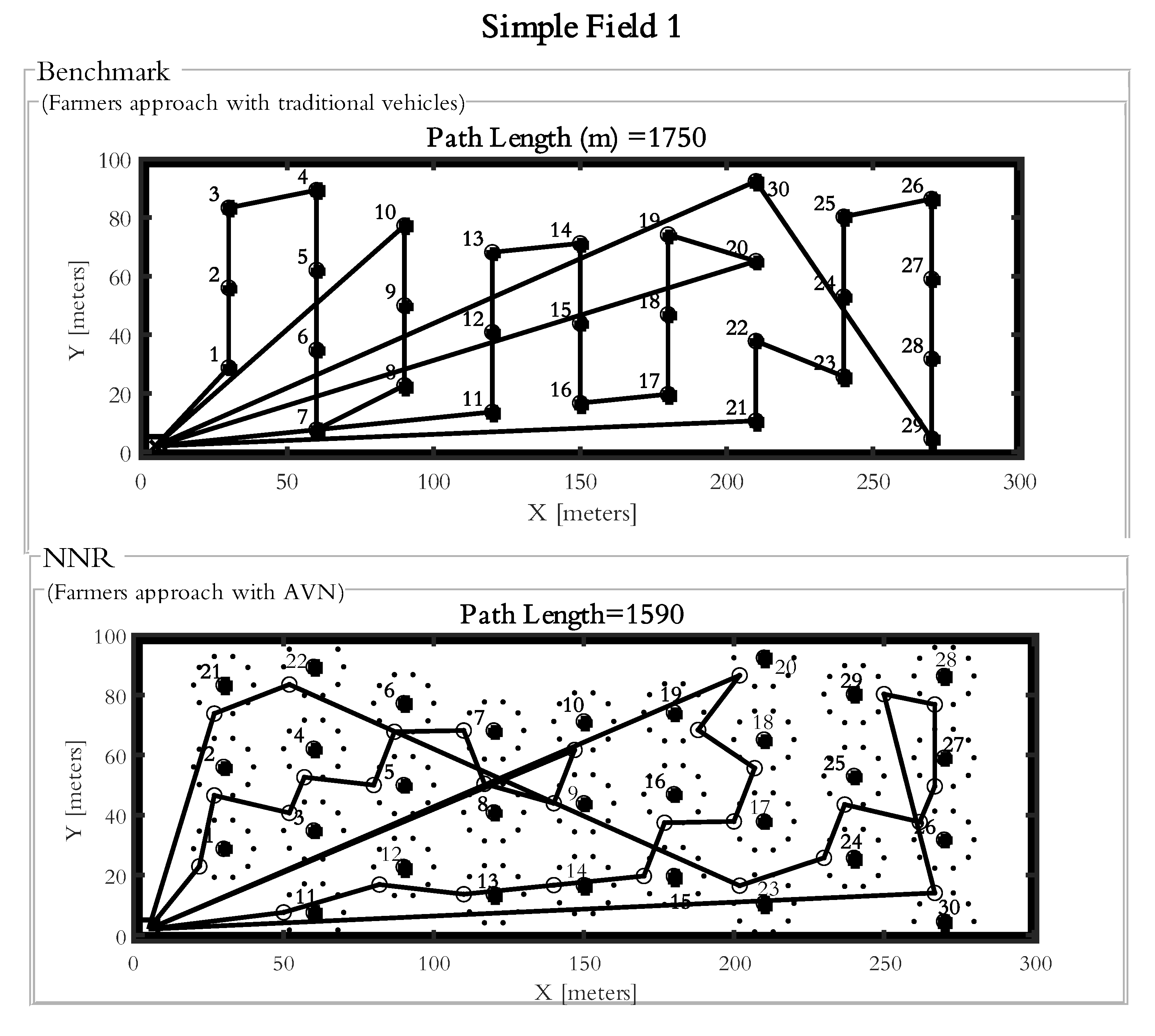
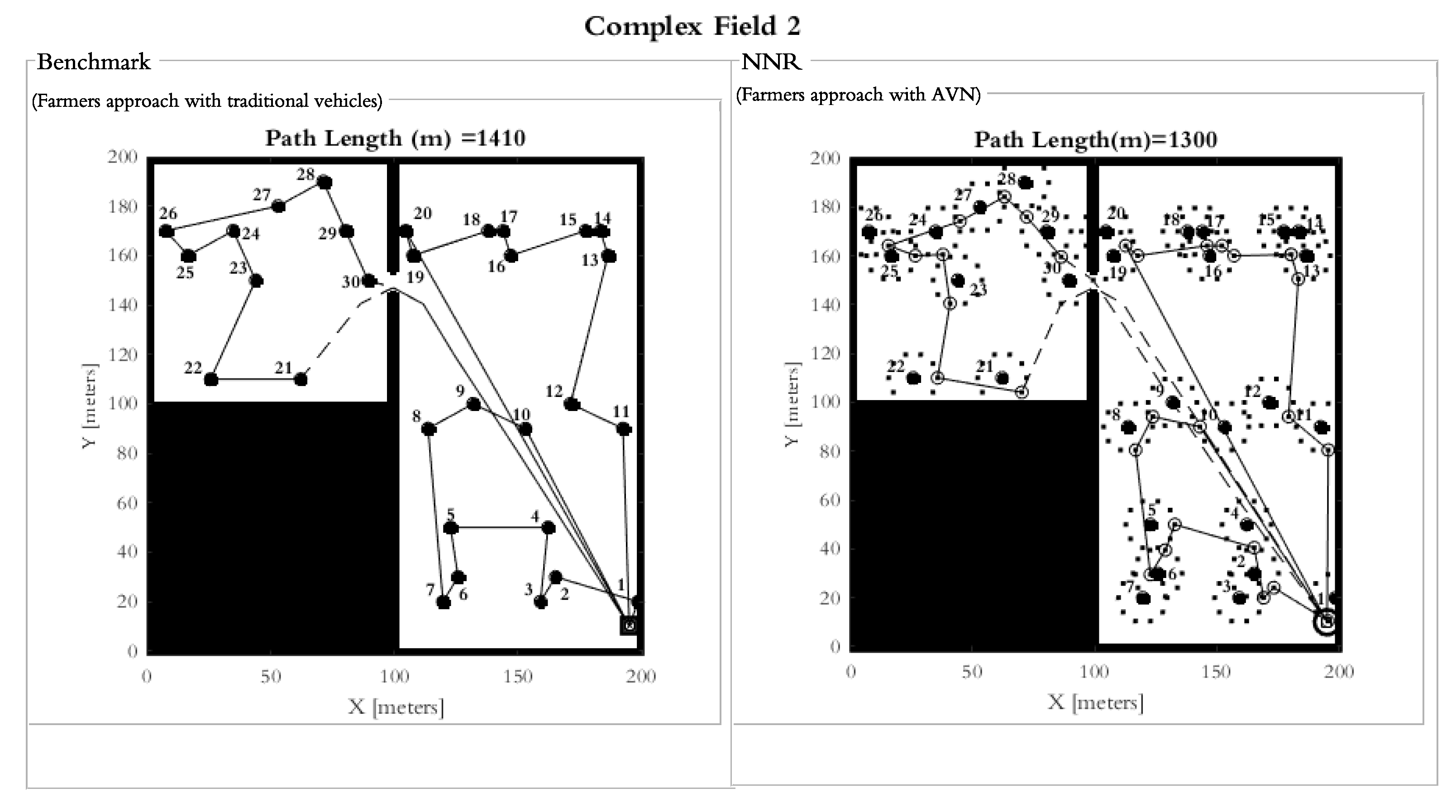
Two different approaches were studied and verified through the testing of situations with outcome pre-knowledge. The first approach imitates the bale collection strategy of farmers by always choosing the closest bales from the current position. The other approach instead uses a GA to optimize the collection order and position within a radius from which the AVN can reach. To investigate the differences in travelled distance (i.e., chosen feasibility) between a traditional and proposed collection approach, two different fields of the same size and with the same number of bales with a pre-determined distribution was studied. One was a simple rectangular field (field 1) and the other was a L-shaped field with more geometrical constraints (field 2). This enables investigations of possible dependencies on field complexity. With the fields selected, some simulation parameters could be set (e.g., grid size, inflation length, number of possible pick-up positions etc.) by conducting verifying tests to find a trade-off between the computational time and accuracy. Then, the experiments were designed by choosing which parameters to vary and thus which simulations to run. To enable comparison, the results from these simulations were then compiled into tables and some paths were also visualized, enabling the analysis of collection order as well as verification on the feasibility.

The traditional approach was generated by considering how humans would operate in a typical agricultural environment for bale collection operation. Generally, a human operator would pick-up the next visible bales closest to the present location. Such a heuristic approach could be programmed by using the nearest neighbor algorithm. Through this approach, two different cases were studied: one with a traditional pick-up vehicle which always has to go to the nearest bales and another with the AVN.

In addition, an optimization approach based on commonly used GA was further developed, thus enabling a comparison to the traditional approach. Here, two different strategies for initial population generation were used to show the effects on convergence.

Verification of the simulations were conducted by running a test simulation on configurations where the results were pre-known. In addition, the results from all simulations were analyzed manually to make sure that the paths were consistent.

2.1. Model Description

In this study, a notion of an AVN (see Figure 1) with a regular forwarder crane of 10 m long was used for the modeling. For comparison, traditional agricultural vehicles (e.g., tractors or loaders) were also modeled. These traditional vehicles are typically equipped with front loaders requiring additional traveling for the loading of each bale (i.e., they cannot load bales onto themselves). This effect is excluded in the traditional vehicle models in this study, leading to underestimation of the travelled distance.

The problem formulation for the bale collection operation with a crane makes it somewhat unique. The AVN can collect bales at a radius R, which makes the situation a close enough traveling salesman problem (CETSP) [23]. The CETSP is a NP hard, combinatorial problem, and some recent solutions for CETSP have been proposed based on the discrete gravitation search algorithm and self-organizing maps [24,25]. However, the vehicle can have different carrying capacities, thus leading to a close enough traveling salesman problem with a capacity constraint. In this study, the collection sequence and collection positions minimizing the total travelled distance was searched for and thus the CETSP is defined as

$$mi{n}_L\left(\mathit{\Sigma }, BP,CP\right)$$

(1)

where $\mathit{\Sigma }$ is the bale pick up sequence; CP is the desired collection position at radius R (specified by AVN reach radius) around the bale positions (BP); $mi{n}_L$ is a function that calculates the minimum length tour at collection positions around each bale.

Agricultural Field Models

The agricultural fields were modeled in two steps. To represent “go” and “no go” areas (obstacles), binary occupancy maps (BOM) [26] were used and to find non-collision paths within the “go” areas, probability roadmaps (PRM) [27] were used.

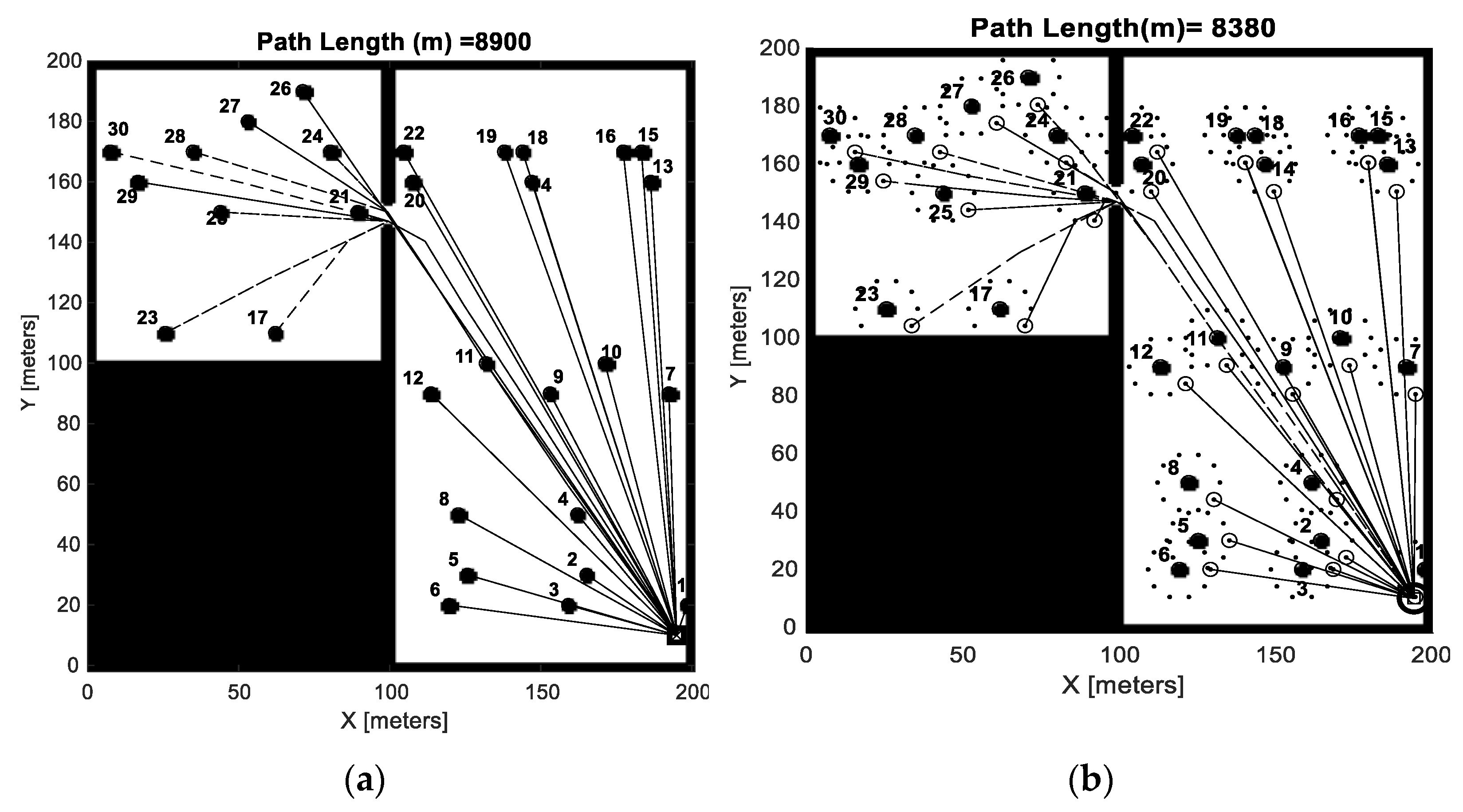
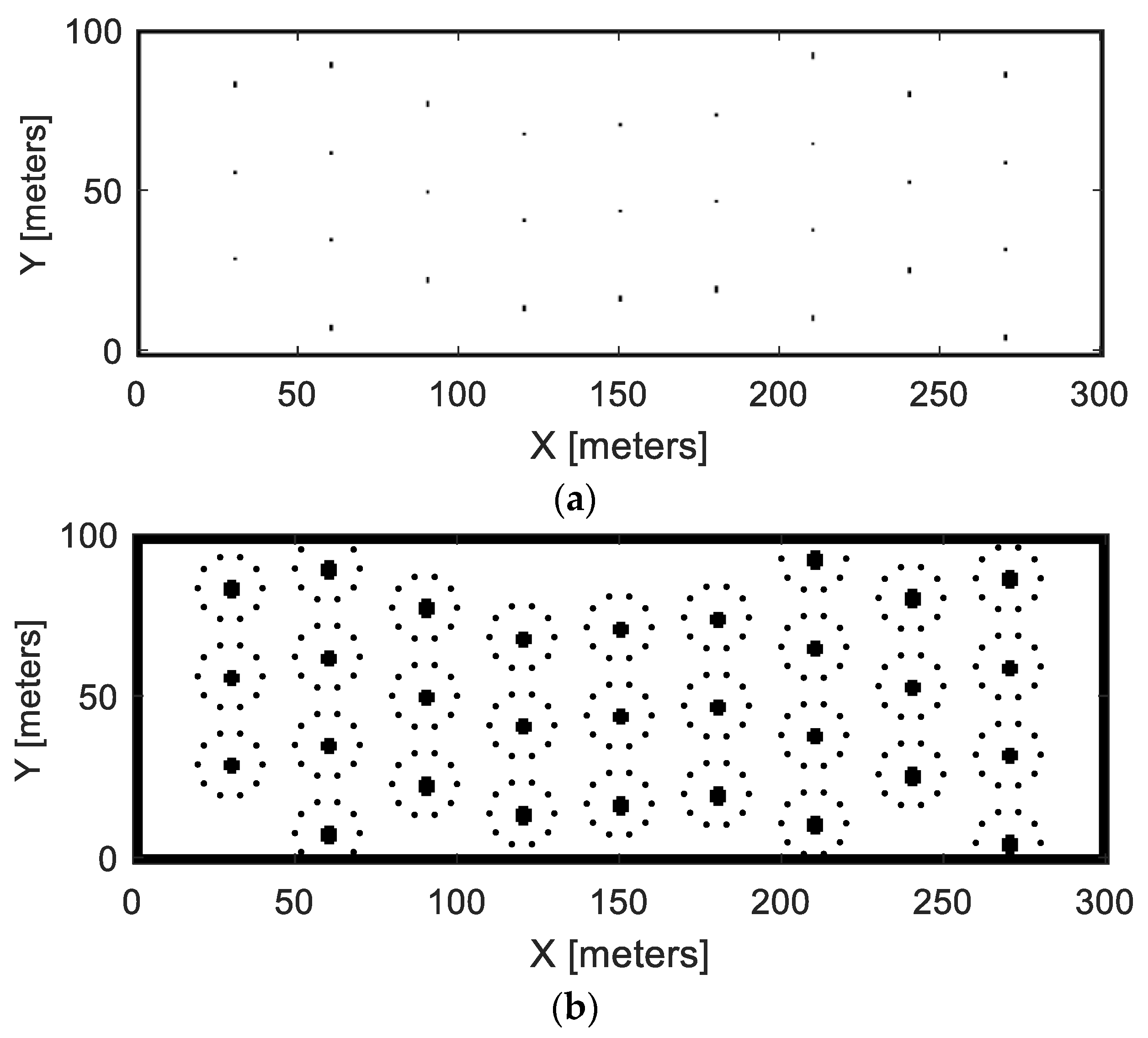
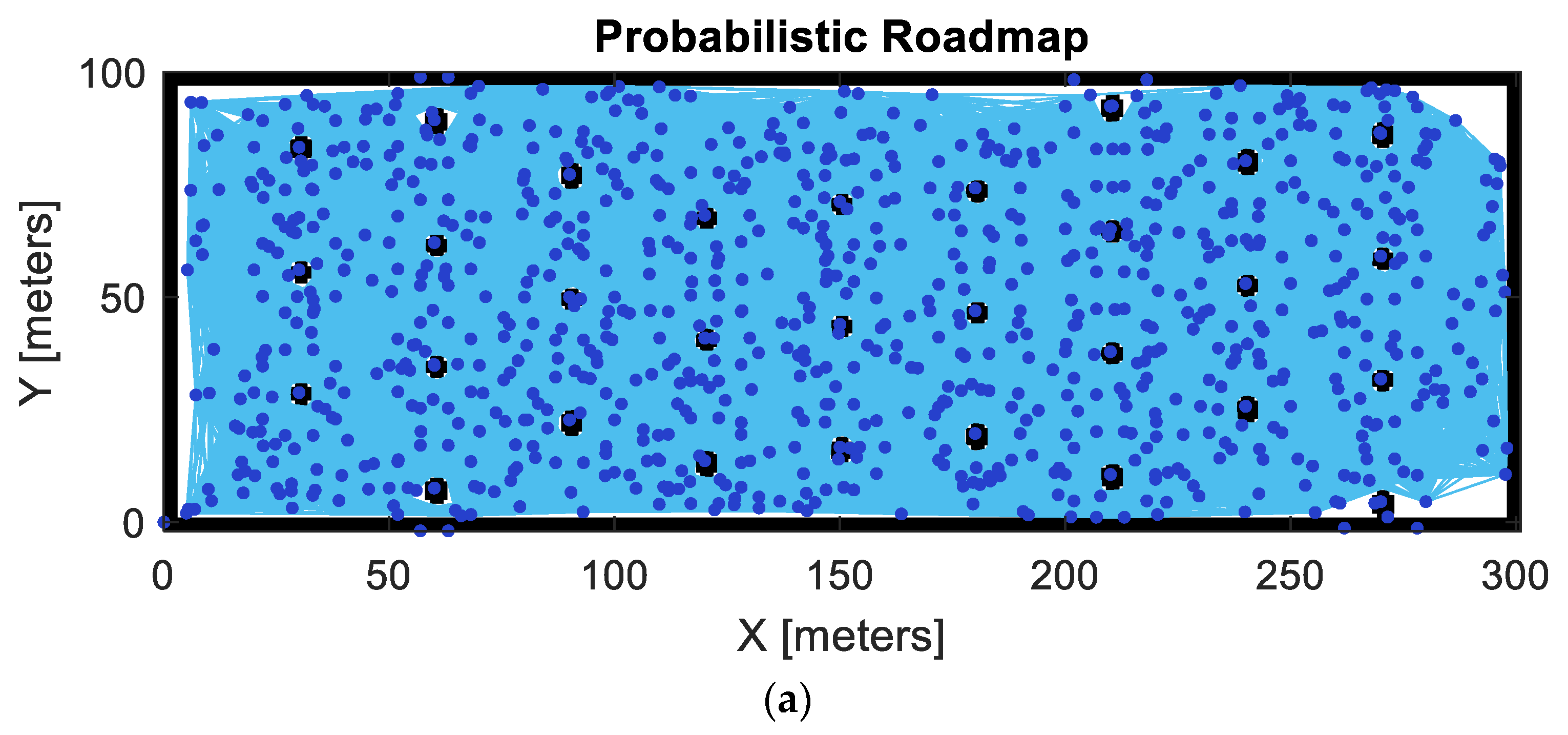
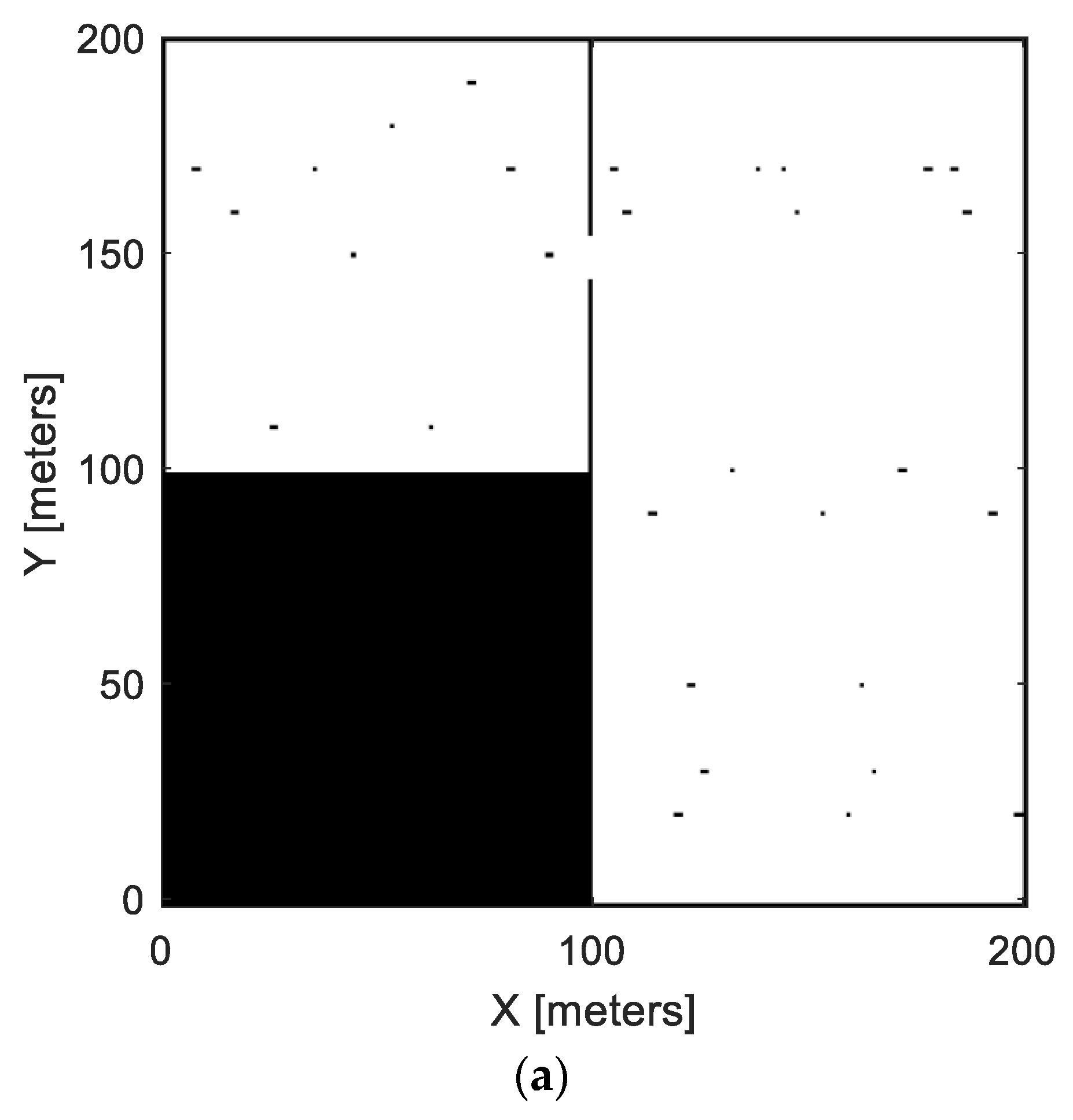
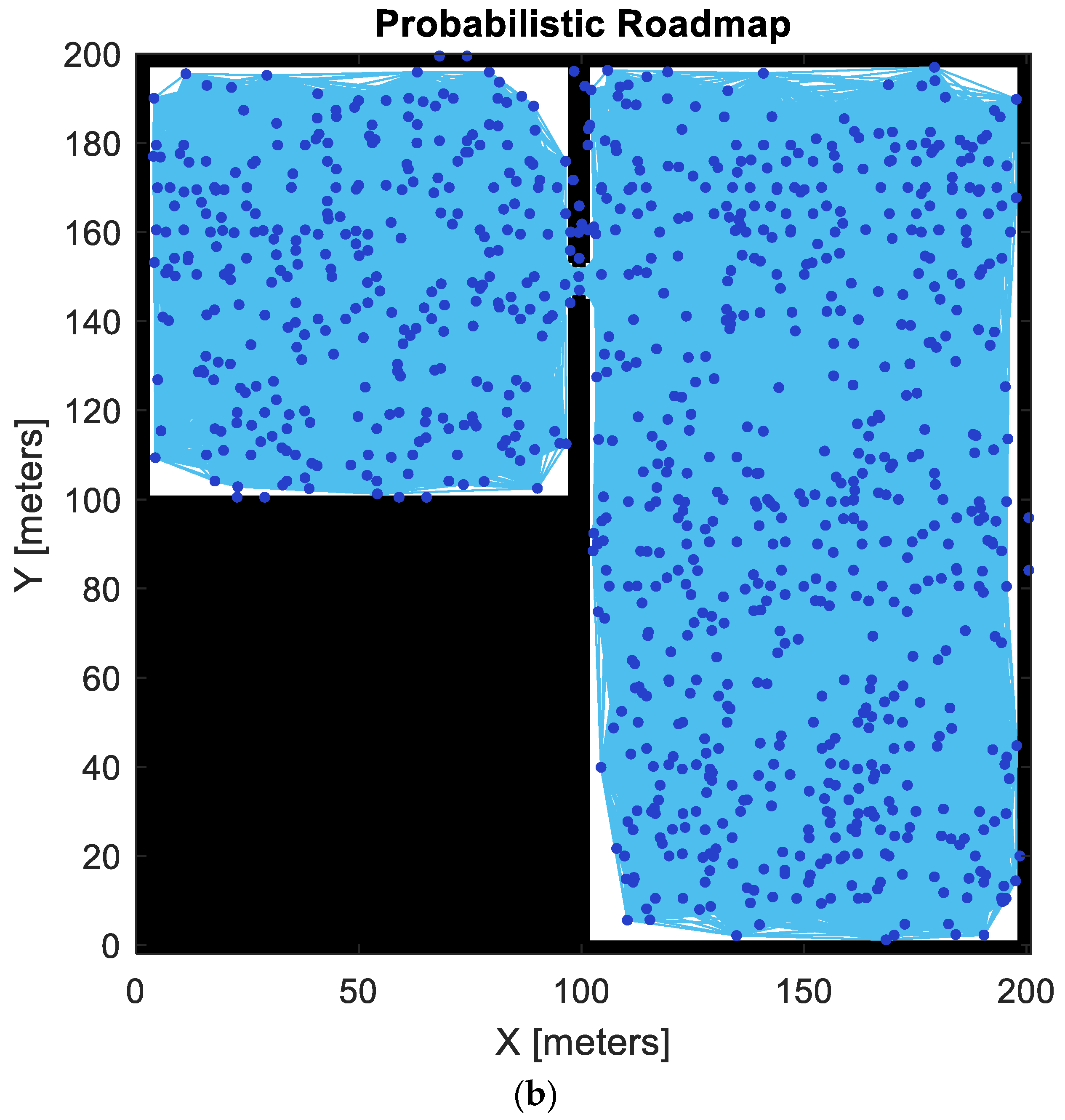
In this research, to investigate the possible effects of field complexity, two different fields were studied. Field 1 (see Figure 2) is a rectangular field without any obstacle areas imitating a quite typical environment for bale collection operations. Field 2 (see Figure 3) on the other hand, is a representation of an irregular more complex agricultural field with obstacle or intrusion areas. For both fields, bales were positioned by calculating the distance, going in straight lines from one end to the other until the whole field was covered, and the harvesting vehicle had collected enough material to form a bale based on the average yield, etc. given in

Table 1. Bale distribution parameters.

Bale Distribution Parameters
Average grass yield	~7000 kg/ha
Average weight of bales	~700 kg
Harvester width	~3.0 m
Distance req to make one bale by harvester	~330 m

.

Figure 2a shows the BOM of field 1 where black dots indicates bales occupancy and Figure 2b shows the inflated BOM of field 1. To reduce the calculation intensity for simulations, only 10 discrete points on each bale collection radius were used, which are represented as black dots surrounding the inflated bales in Figure 2b.

Figure 3a shows the BOM of field 2 where black dots indicates bales occupancy and Figure 3b shows the inflated BOM of field 2 including the discretized collection points at AVN’s reach radius.

The distance traveled to release a bale can then be calculated through

$$d\times HW\times {\check{Y}}_{grass}={\tilde{W}}_{HB}$$

(2)

where d is the distance required to make one bale by harvester; HW is the harvester width; ${\tilde{W}}_{HB}$ is the average weight of one bale; and ${\check{Y}}_{grass}$ is the average grass yield in a typical season. $‘{\times }^{’}$ represents multiplication operator. Based on the parameters in Table 1 and Equation (2), bales were released after a travelled distance of around 330 m (some minor adjustments were made if the release position coincided with the boundary of the field).

Binary Occupancy Maps for Field 1 and Field 2

A typical agricultural environment for the bale collection operation was modeled in 2D using binary occupancy maps. Bales are represented as occupied circle areas and once a bale is picked up, it is removed from the BOM. To take the collection vehicle size into consideration, the occupied areas were further inflated in the BOM. In

Table 2. Binary occupancy map (BOM) setting for both fields.

Binary Occupancy Map Based Settings for Both Fields
Total field area	3 hectares
Grid cell size	1 m
Grid resolution (cells/meter2)	1 m
Inflation	1.3 m

, all BOM settings for both fields (simple and complex) are summarized.

Probabilistic Roadmaps

To further reduce the calculation intensity for the GA-simulations, static PRM was used (stationary nodes and connection lines) to generate the collision free paths. The same number of nodes and connection distance was used for both fields and the chosen PRM parameters are given in

Table 3. Selected PRM settings for the simulation.

PRM Graph Parameters
Number of nodes	1000 (Fixed position nodes + random nodes)	Fixed position nodes	Storage position, start position, end position and potential pickup points for each bale and/or each bales position
		Random nodes	Nodes besides fixed nodes are randomly generated once and remained fixed afterward for all cases
Connection distance	50

.

The quality of the PRM depends on the number of nodes and connection distance and also impacts the calculation intensity. For this study, 1000 nodes and 50 m in connection distance was evaluated as a suitable trade-off.

The “bale storage position, pick-up positions (also bale positions for traditional pick-up vehicle), start- and end position of the vehicle” were pre-defined nodes and then another 1000 randomly generated nodes were added. PRMs for both fields were kept fixed, despite the changes in map (e.g., when bales are picked up) to speed up the computation. However, PRM connection lines did not cross the bale areas even after being removed.

Figure 4 shows the PRM for field 1 (a) and field 2 (b).

2.2. Bales Collection Path Approaches

Two approaches to generate the bale collection paths were studied. The idea was to imitate the bale collection approach of a farmer and compare it to a bale collection approach based on optimization.

2.2.1. Nearest Neighbor Approach

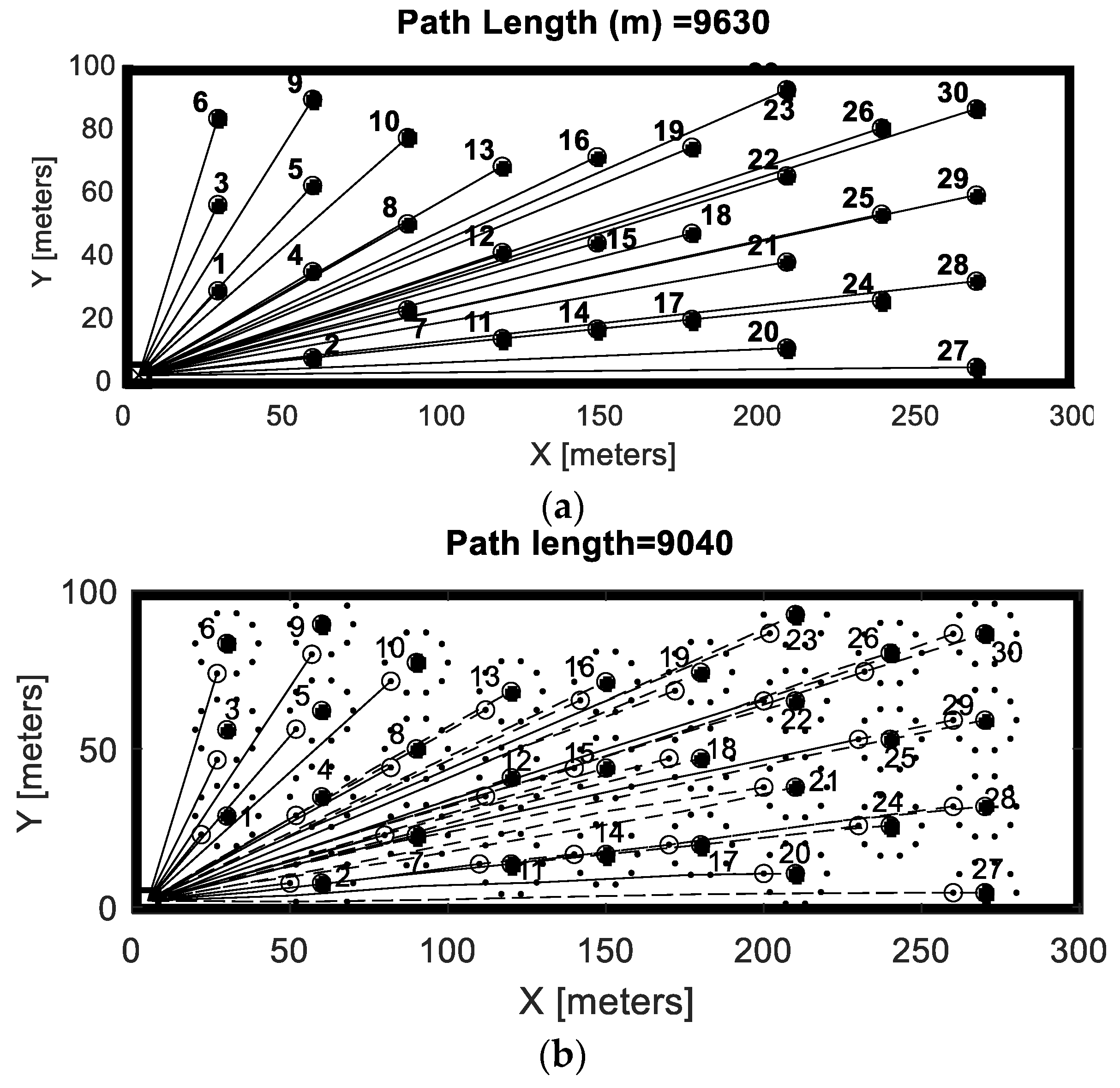
One way of imitating how farmers collect bales, which was used for this study, is through the nearest neighbor approach. It was here assumed that a farmer will choose the nearest bales from its current position and then continue collecting one by one based on proximity. In the case of a traditional collection vehicle, the bale center is used as the collection position. On the other hand, for the AVN, the nearest bale is first derived and then the collection point around the bale that is closest to the Euclidian vector from the previous collection position to the current nearest bale center is derived. A straight-line path is used if no obstacles are intersected, otherwise a collision free path based on PRM is derived. This approach uses the MATLAB© built-in nearest neighbor search algorithm based on Euclidean distance between the set of points in free space. In case when there are obstacles in the space, it may result in false positive in comparison to the farmers’ visual judgment in a real situation.

2.2.2. Optimization Approach

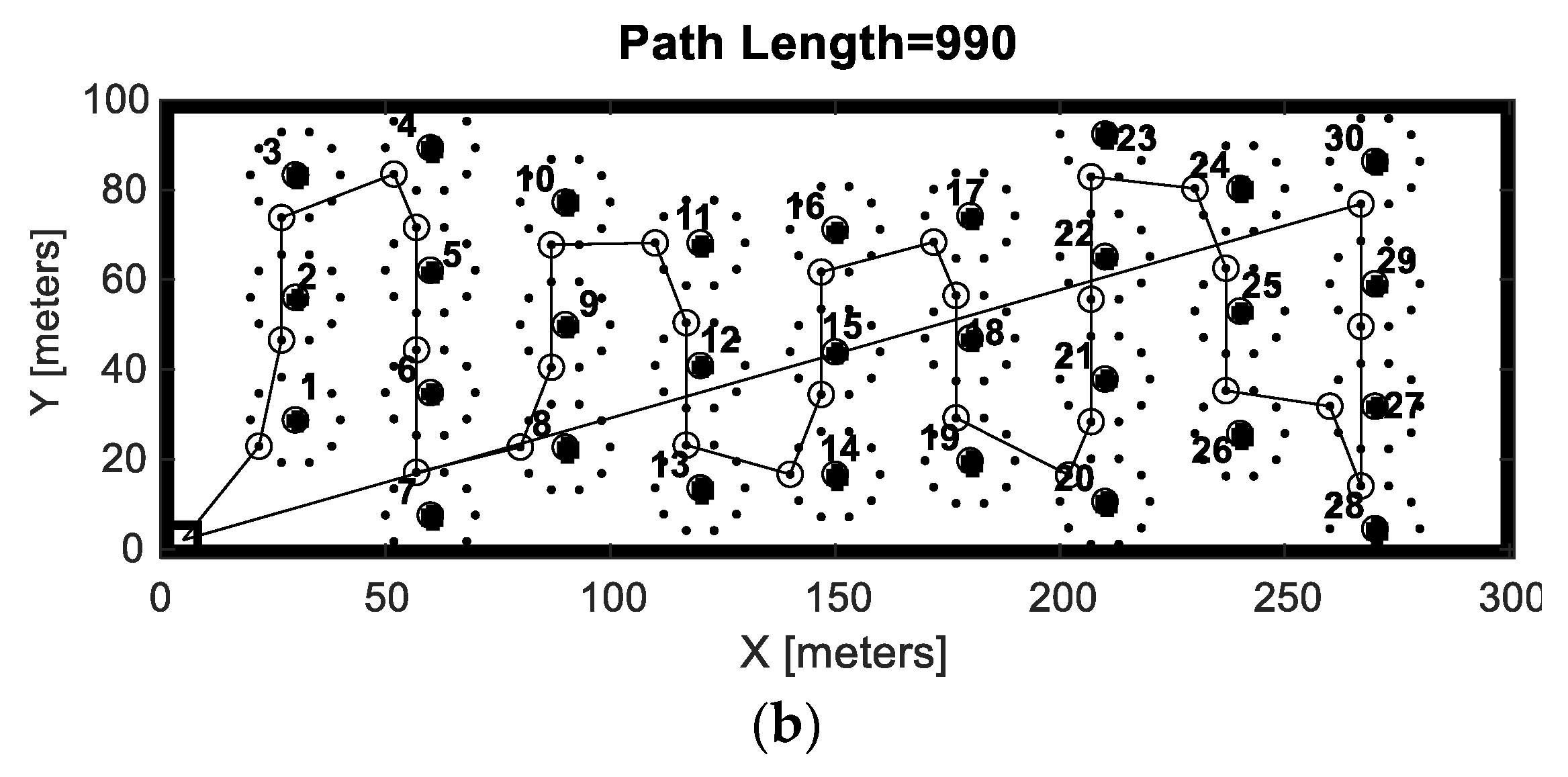
Optimization of the total distance travelled (fitness function) was carried out by use of a GA, which has good performance on finding the global optimum, has possibilities for parallelization, and can be applied to various types of problems. However, GA can become very calculation intensive and therefore, a lot of emphasis has been spent on simplifications, making each iteration as fast as possible.

Since the notion of an agricultural vehicle (see Figure 1) with neighborhood collection capability is used for this study, bales were collected not only in a certain order, but also from a point on a circle with a certain radius (corresponding to the crane length) surrounding the bales. Thus, a traveling solution is defined by a collection order and a set of points on the collection circumference (i.e., collection angles). 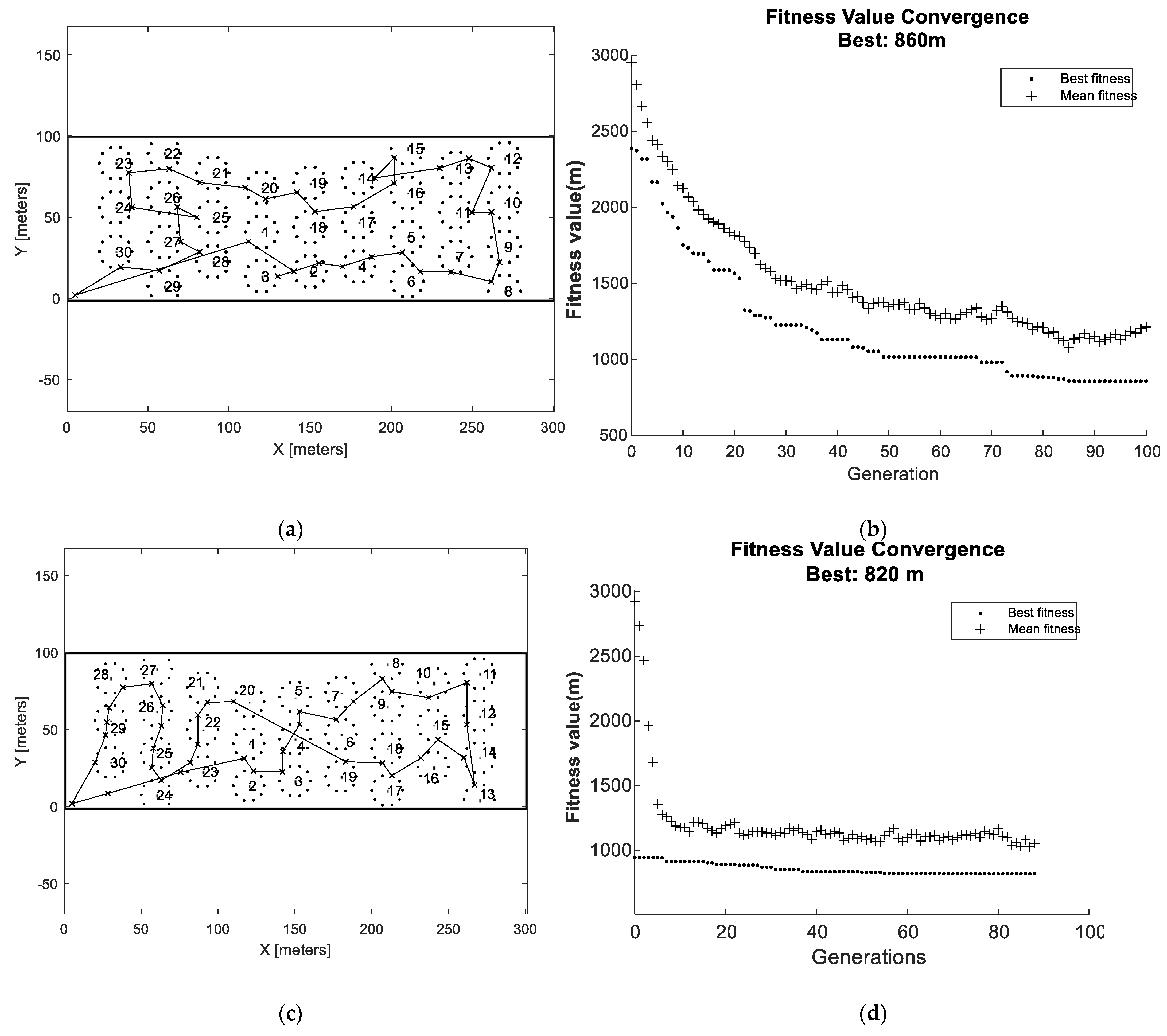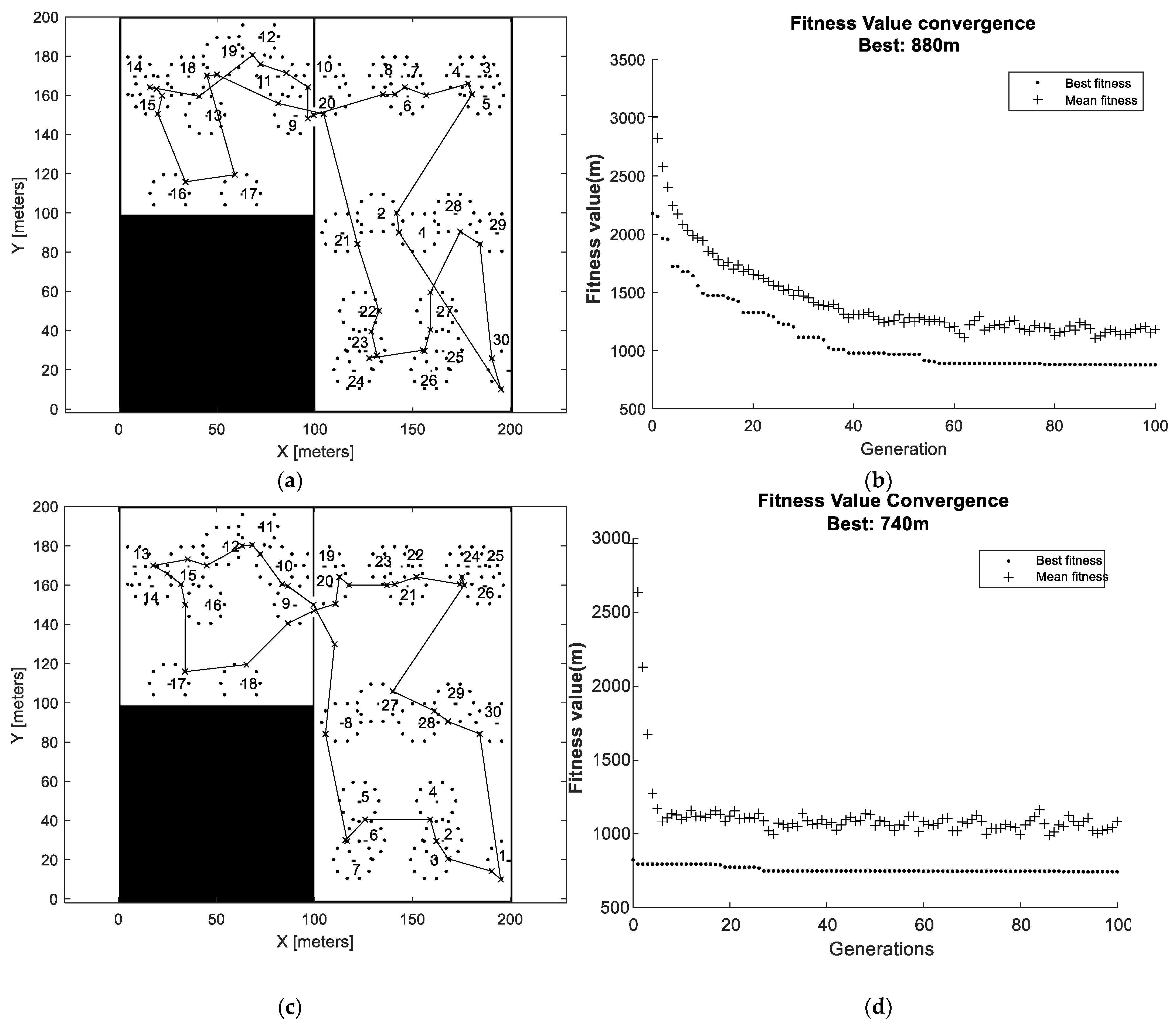Since the collection order is a permutation while collection angles are a set of constrained real numbers between 0 and 2$\pi$ (not a permutation), it was decided to use two GAs. Hence, the first GA (GA1) was used to optimize the collection order represented as chromosome in the population of permutations of the bales’ identities. For each collection order proposed by the first GA, a second GA (GA2) was then used to optimize the collection positions for each bale. To speed up the calculations, a discrete number of collection positions were defined from which GA2 had to choose. In this way, the number of possible combinations were significantly decreased, and integer representation was used for the chromosomes, which also contributes to computational efficiency. For both GAs, the built in “ga”-solver in MATLAB© was used. However, since GA1 is based on permutation chromosomes, custom functions for the initial population, crossovers, and mutations were developed (for GA2, default settings for these properties were used). To enable a comparison of the initial conditions, two different cases of population initialization were tested (i.e., randomized initialization and nearest neighbor initialization). Crossovers were conducted by flipping a random sized part of the chromosomes while the mutations were carried out by swapping two elements in the chromosome. After evaluating the performance by means of computational time and accuracy, the following settings were used for both GAs:

• Population size = 50
• Crossover fraction = 50%
• Function tolerance = 1 × 10⁻⁵
• Elite count = 10
• Maximum nr. of stalling generations = 50
• Maximum nr. of generations = 100

For GA1, vectorization (i.e., working with the complete population for each iteration instead of sequentially working which each chromosome in sequence) and no parallelization was used, while the opposite was used for GA2, thus enabling GA2 to evaluate different sets of collection angles in parallel, which is possible since there exist no dependencies between those solutions.

At the lowest computational level (i.e., for a suggested collection order and set of collection angles), the total travelled distance can be calculated. Here, between two subsequent collection points, a straight line path was derived if no collision in the occupancy map occurred. Otherwise, the PRM was used to find the shortest collision free path (within the pre-generated PRM network). To further improve the computational efficiency, all simulated collection orders were stored together with the, for that order, optimized set of collection positions. For each new generation, this enabled an initial check of whether the suggested collection orders have already been optimized by means of collection angles or not. If not, a new optimization simulation is initiated, otherwise the already stored feasibility value is used.

A 20-core computer was used for the parallel computations, leading to a total simulation time for all set of parameters (field type, carrying capacities) of about 5 days.

3. Results

Simulations with the same set of parameters were carried out for both field 1 and field 2. The simulations included both the nearest neighbor and the optimization approaches. For the nearest neighbor, to enable a fair comparison, two different cases were studied. In the first case, notion of traditional vehicle without distance collection possibilities was modeled and referred to as the “benchmark”. In the other case, the AVN notion was used and referred to as the “nearest neighbor with radius R” (referred as NNR). Additionally, the optimization approach was divided into two cases using the AVN notion. In the first case, random permutations of the pickup sequence were used for the initial population, which here is referred to as “random permutation initialization” (RPI). For the second case, the nearest neighbor collection sequence was included in the initial population, which is referred to as the “nearest neighbor permutation initialization” (NNPI). For each of these four cases, the three different carrying capacities 1, 10, and all bales were evaluated, leading to 12 different simulations for each field. The resulting paths for carrying capacity CC = 10 are shown in the main text while the paths for the remaining simulations can be found in Appendix A.

3.1. Nearest Neighbor Approach

Figure 5 shows the resulting paths for field 1 with CC = 10 of the benchmark-(U) and NNR case (L). Circle ‘o’ represents bales heuristically optimized pickup positions and dots ‘•’ and ‘.’ represents bales positions and discretized pickup position at reach radius respectively. By adding a reach radius, the traveled distance was reduced from 1750 m to 1590 m while the collection sequence remained.

Figure 6 shows the resulting paths for field 2 with CC = 10 of the benchmark-(L) and NNR case (R). By adding a reach radius, the traveled distance was reduced from 1470 m to 1300 m while the collection sequence remained.

3.2. Optimization Approach

Figure 7a shows the resulting paths for field 1 with CC = 10 of the RPI case where ‘x’ represents bales optimized pickup positions. Figure 7b shows the corresponding fitness convergence where black dots ‘·’represent the best fitness in each generation and marker ‘+’ represents the average population fitness value in each generation. Figure 7c shows the resulting path of the NNPI case with the corresponding fitness convergence (d). By incorporating a nearest neighbor optimization as guess in the initial collection sequence population, the travelled distance was reduced from 1470 m to 1360 m.

Figure 8a shows the resulting paths for field 2 with CC = 10 of the RPI case and the corresponding fitness convergence (b). Figure 8c shows the resulting path of the NNPI case with the corresponding fitness convergence (d). By incorporating a nearest neighbor in the initial collection sequence population, the travelled distance was reduced from 1490 m to 1230 m.

3.3. Results Compilation

Results of the travelled distance for all simulations are compiled in

Table 4. Compiled results for field 1.

		Path Distance (m)
	Path Planning Approaches	Nearest Neighbor Approach		Optimization Approach
		(Traditional vehicles)	(AVN notion)	(AVN notion)
	Subcases	Benchmark	NNR	RPI	NNPI
Vehicles Carrying Capacity (CC)	CC = 1	9630	~9040	~9040	~9040
	CC = 10	1750	1550	1470	1360
	CC = all	1160	990	860	820

and

Table 5. Result compilation for field 2.

		Path Distance (m)
	Path Planning Approaches	Nearest Neighbor Approach		Optimization Approach
		(Traditional vehicles)	(AVN notion)	(AVN notion)
	Subcases	Benchmark	NNR	RPI	NNPI
Vehicles Carrying Capacity (CC)	CC = 1	8900	8380	~8380	~8380
	CC = 10	1470	1300	1490	1230
	CC = all	990	830	880	740

where the two path planning approaches and their respective subcases are arranged in columns from left to right for the three different carrying capacities given in rows. For the optimization approach, solutions for CC = 1 had weak dependency on the collection order. Some deviations compared to NNR might occur due to the fact that the discrete collection positions do not necessary coincide with a straight line from the storage location to the bales. Hence the NNR with CC = 1 is an approximation for the optimized approach. Table 4 shows the compiled results of the travelled distance for field 1.

It can be observed in Table 4 that an increasing carrying capacity for all three cases resulted in a significant distance reduction. Percentage reduction in the travelled distance in field 2 for the three carrying capacities are shown in Figure 9.

Figure 10 shows a comparison of the path planning cases for two carrying capacities (CC = 1 will give approximately the same result for the different cases) by means of percentage reduction in the travelled distance. Black bars represent NNR over the benchmark, white bar with solid line borders NNPI over the benchmark and white bar with the dashed dotted border NNPI over NNR.

Table 5 shows the compiled results of travelled distance for field 2.

Percentage reduction in the travelled distance in field 2 for three carrying capacities are shown in Figure 11.

Figure 12 shows comparison path planning cases for two carrying capacities (CC = 1 will give approximately the same result for all cases) by means of a percentage reduction in the travelled distance. The black bar represents the NNR over benchmark, the white bar with solid line borders NNPI over benchmark, and the white bar with dashed dotted border is the NNPI over NNR.

4. Discussion

In order to simplify the computational intensity in optimizing the path planning task for the bale collection operations, there have been a number of approximations made in the modeling, as described in the scope and modeling part of the paper. This includes neglecting vehicle kinetics, considering bale collection only, keeping the PRM network static, discretization of the collection positions, etc. The GA is also significantly dependent on settings for the optimization algorithm, which effects both the accuracy and calculation time. Convergence to an optimal solution is, for instance, highly dependent on the size of the initial population and number of generations. Apart from CC = 1, the benchmark approach will always underestimate the travel distance since the loading stage is excluded from the distance calculation (i.e., relative improvements by the AVN will also be underestimated). Although these approximations will affect the output in an absolute manner, it is plausible that the relative behavior will remain, which was therefore focused on in making conclusions.

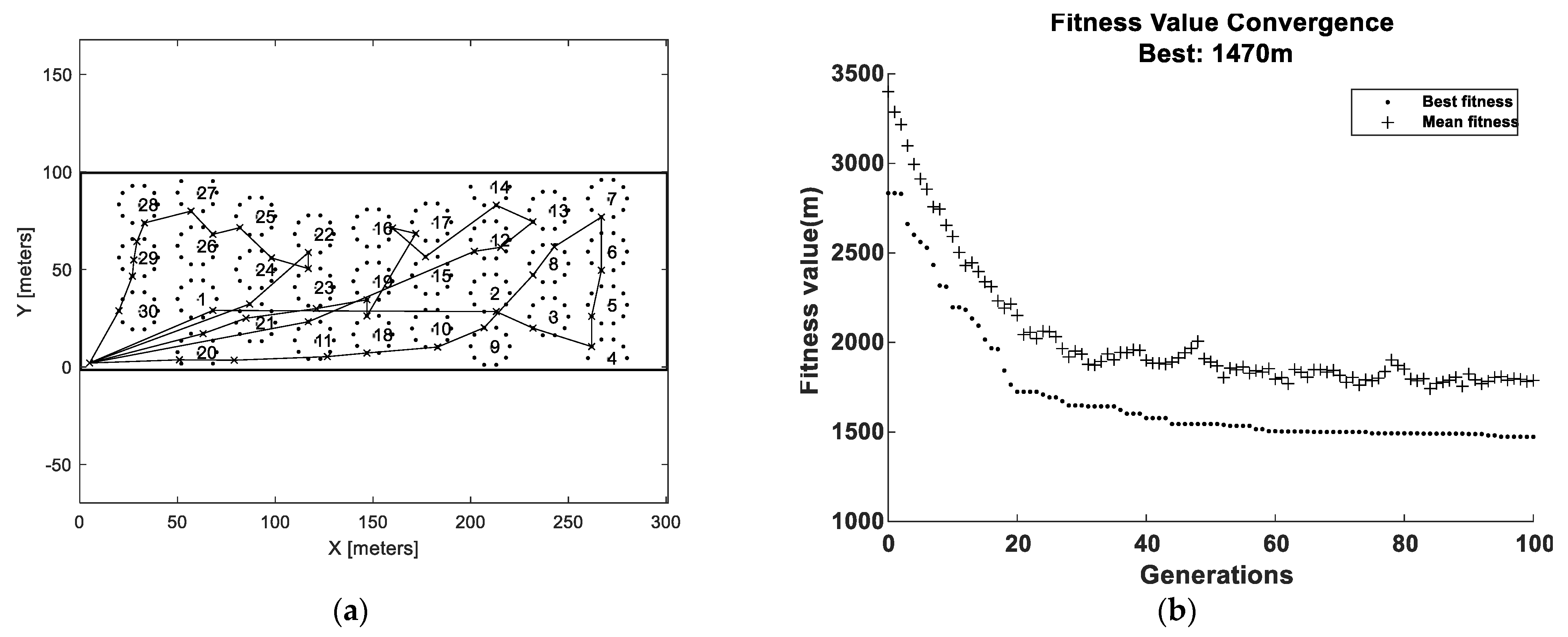
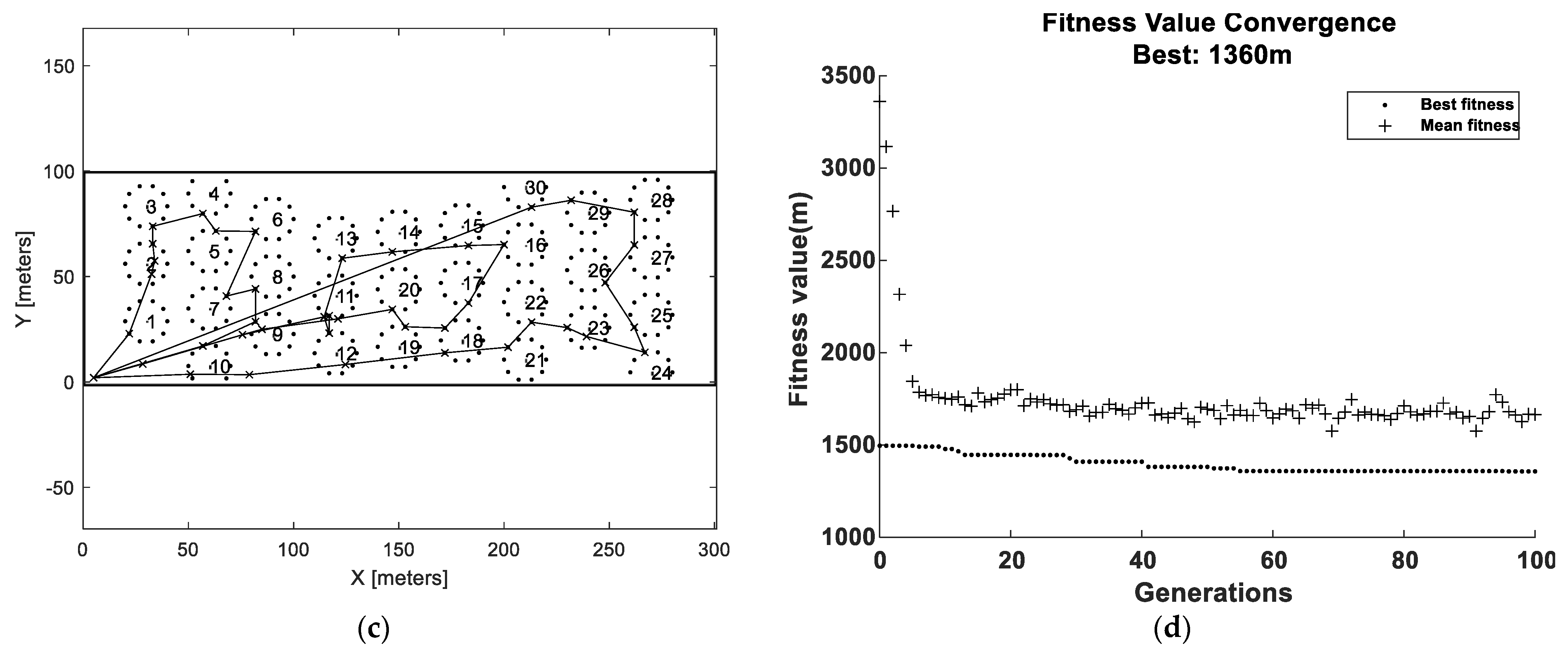
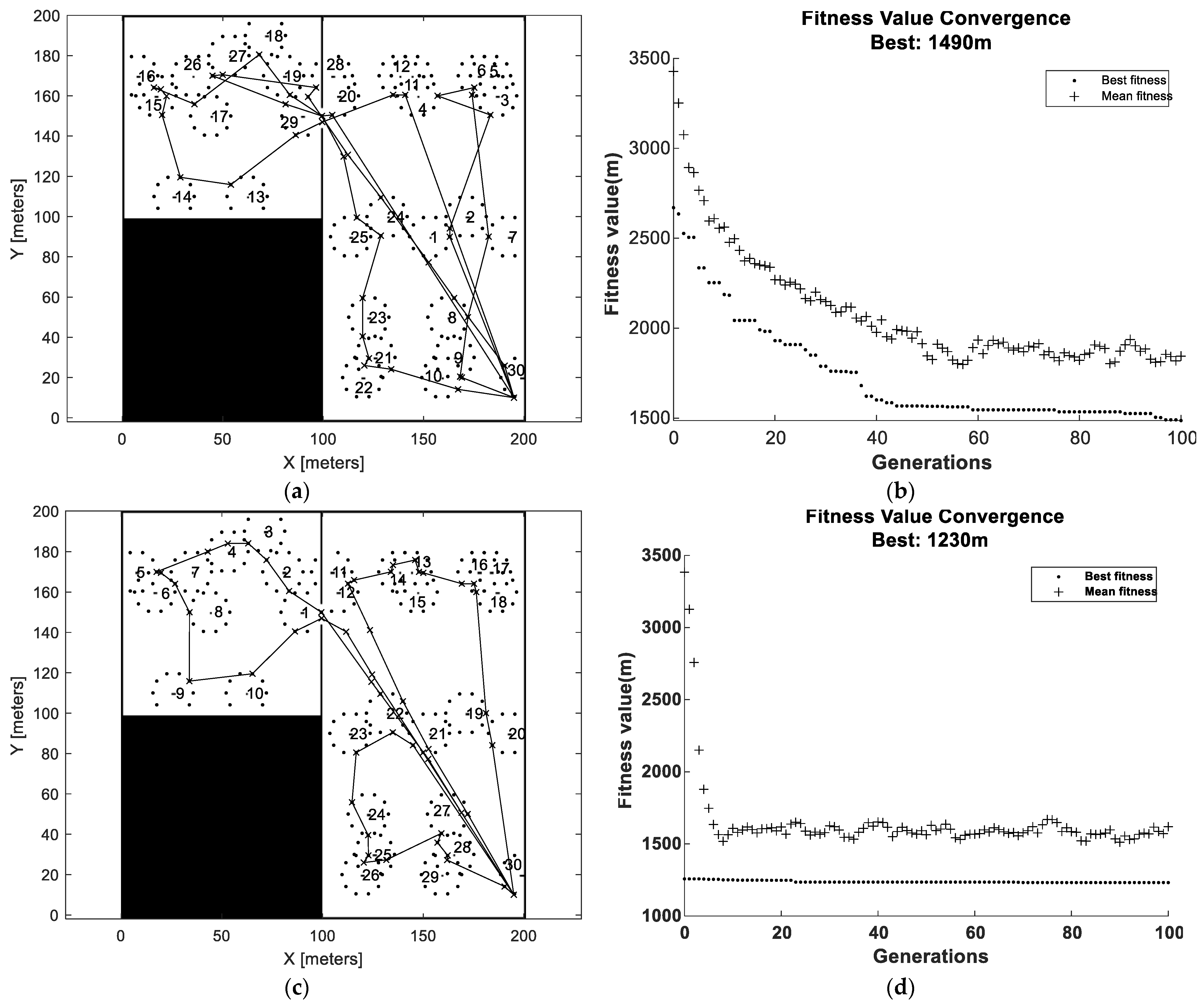
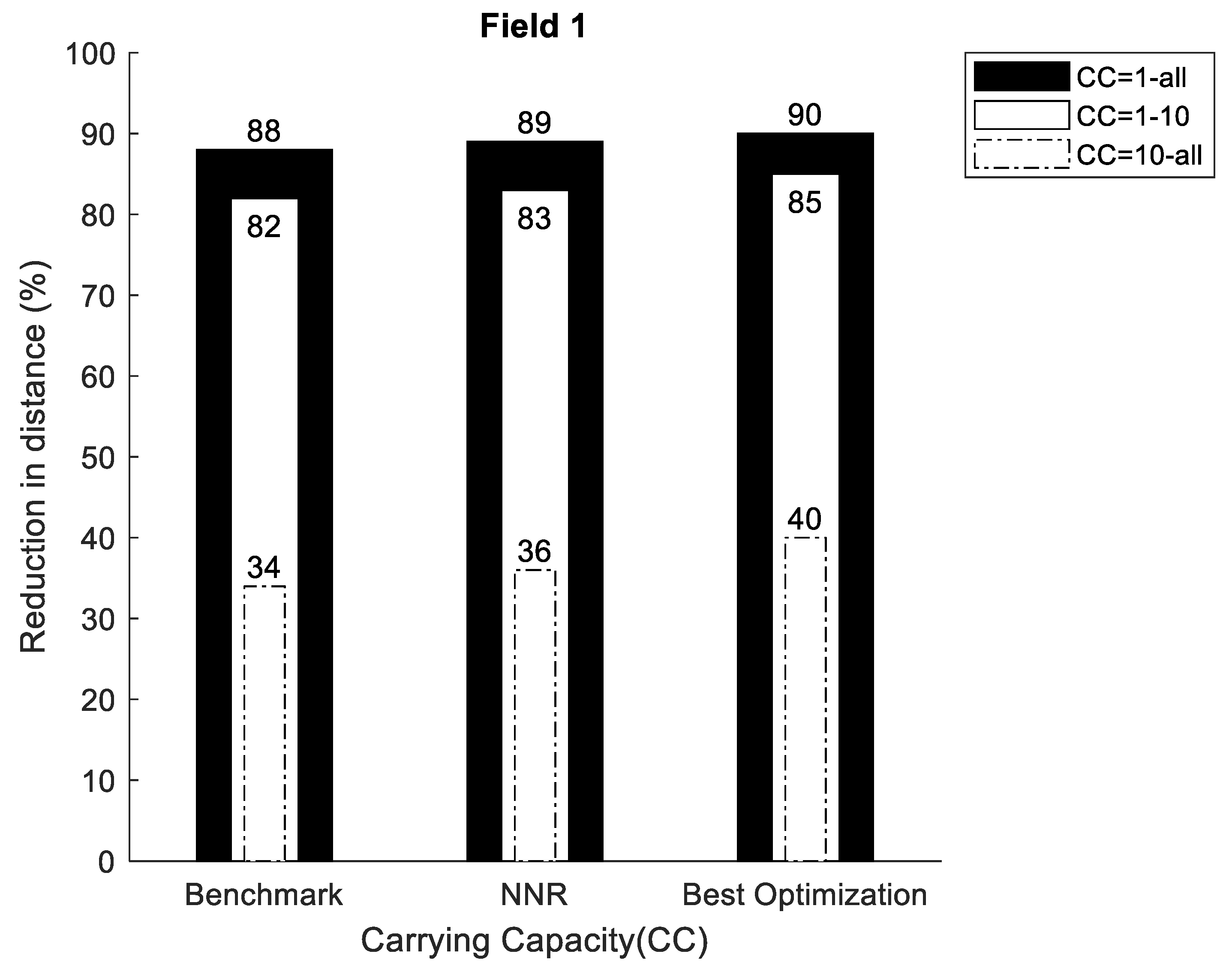
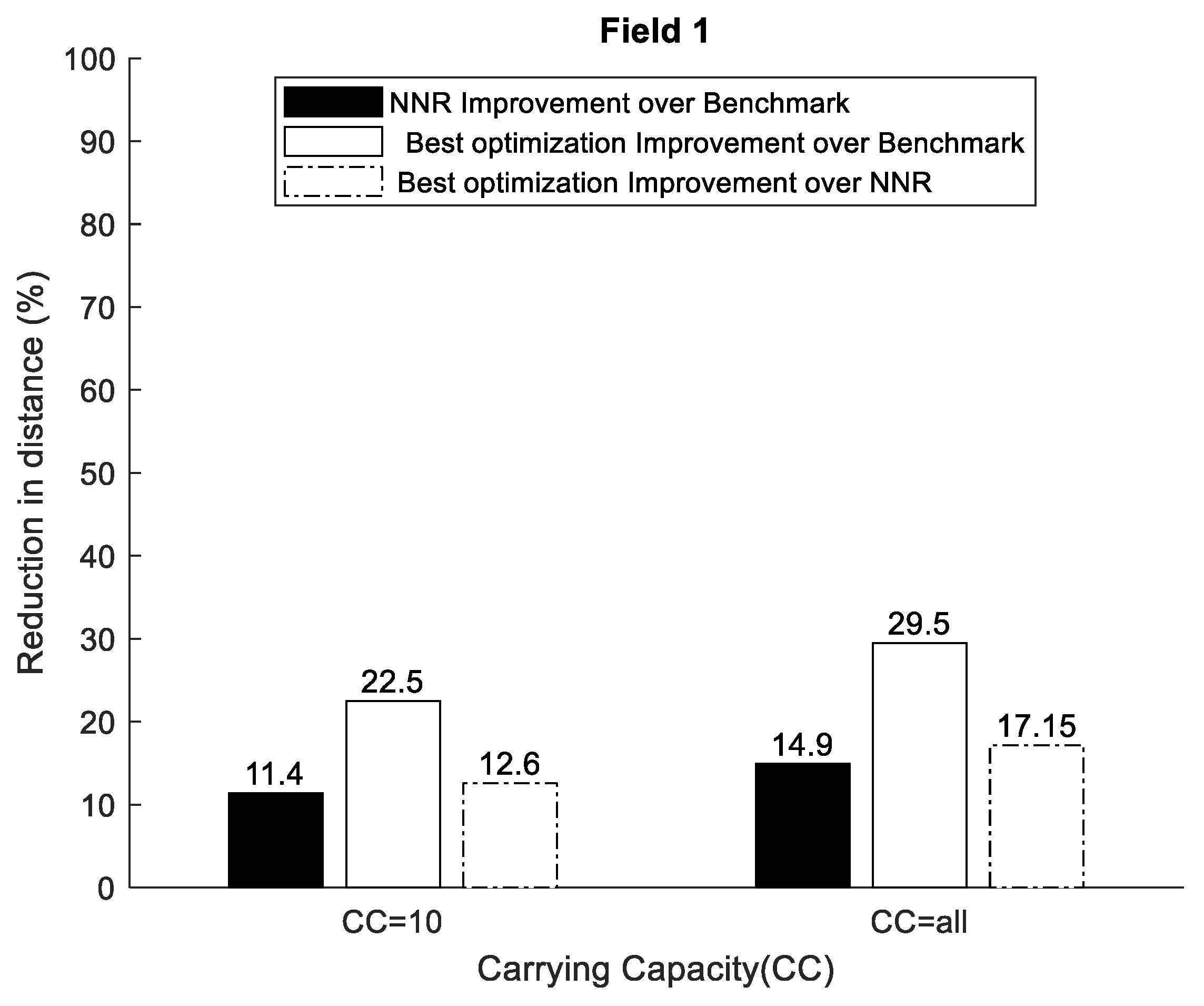
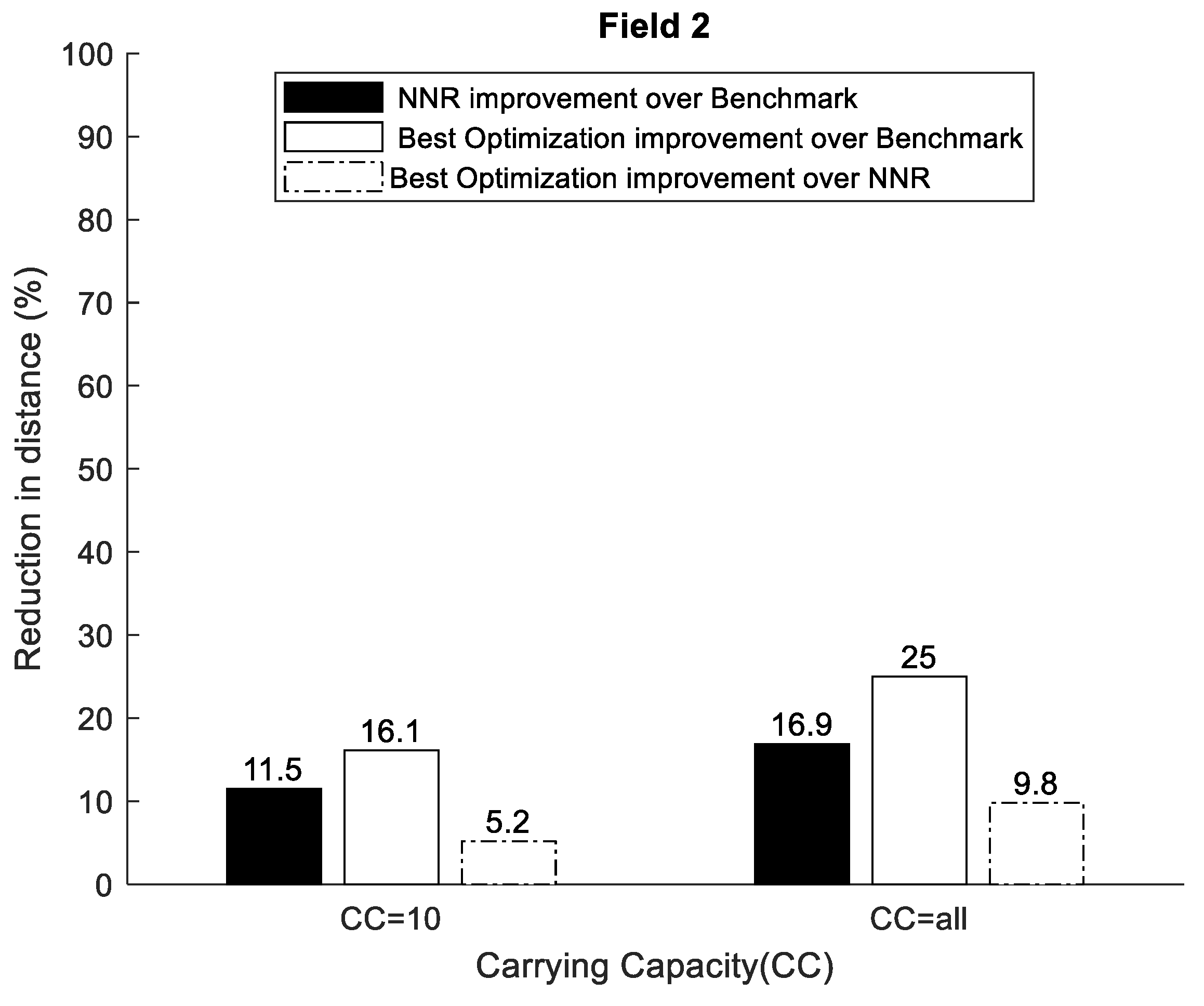
Taking the modeling limitations into consideration, some key insights were gained by analyzing the simulation results. It was found that adding carrying capacity significantly reduced the traveling distance for the bale collection operations. There was an exponential decaying trend in the distance reduction with respect to the carrying capacity. Hence, the bale collection procedure can be significantly improved, even with a small carrying capacity added. Comparing the benchmark with NNR showed that NNR reduced the travelled distance by about 10–20% (depending on field type and carrying capacity). Comparing the nearest neighbor strategy with optimization, the collection order may change for optimization (whether this is generally true or not cannot be concluded by the data presented in this paper). As would be expected, the simulations showed that the optimization approach reduced the travelled distance compared to the nearest neighbor approach. Compared to the benchmark, this reduction was about 20–30% for field 1 and 15–25% for field 2 and compared to NNR, this reduction was around 10–20% for field 1 and around 5–10% for field 2. Thus, the relative travelled distance reduction for the optimized solutions was slightly higher for the regular simple field (Field 1) compared to the complex field (Field 2). These travelled distance improvements can be compared to the similar studies by [21,22], which showed a 6.0 and 6.8% reduction for similar cases, respectively. It should be noted that the convergence to optimal solution strongly depended on the choice of initial population. The results indicate that the nearest neighbor initialization is a better choice than randomly permutated initialization independent of carrying capacities and field complexity (similar results for both fields).

5. Conclusions

It can be concluded that a vehicle with neighborhood collection capabilities and added carrying capacity can significantly reduce the travelled distance for bale collection operations (the benchmark model even gives an underestimation in this study). To generate short paths, the optimization approach is superior compared to the nearest neighbor approach and including the benchmark collection order in the initial population for the genetic algorithm improves the convergence compared to random initialization. Hence, implementing the optimization path planning approach, neighborhood collection capabilities, and adding a carrying capacity will have a significant effect on the farmers’ economic and environmental sustainability. By reducing the working distance through optimized path planning implies less fuel consumption and more cost effectiveness. Although the primary focus in this study was on bale collection operation, it is plausible that the same approach is applicable in similar activities both within agriculture and beyond, for example, in forestry.