Experimental Research on the Physical and Mechanical Properties of the Tussah Cocoon for Leaf-Stripping Machine Development

Abstract

The physical parameters and mechanical properties of the tussah cocoon are of vital importance for the design of a tussah cocoon leaf stripper. In this paper, the freshly harvested tussah cocoons wrapped with fresh leaves (TCFL) and the plucked and dried tussah cocoons (TCDL) were taken as research objects. The physical parameters and mechanical properties of the tussah cocoon with wrapped leaves, leafless tussah cocoons, tussah cocoon shells, tussah pupae, cocoon handle, and oak leaves were measured. The experiment showed that firstly, the radial deformation of the cocoon shell of the tussah cocoon should be controlled to be within 1.05 mm and the axial deformation to be within 1.6 mm. The pressure on the fresh leaf cocoon shell and the dry leaf cocoon shell cannot exceed 14.54 ± 3.16 N and 32.43 ± 7.04 N, respectively. Secondly, when the oak leaves are peeled off, the tensile force on the fresh leaves and dry leaves should be greater than 5.05 ± 3.63 N and 3.35 ± 1.85 N, respectively. Finally, the cocoon stalk can have a negative impact on the leaf-stripping process. These results can provide theoretical support for the design of a tussah leaf stripper to avoid damaging the cocoon shell and tussah pupa during the leaf stripping process.

1. Introduction

The tussah cocoons originated in Shandong, China, and have been reared for over 2000 years [1]. The tussah cocoon is farmed by wild rearing [2]. At present, tussah cocoon farming is mainly carried out in several provinces, including Shandong, Liaoning, Heilongjiang, Jilin, Henan, and Inner Mongolia. Compared with the mulberry silkworm, the tussah cocoon exhibits a low feeding cost. Tussah silk has high elasticity and good toughness, and its silkworm products are attractive in price and quality [3,4].

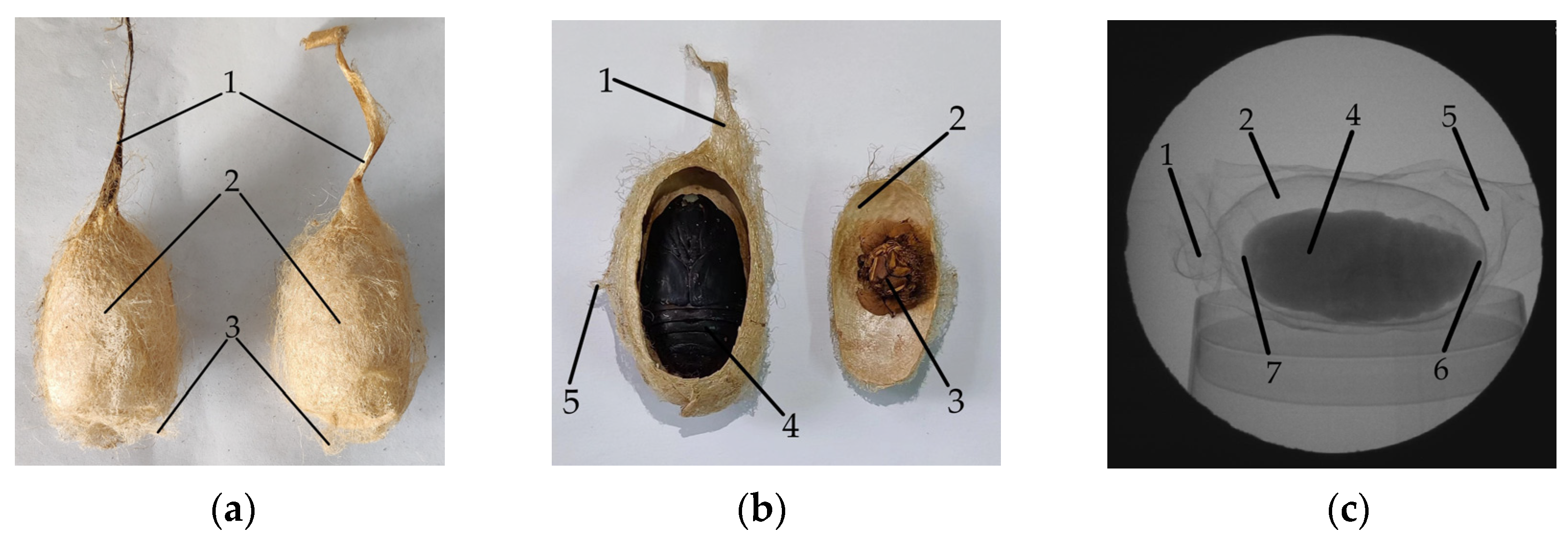
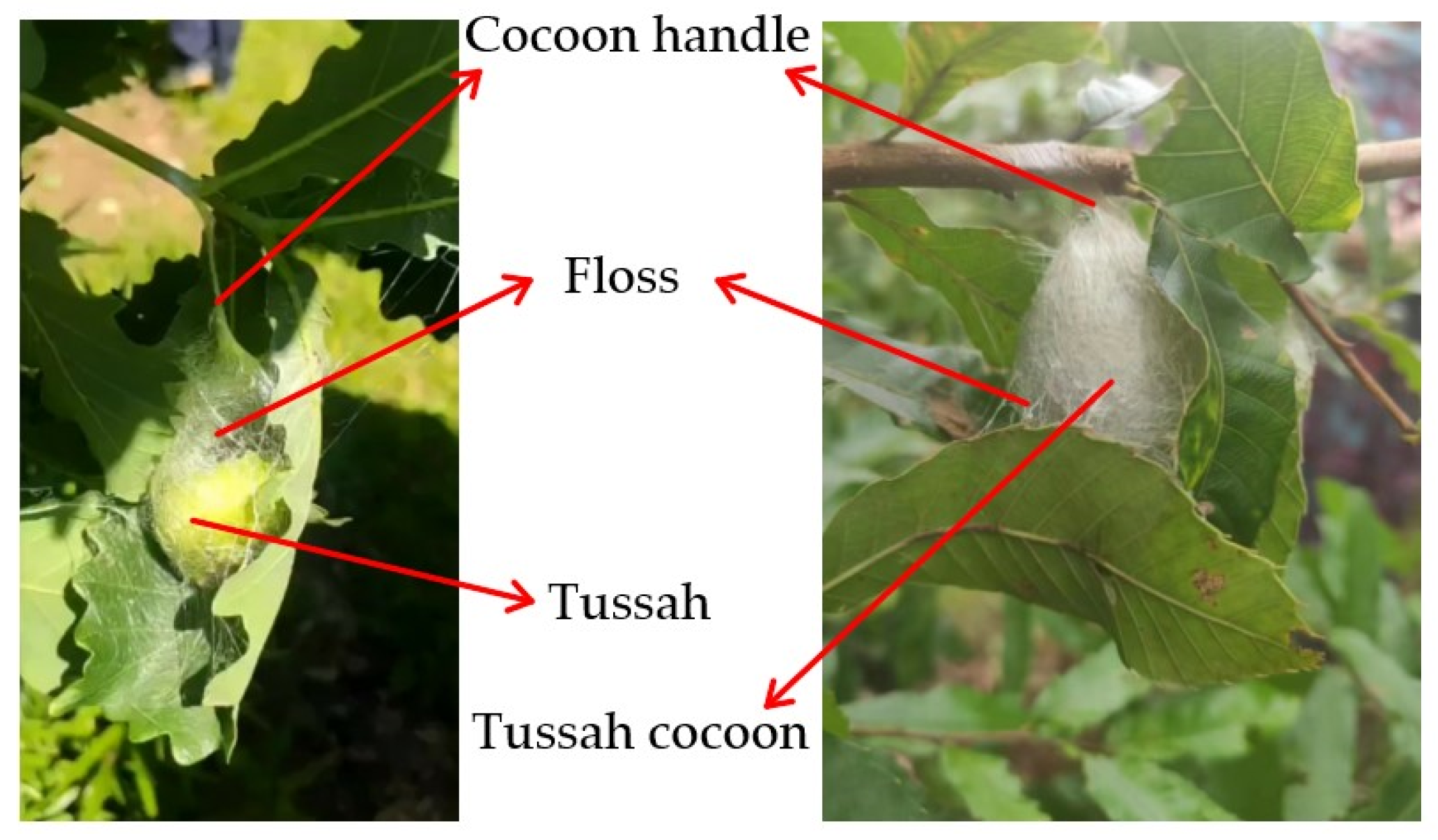
Tussah silk is obtained from tussah cocoons. The tussah cocoon consists of a cocoon handle, cocoon floss, cocoon shell, tussah pupa, and molting, as shown in Figure 1. Tussah cocoons are oval-shaped and the pupae are spindle-shaped. The tussah cocoon and the mulberry silkworm are raised differently and cocooned in different ways. Tussah cocoons are mainly parasitic (free-range) on oak trees. When the tussah in the later stage of the fifth instar is cocooning, it first spins silk and pulls 2~3 tussah leaves to form a skeleton to camouflage and protect itself, and then establishes cocoons in the skeleton. As a result, oak leaves are wrapped on the surface of the tussah cocoon, as shown in Figure 2. Once the tussah has completed its cocooning and pupation, the cocoon can be picked by the silkgrower. When picking the cocoons, the cocoons are first picked from the branches on the oak tree, along with the fresh oak leaves (wrapped leaves), and then the oak leaves wrapped around the cocoons are peeled off.

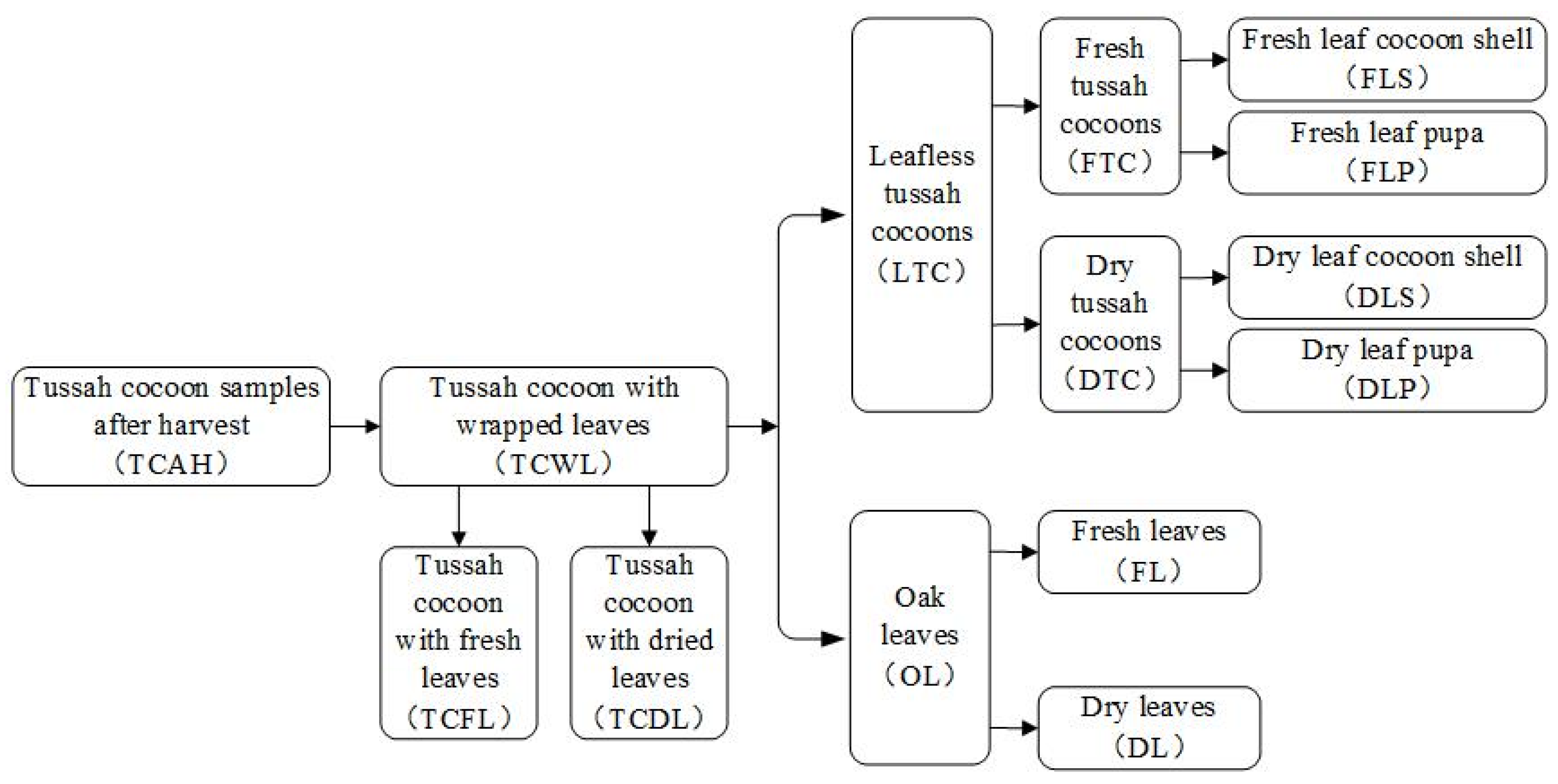
At present, the method of stripping the leaves of the tussah cocoons is mainly manual, both in China and worldwide, and the suitable leaf stripping period is brief. As a result, leaf stripping requires a lot of labor, increasing production costs. In order to reduce the labor input, it is a general trend to develop leaf-stripping machines to realize the mechanization of leaf peeling. The quality of the tussah cocoon (cocoon shell and silkworm pupa) must be guaranteed to the maximum extent during mechanized leaf stripping. In order to design a high-performance tussah cocoon defoliator, the basic physical parameters and mechanical properties of the tussah need to be measured and analyzed to provide data for the design of the leaf stripper. In the process of mechanized leaf stripping, it is necessary to ensure that the leaves are stripped from the tussah cocoons, and that neither the cocoon shells nor the pupae inside the cocoon shells are damaged to avoid damaging the pupae and contaminating the cocoon shells. Therefore, the basic physical parameters and mechanical properties of the oak leaves, tussah cocoons, and pupae need to be measured.

The measurement of physical parameters, including length [5], width [6], thickness [7], volume [8], density [9], mass [10], and moisture content within the material [11], must all be performed. The main methods of measuring mechanical properties include compression [12], bending [13,14,15], shear [16], tensile [17] and puncture [18,19] methods. There are few studies on the physical parameters and mechanical properties of tussah cocoons. Zhao et al. explored the tensile properties of a cocoon shell and measured its mechanical properties, including Young’s modulus and tensile strength. This study provides a reference to guide the biomimetic design of new safety protection materials and structures from the perspective of the microstructure and spatial functional gradient [20]. Chen et al. studied the structure and morphology of 27 different silkworm cocoons. The number and connectivity of layers through the cocoon wall thickness, the amount and distribution of the sericin binder, the diameter and packing density of the silk fibers, and the degrees of orientation of the nonwoven structure were studied to provide assistance in the design of rayon silk [21]. Xue et al. analyzed the thermal insulation performance of the tussah cocoon shell. Both experimental and theoretical analysis showed that tussah cocoons have better thermal insulation properties compared with those of the silkworm, and can be used in the biomimetic design of protective clothing and coatings [22]. At present, research on cocoons is mainly focused on the mechanical properties of mulberry silkworms. The physical parameters and mechanical properties of tussah cocoons have been scarcely studied. The research on the mechanical properties of tussah cocoons is mainly focused on the floss. There is a lack of research on the physical and mechanical parameters of tussah cocoons. Therefore, the physical and mechanical properties of the tussah cocoons at two moisture contents were studied in this paper. The length, diameter, and mass of the tussah cocoon; the length, diameter, and mass of the tussah pupa; and the thickness of the cocoon shell were measured. The axial and radial compression characteristics of the pupae and tussah cocoon were measured. The different stages of the buckling deformation of the cocoon were also analyzed. The magnitude of the detachment force of the cocoon stalk from the tussah cocoon and the peeling force of the tussah cocoon-wrapped leaves was measured. The physical and mechanical properties of tussah cocoons were also refined. These data provided a more comprehensive foundation for the design of the tussah leaf-stripping machine.

When designing the tussah cocoon leaf stripper, the extent of the peeling force and the mechanical properties of the tussah cocoon should be considered. This can ensure the integrity of the tussah cocoon after stripping and the survival rate of the silkworm pupae. Therefore, the steps of this work were as follows: (1) The basic physical parameters of the tussah cocoon, cocoon shell, silkworm pupae, and wrapped leaves were obtained through the physical property testing of each part of the tussah cocoon. The size of the gap between the cocoon shell and the pupa was obtained by analyzing the data. (2) Axial and radial compression tests were carried out on the tussah pupae, tussah cocoons, and tussah cocoon shells. The rupture force of the pupae and the variation of buckling deformation of the tussah cocoon shell and tussah cocoon during compression were obtained in order to reduce the damage to the cocoons and pupae of the tussah cocoon during the mechanical defoliation process. (3) The rupture force of the cocoon stalk and the peeling force of the cocoon leaves were studied. The tearing and puncturing characteristics of oak leaves were also studied. This data was used to design viable method for stripping the oak leaves.

2. Materials and Methods

2.1. Material Preparation

The tussah cocoons wrapped in fresh leaves and the cocoons wrapped in dried leaves were provided by the Si Taizi Research Base of the Liaoning Sericulture Scientific Research Institute, the accountable unit of the National Technical System for the feeding of the tussah sericulture. The tussah cocoons wrapped in fresh leaves were harvested on 28 September 2021. The tussah cocoons wrapped in dried leaves were harvested on 19 September 2021 and dried naturally until 30 September 2021. As shown in Figure 3, samples were prepared from tussah cocoons with well-wrapped leaves (fresh or dried) and complete cocoon stalks. Both samples were sealed, packed in plastic bags, and stored in a refrigerator (4 °C). Fifty tussah samples were measured for each physical property test. Thirty tussah samples were measured for each mechanical property test.

In this paper, the tussah cocoon specimens were divided into two categories: leaf-wrapped tussah cocoons wrapped with tussah leaves, and leafless tussah cocoons manually stripped of tussah leaves. Among them, the tussah cocoons wrapped with fresh leaves were referred to as tussah cocoons with fresh leaves, or TCFL. The tussah cocoons wrapped in tussah leaves after drying were called tussah cocoons with dried leaves, or TCDL. The tussah cocoons with the fresh leaves removed were called fresh tussah cocoons, or FTC. After the leaves are removed from the cocoons with dry leaves, they were called dried tussah cocoons, or DTC. The pupae removed from the fresh tussah cocoons were referred to as fresh leaf pupae (FLP), and their cocoon shells were called fresh leaf cocoon shells (FLS). The pupae removed from the dried tussah cocoons were referred to as dried leaf pupae (DLP), and their cocoon shells were called dried leaf cocoon shells (DLS) (Figure 4). The so-called FTC and DTC, fresh leaf pupae and dried leaf pupae, fresh leaf cocoon shells and dried leaf cocoon shells referred to in this paper are not classifications in the biological or commodity trade sense, but are used only for the convenience of the narrative discussion herein.

2.2. Test Method

2.2.1. Size Measurement of Tussah Cocoons

The tussah cocoon is ellipsoid, and the cross-sectional area perpendicular to the long axis is circular. The length of the cocoon of the tussah mentioned throughout this article did not include the length of the cocoon handle. The length of the long axis and the diameter of the short axis of the TCWL were measured with a high-precision digital vernier caliper (91512, SATA, Shanghai, China). The leaves of the TCWL were firmly attached to the cocoons in the direction of the wrapping. Subsequently, the oak leaves were stripped from the TCWL by hand, and the length and diameter of the LTC were measured using a digital vernier caliper. Finally, the cocoon shell was cut open with scissors to remove the pupae and molt from the LTC, measuring the thickness of the cocoon shell by clamping a single cocoon shell with the external measuring jaws of a vernier caliper. The length (distance from head to tail) and maximum diameter of the pupae were measured with a vernier card, with the vernier measuring claw lightly touching the skin of the pupae. The axial (in the direction of the long axis of the cocoon) and radial (in the direction of the short axis of the cocoon) gaps between the inside of the cocoon and the pupa were calculated. The calculation formulas are shown below.

$$c_a=L-2e-l$$

(1)

$$c_r=D-2e-d$$

(2)

where c_a is the axial gap (mm), c_r is the radial gap (mm), L is the length of the tussah cocoon (mm), e is the thickness of the cocoon shell (mm), l is the length of the pupa (mm), D is the diameter of the tussah cocoon (mm), and d is the diameter of the pupa (mm).

2.2.2. Mass Measurement of Tussah Cocoons

Firstly, the mass of the TCWL was measured using an electronic balance (JJ1023BC, G&G Measurement Plant, Changshu, China). Secondly, the oak leaves were peeled off by hand, and the mass of the peeled leaves (all leaves peeled off from the TCWL) and the LTC were weighed separately. Finally, the cocoon shell was cut open with scissors, and the pupae and molt were removed. The shell and pupae were weighed separately.

2.2.3. Measurement of the Moisture Content of Oak Leaves and Cocoon Shells

The oak leaves and the cocoon shells were cut with scissors (triangular or rectangular pieces with sides less than 10 mm long) and tested for moisture content at a set temperature of 105 °C using a halogen rapid moisture tester (ZTXY-101, Shanghai Zhunquan Instrument Equipment Co, Shanghai, China) [23].

2.2.4. Tussah Cocoons and Pupae Compression Test

Radial and axial compression tests were carried out on the TCWL and LTC using a biomechanical tester (EZ-SX, Shimadzu, Kyoto, Japan). Radial compression tests were carried out on the FLP and the DLP, respectively. The radial compression strain is the compression divided by the diameter and the axial compression strain is the compression divided by the length. The equations for calculating the radial and axial compression strains are shown below.

$${\epsilon }_1=\frac{\Delta X}{D}$$

(3)

$${\epsilon }_2=\frac{\Delta L}{L}$$

(4)

where ε₁ is radial compression strain, ε₂ is axial compression strain, ΔX is radial compression displacement (mm), ΔL is axial compression displacement (mm), D is the maximum diameter of silkworm pupae and cocoons (mm), and L is long axis length of cocoons (mm).

When the pupae were tested in radial compression, the front of the pupae (Figure 5a) was placed face down on the central position of the biomechanical tester carrier, and the indenter of the biomechanical tester applied pressure at the back of the pupae (Figure 5b). The cocoon stalk was reduced using scissors before the axial compression of the cocoon. The cocoon was held by the head facing upwards, and the cocoon was placed vertically with the tail end facing downwards on the central position of the biomechanical tester carrier table. The biomechanical tester was activated, and when the indenter was in contact with the head of the cocoon, the hand was released for normal measurement. The head and tail of the tussah cocoon are shown in Figure 1c. This experiment studied the effects of drying (moisture content) and tussah leaf wrapping on the compressive mechanical properties of tussah cocoons in order to obtain the magnitude of the force required for the fracturing of silkworm pupae.

To study the effect of silkworm pupae on the compression process of tussah cocoons, compression experiments were carried out on empty cocoon shells. Firstly, a small hole with a diameter of 1.6 mm was made from the tail of the LTC using an insect dissecting needle (1.45 mm in diameter, 135 mm in length, Chaozhou Chaoan Caitang Hangyu Medical Equipment Factory, Chaozhou, China). Secondly, the inner tissue of the silkworm pupae in the cocoon shell was crushed and extracted using a disposable syringe (1.6 × 10 TW XZ type, JiangYin Changqiang Medical Devices Co., Ltd., Jiangyin, China). At this time, the silkworm pupae in the cocoon shell only contained a thin layer of pupa skin, eliminating the influence of the silkworm pupae on the silkworm cocoon. Finally, a radial compression test was carried out on the empty cocoon shell, analyzing the effects of the silkworm pupae on the radial compression of the tussah cocoon.

A 50 mm indenter was used for the compression test. The surface of the specimen in contact with the indenter was called the upper contact surface, while the surface of the specimen in contact with the carrier table was called the lower contact surface. The loading speed was set at 10 mm/min for the compression of the pupae and 10 mm/min for the compression of the tussah cocoon and cocoon shell. The length and diameter of the specimen were measured with a vernier caliper before the test.

2.2.5. Tussah Cocoon and Cocoon Stalk Separation Test

As the tussah cocoons were oval-shaped and not easily clamped, the cocoons were cut open at the end using scissors, and the pupae were removed, as shown in Figure 6. The tail of the cocoon shell and the upper end of the cocoon stalk were clamped separately using the biomechanical tester fixture. Subsequently, it was subjected to tensile testing. The test was discontinued when the cocoon floss attached to the cocoon stalk was separated from the cocoon shell. The mass of the cocoon shell after the removal of the pupae was measured before the test. The loading speed was set to 20 mm/min for tensile testing.

2.2.6. Tussah Cocoon-Covered Leaf Stripping Test

One side of the leaf of the TCWL was clamped, and the TCWL hung using the fixture included in the biomechanical tester. Firstly, the biomechanical tester was activated. The fixture was set to remain motionless, and the data recording function of the instrument was switched on. Afterward, the tussah cocoon was gently squeezed and pulled down vertically, by hand. The tussah cocoons were turned slowly during the pull-down process until they were peeled off of the leaves, as shown in Figure 7. The maximum force required to peel off a leaf from a tussah cocoon was observed by recording the change in the load curve during peeling, using a biomechanical tester. Before the test, the length and diameter of the TCWL were measured using vernier calipers.

2.2.7. Tests on the Mechanical Properties of Oak Leaves

Because the fresh leaves were soft and had a high moisture content, bending tests were not carried out. In contrast, dried leaves after drying had a lower moisture content, and were more brittle and curled due to water loss and wrapping around the tussah cocoons, making them less susceptible to bending, tearing, and piercing tests. Therefore, this paper only studied the tearing and piercing of fresh leaves.

(1)

The fresh leaves were stripped intact from the TCFL. The mass of individual oak leaves was measured using an electronic balance. The edges of the fresh leaves were held in place using the fixture accompanying the biomechanical tester and tested for tearing.

(2)

The fresh leaves were stripped intact from the TCFL. Fresh leaves were cut on both sides of the main leaf vein (the main leaf vein was thick and tended to deflect when clamped) using scissors. The cut half of the leaf was fixed to a puncture test bench (The clamping disc was made of acrylic plate, with a disc diameter of 190 mm, a thickness of 10 mm, and a puncture hole diameter of 10 mm) for the puncture test. The diameter of the cylindrical puncture probe was 2 mm. The base of the probe was flat, and the puncture speed was set at 10 mm/min [24].

The puncture strength was calculated by selecting the maximum puncture force from the load-displacement curve of the puncture test. The calculation formula is shown below.

$$P=\frac{F_{max}}{S}$$

(5)

where P is puncture strength (MPa), F_max is maximum puncture force (N), and S is puncture area (mm²).

3. Results and Discussion

Origin 2018 (Origin Lab, Northampton, MA, USA) was used to organize and preprocess the experimental data, as well as to draw the experimental images. The test data were analyzed by ANOVA using SAS 9.2 (Statistical Analysis System, SAS Institute Inc., Kerry, NC, USA) software and tested for significance at the p = 0.05 level.

3.1. Measurement Results and Analysis of Basic Physical Parameters of Tussah Cocoons

3.1.1. Analysis of the Basic Physical Parameters of Tussah Cocoons

It can be seen from

Table 1. Basic physical parameters of tussah cocoons and pupae.

Sample Type	Total Mass/g	Length/mm	Diameter/mm	Number of Wrapped Tussah Leaves/Piece
TCFL	14.65 ± 2.46 a	51.45 ± 3.92 a	29.13 ± 2.75 a	2 ± 1
TCDL	13.76 ± 2.95 b	53.04 ± 3.27 a	28.53 ± 4.51 a	2 ± 1
FTC	12.51 ± 2.11 c	49.94 ± 2.91 b	27.06 ± 1.80 b	/
DTC	11.27 ± 2.16 d	48.48 ± 4.13 b	25.50 ± 3.40 b	/
FLP	9.66 ± 1.84 e	43.64 ± 2.82 c	19.63 ± 1.49 c	/
DLP	10.72 ± 2.14 e	45.38 ± 5.04 c	20.26 ± 1.85 c	/

Note: TCFL—tussah cocoon with fresh leaves; TCDL—tussah cocoon with dried leaves; FTC—fresh tussah cocoon; DTC—dry tussah cocoon; FLP—fresh leaf pupa; DLP—dry leaf pupa. The data in the table is in the form of arithmetic mean ± standard deviation (n = 50). The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05), which is the same as Table 2, Table 3 and Table 4.

and

Table 2. Basic parameters of cocoon shells and oak leaves.

Sample Type	Mass/g	Moisture Content/% (WB)	Cocoon Shell Thickness/mm
FLS	1.287 ± 0.002 a	19.47 ± 2.27 a	0.39 ± 0.09 a
DLS	1.222 ± 0.009 b	13.42 ± 1.04 b	0.35 ± 0.08 a
FL	2.38 ± 0.99 c	35.69 ± 5.79 c	/
DL	1.13 ± 0.45 d	17.22 ± 3.64 d	/

Note: FLS—fresh leaf cocoon shell; DLS—dry leaf cocoon shell; FL—fresh leaves; DL—dry leaves. The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

that there was a significant difference between the moisture content of wrapped leaves and the moisture content of the cocoon shells (p < 0.05). Moisture content had a significant effect (p < 0.05) on the mass of the TCWL, the LTC, the oak leaves, and the cocoon shells. There was a significant difference (p < 0.05) between the mass of the TCWL and that of the LTC. The results indicated that not only did the wrapped leaves lose moisture during the drying process of the cocoons, but also that the cocoon shells of the tussah cocoons lose moisture simultaneously.

From

Table 3. Axial clearances between the cocoon shell and the tussah pupa.

Tussah Cocoon Length Range/mm	Axial Clearance/mm
40~45	3.42 ± 1.09 a
45~50	4.63 ± 1.78 b
50~55	6.26 ± 1.95 c
55~60	7.31 ± 2.04 d

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

and

Table 4. Radial clearances between the cocoon shell and tussah pupa.

Tussah Cocoon Diameter Range/mm	Radial Clearance/mm
15~20	2.92 ± 0.84 a
20~25	4.05 ± 1.46 b
25~30	7.48 ± 1.48 c

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

, it can be seen that with the increase in the diameter (length) of the tussah cocoon, the axial gap (radial gap) between the cocoon shell and the silkworm pupae increased. Table 3 shows that when the length of the tussah cocoon was within the range of 40~45 mm, the axial clearance between the cocoon shell and silkworm pupa was the smallest (3.42 ± 1.09 mm). From Table 4, it can be seen that the smallest radial clearance between the cocoon shell and the pupa (2.92 ± 0.84 mm) was observed when the cocoon diameter of the tussah cocoon was in the range of 15 to 20 mm. Therefore, as long as the deformation of the cocoon shell under pressure did not exceed this gap, the pupae inside the cocoon shell was not damaged by extrusion.

3.1.2. Changes in Moisture Content before and after the Test

Due to the long duration of this test, the specimens were sealed in plastic bags with sealing strips and stored in a refrigerator (4 °C) to ensure the consistency of the test data. At the end of the experiment (after 14 days) the moisture content of the oak leaves wrapped around the tussah cocoons was measured again. The measurement results showed that the moisture content of the fresh leaves was 37.57% ± 4.47%, and the moisture content of the dry leaves was 19.14% ± 2.63%. The moisture content of the oak leaves at this time was not significantly different (p > 0.05) from the moisture content of fresh (35.69% ± 5.79%) and dried (17.22% ± 3.64%) leaves at the start of the trial, which ensured the accuracy and consistency of the data during the trial.

3.2. Experiment using Radial Compression Tests on Tussah Cocoons and Pupae

3.2.1. Radial Compression Analysis of Silkworm Pupae

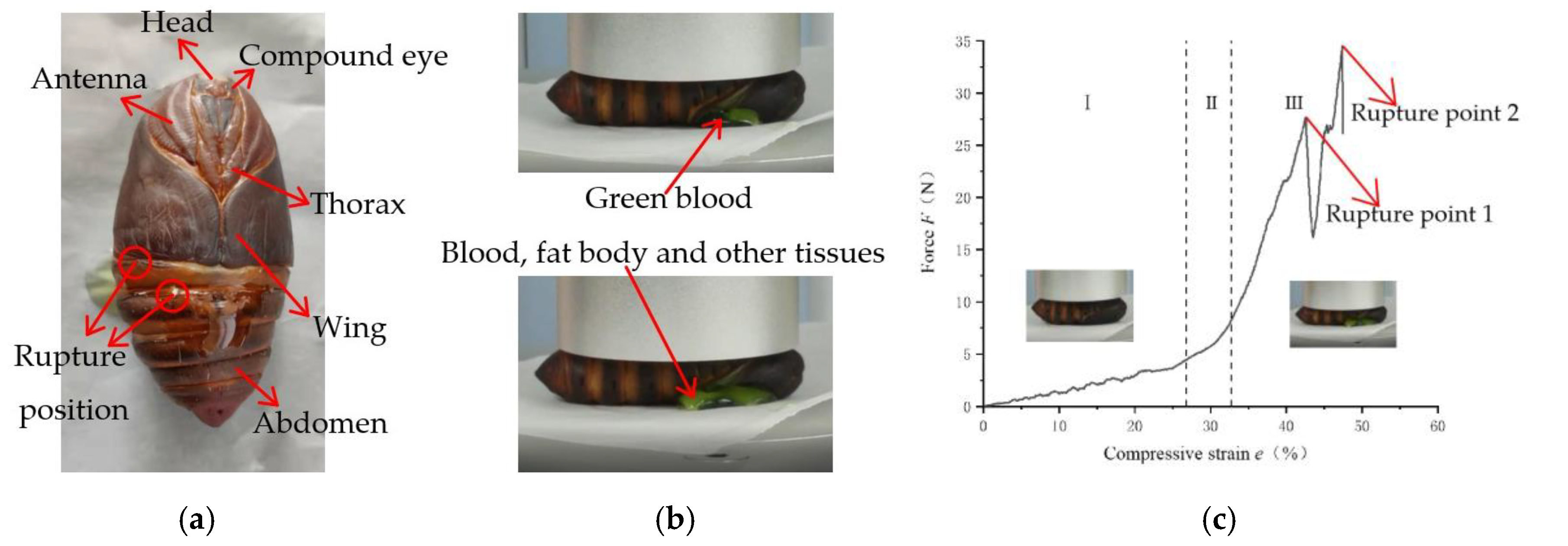
The pupa of the tussah cocoon consists of a head, thorax, and abdomen. The head is small, and the thorax consists of three links, visible only on the back. The abdomen consists of ten segments, the first three of which are covered ventrally by the wings and visible only dorsally, with the fourth, fifth, and sixth ventral segments being larger and freely retractable. The interior of the tussah pupa is filled with green blood, fat bodies, and other tissues. When the silkworm pupae were pressed radially, the abdomen of the pupae elongated axially until the intersegmental membrane ruptured due to pressure transfer.

When the pupae were compressed, the pressure point was located at the junction of the pupae’s wings and abdomen. By observing the compression process of the pupae, it was found that when the pupae were compressed and ruptured, the rupture points occurred mainly at two locations. As shown in Figure 8a, one location was ruptured from the intersegmental membrane joining the abdomen of the pupa, and the other location was ruptured from the intersegmental membrane joining the wing to the abdomen of the pupa. When the pupae ruptured under compression, initially, green blood flowed out, corresponding to the first mutation point (rupture point 1) on the force-compression strain curve, as shown in Figure 8c. Subsequently, tissues such as the fat body in the pupa were pressed out, and therefore, a second mutation point (rupture point 2) appeared on the force–compression strain curve.

As shown in Figure 8c, the force–strain (ratio of compression to the maximum diameter of the pupa) curve of radial compression of the pupa (length and maximum diameter of 42.85 mm and 21.79 mm, respectively) can be divided into three stages.

Stage I (ε = 0~25%): abdominal elongation under pressure. At the beginning of the compressive deformation, the pupae were subjected to radial pressure, and the abdomen of the pupae elongated along the axial direction of the pupae. Then, as the compression increased, the abdominal elongation of the pupa increased. Simultaneously, the pressure on the pupae increased linearly as the radial deformation of the pupae increased.

Stage II (ε = 25~35%): the pressure increased exponentially with compressive strain. The elongation of the pupa’s abdomen reached its limit when the radial compressive strain of the pupa exceeded 25%. At this point, as the compression continued to increase, the forces on the pupa increased exponentially.

Stage III (ε > 35%): pupae fracturing. When the radial compressive strain on the pupae exceeded 35%, the pressure on the pupae increased linearly with the increasing radial compressive deformation. When the pupae reached a radial compressive strain of 40% (pressure reached 26.7 N), the pressure suddenly dropped. At this point, the pressure reached the rupture limit of the pupa, and the pupa ruptured at the point where the ventral segment joins the ventral segment (intersegmental membrane), or where the wing joined the ventral segment (intersegmental membrane). At this moment, the pressure decreased, and the first abrupt change in the force–compression strain curve occurred. The pupae contained a large amount of tissue inside, such as fat bodies, which were difficult to press out when compressed. Therefore, as the compression continued to increase, the pressure on the pupa again increased. When the radial compressive strain of the pupa reached 47% (the pressure reached 34.2 N), tissues, such as fat bodies, within the pupa were pressed out, which caused the pressure to decrease rapidly. At this point, a second abrupt change in the force–compression strain curve occurred.

3.2.2. Radial Compression Analysis of Empty Cocoon Shells and Tussah Cocoon

The force–compression strain (ratio of compression to the short axis length of the cocoon shell) curves for the DLS (length and diameter of 50.93 mm and 28.86 mm, respectively) and the FLS (length and diameter of 50.47 mm and 28.65 mm, respectively) measured in the test are shown in Figure 9a. Figure 9c briefly shows the deformation process of the empty cocoon shell when it was under pressure. As can be seen from Figure 9a, the curve was essentially the same as the first three stages of the force–compression strain curve for a thin-walled spherical metal shell [25,26]. Therefore, the force–compression strain curve of the empty cocoon shell was divided into three stages.

Stage I (ε = 0~7%) was the radial flattening stage of the empty cocoon shell (Figure 9c). In the early stages of compressive deformation, the cocoon shell underwent only elastic deformation. The force–compression strain curve was close to a straight line. Stage II (ε = 7%~39%) was the radially symmetrical buckling stage of the empty cocoon shell (Figure 9c). As the compression displacement continued to increase, the upper and lower contact surfaces of the cocoon shell began to depress symmetrically inwards, and the contact surface became oval (Figure 9c, A). Stage III (ε > 39%) was the radially asymmetric buckling phase stage of the empty cocoon shell (Figure 9c). When the compression was further increased, the upper and lower contact surfaces of the tussah cocoon gradually expanded outwards, and the elliptical contact surface changed to form a new stable asymmetric polygonal shape (Figure 9c, B and C).

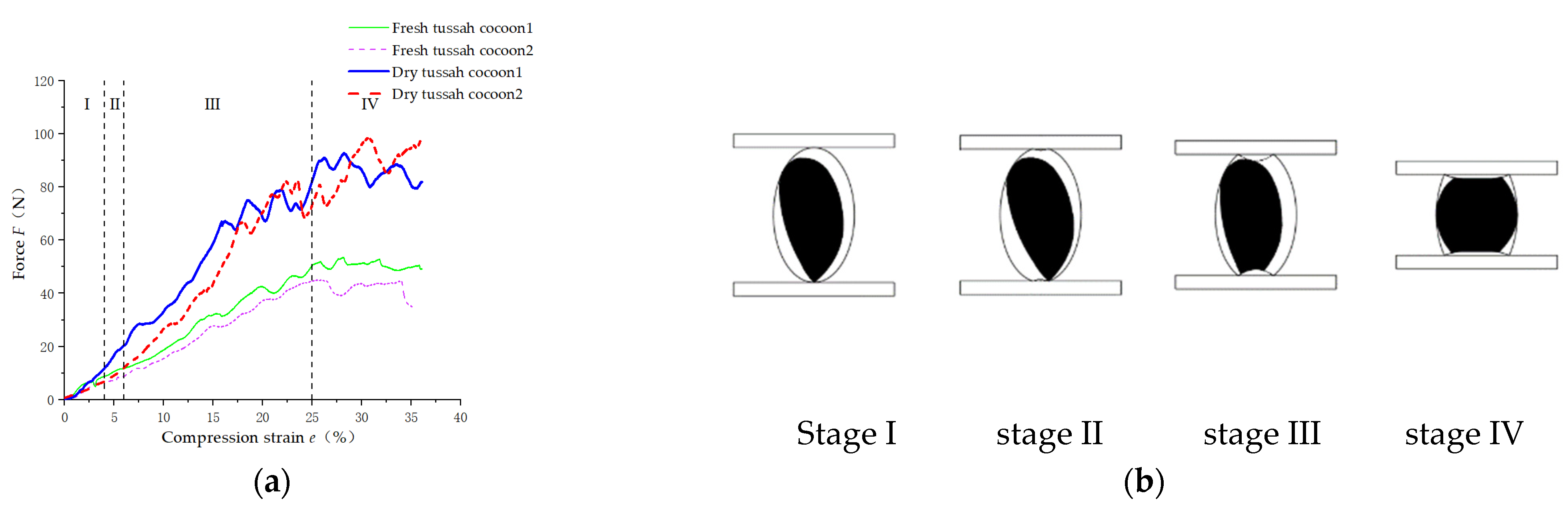
Figure 9b shows the force–strain curves of the pupa-containing DTC (length and diameter 50.77 mm and 28.12 mm, respectively) and the pupa-containing FTC (length and diameter 51.12 mm and 28.21 mm, respectively) under radial compression. The test speed was 10 mm/min. According to the shape of the curve in Figure 9b, the radial pressure deformation process of the tussah cocoon (including the pupa) can be divided into four main stages [27]. The tussah cocoon deformations corresponding to the different stages of the compression process are shown in Figure 9d.

Stage I (ε = 0~7%): radial flattening of the cocoon shell (Figure 9d). Before the cocoon shell collapses, the upper contact surface and the lower contact surface of the tussah cocoon underwent only elastic deformation. The force–strain curve was approximately linear.

Stage II (ε = 7%~12.5%): radial symmetric buckling of cocoon shell (Figure 9d). As the radial deformation of the cocoon shell increased, the pressure on the cocoon shell also increased, and the compression contact surface continued to increase. When the radial deformation of the cocoon shell increased to a certain value, the cocoon shell compression contact surface was symmetrically turned inwards and depressed.

Stage III (ε = 12.5%~32%): radial symmetric buckling of the cocoon and radial synchronous compression of the pupa (Figure 9d). According to Table 4, the radial clearance between the cocoon shell and the pupa was 7.48 ± 1.48 mm when the diameter of the cocoon was in the range of 25~30 mm. Therefore, when the compression reached 3.5 mm and the cocoon strain reached 12.5% (the upper and lower contact surfaces of the cocoon shell concurrently concave), the cocoon shell came into contact with the pupa. As the indenter continued to press down, the cocoon shell was compressed at the same time as the pupa.

Stage IV (ε > 32%): radial symmetric buckling of cocoon shell and synchronous radial compression of cocoon shell and silkworm pupa (Figure 9d). When the flexural deformation of the cocoon shell reached a certain level, the upper and lower contact surfaces formed a stable asymmetric polygonal shape, as shown in Figure 10. When the indenter was pressed down, the pressure increased rapidly. When a sudden decrease in the load curve occurred, it indicated that the pupae had ruptured. At this point, the strain on the tussah cocoons reached 43%, and the critical pressure was 85.72 ± 17.46 N (FTC) or 151.57 ± 52.46 N (DTC).

3.2.3. Combined Radial Compression Analysis of Silkworm Pupae, Empty Cocoon Shells, and Cocoons

The force–deformation curves for the radial compression of pupae, cocoon shells, LTC, and cocoon shells superimposed on the pupae are shown in Figure 11a. The gap between the pupae and the cocoon shell was measured to be around 7 mm in this group. When the tussah cocoon was compressed, the upper and lower contact surfaces of the cocoon bent inward and deformed simultaneously (Figure 9d). Therefore, when the deformation of the tussah cocoon reached about 3.5 mm, the cocoon shell started to extrude the pupa. By observing the size and the trend of the curves of the cocoon shells and the LTC, differences were found in both the size and inflection points of the curves. Then, the force–deformation curves of the cocoon shells and the pupae were superimposed. The superimposed curves were compared with the curves of LTC, and it was found that the trends of the curves were basically the same. The load started to increase exponentially when the deformation was at 9 mm (32% compressive strain), and the pupa ruptured at 12 mm (43% compressive strain). When the LTC was compressed, the pupa expanded and filled the cocoon shell, which limited the expansion of the pupa’s abdomen. (The location of the rupture was on the thorax of the pupa and was different from the location at the point of rupture under pressure in the pupa). Therefore, when the LTC was compressed, the cocoon shell was supported by the silkworm pupa, as shown in Figure 11b. The pressure of the LTC was higher than the superimposed pressure of the cocoon shell and silkworm pupa.

3.2.4. Radial Compression Data Discussion

As can be seen in Table 5, the oak leaves had no significant effect on the radial collapse force on the cocoon shell and the radial rupture force of the pupae inside the shell (p > 0.05). However, the drying of tussah cocoons after harvesting reduced the moisture content of the wrapped leaves and the cocoon shells. There were significant differences (p < 0.05) between the radial mean collapse force of the DLS and the radial mean collapse force of the FLS. Drying also caused a significant difference (p < 0.05) in the total pressure on the cocoon shell when the pupae were radially ruptured. As a result of drying, the average moisture content of the cocoon shell decreased from 19.47% to 13.42%. This increased the radial average collapse force on the cocoon shell by 120.46% and the radial average rupture force of the pupae inside the shell by 76.82%. According to Table 5, it can be seen that there was no significant difference in the radial rupture force between the FLP and the DLP (p > 0.05).

Table 5. Experimental results of radial compression of tussah cocoons and pupa.

Sample	Length/mm	Diameter/mm	Radial Collapse Force of Cocoon Shell/N	Resultant Force of Silkworm Pupae and Cocoon Shell When Silkworm Pupae Breaks/N	Radial Rupture Force of Silkworm Pupa/N
TCFL	50.75 ± 3.17 a	28.08 ± 1.86 a	14.54 ± 3.16 a	91.52 ± 43.42 a	/
FTC	50.71 ± 4.44 a	26.98 ± 1.91 a	12.95 ± 2.16 a	85.72 ± 17.46 a	/
TCDL	51.36 ± 4.04 a	27.95 ± 2.21 a	32.43 ± 7.04 b	162.20 ± 77.78 b	/
DTC	48.06 ± 6.40 a	26.44 ± 2.63 a	28.55 ± 6.93 b	151.57 ± 52.46 b	/
FLP	45.80 ± 3.23 b	20.75 ± 1.88 b	/	/	26.11 ± 6.93 a
DLP	43.82 ± 2.82 b	19.91 ± 1.54 b	/	/	27.29 ± 7.56 a

Note: The data in the table is in the form of arithmetic mean ± standard deviation (n = 30). The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate significant difference (p < 0.05), which is the same as shown in Table 6, Table 7 and Table 8.

Table 5. Experimental results of radial compression of tussah cocoons and pupa.

Sample	Length/mm	Diameter/mm	Radial Collapse Force of Cocoon Shell/N	Resultant Force of Silkworm Pupae and Cocoon Shell When Silkworm Pupae Breaks/N	Radial Rupture Force of Silkworm Pupa/N
TCFL	50.75 ± 3.17 a	28.08 ± 1.86 a	14.54 ± 3.16 a	91.52 ± 43.42 a	/
FTC	50.71 ± 4.44 a	26.98 ± 1.91 a	12.95 ± 2.16 a	85.72 ± 17.46 a	/
TCDL	51.36 ± 4.04 a	27.95 ± 2.21 a	32.43 ± 7.04 b	162.20 ± 77.78 b	/
DTC	48.06 ± 6.40 a	26.44 ± 2.63 a	28.55 ± 6.93 b	151.57 ± 52.46 b	/
FLP	45.80 ± 3.23 b	20.75 ± 1.88 b	/	/	26.11 ± 6.93 a
DLP	43.82 ± 2.82 b	19.91 ± 1.54 b	/	/	27.29 ± 7.56 a

Note: The data in the table is in the form of arithmetic mean ± standard deviation (n = 30). The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate significant difference (p < 0.05), which is the same as shown in Table 6, Table 7 and Table 8.

Table 6. Measurement data for breaking force of tussah silkworm stalks.

Sample	Mass/g	Cocoon Handle Disengagement Force/N
FTC	1.35 ± 1.32 a	29.91 ± 11.15 a
DTC	1.21 ± 1.23 b	36.09 ± 9.98 b

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

Table 6. Measurement data for breaking force of tussah silkworm stalks.

Sample	Mass/g	Cocoon Handle Disengagement Force/N
FTC	1.35 ± 1.32 a	29.91 ± 11.15 a
DTC	1.21 ± 1.23 b	36.09 ± 9.98 b

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

Table 7. Data for mechanical properties of oak leaves.

Type of Test	Mass/g	Maximum Load/N
Fresh leaf tear	2.387 ± 0.998	7.19 ± 2.48
Fresh leaf puncture	1.693 ± 0.499	3.22 ± 2.17

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

Table 7. Data for mechanical properties of oak leaves.

Type of Test	Mass/g	Maximum Load/N
Fresh leaf tear	2.387 ± 0.998	7.19 ± 2.48
Fresh leaf puncture	1.693 ± 0.499	3.22 ± 2.17

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

Table 8. The magnitude of peeling force on tussah cocoon wrapped leaves.

Sample	Tussah Cocoon Size with Wrapped Leaves/mm		Peeling Force of Wrapped Leaves/N
	Length	Diameter
FL	49.59 ± 3.17 a	27.94 ± 2.12 a	5.05 ± 3.63 a
DL	48.83 ± 3.99 a	27.31 ± 2.44 a	3.35 ± 1.85 b

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

Table 8. The magnitude of peeling force on tussah cocoon wrapped leaves.

Sample	Tussah Cocoon Size with Wrapped Leaves/mm		Peeling Force of Wrapped Leaves/N
	Length	Diameter
FL	49.59 ± 3.17 a	27.94 ± 2.12 a	5.05 ± 3.63 a
DL	48.83 ± 3.99 a	27.31 ± 2.44 a	3.35 ± 1.85 b

Note: The same letter after different data in the same column indicates no significant difference (p > 0.05), and different letters indicate a significant difference (p < 0.05).

According to the test results, it can be seen that when the radial compression strain of tussah cocoons was less than 7%, or the radial pressure of TCFL was less than 14.54 ± 3.16 N and the radial pressure of TCDL was less than 32.43 ± 7.04 N, the cocoon shell underwent only elastic deformation. When the diameter of the cocoon was 15 mm, the cocoon shell collapsed, with the smallest deformation of 1.05 mm. However, if the radial strain in the tussah cocoons reached 12.5%, it likely compressed the pupae. Therefore, in order to guarantee the quality of the cocoon shells (because the cocoon shell needs reeling), they must not be plastically deformed, ensuring that the radial strain of the shells is within 7% and that the deformation is less than 1.05 mm.

3.3. Experiment of Axial Compression Tests on Tussah Cocoons

The force–compression strain curves for the DTC (length 51.32 mm, diameter 28.32 mm) and the FTC (length 50.16 mm, diameter 27.91 mm) in axial compression are shown in Figure 12a. The axial compression process is similar to the radial compression process and can be divided into four main stages [28]. The compression changes corresponding to the tussah cocoons are shown in Figure 12b.

Stage I (ε = 0~4%): axial flattening of the cocoon shell (Figure 12b). The axial apical collapse force of the TCDL cocoon shell was measured to be 43.57 ± 4.99 N. The axial apical collapse force of the DLS cocoon shell was measured to be 38.24 ± 7.05 N. There was no significant difference between the two cocoons (p > 0.05). The axial apical collapse force of the TCFL cocoon shell was measured to be 15.34 ± 2.29 N. The axial apical collapse force of the FLS cocoon shell was measured to be 13.45 ± 2.03 N. There was no significant difference between the two cocoons (p > 0.05). However, there was a significant difference (p < 0.05) in the axial collapse force of the cocoon shell between the TCFL and the TCDL. There was also a significant difference (p < 0.05) in the axial collapse force of the cocoon shell between the FLS and the DLS.

Stage II (ε = 4%~6%): axisymmetric buckling of the cocoon shells (Figure 12b). At this stage, there was a gap between the cocoon shell and the pupa axially, which had not yet been pressed into the pupa. As the compression increased, the cocoon shell began to sink inwards.

Stage III (ε = 6%~25%): axisymmetric buckling of the cocoon shell and simultaneous compression of the silkworm pupa (Figure 12b). According to Table 3, the axial clearance between the cocoon shell and the pupa was 6.26 ± 1.95 mm when the cocoon length was between 50~55 mm. Therefore, when the cocoon was pressed by 3 mm (the strain on the cocoon of the silkworm reached 6%), the cocoon shell sagged inward, and the cocoon shell began to squeeze the silkworm pupae. Because the tussah cocoon was ellipsoid, the contact surface between the cocoon shell and the indenter increased continuously during the compression process. The force–compressive strain curve rose in a wavy manner.

Stage IV (ε > 25%): axial asymmetric buckling of the cocoon shell and compression of the silkworm pupa (Figure 13b). When the strain on the cocoon was greater than 44.6%, the cocoon shell layer continued to sink inwards. The force–compression strain curve showed oscillatory changes. However, because the indenter continued to approach the axial center of the cocoon, the contact area between the cocoon and the indenter remained basically unchanged. This produced small changes in the magnitude of the cocoon’s compressive force fluctuations.

When the axial compression strain of the LTC reached 4% (the minimum deformation at the collapse was 1.6 mm when the length of the cocoon was 40 mm), the cocoon shell started to sink inwards. The pressure on the TCFL was less than 15.34 ± 2.29 N, and the cocoon shell only deformed elastically. When the pressure on the TCDL was less than 43.57 ± 4.99 N, the cocoon shell will only deformed elastically. However, the axial collapse force of the cocoon shell was greater than the radial collapse force.

The radial clearance between the cocoon shell and the pupa was minimal (2.92 ± 0.84 mm) when the diameter of the cocoon was in the range of 15 to 20 mm. The axial clearance between the cocoon shell and the pupa was minimal (3.42 ± 1.19 mm) when the cocoon length was in the range of 40~45 mm. Therefore, the radial deformation of the cocoon shell of the tussah cocoon should be controlled within 1.05 mm, and the axial deformation within 1.6 mm. The force required for the radial collapse of the cocoon shell of the TCFL should be within 14.54 ± 3.16 N. The force required for the radial collapse of the cocoon shell of the TCDL should be within 32.43 ± 7.04 N. This can guarantee the quality of the cocoon shell and avoid damage to the pupae.

As can be seen in Figure 9b and Figure 12a, there are differences between stage III and stage IV regarding the radial compression and axial compression of the tussah cocoon. (1) The stage III curves of axial compression fluctuate greatly, and the radial compression fluctuates less. Tussah cocoons are longer in the axial direction, and the size of the upper and lower contact surface changes less during the compression process. When the contact surface is depressed downward, the curve fluctuates significantly. The radial contact surface of tussah cocoons is oval. During the compression process, the ellipse is constantly expanding outward to become larger, and the change is more gentle. Therefore, the curve fluctuation is small. (2) There is an abrupt change in the stage IV curve of radial compression. Stage IV of axial compression continues to fluctuate, without significant abrupt changes. When the tussah cocoons are compressed radially, the curve is flatter. When the pupae rupture, there is a clear abrupt change in the curve. When the tussah cocoons are compressed axially, the curve fluctuates more. When the pupae ruptured, no obvious mutations could be observed.

3.4. Experiments on the Mechanical Properties of the Cocoon Stalk and Leaf Wrapper of Tussah Cocoon

3.4.1. Analysis of Cocoon Stalk and Cocoon Shell Separation Tension

In the tussah cocoon structure, the cocoon stalk was attached to the cocoon floss and wrapped around the cocoon shell through the cocoon floss, as shown in Figure 13a. During the process of the mechanized defoliation of tussah cocoons, the cocoon stalk may have a negative impact on the defoliation process. Therefore, it was necessary to analyze the magnitude of the force when the stalk was detached from the tussah cocoon.

The tensile force–deformation curves of the cocoon stalk of TCFL are shown in Figure 13b. As the tensile deformation continues to increase, the force on the cocoon handle also continued to increase. When the force reached the limit of the detachment of the cocoon stalk from the cocoon shell, the stalk began to be detached gradually from the cocoon shell until it was completely detached.

The cocoon stalk detachment force was 29.91 ± 11.15 N for the FTC. The cocoon stalk detachment force was 36.09 ± 9.98 N for the DTC. There was a significant difference (p < 0.05) between the FTC and the DTC. The cocoon shank detachment force of the FTC was greater than the collapse force of the FLS (14.54 ± 3.16 N). The detachment force of the cocoon stalk of the FTC was greater than the collapse force of the cocoon shell of the TCDL (32.43 ± 7.04 N). Therefore, there was a risk of flexion and deformation of the cocoon before the cocoon stalk broke away from the cocoon shell, which affects the quality of the cocoon shell. Thus, the influence of the cocoon stalk should be taken into account when designing the sericulture cocoon defoliator. During the leaf stripping process, the stripping method must not pull the cocoon stalk off or detach it from the cocoon shell.

3.4.2. Mechanical Properties and Peeling Force Analysis of Tussah Cocoon Oak Leaves

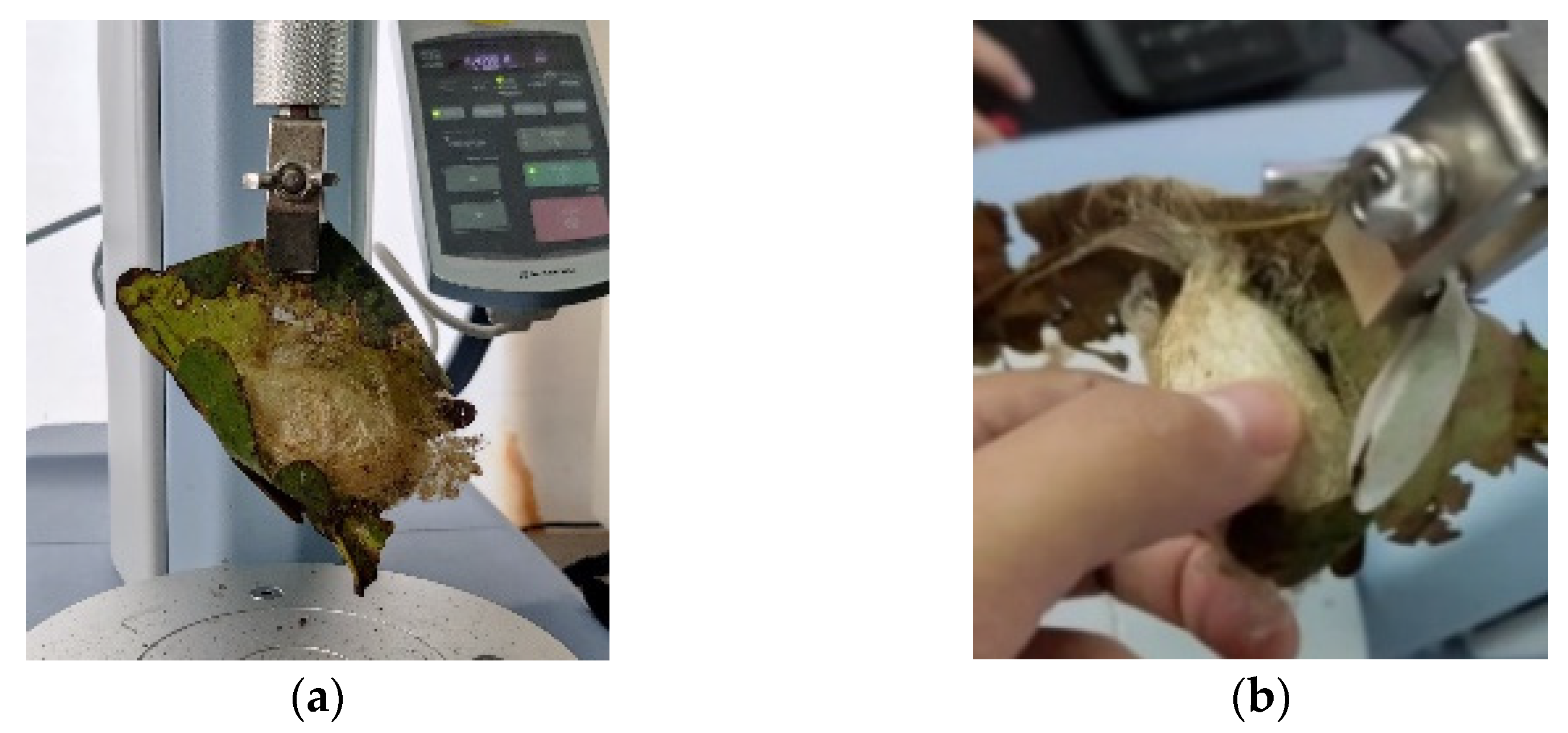
The mechanical properties of oak leaves from the TCFL were tested using a biomechanical tester, and the results are shown in Table 7.

The tearing force of the fresh leaves was 7.19 ± 2.48 N, and the puncture force was 3.22 ± 2.17 N. The puncture strength of the fresh leaves was found to be 1.02 ± 0.69 MPa using Equation (3).

The tussah pupae first spat out silk and curled the leaves into a tube, then formed the cocoon stalk and fixed it to the branch. After that, the silkworm pupa spun a cocoon in the roll-shaped oak leaves. The oak leaves were adhered to the surface of the cocoon shell by the cocoon floss. The magnitude of the peeling force revealed the amount of adhesion of the cocoon floss to the oak leaves.

The oak leaf stripping machine was designed to strip the oak leaves from the surface of the tussah cocoon shell without damaging the shell. This was conducive to the subsequent processing and use of the tussah cocoons. The amount of force required to peel oak leaves from the tussah cocoon was measured to determine the amount of force required for the peeling process. The results are shown in Table 8.

The results showed that the peeling force of whole dried leaves (3.35 ± 1.85 N) was significantly lower than that of the whole fresh leaves (5.05 ± 3.63 N) after the drying of the harvested tussah cocoons. The magnitude of the stripping force of the oak leaves was significantly smaller than the collapse force of the cocoon shell and the detachment force of the cocoon stall.

4. Conclusions

In this paper, the basic physical parameters and mechanical properties of the TCWL, the LTC, the cocoons shell, the pupa, and the oak leaves were studied. These experiments provide a detailed data base for the study of the tussah leaf strippers. The foundation and suggestions provided for the design of the tussah cocoon leaf-stripping machine are as follows:

(1)

When designing the leaf-stripping machine for tussah, the large deformation of the tussah cocoon shell should be avoided. The radial deformation of the cocoon shell of the tussah cocoon should be controlled to be within 1.05 mm and the axial deformation to be within 1.6 mm. At this point, the cocoon shell quality is safeguarded, and damage to the pupae can be avoided.

(2)

The pressure required for the radial collapse of the cocoon shell of the TCFL was 14.54 ± 3.16 N, and the force required for the axial collapse was 15.34 ± 2.29 N. The pressure required for the radial collapse of the cocoon shell of the TCDL was 32.43 ± 7.04 N, and the force required for the axial collapse was 43.57 ± 4.99 N. Therefore, in order to obtain complete tussah cocoons, it should be ensured that the force of the TCDL is less than 32.43 ± 7.04 N, and the force of the TCFL is less than 14.54 ± 3.16 N.

(3)

The cocoon shank detachment force of the TCFL was greater than the force of the cocoon shell collapse of the TCFL. The cocoon shank detachment force of the TCDL was greater than the force of the cocoon shell collapse of the TCDL. Therefore, the adverse effects of the cocoon stalk on the leaf-stripping process should be taken into consideration when designing a tussah cocoon leaf-stripping machine.

(4)

The leaf peeling force was 3.35 ± 1.85 N for TCDL and 5.05 ± 3.63 N for TCFL. When the oak leaves were peeled off, the pulling force on the fresh oak leaves and dry oak leaves should be greater than their peeling force, respectively. Therefore, when designing the tussah cocoon leaf-stripping machine, it should be ensured that the force on the oak leaves during leaf stripping is greater than 3.35 ± 1.85 N (TCDL) and 5.05 ± 3.63 N (TCFL).

(5)

Tussah cocoons with a high water content have lower cocoon shell hardness, making it easier for the cocoon shell to be compressed. It can be seen from Table 8 that the peeling force required for dried leaves is less than that for fresh leaves, which makes it easier to peel the dried leaves from the TCFL. However, the leaves of the TCFL are very brittle, making it difficult to peel the oak leaves cleanly. Therefore, when designing a tussah cocoon leaf-stripping machine, these conditions should be considered comprehensively.