Pear Tree Growth Simulation and Soil Moisture Assessment Considering Pruning
Abstract
1. Introduction
2. Materials and Methods
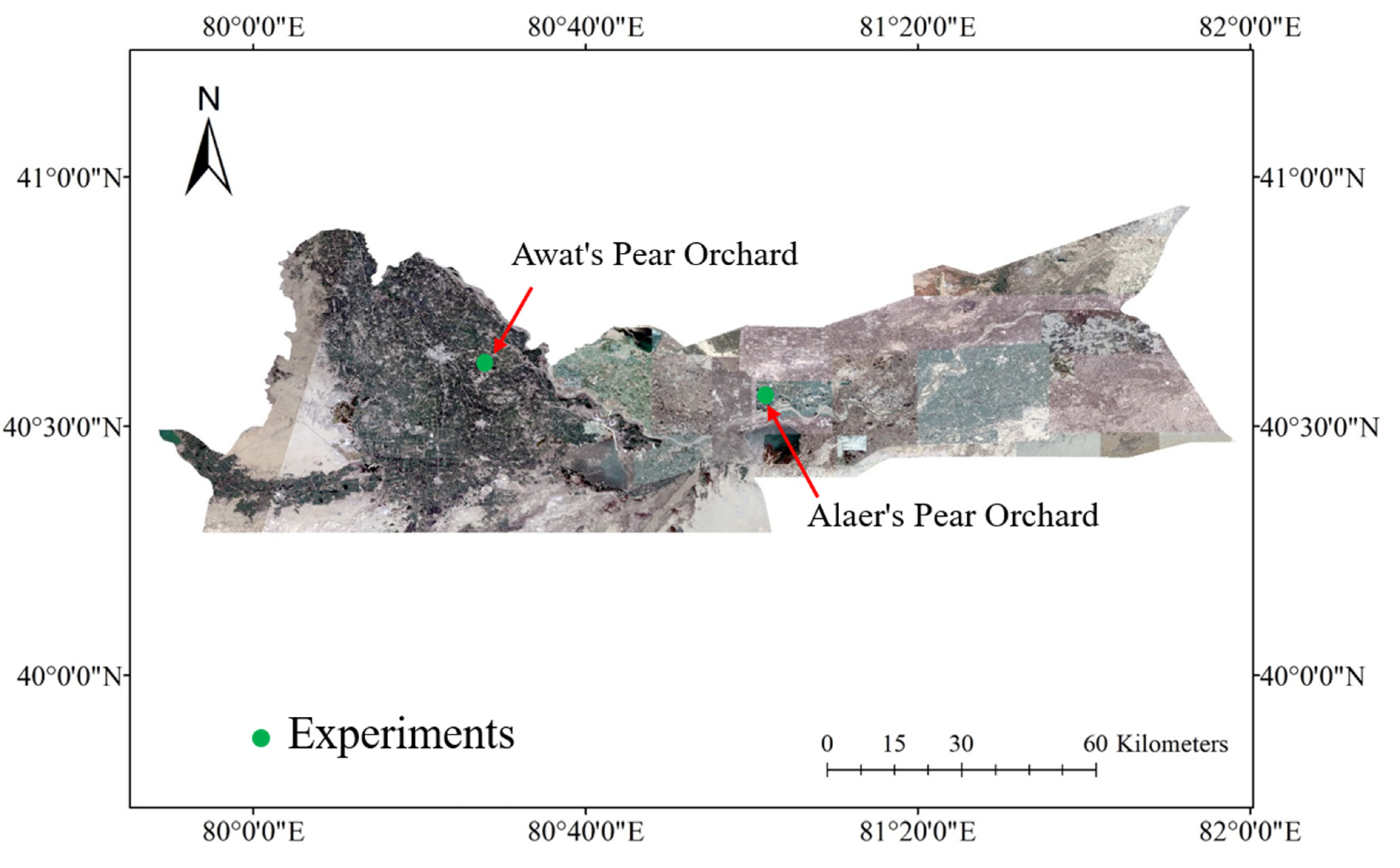
2.1. Field Experiments Design
2.2. Field Data Measurements and Observation
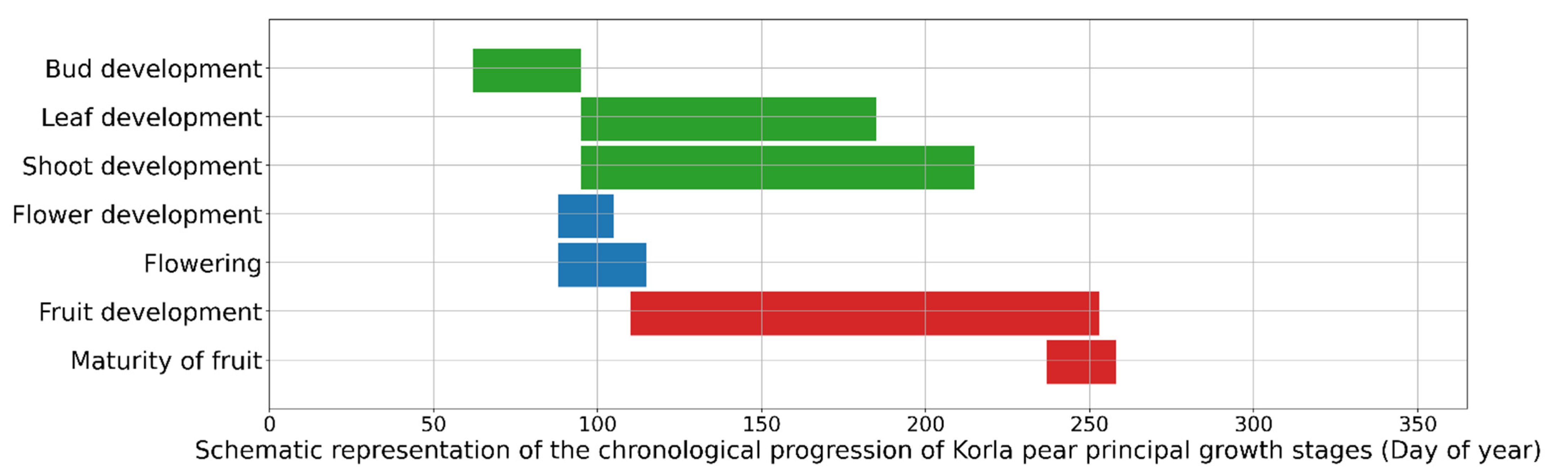
- Phenology time: To calibrate the simulation performance of phenological parameters, emergence (leaf blade starts to unfold), flowering (fruit begins to develop), and maturity dates (dry weight of fruit is not increasing) were observed during the growing period. The variation in the time series of the main fertility stages of Korla pear is shown in Figure 3.
- Initial total dry weight (TDWI): Measurements of the initial buds were used to calculate the TDWI.
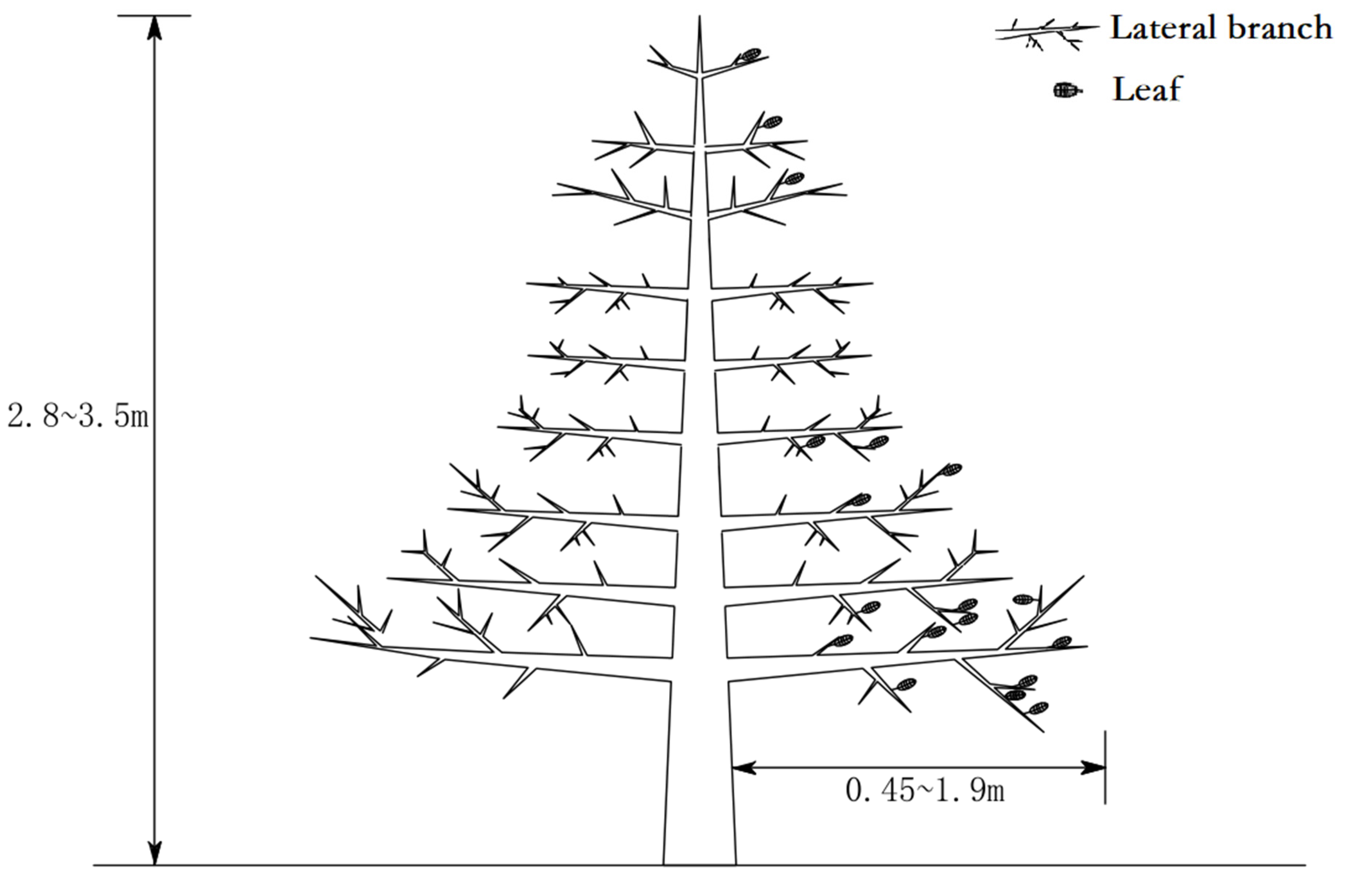
- Dry weight: The dry matter mass of leaves and fruits was measured about 13 times during the growth cycle, as shown in Figure 4a. The phenotypic parameters (length, diameter, etc.) of the branches were measured at different periods, and then the density of branches with different diameters was measured (as shown in Figure 4b) to calculate the dry matter of the stems. A number of fruits and leaves were collected at each treatment, dried and treated, and then statistically converted with the observed data to obtain the dry matter mass of each treatment. After fruit harvest, leaf drop nets were placed to collect leaves from the whole tree, as shown in Figure 4c.
- Canopy structure parameters: LAI and diffuse visible light extinction coefficient of the experimental area were measured about 10 times, especially before and after pruning pear trees, and specific leaf area parameters were measured to obtain diffuse visible light extinction coefficients and verify the performance of simulated LAI.
- Photosynthesis (CO2 assimilation) parameters: Parameters such as net photosynthetic rate was measured with an LI-COR 6400XT instrument (LI-COR, United States). Maximum CO2 assimilation rate and light-use efficiency parameters at optimal developmental temperature were obtained by calculation. Leaf area index (LAI), photosynthetically effective intercepted radiation and corresponding radiation abatement coefficients were measured nondestructively twice a week throughout the growth cycle using a plant canopy analyzer (LI-COR LAI-2000).
- Soil moisture content: The sampled soil at every 20 cm (0~100 cm) was brought back to the laboratory and weighed after drying at 85 °C to a constant weight to calculate soil moisture. The field water-holding capacity and soil-water content in saturated conditions were measured using the cutting ring method before seedling emergence. The undisturbed soil was collected at the experimental site and brought back to the laboratory, and the soil-water content was saturated under the conditions of manual intervention. The soil-water content of the undisturbed soil at this time was measured as the saturated soil water content. If the undisturbed soil saturated with water content was placed on top of the air-dried soil, so that the air-dried soil absorbed the gravitational water in the undisturbed soil, then the undisturbed soil water content was measured at this time, to obtain the field water-holding capacity.
- Yield: To evaluate the simulated yield, the weight of all pears from each tree was measured at harvest and the total dry weight of the pears was calculated from the pears’ measured water content.
- Agromanagement actions: Irrigation, fertilization and pruning times of pear orchards were observed and recorded.
- Removed biomass was collected and weighed: After summer pruning, all removed stems, fruits and leaves were collected from each test area. They were dried in a forced-air oven at 105 °C for 30 min and then at 85 °C to a constant weight, after which all samples were weighed.
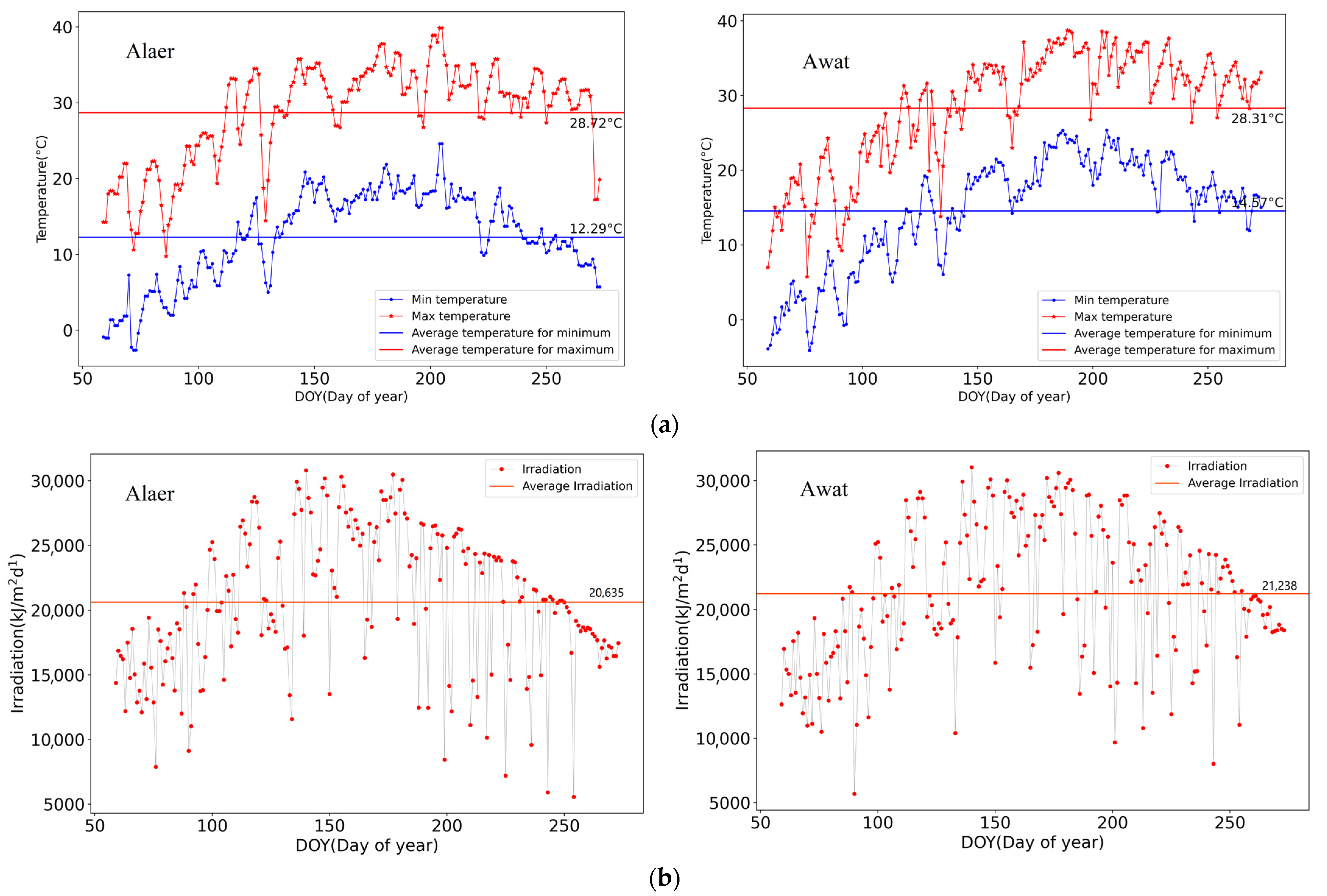
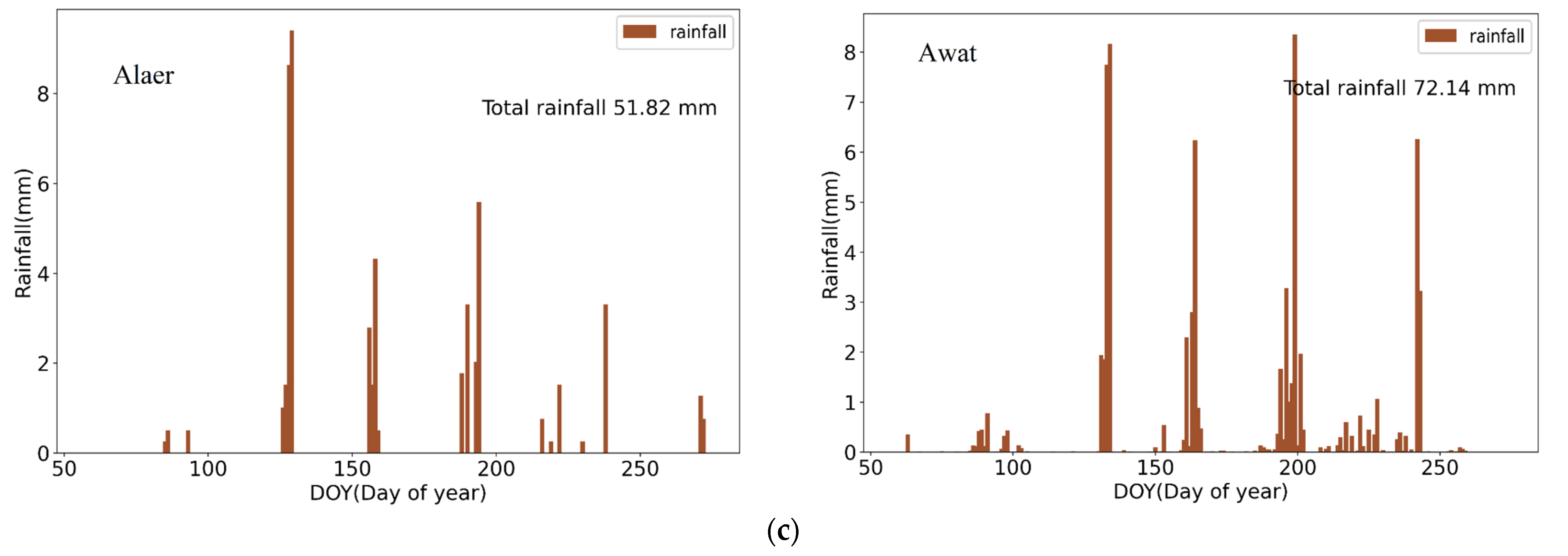
- Weather data: Small weather stations in the pear orchard were used to collect the meteorological input parameters required by WOFOST model. Figure 5 shows the daily maximum and minimum temperature (daily average temperature 12.3~28.7 °C), daily total precipitation and radiation during the main growth period of pear trees in two orchards. The daily minimum and maximum temperatures showed a tendency to rise and then fall, and the daily temperature difference was large. The annual rainfall in the study area was less than 100 mm. The water needs of pear trees mainly depended on irrigation. Although most of the rainfall occurred in summer, the amount of rainfall was very small. The total daily radiation of the two pear orchards was strong, which was conducive to plants’ photosynthesis.
2.3. Modification of WOFOST Model
2.4. Calibration of WOFOST Model
2.5. Evaluation of Simulated Performance
3. Results
3.1. Calibration Performance
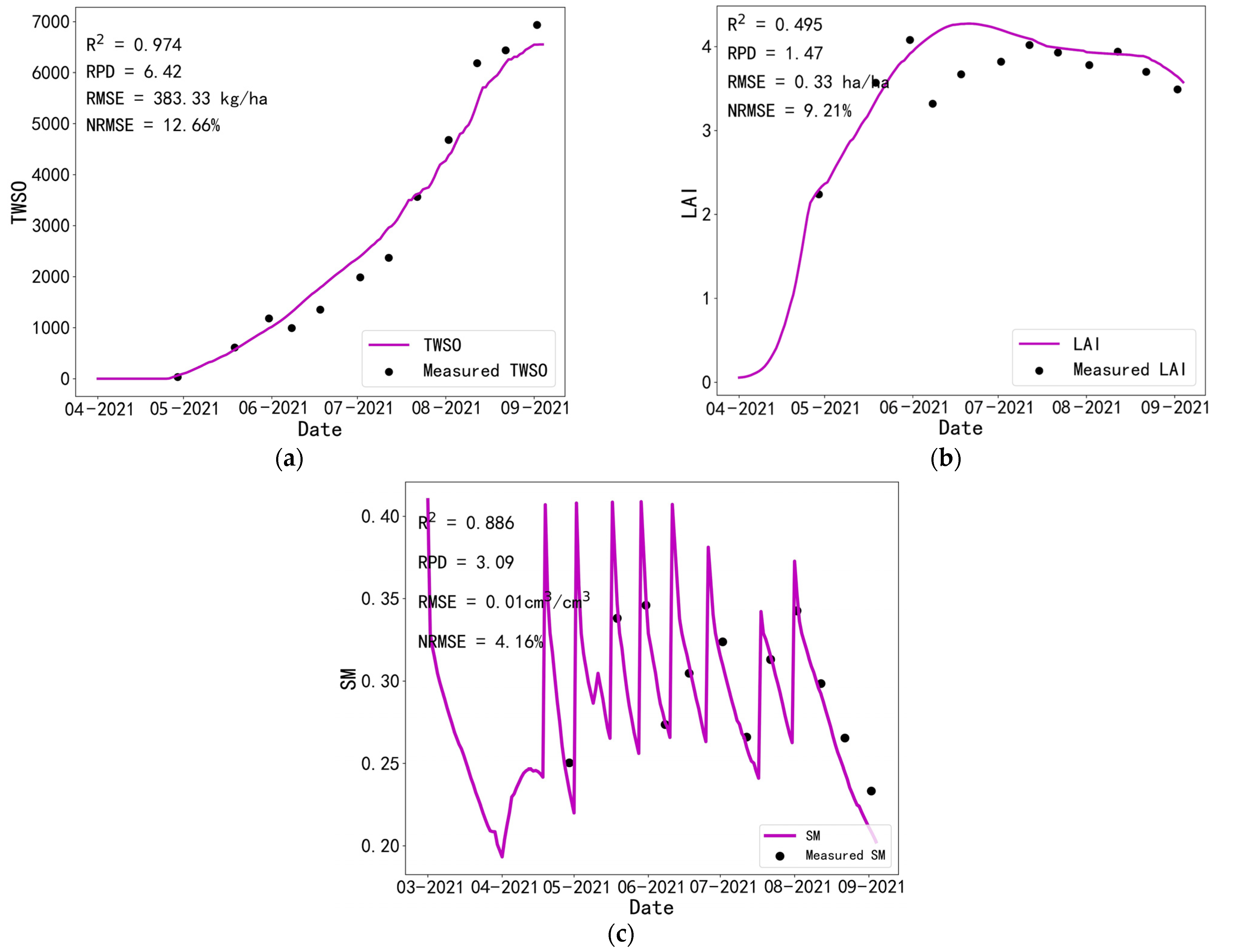
3.1.1. Performance of the Unmodified Model
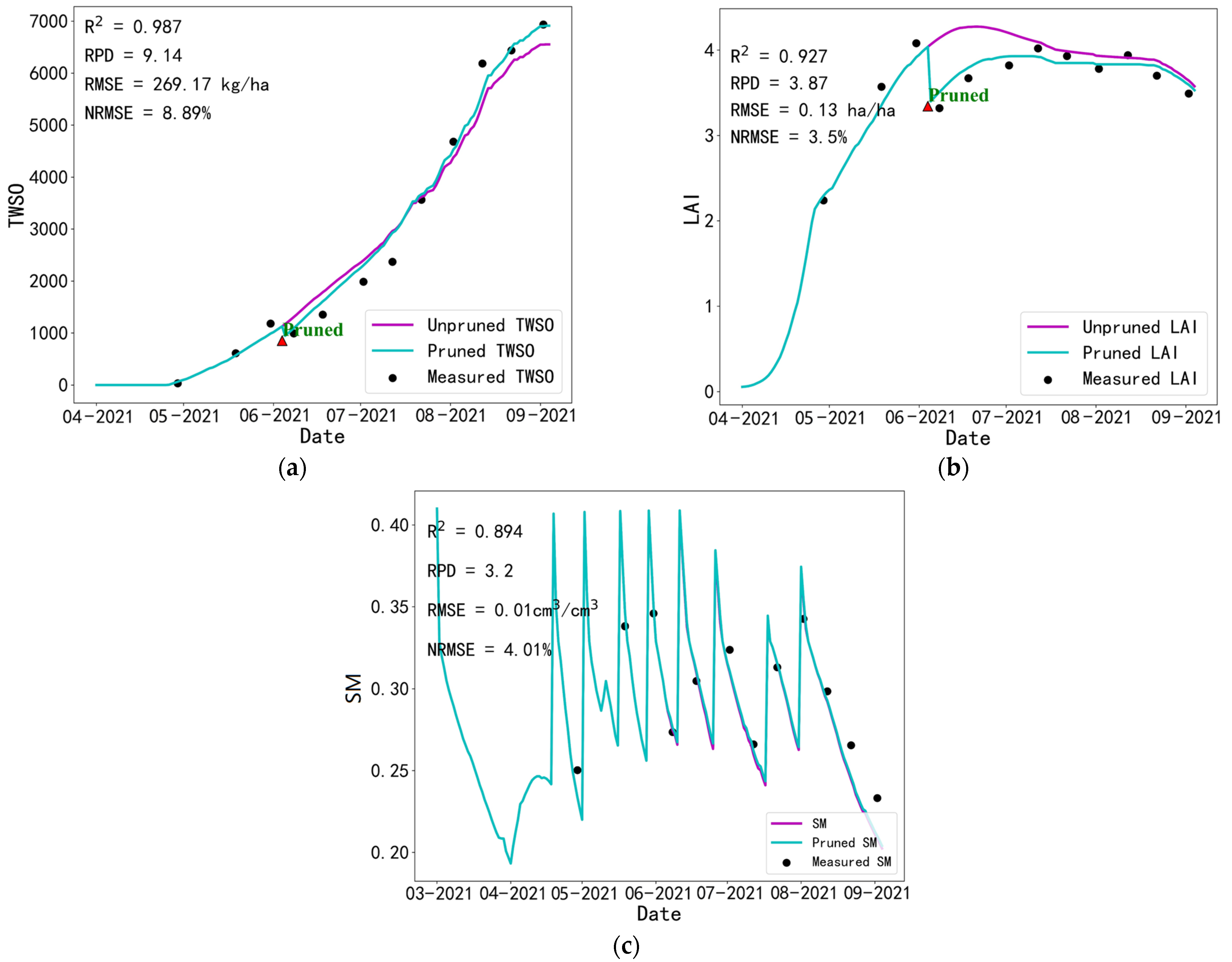
3.1.2. Performance of the Modified Model
3.2. Validation and Evaluation
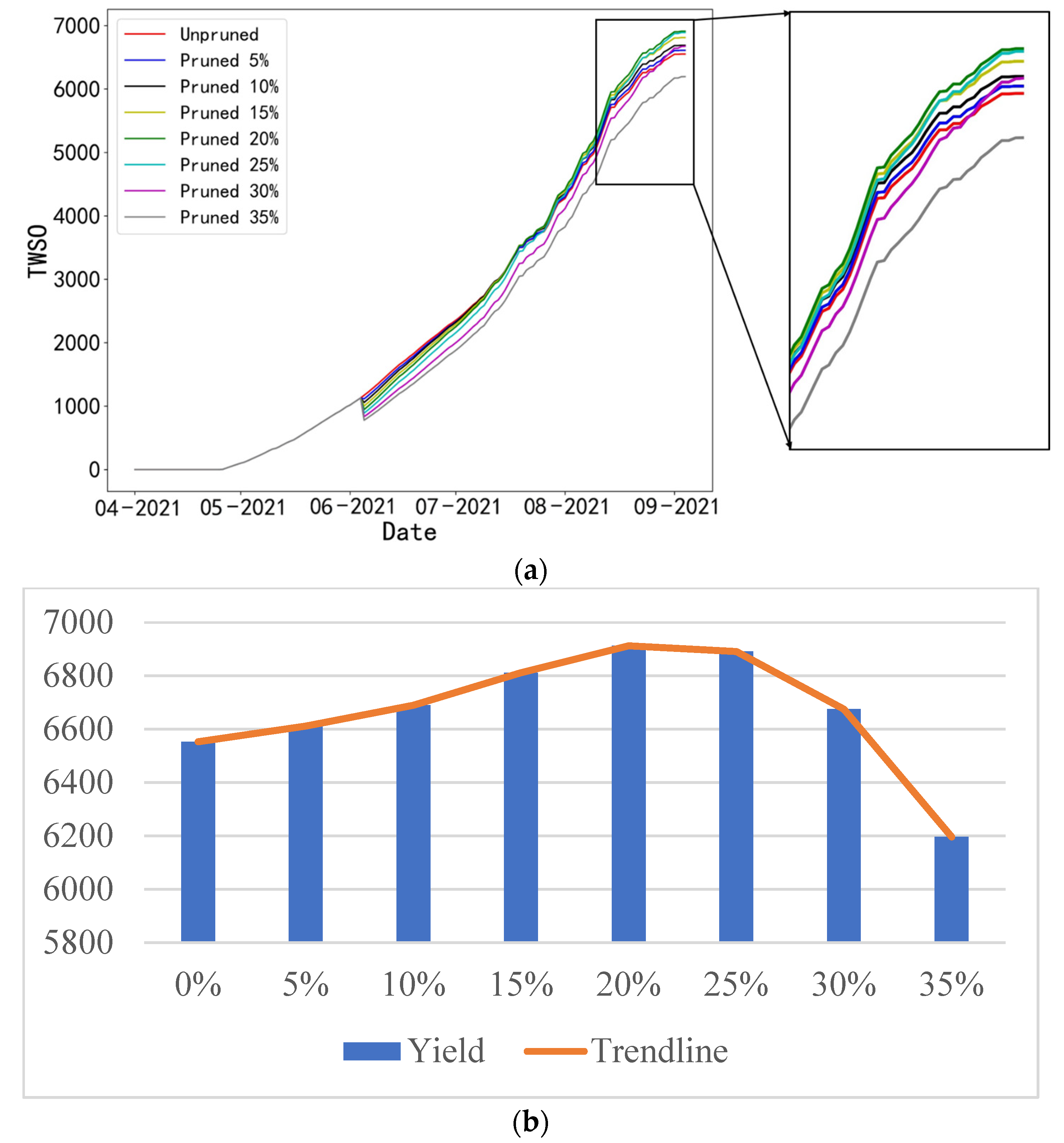
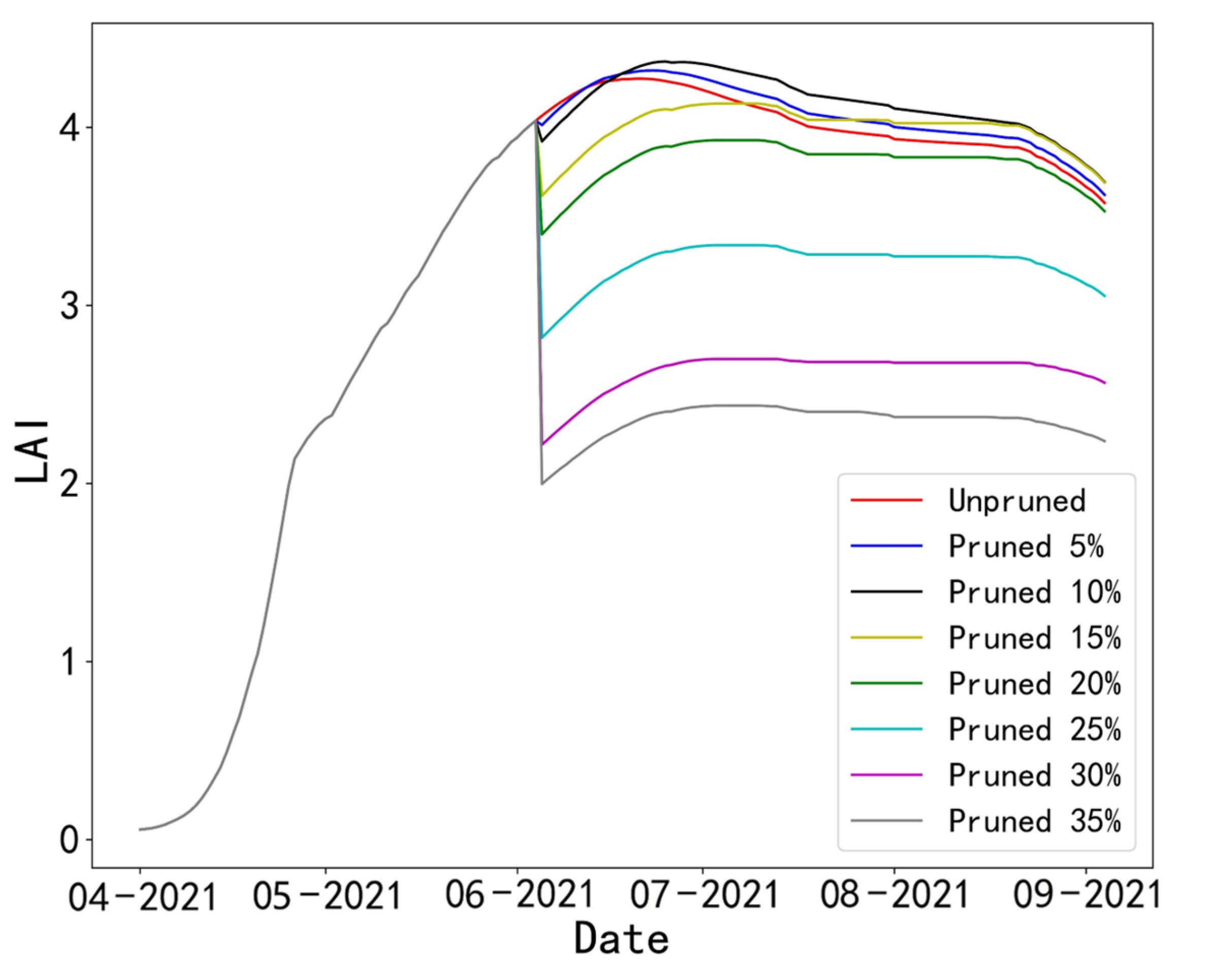
3.2.1. Performance of the Simulated TWSO and LAI Growth Dynamics
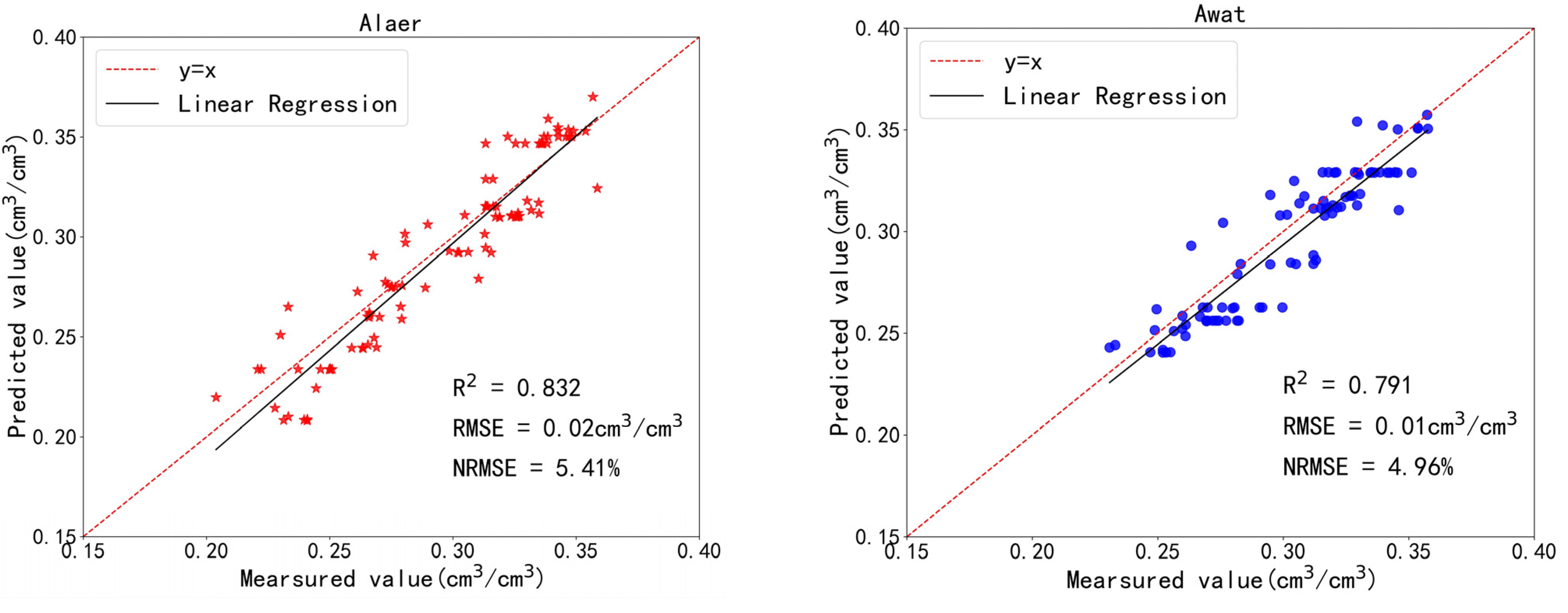
3.2.2. Performance of the Simulated Soil Moisture
3.2.3. Performance of the Simulated Final TAGP Based on Modified Model
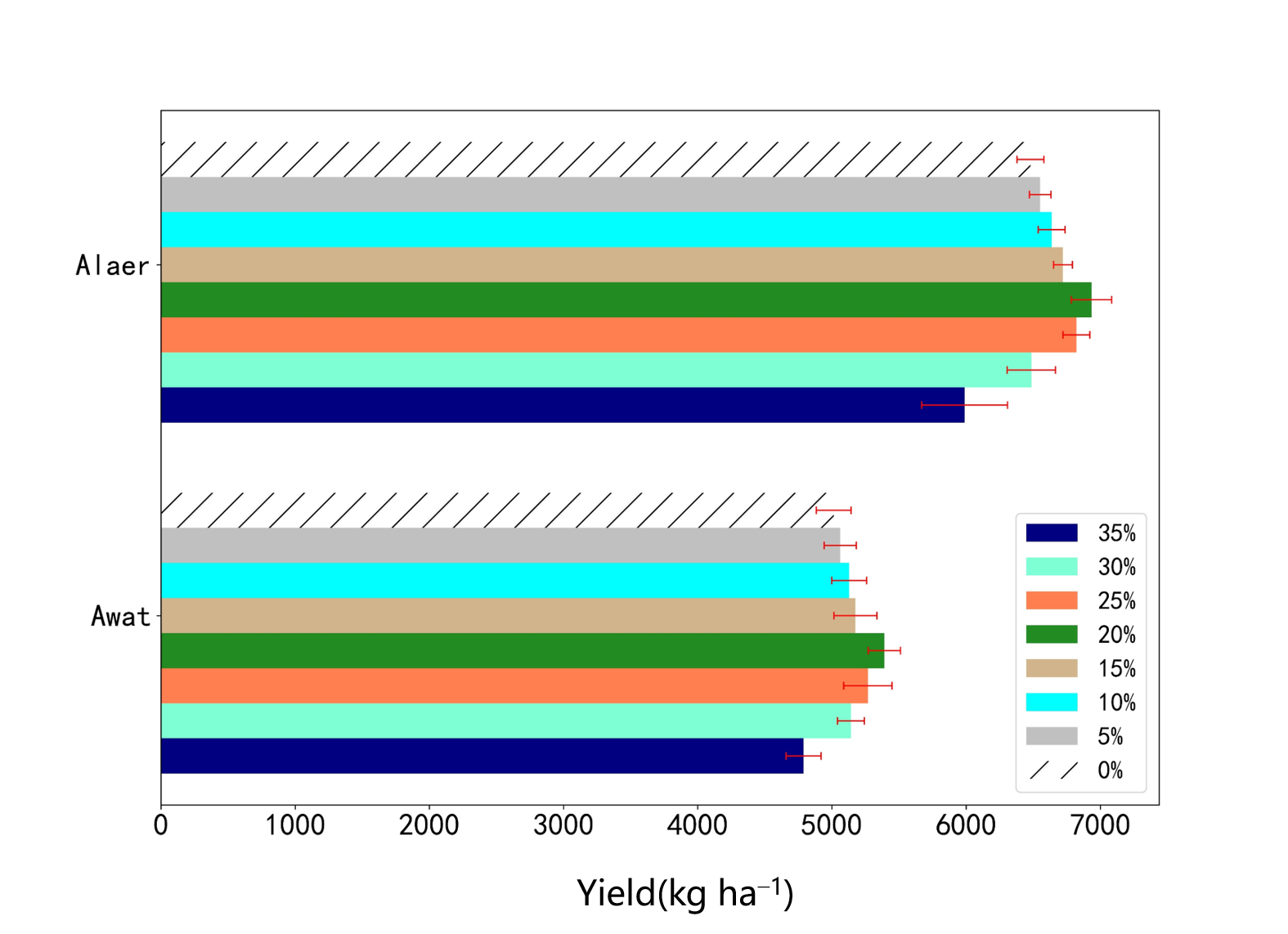
3.3. Simulated Yield under Different Pruning Intensities Based on Modified Model
3.4. Simulated LAI under Different Pruning Intensities
4. Discussion
4.1. Performance of the Improved Model in Pear Tree Growth Simulation and Soil Moisturre Assessment
4.2. Model Modification and Calibration
4.3. Model Modification Analysis Considering Pruning
4.4. Effect of Meteorological Differences on the Yield of Pear Orchards
4.5. Limitations of the Modified Model and Future Research Prospects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Input Main Soil Parameters | Description | Value (Alaer) | Value (Awat) |
|---|---|---|---|
| SMW | Soil moisture content at wilting point [cm3/cm3] | 0.074 | 0.075 |
| SMFCF | Soil moisture content at field capacity [cm3/cm3] | 0.329 | 0.324 |
| SM0 | Soil moisture content at saturation [cm3/cm3] | 0.410 | 0.410 |
| K0 | Hydraulic conductivity of saturated soil [cm day−1] | 23.97 | 23.85 |
| SOPE | Maximum percolation rate root zone [cm day−1] | 1.37 | 1.41 |
| KSUB | Maximum percolation rate subsoil [cm day−1] | 2.03 | 2.05 |
| SMATB | Soil moisture content as function of pF [log (cm); cm3 cm−3] | Measured soil water retention (as function of pF) | Measured soil water retention (as function of pF) |
| CONTB | hydraulic conductivity as function of pF | Measured hydraulic conductivity | Measured hydraulic conductivity |
Appendix B
| Calibrated Crop Parameters | Description | Value | Units |
|---|---|---|---|
| TBASEM | Base temperature for emergence | 10 | °C |
| TEFFMX | Maximum effective temperature for emergence | 30 | °C |
| TSUMEM | Temperature sum from sowing to emergence | 100 | °C |
| TSUM1 | Temperature sum from emergence to anthesis | 140 | °C d−1 |
| TSUM2 | Temperature sum from anthesis to maturity | 1880 | °C d−1 |
| DTMSTB | Daily increase in temperature sum as a function of daily mean temperature | (0−10−35.5−40 °C) = 0.0−0.0−25.5−25.5 °C d−1 | °C d−1 |
| TDWI | Initial total crop dry weight | 41.9 | kg ha−1 |
| LAIEM | LAI at emergence | 0.0007 | ha ha−1 |
| RGRLAI | Maximum relative increase in LAI | 0.060 | ha ha−1 d−1 |
| SLATB | Specific leaf area as a function of DVS | (0.0−0.55−1.0−2.0) = 0.0020−0.0018-0.0016−0.0016 ha kg−1 | ha kg−1 |
| SPAN | Life span of leaves growing at 35 Celsius | 85 | [days] |
| TBASE | Lower threshold temp. for ageing of leaves | 10.0 | °C |
| KDIFTB | Extinction coefficient for diffuse visible light as function of DVS | (0.0−1.260−1.261-2.0) = 0.46−0.83−0.69−0.79 | - |
| EFFTB | Initial light-use efficiency of CO2 assimilation of single leaves as function of daily temperature | (19.5, 36.0) = 0.53−0.53 | kg ha−1 hr−1 J−1 m2 s |
| AMAXTB | Maximum leaf CO2 assimilation rate as a function of development stage of the crop | (0.0, 1.6, 2.0) = 39.0−43.0−24.0 | kg ha−1 hr−1 |
| TMPFTB | Reduction factor of AMAX as function of daily mean temperature | (10−19.5−35.5−40) = 0−1−1−0 | - |
| CVL | Conversion efficiency of assimilates into leaf | 0.73 | kg kg−1 |
| CVO | Conversion efficiency of assimilates into storage organ | 0.72 | kg kg−1 |
| CVR | Conversion efficiency of assimilates into root | 0.690 | kg kg−1 |
| CVS | Conversion efficiency of assimilates into stem | 0.65 | kg kg−1 |
| Q10 | Relative increase in maintenance respiration rate with each 10 degrees increase in temperature | 2.0 | - |
| RML | Relative maintenance respiration rate for leaves | 0.0350 | - |
| RMO | Relative maintenance respiration rate for storage organs | 0.0130 | - |
| RMR | Relative maintenance respiration rate for roots | 0.0120 | - |
| RMS | Relative maintenance respiration rate for stems | 0.0100 | - |
| FRTB | Fraction of total dry matter increase partitioned to roots as a function of development stage | (0.0−1.57−2.0) = 0.3−0.0−0.0 | kg kg−1 |
| FLTB | Fraction of above ground dry matter increase partitioned to leaves as a function of development stage | (0.00−0.34−0.51−0.97−1.00−1.50−1.80−2.00) = 0.95−0.90−0.85−0.60−0.20−0−0−0 | kg kg−1 |
| FSTB | Fraction of above ground dry matter increase partitioned to stems as a function of development stage | (0.00−0.34−0.51−0.97−1.00−1.50−1.80−2.00) = 0.05−0.10−0.15−0.40−0.70−0.75−0.10−0 | kg kg−1 |
| FOTB | Fraction of above ground dry matter increase partitioned to storage organs as a function of development stage | (0.00−0.34−0.51−0.97−1.00−1.50−1.80−2.00) = 0.0−0.0−0.0−0.0−0.10−0.25−0.90−1 | kg kg−1 |
| PERDL | Maximum relative death rate of leaves due to water stress | 0.03 | - |
| RDRSTB | Relative death rate of stems as a function of development stage | (0.0−1.0−1.5−2.0) = 0−0−0.02−0.02 | - |
| CFET | Correction factor for potential transpiration rate | 1.02 | - |
| DEPNR | Dependency number for crop sensitivity to soil moisture stress | 1.5 | - |
| RDI | Initial rooting depth | 10 | cm |
| RRI | Daily increase in rooting depth | 1.2 | cm d−1 |
| RDMCR | Maximum rooting depth of the crop | 120 | cm |
References
- Wu, J.; Wang, Y.; Xu, J.; Korban, S.S.; Fei, Z.; Tao, S.; Ming, R.; Tai, S.; Khan, A.M.; Postman, J.D.; et al. Diversification and Independent Domestication of Asian and European Pears. Genome Biol. 2018, 19, 77. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zhao, Z.; Wang, W.; Ma, Y.; Huang, X. Yield and Growth of Mature Pear Trees under Water Deficit during Slow Fruit Growth Stages in Sparse Planting Orchard. Sci. Hortic. 2013, 164, 189–195. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, W.; Wu, Y.; Xu, M.; Huang, X.; Ma, Y.; Ren, D. Leaf Physiological Responses of Mature Pear Trees to Regulated Deficit Irrigation in Field Conditions under Desert Climate. Sci. Hortic. 2015, 187, 122–130. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, M.; Liu, J.; Wang, W.; Liu, S. Fertilizer and Soil Nitrogen Utilization of Pear Trees as Affected by the Timing of Split Fertilizer Application in Rain-Fed Orchard. Sci. Hortic. 2019, 252, 363–369. [Google Scholar] [CrossRef]
- Colpaert, B.; Steppe, K.; Gomand, A.; Vanhoutte, B.; Remy, S.; Boeckx, P. Experimental Approach to Assess Fertilizer Nitrogen Use, Distribution, and Loss in Pear Fruit Trees. Plant Physiol. Biochem. 2021, 165, 207–216. [Google Scholar] [CrossRef]
- Hallgren, S.W. Tree Physiology|Shoot Growth and Canopy Development. Encycl. For. Sci. 2004, 1600–1606. [Google Scholar] [CrossRef]
- Persello, S.; Grechi, I.; Boudon, F.; Normand, F. Nature Abhors a Vacuum: Deciphering the Vegetative Reaction of the Mango Tree to Pruning. Eur. J. Agron. 2019, 104, 85–96. [Google Scholar] [CrossRef]
- Kumar, M.; Rawat, V.; Rawat, J.M.S.; Tomar, Y.K. Effect of Pruning Intensity on Peach Yield and Fruit Quality. Sci. Hortic. 2010, 125, 218–221. [Google Scholar] [CrossRef]
- Doll, U.; Mosqueira, D.; Mosqueira, J.; González, B.; Vogel, H. Pruning Maqui (Aristotelia Chilensis (Molina) Stuntz) to Optimize Fruit Production. J. Appl. Res. Med. Aromat. Plants 2017, 6, 10–14. [Google Scholar] [CrossRef]
- Hampson, C.R.; Quamme, H.A.; Brownlee, R.T. Canopy Growth, Yield, and Fruit Quality of “Royal Gala” Apple Trees Grown for Eight Years in Five Tree Training Systems. HortScience 2002, 37, 627–631. [Google Scholar] [CrossRef]
- Passos, L.C.; da Silva, J.R.; Rodrigues, W.P.; de Reis, F.O.; da Vasconcellos, M.A.S.; Machado Filho, J.A.; Campostrini, E. Leaf Photosynthetic Responses of Passion Fruit Genotypes to Varying Sunlight Exposure within the Canopies. Exp. Plant. Physiol. 2018, 30, 103–112. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, K.; Chen, L. Response of Photosynthetic Plasticity of Paeonia Suffruticosa to Changed Light Environments. Env. Exp. Bot. 2003, 49, 121–133. [Google Scholar] [CrossRef]
- Li, Y.; Xin, G.; Wei, M.; Shi, Q.; Yang, F.; Wang, X. Carbohydrate Accumulation and Sucrose Metabolism Responses in Tomato Seedling Leaves When Subjected to Different Light Qualities. Sci. Hortic. 2017, 225, 490–497. [Google Scholar] [CrossRef]
- Vosnjak, M.; Mrzlic, D.; Usenik, V. Summer Pruning of Sweet Cherry: A Way to Control Sugar Content in Different Organs. J. Sci. Food Agric. 2022, 102, 1216–1224. [Google Scholar] [CrossRef]
- Mierowska, A.; Keutgen, N.; Huysamer, M.; Smith, V. Photosynthetic Acclimation of Apple Spur Leaves to Summer-Pruning. Sci. Hortic. 2002, 92, 9–27. [Google Scholar] [CrossRef]
- Palmer, J.W.; Avery, D.J.; Wertheim, S.J. Effect of Apple Tree Spacing and Summer Pruning on Leaf Area Distribution and Light Interception. Sci. Hortic. 1992, 52, 303–312. [Google Scholar] [CrossRef]
- Schaffer, B.; Gaye, G.O. Effects of Pruning on Light Interception, Specific Leaf Density and Leaf Chlorophyll Content of Mango. Sci. Hortic. 1989, 41, 55–61. [Google Scholar] [CrossRef]
- Di, D.; Delle, S.; Vegetali, P.; Suolo, D.; Ambiente, E.D.; Of, P.; Fruit, W.; Di, D.; Delle, S.; Vegetali, P.; et al. Basic Considerations about Pruning Deciduous Fruit Trees. In Advances in Horticultural Science; Firenze University Press: Firenze, Italy, 2019; Volume 25, pp. 129–204. [Google Scholar]
- Ye, M.; Zhao, X.; Biswas, A.; Huo, G.; Yang, B.; Zou, Y.; Siddique, K.H.M.; Gao, X. Measurements and Modeling of Hydrological Responses to Summer Pruning in Dryland Apple Orchards. J. Hydrol. 2021, 594, 125651. [Google Scholar] [CrossRef]
- Yin, X.; Struik, P.C.; Goudriaan, J. On the Needs for Combining Physiological Principles and Mathematics to Improve Crop Models. Field Crops Res. 2021, 271, 108254. [Google Scholar] [CrossRef]
- Chenu, K.; Porter, J.R.; Martre, P.; Basso, B.; Chapman, S.C.; Ewert, F.; Bindi, M.; Asseng, S. Contribution of Crop Models to Adaptation in Wheat. Trends Plant Sci. 2017, 22, 472–490. [Google Scholar] [CrossRef]
- Soltani, A.; Sinclair, T.R. Modeling Physiology of Crop Development, Growth and Yield. In Modeling Physiology of Crop Development, Growth and Yield; CABi Publishing: Wallingford, UK, 2012; pp. 1–322. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A Review of Data Assimilation of Remote Sensing and Crop Models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.H.; Wu, Y.; et al. Assimilation of Remote Sensing into Crop Growth Models: Current Status and Perspectives. Agric. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Hoogenboom, G. Contribution of Agrometeorology to the Simulation of Crop Production and Its Applications. Agric. Meteorol. 2000, 103, 137–157. [Google Scholar] [CrossRef]
- Matthews, R.; Stephens, W.; Hess, T.; Middleton, T.; Graves, A. Applications of Crop/Soil Simulation Models in Tropical Agricultural Systems. Adv. Agron. 2002, 76, 31–124. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT Cropping System Model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Bergez, J.E.; Raynal, H.; Launay, M.; Beaudoin, N.; Casellas, E.; Caubel, J.; Chabrier, P.; Coucheney, E.; Dury, J.; Garcia de Cortazar-Atauri, I.; et al. Evolution of the STICS Crop Model to Tackle New Environmental Issues: New Formalisms and Integration in the Modelling and Simulation Platform RECORD. Environ. Model. Softw. 2014, 62, 370–384. [Google Scholar] [CrossRef]
- Vanuytrecht, E.; Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E.; Heng, L.K.; Garcia Vila, M.; Mejias Moreno, P. AquaCrop: FAO’s Crop Water Productivity and Yield Response Model. Environ. Model. Softw. 2014, 62, 351–360. [Google Scholar] [CrossRef]
- de Wit, A.; Boogaard, H.; Fumagalli, D.; Janssen, S.; Knapen, R.; van Kraalingen, D.; Supit, I.; van der Wijngaart, R.; van Diepen, K. 25 Years of the WOFOST Cropping Systems Model. Agric. Syst 2019, 168, 154–167. [Google Scholar] [CrossRef]
- Nendel, C.; Berg, M.; Kersebaum, K.C.; Mirschel, W.; Specka, X.; Wegehenkel, M.; Wenkel, K.O.; Wieland, R. The MONICA Model: Testing Predictability for Crop Growth, Soil Moisture and Nitrogen Dynamics. Ecol. Model. 2011, 222, 1614–1625. [Google Scholar] [CrossRef]
- Brown, H.; Huth, N.; Holzworth, D. Crop Model Improvement in APSIM: Using Wheat as a Case Study. Eur. J. Agron. 2018, 100, 141–150. [Google Scholar] [CrossRef]
- Ceglar, A.; van der Wijngaart, R.; de Wit, A.; Lecerf, R.; Boogaard, H.; Seguini, L.; van den Berg, M.; Toreti, A.; Zampieri, M.; Fumagalli, D.; et al. Improving WOFOST Model to Simulate Winter Wheat Phenology in Europe: Evaluation and Effects on Yield. Agric. Syst. 2019, 168, 168–180. [Google Scholar] [CrossRef]
- Sandhu, R.; Irmak, S. Performance of AquaCrop Model in Simulating Maize Growth, Yield, and Evapotranspiration under Rainfed, Limited and Full Irrigation. Agric. Water Manag. 2019, 223, 105687. [Google Scholar] [CrossRef]
- Xu, J.; Bai, W.; Li, Y.; Wang, H.; Yang, S.; Wei, Z. Modeling Rice Development and Field Water Balance Using AquaCrop Model under Drying-Wetting Cycle Condition in Eastern China. Agric. Water Manag. 2019, 213, 289–297. [Google Scholar] [CrossRef]
- Wolf, J. Comparison of Two Potato Simulation Models under Climate Change. II. Application of Climate Change Scenarios. Clim. Res. 2002, 21, 187–198. [Google Scholar] [CrossRef]
- Li, M.; Du, Y.; Zhang, F.; Fan, J.; Ning, Y.; Cheng, H.; Xiao, C. Modification of CSM-CROPGRO-Cotton Model for Simulating Cotton Growth and Yield under Various Deficit Irrigation Strategies. Comput. Electron. Agric. 2020, 179, 105843. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, L.; Jiang, J.; Fan, Y.; Zhang, X. Review of Application of EPIC Crop Growth Model. Ecol. Model. 2022, 467, 109952. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Wang, Y.; Sun, H.; Hannaford, J.; Su, Z.; Barker, L.J.; Qu, Y. Drought Risk Assessment of Spring Maize Based on APSIM Crop Model in Liaoning Province, China. Int. J. Disaster Risk Reduct. 2020, 45, 101483. [Google Scholar] [CrossRef]
- Constantin, J.; le Bas, C.; Justes, E. Large-Scale Assessment of Optimal Emergence and Destruction Dates for Cover Crops to Reduce Nitrate Leaching in Temperate Conditions Using the STICS Soil–Crop Model. Eur. J. Agron. 2015, 69, 75–87. [Google Scholar] [CrossRef]
- Bai, T.C.; Wang, T.; Zhang, N.N.; Chen, Y.Q.; Mercatoris, B. Growth Simulation and Yield Prediction for Perennial Jujube Fruit Tree by Integrating Age into the WOFOST Model. J. Integr. Agric. 2020, 19, 721–734. [Google Scholar] [CrossRef]
- de Wit, A.J.W.; Boogaard, H.L.; Supit, I.; van den Berg, M. System Description of the WOFOST 7.2 Cropping Systems Model; WOFOST: Wageningen, The Netherlands, 2020; p. 120. [Google Scholar]
- van Diepen, C.A.; Wolf, J.; van Keulen, H.; Rappoldt, C. WOFOST: A Simulation Model of Crop Production. Soil Use Manag. 1989, 5, 16–24. [Google Scholar] [CrossRef]
- Van Ittersum, M.K.; Leffelaar, P.A.; Van Keulen, H.; Kropff, M.J.; Bastiaans, L.; Goudriaan, J. On Approaches and Applications of the Wageningen Crop Models. Eur. J. Agron. 2003, 18, 201–234. [Google Scholar] [CrossRef]
- Bassu, S.; Fumagalli, D.; Toreti, A.; Ceglar, A.; Giunta, F.; Motzo, R.; Zajac, Z.; Niemeyer, S. Modelling Potential Maize Yield with Climate and Crop Conditions around Flowering. Field Crops Res. 2021, 271, 108226. [Google Scholar] [CrossRef]
- Ogutu, G.E.O.; Franssen, W.H.P.; Supit, I.; Omondi, P.; Hutjes, R.W.A. Probabilistic Maize Yield Prediction over East Africa Using Dynamic Ensemble Seasonal Climate Forecasts. Agric. Meteorol. 2018, 250–251, 243–261. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving Winter Wheat Yield Estimation by Assimilation of the Leaf Area Index from Landsat TM and MODIS Data into the WOFOST Model. Agric. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- De Wit, A. Available online: https://pcse.readthedocs.io/en/stable/ (accessed on 6 March 2021).
- Bai, T.; Zhang, N.; Wang, T.; Wang, D.; Yu, C.; Meng, W.; Fei, H.; Chen, R.; Li, Y.; Zhou, B. Simulating on the Effects of Irrigation on Jujube Tree Growth, Evapotranspiration and Water Use Based on Crop Growth Model. Agric. Water Manag. 2021, 243, 106517. [Google Scholar] [CrossRef]
- van Dam, J.; Groenendijk, P.; Hendriks, R.; Jacobs, C. Alterra Report1649-Swap32 Theory Description and User Manual; Alterra: Wageningen, The Netherlands, 2009. [Google Scholar]
- Hao, S.; Ryu, D.; Western, A.; Perry, E.; Bogena, H.; Franssen, H.J.H. Performance of a Wheat Yield Prediction Model and Factors Influencing the Performance: A Review and Meta-Analysis. Agric. Syst. 2021, 194, 103278. [Google Scholar] [CrossRef]
- Akumaga, U.; Tarhule, A.; Yusuf, A.A. Validation and Testing of the FAO AquaCrop Model under Different Levels of Nitrogen Fertilizer on Rainfed Maize in Nigeria, West Africa. Agric. Meteorol. 2017, 232, 225–234. [Google Scholar] [CrossRef]
- Fleming, A.; Schenkel, F.S.; Chen, J.; Malchiodi, F.; Bonfatti, V.; Ali, R.A.; Mallard, B.; Corredig, M.; Miglior, F. Prediction of Milk Fatty Acid Content with Mid-Infrared Spectroscopy in Canadian Dairy Cattle Using Differently Distributed Model Development Sets. J. Dairy Sci. 2017, 100, 5073–5081. [Google Scholar] [CrossRef]
- Wang, D.; Wang, C.; Xu, L.; Bai, T.; Yang, G. Simulating Growth and Evaluating the Regional Adaptability of Cotton Fields with Non-Film Mulching in Xinjiang. Agriculture 2022, 12, 895. [Google Scholar] [CrossRef]
- Wang, L.; Wu, W.; Xiao, J.; Huang, Q.; Hu, Y. Effects of Different Drip Irrigation Modes on Water Use Efficiency of Pear Trees in Northern China. Agric. Water Manag. 2021, 245, 106660. [Google Scholar] [CrossRef]
- Malone, R.W.; Huth, N.; Carberry, P.S.; Ma, L.; Kaspar, T.C.; Karlen, D.L.; Meade, T.; Kanwar, R.S.; Heilman, P. Evaluating and Predicting Agricultural Management Effects under Tile Drainage Using Modified APSIM. Geoderma 2007, 140, 310–322. [Google Scholar] [CrossRef]
- Zhao, Y.; Mao, X.; Shukla, M.K. A Modified SWAP Model for Soil Water and Heat Dynamics and Seed–Maize Growth under Film Mulching. Agric. Meteorol. 2020, 292–293, 108127. [Google Scholar] [CrossRef]
- Qiu, R.; Li, L.; Liu, C.; Wang, Z.; Zhang, B.; Liu, Z. Evapotranspiration Estimation Using a Modified Crop Coefficient Model in a Rotated Rice-Winter Wheat System. Agric. Water Manag. 2022, 264, 107501. [Google Scholar] [CrossRef]
- Castrignanò, A.; Katerji, N.; Karam, F.; Mastrorilli, M.; Hamdy, A. A Modified Version of CERES-Maize Model for Predicting Crop Response to Salinity Stress. Ecol. Model. 1998, 111, 107–120. [Google Scholar] [CrossRef]
- du Toit, E.S.; Sithole, J.; Vorster, J. Pruning Intensity Influences Growth, Flower and Fruit Development of Moringa Oleifera Lam. under Sub-Optimal Growing Conditions in Gauteng, South Africa. S. Afr. J. Bot. 2020, 129, 448–456. [Google Scholar] [CrossRef]
- de Alcântara Barbosa, C.M.; Pio, R.; de Souza, F.B.M.; Bisi, R.B.; Bettiol Neto, J.E.; da Hora Farias, D. Phenological Evaluation for Determination of Pruning Strategies on Pear Trees in the Tropics. Sci. Hortic. 2018, 240, 326–332. [Google Scholar] [CrossRef]
- Molina, A.J.; Aranda, X.; Llorens, P.; Galindo, A.; Biel, C. Sap Flow of a Wild Cherry Tree Plantation Growing under Mediterranean Conditions: Assessing the Role of Environmental Conditions on Canopy Conductance and the Effect of Branch Pruning on Water Productivity. Agric. Water Manag. 2019, 218, 222–233. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, X.; Wang, Y.; Ma, J.; Wei, X.; Chen, D. Effects of Pruning Intensity on Jujube Transpiration and Soil Moisture of Plantation in the Loess Plateau. IOP Conf Ser. Earth Env. Sci. 2017, 52, 012048. [Google Scholar] [CrossRef]
- Greer, D.H.; Weedon, M.M. Modelling Photosynthetic Responses to Temperature of Grapevine (Vitis Vinifera Cv. Semillon) Leaves on Vines Grown in a Hot Climate. Plant. Cell Env. 2012, 35, 1050–1064. [Google Scholar] [CrossRef]
- Crafts-Brandner, S.J.; Salvucci, M.E. Sensitivity of Photosynthesis in a C4 Plant, Maize, to Heat Stress. Plant. Physiol. 2002, 129, 1773–1780. [Google Scholar] [CrossRef]
- Hasanuzzaman, M.; Nahar, K.; Alam, M.M.; Roychowdhury, R.; Fujita, M. Physiological, Biochemical, and Molecular Mechanisms of Heat Stress Tolerance in Plants. Int. J. Mol. Sci. 2013, 14, 9643–9684. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Wei, J.; Zhang, G.; Sun, X.; Wang, W.; Wu, C.; Tang, M.; Gan, Z.; Xu, X.; Chen, S.; et al. Effects of Cooling Measures on ‘Nijisseiki’ Pear (Pyrus Pyrifolia) Tree Growth and Fruit Quality in the Hot Climate. Sci. Hortic. 2018, 238, 318–324. [Google Scholar] [CrossRef]
- Schrader, L.; Sun, J.; Zhang, J.; Felicetti, D.; Tianz, J. Heat and Light-Induced Apple Skin Disorders: Causes and Prevention. Acta Hortic. 2008, 772, 51–58. [Google Scholar] [CrossRef]
- Niu, Y.; Chen, X.; Zhou, W.; Li, W.; Zhao, S.; Nasir, M.; Dong, S.; Zhang, S.; Liao, K. Genetic Relationship between the ‘Korla Fragrant Pear’ and Local Pear Varieties in Xinjiang Based on Floral Organ Characteristics. Sci. Hortic. 2019, 257, 108621. [Google Scholar] [CrossRef]
- Menzel, C.M.; le Lagadec, M.D. Can the Productivity of Mango Orchards Be Increased by Using High-Density Plantings? Sci. Hortic. 2017, 219, 222–263. [Google Scholar] [CrossRef]
- Siad, S.M.; Iacobellis, V.; Zdruli, P.; Gioia, A.; Stavi, I.; Hoogenboom, G. A Review of Coupled Hydrologic and Crop Growth Models. Agric. Water Manag. 2019, 224, 105746. [Google Scholar] [CrossRef]
- Chapagain, R.; Remenyi, T.A.; Harris, R.M.B.; Mohammed, C.L.; Huth, N.; Wallach, D.; Rezaei, E.E.; Ojeda, J.J. Decomposing Crop Model Uncertainty: A Systematic Review. Field Crops Res. 2022, 279, 108448. [Google Scholar] [CrossRef]
- He, L.I.; Jiang, Z.W.; Chen, Z.X.; Ren, J.Q.; Bin, L.I. Hasituya Assimilation of Temporal-Spatial Leaf Area Index into the CERES-Wheat Model with Ensemble Kalman Filter and Uncertainty Assessment for Improving Winter Wheat Yield Estimation. J. Integr. Agric. 2017, 16, 2283–2299. [Google Scholar] [CrossRef]
- Cui, N.; Du, T.; Li, F.; Tong, L.; Kang, S.; Wang, M.; Liu, X.; Li, Z. Response of Vegetative Growth and Fruit Development to Regulated Deficit Irrigation at Different Growth Stages of Pear-Jujube Tree. Agric. Water Manag. 2009, 96, 1237–1246. [Google Scholar] [CrossRef]
- Cui, N.; Du, T.; Kang, S.; Li, F.; Zhang, J.; Wang, M.; Li, Z. Regulated Deficit Irrigation Improved Fruit Quality and Water Use Efficiency of Pear-Jujube Trees. Agric. Water Manag. 2008, 95, 489–497. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Yuan, Y.; Xu, J.; Tu, C.; Fisk, C.; Zhang, W.; Chen, X.; Ritchie, D.; Hu, S. Irrigation and Weed Control Alter Soil Microbiology and Nutrient Availability in North Carolina Sandhill Peach Orchards. Sci. Total Environ. 2018, 615, 517–525. [Google Scholar] [CrossRef] [PubMed]
- Paušič, A.; Tojnko, S.; Lešnik, M. Permanent, Undisturbed, in-Row Living Mulch: A Realistic Option to Replace Glyphosate-Dominated Chemical Weed Control in Intensive Pear Orchards. Agric. Ecosyst. Environ. 2021, 318, 107502. [Google Scholar] [CrossRef]
- Hammermeister, A.M. Organic Weed Management in Perennial Fruits. Sci. Hortic. 2016, 208, 28–42. [Google Scholar] [CrossRef]

| Pruning Intensity | Unpruned | Pruned 5% | Pruned 10% | Pruned 15% | Pruned 20% | Pruned 25% | Pruned 30% | Pruned 35% | |
|---|---|---|---|---|---|---|---|---|---|
| DVS | |||||||||
| DVS = 0.0 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | |
| DVS = 1.260 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | |
| DVS = 1.261 | 0.83 | 0.80 | 0.75 | 0.72 | 0.69 | 0.66 | 0.63 | 0.60 | |
| DVS = 2.0 | 0.83 | 0.83 | 0.83 | 0.81 | 0.79 | 0.76 | 0.74 | 0.71 | |
| Region | Pruning Intensity | Unmodified Model | Modified Model | ||||
|---|---|---|---|---|---|---|---|
| RMSE (kg ha−1) | NRMSE (%) | RMSE (kg ha−1) | NRMSE (%) | ||||
| Alaer | 0% | 0.969 | 408.69 | 14.07 | 0.969 | 408.69 | 14.07 |
| 5% | 0.973 | 385.39 | 12.95 | 0.976 | 362.69 | 12.19 | |
| 10% | 0.965 | 450.18 | 15.30 | 0.972 | 401.41 | 13.64 | |
| 15% | 0.964 | 455.65 | 15.45 | 0.975 | 376.99 | 12.78 | |
| 25% | 0.948 | 564.28 | 19.51 | 0.968 | 438.73 | 15.17 | |
| 30% | 0.921 | 636.73 | 23.83 | 0.955 | 479.15 | 17.93 | |
| 35% | 0.917 | 630.65 | 24.17 | 0.956 | 458.92 | 17.59 | |
| Awat | 0% | 0.945 | 429.45 | 18.22 | 0.945 | 429.45 | 18.22 |
| 5% | 0.939 | 438.87 | 17.37 | 0.943 | 428.09 | 16.94 | |
| 10% | 0.948 | 402.04 | 17.19 | 0.959 | 357.23 | 15.27 | |
| 15% | 0.92 | 514.36 | 20.72 | 0.939 | 449.65 | 18.11 | |
| 20% | 0.941 | 424.48 | 18.93 | 0.964 | 329.45 | 14.69 | |
| 25% | 0.839 | 630.16 | 32.90 | 0.899 | 500.10 | 26.11 | |
| 30% | 0.910 | 476.98 | 23.78 | 0.948 | 360.83 | 17.99 | |
| 35% | 0.784 | 650.80 | 35.01 | 0.919 | 399.29 | 21.48 | |
| Region | Pruning Intensity | Unmodified Model | Modified Model | ||||
|---|---|---|---|---|---|---|---|
| RMSE (ha ha−1) | NRMSE (%) | RMSE (ha ha−1) | NRMSE (%) | ||||
| Alaer | 0% | 0.924 | 0.13 | 3.42 | 0.924 | 0.13 | 3.42 |
| 5% | 0.903 | 0.15 | 3.99 | 0.908 | 0.15 | 3.90 | |
| 10% | 0.875 | 0.18 | 4.70 | 0.914 | 0.15 | 3.88 | |
| 15% | 0.882 | 0.17 | 4.12 | 0.911 | 0.16 | 3.96 | |
| 25% | −1.919 | 0.71 | 21.93 | 0.904 | 0.13 | 3.99 | |
| 30% | −4.248 | 1.32 | 47.37 | 0.885 | 0.19 | 7.01 | |
| 35% | −5.209 | 1.57 | 62.92 | 0.905 | 0.19 | 7.77 | |
| Awat | 0% | 0.899 | 0.21 | 5.44 | 0.899 | 0.21 | 5.44 |
| 5% | 0.884 | 0.22 | 5.56 | 0.903 | 0.20 | 5.08 | |
| 10% | 0.852 | 0.23 | 5.92 | 0.920 | 0.17 | 4.37 | |
| 15% | 0.848 | 0.25 | 6.45 | 0.894 | 0.21 | 5.38 | |
| 20% | 0.567 | 0.36 | 9.79 | 0.916 | 0.16 | 4.30 | |
| 25% | −0.049 | 0.57 | 16.94 | 0.849 | 0.22 | 6.42 | |
| 30% | −3.077 | 0.94 | 30.39 | 0.868 | 0.17 | 5.47 | |
| 35% | −4.902 | 1.46 | 55.76 | 0.860 | 0.23 | 8.60 | |
| Region | Pruning Intensity | Unmodified Model | Modified Model | ||||
|---|---|---|---|---|---|---|---|
| RMSE (cm3 cm−3) | NRMSE (%) | RMSE (cm3 cm−3) | NRMSE (%) | ||||
| Alaer | 0% | 0.866 | 0.011 | 4.54 | 0.866 | 0.011 | 4.54 |
| 5% | 0.878 | 0.011 | 4.28 | 0.878 | 0.010 | 4.28 | |
| 10% | 0.829 | 0.022 | 5.03 | 0.834 | 0.020 | 4.99 | |
| 15% | 0.832 | 0.021 | 5.01 | 0.836 | 0.018 | 4.94 | |
| 25% | 0.791 | 0.022 | 5.95 | 0.827 | 0.020 | 5.43 | |
| 30% | 0.535 | 0.032 | 8.95 | 0.733 | 0.022 | 6.79 | |
| 35% | 0.658 | 0.029 | 8.63 | 0.715 | 0.021 | 7.47 | |
| Awat | 0% | 0.779 | 0.013 | 4.49 | 0.779 | 0.013 | 4.49 |
| 5% | 0.798 | 0.021 | 5.15 | 0.801 | 0.021 | 5.14 | |
| 10% | 0.799 | 0.010 | 4.74 | 0.804 | 0.010 | 4.68 | |
| 15% | 0.743 | 0.021 | 5.60 | 0.767 | 0.022 | 5.33 | |
| 20% | 0.799 | 0.010 | 4.64 | 0.806 | 0.010 | 4.56 | |
| 25% | 0.698 | 0.021 | 5.85 | 0.703 | 0.020 | 5.79 | |
| 30% | 0.626 | 0.023 | 5.86 | 0.763 | 0.017 | 4.67 | |
| 35% | 0.369 | 0.026 | 8.77 | 0.744 | 0.020 | 5.59 | |
| Pruning Intensity | Alaer | Awat | ||||
|---|---|---|---|---|---|---|
| Simulated Values (t ha−1) | Measured Values (t ha−1) | Relative Error (%) | Simulated Values (t ha−1) | Measured Values (t ha−1) | Relative Error (%) | |
| 0% | 22.67 | 24.73 | 8.33 | 20.09 | 18.22 | 10.25 |
| 5% | 22.57 | 20.49 | 10.14 | 19.95 | 22.43 | 11.04 |
| 10% | 22.54 | 19.45 | 15.91 | 19.92 | 21.75 | 8.39 |
| 15% | 22.35 | 23.97 | 6.77 | 19.75 | 17.21 | 14.76 |
| 20% | 22.15 | 21.38 | 3.61 | 19.50 | 18.46 | 5.65 |
| 25% | 21.33 | 18.73 | 13.90 | 19.04 | 15.33 | 24.23 |
| 30% | 19.93 | 22.34 | 10.79 | 18.11 | 16.15 | 12.11 |
| 35% | 18.60 | 15.11 | 23.07 | 16.53 | 14.33 | 15.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, N.; Li, M.; Li, L.; Bai, T. Pear Tree Growth Simulation and Soil Moisture Assessment Considering Pruning. Agriculture 2022, 12, 1653. https://doi.org/10.3390/agriculture12101653
Wang C, Zhang N, Li M, Li L, Bai T. Pear Tree Growth Simulation and Soil Moisture Assessment Considering Pruning. Agriculture. 2022; 12(10):1653. https://doi.org/10.3390/agriculture12101653
Chicago/Turabian StyleWang, Chengkun, Nannan Zhang, Mingzhe Li, Li Li, and Tiecheng Bai. 2022. "Pear Tree Growth Simulation and Soil Moisture Assessment Considering Pruning" Agriculture 12, no. 10: 1653. https://doi.org/10.3390/agriculture12101653
APA StyleWang, C., Zhang, N., Li, M., Li, L., & Bai, T. (2022). Pear Tree Growth Simulation and Soil Moisture Assessment Considering Pruning. Agriculture, 12(10), 1653. https://doi.org/10.3390/agriculture12101653







