Abstract
We created a subsurface drip irrigation (SDI)-specific variable flow emitter (VFE) that switches working stages automatically based on the inlet pressure (H) to achieve a step change in the flow rate. At working stage I (H = 0.1 MPa), namely the conventional water supply stage, the VFE provided a normal flow rate (qI) of 1–2 L/h for crop irrigation. At working stage II (H > 0.1 MPa; exceeding the design pressure), VFE delivered a larger flow rate (qII). The larger qII facilitated water movement upward from the underground to the surface seedbed during the crop planting, thus ameliorating crop germination issues under SDI. We focused on the impacts of four structural parameters of the flow channel: tooth height (E), tooth spacing (B), tooth angle (A), and flow channel depth (D) on the qI and VFE-flow index (x) at working stage I. Computational fluid dynamic (CFD) simulations were conducted along with a physical laboratory test to develop VFE using computerized numerical control (CNC) technology (accuracy = 0.05 mm). Nine VFEs were designed using an L9(34) orthogonal test. The combination of tetrahedral meshing with a six-layer boundary layer and the realizable k–ε turbulence model was found suitable for CFD simulations. The standard root-mean-square error (nRMSE) of the measured and simulated qIs was a minimum of 7.4%. The four parameters influenced qIs as D > B > E > A, and the four factors influenced the xs as B > E > D > A. Based on the numerical simulation data, multiple linear regression models were constructed for the qIs and xs with four parameters when H = 0.1 MPa. Aiming for the minimum x, the optimal combination of the flow channel structural parameters corresponding to different qIs was determined by the ergodic optimization algorithm. When qI was 1.5 L/h, the optimal structural combinations were E = 1.2 mm, B = 1.8 mm, A = 42°, and D = 1 mm. The VFE with a qI of 1.5 L/h was created by CNC technology. The relative errors of the measured and predicted qIs using the regression model were −0.19–6.31%, and their nRMSE was 6.76%. Thus, optimizing the flow channel structural parameters based on a multiple linear regression model and the ergodic optimization algorithm is a highly precise theoretical base for VFE development.
1. Introduction
Subsurface drip irrigation (SDI) is a technique with great water-saving potential and a major impact on improving the yield and quality of crops [1]. It can transport water and nutrients directly to the root zone of crops and has considerable advantages, such as improving water use efficiency, reducing weed growth, and eliminating the need to replace driplines annually [2,3,4,5,6]. An SDI system can be operated for more than 10 years, and the dripline must be buried below the plow layer when the soil is cultivated [7]. The upward movement of water is slower than the downward movement owing to gravity. Rotary tillage before sowing makes the surface soil dry and loose, reducing the hydraulic conductivity of the soil surface layer and further restraining the upward movement of water to the surface seedbed [8,9,10], resulting in difficult crop germination and low yield [11,12]. In a study by Mo et al. [13,14], the emergence rate of SDI spring maize was less than 80% when the depth of the dripline was 30–35 cm, the flow rate of the emitter was 1.05 L/h, and the irrigation volume of emergence water was 15–60 mm. In the Xinjiang Production and Construction Corps, China, the total planting area of corn and cotton production using SDI decreased from 8000 ha to 70 ha over the last nine years [15], and one of the primary reasons for this decrease was germination issues [9,13]. In recent years, SDI has been promoted in northeast, northwest, and south China based on actual production demand, and over 6600 ha has been installed [16]. However, the problem of low crop emergence rate has not been resolved yet and is a scientific problem that hinders the large-scale application of SDI.
The emitter flow rate has a profound effect on the geometry of soil wetting patterns [17]. When the flow rate is greater than the saturated hydraulic conductivity of the soil, the partial soil moisture content can reach a high value in a short period of time, thereby increasing the water potential gradient, accelerating the migration of the wetting front, and increasing the soil moisture content at the same location as the water flow rate. The infiltration rate of SDI soil water and the distance of the upward migration of water increase as the discharge of the emitter under sandy loam soil increases [18,19,20]. The upward migration distance of soil water and the wetting area of the surface increased with the flow rate for low infiltration soils in Jordan [21]. The wetting can reach the soil surface when the drip irrigation zone depth is 30 cm, and the flow rate is greater than 8 L/h [22]. In both sandy and loam soil box experiments, the flow rate had a major impact on the moisture content of the upper 0–20 cm of soil, which increased along with the flow rate [23]. When the flow rate was increased from 0.5 to 1.4 L/h, the upward water transport distance increased by 54.3% [24]. At present, most emitters for SDI have a flow rate of 1–2 L/h [25,26], which was mainly designed for the crop water demand at the conventional water supply stage and did not take pre-emergence irrigation under SDI into account.
To address the problem of seedling emergence in SDI, our team has proposed a new variable flow emitter (VFE). Through the synergistic interaction of the flow channel and elastomer, the water supply pressure is used as the driving force to achieve a step change in flow rate. The VFE delivers a conventional flow rate of 1–2 L/h at a working pressure of 0.1 MPa during most crop growth stages at working stage I. When the inlet pressure reached the design valve, the VFE provided a sudden increase in the flow rate that was greater than the saturated soil water conductivity, thus promoting the upward migration of soil water and improving the soil moisture content around the seeds. This working stage (i.e., working stage II) provides pre-emergence irrigation in SDI. A VFE is a new emitter structure type, and no prior information was available to guide us in developing it. Since working stage I forms the basis of working stage II, and most of the working stage of the VFE is stage I, the research and development of the VFE should initially focus on stage I.
The flow rate and flow index are two primary hydraulic performance indexes of an emitter, also important to the VFE at working stage I. The optimum flow rate should be selected based on the soil texture, crop water consumption law, and other factors [26,27,28]. The flow index indicates the sensitivity of the flow rate to the working pressure; the lower the flow index, the more uniform the irrigation, the greater the laying distance of the dripline, and the smaller the investment [29,30,31,32,33,34]. Therefore, the majority of research and development of new emitters have been carried out with the goal of reducing the flow index. Because of the complex structure and small size of the flow channel [35,36,37], researchers have focused on the response law of the macroscopic hydraulic performance of the emitter to structural parameters by processing prototype emitter models [38,39], scaled-up emitter models [40,41], or dripline production [42,43].
With the advancement of computer fluid simulation technology, researchers have begun using numerical simulation as the primary method and hydraulic performance testing as the auxiliary verification method to thoroughly investigate the cooperative mutual feed relationship between the hydraulic performance of the emitter, the internal flow field of the flow channel, and the flow channel structure [44,45]. The flow index is closely related to the length, width, and depth of the flow channel, height, angle, and spacing of the tooth, and other structural parameters [46]. Because of disparities between the emitter structure and test conditions, there is no unified conclusion on the sequence of the flow index affected by the flow channel structural parameters; however, most research results show that tooth spacing has a substantial impact on the flow index [47,48,49,50].
Based on measured or simulated data of emitter hydraulic performance, researchers have created many mathematical regression models of the flow rate and index using flow channel structural parameters. The relative errors between the predicted values of the regression model and the measured values ranged between 3.8% and 37.0%. In addition, researchers have used genetic algorithms [50,51], artificial neural networks [52,53], gene expression programming [54], and other artificial intelligence learning methods to develop a mathematical model of the hydraulic performance and structural parameters of the emitter. This can improve the simulation accuracy of the hydraulic performance of the emitter and reduce the relative error between the predicted value of the model and the measured value by 3.0–15.8%. Because the number of independent variables in mathematical regression models of the flow rate and flow channel structural parameters are typically more than three, emitter manufacturers were unable to determine the optimal combination of structural parameters for the flow channel and could only obtain a value range.
In this study, computerized numerical control (CNC) technology was used to process the VFE and its testing device, and physical test data were used to determine the appropriate mathematical simulation method for computational fluid dynamic (CFD) simulation of the hydraulic performance of the VFE at working stage I. Regression models of the VFE-flow rate, flow index, and flow channel structural parameters were constructed using the determined CFD simulation method. Third, an ergodic optimization algorithm (EOA) was used to obtain the three optimal combinations of flow channel structural parameters corresponding to the flow rate range of 1–2 L/h, with the goal of obtaining the minimum flow index. The samples were then processed by CNC, and the prediction results of the regression model were verified using the hydraulic performance measurements. The combination of CFD simulation, regression model development, and EOA proposed in this study can provide a new concept for rapid and accurate acquisition of the optimal flow channel structural parameter combination of VFE.
2. Materials and Methods
2.1. Structural Design and Working Principles of Variable Flow Emitters
A variable flow emitter (VFE) primarily consists of the shell body (1), cylindrical elastomer (2), core body (3), and base (4). The core body was cylindrical, and it was possible to securely wrap the cylindrical elastomer around it. The cylindrical elastomer and core body were installed on the base, formed a sealed body with the shell body, and were attached to the inner wall of the dripline. A cavity body was positioned between the outer surface of the cylindrical elastomer, shell body, and base. When the cylindrical elastomer was unstressed, a number of grooves on the outer surface of the core body were bent back and forth to form a flow channel with the inner surface of the cylindrical elastomer (Figure 1 and Figure 2).
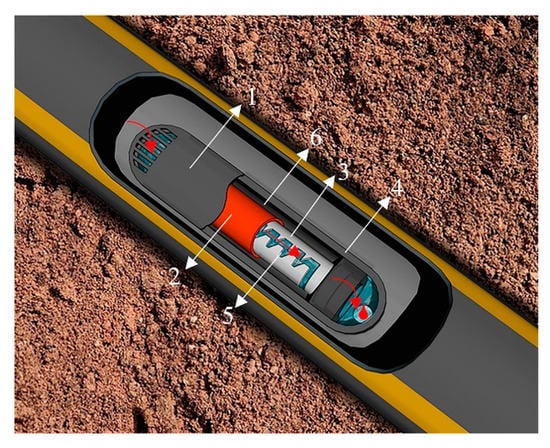
Figure 1.
Schematic illustration of variable flow emitter structure. Note: 1. Shell body; 2. Cylindrical elastomer; 3. Core body; 4. Base part; 5. Flow channel; 6. Cavity body.
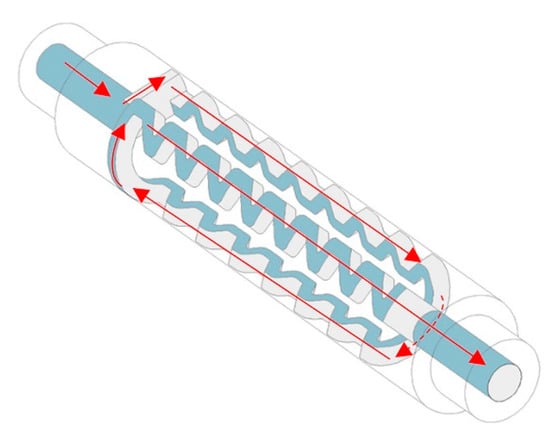
Figure 2.
Axonometric diagram of the movement route of the water in the flow channel (the red arrow).
As shown in Figure 3, the VFE had two functions that corresponded to two working stages: the conventional flow rate supply stage I and the large-flow rate supply stage II. Both these stages are mainly regulated by the working pressure (H) of the emitter. When H was below the design working pressure, the pressure in the flow channel was insufficient to separate the cylindrical elastomer from the surface of the core body, which meant water could only flow via the flow channel (5). At this instance, the VFE was in working stage I. During this stage, when H was 0.1 MPa, the flow rate (qI) of VFE was 1–2 L/h, which was typical for SDI. When H was greater than the design working pressure, the pressure in the flow channel could cause the cylindrical elastomer to expand and deform in the cavity body. The cylindrical elastomer would exit the groove, and the increase in the section of the flow channel would result in a higher flow rate (qII), which realized a step change in the flow rate of the VFE. At this instance, the VFE shifted to working stage II. At this time, the self-cleaning function of VFE was also started, and the sediment that accumulated in the flow channel could be flushed out due to the expansion of the flow section so as to improve the anti-clogging performance of the emitter.
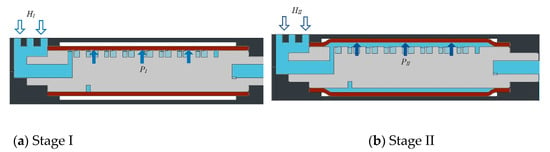
Figure 3.
A sectional view of the variable flow emitter in the working stage I (a) and stage II (b). Note: PI and qI are the pressure of the internal flow of the flow channel on the elastomer and the outflow flow rate in the conventional flow supply stage I, respectively. PII and qII are the pressure of the internal water flow of the flow channel on the elastomer and the outflow flow rate in the larger flow supply stage II, respectively.
The majority of the working stage of VFE during the entire crop growth period was stage I, which was the basis of working stage II. Therefore, exploring the quantitative characterization relationship between qI and the flow index (x) in working stage I with the structural parameters of the flow channel and elucidating the appropriate combination of structural parameters corresponding to different qI was an important prerequisite for the development of VFE. Consequently, this study focused solely on working stage I.
2.2. Analysis of Flow Channel Structural Parameter Affecting Hydraulic Performance of VFE in the Working Stage I
The flow channel for VFE is N-type, which can increase the turbulent kinetic energy in the mainstream area and low-speed area, increase the migration rate of sand in the flow channel, and improve the clogging resistance of VFE [36]. Four structure factors of the flow channel with great influence on x, namely tooth height (E), tooth spacing (B), tooth angle (A), and flow channel depth (D) are selected to study the response law of qI and x to H for VFE in the working stage I (Figure 4).
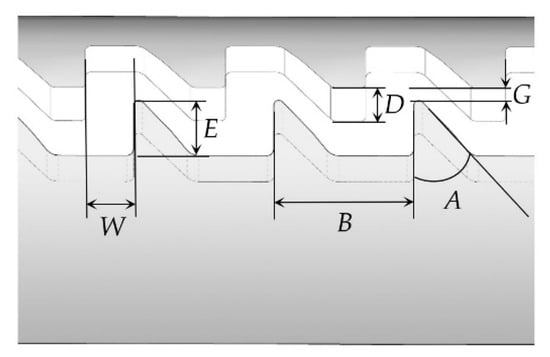
Figure 4.
Structural perspective of the flow channel in variable flow emitter.
2.2.1. Experiment Design
In order to improve the anti-clog performance of the emitter, the value range of W, D, and G in the existing published references is 0.5–1.3 mm, 0.5–1.3 mm, and 0 mm [15,48,55,56,57]. Fluent (Ansys, Canonsburg, PA, USA) is often used for structural design and performance optimization of emitters [58]. Aiming at the VFE flow rate of 1–2 L/h when H is 0.1 MPa, this study uses Fluent to conduct preliminary simulation and determines that E was 0.6–1.0 mm, B was 1.8–2.2 mm, A was 34–42°, and D was 0.6–1.0 mm. In addition, W and G were fixed values of 0.5 and 0 mm. For E, B, A, and D, three levels were selected for each factor, and the orthogonal test, L9(34), was used for the experimental design. The flow channel structural parameters of nine VFEs designed by orthogonal experiment are shown in Table 1, No. 1–9. The VFE of serial number 10 is used to adjust the parameters of the Fluent model for the simulation of the flow of VFE under different H.

Table 1.
Experiment design.
2.2.2. Hydraulic Performance Test Method and Test Index
A special testing device for the hydraulic performance of VFE was created. The structure of the testing device and the NO. 10 VFE (Table 1) were both designed using Unigraphics NX 10.0 (Siemens PLM Software, USA), and manufactured by the computerized numerical control (CNC) technology with a machining accuracy of 0.05 mm. The processed material was brass (Figure 5 and Figure 6). In order to verify the machining accuracy of CNC technology, a 2.5-dimensional image size measuring instrument (JTMS-3020, accuracy ≤ (2.5+ measuring length/100) μm, Jiateng Precision Equipment (Tianjin) Co., LTD., Tianjin, China) was used for structural size rechecking.

Figure 5.
The flow channel on the core body of a variable flow emitter is carved using computerized numerical control technology.

Figure 6.
Schematic diagram of the variable flow emitter and testing device made by the computerized numerical control technology. Note: 1. Teflon elastomer; 2. Core body; 3. Special test equipment; 4. Screw; 5. Nut.
In order to study the hydraulic performance changes of VFE in working stage I, it is necessary to keep the cylindrical elastomer from deforming. The Teflon elastomer with an elastic modulus of 60 MPa was selected on the outer surface of the core body to ensure the sealing of the flow channel under H, and that the deformation of the channel section was as small as possible.
The hydraulic performance test of VFE is located in the National Water-saving Irrigation Engineering Technology Research Center (Beijing, China), and the hydraulic performance test bench is shown in Figure 7. Circulating water was used in the experiment, and the water temperature was maintained at (23 ± 2) °C. The test was in accordance with the test of Platic equipment for water savine irrigation-Part 3:Drip pipe and drip tape inlaid with emitters inside (GB/T 19812.3-2017). The pre-test procedure was as follows: the valve (6) was closed; the bucket (8) was placed under the special test device (7); the centrifugal pump (2) was started; the pressure gauge (5) was set to monitor H through the ball valve (4); and H was set as 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, 0.11, 0.12, and 0.15 MPa. Once the pressure gauge (5) reading was stable, the valve (6) was opened, and the test system was started. The test duration was 5 min. The water volume of the VFE was measured using a measuring cylinder with an accuracy of 1 mL, and the test was repeated three times. The centrifugal pump model was CDLF410, and the flow rate is 4 m³/h, the head is 0.81 MPa, and it was purchased from South Pump Industry, Zhejiang, China. The pressure gauge range was 0–0.6 MPa with an accuracy level of 0.005 and was acquired from Yangquan Instrument (Shanxi, China); 120 mesh filters (mesh diameter 0.125 mm) were acquired from Netafim, Israel.
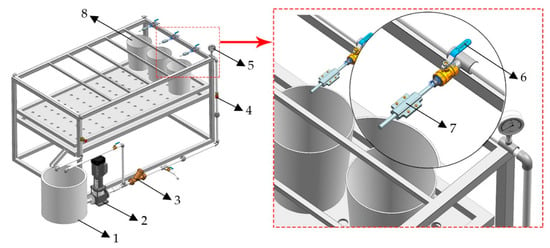
Figure 7.
Hydraulic performance test platform for variable flow emitter. Note: 1. Water storage tank; 2. Centrifugal pump; 3. Filter; 4. Ball valve; 5. Pressure gauge; 6. Valve; 7. Special testing device; and 8. Bucket.
Based on the qI (L/h) values corresponding to different H (MPa) values, Equation (1) can be used to determine the flow coefficient (k) and x of the VFE in working stage I.
qI = k × Hx
2.3. The Numerical Simulation
2.3.1. Determination of the Meshing and Turbulence Model Using Fluent Software
The main factors affecting the accuracy of the Fluent simulation included the selection of the meshing method and turbulence model [47]. In the numerical simulation of VFE No. 10 (Table 1), we initially set the three meshing models of tetrahedral meshing without a boundary layer (TWBL), tetrahedral meshing with the 6-layer boundary layer (TBL), and hexahedral meshing (HEX) with the same turbulence model as that of standard k-ε. Second, five turbulence models were established as standard k-ε, RNG k-ε, realizable k-ε, kω, and RSM using the same meshing model as TBL. When H was 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, 0.11, 0.12, and 0.15 MPa, the consistency between the simulated flow rate and the measured flow rate was evaluated by the standard root-mean-square error (nRMSE) (Equation (2)) [59,60,61].
where Si and Ei represented the measured and simulated values, respectively; n was the number of measured data; and Eave, the mean of the measured data. The model evaluation criteria were as follows: nRMSE ≤ 10%, excellent agreement between the simulated and measured rates; 10% < nRMSE < 20%, good; 20% ≤ nRMSE ≤ 30%, fair; and nRMSE > 30%, poor.
2.3.2. Influence of the Flow Channel Structural Parameters on the Hydraulic Performance of VFE
Once the appropriate meshes and turbulence models of the Fluent for the VFE in working stage I were determined, the hydraulic performance, including the flow rate under different H values and the flow index of the nine VFEs, were simulated (Table 1), and quantitative representation models of these two indexes and the four structural parameters of flow channel were constructed.
3. Results
3.1. Establishment of the Meshing and Turbulence Model
The number of grids for TWBL, TBL, and HEX were 0.535 million, 0.757 million, and 0.115 million, respectively. Table 2 displays the measured flow rate (qIm) and simulated flow rate (qIs) of the variable flow emitter (VFE)in working stage I for different meshing and turbulence models when H was 0.05–0.15 MPa. When the turbulence model was standard k-ε, the difference between qIm and qIs using tetrahedral meshing with a six-layer boundary layer (TBL) was the smallest, with an nRMSE = 8.4%, indicating that the simulation result is in excellent agreement. When the meshing model was TBL, the nRMSE corresponding to the other four turbulence models was less than 10%, except for the kω turbulence model, and the simulated value using the realizable k–ε turbulence model came the closest to the measured value (nRMSE = 7.4%). Therefore, a combination of the TBL meshing model and realizable k–ε turbulence model should be adopted in the simulation of qIs of VFE using the Fluent software.

Table 2.
Comparison between measured and simulated flow rates of the VFE in working stage I.
3.2. Simulation Results of the Emitter Flow Rate and Flow Index of Variable Flow Emitters
Figure 8 shows the variation curve of qIs with respect to H following the numerical simulation of the nine VFEs in Table 1 using the TBL meshing model and the realizable k–ε turbulence model. When H = 0.1 MPa, the simulated flow rate (qIs0.1) of VFE was 1.05–2.21 L/h, which was close to the desired range of 1–2 L/h. After fitting qIs and H to the power function, the simulated flow indexes (xs) of these nine VFEs were between 0.4870 and 0.5148, all of which were within the range of the flow index of the most widely used non-pressure compensated emitters currently on the market [52,62] (Table 3).
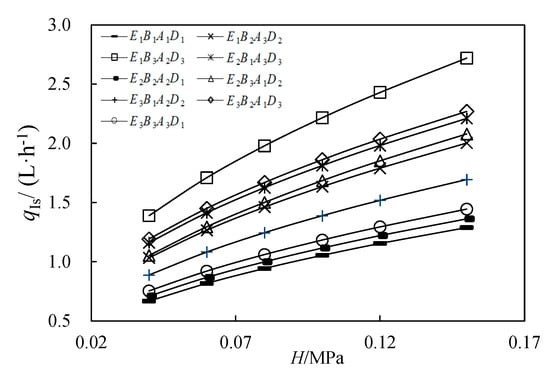
Figure 8.
Simulated flow rates (qIs) of the nine variable flow emitters in working stage I and the working pressure (H).

Table 3.
The simulated flow rates at H = 0.1 MPa (qIs0.1) and the simulated flow indexes (xs) of the variable flow emitter in working stage I.
3.3. Range Analysis of Hydraulic Performance of Variable Flow Emitter
Range analysis provides the degree of influence of the change in test factor level on the index, allowing for the determination of the optimal level of the factor and the order of factors affecting the hydraulic performance of the VFE in working stage I [63]. The range analysis of factors in the orthogonal test of the hydraulic performance of the VFE is presented in Table 4, where q1, q2, q3, and x1, x2, and x3 are the respective mean values of qIs0.1 and xs corresponding to levels 1, 2, and 3 (which can be calculated from Table 3), and R is the range of corresponding factors. The higher the value of R, the greater the influence of that factor on the test index. Within the level range of this experimental factor study, the order of the influence of each experimental factor on qIs0.1 was D > B > E > A, whereas the order of the influence of each experimental factor on xs was B > E > D > A.

Table 4.
Range analysis table of orthogonal test.
qIs0.1 was negatively correlated with E, positively correlated with B and D, and had a modest variation with A. xs was positively correlated with B, negatively correlated with E and A, and variable (an initial increased and subsequent decreased) correlation with D (Figure 9). Within the flow rate range of 1–2 L/h, the optimal combination of the flow channel structural parameters was E3B1A3D3 with E = 1.2 mm, B = 1.8 mm, A = 42°, and D = 1 mm, using the minimum value of xs as the preference principle [64,65,66].
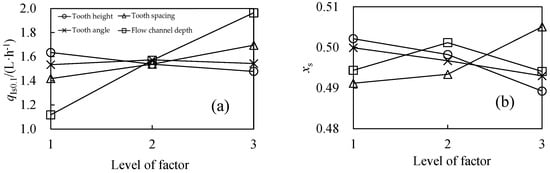
Figure 9.
Effect of flow channel structural parameters on (a) the simulated flow rate (qIs0.1) and (b) flow index (xs) of the variable flow emitter in working stage I.
3.4. Linear Regression Model for Hydraulic Performance of the Variable Flow Emitter
In this study, multiple linear regression equations of the flow rate at H = 0.1 MPa (qIs0.1) and flow index (xs) with E, B, A, and D were developed based on simulation data. The constant term and regression coefficients of E, B, and D had a significant effect on the multi-linear regression equation of qIs0.1 (p < 0.05); however, A did not have a significant effect on the linear regression equation of qIs0.1 (p > 0.1). The constant terms E and B had a significant influence on the linear regression equation of xs at p < 0.1 and p < 0.05, respectively. However, the influence of A and D on the linear regression equation of xs did not reach the significance level (p > 0.1) (Table 5). To simplify the regression model, factor A was removed from the qIs0.1 regression model. In order to determine A in the optimal flow channel structure, only factor D was removed from the regression model of xs. After optimization, the coefficient of determination (R2) of the multiple linear regression equation for qIs0.1 and xs were 0.99 and 0.80, respectively (Table 6). Both coefficients reached significance (p < 0.05) (Table 7), which indicated a strong match.

Table 5.
Significance analysis of multiple linear regression coefficients for the hydraulic performance of flow rate at H = 0.1 MPa (qIs0.1) and flow index (xs) with structural parameters.

Table 6.
Multiple linear regression model for the hydraulic performance of flow rate at H = 0.1 MPa (qIs0.1) and flow index (xs) with structural parameters.

Table 7.
Multivariate linear regression equation analysis of variance.
3.5. Optimization and Verification of the Flow Channel Structural Parameters Using the Ergodic Optimization Algorithm
The flow rate of the VFE in working stage I was determined by factors such as soil texture and crop water consumption. Based on the multiple linear regression model in Table 6, an ergodic optimization algorithm (EOA) was developed using Visual Studio 2019 (Microsoft Visual Studio, US) with the following constraints: 0.6 mm ≤ E ≤ 1.0 mm, ΔE = 0.1 mm; 1.8 mm ≤ B ≤ 2.2 mm, ΔB = 0.1 mm; 34° ≤ A ≤ 42°, ΔA = 1°; 0.6 mm ≤ D ≤ 1.0 mm, ΔD = 0.1 mm. The EOA calculated the optimal combination of flow channel structure parameters for qI0.1 values of 1.03, 1.5, and 2.0 L/h to meet the minimum x aim (Table 8). The relative errors between x using the multiple linear regression model and xs using the Fluent model were −0.7–0.3% for the three VFEs.

Table 8.
Optimal combination of flow channel structural parameters for different flow rates at H = 0.1 MPa (qI0.1).
After CNC processing, the dimensions of the flow channel structural parameters of the VFE with qI0.1 of 1.5 L/h (VFE-1.5) were measured with a 2.5-dimension image size measuring instrument (Table 9). After three measurements, it was found that the difference between the design size and the actual size was modest, and the relative error was 0.24–6.33%, indicating that CNC processing accuracy was high.

Table 9.
Comparison of the actual and design size of the flow channel structure of the processed variable flow emitter when the flow rate (qI0.1) was 1.5 L/h.
The flow rate (qIm) of VFE-1.5 was measured at H = 0.02–0.16 MPa, and compared with the qI predicted by the qI-H formula in Table 8 revealed that when H < 0.06 MPa, qIm was slightly smaller than qI, with a relative error of -6.31%–0.19%. When H ≥ 0.06 MPa, qIm was slightly larger than qI, and the relative error was 1.13%–4.40% (Table 10). For H = 0.02–0.16 Mpa, the nRMSE of qIm and qI was 6.76%, showing excellent agreement between them.

Table 10.
Relative error between the measured flow rate (qIm) and the predicted flow rate (qI) when qI0.1 was 1.5 L/h based on the formula in Table 8.
4. Discussion
4.1. Influence of Meshing and Turbulence Model on the Accuracy of Fluent Simulation on Flow Rate
At present, most numerical simulation studies related to the development of emitters only focus on the influence of turbulence model selection on simulation accuracy [67,68]. In this study, we simulate and analyze the simulation accuracy of three meshing models and five turbulence models on the flow rate and flow index of the variable flow emitter (VFE) in working stage I with the aid of Fluent software. Consistent with the study results by Jin et al. and Tian et al. [65,68], the simulation accuracy of tetrahedral meshing with a 6-layer boundary layer (TBL) and the realizable k–ε turbulence model was the highest in our study too. Feng et al. [69] believe that the RNG k–ε turbulence model is more suitable than the realizable k–ε model for simulating the flow field in a triangular channel when considering computational efficiency. The RNG k–ε and realizable k–ε turbulence models in this study can be used in the same grid partition. However, the nRMSE of the latter model was 1.4% lower than that of the former model; therefore, the realizable k–ε turbulence model is selected as the optimal model in this study.
4.2. Analysis of the Influence of Flow Channel Structural Parameters on the Hydraulic Performance of Variable Flow Emitters
The flow rates of nine VFEs were simulated using the TBL and realizable k–ε turbulence models, and the corresponding flow indexes were obtained. The order of influences of each test factor on the flow index, as determined by range analysis, was B > E > D > A. In previous research, it has been determined that D has little influence on the flow index [50,70]. In addition, no consistent conclusion has been reached regarding the flow channel structural parameters that have a significant influence on the flow index for different flow channel structure forms. Wang et al. and Cao et al. [52,58] believe that B has the greatest influence on the flow index for triangular flow channels. Hu et al. [50] believe E has the greatest influence on the flow index for trapezoidal flow channels. Therefore, in light of a new type of emitter, it is crucial to investigate the influence of the channel structure parameters on the flow index.
4.3. Construction of Regression Model for the Hydraulic Performance of a Variable Flow Emitter and Flow Channel Structure Optimization
We assessed a multiple linear regression model with a flow rate of H = 0.1 MPa (qI0.1), x, and flow channel structural parameters using the Fluent simulation results. To simplify the model, it was necessary to exclude factors that have an insignificant influence. Specifically, A (p = 0.76595) in the qI0.1 regression model and D (p = 0.96564) and A (p = 0.24303) in the x regression model. However, considering that A is one of the four structural parameters of the flow channel and that factor p = 0.32 was retained in the regression model in the work by Yang et al. [47], factor A was retained in the x regression model in the current study.
Currently, there are few research results pertaining to the joint solution of multiple linear regression models developed using emitter flow rate, flow index, and flow channel structure parameters. Based on the regression model and ergodic optimization algorithm (EOA), this study determines the optimal parameter combinations of the flow channel structure corresponding to the minimum x for varying qI0.1. For the VFE with qI0.1 = 1.5 L/h, the measured flow rate (qIm) in working stage I was initially slightly lower than the formula-based calculated flow rate (qI) and subsequently raised to a value slightly higher than qI with an increase in H. In order to ensure the tightness of the flow channel of the VFE in working stage I, the inner diameter of the cylindrical elastomer with small elasticity was kept slightly smaller than the outer diameter of the core body, and the elastomer would embed a small part of the flow channel, resulting in the actual size of the flow channel depth (Da) being less than that of design value (D), giving rise to the actual water flow channel section less than the designed section. qI was calculated using the Fluent simulation based on D, while qIm was obtained using the test based on Da causing qIm < qI when H < 0.6 MPa. When H ≥ 0.6 MPa, the Da would be larger than D owing to the small elasticity of the cylindrical elastomer; therefore, qIm > qI. When H was 0.02–0.16 MPa, the nRMSE of qIm and qI was less than 10%, indicating excellent agreement between them. Therefore, the accuracy of the method based on the regression model and EOA to determine the optimal combination of flow channel structural parameters with the minimum flow index was greater. This method can shorten the development time of new emitters.
For SDI, when the pump is turned off, the negative pressure generated in the pipe network system will suck the soil particles into the flow channel, causing the emitter to clog. Although the VEF can be self-cleaning at working stage II, it still needs to improve its anti-siphoning property by improving the structure.
5. Conclusions
Using an orthogonal experimental design and a combination of test and numerical simulation, the responses of the flow rate and flow index of the variable flow emitter (VFE) to the structural parameters of the flow channel in working stage I was investigated. An optimization method of flow channel structural parameters based on a multiple linear regression model and ergodic optimization algorithm (EOA) was constructed. The main conclusions were as follows:
- The combination of tetrahedral meshing with six-layer boundary layer TBL and the realizable k-ε turbulence model was suitable for the flow rate simulation of VFE using Fluent software.
- The results of the range analysis show that the order of influence of the flow channel structure factors on the flow rate was D > B > E > A, while the primary order of influence of the flow index was B > E > D > A.
- With the aim of minimizing the flow index, the optimal combination of the structural parameters of the flow channel corresponding to different flow rates was obtained on the basis of multiple linear regression modeling of the flow rate, flow index, and flow channel structural parameters, in conjunction with the EOA.
- A VFE with a flow rate of 1.5 L/h at H = 0.1 MPa was developed using CNC processing technology, and its hydraulic performance was tested. The nRMSE value of the measured flow rate and calculated flow rate using the formula was 6.76%, and the prediction accuracy of the model was high.
6. Patents
The contents of this research have been patented by our team, and the patent information is as follows: Yan, M.; Jiandong, W.; Yanqun, Z.; Qiaoling, L; Shihong, G.; Di, X.; Xiaoyan, G. Drip Irrigation Emitter and Drip Irrigation System. Chinese patent CN112205282B; Beijing, China, 2021.
Author Contributions
Conceptualization, Y.M.; methodology, N.G. and Y.M.; software, N.G.; validation, Y.M., L.Y. and S.G.; formal analysis, N.G., Y.M. and J.W.; investigation, N.G. and Y.M.; writing—original draft preparation, N.G.; writing—review and editing, Y.M. and L.Y.; funding acquisition, Y.M. and L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported the Research and Development Support Program of China Institute of Water Resources and Hydropower Research (ID0145B042021), the National Science Foundation of China (51909276 and 51979288), and the Agricultural Science and Technology Innovation Program (No 2021-2025).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| SDI | Subsurface drip irrigation |
| VFE | Variable flow emitter |
| EOA | Ergodic optimization algorithm |
| x | Flow index |
| qI | Flow rate at working stage I, (L·h−1) |
| qII | Flow rate at working stage II, (L·h−1) |
| k | Flow coefficient |
| H | Water pressure, (MPa) |
| HI | Water pressure at working stage I, (MPa) |
| HII | Water pressure at working stage II, (MPa) |
| PI | The pressure in the flow channel at working stage I |
| PII | The pressure in the flow channel at working stage II |
| E | Tooth height |
| B | Tooth spacing |
| A | Tooth Angle |
| D | Flow channel depth |
| Da | The actual size of the flow channel depth |
| TWBL | Tetrahedros meshing without boundary layer |
| TBL | Tetrahedros meshing with six-layer boundary layer |
| HEX | Hexahedral meshing |
| nRSME | Normalized root-mean-square error |
| Si | Observation value |
| Ei | Estimation value |
| n | The number of observed data |
| Eave | Average of the observed data |
| R2 | Coefficient of determination |
| qIm | Measured value of emitter flow rate |
| qIs | Simulation value of emitter flow rate based on ergodic optimization algorithm, (L·h−1) |
| qIs0.1 | Simulation value of emitter flow rate based on ergodic optimization algorithm under the pressure of 0.1MPa, (L·h−1) |
| xs | Simulation value of emitter flow index based on ergodic optimization algorithm |
| qI0.1 | Flow rate at working stage I when the flow index is minimum under the pressure of 0.1MPa, (L·h−1) |
References
- Cai, Y.; Wu, P.; Zhang, L.; Zhu, D.; Chen, J.; Wu, S.; Zhao, X. Simulation of soil water movement under subsurface irrigation with porous ceramic emitter. Agr. Water Manag. 2017, 192, 244–256. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, X.; Wu, P.; Zhang, L.; Zhu, D.; Chen, J.; Lin, L. Ceramic patch type subsurface drip irrigation line: Construction and hydraulic properties. Biosyst. Eng. 2019, 182, 29–37. [Google Scholar] [CrossRef]
- Wang, J.; Yang, T.; Wei, T.; Chen, R.; Yuan, S. Experimental determination of local head loss of non-coaxial emitters in thin-wall lay-flat polyethylene pipes. Biosyst. Eng. 2020, 190, 71–86. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, L.; Wu, P.; Cai, Y.; Zhao, X.; Yao, C. Hydraulic performance and parameter optimisation of a microporous ceramic emitter using computational fluid dynamics, artificial neural network and multi-objective genetic algorithm. Biosyst. Eng. 2020, 189, 11–23. [Google Scholar] [CrossRef]
- Petit, J.; Ait-Mouheb, N.; Mas García, S.; Metz, M.; Molle, B.; Bendoula, R. Potential of visible/near infrared spectroscopy coupled with chemometric methods for discriminating and estimating the thickness of clogging in drip-irrigation. Biosyst. Eng. 2021, 209, 246–255. [Google Scholar] [CrossRef]
- Roberts, T.L.; White, S.A.; Warrick, A.W.; Thompson, T.L. Tape depth and germination method influence patterns of salt accumulation with subsurface drip irrigation. Agr. Water Manag. 2008, 95, 669–677. [Google Scholar] [CrossRef]
- Huang, X.; Li, G. Present Situation and Development of Subsurface Drip Irrigation. Trans. CSAE 2002, 18, 176–181. [Google Scholar]
- Guo, S.; Mo, Y.; Wu, Z.; Wang, J.; Zhang, Y.; Gong, S.; Xu, M.; Guo, B.; Shen, X. Changes in Radiation in Canopy and the Yield of Maize in Response to Planting Density and Irrigation amountsThe Effects of Furrow Depth in Alternate Row Planting on Germination and Yield of Spring Maize under Subsurface Drip Irrigation in North China Plain. J. Irrig. Drain. 2021, 40, 27–34. [Google Scholar]
- Mo, Y.; Li, G.; Cai, M.; Wang, D.; Xu, X.; Bian, X. Selection of suitable technical parameters for alternate row/bed planting with high maize emergence under subsurface drip irrigation based on HYDRUS-2D model. Trans. Chin. Soc. Agric. Eng. 2017, 33, 105–112. [Google Scholar]
- Kandelous, M.M.; Šimůnek, J. Numerical simulations of water movement in a subsurface drip irrigation system under field and laboratory conditions using HYDRUS-2D. Agr. Water Manag. 2010, 97, 1070–1076. [Google Scholar] [CrossRef]
- Lamm, F.R.; Trooien, T.P. Dripline depth effects on corn production when crop establishment is nonlimiting. Appl. Eng. Agric. 2005, 21, 835–840. [Google Scholar] [CrossRef]
- Lamm, F.R.; Abou Kheira, A.A.; Trooien, T.P. Sunflower, soybean, and grain sorghum crop production as affected by dripline depth. Appl. Eng. Agric. 2010, 26, 873–882. [Google Scholar] [CrossRef]
- Mo, Y.; Li, G.; Wang, D.; Lamm, F.R.; Wang, J.; Zhang, Y.; Cai, M.; Gong, S. Planting and preemergence irrigation procedures to enhance germination of subsurface drip irrigated corn. Agr. Water Manag. 2020, 242, 106412. [Google Scholar] [CrossRef]
- Mo, Y.; Li, G.; Wang, D. A sowing method for subsurface drip irrigation that increases the emergence rate, yield, and water use efficiency in spring corn. Agr. Water Manag. 2017, 179, 288–295. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, B.; Yang, P. Research advances in drip irrigation emitter clogging mechanism and controlling methods. J. Hydraul. Eng. 2018, 49, 103–114. [Google Scholar]
- Wu, F.; Zai, S.; Xu, J.; Wang, H. Application Modes and Inspiration of Subsurface Drip Irrigation. J. North China Univ. Water Resour. Electr. Power Nat. Sci. Ed. 2016, 37, 19–22. [Google Scholar]
- Xi, B.; Wang, P.; Fu, T.; Zhang, W. Optimal coupling combinations among discharge rate, lateral depth and irrigation frequency for subsurface drip-irrigated triploid Populus tomentosa pulp plantation. Life Sci. J. 2013, 10, 4466–4476. [Google Scholar]
- Li, H. Experiments and Numerical Simulations of Soil-Water Movement in Subsurface Drip Irrigation. Master’s Thesis, Wuhan University, Wuhan, China, 2005. [Google Scholar]
- Sun, L.; Luo, J.; Li, X. Effects of Dripper Discharge on Soil-water Movement under Subsurface Drip Irrigation. Water Sav. Irrig. 2012, 41–44. [Google Scholar]
- Zhang, K. Influence of Water Movement in Soil under Micro-Irrigation by Using Numerical Simulation. Master’s Thesis, Northwest A&F University, Yanglin, China, 2015. [Google Scholar]
- Ma, X.G.; Shen, Z.Z.; Zhang, W.J.; Wei, J.S.; Jie, R. Experimental study of wetted soil volumes in a sandy loam under subsurface drip irrigation in the East Sandy Land of the Yellow River. J. Food Agric. Environ. 2013, 11, 987–992. [Google Scholar]
- Al-Mefleh, N.K.; Abu-Zreig, M. Field evaluation of arid soils wetting pattern in subsurface drip irrigation scheme. CLEAN Soil Air Water 2013, 41, 651–656. [Google Scholar] [CrossRef]
- Li, J.; Yang, F.; Li, Y. Water and nitrogen distribution under subsurface drip fertigation as affected by layered-textural soils. Trans. Chin. Soc. Agric. Eng. 2009, 25, 25–31. [Google Scholar]
- Wang, C. The Experiment Research on the Soil Moisture Dynamic Change of Soil Water Movement under Subsurface Drip Irrigation. Master’s Thesis, Northwest A&F University, Yanglin, China, 2011. [Google Scholar]
- Sun, Z.; Huang, L.; Yang, P.; Qiu, L.; Zhang, Y. Effect of lower irrigation limit anf emitter flow on winter wheat growth under subsurface drip irrigation. J. Agric. Univ. 2019, 24, 41–50. [Google Scholar]
- Li, J.; Yang, F.; Liu, Y.; Yan, L. Performance of low-discharge emitters buried in soil as affected by layered-textural soils. Trans. CSAE 2009, 25, 1–6. [Google Scholar]
- Wang, X.; Bai, D.; Li, Z.; Li, G. Influence of soilphysical properties on emitter discharge of subsurface drip irrigation. J. Arid Land Resour. Environ. 2009, 23, 126–129. [Google Scholar]
- Li, G.; Bai, D.; Wang, X.; Fu, J. Effect of Different Textural Soils on Hydraulic Characteristics of Emitters under Subsurface Drip Irrigation. Trans. Chin. Soc. Agric. Mach. 2009, 40, 58–62. [Google Scholar]
- Baiamonte, G. Advances in designing drip irrigation laterals. Agr. Water Manag. 2018, 199, 157–174. [Google Scholar] [CrossRef]
- Yıldırım, G.; Agıralioglu, N. Linear Solution for Hydraulic Analysis of Tapered Microirrigation Laterals. J. Irrig. Drain. Eng. 2004, 130, 78–87. [Google Scholar] [CrossRef]
- Li, Y.K.; Yang, P.L.; Xu, T.W.; Liu, H.L.; Liu, H.S.; Xu, F.P. Hydraulic property and flow characteristics of three labyronth flow patns of drip irrigation emitters under micro-pressure. Trans. ASABE 2009, 4, 1129–1138. [Google Scholar]
- Zhang, J.; Zhao, W.; Tang, Y.; Lu, B. Anti-clogging performance evaluation and parameterized design of emitters with labyrinth channels. Comput. Electron. Agr. 2010, 74, 59–65. [Google Scholar] [CrossRef]
- Camp, C.R. Subsurface drip irrigation: A review. Trans. ASAE 1998, 41, 1353–1367. [Google Scholar] [CrossRef]
- Nakayama, F.S.U.W.; Bucks, D.A. Water quality in drip/trickle irrigation: A review. Irrig. Sci. 1991, 12, 187–192. [Google Scholar] [CrossRef]
- Zhang, W.; Niu, W.; Li, G.; Wang, J.; Wang, Y.; Dong, A. Lateral inner environment changes and effects on emitter clogging risk for different irrigation times. Agr. Water Manag. 2020, 233, 106069. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Zhang, Y.; Wang, H.; Ma, X.; Mo, Y. Anti-clogging performance optimization for dentiform labyrinth emitters. Irrig. Sci. 2020, 38, 275–285. [Google Scholar] [CrossRef]
- Wei, Q.; Shi, Y.; Dong, W.; Lu, G.; Huang, S. Study on hydraulic performance of drip emitters by computational fluid dynamics. Agr. Water Manag. 2006, 84, 130–136. [Google Scholar] [CrossRef]
- Kang, M.; Li, Z.; Xu, T.; Wang, Z. Numerical Simulation of Double Inner Teeth Rectangular Labyrinth Channel Emitter Based on Orthogonal Test. Yellow River 2019, 41, 156–160. [Google Scholar]
- Xu, T.; Zhang, L. Hydraulic performance and energy dissipation effect of pit structure flow channel emitter. IFAC Pap. 2019, 52, 143–148. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Qiu, X.; Wang, J. Modeling of hydraulic characteristics through labyrinth emitterin drip irrigation using computational fluid dynamics. Trans. CSAE 2005, 21, 12–16. [Google Scholar]
- Wei, Z.; Zhao, W.; Tang, Y.; Lu, B.; Zhang, M. Anti-clogging design method for the labyrinth channels of drip irrigation emitters. Trans. CSAE 2005, 21, 1–7. [Google Scholar]
- Chen, X.; Wei, Z.; Wei, C.; He, K. Effect of compensation chamber structure on the hydraulic performance of pressure compensating drip emitters. Biosyst. Eng. 2022, 214, 107–121. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, F.; Peng, G.; Fan, Y.; Li, J. Experimental Research on Dissipating Process in the Interior of Labyrinth Emitter. J. Irrig. Drain. 2008, 27, 39–42. [Google Scholar]
- Li, Y.; Yang, P.; Xu, T.; Ren, S.; Lin, X.; Wei, R.; Xu, H. CFD and digital particle tracking to assess flow characteristics in the labyrinth flow path of a drip irrigation emitter. Irrig. Sci. 2008, 26, 427–438. [Google Scholar] [CrossRef]
- Paxson, G.; Savage, B. Labyrinth Spillways: Comparison of Two Popular USA Design Methods and Consideration of Non-Standard Approach Conditions and Geometries; International Junior Researcher and Engineer Workshop on Hydraulic Structures; Division of Civil Engineering, University of Brisbane: Queensland, BNE, Australia, 2006; pp. 37–46. [Google Scholar]
- Zhang, L.; Li, S. Numerical Experimental Investigation of Douche Hydraulic Performance on Drop Irrigation of Tooyh-Type Labyrintn Channel. Water Resour. Power 2017, 35, 103–106. [Google Scholar]
- Yang, B.; Zhang, G.; Wang, J.; Gong, S.; Wang, H.; Mo, Y. Numerical Simulation of Hydraulic Performance of Tooth-form Channel of Labyrinth Emitter. J. Irrig. Drain. 2019, 38, 71–76. [Google Scholar]
- Wang, J.; Gong, S.; Li, G.; Zhao, Y. The influence of geometrical parameters of dental flow passage of labyrinth emitter on the hydraulic performance under low working pressure. J. Hydraul. Eng. 2014, 45, 72–78. [Google Scholar]
- Zhang, J.; Hong, J.; Zhao, W.; Lu, B. Parameterized Design of Labyrinth-Channel Emitters Based on Orthogonal Experiments. J. Xi’an Jiaotong Univ. 2006, 40, 31–35. [Google Scholar]
- Hu, Y.; Peng, J.; Yin, F.; Liu, X.; Li, N. Optimization of trapezoidal labyrinth emitter channel based on MATLAB and COMSOL co-simulation. Trans. Chin. Soc. Agric. Eng. 2020, 36, 158–164. [Google Scholar]
- Guo, L.; Bai, D.; Cheng, P.; Zhou, W. Optimization design of triangular labyrinth channel in drip irrigation emitter. J. Drain. Irrig. Mach. Eng. 2015, 33, 634–639. [Google Scholar]
- Cao, L. Study on Hydraulic Performance of Buried Labyrinth Dropper. Master’s Thesis, HeBei Agricultural University, Baoding, China, 2019. [Google Scholar]
- Seyedzadeh, A.; Maroufpoor, S.; Maroufpoor, E.; Shiri, J.; Bozorg-Haddad, O.; Gavazi, F. Artificial intelligence approach to estimate discharge of drip tape irrigation based on temperature and pressure. Agr. Water Manag. 2020, 228, 105905. [Google Scholar] [CrossRef]
- Mattar, M.A.; Alamoud, A.I. Gene expression programming approach for modeling the hydraulic performance of labyrinth-channel emitters. Comput. Electron. Agr. 2017, 142, 450–460. [Google Scholar] [CrossRef]
- Mo, Y.; Zhao, X.; Wang, J.; Zhang, Y.; Gong, S.; Xia, H.; Li, Q.; Wang, Y. Design and structural optimization of the automatic flushing valve with exhaust function. Trans. Chin. Soc. Agric. Eng. 2022, 38, 72–79. [Google Scholar]
- Li, Y.; Yang, P.; Ren, S.; Xu, T. Hydraulic Characterizations of Tortuous Flow in Path Drip Irrigation Emitter. J. Hydrodyn. Ser. B 2006, 18, 449–457. [Google Scholar] [CrossRef]
- Yu, L.; Wu, P.; Niu, W. Influence of the Offset of Labyrinth Channels of Drip Emitters on Hydraulic and Anti-clogging Performance. Trans. Chin. Soc. Agric. Mach. 2011, 42, 64–73. [Google Scholar]
- Wang, J. Experiment and Numerical Simulation of Hydraulic Performance on Emitter of Dripline. Master’s Thesis, Tianjin Agricultural University, Tianjin, China, 2020. [Google Scholar]
- Bannayan, M.; Hoogenboom, G. Using pattern recognition for estimating cultivar coefficients of a crop simulation model. Field Crop Res. 2009, 111, 290–302. [Google Scholar] [CrossRef]
- Dettori, M.; Cesaraccio, C.; Motroni, A.; Spano, D.; Duce, P. Using CERES-Wheat to simulate durum wheat production and phenology in Southern Sardinia, Italy. Field Crop Res. 2011, 120, 179–188. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Yang, B.; Mo, Y.; Zhang, Y.; Ma, X. Simulation and Optimization of Venturi Injector by Machine Learning Algorithms. J. Irrig. Drain. Eng. 2020, 146, 04020021. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Y.; Shi, K. Research on the Parametric Design of Improved Bidirectional Drip Irrigation Emitter. China Rural. Water Hydropower 2020, 108–112. [Google Scholar]
- Zhuang, C.; He, C. Fundamentals of Applied Mathematical Statistics, 4th ed.; South China University of Technology Press: Guangzhou, China, 2013; p. 436. [Google Scholar]
- Wang, W.; Wang, F.; Yan, H. Study on CFD Method for Flow Simulation in Labyrinth Emitter. Trans. Chin. Soc. Agric. Mach. 2006, 37, 70–73. [Google Scholar]
- Tian, J.; Bai, D.; Yu, F.; Wang, X.; Guo, L. Numerical simulation of hydraulic performance on bidirectional flow channel of drip irrigation emitter using Fluent. Trans. Chin. Soc. Agric. Eng. 2014, 30, 65–71. [Google Scholar]
- Zheng, G.; Ma, J.; He, S.; Zhou, J.; Li, Y.; Liu, Y. The Effect of Low Pressure on the Hydraulic Technical Performance of Different Emitters. Water Sav. Irrig. 2021, 74–77. [Google Scholar]
- Nie, L.; Shi, Y.; Wei, Q.; Lu, G.; Dong, W. Research on Adaptability of Different Turbulent Models Based on Flow Discharge of the Drip Emitters. Water Sav. Irrig. 2008, 13–17. [Google Scholar]
- Jin, W.; Zhang, H. Numerical Simulating Approaches and Experiment on Micro-scales Flow Field. Trans. Chin. Soc. Agric. Mach. 2010, 41, 67–71. [Google Scholar]
- Feng, J.; Li, Y.; Wang, W.; Xue, S. Effect of optimization forms of flow path on emitter hydraulic and anti-clogging performance in drip irrigation system. Irrig. Sci. 2018, 36, 37–47. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Shan, B.; Wang, G. Structural Design and Optimization of Triangle Circulation Drip Irrigation Emitters. Trans. Chin. Soc. Agric. Mach. 2010, 41, 43–46. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).


