Winter Wheat Cultivar Recommendation Based on Expected Environment Productivity
Abstract
1. Introduction
2. Materials and Methods
2.1. Yield Dataset and Environmental Variables
2.2. Statistical Analyses
2.2.1. Adjustment of Mean Yield of Cultivars in Different Environmental Conditions
2.2.2. Assessment of the Impact of Environmental Conditions on Yield
DLjl + c15 × DL2+ c16 × HTC1,jl 2 + c26 × HTC11,jl2 + ejkl
2.2.3. Calculation of Cultivar Yield in Relation to the Average Yield in a Given Environment
2.2.4. Cultivar Recommendation and Comparison with the COBORU Recommendation
2.2.5. Method Validation
- (1)
- Ranking of cultivars calculated for environments with productivity 7 t/ha, obtained based on the data from the years 2015–2019, denoted R7 (2015–2019);
- (2)
- Ranking of cultivars calculated for environments with productivity 10 t/ha, obtained based on the data from the years 2015–2019, R10 (2015–2019);
- (3)
- Ranking of cultivars calculated for environments with productivity 7 t/ha, obtained based on the data from the year 2018 [11], R7 (2018);
- (4)
- Ranking of cultivars calculated for environments with productivity 10 t/ha, obtained based on the data from the year 2018 [11], R10 (2018);
- (5)
- Ranking of cultivars based on the recommendation of COBORU, R (COBORU).
3. Results
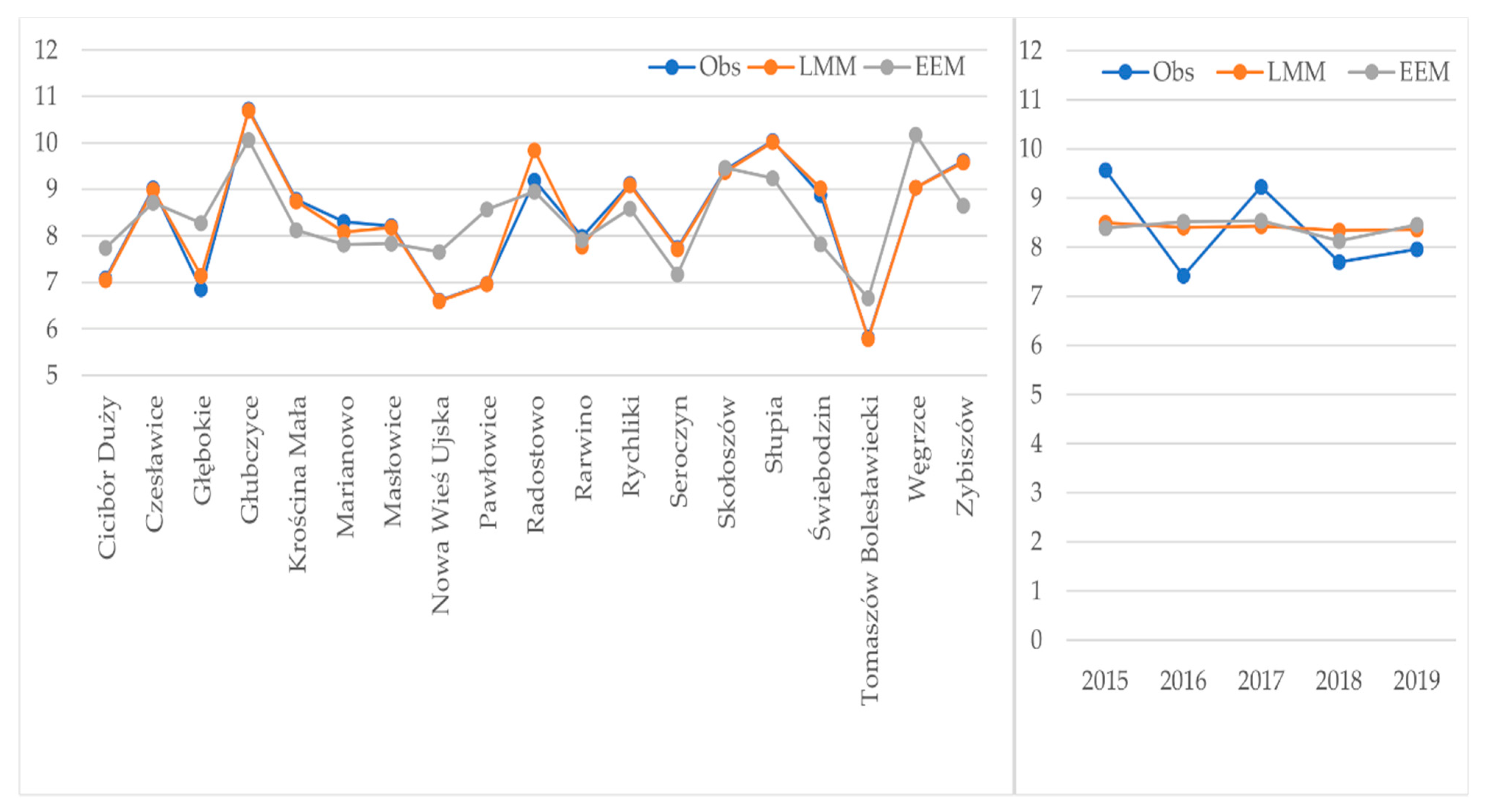
3.1. Average Yield per Trial Locations: Observed, Adjusted Using Linear Mixed Model and Estimated Using the Explanatory Environmental Model (EEM)
3.2. Assessment of the Impact of Environmental Conditions on Yield
3.3. Cultivar Recommendation
3.4. Method Validation and Comparison COBORU Recommendation
4. Discussion
4.1. Average Yield in Trial Locations: Observed, Adjusted Using Linear Mixed Model and Assessed Using Explanatory Environmental Model
4.2. Assessment of the Impact of Environmental Conditions on Yield
4.3. Cultivar Recommendation
4.4. Method Validation and Comparison with the COBORU Recommendation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brockerhoff, H. LSV Winterweizensorten—Mehrjährige Ertragsleistung. 2020. Available online: https://www.landwirtschaftskammer.de/landwirtschaft/ackerbau/pdf/tabellen-winterweizen-sv-2020.pdf (accessed on 18 August 2020).
- AHDB Recommended Lists for Cereals and Oilseeds 2020/21 Summer Edition. Available online: https://projectblue.blob.core.windows.net/media/Default/Imported%20Publication%20Docs/AHDB%20Cereals%20&%20Oilseeds/Varieties/RL2020-21/AHDB%20Recommended%20Lists%20for%20cereals%20and%20oilseeds%202020-21%20(summer%20edition).pdf (accessed on 18 August 2020).
- Department of Agriculture, Food and the Marine. 2020. Winter Cereal Recommended Lists 2020. Available online: https://www.agriculture.gov.ie/media/migration/publications/2019/1WinterCerealRecommendedLists160919.pdf (accessed on 18 August 2020).
- COBORU. Listy Odmian Zalecanych do Uprawy na Obszarze Województw 2020 (Lists of Varieties Recommended for Cultivation on the Territory of the Voivodeship in 2020, in Polish). Available online: https://coboru.gov.pl/Publikacje_COBORU/LOZ/LOZ_2020.pdf (accessed on 12 August 2020).
- AHDB. Variety Selection Tool for Cereals and Oilseeds. Available online: https://ahdb.org.uk/vst (accessed on 18 August 2020).
- Sortenberatung, N.R.W. Available online: http://www.sortenberatung.de/ (accessed on 18 August 2020).
- Gozdowski, D.; Stępień, M.; Samborski, S.; Dobers, E.S.; Szatyłowicz, J.; Chormański, J. Determination of the most relevant soil properties for the delineation of management zones in production fields. Commun. Soil Sci. Plant Anal. 2014, 45, 2289–2304. [Google Scholar] [CrossRef]
- Barbanti, L.; Adroher, J.; Damian, J.M.; Di Virgilio, N.; Falsone, G.; Zucchelli, M.; Martelli, R. Assessing wheat spatial variation based on proximal and remote spectral vegetation indices and soil properties. Ital. J. Agron. 2018, 13, 21–30. [Google Scholar] [CrossRef]
- Carew, R.; Smith, E.G.; Grant, C. Factors influencing wheat yield and variability: Evidence from Manitoba, Canada. J. Agric. Appl. Econ. 2009, 41, 625–639. [Google Scholar] [CrossRef]
- Babushkina, E.A.; Belokopytova, L.V.; Zhirnova, D.F.; Shah, S.K.; Kostyakova, T.V. Climatically driven yield variability of major crops in Khakassia (South Siberia). Int. J. Biometeorol. 2018, 62, 939–948. [Google Scholar] [CrossRef]
- Iwańska, M.; Paderewski, J.; Stępień, M.; Rodrigues, P.C. Adaptation of Winter Wheat Cultivars to Different Environments: A Case Study in Poland. Agronomy 2020, 10, 632. [Google Scholar] [CrossRef]
- Senapati, N.; Griffiths, S.; Hawkesford, M.; Shewry, P.R.; Semenov, M.A. Substantial increase in yield predicted by wheat ideotypes for Europe under future climate. Clim. Res. 2020, 80, 189–201. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Drivers of within-field spatial and temporal variability of crop yield across the US Midwest. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Zhang, Q.; Sun, P.; Song, C. Impact of Droughts on Winter Wheat Yield in Different Growth Stages during 2001–2016 in Eastern China. Int. J. Disaster Risk Sci. 2018, 9, 376–391. [Google Scholar] [CrossRef]
- Iwańska, M.; Stępień, M. The effect of soil and weather conditions on yields of winter wheat in multi-environmental trials. Biom. Lett. 2019, 56, 263–279. [Google Scholar] [CrossRef]
- Hanson, A.D.; Nelsen, C.E. Water: Adaptation of crops to drought-prone environments. In The Biology of Crop Productivity; Carlson, P.S., Ed.; Academic Press: New York, NY, USA, 1980; pp. 77–152. [Google Scholar]
- Senapati, N.; Stratonovitch, P.; Paul, M.J.; Semenov, M.A. Drought tolerance during reproductive development is important for increasing wheat yield potential under climate change in Europe. J. Exp. Bot. 2019, 70, 2549–2560. [Google Scholar] [CrossRef] [PubMed]
- Kristensen, K.; Schelde, K.; Olesen, K.E. Winter wheat field response to climate variability in Denmark. J. Appl. Sci. 2011, 149, 33–47. [Google Scholar]
- Selyaninov, G.T. Methods of climate description to agricultural purposes. In World Climate and Agriculture Handbook; Selyaninov, G.T., Ed.; Gidrometeoizdat: Leningrad, Russia, 1937; pp. 5–27. [Google Scholar]
- Rubel, F.; Kottek, M. Observed and projected climate shifts 1901–2100 depicted by world maps of the Köppen-Geiger climate classification. Meteorol. Z. 2010, 19, 135–141. [Google Scholar] [CrossRef]
- Mądry, W.; Paderewski, J.; Gozdowski, D.; Rozbicki, J.; Golba, J.; Piechociński, M.; Studnicki, M.; Derejko, A. Adaptation of winter wheat cultivars to crop managements and polish agricultural environments. Turk. J. Field Crop. 2013, 8, 118–127. [Google Scholar]
- Studnicki, M.; Derejko, A.; Wójcik–Gront, E.; Kosma, M. Adaptation patterns of winter wheat cultivars in agro–ecological regions. Sci. Agric. 2019, 76, 148–156. [Google Scholar] [CrossRef]
- Paderewski, J.; Rodrigues, P.C. The usefulness of EM-AMMI to study the influence of missing data pattern and application to Polish post-registration winter wheat data. Aust. J. Crop Sci. 2014, 8, 640. [Google Scholar]
- Studnicki, M.; Paderewski, J.; Piepho, H.P.; Wójcik-Gront, E. Prediction accuracy and consistency in cultivar ranking for factor-analytic linear mixed models for winter wheat multienvironmental trials. Crop Sci. 2017, 57, 2506–2516. [Google Scholar] [CrossRef]
- Aguate, F.; Crossa, J.; Balzarini, M. Effect of Missing Values on Variance Component Estimates in Multienvironment Trials. Crop Sci. 2019, 59, 508–517. [Google Scholar] [CrossRef]
- Iwańska, M.; Stępień, M. The effect of soil and course of weather conditions during the growth and maturation of winter wheat on yields in multi-environmental trials. In Proceedings of the XLIXth International Biometrical Colloquium, Siedlce, Poland, 8–12 September 2019. [Google Scholar] [CrossRef]
- Witek, T.; Górski, T.; Kern, H.; Bartoszewski, Z.; Biesiadzki, A.; Budzyńska, K.; Demidowicz, G.; Deputat, T.; Flaczyk, Z.; Gałecki, Z.; et al. Waloryzacja Rolniczej Przestrzeni Produkcyjnej Polski wg Gmin (Valorization of Productive Agricultural Area of Poland in Districts, in Polish); IUNG: Puławy, Poland, 1981; pp. 1–416. [Google Scholar]
- Skowera, B.; Puła, J. Skrajne warunki pluwiotermiczne w okresie wiosennym na obszarze Polski w latach 1971–2000 (Pluviometric extreme conditions in spring season in Poland in the years 1971–2000, in Polish). Acta Agrophys. 2004, 3, 171–177. [Google Scholar]
- Szewrański, S.; Kazak, J.; Żmuda, R.; Wawer, R. Indicator-based assessment for soil resource management in the Wrocław larger urban zone of Poland. Pol. J. Environ. Stud. 2017, 26, 2239–2248. [Google Scholar] [CrossRef]
- Adomski, C. Agrometeorologia; PWRiL: Warsaw, Poland, 1987; pp. 1–544. [Google Scholar]
- Jadczyszyn, J.; Niedźwiecki, J.; Debaene, G. Analysis of agronomic categories in different soil texture classification systems. Pol. J. Soil Sci. 2016, 49, 61–72. [Google Scholar] [CrossRef]
- Zadoks, J.C.; Chang, T.T.; Konzak, C.F. A decimal code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar] [CrossRef]
- Meier, U. Growth Stages of Plants—Entwicklungsstadien von Pflanzen—Estadios de las Plantas—Dévelopement des Plantes; Blackwell Wissenschaftsverlag, BBCH-Monograph: Berlin, Germany; Wien, NY, USA, 1997; pp. 1–158. [Google Scholar]
- Økland, R.H. On the variation explained by ordinationand constrained ordination axes. J. Veg. Sci. 1999, 10, 131–136. [Google Scholar] [CrossRef]
- Amenta, P.; D’Ambra, L. Constrained principal component analysis with external information. Stat. Appl. 2000, 12, 7–29. [Google Scholar]
- Paderewski, J.; Rodrigues, P.C. Constrained AMMI Model: Application to Polish Winter Wheat Post-Registration Data. Crop Sci. 2018, 58, 1458–1469. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, 2–8 September 1971; Petrov, B.N., Csáki, F., Eds.; Springer: New York, NY, USA, 1992; pp. 610–624. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Harrell, F.E. Regression Modeling Strategies; Springer: New York, NY, USA, 2001. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R–project.org/ (accessed on 15 July 2020).
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Soft. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Soft. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Piepho, H.P. Empirical best linear unbiased prediction in cultivar trials using factor-analytic variance-covariance structures. Theor. Appl. Genet. 1998, 97, 195–201. [Google Scholar] [CrossRef]
- Rozbicki, J.; Gozdowski, D.; Studnicki, M.; Mądry, W.; Golba, J.; Sobczyński, G.; Wijata, M. Management intensity effects on grain yield and its quality traits of winter wheat cultivars in different environments in Poland. Biotechnology 2019, 22, 2. Available online: http://www.ejpau.media.pl/volume22/issue1/art–01.html (accessed on 24 October 2019). [CrossRef]
- Fotyma, M.; Zięba, S. Przyrodnicze i Gospodarcze Podstawy Wapnowania Gleb (Natural and Economic Base of Soil Liming, in Polish); PWRiL: Warszawa, Poland, 1988; pp. 1–251. [Google Scholar]
- Schnug, E.; Heym, J.; Achwan, F. Establishing critical values for soil and plant analysis by means of the boundary line development system (Bolides). Commun. Soil Sci. Plant Anal. 1996, 27, 2739–2748. [Google Scholar] [CrossRef]
- Farhoodi, A.; Coventry, D.R. Field crop responses to lime in mid–north region of South Australia. Field Crop. Res. 2008, 108, 45–53. [Google Scholar] [CrossRef]
- Miller, L. Summary of Yield Responses from Liming. 2017. Available online: http://www.sfs.org.au/Liming%20and%20soil%20acidity%20article/2017%20Results%20Book%20Summary%20Yield%20Responses%20from%20liming.pdf (accessed on 30 October 2019).
- Musgrave, M.E. Waterlogging effects on yield and photosynthesis in eight winter wheat cultivars. Crop Sci. 1994, 34, 1314–1318. [Google Scholar] [CrossRef]
- Ding, J.; Liang, P.; Wu, P.; Zhu, M.; Li, C.; Zhu, X.; Guo, W. Identifying the Critical Stage near Anthesis for Waterlogging on Wheat Yield and Its Components in the Yangtze River Basin, China. Agronomy 2020, 10, 130. [Google Scholar] [CrossRef]
- GUS. Production of Agricultural and Horticultural Crops in 2019. Available online: https://stat.gov.pl/download/gfx/portalinformacyjny/en/defaultaktualnosci/3332/2/4/1/produkcja_upraw_rolnych_i_ogrodniczych_w_2019_r..pdf (accessed on 18 August 2020).

| Variable Name | Unit | Description and Interpretation | Number per Location and Cropping Season | Source |
|---|---|---|---|---|
| Air temperature (T) | °C | Mean air temperature in 10-day period from the first period in April to the second period in July | 11 | COBORU |
| Precipitation (P) | mm | Sum of rainfall in 10-day period from the first period in April to the second period in July | 11 | |
| Selyaninov Hydrothermal coefficient (HTC) | 10 mm/°C | HTC = 10 × ƩP/ƩT | 11 | Skowera and Puła [28], simplified (calculation based on COBORU data) |
| Climatic water balance (CWB) | mm | The difference between the precipitations and the potential evapotranspiration for a total period of 60 days, reported every 10 days | 5 | ADMS for the district in which the experiment is located |
| Drought length (DL) | 10-day period | The number of ADMS reports indicating the threat of drought between 1 April and 10 July 2015–2019 as according to the ADMS website adjusted to agronomic category | 1 | |
| Arable land suitability group (LS) | points | Arable land suitability for each trial location. The full scale ranges from 18 to 94 points, with higher values for better, more wheat-suitable soils [29] | 1 | COBORU |
| Soil pH | unitless | Measured in 1 M KCl extract | 1 |
| Variable | Coefficients b | Sum of Squares b | d.f. | F-Ratio | p-Value |
|---|---|---|---|---|---|
| Intercept (m*) | 6.110 | 27.911 | 1 | 15.524 | <0.001 *** |
| Mk (MIM_HIM) | −0.501 | 46.111 | 1 | 25.646 | <0.001 *** |
| LS | 0.079 | 116.054 | 1 | 64.547 | <0.001 *** |
| Soil pH | −0.585 | 9.990 | 1 | 5.556 | 0.0196 * |
| DL | 0.520 | 4.008 | 1 | 2.229 | 0.1373 |
| DL2 | −0.186 | 7.979 | 1 | 4.438 | 0.0366 * |
| HTCApril_1_dec | 0.006 | 4.401 | 1 | 2.448 | 0.1196 |
| HTCApril_2_dec2 | 0.143 | 6.029 | 1 | 3.353 | 0.0688 (.) |
| HTCMay_1_dec | −0.157 | 5.571 | 1 | 3.099 | 0.0802 (.) |
| HTCMay_3_dec | 0.283 | 7.298 | 1 | 4.059 | 0.0455 * |
| HTCMay_3_dec2 | −0.025 | 5.193 | 1 | 2.888 | 0.0911 (.) |
| HTCJune_1_dec2 | 0.098 | 8.195 | 1 | 4.558 | 0.0342 * |
| HTCJune_2_dec | 0.180 | 3.390 | 1 | 1.885 | 0.1716 |
| HTCJuly_1_dec | −0.806 | 9.839 | 1 | 5.472 | 0.0205 * |
| HTCJuly_1_dec2 | 0.166 | 8.455 | 1 | 4.703 | 0.0315 * |
| Residuals | 302.062 | 168 |
| Cultivar | Mean Winter Wheat Productivity Level t/ha | Adaptation (Yield Range, t/ha) ** | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 7 | 8 | 9 | 10 | 11 | ||||||||
| Yecv | Rank | Yecv | Rank | Yecv | Rank | Yecv | Rank | Yecv | Rank | Yecv | Rank | ||
| Rotax | 6.60 | (1) | 7.55 | (1) | 8.49 | (1) | 9.44 | (5) | 10.38 | (8) | 11.33 | (13) | w ** |
| Artist | 6.49 | (2) | 7.48 | (2) | 8.46 | (2) | 9.45 | (3) | 10.44 | (4) | 11.43 | (5) | w |
| Hybery | 6.47 | (3) | 7.46 | (3) | 8.45 | (3) | 9.44 | (4) | 10.43 | (6) | 11.42 | (6) | w |
| SY Orofino | 6.46 | (4) | 7.43 | (4) | 8.41 | (8) | 9.38 | (11) | 10.36 | (11) | 11.34 | (11) | w |
| Kredo | 6.45 | (5) | 7.43 | (5) | 8.41 | (9) | 9.39 | (10) | 10.37 | (10) | 11.34 | (9) | w |
| Viborg | 6.44 | (6) | 7.42 | (7) | 8.41 | (7) | 9.39 | (9) | 10.38 | (9) | 11.37 | (8) | w |
| Sikorka | 6.42 | (7) | 7.43 | (6) | 8.43 | (5) | 9.44 | (6) | 10.44 | (5) | 11.44 | (4) | w |
| Linus | 6.41 | (8) | 7.40 | (9) | 8.40 | (10) | 9.39 | (7) | 10.39 | (7) | 11.39 | (7) | w |
| Błyskawica | 6.39 | (9) | 7.42 | (8) | 8.44 | (4) | 9.47 | (1) | 10.49 | (1) | 11.52 | (3) | w |
| KWS Kiran | 6.37 | (10) | 7.34 | (12) | 8.31 | (13) | 9.28 | (15) | 10.25 | (18) | 11.22 | (22) | n (6–10) |
| RGT Bilanz | 6.36 | (11) | 7.39 | (10) | 8.42 | (6) | 9.46 | (2) | 10.49 | (2) | 11.52 | (2) | w |
| Euforia | 6.35 | (12) | 7.35 | (11) | 8.34 | (11) | 9.34 | (12) | 10.33 | (12) | 11.33 | (14) | w |
| Franz | 6.34 | (13) | 7.31 | (13) | 8.28 | (14) | 9.26 | (18) | 10.23 | (22) | 11.21 | (23) | n (6–9) |
| KWS Dakotana | 6.30 | (14) | 7.25 | (18) | 8.20 | (24) | 9.15 | (25) | 10.10 | (26) | 11.05 | (26) | n (6–7) |
| Mirek | 6.30 | (15) | 7.26 | (16) | 8.22 | (23) | 9.17 | (24) | 10.13 | (25) | 11.09 | (25) | n (6–7) |
| Oxal | 6.26 | (16) | 7.25 | (20) | 8.23 | (22) | 9.22 | (22) | 10.21 | (23) | 11.20 | (24) | n (6–7) |
| RGT Kilimanjaro | 6.26 | (17) | 7.25 | (17) | 8.25 | (17) | 9.25 | (20) | 10.24 | (21) | 11.24 | (21) | n (6–9) |
| Apostel | 6.25 | (18) | 7.27 | (14) | 8.28 | (15) | 9.30 | (13) | 10.32 | (14) | 11.33 | (12) | w |
| Bonanza | 6.25 | (19) | 7.19 | (25) | 8.12 | (25) | 9.06 | (27) | 10.00 | (27) | 10.94 | (27) | n (6) |
| Sfera | 6.25 | (20) | 7.25 | (19) | 8.25 | (19) | 9.25 | (19) | 10.25 | (19) | 11.25 | (19) | w |
| Plejada | 6.24 | (21) | 7.24 | (22) | 8.24 | (20) | 9.25 | (21) | 10.25 | (20) | 11.25 | (20) | n (10–11) |
| Tobak | 6.22 | (22) | 7.25 | (21) | 8.27 | (16) | 9.29 | (14) | 10.32 | (13) | 11.34 | (10) | n (8–11) |
| Opcja | 6.21 | (23) | 7.23 | (23) | 8.25 | (18) | 9.27 | (16) | 10.29 | (15) | 11.31 | (18) | n (8–11) |
| Frisky | 6.20 | (24) | 7.27 | (15) | 8.33 | (12) | 9.39 | (8) | 10.46 | (3) | 11.52 | (1) | n (7–11) |
| Rivero | 6.18 | (25) | 7.21 | (24) | 8.24 | (21) | 9.26 | (17) | 10.29 | (16) | 11.32 | (17) | n (9–11) |
| Mulan | 5.99 | (26) | 7.05 | (26) | 8.12 | (26) | 9.19 | (23) | 10.25 | (17) | 11.32 | (15) | n (10–11) |
| Arkadia | 5.72 | (27) | 6.84 | (27) | 7.96 | (27) | 9.08 | (26) | 10.20 | (24) | 11.32 | (16) | n (11) |
| R7 (2015–2019) | R7 (2018) | R10 (2015–2019) | R10 (2018) | R (COBORU) | |
|---|---|---|---|---|---|
| R7 (2015–2019) | 1.00 | 0.63 *** | 0.82 *** | 0.68 *** | 0.42 * |
| R7 (2018) | 0.63 *** | 1.00 | 0.41 (.) | 0.68 *** | 0.26 (ns) |
| R10 (2015–2019) | 0.82 *** | 0.41 (.) | 1.00 | 0.59 *** | 0.33 (ns) |
| R10 (2018) | 0.68 *** | 0.68 *** | 0.59 *** | 1.00 | 0.09 (ns) |
| R (COBORU) | 0.42 * | 0.26 (ns) | 0.33 (ns) | 0.09 (ns) | 1.00 |
| Cultivar | Type * | Mean Winter Wheat Productivity Level t/ha | COBORU Recommendation (No of Provinces) | |||
|---|---|---|---|---|---|---|
| 7 | 10 | |||||
| 2018 | 2015–2019 | 2018 | 2015–2019 | |||
| Artist | B | 1 | 2 | 10 | 4 | 1 (15) |
| RGT Kilimanjaro | A | 14 | 17 | 7 | 21 | 2 (13) |
| Linus | A | 19 | 9 | 13 | 7 | 3 (12) |
| RGT Bilanz | B | 3 | 10 | 1 | 2 | 4 (11) |
| Hondia | A | 16 | 38 | 19 | 19 | 5.5 (8) |
| Rotax | B | 5 | 1 | 15 | 8 | 5.5 (8) |
| Formacja | A | 15 | 46 | 12 | 42 | 7 (7) |
| Euforia | A | n.d. | 11 | n.d. | 12 | 8.5 (6) |
| Patras | A | 8 | 29 | 11 | 27 | 8.5 (6) |
| Belissa | B | 6 | 31 | 20 | 26 | 10.5 (5) |
| Owacja | B | n.d. | 48 | n.d. | 52 | 10.5 (5) |
| KWS Spencer | A | 17 | 52 | 18 | 61 | 13 (4) |
| Medalistka | B | 20 | 44 | 23 | 36 | 13 (4) |
| Ostroga | A | 25 | 83 | 25 | 87 | 13 (4) |
| Arkadia | A | 22 | 75 | 22 | 24 | 17 (3) |
| Delawar | A | 18 | 54 | 10 | 29 | 17 (3) |
| Fakir | B | n.d. | 39 | n.d. | 67 | 17 (3) |
| LG Jutta | B | 4 | 66 | 14 | 77 | 17 (3) |
| Tytanika | B | 21 | 65 | 21 | 64 | 17 (3) |
| Bonanza | B | 2 | 27 | 8 | 55 | 23.5 (2) |
| Hybery | B | 11 | 3 | 4 | 6 | 23.5 (2) |
| KWS Dakotana | A | n.d. | 18 | n.d. | 41 | 23.5 (2) |
| KWS Firebird | A | 14 | 67 | 16 | 75 | 23.5(2) |
| Plejada | B | n.d. | 22 | n.d. | 20 | 23.5 (2) |
| Rivero | B | 9 | 24 | 9 | 16 | 23.5 (2) |
| RGT Metronom | A | n.d. | 53 | n.d. | 49 | 23.5 (2) |
| SY Orofino | B | n.d. | 4 | n.d. | 11 | 23.5 (2) |
| Apostel | A | n.d. | 14 | n.d. | 14 | 31.5 (1) |
| Błyskawica | B | n.d. | 8 | n.d. | 1 | 31.5 (1) |
| Frisky | C | 7 | 15 | 2 | 3 | 31.5 (1) |
| Kometa | B | n.d. | 57 | n.d. | 57 | 31.5 (1) |
| KWS Ozon | B | 24 | 59 | 24 | 50 | 31.5 (1) |
| Natula | A | n.d. | 70 | n.d. | 68 | 31.5 (1) |
| Pokusa | B | 23 | 56 | 17 | 30 | 31.5 (1) |
| Sailor | A | n.d. | 76 | n.d. | 76 | 31.5 (1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwańska, M.; Paderewski, J.; Stępień, M.; Rodrigues, P.C. Winter Wheat Cultivar Recommendation Based on Expected Environment Productivity. Agriculture 2021, 11, 522. https://doi.org/10.3390/agriculture11060522
Iwańska M, Paderewski J, Stępień M, Rodrigues PC. Winter Wheat Cultivar Recommendation Based on Expected Environment Productivity. Agriculture. 2021; 11(6):522. https://doi.org/10.3390/agriculture11060522
Chicago/Turabian StyleIwańska, Marzena, Jakub Paderewski, Michał Stępień, and Paulo Canas Rodrigues. 2021. "Winter Wheat Cultivar Recommendation Based on Expected Environment Productivity" Agriculture 11, no. 6: 522. https://doi.org/10.3390/agriculture11060522
APA StyleIwańska, M., Paderewski, J., Stępień, M., & Rodrigues, P. C. (2021). Winter Wheat Cultivar Recommendation Based on Expected Environment Productivity. Agriculture, 11(6), 522. https://doi.org/10.3390/agriculture11060522







