1. Introduction
Traditionally, pig production and processing are important elements of agricultural production in Poland and Hungary. In both countries, all meat products awarded Protected Geographical Indication or Protected Designation of Origin are made of pork. According to Food and Agriculture Organization of the United Nations (FAO) [
1], each Polish person consumed 88.5 kg of meat in 2018, 65% of which was pork. In Hungary, these values were 84 kg and 64%, respectively.
Furthermore, in Poland and Hungary, pig production is a relatively more important direction of agricultural production than it is generally in the European Union (EU) and Central and Eastern European (CEE) countries. According to the economic accounts for agriculture (EAA) [
2] in 2019, 13% and 10% of the total value of agricultural production in Poland and Hungary, respectively, can be attributed to pig production, ranking the countries fifth and tenth in the EU for this parameter, respectively. The above observations prove the importance of researching this industry. All the countries where pig production is equally or more important (Denmark, Belgium, Spain, Germany, Austria, and the Netherlands) are “old” EU−15 member states. Due to their communist past and the smaller scale of production on Polish and Hungarian farms [
3], other major pig producers in EU are not fully comparable. This fact justifies the limitation of the comparative study to Poland and Hungary.
Additionally, in a comparison of specialization and competitiveness in animal production undertaken by Tłuczak [
4], Poland and Hungary were classified as being in the same group for pig production as unspecialized countries that lack a competitive advantage. Additionally, in a classification provided by Baráth and Fertő [
5], the Hungarian situation is the closest match to that of Poland. On the other hand, after EU accession in 2004, the pig production industry in both countries significantly decreased. We can observe a decline in the number of specialized farms, number of animals bred, and in the trade balance; and all this under conditions of relatively stable prices and increasing demand in the long term (see
Section 2 for details).
The aim of this paper was to evaluate this situation using stochastic frontier analysis (SFA). In particular, we assess whether the decline in the industry can be associated with production efficiency, technological change, or the general level of technological development. In the assessment, individual, farm-level data from the Farm Accountancy Data Network (FADN) were used for pig-production-specialized farms in Poland and Hungary during period 2004–2015.
Additionally, the scale of negative changes was different in both countries, which is the basis for the hypothesis of farm heterogeneity in Poland and Hungary. There are two common sources of farm heterogeneity that need to be accounted for in performance analysis [
6]. The first is the diversity of production conditions among sample farms. Although in the case of livestock production, some factors (such as soil type, latitude, altitude, precipitation) are less important, differences may remain in market organization, infrastructure, distance from the service center, etc. Unfortunately, data for measuring these conditions are rarely available, but unobserved heterogeneity can be distinguished from farm inefficiency using an appropriate SFA approach [
7,
8]. The second source of heterogeneity results from differences in the technology that is used and is called technological heterogeneity. In pig production, this may arise from varying degrees of mechanization, or simply from the breeding of different breeds of pigs. Alem [
9] argues that there are several econometric techniques for dealing with this problem, including cluster algorithms, random parameter, latent class, and metafrontier approaches. In the empirical analysis, we employed the latter approach.
This paper contributes to knowledge about agricultural production performance. Empirical studies on technical efficiency in the pork industry are still limited, especially in terms of cross-country comparison. To the best of our knowledge, there has been no comparative analysis of the pig industries in Poland and Hungary. This paper is organized as follows. In
Section 2, we present a short description of pig production in Poland and Hungary.
Section 3 describes the empirical database and the methodology. In
Section 4, we present the results, compare them with previous findings, and based on this formulate recommendations for agricultural policy in both countries.
Section 5 concludes.
2. The Specificity and Dynamics of Pig Production in Poland and Hungary
Although the pork industry has traditionally been important in Hungary and Poland, we can observe some differences in the countries’ pig production farms. The pork industry has declined in size in both countries, but negative changes have been more severe in Poland (
Table 1). These differences in dynamics deserve deeper investigation.
The first issue to consider is structural change. The process of concentration was more intense in Poland, where from 2005 to 2016, the average number of animals per holding increased more than four-fold (in Hungary, the number doubled). For both countries, the disappearance of the smallest farms was rather the result of the more rapid decrease in the number of farms than a decrease in number of animals. Csonka and Fertő [
13] analyzed structural change in pork production in Hungary. They identified an intensification and concentration process that is most visible in the disappearance of small and medium-sized farms. In comparison to other CEE countries, Hungary may be described as having a “dual pig industry,” with a large share of both small- and large-scale farms. According to Kovacs [
14], this situation is a consequence of agrarian reforms undertaken after 1989 when the land of well-developed, large-scale agricultural holdings was partitioned and distributed to individual farmers. However, some farmers continued to cooperate or decided to establish legal entities, permitting the survival of some larger-scale holdings. In Poland, medium-scale farms predominate. This may also be connected to the communist period, when family farms in this country remained relatively intact [
15].
Potori, Chmieliński, and Krawat-Woźniak [
16] presented a comprehensive comparative analysis of Polish and Hungarian agriculture. They found a more dualistic nature of agriculture in Hungary, i.e., the coexistence of large, commercial farms alongside small-scale subsistence farms. In Poland, the authors identified a stronger positive impact of EU support on agricultural development. They also stated that Polish farmers were better prepared for EU accession and competition on the common market, allowing Poland to become a net exporter of food products with higher value added. However, this statement is not proven by the data presented in
Table 1. When it comes to the pork trade, the balance was generally maintained in the case of Hungary, while Poland became a net importer—mainly due to the weak international competitiveness of Polish pork farms, which resulted in the substitution of domestic production with imports [
17]. This phenomenon is particularly significant in relation to piglet supply [
18]. Among other reasons for the decline in pork production in Poland, we can mention the trade embargo imposed by Russia, and the spread of African swine fewer (ASF). A particularly sharp decline in the number of pregnant sows and piglets can be explained by the fact that keeping sows and rearing piglets requires much more knowledge than the process of fattening does. Adapting pigsties to piglet production is a difficult and expensive task, thus many small farms are not interested or able to undertake such specialization [
19].
Hungary faced similar problems after EU accession. Because of the common EU market, the proportion of cheap imported pigs increased, depressing domestic prices and increasing production-related losses. Strict environmental and animal welfare requirements also represented a big burden for farmers in terms of cost structure. The price boom of 2008 also negatively affected the Hungarian pig industry because most farmers had no cropland for growing feed. Finally, those farms which had arable land for feed growing could count on a secure income from the latter due to the single area payment scheme and a secure cereal market; the risky market situation and cost of investment required to maintain competitiveness resulted in many pig-keeping farms ceasing production. After the worst year in 2013, the situation partly started to improve thanks to the National Pig Strategy that was accepted by the government in 2012, in addition to value added tax reductions [
20].
Some of the tendencies identified here may be associated with consumers’ dietary changes and generally the demand side. Overall trends in meat consumption in Poland were described by Trajer and Mieczkowski [
21], who identified relatively stable pork consumption with a temporary decrease around 2013, and the substitution of beef consumption with poultry. The latter authors described this trend as a result of the high level of price competitiveness, dietary properties, and changes in diets in favor of lower calorie, low-fat options. According to FAO data (
Table 1), trends in meat consumption in Hungary were the opposite with regard to poultry, which significantly declined in favor of pork.
In summary, the results of earlier comparative analyses are inconclusive. In terms of labor, efficiency was higher in Hungary, while efficiency was higher for land in Poland [
16]. Similarly, some research indicates the higher efficiency of the agricultural industry in Hungary [
22,
23], but other work in Poland [
24,
25] have explained this to some extent by the different time periods that were analyzed and differences in methodology. However, none of this research was specifically concentrated on pig production. To obtain more comparable results, we applied technical efficiency analysis. The goal of this research was to examine how changes in industry dynamics are associated with differences in the technical efficiency of farms and technological gaps using the metafrontier approach.
3. Materials and Methods
We used Farm Accountancy Data Network (FADN) data for individual farms specialized in pig production (defined as more than two-thirds of standard output coming from the latter activity). An important feature of FADN data is their representativeness. This covers “commercial” farms, specified for Poland and Hungary as farms having more than EUR 4000 of standard output. For Poland and Hungary during the period 2004–2015, the sample size was 13,588 and 756, respectively. The average number of observations per year was thus 1132 for Poland and 63 for Hungary. However, the FADN database uses rotational sampling, which makes the panel unbalanced. More detailed information about the sample characteristics is presented in
Table 2. The value of the total output, depreciation, and total specific cost were deflated to constant 2010 prices using nominal price indices from Eurostat (aact_eaa05) and FADN annual currency exchange rates.
The data show that farms are, on average, larger in Hungary, but more differentiated in Poland. The average pork-specialized farm in Hungary is more than five times as big in terms of output and number of pigs as in Poland, and almost four times as big in terms of employment. Similarly, the depreciation and total specific costs were almost four (six) times as high, respectively. When it comes to sample diversity, this is much higher in Poland in terms of output, labor input, and number of pigs, and slightly lower in the case of depreciation and total specific costs. This may be due to the generally larger sample.
The data were used to assess differences in the efficiency of pig production farms in Poland and Hungary. We followed the most commonly used [
9] two-step strategy of metafrontier assessment proposed by O’Donnell et al. [
26]. In line with this approach, the analysis was divided into two steps. First, efficiency was calculated using stochastic frontier analysis (SFA). In the second step, a linear programming method was used to identify the metafrontier. Although we identified a few studies that were methodically similar to ours, it is possible to distinguish a clear research gap. The analysis of farms specialized in pig production is scarce, particularly in the context of European agriculture. Some studies in this field that applied a metafrontier approach refer to China. In particular, Zhang et al. [
27] analyzed pork production. One piece of work exists that refers to pork production in EU member states [
28], but this application used the metafrontier approach to examine total factor productivity, not efficiency. Therefore, to the best of our knowledge, pork-specialized farms in Poland and Hungary have not yet been the subject of a comparative efficiency analysis corrected for technological heterogeneity with the metafrontier method. Dakpo et al. [
29] compared total factor productivity changes among different types of farming in France, but without a focus on pork. Cechura et al. [
30] compared 24 EU countries but only concentrated on dairy farms. Latruffe, Fogarasi and Desjeux [
31] compared Hungary and France, but only analyzed farms specialized in dairy and cereal, oilseed and protein crops. Beyond this research, some works referred to pork production only in Hungary [
32] or Poland [
33], but neither of these covered the research topic addressed herein.
In our approach, a general stochastic production frontier model can be defined as
where
is the output produced by farm
i at time
t = 1, 2, …,
T;
is a vector of factor inputs;
i = 1, 2, …,
N denotes N farms at time
t;
is the error term; and
represents the technical efficiency of farm
i. Furthermore,
and
are assumed to be independent and identically distributed (
iid) with variances
and
, respectively. Another common assumption is that all farms operate with the same working environments (a common technology assumption). However, both our literature review and descriptive statistics suggest that pig farms use different technologies in Poland and Hungary.
To address the issue of technological heterogeneity, we estimated separate production functions. Furthermore, it is possible to account for within-country heterogeneity between farms by applying the “true” random effects (TREs) model proposed by Greene [
7,
8]. TRE models assume a time-invariant, firm-specific random term (
θi), which is supposed to capture cross-firm heterogeneity and distinguish it from time-varying inefficiency (
). In its most general form, the model can be written as
In the context of technological heterogeneity in
k countries where
is the output for farm
i during the
tth period for the
kth region,
denotes the input vector for farm
i at time
t in region
k;
represents the error;
denotes the inefficiency of farm
i at time
t in region
k; and
is a vector of unknown parameters to be estimated for the
kth region. Thus, we can rewrite Equation (1) as
We modeled technology assuming a Cobb–Douglas function. Furthermore, we assumed a normal-half normal distribution of error and inefficiency terms and to account for the technological change, including a time trend (t) in the deterministic component of the model. The final form of the model is thus:
where SE131 was the total output in 2010 EUR; SE010 was the total labor input in annual work units (full-time person equivalent); SE360 was the depreciation in 2010 EUR; SE281 was the total specific cost in 2010 EUR (feed and other specific costs); SE100 was the number of pigs. The model was estimated using the maximum simulated likelihood method in NLOGIT. For a robustness check and to assess whether the separation of time-invariant cross-farm heterogeneity was justified, we also calculated a Battese and Coelli [
34] type model. Results are presented in the
Appendix A.
The technical efficiency (
) of the
ith farm at the region–
k frontier can be computed from the equation:
In the second step, following O’Donnell et al. [
26], a metafrontier function that envelops the estimated group frontiers can be obtained by solving the following optimization problem:
where
k is the estimated coefficient vector associated with the group-k stochastic frontier. Since these estimated coefficient vectors are fixed and the function
f(.) is log-linear in the parameters (as assumed in the empirical application in this paper), the LP problem becomes:
where
is the arithmetic average of the
xit-vectors over all farms during all periods.
After solving the LP problem defined by Equation (7), estimates of metatechnology ratios and technical efficiencies with respect to the metafrontier can be obtained using the following decomposition:
The first term on the right-hand side is the technical efficiency (TE) of the
ith firm during the
tth period with respect to the country-k frontier. The second term on the right-hand side is the metatechnology ratio (MTR) for the
ith firm during the
tth period (in the
kth country). The constraints in the LP problem defined by Equation (7) guarantee that metatechnology ratios estimated in this manner will lie in the unit interval. Finally, the technical efficiency of the
ith firm during the
tth period with respect to the metafrontier is:
Thus, the technical efficiency relative to the metafrontier is defined in an analogous way to Equation (5): it is the ratio of the observed output relative to the frontier output, adjusted for the corresponding random error. In practice, it is convenient to predict technical efficiency with respect to the metafrontier using the decomposition:
where
and
are the predictors discussed in connection with Equations (5) and (8). The calculation of the metafrontier was performed in R using codes provided for SHAZAM by O’Donnell et al. [
26].
4. Results and Discussion
Table 3 shows our estimations for both countries. The estimated time trend variable (t) can be interpreted as the average annual rate of technical change [
35]. In the case of Poland and Hungary, this parameter is negative and significant, implying a technological decline in pig production in both countries. This is a potential explanation for the general decline in the pork industry. Alternatively, it might capture environmental changes, especially regulations related to animal welfare.
Production elasticities can be assessed by an analysis of the production function coefficients. Interestingly, the relative importance of different production factors varies between Poland and Hungary, which is another justification for the metafrontier approach. In Poland, specific costs have a greater influence on pig production compared to other outputs. The second most important input is the number of animals. In Hungary, the order of priority for these inputs was the opposite, and the difference in elasticity was smaller. We can also observe the greater relative importance of labor in Hungary, but in general, the elasticity of production was low for this factor in both countries. The least important factor, which, however, is still highly significant, is fixed capital depreciation. These findings are valuable in relation to making interventions in the pig production industry.
The sum of the elasticities can be interpreted as a returns-to-scale parameter, which informs about the proportionality of changes in output after the amounts of all inputs in production are changed by the same factor. This value is similar for both countries, and higher than 1, which would imply increasing returns to scale. This means that an increase in inputs would cause a higher than proportional increase in output. This result is a prerequisite for further expansion in farm production scale. This is not surprising, knowing that the average farm size is larger in other EU countries specialized in pig production (e.g., Denmark, Belgium, Spain, and Germany). Furthermore, increasing returns to scale are common in pig production [
28].
Other parameters inform us about the proper model specification. A significant value of θ suggests that taking into account time-invariant, farm-specific heterogeneity was justified. Another reason for using a “true” random effects model is comparing AIC values between the discussed models, and calculating a robustness check for Battese and Coelli [
34] type models (see
Appendix A). In both cases, AIC was lower for the TRE (−8715.9 and 115.1) than the BC models (−8452.7 and 136.5), which is a sign of the better fit of the model. Significant values for σ
u indicate that there was inefficiency among farms for pig production in both countries. Its relative importance in comparison to stochastic noise is represented by λ; note that it was much higher in the case of Hungary. In Poland, it was below 1, indicating that most of the variability in output unexplained by the model was due to random error rather than inefficiency.
More conclusions about the efficiency of production can be drawn from the results presented in
Table 4. Differences between the parameters were checked using the Mann–Whitney test.
Regarding the technical efficiency of pig production, in comparison to the countries’ own frontiers (
), higher mean values are achieved in Poland. The difference is approximately 10.5%. The average technical efficiency score of 0.908 in Poland indicates that pig production output was at approximately 91% of its potential given the regional technology. In comparison with previously obtained results, our efficiency scores are only slightly lower than those presented in a study by Cechura et al. [
28] (Poland 0.925, Hungary 0.825)—the latter of which conducted research on a similar sample using the SFA method, assuming a translog production function. However, the scores are higher than the estimates obtained by Latruffe et al. [
32] (Hungary 0.423–0.553) and Syp and Osuch [
33] (Poland 0.747), though the methods and research sample in these pieces of work differed more from our approach.
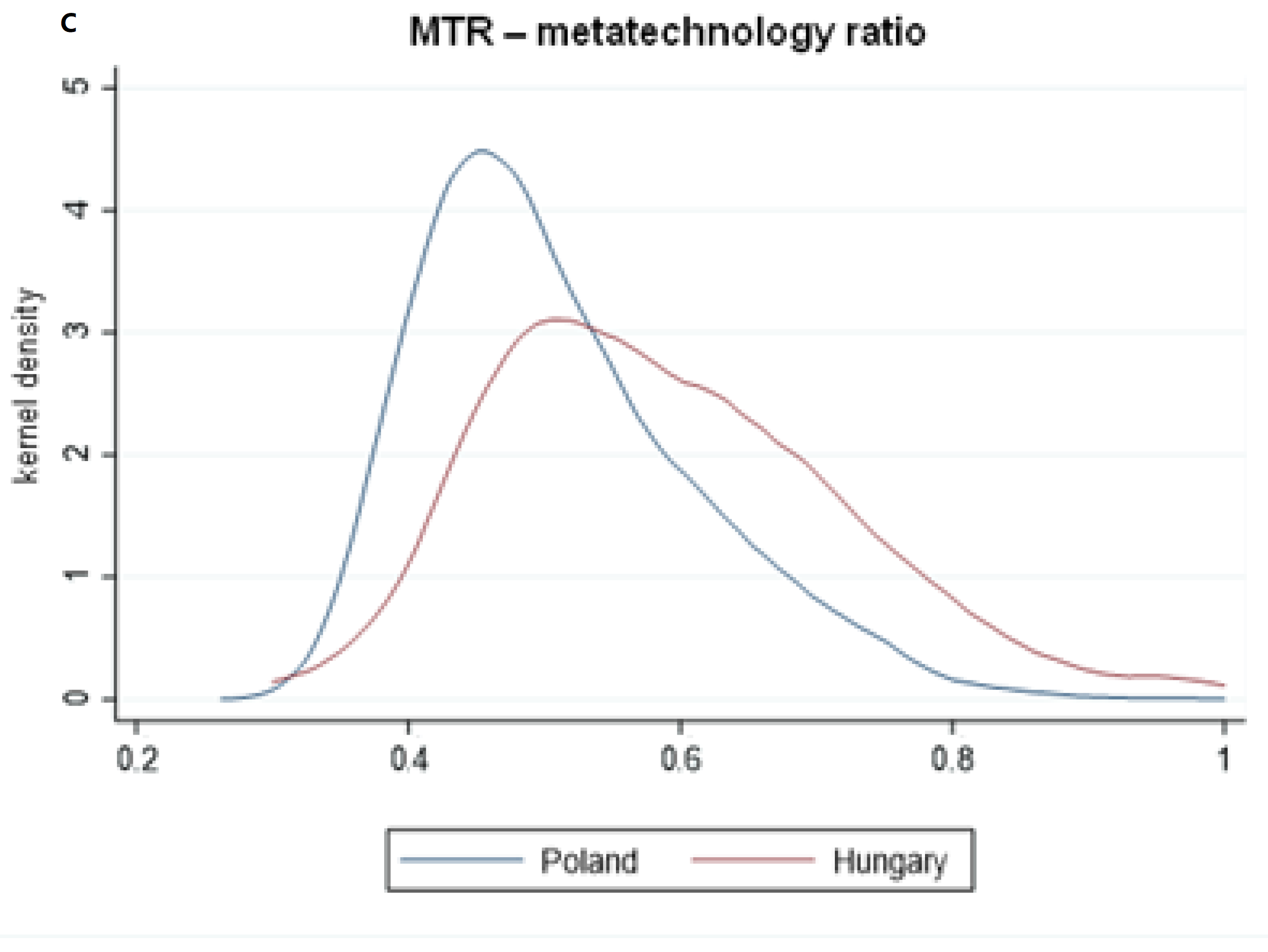
However, increasing the comparability of technical efficiency results is possible by comparing farm results with those for the metafrontier (). These values are much lower for both countries. Furthermore, from this perspective, farms in Hungary were more efficient than those in Poland. Despite the seemingly small difference (1.3 p.p.), according to the Mann–Whitney test, the result is statistically significant, and suggests even more differentiated values for the metatechnology ratio. In general, a lower (higher) value implies a larger (smaller) technology gap between the individual frontier and the metafrontier. An score of 1 indicates that a farmer applies the best technology available in the region (i.e., an score equal to 1 is equivalent to the point at which the individual regional frontier coincides with the metafrontier). Our results indicate that, on average, pig production farms in Hungary during the period 2004–2015 were more technologically developed (i.e., higher ) but also less efficient in relation to the country frontier (lower ); however, greater technological development resulted in generally higher efficiency in relation to the metafrontier (higher ).
Regarding these results, the dual structure of the pig production industry in Hungary was again visible [
13]: a small share of large, well technologically developed and efficient farms has “pushed” the production frontier forward, leaving behind most other farms and resulting in lower values for mean technical efficiency. The former farms are also more efficient than the top Polish farms, as is visible in the higher values for the max
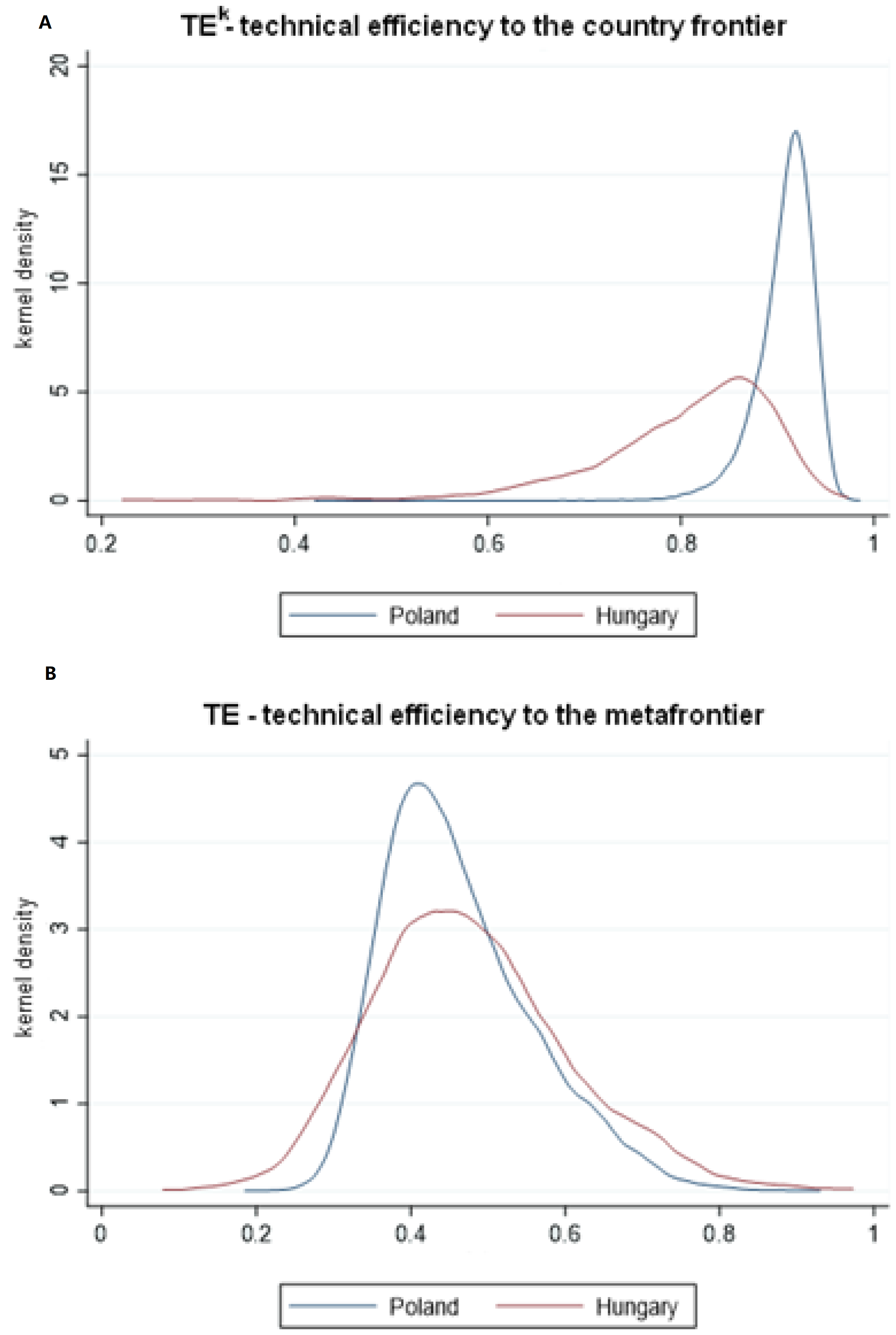
in Hungary. On the other hand, the minimum values of this parameter are much lower in Hungary than in Poland, proving the greater range of efficiency of Hungarian pork-producing farms. This can also be observed in the shape of kernel density plots for all three parameters presented in
Figure 1. The kurtosis of efficiency distribution is much higher for Poland.
Although the polarization of efficiency is more severe in Hungary, the generally low level of technological readiness must be perceived as a serious problem in both countries. The average metatechnology ratio of 0.51 and 0.59 is higher than reported for grain production in Norway (0.59–0.82) [
9]; milk production in Norway (0.96–0.98) [
36]; crop and milk production in Hungary and France (0.76–0.98) [
31]; organic farming in Alpine regions (0.65–0.75) [
37]; citrus farming in Spain (0.88–0.96) [
38]; and olive farming in Spain (0.89–0.98) [
39]. This leads to the conclusion that both countries should devote more resources to disseminating good practices and modern methods of pig breeding.
5. Conclusions
The goal of this paper was to measure the performance and technological gap associated with pig production in two central European countries—Hungary and Poland. We took into account the unobserved heterogeneity and technological differences by using a “true” random effects model [
7,
8] and a metafrontier model [
26]. We found that both countries underwent technological decline during the period analyzed. Furthermore, the estimated production functions are different for both countries in terms of production elasticity. In Poland, the most important production factor was feed and other specific costs, while in Hungary it was the number of animals. Our estimations suggest the presence of increasing returns to scale in both countries, which is a prerequisite for further concentration in the industry. Estimated average country-level efficiency for Poland (0.91) was statistically higher than in Hungary (0.8). However, the results suggest that pig-producing farms in both countries suboptimally use technology, given the countries’ overall technological status. This study also showed that the metatechnology ratio was higher for Hungary (0.59) than for Poland (0.51), meaning that farmers in Poland were further from the metafrontier than those operating in Hungary. This helps explain the more severe decline in the pig production industry in the former country. In addition, the analysis of kernel density plots of efficiency parameters revealed that farms in Hungary were more dispersed.
Consequently, interventions aimed at improving the performance of the pig production industry in Poland and Hungary need to address the problem of the low level of technological development of farms, but with different means, taking into account the heterogeneity identified in this study. First, the general decline which affected the pig production industry in Poland and Hungary after their accession to the EU in 2004 can be explained to some extent by the negative technical change observed during the period of analysis. This might be a consequence of regulations related to animal production—e.g., different animal welfare measures, while the technology used on some farms might be outdated. However, further research is needed to investigate the factors that potentially explain this decline. An important policy implication of this result is that further investment is needed to improve the related technology in both countries to improve the competitiveness of the industry and maintain a high level of animal welfare standards. Second, the average technical efficiency estimates compared to the country frontier are low in Hungary and high in Poland, suggesting that different policy measures could be effective in each country: for example, there is room to increase productivity through technical efficiency improvements (e.g., through extension programs) for Hungary; however, this approach would be less effective in Poland.
In identifying the limitations of the research approach, which at the same time indicate directions for future research, three main improvements are suggested. First, if appropriate data are available, it would be interesting to adjust estimations of pig production efficiency in accordance with the related environmental footprints. This can be done by applying a bad outputs framework. Second, a dynamic analysis and the application of total factor productivity indices could shed new light on changes in the industry during the period under analysis. Finally, research robustness could be improved by relaxing assumptions about the functional forms of production function and inefficiency distribution. To achieve this, nonparametric or semiparametric estimation methods could be used.