1. Introduction
Cerebral palsy (CP) encompasses a heterogeneous group of motor impairments in childhood that affect the development of movement and posture, causing activity limitation [
1]. The prevalence of CP is 2.1 cases per 1000 in high-income countries and occurs in up to 10% of infants at highest risk [
2]. CP is a diagnosis based on clinical and neurological signs and is typically determined between age 12 and 24 months [
3]. Earlier identification of infants with CP would improve access to community services [
4], improve well-being for parents [
5] and provide social and economic support for those infants and families in need of care [
6]. Early identification would also facilitate earlier onset of therapies and treatments in the period when plasticity of the infant brain is at its highest [
7]. Today, the most accurate risk assessments of CP in infants before 5 months of age are the observational general movement assessment (GMA) and cerebral imaging [
3]. However, these risk assessments are either based on qualitative perception, requiring considerable training and clinical expertise (GMA), or demand highly expensive equipment (cerebral imaging) [
8]. Thus, research on low-cost alternatives for early risk assessment of CP based on automatic and objective detection of infant spontaneous movements has rapidly increased the last two decades [
9,
10].
Automatic detection of infant spontaneous movements is based on several types of technology including 3D motion capture, inertial sensors, and video recordings [
9]. The most clinically feasible technology is a video recording, which is non-intrusive, not dependent on body worn reflective markers or inertial sensors, and available in most clinical and home-based settings using commercially available video and smartphone cameras [
10]. Because of the clinical use of observational GMA, large databases of video recordings and CP outcomes are becoming available. These serve as rich sources of data that are important for the generation of robust prediction models based on machine learning. Furthermore, novel methods within machine learning and computer vision have improved possibilities for automated infant motion tracking and facilitated the further development of a computer-based assessment of infant movement kinematics [
11]. Several studies have predicted CP based on an automatic movement assessment from infant video recordings with performance comparable to observational GMA [
12,
13,
14,
15,
16]. A summary of the results of these studies, the methods used, and sample sizes are shown in
Table 1. Kanemura et al. [
17] also found that infants developing CP had higher average velocity and jerky movements of the legs. However, this study did not report the sensitivity and specificity of the method predicting CP.
Despite promising results, previous studies using automatic assessment of spontaneous infant movements have several fundamental shortcomings: First, all studies, except the study of Orlandi et al. [
16], are based on convenience samples that do not reflect typical clinical cohorts. Second, study samples are small (
N = 13–16) in terms of number of children with CP, and it is uncertain whether the prediction models in these studies have external validity for application in a representative population of high-risk infants. Third, the construct validity of the movement features included in previous prediction models is questionable. Observational GMA defines that infant spontaneous movements have complexity denoted by a flow of changes in the movement direction of the participating body parts and variation across time where the infant explores the movement possibilities that the body offers. These spatial and temporal changes in movements are tightly intertwined [
18]. The spatial and temporal changes in these movement features are difficult to represent as a single feature across the entire video recording, as was carried out in a previous study using the standard deviation of the center of motion [
12]. Our hypothesis is that complex and variable spontaneous movements could be characterized by multiple features of temporal modulation in movement frequencies and covariation that will outperform single features, and that spatial and temporal changes in infant movement can be assessed by dividing the video recording into smaller movement periods to obtain a percentage (i.e., proportion) of periods with CP risk-related movements. Furthermore, previous studies have not investigated the relationship between CP prediction models and gross motor function in children with CP. These are important elements to ensure the construct validity and, consequently, the feasibility of the CP prediction model for clinical decision support.
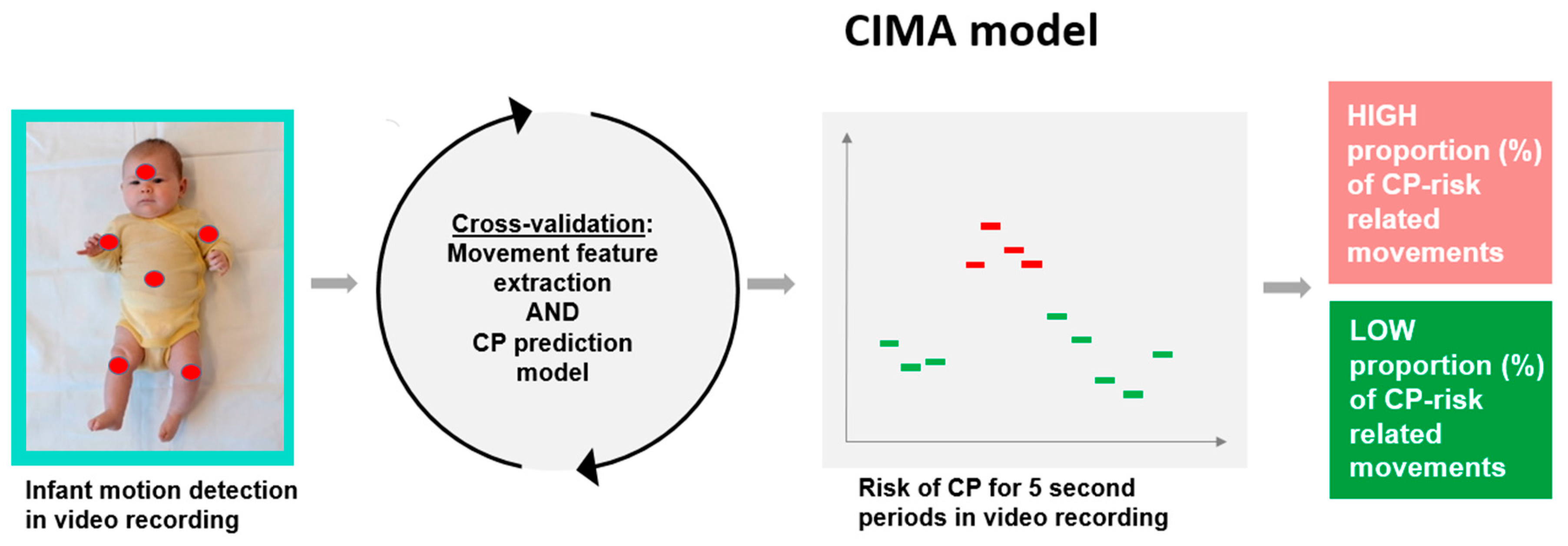
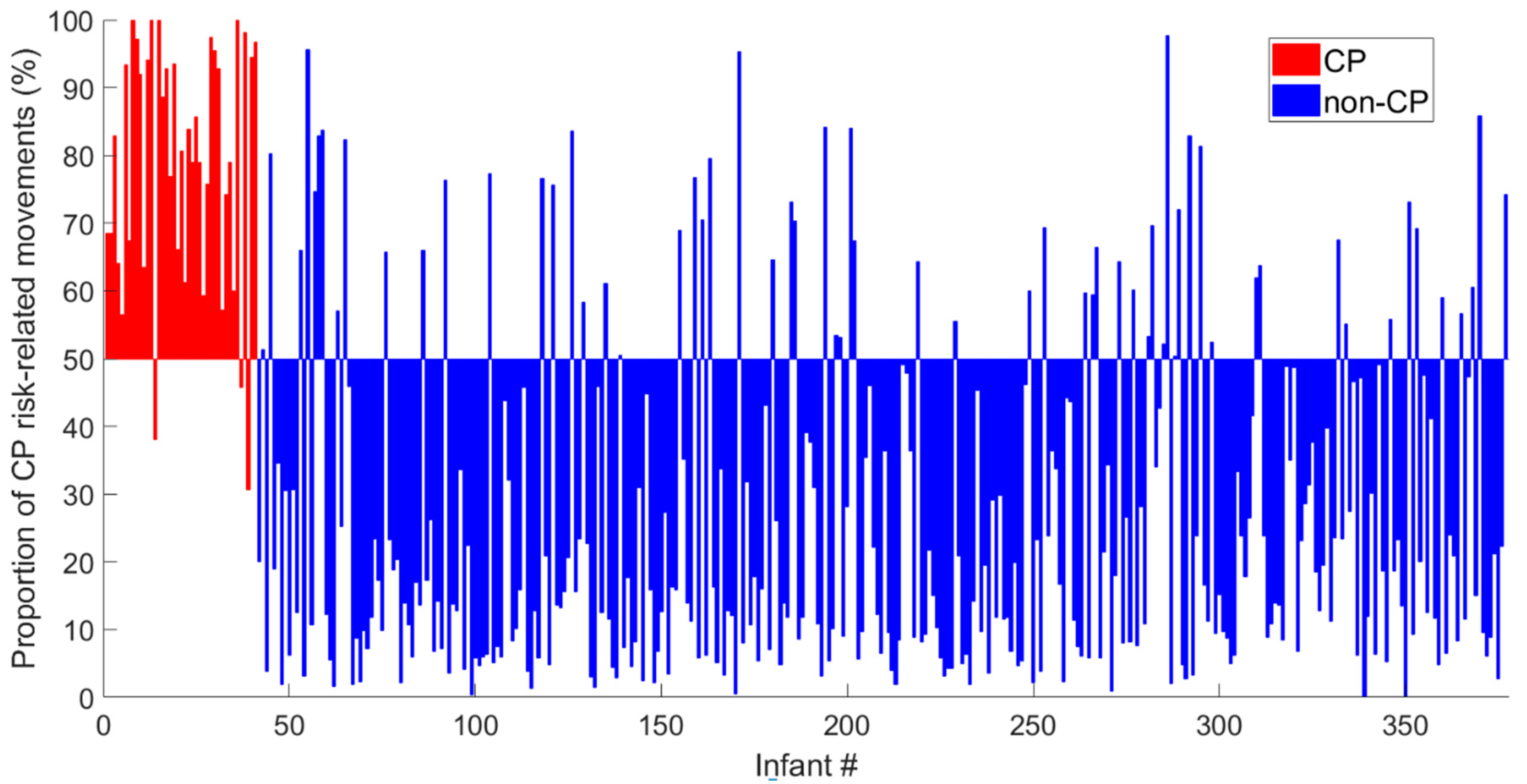
The aim of the present study was to present a novel machine-learning model, the Computer-based Infant Movement Assessment (CIMA) model, for clinically feasible early CP prediction and for the prediction of ambulatory (gross motor function classification scale (GMFCS I–III) versus non-ambulatory function (GMFCS IV–V) in children with CP.
4. Discussion
This study presents a novel machine-learning model, the CIMA model, for the early prediction of CP with an accuracy comparable to the General Movement Assessment (GMA) and neonatal cerebral imaging. Furthermore, the CIMA model differentiated children with ambulatory CP from those with non-ambulatory CP. These findings motivate the further development of a clinical decision support system based on video recordings and machine-learning assessment that can easily be applied for screening of high-risk infants.
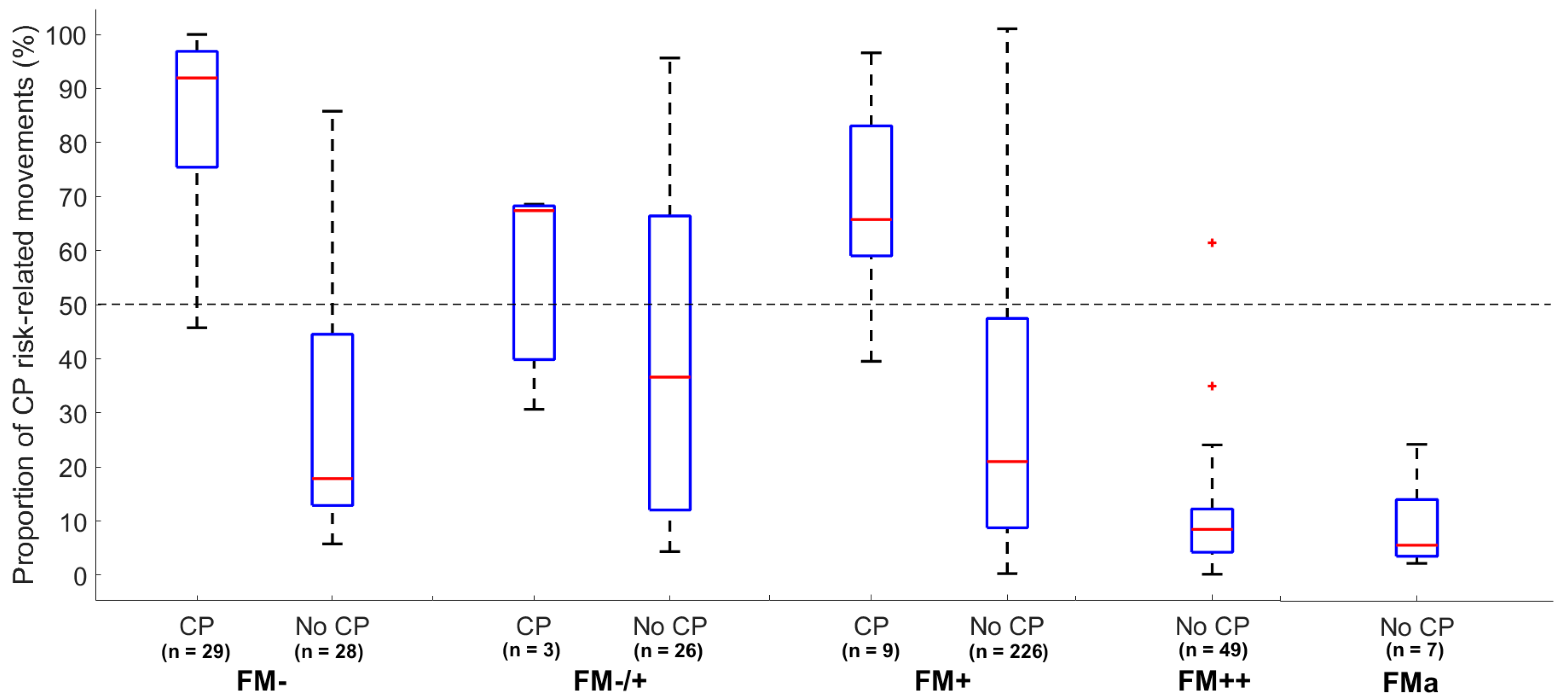
In the present study, the CIMA model was developed based on CP outcome. This is in contrast to others who have presented machine-learning models for automated CP prediction based on the identification of abnormal general movements and absence of FMs [
9]. The video recordings in the present study were performed during the fidgety movements period, making it likely that the CIMA model captures some of the features which are typical for FM. Hence, the selected features in the CIMA model (i.e., movement covariation, frequencies and amplitudes) have the potential to reflect complexity and variability of the infant spontaneous movements which is typical for FM [
27]. Both CIMA and GMA deliver a high number of false positives, but the assessments are weakly correlated with
r = 0.24 to 0.30 (see
Appendix F for details). The false positive cases of the CIMA method are mainly in the intermittent FM category (FM+), whereas the false positive of the GMA is, by definition, in the absent and the sporadic FM category (FM−/+ and FM+). The CIMA model identified children without CP who were classified with absence of FMs (i.e., FM−) with a low proportion of CP risk-related movements. These results suggest that the CIMA model and GMA identifies different false positive cases and may identify different features of infant spontaneous movements. Thus, machine-learning approaches, like the CIMA model, could be used to detect false positive cases within the group of infants with absence of FMs. Further research could relate the movements features used in the CIMA model to the different motor phenotypes recently suggested for infants developing CP in order to gain a deeper knowledge of the appearance of false positive cases in the CIMA model [
31].
The ability of the CIMA model to predict ambulatory versus non-ambulatory function in children with CP suggests a continuum in the proportion (%) of periods with CP risk-related movements, which is related to later motor function. However, the present CIMA model cannot reveal how the chosen movement features change according to later motor function. For the time being, we can, therefore, only speculate that reduced covariation between body parts and reduced variation in movement frequencies and amplitudes are typical for infants who develop CP and that the same movement features are related to the severity of CP.
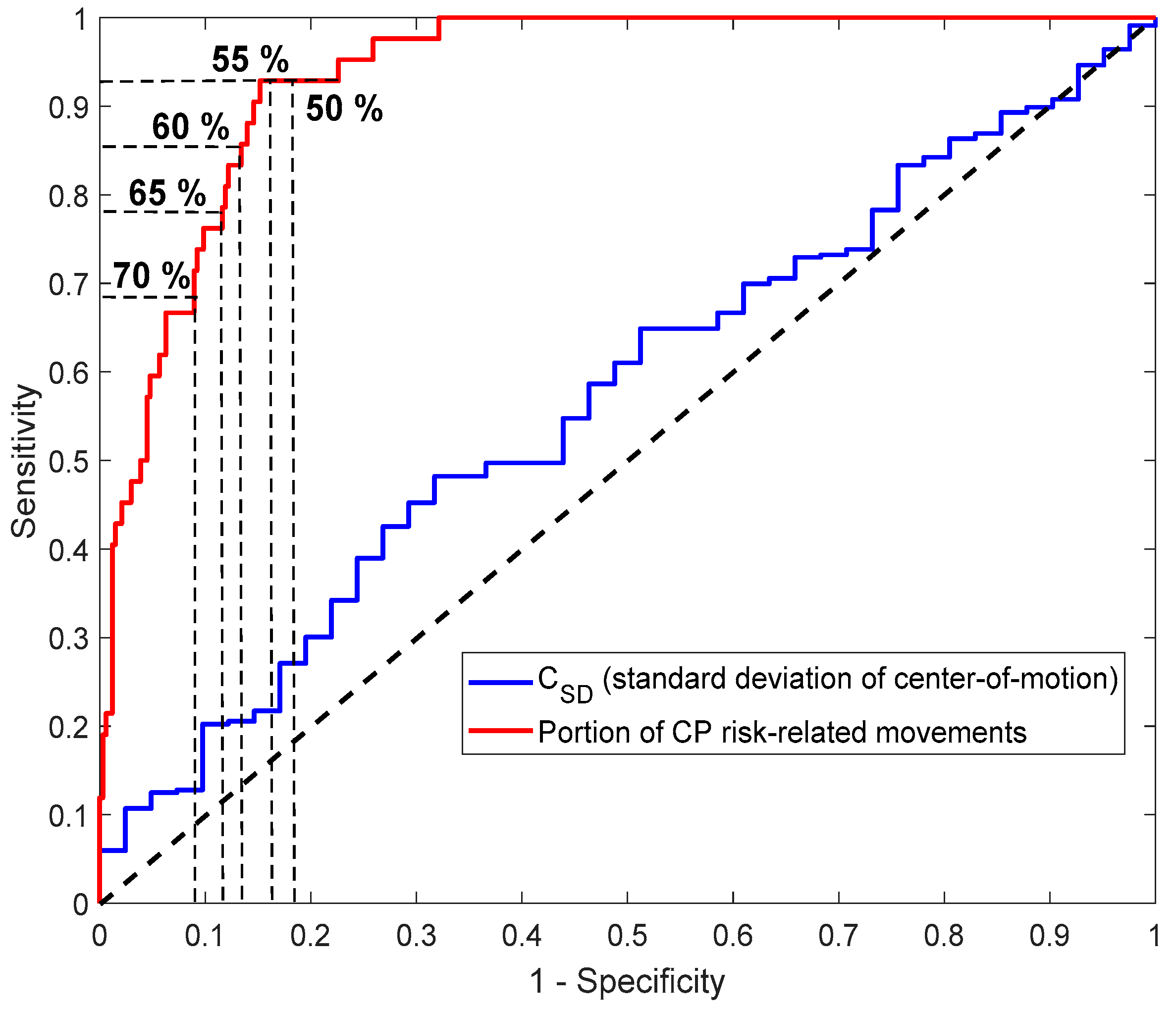
The proportion (%) of time periods with abnormal movements identified by the CIMA model was shown to outperform the CP prediction ability of the standard deviation of the center of motion (C
SD) used in several previous computer-based studies by our group [
12,
30]. The previously developed C
SD was based on a frame differencing method which may be susceptible to differences in contrasts, light, and infant clothing, which may vary more in this larger multi-site cohort of infants. Furthermore, as the sample size and heterogeneity of children with CP increase, it becomes more challenging for a single predefined feature, such as C
SD, to contain information of various characteristics of the infant movement repertoire relevant for a clinical outcome such as CP. Thus, we argue that it is likely that the predictive performance of other suggested single features such as relative movement frequency [
15] and mean and minimum velocity [
30] will potentially decay in larger multi-site populations of high-risk infants. The performance of the presented CIMA model suggests that overall variables, such as the proportion (%) of periods with CP risk-related movements, should be based on a cluster of movement features rather than single “key” features.
The CIMA model has several clinical and methodological limitations. First, the large distance optical flow method is not fully automatic and requires manual annotation. Thus, even though the CIMA model could be a clinically feasible alternative to observational GMA, additional resources for manual annotation are necessary at this point. Furthermore, the horizontal and vertical coordinates of the pixel centers of the six labeled infant body parts are not directly related to biomechanical features such as the joint center position or the body part’s center of mass. Consequently, the present infant movement tracker based on large distance optical flow does not provide accurate biomechanical descriptors of the infant movements. Thus, the selected features and PLS regression components of the CIMA model will be dependent on the specific motion tracker system used. Further studies should emphasize on developing fully automated movement tracker technology able to identify joint center position and the body segment’s center of mass (i.e., full biomechanical 2D model), which will have the potential to identify specific and definable biomarkers of later motor impairments. Advancement in computer vision and the development of deep convolutional neural networks make it possible to identify joint centers and body segment position with high precision [
11,
32]. Such a movement tracker will generate universal pools of biomechanical descriptors for the CIMA model that are not dependent on manual annotations and the choice of movement assessment technology (e.g., 3D motion capture and inertial body worn sensors).
Secondly, the CIMA model is trained on video recordings from a standardized camera setup with a static mounted camera [
12]. To improve clinical feasibility, the CIMA model should be trained on video recordings from hand-held smartphone cameras. Thus, a fully automated movement tracker system suggested above could include filters and post-processing procedures to remove motion artifacts of hand-held smartphone recordings [
11]. This will integrate the CIMA model into future app-based platforms for clinical decision support.
Thirdly, the present model was created from 5 second non-overlapping time periods. It is highly unlikely that all 5 second periods within a video recording contain infant movements related to risk of CP outcome. As an example, infants with or without CP may be quiet with little movements within a 5 second time period. These time periods containing only short movement sequences will get different CIMA model labels according to the CP outcome. Thus, the labeling of the short periods may contribute to noise and, consequently, this may affect the estimated percentage (%) of periods with CP risk-related movements. A remedy for these limitations is to use the classification score provided by linear discriminative analysis to weight the influence of each time interval. This solution was implemented in our study but did not change the reported overall performance of the CIMA model.
Fourth, the present study did not provide test–retest reliability of the proportion of CP risk-related movements. The intra-session test-reliability of observational GMA is reported to be high [
33]. Further test–retest reliability studies are necessary before concluding that the CIMA model is a clinically feasible alternative to observational GMA.
Finally, the present study should be replicated on new samples of high-risk infants to assess the external validity of the CIMA model. The present multi-center study comprised a heterogenous selection of infants (shown in
Appendix A,
Table A1). The predictive values of a specific method will differ based on the prevalence of the outcome, and this should be taken into consideration in the interpretation of the results. The international community of infant movement assessment should collaborate on generating larger databases of infant video data working as a foundation for the development of more robust machine-learning algorithms for the classification of infant motor repertoire and the prediction of later motor impairments. The investigation of neurophysiological correlates (functional magnetic resonance imaging (fMRI), ultrasound, electroencephalography (EEG) and magnetic resonance imaging (MRI)) to the outcome of the CIMA model is also an important direction of future research to improve the model’s construct validity and establish new biomarkers of later motor impairments.