Geospatial-Temporal and Demand Models for Opioid Admissions, Implications for Policy
Abstract
:1. Introduction
2. Experimental Section
2.1. Data
2.2. Geospatial Analysis
2.3. Explanatory Analysis
2.4. Variables
2.5. Software
3. Results
3.1. Descriptive Statistics—Missing Data
3.2. Descriptive Statistics—Quantitative Data
3.3. Descriptive Statistics—Categorical Data
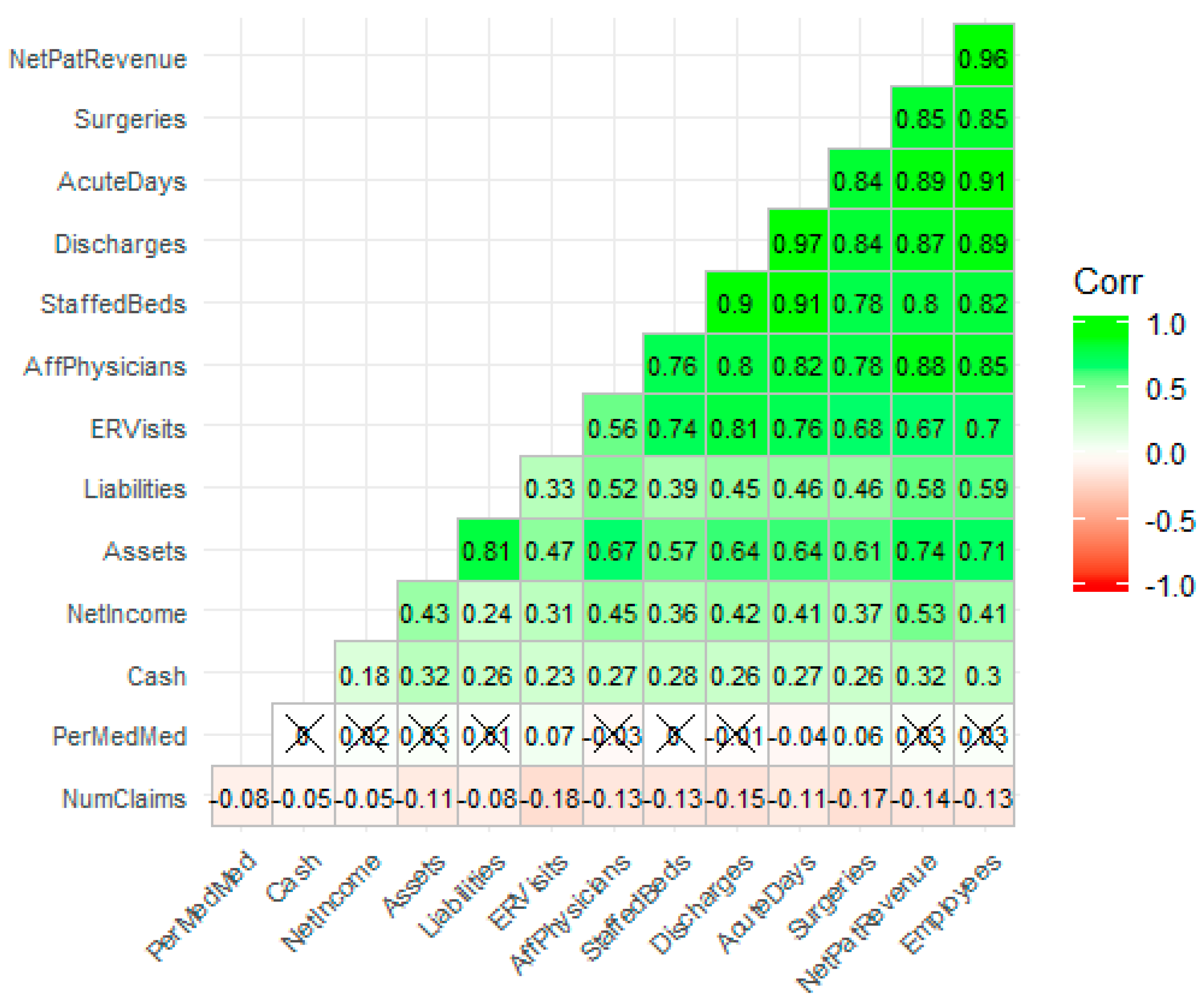
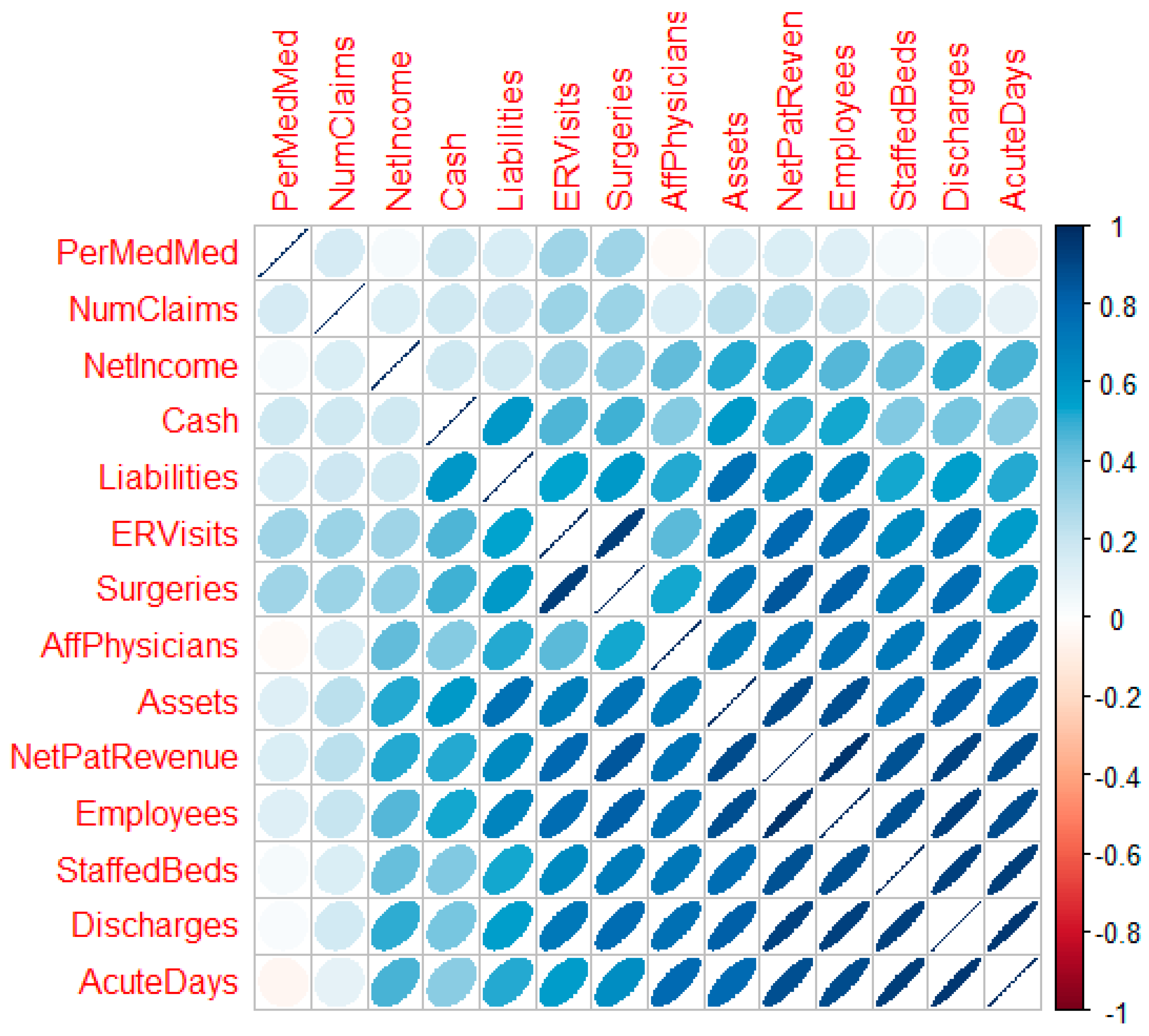
3.4. Descriptive Statistics—Correlational Analysis
3.5. Exploratory Data Analysis—Feature Engineering and Transformations
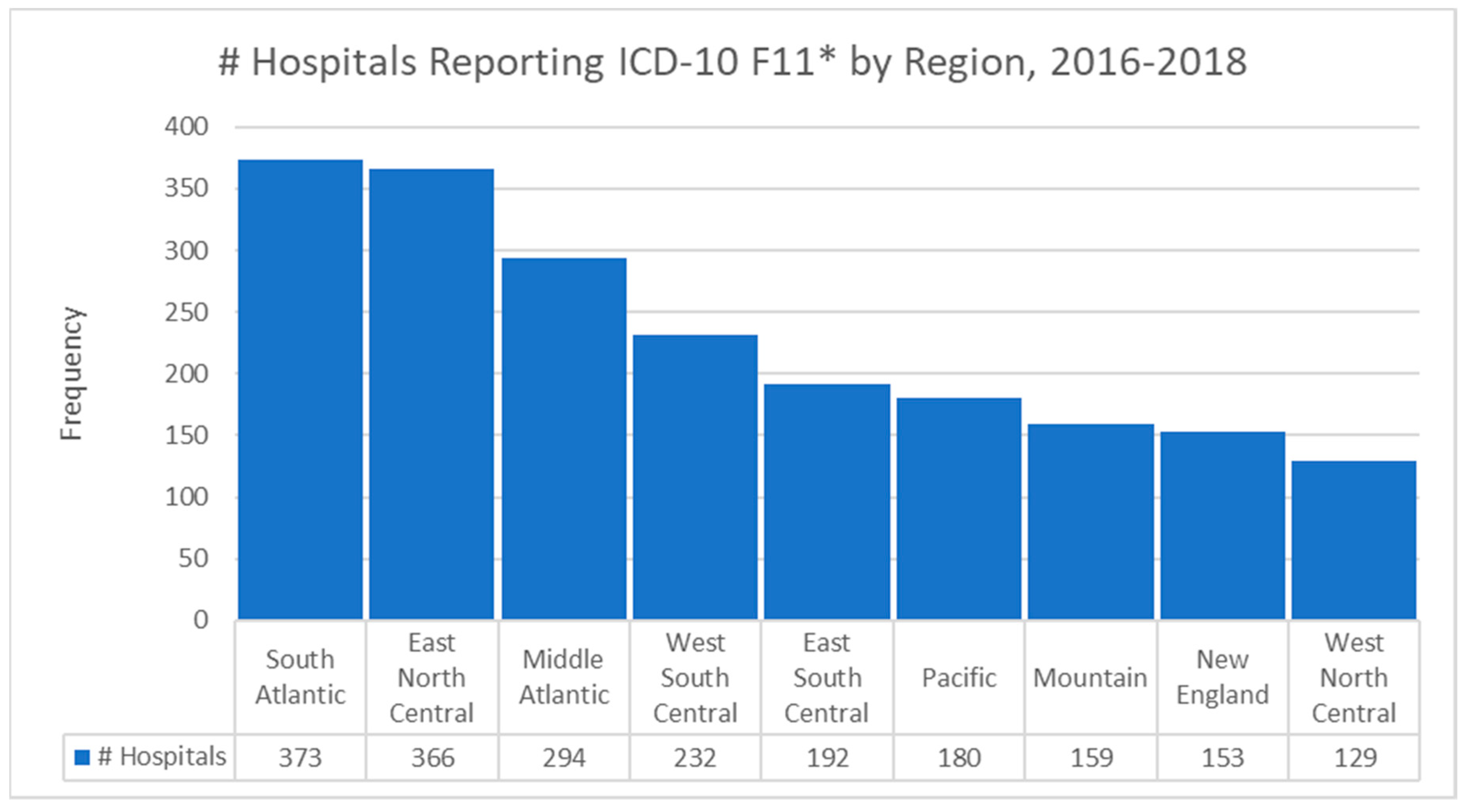
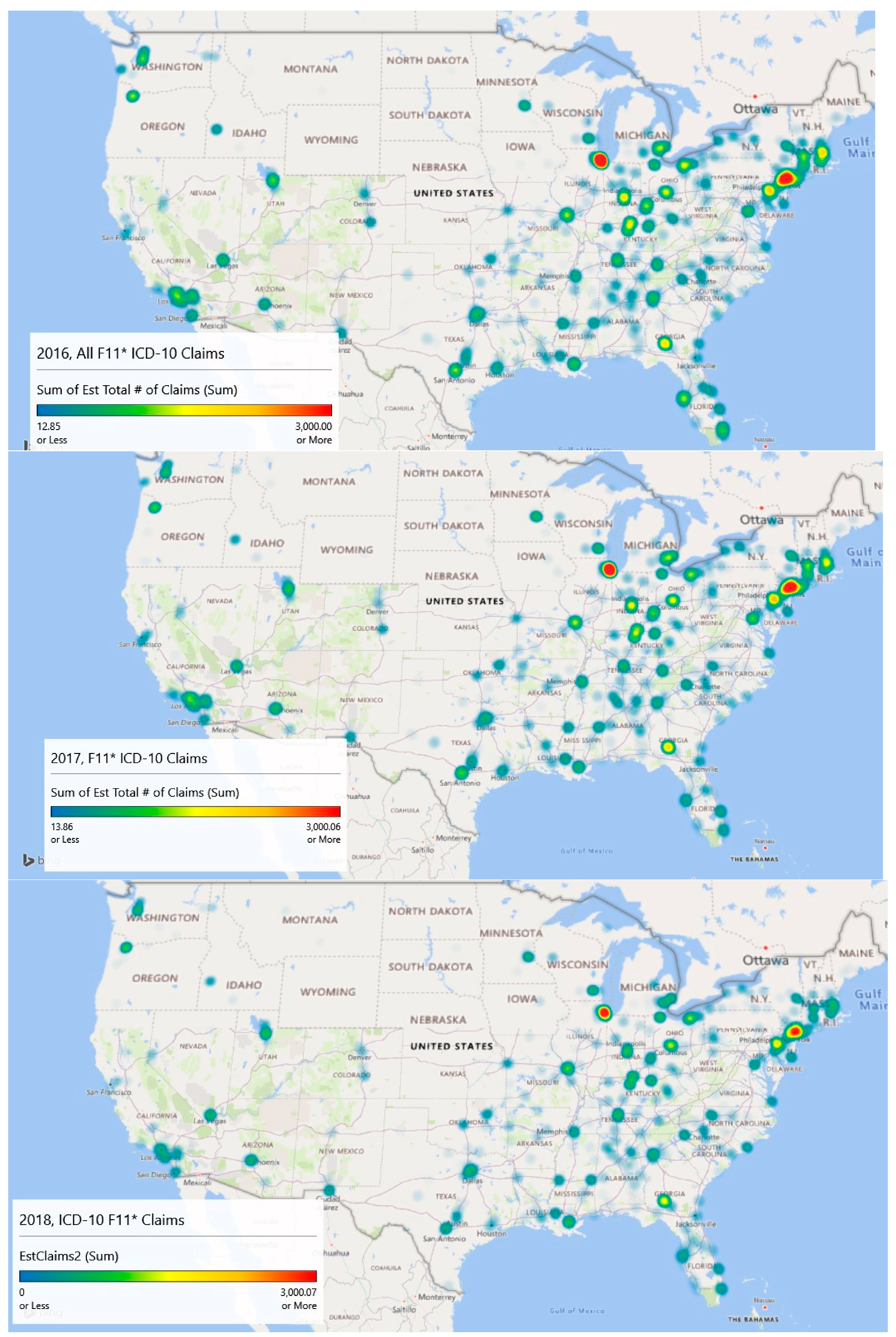
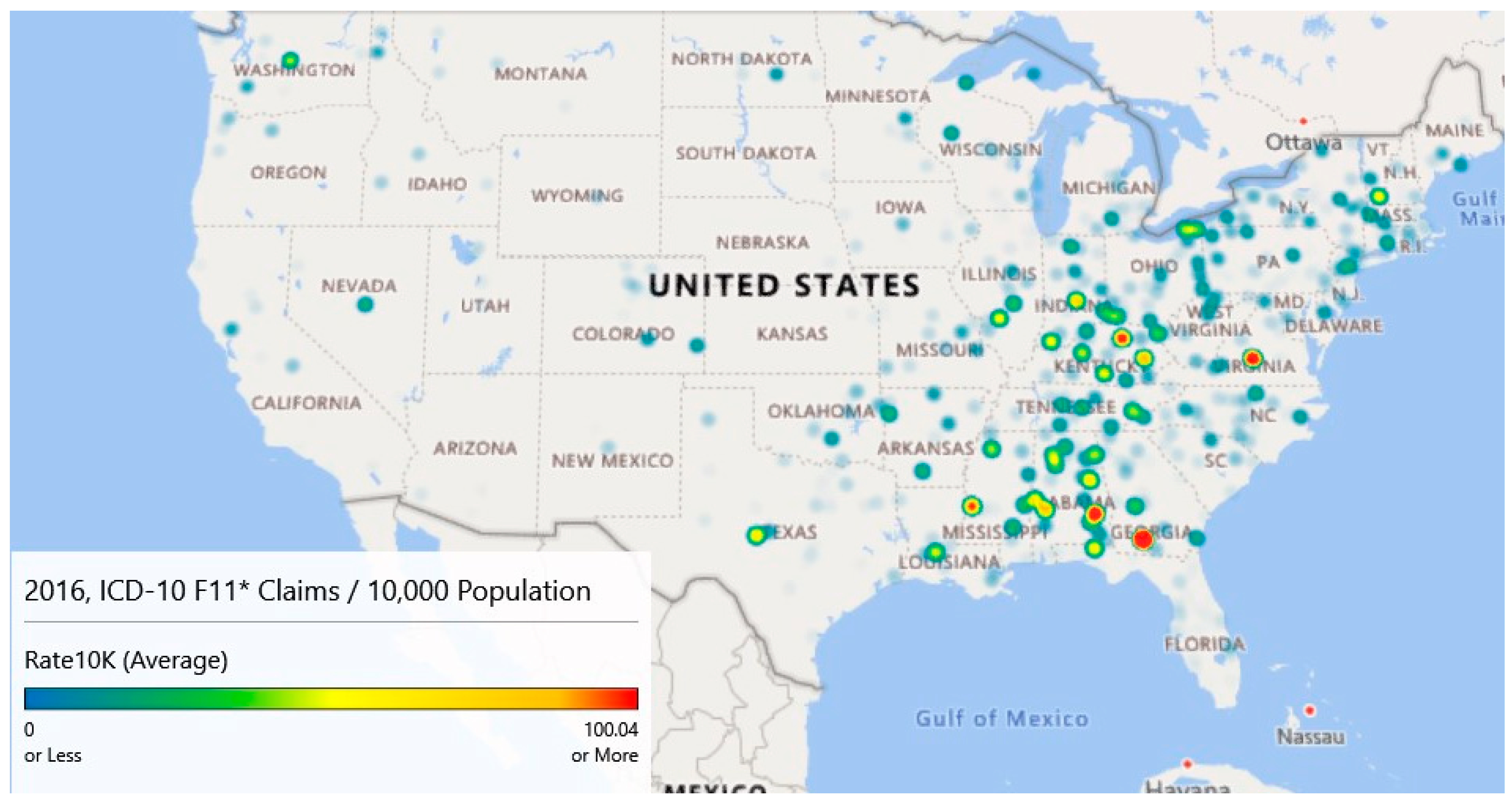
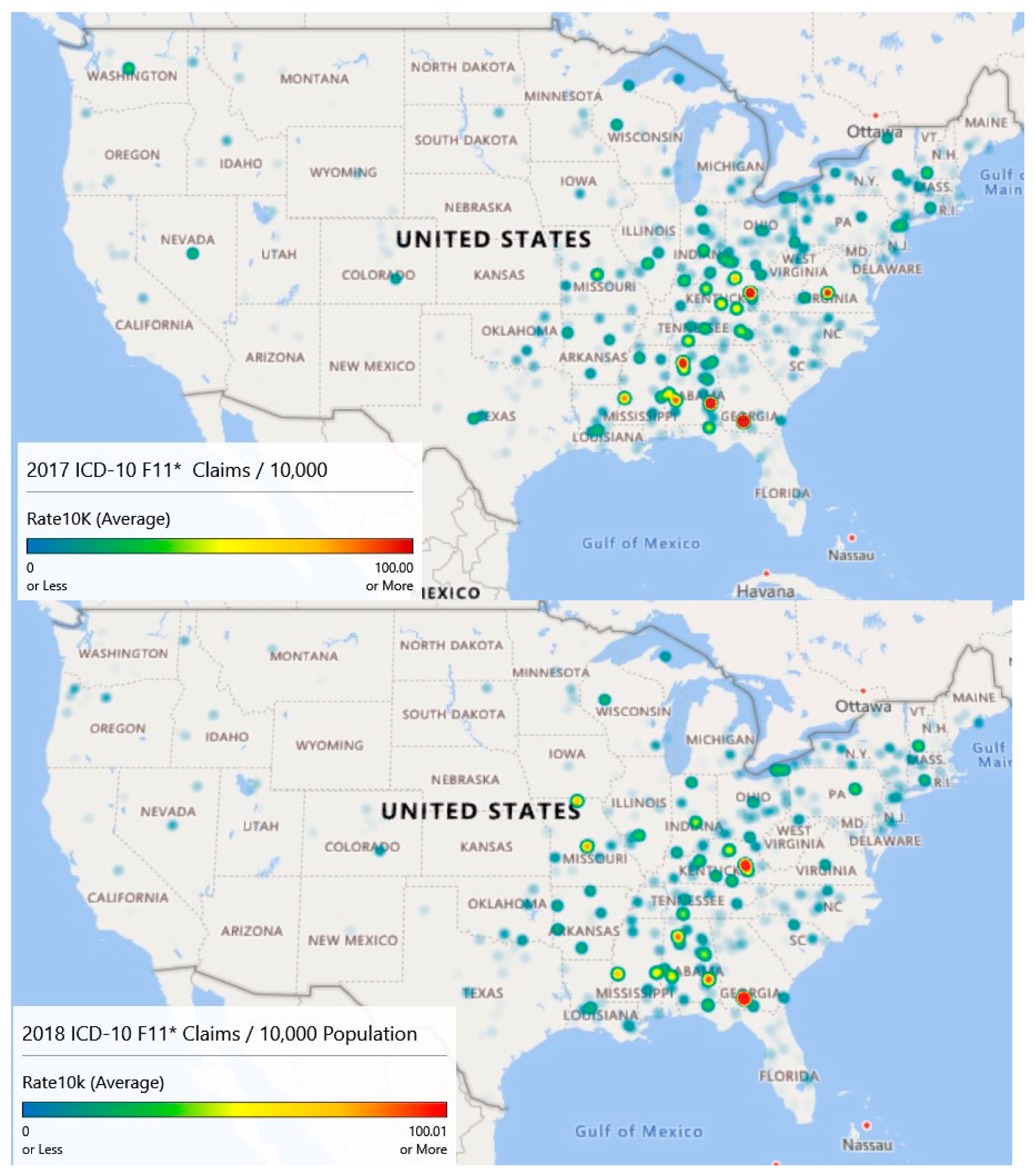
3.6. Geospatial Analysis Results—Zip Code Unit of Analysis
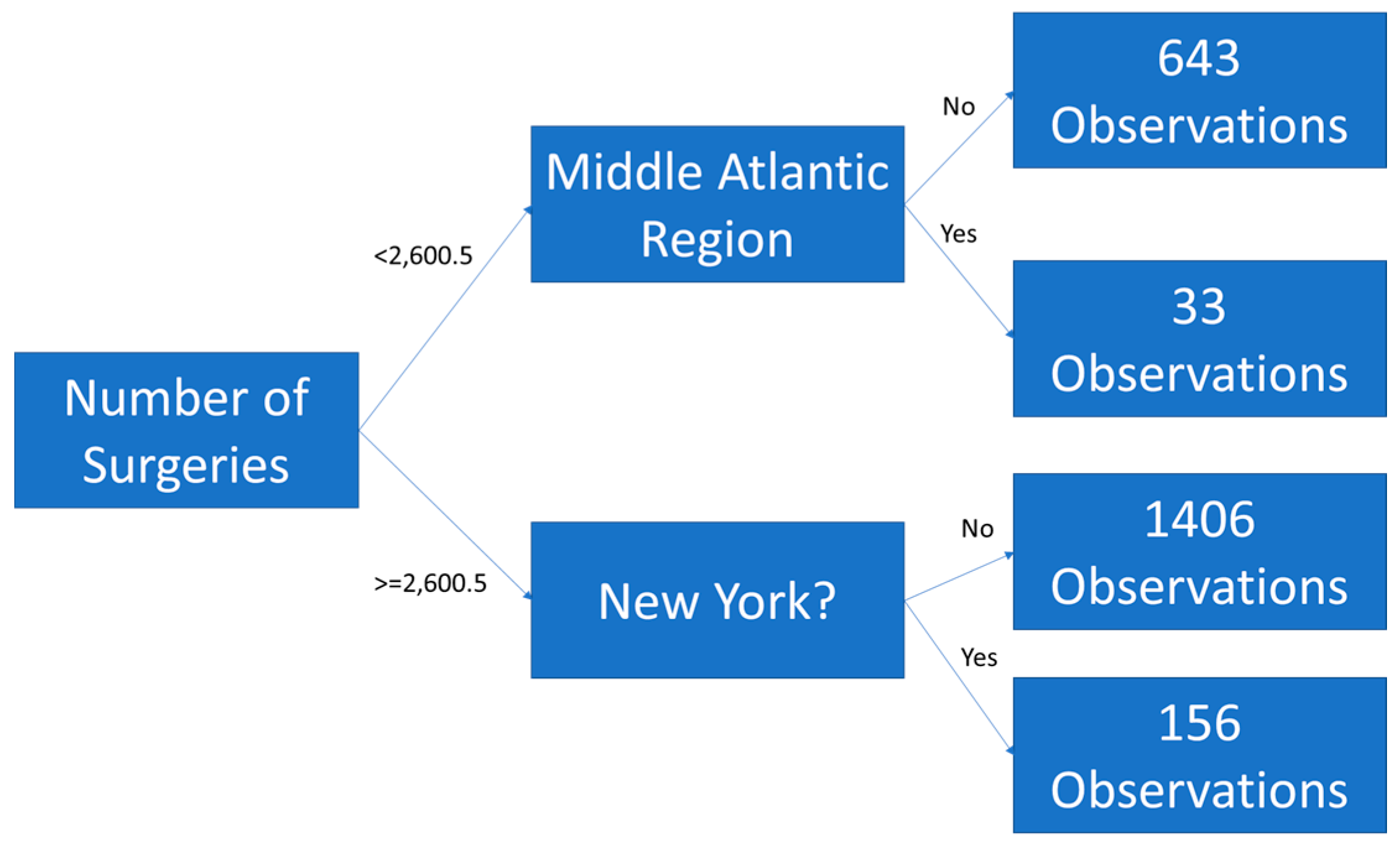
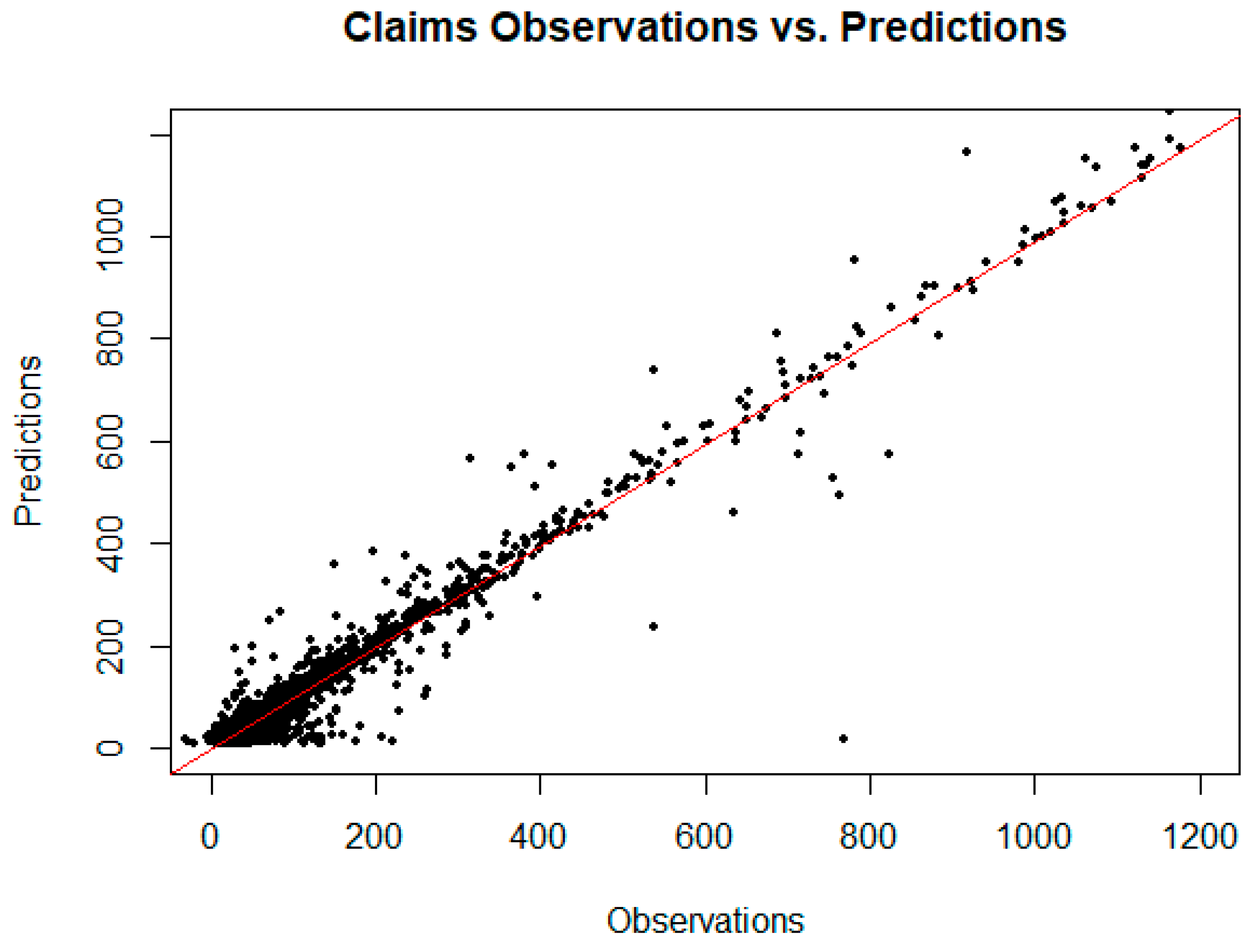
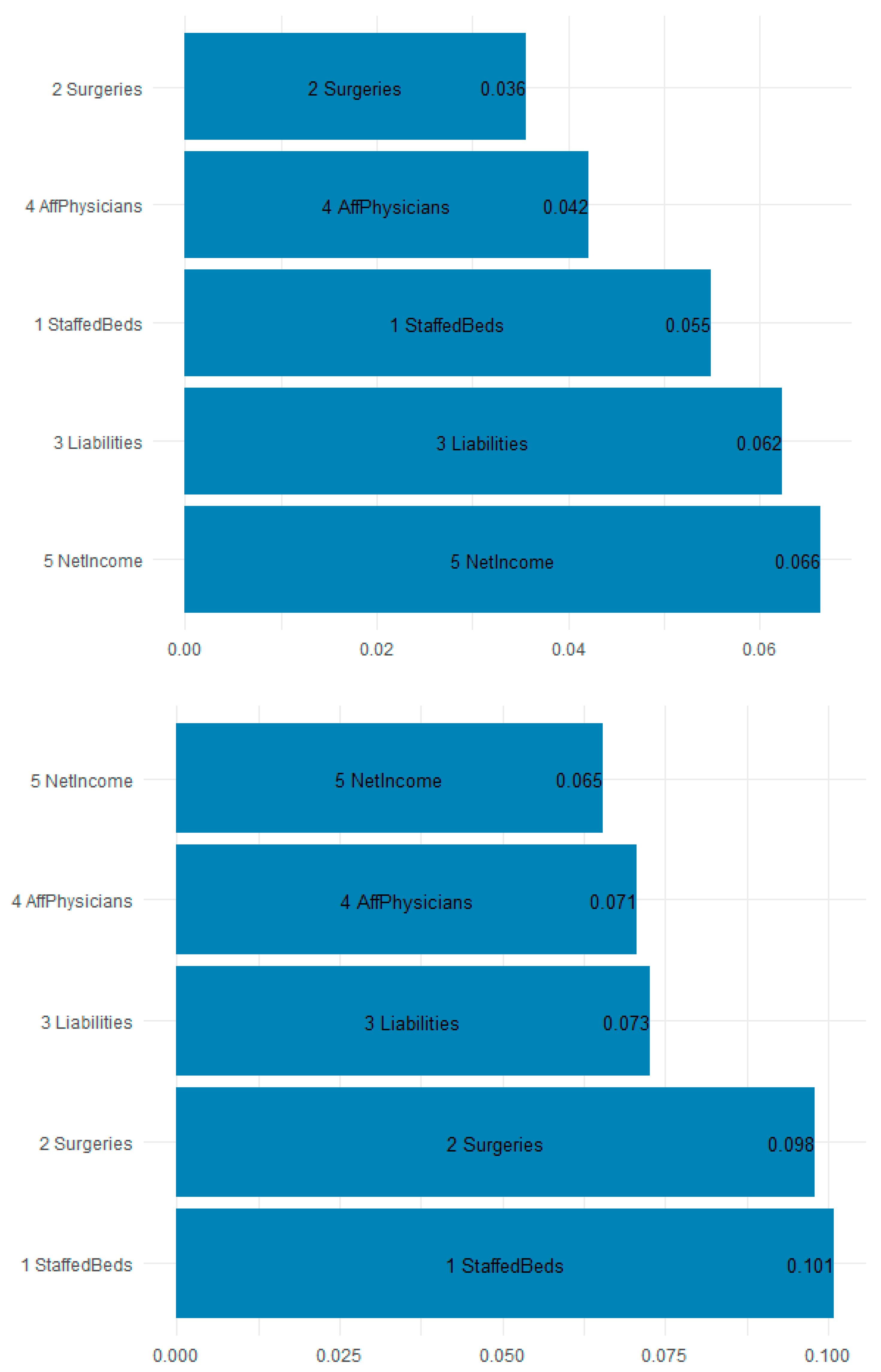
3.7. Explanatory Modeling Results
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
| F11 Opioid Related Disorders | F11.24 with Opioid-Induced Mood Disorder |
|---|---|
| F11.1 Opioid abuse | F11.25 Opioid dependence with opioid-induced psychotic disorder |
| F11.10 …… uncomplicated | F11.250 …… with delusions |
| F11.11 …… in remission | F11.251 …… with hallucinations |
| F11.12 Opioid abuse with intoxication | F11.259 …… unspecified |
| F11.120 …… uncomplicated | F11.28 Opioid dependence with other opioid-induced disorder |
| F11.121 …… delirium | F11.281 Opioid dependence with opioid-induced sexual dysfunction |
| F11.122 …… with perceptual disturbance | F11.282 Opioid dependence with opioid-induced sleep disorder |
| F11.129 …… unspecified | F11.288 Opioid dependence with other opioid-induced disorder |
| F11.14 …… with opioid-induced mood disorder | F11.29 …… with unspecified opioid-induced disorder |
| F11.15 Opioid abuse with opioid-induced psychotic disorder | F11.9 Opioid use, unspecified |
| F11.150 …… with delusions | F11.90 …… uncomplicated |
| F11.151 …… with hallucinations | F11.92 Opioid use, unspecified with intoxication |
| F11.159 …… unspecified | F11.920 …… uncomplicated |
| F11.18 Opioid abuse with other opioid-induced disorder | F11.921 …… delirium |
| F11.181 Opioid abuse with opioid-induced sexual dysfunction | F11.922 …… with perceptual disturbance |
| F11.182 Opioid abuse with opioid-induced sleep disorder | F11.929 …… unspecified |
| F11.188 Opioid abuse with other opioid-induced disorder | F11.93 …… with withdrawal |
| F11.19 …… with unspecified opioid-induced disorder | F11.94 …… with opioid-induced mood disorder |
| F11.2 Opioid dependence | F11.95 Opioid use, unspecified with opioid-induced psychotic disorder |
| F11.20 …… uncomplicated | F11.950 …… with delusions |
| F11.21 …… in remission | F11.951 …… with hallucinations |
| F11.22 Opioid dependence with intoxication | F11.959 …… unspecified |
| F11.220 …… uncomplicated | F11.98 Opioid use, unspecified with other specified opioid-induced disorder |
| F11.221 …… delirium | F11.981 Opioid use, unspecified with opioid-induced sexual dysfunction |
| F11.222 …… with perceptual disturbance | F11.982 Opioid use, unspecified with opioid-induced sleep disorder |
| F11.229 …… unspecified | F11.988 Opioid use, unspecified with other opioid-induced disorder |
| F11.23 …… with withdrawal | F11.99 …… with unspecified opioid-induced disorder |
References
- What is the U.S. Opioid Epidemic? 2017. Available online: http://www.webcitation.org/78Jgiy2wz (accessed on 12 May 2019).
- Center, B.P. Tracking Federal Funding to Combat the Opioid Crisis. 2019. Available online: https://bipartisanpolicy.org/library/tracking-federal-funding-to-combat-the-opioid-crisis/ (accessed on 12 May 2019).
- McCance-Katz, E. The National Survey on Drug Use and Health. 2017. Available online: https://www.samhsa.gov/data/sites/default/files/nsduh-ppt-09-2018.pdf (accessed on 12 May 2019).
- Nearly 60 Doctors, Other Medical Workers Charged In Federal Opioid Sting. 2019. Available online: https://www.npr.org/2019/04/17/714014919/nearly-60-docs-other-medical-workers-face-charges-in-federal-opioid-sting (accessed on 12 May 2019).
- Jury Finds Podiatrist Guilty of Operating Pill Mill. 2019. Available online: https://www.justice.gov/usao-ndga/pr/jury-finds-podiatrist-guilty-operating-pill-mill (accessed on 12 May 2019).
- Virginia Doctor Convicted on 861 Federal Counts of Drug Distribution, Including Distribution Resulting in Death: Faces Mandatory Minimum of 20 Years in Federal Prison. 2019. Available online: https://www.justice.gov/usao-wdva/pr/virginia-doctor-convicted-861-federal-counts-drug-distribution-including-distribution (accessed on 12 May 2019).
- Southern District of Florida Charges 124 Individuals Responsible for $337 Million in False Billing as Part of National Healthcare Fraud Takedown. 2018. Available online: https://www.justice.gov/usao-sdfl/pr/southern-district-florida-charges-124-individuals-responsible-337-million-false-billing (accessed on 12 May 2019).
- Fentanyl Flows from China: An Update since 2017. 2018. Available online: https://www.uscc.gov/sites/default/files/Research/Fentanyl%20Flows%20from%20China.pdf (accessed on 12 May 2019).
- China Policies to Promote Local Production of Pharmaceutical Products and Protect Health; World Health Organization: Geneva, Switzerland, 2017.
- Deprez, E.; Hui, L.; Wills, K. Deadly Chinese fentanyl is creating a new era of drug kingpins. Bloomberg 2018. Available online: https://www.bloomberg.com/news/features/2018-05-22/deadly-chinese-fentanyl-is-creating-a-new-era-of-drug-kingpins (accessed on 12 May 2019).
- China’s Fentanyl Production, Export Fueling U.S. Opioid Crisis, Schumer Says. 2018. Available online: https://www.amny.com/news/china-fentanyl-schumer-1.18531808 (accessed on 12 May 2019).
- Dudley, S.; Bonello, D.; Lopez-Aranda, J.; Moreno, M.; Clavel, T.; Kjelstad, B.; Restepo, J.J. Mexico’s Role in the Deadly Rise of Fentanyl. 2019. Available online: https://www.insightcrime.org/wp-content/uploads/2019/02/Fentanyl-Report-InSight-Crime-19-02-11.pdf (accessed on 12 May, 2019).
- Definitive Healthcare. 2019. Available online: http://www.webcitation.org/788Bun3Wb (accessed on 12 May 2019).
- Annual Estimates of the Resident Population: April 1, 2010 to July 1, 2018. American Factfinder, 2019. Available online: https://factfinder.census.gov/faces/tableservices/jsf/pages/productview.xhtml?src=bkmk, (accessed on 12 June 2019).
- Gehlenborg, N.; Wong, B. Heat maps. Nat. Methods 2012, 9. [Google Scholar] [CrossRef]
- Lee, D.C.; Yi, S.S.; Athens, J.K.; Vinson, A.J.; Wall, S.P.; Ravenell, J.E. Using Geospatial analysis and emergency claims data to improve minority health surveillance. J. Racial Ethn. Health Disparities 2018, 5, 712–720. [Google Scholar] [CrossRef] [PubMed]
- MacQuillan, E.L.; Curtis, A.B.; Baker, K.M.; Paul, R.; Back, Y.O. Using GIS mapping to target public health interventions: Examining birth outcomes across GIS techniques. J. Community Health 2017, 42, 633–638. [Google Scholar] [CrossRef] [PubMed]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Singh, S.; Understanding the bias-variance trade-off. Towards Data Science 2018. Available online: https://towardsdatascience.com/understanding-the-bias-variance-tradeoff-165e6942b229 (accessed on 12 June 2019).
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Census Regions and Divisions of the United States. 2019. Available online: https://www2.census.gov/geo/pdfs/maps-data/maps/reference/us_regdiv.pdf (accessed on 11 June 2019).
- R Core Development Team. R: A Language and Environment for Statistical Computing; The R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Kassambra, A. ggcorplot: Visualization of a correlation matrix using ‘ggplot2’. 2018. Available online: http://www.sthda.com/english/wiki/ggcorrplot-visualization-of-a-correlation-matrix-using-ggplot2 (accessed on 12 May 2019).
- Weisburg, S.; Fox, J. A {R} Companion to Applied Regression, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2011. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. B Stat. Methodol. 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Wei, T.; Simko, V. R Package “corrplot:” Visualization of a Correlation Matrix. 2017. Available online: https://cran.r-project.org/web/packages/corrplot/corrplot.pdf (accessed on 12 May 2019).
- New Jersey’s drug addiction crisis. 2019. Available online: https://www.njtvonline.org/addiction/, (accessed on 12 May 2019).
- Ekin, T.; Musal, R.; Fulton, L. Overpayment models for medical audits. J. Appl. Stat. 2015, 42, 2391–2405. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; He, T. Xgboost: Extreme gradient boosting. 2018. Available online: https://cran.r-project.org/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 12 May 2019).
- Data trends: Opioid prescribing, overdose deaths, and more. 2019. Available online: http://core-rems.org/data-trends-opioid-prescribing-overdose-deaths-and-more/ (accessed on 12 May 2019).
- Emergency department data show rapid increases in opioid overdoses. Available online: https://www.cdc.gov/media/releases/2018/p0306-vs-opioids-overdoses.html (accessed on 12 May 2019).
| Financial Variables | Defined | Measurement |
| Net Patient Revenue | Gross Patient Revenue less attributable expenses | Ratio |
| Net Income | Income less costs, expenses, and taxes | Ratio |
| Cash on Hand | Cash available to the organization | Ratio |
| Assets | Company owned | Ratio |
| Liabilities | Company owes | Ratio |
| Workload Variables | Defined | Measurement |
| Discharges | Number of patients discharged from admission | Integer |
| ER Visits | Number of emergency room visits | Integer |
| Surgeries | Number of surgeries performed | Integer |
| Acute Days | Number of acute bed days of hospital | Integer |
| Technical Variables | Defined | Measurement |
| Staffed Beds | Number of staffed beds operated by hospital | Integer |
| Affiliated Physicians | Number of physicians affiliated with hospital | Integer |
| Employees | Number of direct employees of hospital | Integer |
| % Medicare /caid Patients | Percent of patients reimbursing through Medicare/caid | Ratio |
| Ownership | Governmental, Proprietary, Voluntary Non-Profit | Categorical |
| Medical School Affiliation | None, Limited, Major, Graduate Affiliation | Categorical |
| Hospital Type | Children, Critical Access, Long-Term, Psychiatric, Rehab, Short-Term | Categorical |
| Region 1: Northeast |
| New England (Connecticut, Maine, Massachusetts, New Hampshire, Rhode Island, Vermont) |
| Mid-Atlantic (New Jersey, New York, and Pennsylvania) |
| Region 2: Midwest |
| East North Central (Illinois, Indiana, Michigan, Ohio, Wisconsin) |
| West North Central (Iowa, Kansas, Minnesota, Missouri, Nebraska, North Dakota, South Dakota) |
| Region 3: South |
| South Atlantic (Delaware, Florida, Georgia, Maryland, North Carolina, South Carolina, Virginia, Washington D.C., West Virginia) |
| East South Central (Alabama, Kentucky, Mississippi, Tennessee) |
| West South Central (Arkansas, Louisiana, Oklahoma, Texas) |
| Region 4: West |
| Mountain (Arizona, Colorado, Idaho, Montana, Nevada, New Mexico, Utah, Wyoming) |
| Pacific (Alaska, California, Hawaii, Oregon, Washington) |
| N = 2090 | Variable Name | Mean | SD | Median | 10% Trimmed |
|---|---|---|---|---|---|
| Claims | NumClaims | 103.47 | 198.19 | 33 | 57.14 |
| Staffed Beds | StaffedBeds | 273.53 | 227.59 | 214 | 240.19 |
| Discharges | Discharges | 14,039.67 | 13,572.68 | 10,306.00 | 11,934.51 |
| ER Visits | ERVisits | 50,642.37 | 49,459.27 | 43,564.50 | 44,229.24 |
| Surgeries | Surgeries | 10,113.16 | 12,165.17 | 7,142.00 | 7,992.79 |
| Acute Bed Days | AcuteDays | 72,140.06 | 72,658.04 | 49,710.00 | 59,421.91 |
| Physicians | AffPhysicians | 384.89 | 391.09 | 312 | 318.58 |
| Employees | Employees | 1,968.09 | 2,458.91 | 1,222.50 | 1,475.25 |
| % Medicare/caid | PerMedMed | 42.00% | 16.00% | 42.00% | 42.00% |
| Net Patient Revenue ($1 M) | NetPatRevenue | $403.07 | $519.72 | $247.83 | $298.78 |
| Net Income ($1 M) | NetIncome | $30.25 | $109.98 | $8.12 | $18.94 |
| Cash on Hand ($1 M) | Cash | $36.59 | $182.67 | $1.35 | $10.53 |
| Assets ($1 M) | Assets | $524.23 | $961.34 | $206.53 | $317.09 |
| Liabilities ($1 M) | Liabilities | $212.69 | $542.10 | $70.82 | $125.23 |
| Color | Percentile Value | Lower Value | Higher Value |
|---|---|---|---|
| Blue | 0% | 0 | 0 |
| Blue Green | (0, 25%) | 1 | 749 |
| Green | 25% | 750 | 750 |
| Green Yellow | (25%, 50%) | 751 | 1499 |
| Yellow | 50% | 1500 | 1500 |
| Yellow Orange | (50%, 75%) | 1501 | 2249 |
| Orange | 75% | 2250 | 2250 |
| Orange Red | (75%, 100%) | 2251.00 | 2999.00 |
| Red | 100% | 3000.00 | 3000.00 |
| Feature | Gain |
|---|---|
| Staffed Beds | 10.09% |
| Surgeries | 9.79% |
| Liabilities | 7.27% |
| Affiliated Physicians | 7.07% |
| Net Income | 6.54% |
| ER Visits | 5.46% |
| % Medicare/caid | 5.32% |
| Employees | 5.20% |
| Year 2018 | 5.04% |
| Illinois | 4.35% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fulton, L.; Dong, Z.; Zhan, F.B.; Kruse, C.S.; Stigler Granados, P. Geospatial-Temporal and Demand Models for Opioid Admissions, Implications for Policy. J. Clin. Med. 2019, 8, 993. https://doi.org/10.3390/jcm8070993
Fulton L, Dong Z, Zhan FB, Kruse CS, Stigler Granados P. Geospatial-Temporal and Demand Models for Opioid Admissions, Implications for Policy. Journal of Clinical Medicine. 2019; 8(7):993. https://doi.org/10.3390/jcm8070993
Chicago/Turabian StyleFulton, Lawrence, Zhijie Dong, F. Benjamin Zhan, Clemens Scott Kruse, and Paula Stigler Granados. 2019. "Geospatial-Temporal and Demand Models for Opioid Admissions, Implications for Policy" Journal of Clinical Medicine 8, no. 7: 993. https://doi.org/10.3390/jcm8070993
APA StyleFulton, L., Dong, Z., Zhan, F. B., Kruse, C. S., & Stigler Granados, P. (2019). Geospatial-Temporal and Demand Models for Opioid Admissions, Implications for Policy. Journal of Clinical Medicine, 8(7), 993. https://doi.org/10.3390/jcm8070993







