The Influence of the Joint Volume on the Prevention of Impingement and Elbow-at-Side Rotations: Could the 36 mm Sphere with an Inferior Offset of 2 mm Be the New Gold Standard?
Abstract
1. Introduction
2. Materials and Methods
- -
- For the 36 mm diameter sphere, the following were used:
- Standard center: 36 + 0.
- Eccentric with 2 mm lower offset: 36 + 2.
- 5 mm lateralized (equivalent to a BIO (Biologic Increased Offset) or a MIO (Metallic Increased Offset)—RSA (Reverse Shoulder Arthroplasty): 36 + 5.
- 7 mm lateralized: 36 + 7.
- -
- For the 42 mm diameter sphere, the following were used:
- Standard center: 42 + 0.
- Offset by 7 mm: 42 + 7.
- Offset by 10 mm: 42 + 10.
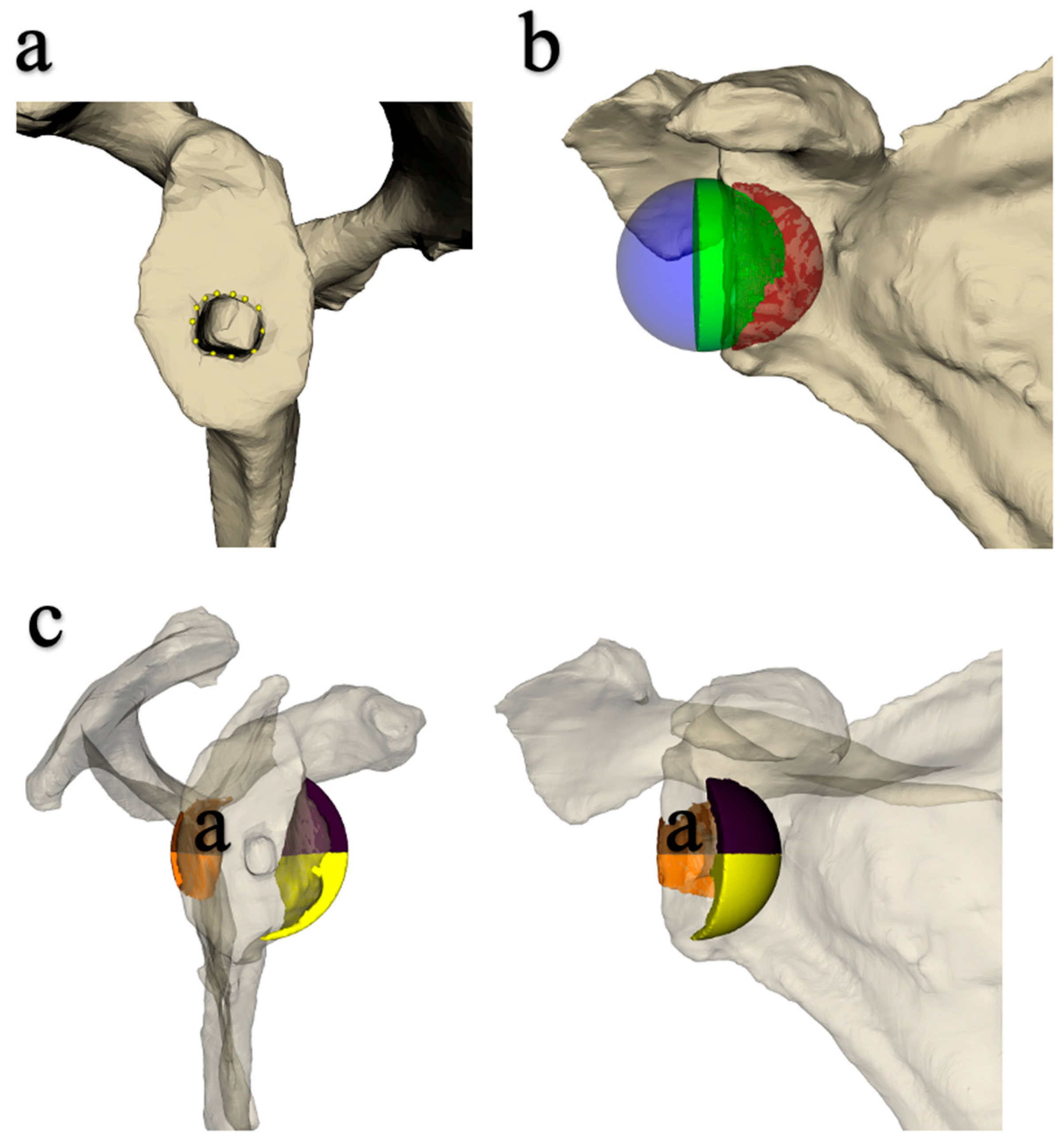
2.1. Implantation of the Prosthesis and Measurement of Joint Mobility
2.2. Data Acquisition Protocol
2.3. Statistical Analysis
3. Results
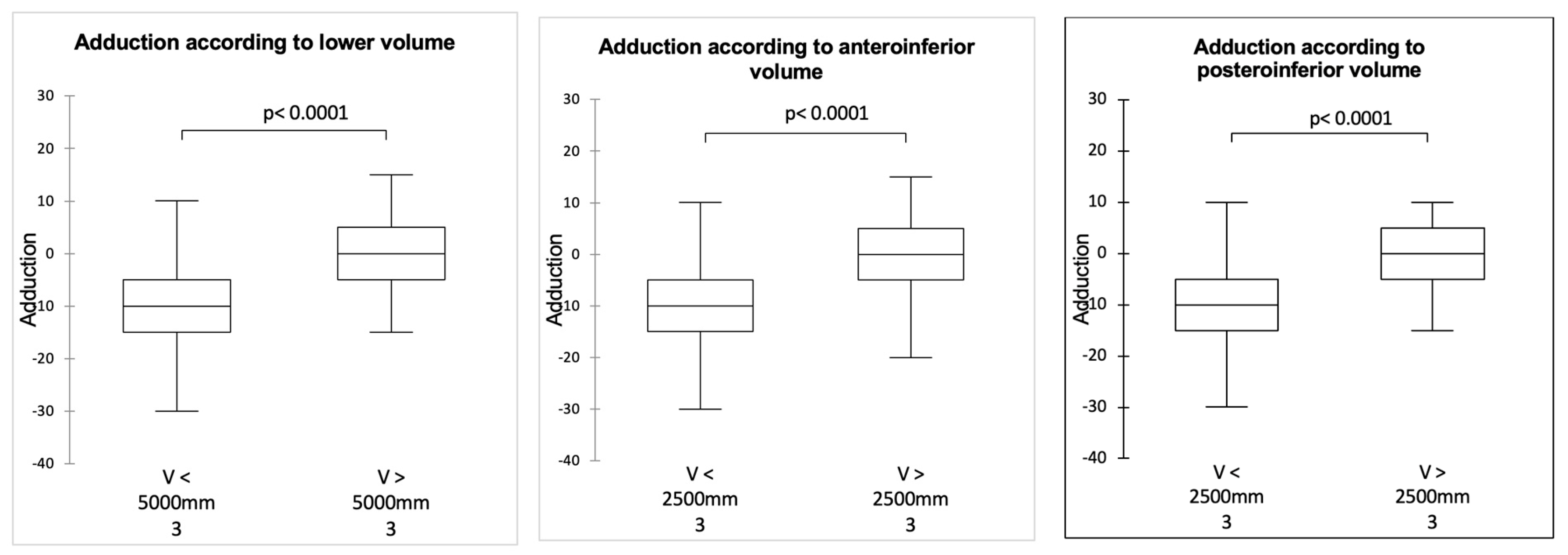
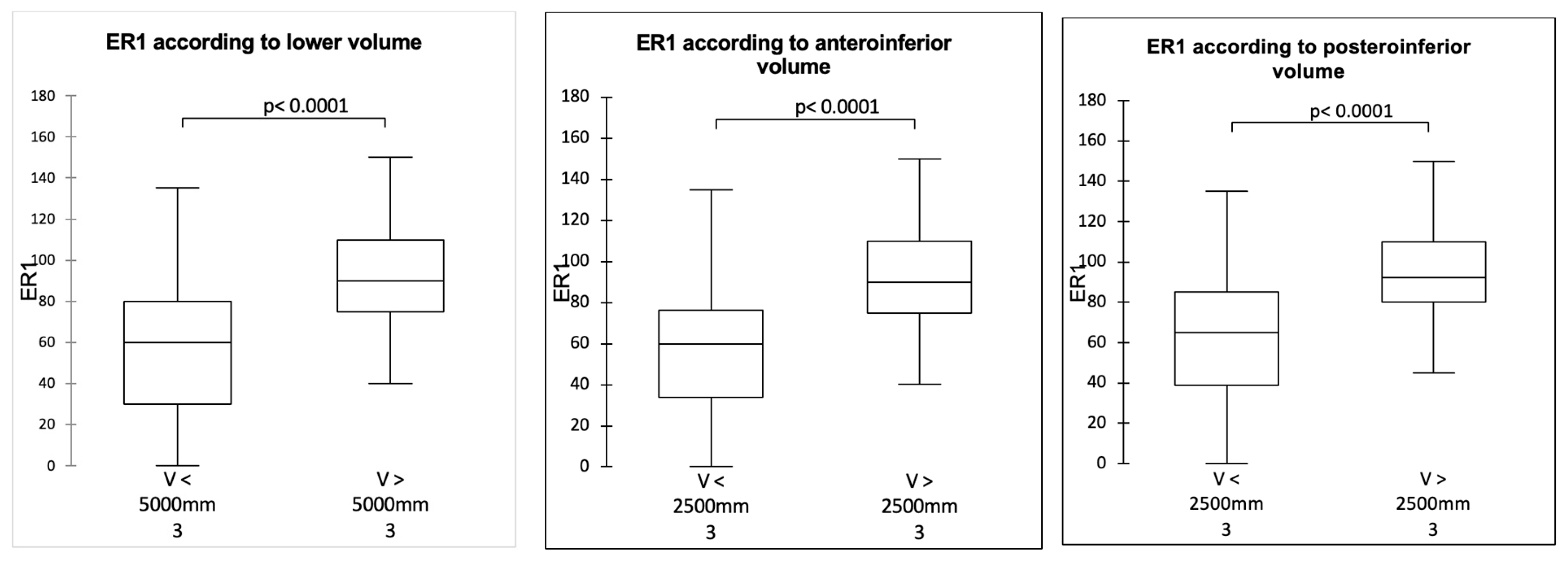
3.1. Influence of Sphere Design on Mobility in Adduction, ER1, and IR1 (Table 2, Table 3 and Table 4)
| 36 | 36 + 2 | 36 + 5 | 36 + 7 | 42 | 42 + 7 | 42 + 10 | |
|---|---|---|---|---|---|---|---|
| 36 | 1 | 0.037 | 0.007 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| 36 + 2 | 1 | 1.000 | 0.663 | 0.477 | 0.002 | <0.0001 | |
| 36 + 5 | 1 | 0.682 | 0.615 | 0.000 | <0.0001 | ||
| 36 + 7 | 1 | 1.000 | 0.020 | 0.000 | |||
| 42 | 1 | 0.318 | 0.016 | ||||
| 42 + 7 | 1 | 0.800 |
| 36 | 36 + 2 | 36 + 5 | 36 + 7 | 42 | 42 + 7 | 42 + 10 | |
|---|---|---|---|---|---|---|---|
| 36 | 1 | 0.010 | 0.126 | 0.001 | <0.0001 | <0.0001 | <0.0001 |
| 36 + 2 | 1 | 0.993 | 0.997 | 0.751 | 0.011 | 0.000 | |
| 36 + 5 | 1 | 0.661 | 0.139 | 0.000 | <0.0001 | ||
| 36 + 7 | 1 | 0.970 | 0.019 | 0.000 | |||
| 42 | 1 | 0.191 | 0.007 | ||||
| 42 + 7 | 1 | 0.902 |
| 36 | 36 + 2 | 36 + 5 | 36 + 7 | 42 | 42 + 7 | 42 + 10 | |
|---|---|---|---|---|---|---|---|
| 36 | 1 | 0.022 | 0.198 | 0.012 | <0.0001 | <0.0001 | <0.0001 |
| 36 + 2 | 1 | 0.976 | 1.000 | 0.868 | 0.191 | 0.099 | |
| 36 + 5 | 1 | 0.997 | 0.321 | 0.025 | 0.007 | ||
| 36 + 7 | 1 | 0.653 | 0.059 | 0.014 | |||
| 42 | 1 | 0.988 | 0.909 | ||||
| 42 + 7 | 1 | 1.000 |
3.2. Influence of Sphere Design on Joint Volume (Inferior, Posteroinferior and Anteroinferior)
3.3. Correlation Between Joint Volume and Mobility
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grammont Inverted Total Shoulder Arthroplasty in the Treatment of Glenohumeral Osteoarthritis with Massive Rupture of the Cuff. Results of a Multicentre Study of 80 Shoulders-PubMed. Available online: https://pubmed.ncbi.nlm.nih.gov/15125127/ (accessed on 2 January 2024).
- Chelli, M.; Boileau, P.; Domos, P.; Clavert, P.; Berhouet, J.; Collin, P.; Walch, G.; Favard, L. Survivorship of Reverse Shoulder Arthroplasty According to Indication, Age and Gender. J. Clin. Med. 2022, 11, 2677. [Google Scholar] [CrossRef] [PubMed]
- Kozak, T.; Bauer, S.; Walch, G.; Al-Karawi, S.; Blakeney, W. An Update on Reverse Total Shoulder Arthroplasty: Current Indications, New Designs, Same Old Problems. EFORT Open Rev. 2021, 6, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Larose, G.; Virk, M.S. The Evolution of Reverse Total Shoulder Arthroplasty and Its Current Use in the Treatment of Proximal Humerus Fractures in the Older Population. J. Clin. Med. 2022, 11, 5832. [Google Scholar] [CrossRef] [PubMed]
- Coward, J.C.; Bauer, S.; Babic, S.M.; Coron, C.; Okamoto, T.; Blakeney, W.G. Understanding Shoulder Pseudoparalysis. Part II: Treatment. EFORT Open Rev. 2022, 7, 227–239. [Google Scholar] [CrossRef]
- Boileau, P.; Morin-Salvo, N.; Bessière, C.; Chelli, M.; Gauci, M.-O.; Lemmex, D.B. Bony Increased-Offset-Reverse Shoulder Arthroplasty: 5 to 10 Years’ Follow-Up. J. Shoulder Elb. Surg. 2020, 29, 2111–2122. [Google Scholar] [CrossRef]
- Lévigne, C.; Boileau, P.; Favard, L.; Garaud, P.; Molé, D.; Sirveaux, F.; Walch, G. Scapular Notching in Reverse Shoulder Arthroplasty. J. Shoulder Elb. Surg. 2008, 17, 925–935. [Google Scholar] [CrossRef]
- Lévigne, C.; Garret, J.; Boileau, P.; Alami, G.; Favard, L.; Walch, G. Scapular Notching in Reverse Shoulder Arthroplasty: Is It Important to Avoid It and How? Clin. Orthop. Relat. Res. 2011, 469, 2512–2520. [Google Scholar] [CrossRef]
- Nyffeler, R.W.; Werner, C.M.L.; Simmen, B.R.; Gerber, C. Analysis of a Retrieved Delta III Total Shoulder Prosthesis. J. Bone Joint Surg. Br. 2004, 86, 1187–1191. [Google Scholar] [CrossRef]
- Boileau, P.; Watkinson, D.; Hatzidakis, A.M.; Hovorka, I. Neer Award 2005: The Grammont Reverse Shoulder Prosthesis: Results in Cuff Tear Arthritis, Fracture Sequelae, and Revision Arthroplasty. J. Shoulder Elb. Surg. 2006, 15, 527–540. [Google Scholar] [CrossRef]
- Rol, M.; Favard, L.; Berhouet, J. Factors Associated with Internal Rotation Outcomes after Reverse Shoulder Arthroplasty. Orthop. Traumatol. Surg. Res. 2019, 105, 1515–1519. [Google Scholar] [CrossRef]
- Huish, E.G.; Athwal, G.S.; Neyton, L.; Walch, G. Adjusting Implant Size and Position Can Improve Internal Rotation After Reverse Total Shoulder Arthroplasty in a Three-Dimensional Computational Model. Clin. Orthop. Relat. Res. 2021, 479, 198–204. [Google Scholar] [CrossRef] [PubMed]
- Gibian, J.T.; Sokrab, R.; Hill, J.R.; Keener, J.D.; Zmistowski, B.M. Predictors of Internal Rotation after Reverse Shoulder Arthroplasty. Arch. Bone Jt. Surg. 2023, 11, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Luster, T.G.; Dean, R.S.; Trasolini, N.A.; Eichinger, J.K.; Parada, S.A.; Ralston, R.K.; Waterman, B.R. Predictive Factors Influencing Internal Rotation Following Reverse Total Shoulder Arthroplasty. J. Shoulder Elb. Surg. 2024, 33, 1200–1208. [Google Scholar] [CrossRef] [PubMed]
- Rohman, E.; King, J.J.; Roche, C.P.; Fan, W.; Kilian, C.M.; Papandrea, R.F. Factors Associated with Improvement or Loss of Internal Rotation after Reverse Shoulder Arthroplasty. J. Shoulder Elb. Surg. 2022, 31, e346–e358. [Google Scholar] [CrossRef]
- Adam, M.F.; Lädermann, A.; Denard, P.J.; Lacerda, F.; Collin, P. Preoperative Diagnosis and Rotator Cuff Status Impact Functional Internal Rotation Following Reverse Shoulder Arthroplasty. J. Shoulder Elb. Surg. 2024, 33, 1570–1576. [Google Scholar] [CrossRef]
- Berhouet, J.; Garaud, P.; Slimane, M.; Nicot, J.; Banah, J.; Waynberger, E.; Favard, L. Effect of Scapular Pillar Anatomy on Scapular Impingement in Adduction and Rotation after Reverse Shoulder Arthroplasty. Orthop. Traumatol. Surg. Res. 2014, 100, 495–502. [Google Scholar] [CrossRef]
- Berhouet, J.; Samargandi, R.; Favard, L.; Turbillon, C.; Jacquot, A.; Gauci, M.-O. The Real Post-Operative Range of Motion Differs from the Virtual Pre-Operative Planned Range of Motion in Reverse Shoulder Arthroplasty. J. Pers. Med. 2023, 13, 765. [Google Scholar] [CrossRef]
- Baumgarten, K.M. Accuracy of Blueprint Software in Predicting Range of Motion 1 Year after Reverse Total Shoulder Arthroplasty. J. Shoulder Elb. Surg. 2023, 32, 1088–1094. [Google Scholar] [CrossRef]
- Thomas, L.G.; Chalmers, P.N.; Henninger, H.B.; Davis, E.W.; Tashjian, R.Z. Preoperative Planning Software Does Not Accurately Predict Range of Motion in Reverse Total Shoulder Arthroplasty. J. Am. Acad. Orthop. Surg. 2024, 32, e378–e386. [Google Scholar] [CrossRef]
- Kelly, J.D.; Humphrey, C.S.; Norris, T.R. Optimizing Glenosphere Position and Fixation in Reverse Shoulder Arthroplasty, Part One: The Twelve-Mm Rule. J. Shoulder Elb. Surg. 2008, 17, 589–594. [Google Scholar] [CrossRef]
- Falaise, V.; Levigne, C.; Favard, L. SOFEC Scapular Notching in Reverse Shoulder Arthroplasties: The Influence of Glenometaphyseal Angle. Orthop. Traumatol. Surg. Res. 2011, 97, S131–S137. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, S.; Levy, J.C.; Lee, W.E.; Keller, T.S.; Maitland, M.E. Center of Rotation Affects Abduction Range of Motion of Reverse Shoulder Arthroplasty. Clin. Orthop. Relat. Res. 2007, 458, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.M.; Nguyen, M.; Groneck, A. Internal Rotation Limitation Is Prevalent Following Modern Reverse Shoulder Arthroplasty and Negatively Affects Patients’ Subjective Rating of the Procedure. J. Shoulder Elb. Surg. 2024, 33, 2646–2654. [Google Scholar] [CrossRef] [PubMed]
- Bauer, S.; Blakeney, W.G.; Goyal, N.; Flayac, H.; Wang, A.; Corbaz, J. Posteroinferior Relevant Scapular Neck Offset in Reverse Shoulder Arthroplasty: Key Player for Motion and Friction-Type Impingement in a Computer Model. J. Shoulder Elb. Surg. 2022, 31, 2638–2646. [Google Scholar] [CrossRef]
- Kolmodin, J.; Davidson, I.U.; Jun, B.J.; Sodhi, N.; Subhas, N.; Patterson, T.E.; Li, Z.-M.; Iannotti, J.P.; Ricchetti, E.T. Scapular Notching After Reverse Total Shoulder Arthroplasty: Prediction Using Patient-Specific Osseous Anatomy, Implant Location, and Shoulder Motion. J. Bone Jt. Surg. 2018, 100, 1095–1103. [Google Scholar] [CrossRef]
- Simovitch, R.W.; Zumstein, M.A.; Lohri, E.; Helmy, N.; Gerber, C. Predictors of Scapular Notching in Patients Managed with the Delta III Reverse Total Shoulder Replacement. J. Bone Jt. Surg. Am. 2007, 89, 588–600. [Google Scholar] [CrossRef]
- Krämer, M.; Bäunker, A.; Wellmann, M.; Hurschler, C.; Smith, T. Implant Impingement during Internal Rotation after Reverse Shoulder Arthroplasty. The Effect of Implant Configuration and Scapula Anatomy: A Biomechanical Study. Clin. Biomech. 2016, 33, 111–116. [Google Scholar] [CrossRef]
- Simovitch, R.; Flurin, P.-H.; Wright, T.; Zuckerman, J.D.; Roche, C.P. Quantifying Success after Total Shoulder Arthroplasty: The Minimal Clinically Important Difference. J. Shoulder Elbow Surg. 2018, 27, 298–305. [Google Scholar] [CrossRef]
- Bauer, S.; Corbaz, J.; Athwal, G.S.; Walch, G.; Blakeney, W.G. Lateralization in Reverse Shoulder Arthroplasty. J. Clin. Med. 2021, 10, 5380. [Google Scholar] [CrossRef]
- Arenas-Miquelez, A.; Murphy, R.J.; Rosa, A.; Caironi, D.; Zumstein, M.A. Impact of Humeral and Glenoid Component Variations on Range of Motion in Reverse Geometry Total Shoulder Arthroplasty: A Standardized Computer Model Study. J. Shoulder Elb. Surg. 2021, 30, 763–771. [Google Scholar] [CrossRef]
- King, J.J.; Hones, K.M.; Wright, T.W.; Roche, C.; Zuckerman, J.D.; Flurin, P.H.; Schoch, B.S. Does Isolated Glenosphere Lateralization Affect Outcomes in Reverse Shoulder Arthroplasty? Orthop. Traumatol. Surg. Res. 2023, 109, 103401. [Google Scholar] [CrossRef] [PubMed]
- Berhouet, J.; Samargandi, R.; Jacquot, A.; Favard, L.; Boileau, P.; Gauci, M.-O. Restoration of Internal Rotation after Reverse Shoulder Arthroplasty May Vary Depending on Etiology in Patients Younger than 60 Years of Age: A Multicenter Retrospective Study. J. ISAKOS 2024, 9, 620–627. [Google Scholar] [CrossRef] [PubMed]
- Werner, B.S.; Ascione, F.; Bugelli, G.; Walch, G. Does Arm Lengthening Affect the Functional Outcome in Onlay Reverse Shoulder Arthroplasty? J. Shoulder Elb. Surg. 2017, 26, 2152–2157. [Google Scholar] [CrossRef] [PubMed]
- Nyffeler, R.W.; Werner, C.M.L.; Gerber, C. Biomechanical Relevance of Glenoid Component Positioning in the Reverse Delta III Total Shoulder Prosthesis. J. Shoulder Elb. Surg. 2005, 14, 524–528. [Google Scholar] [CrossRef]
- Haidamous, G.; Cabarcas, B.; Ohanisian, L.; Simon, P.; Christmas, K.N.; Wilder, L.; Achors, K.; Mighell, M.A.; Frankle, M.A. Does Improved External Rotation Following Reverse Shoulder Arthroplasty Impact Clinical Outcomes in Patients with Rotator Cuff Pathology and External Rotation Less than 0°? J. Shoulder Elb. Surg. 2023, 32, 68–75. [Google Scholar] [CrossRef]



| Sphere | Supply (°) | ER1 (°) | IR1(°) | Lower Volume (mm’) | Anteroinferior Volume (mm’) | Posteroinferior Volume (mm’) |
|---|---|---|---|---|---|---|
| 36 | −16.5 [−35–5] | 32.4 [0–125] | 28.2 [0–100] | 2419.9 [1349.2–4091.6] | 1444.9 [342.5–2260.7] | 973.6 [89.4–1957] |
| 36 + 2 | −9.3 [−30–15] | 64.6 [0–135] | 55.9 [0–130] | 2855.6 [1580.5–4451.8] | 1713.0 [435.5–2369.9] | 1138.7 [299–2126.3] |
| 36 + 5 | −9.1 [−20–5] | 55.9 [0–135] | 48.2 [0–100] | 3465.6 [2589.5–4552.1] | 1866.4 [1301.7–2408.9] | 1597.6 [946.8–2189.9] |
| 36 + 7 | −6.3 [−20–10] | 70.4 [0–130] | 54.7 [0–105] | 3980.7 [3264.8–4797.5] | 2078.2 [1762.7–2507.4] | 1899.5 [1402.4–2326.8] |
| 42 | −5.1 [−25–15] | 77.2 [−0–150] | 67.6 [0–140] | 5453.5 [3907.7–7527.3] | 3102.0 [1636.2–4143.3] | 2346.6 [1075.6–3652.6] |
| 42 + 7 | −0.7 [−15–10] | 94.1 [45–145] | 74.7 [15–120] | 6850.0 [5497.7–7961] | 3619.0 [2759.7–4352.6] | 3225.5 [2218.7–3826.1] |
| 42 + 10 | 1.8 [−15–10] | 101.0 [55–145] | 77.5 [20–125] | 7606.3 [6518.6–8505.8] | 3923.8 [3416.5–4494.5] | 3678.3 [2929.7–4175.6] |
| 36 + 2 mm Sphere | 36 + 5 mm Sphere | 36 + 7 mm Sphere | 42 + 0 Sphere | |
|---|---|---|---|---|
| Inferior volume | 18% | 43% | 65% | 125% |
| Anteroinferior volume | 19% | 29% | 44% | 115% |
| Posteroinferior volume | 17% | 64% | 95% | 141% |
| 42 + 7 Sphere | 42 + 10 Sphere | |
|---|---|---|
| Inferior volume | 26% | 39% |
| Anteroinferior volume | 17% | 26% |
| Posteroinferior volume | 37% | 57% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Besnard, M.; Samargandi, R.; Abualross, O.; Berhouet, J. The Influence of the Joint Volume on the Prevention of Impingement and Elbow-at-Side Rotations: Could the 36 mm Sphere with an Inferior Offset of 2 mm Be the New Gold Standard? J. Clin. Med. 2025, 14, 2324. https://doi.org/10.3390/jcm14072324
Besnard M, Samargandi R, Abualross O, Berhouet J. The Influence of the Joint Volume on the Prevention of Impingement and Elbow-at-Side Rotations: Could the 36 mm Sphere with an Inferior Offset of 2 mm Be the New Gold Standard? Journal of Clinical Medicine. 2025; 14(7):2324. https://doi.org/10.3390/jcm14072324
Chicago/Turabian StyleBesnard, Marion, Ramy Samargandi, Osamah Abualross, and Julien Berhouet. 2025. "The Influence of the Joint Volume on the Prevention of Impingement and Elbow-at-Side Rotations: Could the 36 mm Sphere with an Inferior Offset of 2 mm Be the New Gold Standard?" Journal of Clinical Medicine 14, no. 7: 2324. https://doi.org/10.3390/jcm14072324
APA StyleBesnard, M., Samargandi, R., Abualross, O., & Berhouet, J. (2025). The Influence of the Joint Volume on the Prevention of Impingement and Elbow-at-Side Rotations: Could the 36 mm Sphere with an Inferior Offset of 2 mm Be the New Gold Standard? Journal of Clinical Medicine, 14(7), 2324. https://doi.org/10.3390/jcm14072324






