Improving Sepsis Prediction in the ICU with Explainable Artificial Intelligence: The Promise of Bayesian Networks
Abstract
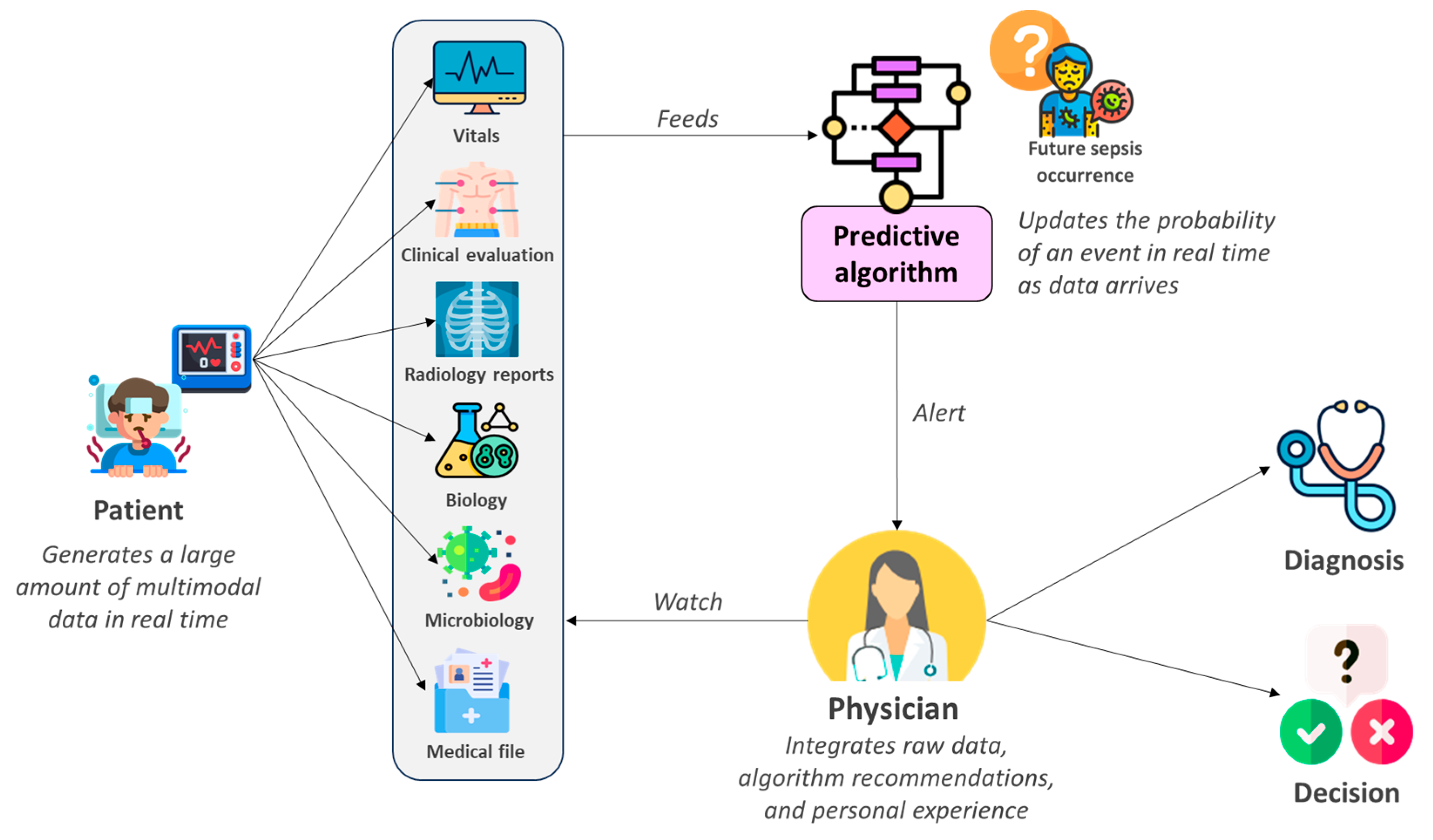
1. Introduction
2. Why Are Traditional AI Models Struggling to Gain Acceptance in Intensive Care?
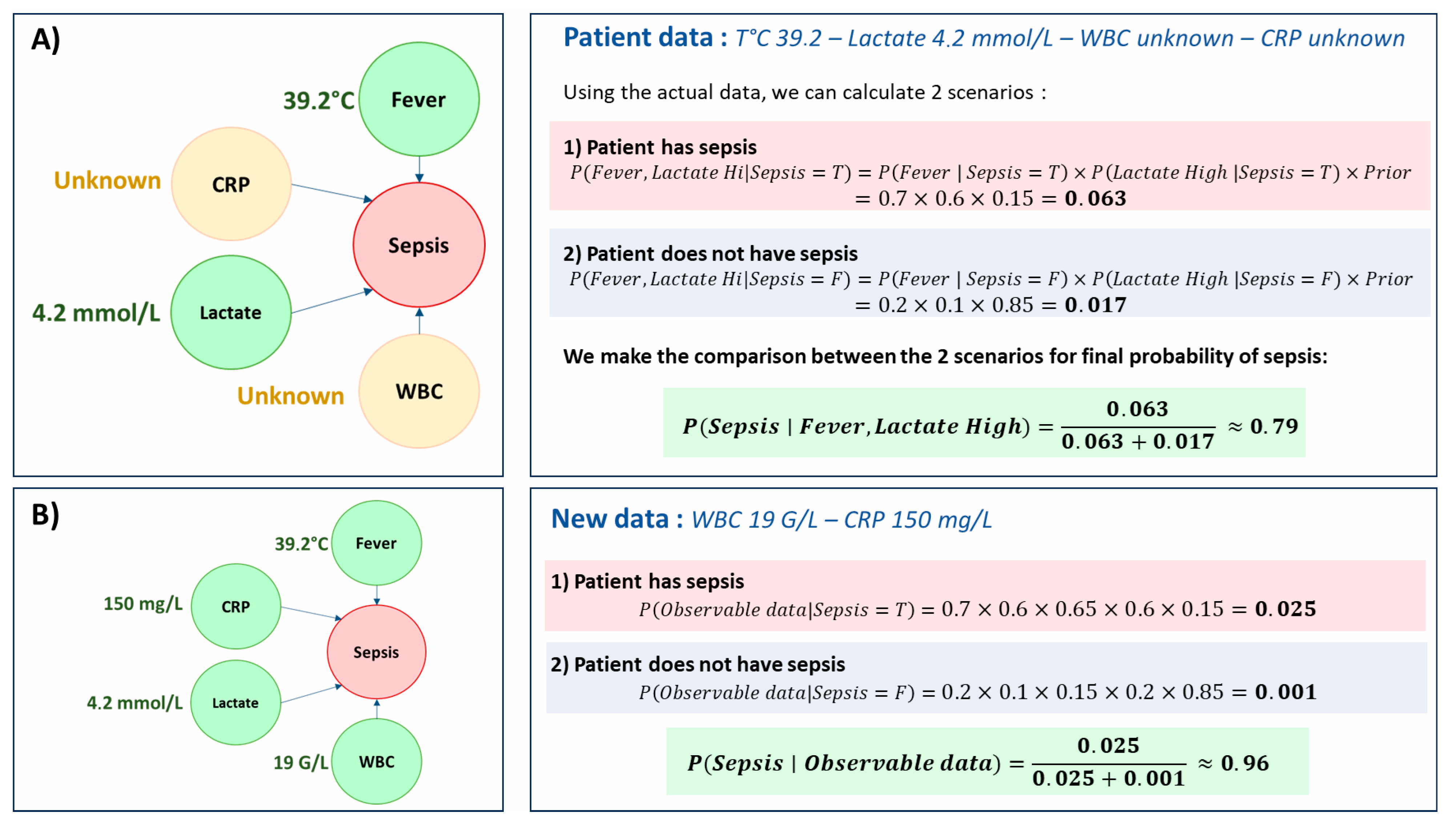
3. Conditional Probability Models: Principles and Foundations
3.1. Definition
- H: a hypothesis (e.g., “the patient has sepsis”),
- D: observed data (e.g., “elevated lactate levels”),
- P(H): the prior probability of the hypothesis (without knowledge of the test),
- P(D∣H): the likelihood, i.e., the probability of observing D if H is true,
- P(D): the total probability of observing D (all causes combined),
- P(H∣D): the posterior probability, i.e., the revised belief about H after seeing D.
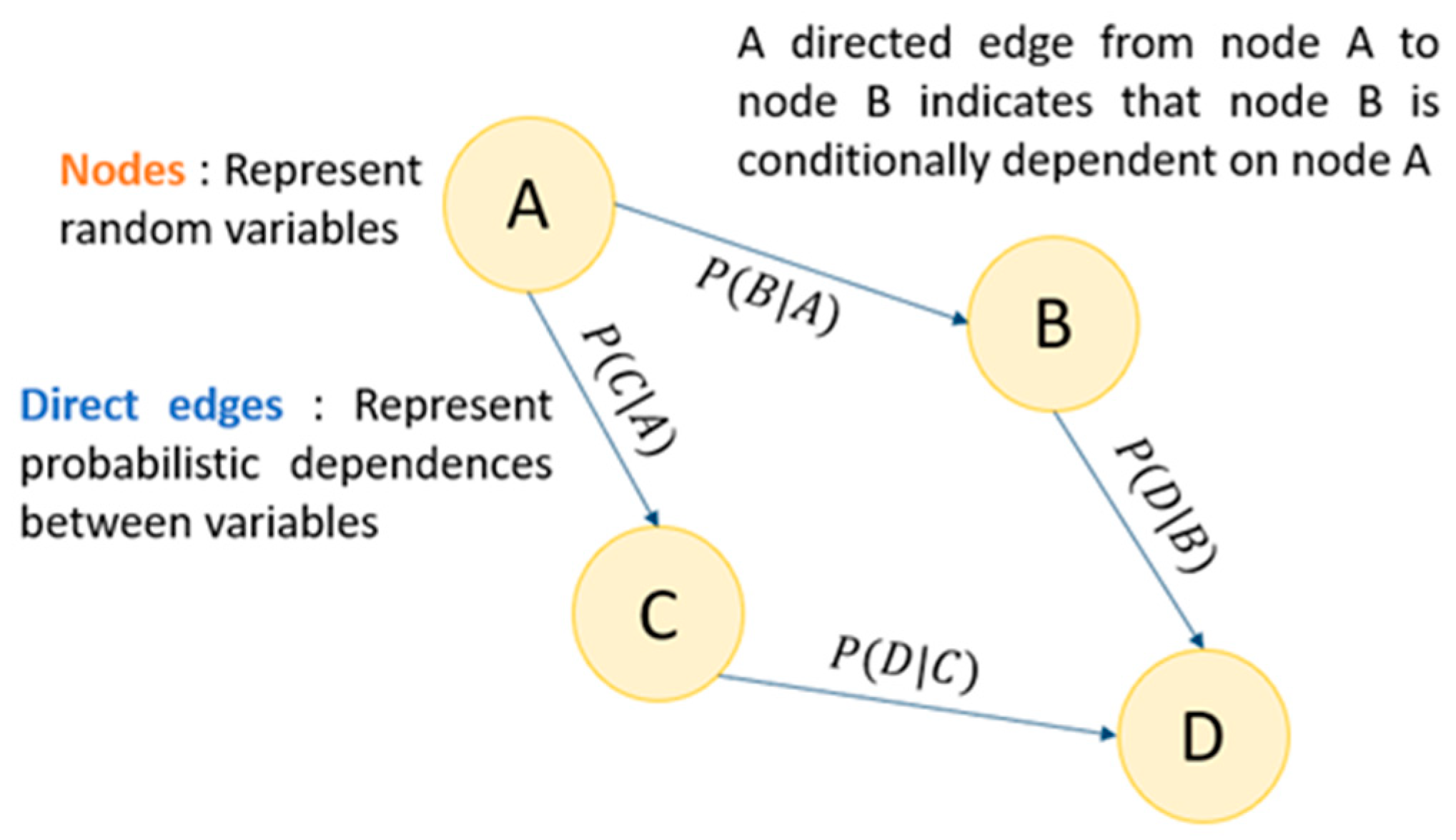
3.2. Bayesian Network Structure
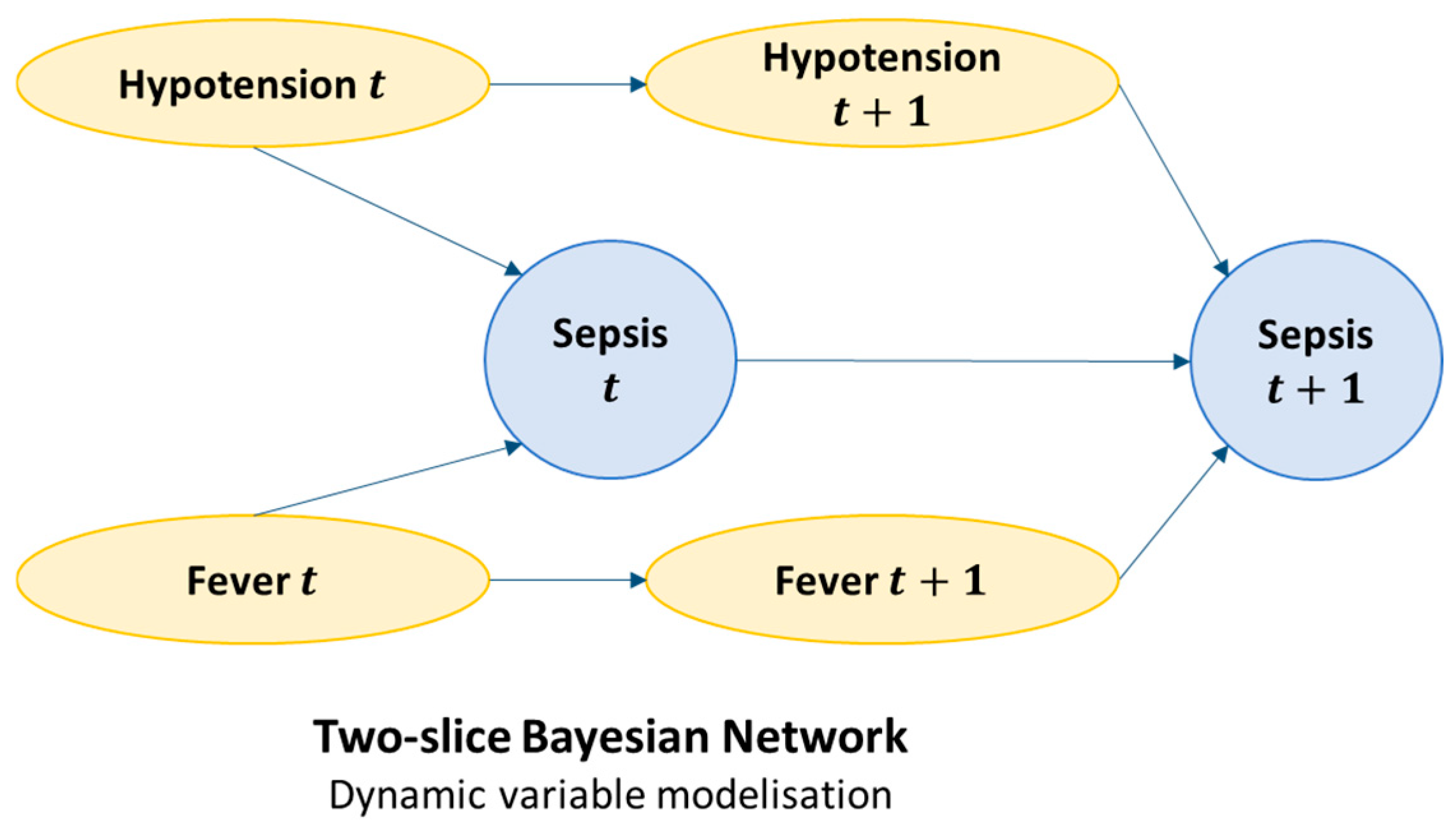
3.3. Dynamic Bayesian Model (DBN) and Real Time Prediction
3.4. Construction and Learning Methodology
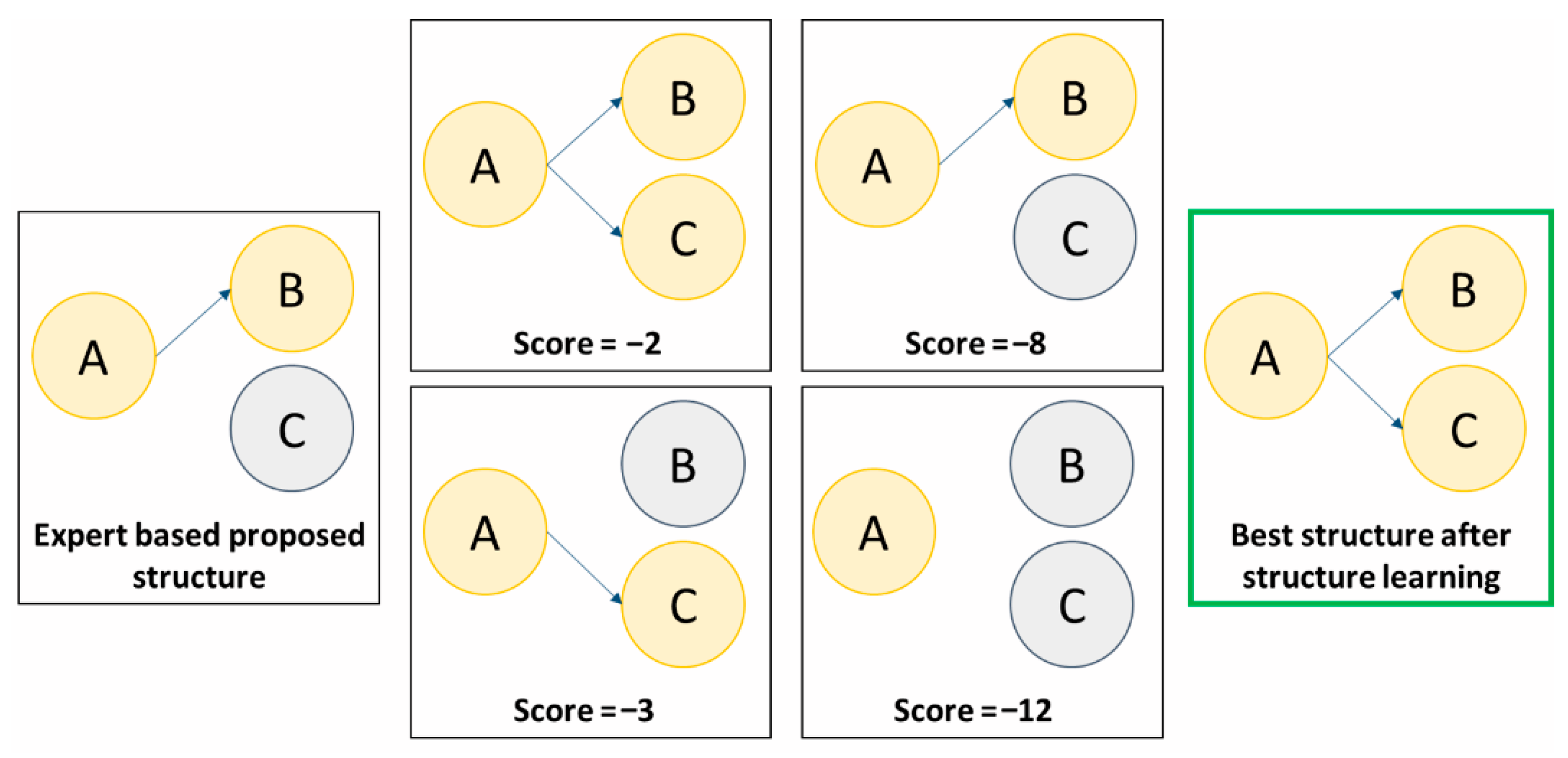
3.4.1. Building the Network Structure
3.4.2. Network Probability Learning
Frequentist Methods
Bayesian Methods
3.4.3. Validation of the Learned Network
- Quantitative evaluation: Often based on predictive performance metrics (AUROC, sensitivity, specificity, positive and negative predictive value, likelihood ratio and accuracy), but also on more global scores (Bayesian Information Criterion or Akaike Information Criterion). This analysis makes it possible to verify the clinical usefulness of the BN and compare it to other algorithms or scores available for the same prediction task.
- Qualitative evaluation: This is more a matter for the domain expert, who is responsible for verifying the pathophysiological consistency between the various relationships established by the network. This “expert-based” verification makes it possible to check that the structure learning has not implemented false relationships between variables (e.g., fever increases the leukocyte count).
4. Why Does Modeling Clinical Relationships Change the Game in Predicting Sepsis?
5. Practical Applications of Bayesian Models in Predicting Sepsis
5.1. Early Diagnosis Assistance
5.2. Assistance with Sorting and Prognosis
5.3. Assistance with Treatment Strategy
| Study | Prediction Outcome | Algorithms | Main Results | Population | Prediction Horizon | Data Used in Algorithm |
|---|---|---|---|---|---|---|
| Nachimuthu & Haug, 2012 [30] | Sepsis: SIRS (at least 2 criterions) + suspected infection | Dynamic Bayesian Networks (DBN) | DBN: AUROC: 0.94 Se 0.86; Sp 0.95 | ER patients; n = 741 patients. | Prediction of sepsis within the first 24 h | WBC, immature neutrophil %, HR, MAP, DBP, SBP, temperature, RR, PaCO2, age |
| Henry et al., 2015 [14] | Septic shock: Sepsis (SIRS + suspected infection) + hypotension after ≥20 mL/kg fluid resuscitation in past 24 h | TREWScore: Cox model Comparators: SIRS, MEWS | TREWScore: AUROC: 0.83 Sp 0.67; Se 0.85 SIRS: Se 0.74; Sp 0.64 | MIMIC-II database. n = 16,234 patients. | Real-time risk update with no fixed window | GCS, platelets, BUN/creatinine ratio, arterial pH, temperature, RR, WBC, bicarbonate, HR/SBP (shock index), SBP, HR |
| Haug et Ferraro, 2016 [38] | Sepsis: Retrospective identification by ICD codes in EHR. | - Bayesian Network (BN) - Tree-Augmented Naïve Bayesian Network (TAN) | BN: AUROC: 0.97 Se 0.60; PPV: 0.38 TAN: AUROC: 0.97 Se 0.60; PPV: 0.37 | ER patients. n = 186,725 patients | Prediction using data from first 90 min | Age, MAP, temperature, HR, WBC |
| Desautels et al., 2016 [32] | Sepsis: SEPSIS-III criteria | Insight (Gradient Tree Boosting) Comparators: SOFA, qSOFA, MEWS, SIRS | Insight: AUROC: 0.74 Se 0.80; Sp 0.54 SOFA: AUROC: 0.73 Se 0.80; Sp 0.48 | MIMIC-III dataset. n = 22,853 ICU stays. | Sepsis prediction 4 h in advance using 2-h window | Age, RR, DBP, SBP, temperature, SaO2, GCS |
| Barton et al., 2019 [39] | Sepsis: SEPSIS-III criteria | XGBoost Comparators: SOFA, qSOFA, MEWS, SIRS | XGBoost: AUROC: 0.84 Se 0.80; Sp 0.72 SOFA: AUROC: 0.72 Se 0.78; Sp 0.59 | MIMIC-III n = 21,507 patients | Sepsis prediction up to 24 h in advance | SaO2, HR, SBP, DBP, temperature, RR |
| Gupta et al., 2020 [27] | Sepsis: SEPSIS-III criteria Diagnosis inferred via mortality | Tree-Augmented Naïve Bayesian Network (TAN) Comparators: SIRS, qSOFA, MEWS, SOFA scores | TAN: AUROC: 0.84 Se 0.71; Sp 0.80 SOFA: AUROC: 0.80 Se 0.71; Sp 0.75 | Cerner Corporations HIPAA-compliant Health Facts database n = 63 million patients | Real-time sepsis risk update as data arrives | SBP, GCS, RR, WBC, creatinine, PaO2/FiO2 |
| Shashikumar et al., 2021 [40] | Sepsis: SEPSIS-III criteria | Deep Artificial Intelligence Sepsis Expert (DeepAISE): Gated Recurrent Unit multi-layer deep network | DeepAISE: AUROC: 0.90 Se 0.85; Sp 0.80 | ICU patients. n = 25,820 patients | Sepsis prediction 4 h in advance | 65 features incl. MAP, HR, SpO2, SBP, DBP, RR, GCS, PaO2, FiO2, WBC, creatinine, BUN, lactate, CRP, demographics |
| Valik et al., 2023 [31] | Sepsis: SEPSIS-III criteria | SepsisFinder (CPN) Comparators: LightGBM, NEWS2 | SepsisFinder: AUROC: 0.95 Se 0.85; Sp 0.97 LightGBM: AUROC: 0.949 | Non-ICU hospital admissions n = 55,655 | Sepsis prediction within 48 h | HR, MAP, RR, SpO2, O2 flow, GCS, CRP, WBC, platelets, bilirubin, creatinine, BUN, albumin, lactate, HCO3, pH, department, time since surgery |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| AUROC | Area Under the Receiver Operating Characteristic Curve |
| BN | Bayesian Network |
| BUN | Blood Urea Nitrogen |
| CRP | C-Reactive Protein |
| CPT | Conditional Probability Table |
| DBN | Dynamic Bayesian Network |
| DBP | Diastolic Blood Pressure |
| EHR | Electronic Health Record |
| FiO2 | Fraction of Inspired Oxygen |
| GCS | Glasgow Coma Scale |
| HR | Heart Rate |
| MAP | Mean Arterial Pressure |
| MEWS | Modified Early Warning Score |
| MIMIC | Medical Information Mart for Intensive Care |
| O2 flow | Oxygen Flow Rate |
| PaCO2 | Partial Pressure of Arterial Carbon Dioxide |
| PaO2/FiO2 | Partial Pressure of Arterial Oxygen/Fraction of Inspired Oxygen |
| pH | Arterial pH |
| PPV | Positive Predictive Value |
| qSOFA | quick Sequential Organ Failure Assessment |
| RR | Respiratory Rate |
| SaO2 | Arterial Oxygen Saturation |
| SBP | Systolic Blood Pressure |
| Se | Sensitivity |
| SIRS | Systemic Inflammatory Response Syndrome |
| SOFA | Sequential Organ Failure Assessment |
| Sp | Specificity |
| SpO2 | Peripheral Oxygen Saturation |
| TAN | Tree-Augmented Naive Bayes |
| T° | Temperature |
| WBC | White Blood Cell count |
| xAI | Explainable Artificial Intelligence |
References
- Rudd, K.E.; Johnson, S.C.; Agesa, K.M.; Shackelford, K.A.; Tsoi, D.; Kievlan, D.R.; Colombara, D.V.; Ikuta, K.S.; Kissoon, N.; Finfer, S.; et al. Global, regional, and national sepsis incidence and mortality, 1990–2017: Analysis for the Global Burden of Disease Study. Lancet 2020, 395, 200–211. [Google Scholar] [CrossRef] [PubMed]
- Singer, M.; Deutschman, C.S.; Seymour, C.W.; Shankar-Hari, M.; Annane, D.; Bauer, M.; Bellomo, R.; Bernard, G.R.; Chiche, J.D.; Coopersmith, C.M.; et al. The Third International Consensus Definitions for Sepsis and Septic Shock (Sepsis-3). JAMA 2016, 315, 801–810. [Google Scholar] [CrossRef] [PubMed]
- Evans, L.; Rhodes, A.; Alhazzani, W.; Antonelli, M.; Coopersmith, C.M.; French, C.; Machado, F.R.; Mcintyre, L.; Ostermann, M.; Prescott, H.C.; et al. Surviving sepsis campaign: International guidelines for management of sepsis and septic shock 2021. Crit. Care Med. 2021, 11, e1063–e1143. [Google Scholar] [CrossRef]
- Seymour, C.W.; Gesten, F.; Prescott, H.C.; Friedrich, M.E.; Iwashyna, T.J.; Phillips, G.S.; Lemeshow, S.; Osborn, T.; Terry, K.M.; Levy, M.M. Time to Treatment and Mortality during Mandated Emergency Care for Sepsis. N. Engl. J. Med. 2017, 376, 2235–2244. [Google Scholar] [CrossRef] [PubMed]
- Liu, V.X.; Fielding-Singh, V.; Greene, J.D.; Baker, J.M.; Iwashyna, T.J.; Bhattacharya, J.; Escobar, G.J. The Timing of Early Antibiotics and Hospital Mortality in Sepsis. Am. J. Respir. Crit. Care Med. 2017, 196, 856–863. [Google Scholar] [CrossRef]
- Isaranuwatchai, S.; Buppanharun, J.; Thongbun, T.; Thavornwattana, K.; Harnphadungkit, M.; Siripongboonsitti, T. Early antibiotics administration reduces mortality in sepsis patients in tertiary care hospital. BMC Infect. Dis. 2025, 25, 136. [Google Scholar] [CrossRef]
- Adams, R.; Henry, K.E.; Sridharan, A.; Soleimani, H.; Zhan, A.; Rawat, N.; Johnson, L.; Hager, D.N.; Cosgrove, S.E.; Markowski, A.; et al. Prospective, multi-site study of patient outcomes after implementation of the TREWS machine learning-based early warning system for sepsis. Nat. Med. 2022, 28, 1455–1460. [Google Scholar] [CrossRef]
- Lauritsen, S.M.; Kalør, M.E.; Kongsgaard, E.L.; Lauritsen, K.M.; Jørgensen, M.J.; Lange, J.; Thiesson, B. Early detection of sepsis utilizing deep learning on electronic health record event sequences. Artif. Intell. Med. 2020, 104, 101820. [Google Scholar] [CrossRef]
- Van de Sande, D.; van Genderen, M.E.; Huiskens, J.; Gommers, D.; van Bommel, J. Moving from bytes to bedside: A systematic review on the use of artificial intelligence in the intensive care unit. Intensive Care Med. 2021, 47, 750–760. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. 2019, 51, 1–42. [Google Scholar] [CrossRef]
- Champendal, M.; Müller, H.; Prior, J.O.; dos Reis, C.S. A scoping review of interpretability and explainability concerning artificial intelligence methods in medical imaging. Eur. J. Radiol. 2023, 169, 111159. [Google Scholar] [CrossRef]
- Goh, G.S.W.; Lapuschkin, S.; Weber, L.; Samek, W.; Binder, A. Understanding Integrated Gradients with SmoothTaylor for Deep Neural Network Attribution. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 4949–4956. [Google Scholar] [CrossRef]
- Gavito, A.T.; Klabjan, D.; Utke, J. Multi-Layer Attention-Based Explainability via Transformers for Tabular Data. arXiv 2024. [Google Scholar] [CrossRef]
- Henry, K.E.; Hager, D.N.; Pronovost, P.J.; Saria, S. A targeted real-time early warning score (TREWScore) for septic shock. Sci. Transl. Med. 2015, 7, 299ra122. [Google Scholar] [CrossRef] [PubMed]
- Polotskaya, K.; Muñoz-Valencia, C.S.; Rabasa, A.; Quesada-Rico, J.A.; Orozco-Beltrán, D.; Barber, X. Bayesian Networks for the Diagnosis and Prognosis of Diseases: A Scoping Review. Mach. Learn. Knowl. Extr. 2024, 6, 1243–1262. [Google Scholar] [CrossRef]
- Pearl, J. From Bayesian Networks to Causal Networks. In Mathematical Models for Handling Partial Knowledge in Artificial Intelligence; Springer: Boston, MA, USA, 1995; pp. 157–182. Available online: https://link.springer.com/chapter/10.1007/978-1-4899-1424-8_9 (accessed on 10 August 2025).
- Russell, S.J.; Norvig, P.; Davis, E. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010; p. 1132. [Google Scholar]
- Schupbach, J.; Pryor, E.; Webster, K.; Sheppard, J. Combining Dynamic Bayesian Networks and Continuous Time Bayesian Networks for Diagnostic and Prognostic Modeling. In Proceedings of the 2022 IEEE AUTOTESTCON, National Harbor, MD, USA, 29 August–1 September 2022; pp. 1–8. Available online: https://ieeexplore.ieee.org/document/9984758/ (accessed on 10 August 2025).
- Tsamardinos, I.; Brown, L.E.; Aliferis, C.F. The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 2006, 65, 31–78. [Google Scholar] [CrossRef]
- Scutari, M.; Graafland, C.E.; Gutiérrez, J.M. Who Learns Better Bayesian Network Structures: Accuracy and Speed of Structure Learning Algorithms. arXiv 2019. [Google Scholar] [CrossRef]
- Kochenderfer, M.J.; Wheeler, T.A.; Wray, K.H. Algorithms for Decision Making; MIT Press: Cambridge, MA, USA, 2022; p. 1. [Google Scholar]
- Ben, F.; Kalti, K.; Ali, M. The threshold EM algorithm for parameter learning in bayesian network with incomplete data. Int. J. Adv. Comput. Sci. Appl. 2011, 2. [Google Scholar] [CrossRef][Green Version]
- Nicora, G.; Catalano, M.; Bortolotto, C.; Achilli, M.F.; Messana, G.; Lo Tito, A.; Consonni, A.; Cutti, S.; Comotto, F.; Stella, G.M.; et al. Bayesian Networks in the Management of Hospital Admissions: A Comparison between Explainable AI and Black Box AI during the Pandemic. J. Imaging 2024, 10, 117. [Google Scholar] [CrossRef]
- Health C for D and R. Artificial Intelligence in Software as a Medical Device. FDA. 2025. Available online: https://www.fda.gov/medical-devices/software-medical-device-samd/artificial-intelligence-software-medical-device (accessed on 19 July 2025).
- Zagzebski, L.T. Virtues of the Mind: An Inquiry into the Nature of Virtue and the Ethical Foundations of Knowledge; Cambridge University Press: New York, NY, USA, 1996; p. 365. [Google Scholar]
- Kidd, I.J. Intellectual Humility, Confidence, and Argumentation. Topoi 2016, 35, 395–402. [Google Scholar] [CrossRef]
- Gupta, A.; Liu, T.; Shepherd, S. Clinical decision support system to assess the risk of sepsis using Tree Augmented Bayesian networks and electronic medical record data. Health Inform. J. 2020, 26, 841–861. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, J.; Xu, X.; Yin, C.; Lu, Y.; Yao, B.; Tory, M.; Padilla, L.M.; Caterino, J.; Zhang, P.; et al. Rethinking Human-AI Collaboration in Complex Medical Decision Making: A Case Study in Sepsis Diagnosis. In Proceedings of the 2024 CHI Conference on Human Factors in Computing System, Honolulu, HI, USA, 11–16 May 2024; pp. 1–18. [Google Scholar] [CrossRef]
- Senoner, J.; Schallmoser, S.; Kratzwald, B.; Feuerriegel, S.; Netland, T. Explainable AI improves task performance in human-AI collaboration. arXiv 2024. [Google Scholar] [CrossRef] [PubMed]
- Nachimuthu, S.K.; Haug, P.J. Early detection of sepsis in the emergency department using Dynamic Bayesian Networks. AMIA Annu. Symp. Proc. 2012, 2012, 653–662. [Google Scholar]
- Valik, J.K.; Ward, L.; Tanushi, H.; Johansson, A.F.; Färnert, A.; Mogensen, M.L.; Pickering, B.W.; Herasevich, V.; Dalianis, H.; Henriksson, A.; et al. Predicting sepsis onset using a machine learned causal probabilistic network algorithm based on electronic health records data. Sci. Rep. 2023, 13, 11760. [Google Scholar] [CrossRef]
- Desautels, T.; Calvert, J.; Hoffman, J.; Jay, M.; Kerem, Y.; Shieh, L.; Shimabukuro, D.; Chettipally, U.; Feldman, M.D.; Barton, C.; et al. Prediction of Sepsis in the Intensive Care Unit With Minimal Electronic Health Record Data: A Machine Learning Approach. JMIR Med. Inform. 2016, 4, e5909. [Google Scholar] [CrossRef]
- Agard, G.; Roman, C.; Guervilly, C.; Forel, J.-M.; Orléans, V.; Barrau, D.; Auquier, P.; Ouladsine, M.; Boyer, L.; Hraiech, S. An Innovative Deep Learning Approach for Ventilator-Associated Pneumonia (VAP) Prediction in Intensive Care Units—Pneumonia Risk Evaluation and Diagnostic Intelligence via Computational Technology (PREDICT). J. Clin. Med. 2025, 14, 3380. [Google Scholar] [CrossRef]
- Wang, T.; Velez, T.; Apostolova, E.; Tschampel, T.; Ngo, T.L.; Hardison, J. Semantically Enhanced Dynamic Bayesian Network for Detecting Sepsis Mortality Risk in ICU Patients with Infection. arXiv 2018. [Google Scholar] [CrossRef]
- Peelen, L.; de Keizer, N.F.; de Jonge, E.; Bosman, R.-J.; Abu-Hanna, A.; Peek, N. Using hierarchical dynamic Bayesian networks to investigate dynamics of organ failure in patients in the Intensive Care Unit. J. Biomed. Inform. 2010, 43, 273–286. [Google Scholar] [CrossRef]
- Leibovici, L.; Paul, M.; Nielsen, A.D.; Tacconelli, E.; Andreassen, S. The TREAT project: Decision support and prediction using causal probabilistic networks. Int. J. Antimicrob. Agents 2007, 30, 93–102. [Google Scholar] [CrossRef]
- Petrungaro, B.; Kitson, N.K. Constantinou AC. Investigating potential causes of Sepsis with Bayesian network structure learning. arXiv 2025. [Google Scholar] [CrossRef]
- Haug, P.; Ferraro, J. Using a Semi-Automated Modeling Environment to Construct a Bayesian, Sepsis Diagnostic System. In Proceedings of the 7th ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics, Seattle, WA, USA, 2–5 October 2016; pp. 571–578. [Google Scholar] [CrossRef]
- Barton, C.; Chettipally, U.; Zhou, Y.; Jiang, Z.; Lynn-Palevsky, A.; Le, S.; Calvert, J.; Das, R. Evaluation of a machine learning algorithm for up to 48-hour advance prediction of sepsis using six vital signs. Comput. Biol. Med. 2019, 109, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Shashikumar, S.P.; Josef, C.S.; Sharma, A.; Nemati, S. DeepAISE—An interpretable and recurrent neural survival model for early prediction of sepsis. Artif. Intell. Med. 2021, 113, 102036. [Google Scholar] [CrossRef]
- Li, F.; Ding, P.; Mealli, F. Bayesian causal inference: A critical review. Philos. Trans. R. Soc. A 2023, 381, 20220153. [Google Scholar] [CrossRef]
- Kungurtsev, V.; Idlahcen, F.; Rysavy, P.; Rytir, P.; Wodecki, A. Learning Dynamic Bayesian Networks from Data: Foundations, First Principles and Numerical Comparisons. arXiv 2024. [Google Scholar] [CrossRef]
- U.S. Food & Drug Administration. Clinical Decision Support Software—Guidance for Industry and Food and Drug Administration Staff; U.S. Food & Drug Administration: Silver Spring, MD, USA, 2022. [Google Scholar]
- Mello, M.M.; Guha, N. Understanding Liability Risk from Using Health Care Artificial Intelligence Tools. N. Engl. J. Med. 2024, 390, 271–278. [Google Scholar] [CrossRef]

| Dimension | Typical Metric/Approach | Relevance for Clinical Adoption |
|---|---|---|
| Predictive performance | AUROC, AUPRC, sensitivity, specificity, calibration curves | Necessary to establish baseline model accuracy, but not sufficient for bedside use |
| Robustness to missing or noisy data | Performance under simulated missingness, imputation strategies, sensitivity analyses | Critical in ICU where incomplete data is common (labs not yet available) |
| Explainability/Interpretability | Intrinsic model transparency (BN), post-hoc methods (SHAP, LIME) | Determines whether clinicians can understand and trust the recommendation |
| Uncertainty quantification | Confidence intervals, posterior distributions, predictive intervals | Helps avoid over-reliance on predictions and supports cautious decision-making |
| Alignment with clinical reasoning | Face validity, concordance with known causal relationships | Facilitates clinician acceptance and integration into decision-making processes |
| Workflow integration | Real-time capability, compatibility with EHR systems, usability testing | Ensures feasibility of deployment in high-intensity ICU settings |
| Impact on outcomes | Prospective validation, randomized controlled trials. | Ultimately, the only measure that justifies clinical adoption |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agard, G.; Roman, C.; Guervilly, C.; Ouladsine, M.; Boyer, L.; Hraiech, S. Improving Sepsis Prediction in the ICU with Explainable Artificial Intelligence: The Promise of Bayesian Networks. J. Clin. Med. 2025, 14, 6463. https://doi.org/10.3390/jcm14186463
Agard G, Roman C, Guervilly C, Ouladsine M, Boyer L, Hraiech S. Improving Sepsis Prediction in the ICU with Explainable Artificial Intelligence: The Promise of Bayesian Networks. Journal of Clinical Medicine. 2025; 14(18):6463. https://doi.org/10.3390/jcm14186463
Chicago/Turabian StyleAgard, Geoffray, Christophe Roman, Christophe Guervilly, Mustapha Ouladsine, Laurent Boyer, and Sami Hraiech. 2025. "Improving Sepsis Prediction in the ICU with Explainable Artificial Intelligence: The Promise of Bayesian Networks" Journal of Clinical Medicine 14, no. 18: 6463. https://doi.org/10.3390/jcm14186463
APA StyleAgard, G., Roman, C., Guervilly, C., Ouladsine, M., Boyer, L., & Hraiech, S. (2025). Improving Sepsis Prediction in the ICU with Explainable Artificial Intelligence: The Promise of Bayesian Networks. Journal of Clinical Medicine, 14(18), 6463. https://doi.org/10.3390/jcm14186463








