Missing Data in Orthopaedic Clinical Outcomes Research: A Sensitivity Analysis of Imputation Techniques Utilizing a Large Multicenter Total Shoulder Arthroplasty Database
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source
2.2. Clinical Outcome Measures
2.3. Demographic and Surgical Covariates
2.4. Introduction of Data Missingness
2.5. Imputation Strategies
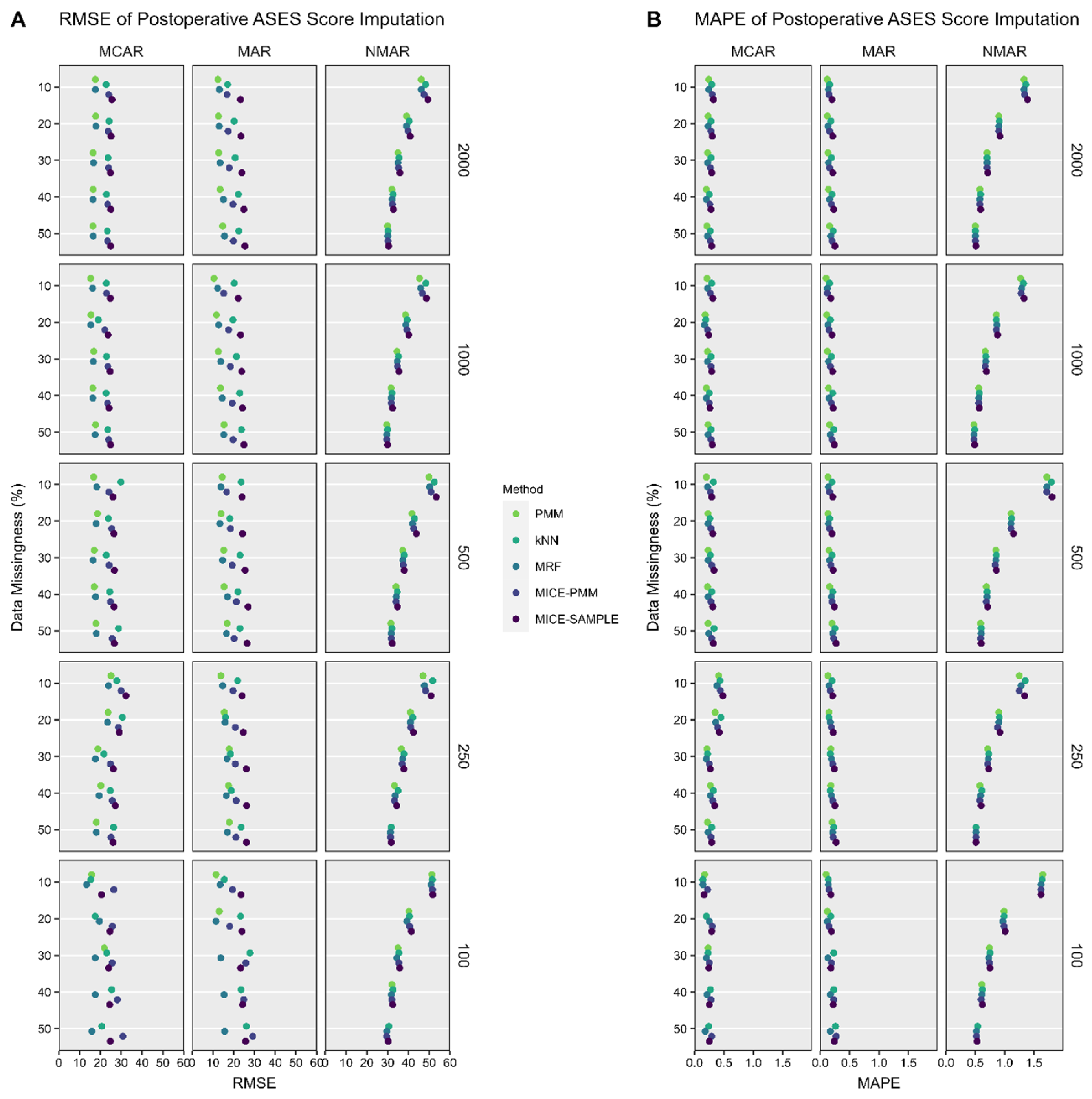
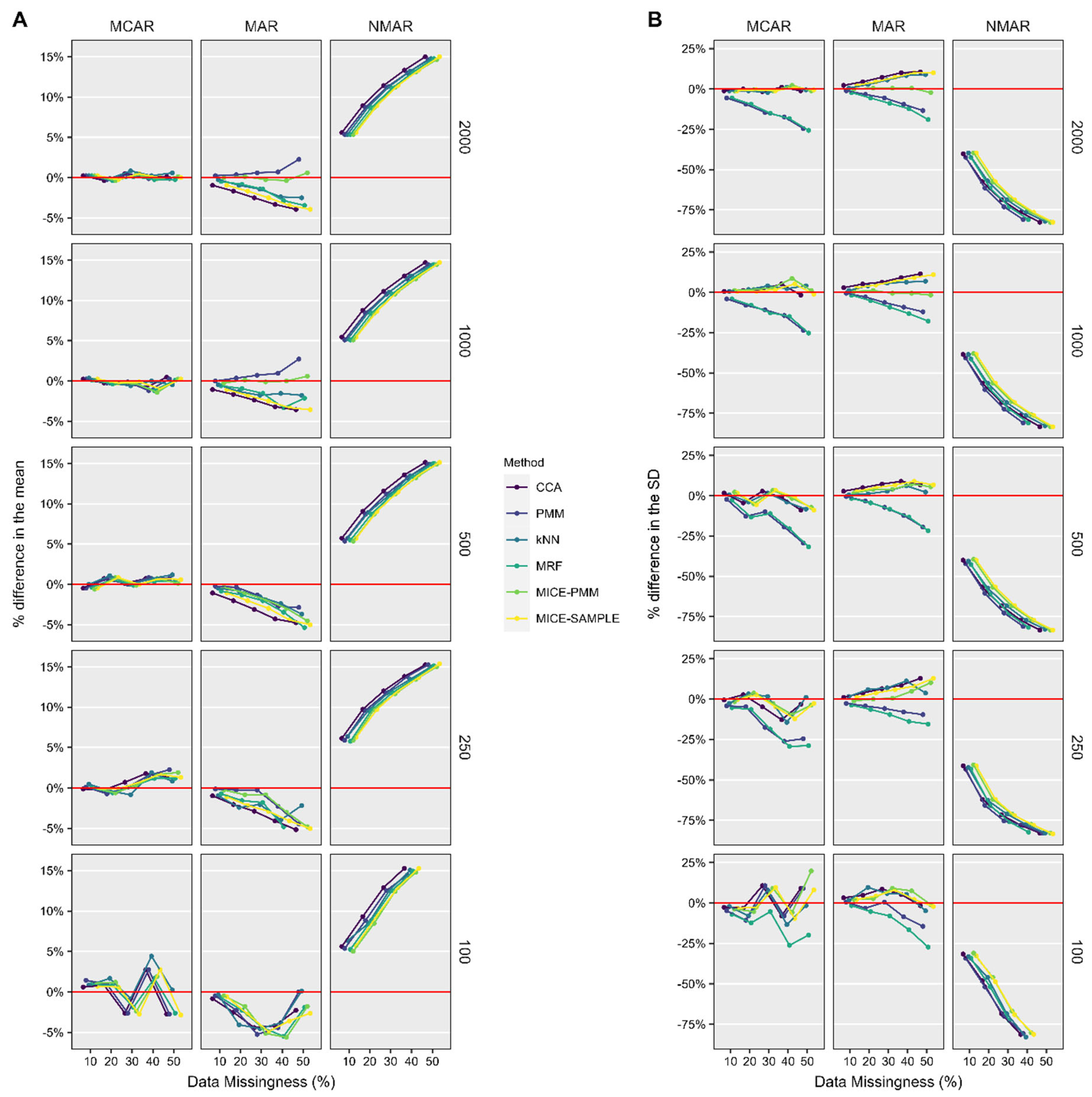
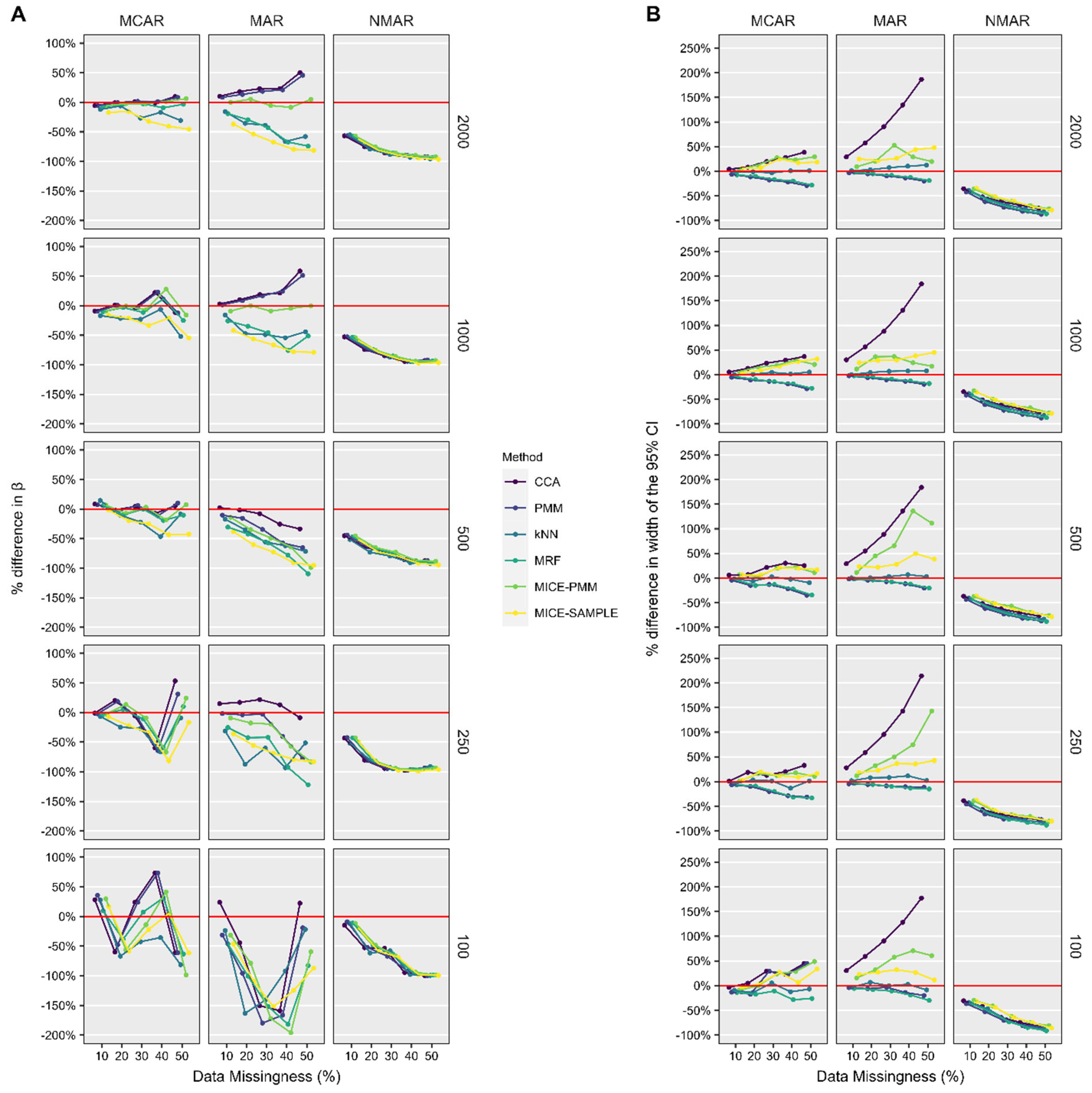
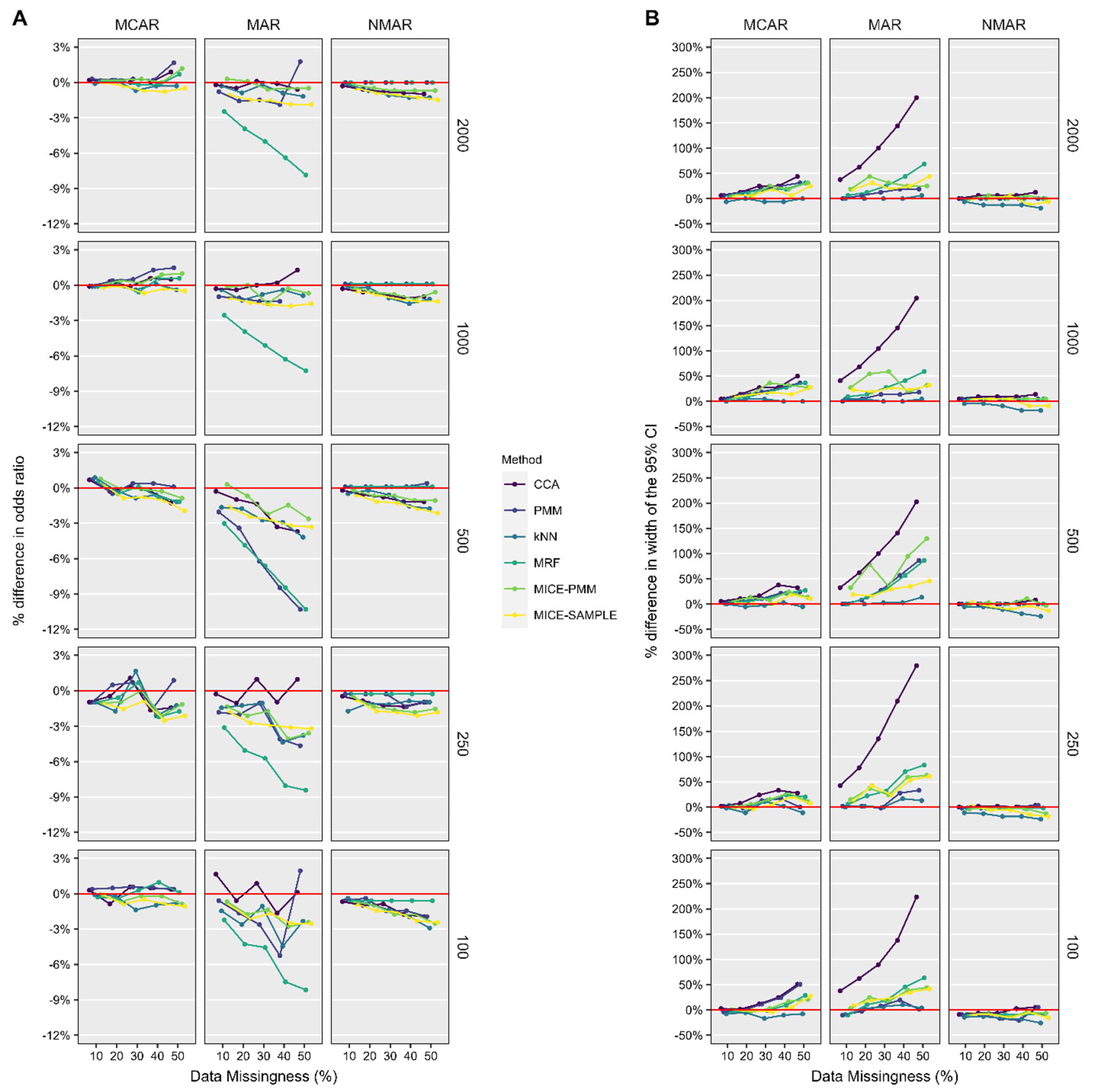
2.6. Performance Assessment
3. Results
3.1. Patient Characteristics
3.2. ASES Score
3.3. ASES Score Imputed with Correlated Scores Available
3.4. Forward Elevation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sterne, J.A.C.; White, I.R.; Carlin, J.B.; Spratt, M.; Royston, P.; Kenward, M.G.; Wood, A.M.; Carpenter, J.R. Multiple imputation for missing data in epidemiological and clinical research: Potential and pitfalls. BMJ 2009, 338, b2393. [Google Scholar] [CrossRef] [PubMed]
- Schafer, J.L. Multiple Imputation: A Primer. Stat. Methods Med. Res. 1999, 8, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Ondeck, N.T.; Fu, M.C.; Skrip, L.A.; McLynn, R.P.; Su, E.P.; Grauer, J.N. Treatments of Missing Values in Large National Data Affect Conclusions: The Impact of Multiple Imputation on Arthroplasty Research. J. Arthroplast. 2018, 33, 661–667. [Google Scholar] [CrossRef]
- Richards, R.R.; An, K.N.; Bigliani, L.U.; Friedman, R.J.; Gartsman, G.M.; Gristina, A.G.; Iannotti, J.P.; Mow, V.C.; Sidles, J.A.; Zuckerman, J.D. A standardized method for the assessment of shoulder function. J. Shoulder Elb. Surg. 1994, 3, 347–352. [Google Scholar] [CrossRef]
- Narulla, R.; Song, M.; Karunaratne, S.; Smithers, C.; Petchell, J. Trends in shoulder surgery patient-reported outcome measures. JSES Int. 2023, 7, 653–661. [Google Scholar] [CrossRef]
- Constant, C.R.; Murley, A.H. A clinical method of functional assessment of the shoulder. Clin. Orthop. Relat. Res. 1987, 214, 160–164. [Google Scholar] [CrossRef]
- Roche, C.; Kumar, V.; Overman, S.; Simovitch, R.; Flurin, P.-H.; Wright, T.; Routman, H.; Teredesai, A.; Zuckerman, J. Validation of a machine learning–derived clinical metric to quantify outcomes after total shoulder arthroplasty. J. Shoulder Elb. Surg. 2021, 30, 2211–2224. [Google Scholar] [CrossRef]
- Wong, S.E.; Zhang, A.L.; Berliner, J.L.; Ma, C.B.; Feeley, B.T. Preoperative patient-reported scores can predict postoperative outcomes after shoulder arthroplasty. J. Shoulder Elb. Surg. 2016, 25, 913–919. [Google Scholar] [CrossRef]
- Friedman, R.J.; Eichinger, J.; Schoch, B.; Wright, T.; Zuckerman, J.; Flurin, P.-H.; Bolch, C.; Roche, C. Preoperative parameters that predict postoperative patient-reported outcome measures and range of motion with anatomic and reverse total shoulder arthroplasty. JSES Open Access 2019, 3, 266–272. [Google Scholar] [CrossRef]
- Chen, R.E.; Papuga, M.O.; Nicandri, G.T.; Miller, R.J.; Voloshin, I. Preoperative Patient-Reported Outcomes Measurement Information System (PROMIS) scores predict postoperative outcome in total shoulder arthroplasty patients. J. Shoulder Elb. Surg. 2019, 28, 547–554. [Google Scholar] [CrossRef]
- Gower, J.C. A General Coefficient of Similarity and Some of Its Properties. Biometrics 1971, 27, 857–871. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Bühlmann, P. MissForest—Non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [PubMed]
- Van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Dowdle, S.B.; Glass, N.; Anthony, C.A.; Hettrich, C.M. Use of PROMIS for Patients Undergoing Primary Total Shoulder Arthroplasty. Orthop. J. Sports Med. 2017, 5, 2325967117726044. [Google Scholar] [CrossRef]
- Cella, D.; Yount, S.; Rothrock, N.; Gershon, R.; Cook, K.; Reeve, B.; Ader, D.; Fries, J.F.; Bruce, B.; Rose, M.; et al. The Patient-Reported Outcomes Measurement Information System (PROMIS): Progress of an NIH Roadmap Cooperative Group During its First Two Years. Med. Care 2007, 45, S3. [Google Scholar] [CrossRef]
- Roach, K.E.; Budiman-Mak, E.; Songsiridej, N.; Lertratanakul, Y. Development of a shoulder pain and disability index. Arthritis Care Res. 1991, 4, 143–149. [Google Scholar] [CrossRef]
- Lippitt, S.; Matsen, F.; Fu, F.; Hawkins, R. A practical tool for evaluating function: The Simple Shoulder Test. In The Shoulder: A Balance of Mobility and Stability; American Academy of Orthopaedic Surgeons: Rosemont, IL, USA, 1993. [Google Scholar]
- Gowd, A.K.; Charles, M.D.; Liu, J.N.; Lalehzarian, S.P.; Cabarcas, B.C.; Manderle, B.J.; Nicholson, G.P.; Romeo, A.A.; Verma, N.N. Single Assessment Numeric Evaluation (SANE) is a reliable metric to measure clinically significant improvements following shoulder arthroplasty. J. Shoulder Elb. Surg. 2019, 28, 2238–2246. [Google Scholar] [CrossRef]
- Amstutz, H.C.; Sew Hoy, A.L.; Clarke, I.C. UCLA anatomic total shoulder arthroplasty. Clin. Orthop. Relat. Res. 1981, 155, 7–20. [Google Scholar] [CrossRef]
- Tashjian, R.Z.; Hung, M.; Keener, J.D.; Bowen, R.C.; McAllister, J.; Chen, W.; Ebersole, G.; Granger, E.K.; Chamberlain, A.M. Determining the minimal clinically important difference for the American Shoulder and Elbow Surgeons score, Simple Shoulder Test, and visual analog scale (VAS) measuring pain after shoulder arthroplasty. J. Shoulder Elb. Surg. 2017, 26, 144–148. [Google Scholar] [CrossRef]
- Michael, R.J.; Williams, B.A.; Laguerre, M.D.; Struk, A.M.; Schoch, B.S.; Wright, T.W.; Farmer, K.W.; Vasilopoulos, T.; King, J.J. Correlation of multiple patient-reported outcome measures across follow-up in patients undergoing primary shoulder arthroplasty. J. Shoulder Elb. Surg. 2019, 28, 1869–1876. [Google Scholar] [CrossRef]
- King, J.J.; Wright, L.; Hao, K.A.; Roche, C.; Wright, T.W.; Vasilopoulos, T.; Zuckerman, J.D.; Flurin, P.-H.; Schoch, B.S. The Shoulder Arthroplasty Smart Score Correlates Well With Legacy Outcome Scores Without a Ceiling Effect. J. Am. Acad. Orthop. Surg. 2023, 31, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Pereira, R.C.; Abreu, P.H.; Rodrigues, P.P.; Figueiredo, M.A.T. Imputation of data Missing Not at Random: Artificial generation and benchmark analysis. Expert Syst. Appl. 2024, 249, 123654. [Google Scholar] [CrossRef]

| Missingness Pattern | Definition and Example |
|---|---|
| Missing Completely At Random (MCAR) | No systematic differences between missing and observed values are present. For example, ASES scores may be missing because clinic coordinators forgot to administer questionnaires that particular day. |
| Missing At Random (MAR) | Systematic difference between missing and observed values can be explained by differences in observed data. For example, missing ASES scores may be lower than recorded ASES scores, but only because females were less likely than males to fill out the questionnaire. In this scenario, if considering only the subgroup of patients who are female, the assumption can be made that the missing data for females should be similar, and hence can be imputed from the collected data for females. Therefore, if sex is used as a predictive factor in the imputation model, imputation methods are appropriate for use with this dataset. |
| Not Missing At Random (NMAR) | Even after the observed data are considered, systematic differences remain between the missing and observed values. For example, patients with low ASES scores may be more likely to have missing values because they sought treatment at a different institution. |
| Patient # | Sex | Postoperative ASES Score | MCAR | MAR | NMAR |
|---|---|---|---|---|---|
| 1 | M | 40 | ? | 40 | ? |
| 2 | M | 83 | 83 | 83 | 83 |
| 3 | F | 65 | 65 | ? | ? |
| 4 | M | 88 | ? | 88 | 88 |
| 5 | F | 85 | 85 | ? | 85 |
| 6 | F | 25 | 25 | ? | ? |
| 7 | F | 35 | ? | ? | ? |
| 8 | M | 87 | ? | 87 | 87 |
| 9 | F | 62 | ? | ? | ? |
| 10 | F | 85 | 85 | 85 | 85 |
| Method | Definition | Advantages | Disadvantages |
|---|---|---|---|
| Complete-case analysis (CCA) | Only patients with complete information are analyzed. Patients with missing data are excluded from analysis. |
|
|
| Single imputation | |||
| Predictive mean matching (PMM) | Missing values are imputed by first predicting them using a regression model based on observed values of other variables, then replacing the missing value with a value from a donor pool of observed values that are closest to the predicted value. |
|
|
| k-Nearest Neighbor (kNN) | Missing values are imputed by averaging or interpolating values from the k most similar observations (nearest neighbors) based on other variables. |
|
|
| Multivariate random forest (MRF) | Missing values are imputed by building a random forest model for each variable with missing values and imputing missing values by averaging predictions from multiple trees in the forest. |
|
|
| Multiple imputation | |||
| MICE with PMM, M = 30 (MICE-PMM-30) | Missing values are imputed using predictive mean matching within each iteration of the MICE algorithm. |
|
|
| MICE with random sampling, M = 30 (MICE-SAMPLE-30) | Missing values are imputed by drawing random samples from the predictive distribution within each iteration of the MICE algorithm. |
|
|
| Variable | Combined (n = 2204) | aTSA (n = 795) | rTSA (n = 1409) |
|---|---|---|---|
| Age at surgery (years) | 69.3 ± 8.0 | 65.4 ± 7.7 | 71.6 ± 7.3 |
| BMI (kg/m2) | 29.6 ± 6.2 | 30.6 ± 6.4 | 29.1 ± 6.0 |
| Follow-up (months) | 30.3 ± 12.3 | 31.3 ± 14.1 | 29.8 ± 11.1 |
| Female sex | 55.6% (1226) | 49.3% (392) | 59.2% (834) |
| Dominant side surgery | 61.2% (1348) | 57.9% (460) | 63.0% (888) |
| Comorbidities | |||
| None | 29.2% (644) | 35.1% (279) | 25.9% (365) |
| Hypertension | 57.0% (1256) | 51.6% (410) | 60.0% (846) |
| Heart disease | 15.7% (346) | 13.3% (106) | 17.0% (240) |
| Diabetes | 14.9% (328) | 12.8% (102) | 16.0% (226) |
| Tobacco use | 8.1% (178) | 8.9% (71) | 7.6% (107) |
| Preoperative diagnosis | |||
| Osteoarthritis | 65.5% (1444) | 94.6% (752) | 49.1% (692) |
| Avascular necrosis | 1.7% (38) | 1.9% (15) | 1.6% (23) |
| Rotator cuff tear | 7.2% (159) | 0.4% (3) | 11.1% (156) |
| Cuff tear arthropathy | 22.7% (500) | 0.9% (7) | 35.0% (493) |
| Rheumatoid arthritis | 2.9% (63) | 2.3% (18) | 3.2% (45) |
| Subscapularis repair | - | - | 37.8% (533) |
| Cemented humeral component | 5.4% (118) | 5.5% (44) | 5.3% (74) |
| Previous surgery on shoulder | 23.8% (524) | 16.2% (129) | 28.0% (395) |
| Estimated blood loss (mL) | 200 (100–300) | 200 (100–300) | 160 (100–300) |
| Preoperative outcome measures | |||
| ASES score | 38.6 ± 16.0 | 38.9 ± 16.0 | 38.4 ± 16.1 |
| Active FE (°) | 93 ± 36 | 102 ± 32 | 88 ± 37 |
| Postoperative outcome measures | |||
| ASES score | 84.4 ± 17.6 | 86.6 ± 17.3 | 83.1 ± 17.7 |
| Active FE (°) | 145 ± 24 | 149 ± 25 | 142 ± 24 |
| Improvement in outcome measures | |||
| ASES score | 45.8 ± 20.9 | 47.7 ± 21.0 | 44.7 ± 20.8 |
| Active FE (°) | 51 ± 38 | 47 ± 35 | 53 ± 39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, K.A.; Vasilopoulos, T.; Elwell, J.; Roche, C.P.; Hones, K.M.; Wright, J.O.; King, J.J.; Wright, T.W.; Simovitch, R.W.; Schoch, B.S. Missing Data in Orthopaedic Clinical Outcomes Research: A Sensitivity Analysis of Imputation Techniques Utilizing a Large Multicenter Total Shoulder Arthroplasty Database. J. Clin. Med. 2025, 14, 3829. https://doi.org/10.3390/jcm14113829
Hao KA, Vasilopoulos T, Elwell J, Roche CP, Hones KM, Wright JO, King JJ, Wright TW, Simovitch RW, Schoch BS. Missing Data in Orthopaedic Clinical Outcomes Research: A Sensitivity Analysis of Imputation Techniques Utilizing a Large Multicenter Total Shoulder Arthroplasty Database. Journal of Clinical Medicine. 2025; 14(11):3829. https://doi.org/10.3390/jcm14113829
Chicago/Turabian StyleHao, Kevin A., Terrie Vasilopoulos, Josie Elwell, Christopher P. Roche, Keegan M. Hones, Jonathan O. Wright, Joseph J. King, Thomas W. Wright, Ryan W. Simovitch, and Bradley S. Schoch. 2025. "Missing Data in Orthopaedic Clinical Outcomes Research: A Sensitivity Analysis of Imputation Techniques Utilizing a Large Multicenter Total Shoulder Arthroplasty Database" Journal of Clinical Medicine 14, no. 11: 3829. https://doi.org/10.3390/jcm14113829
APA StyleHao, K. A., Vasilopoulos, T., Elwell, J., Roche, C. P., Hones, K. M., Wright, J. O., King, J. J., Wright, T. W., Simovitch, R. W., & Schoch, B. S. (2025). Missing Data in Orthopaedic Clinical Outcomes Research: A Sensitivity Analysis of Imputation Techniques Utilizing a Large Multicenter Total Shoulder Arthroplasty Database. Journal of Clinical Medicine, 14(11), 3829. https://doi.org/10.3390/jcm14113829





