Texture Analysis for the Bone Age Assessment from MRI Images of Adolescent Wrists in Boys
Abstract
1. Introduction
2. Materials and Methods
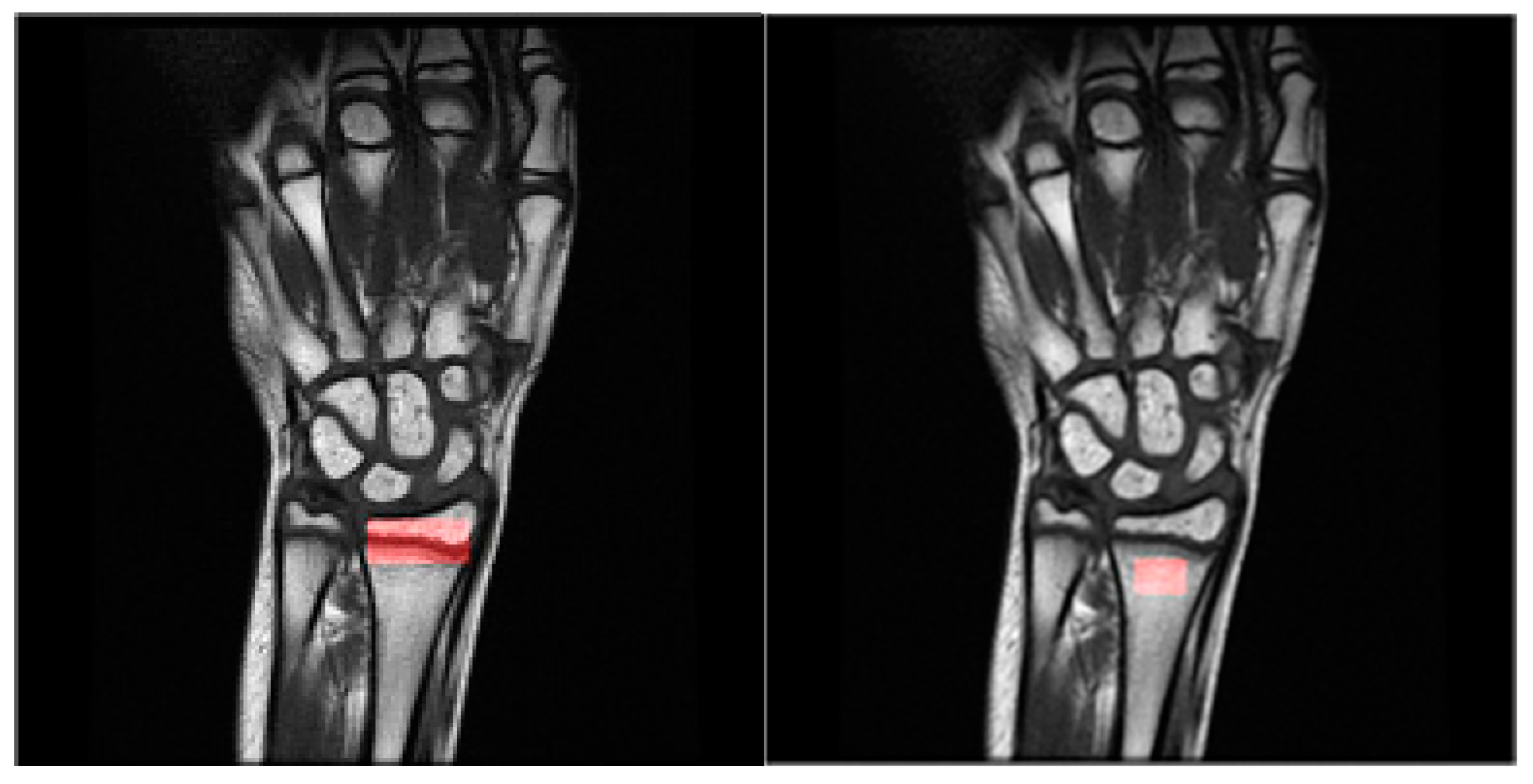
2.1. Data Acquisition
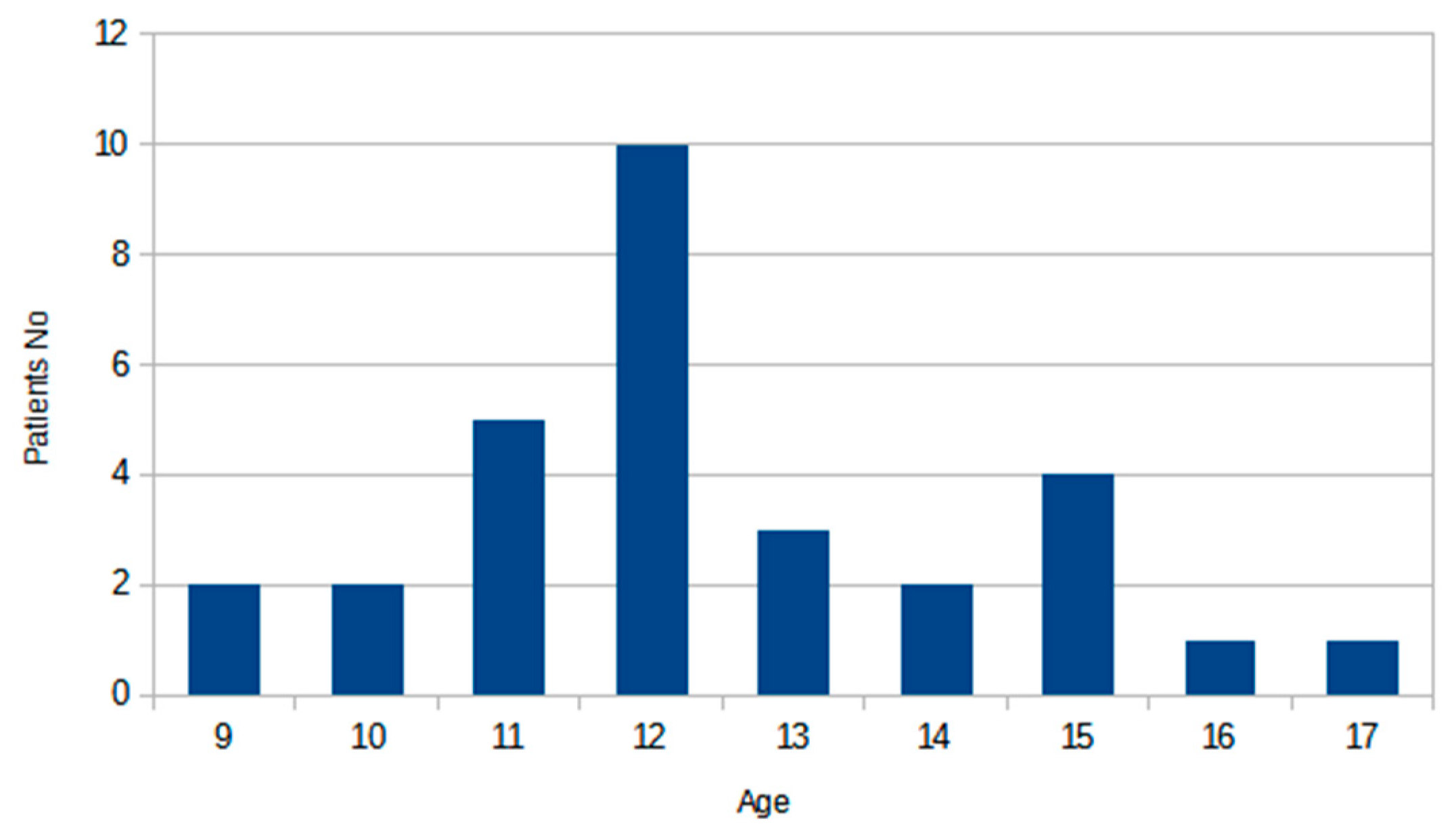
2.2. Dataset Description
2.3. Data Analysis Methods and Methodology
2.4. Experiment Setup
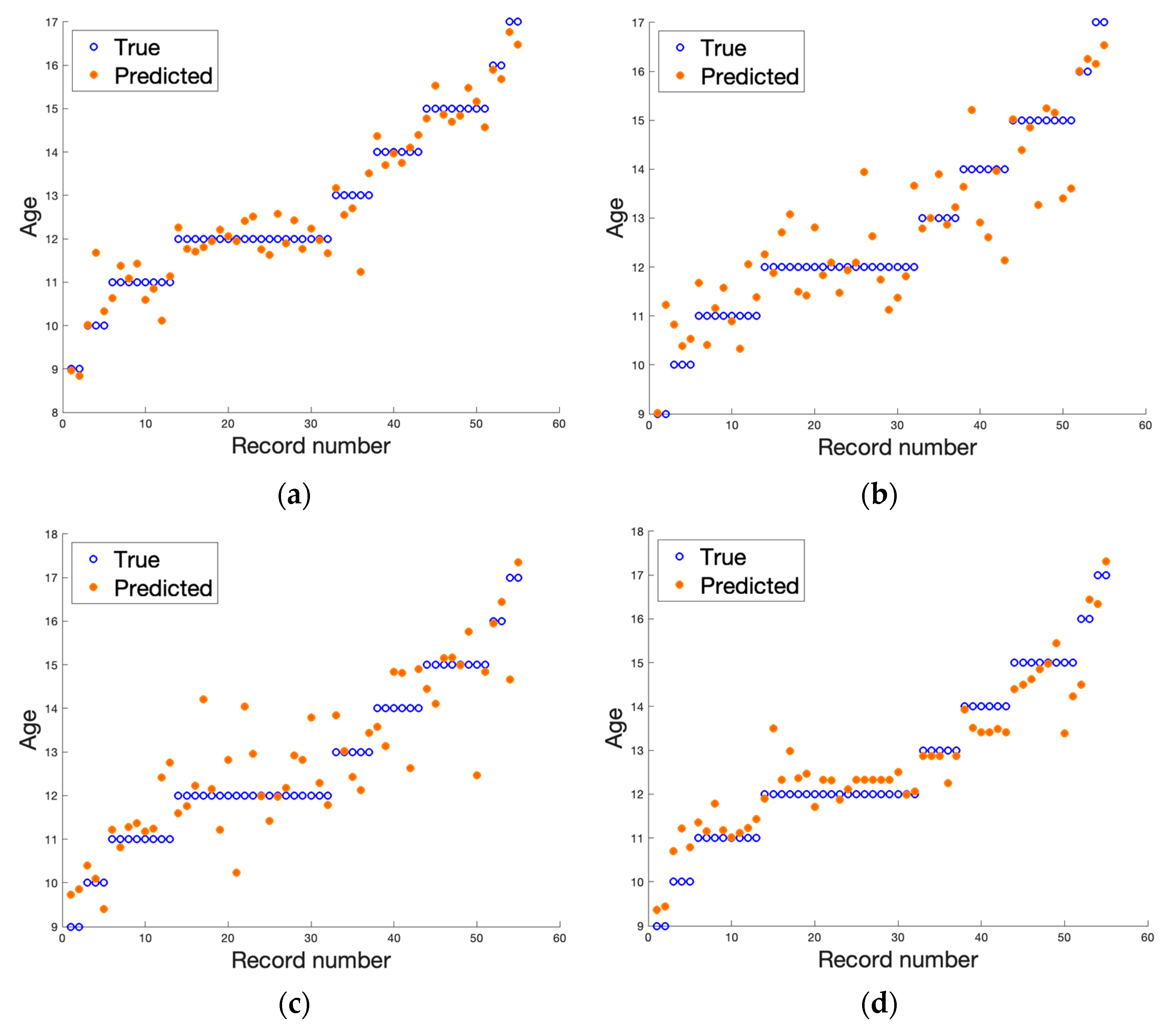
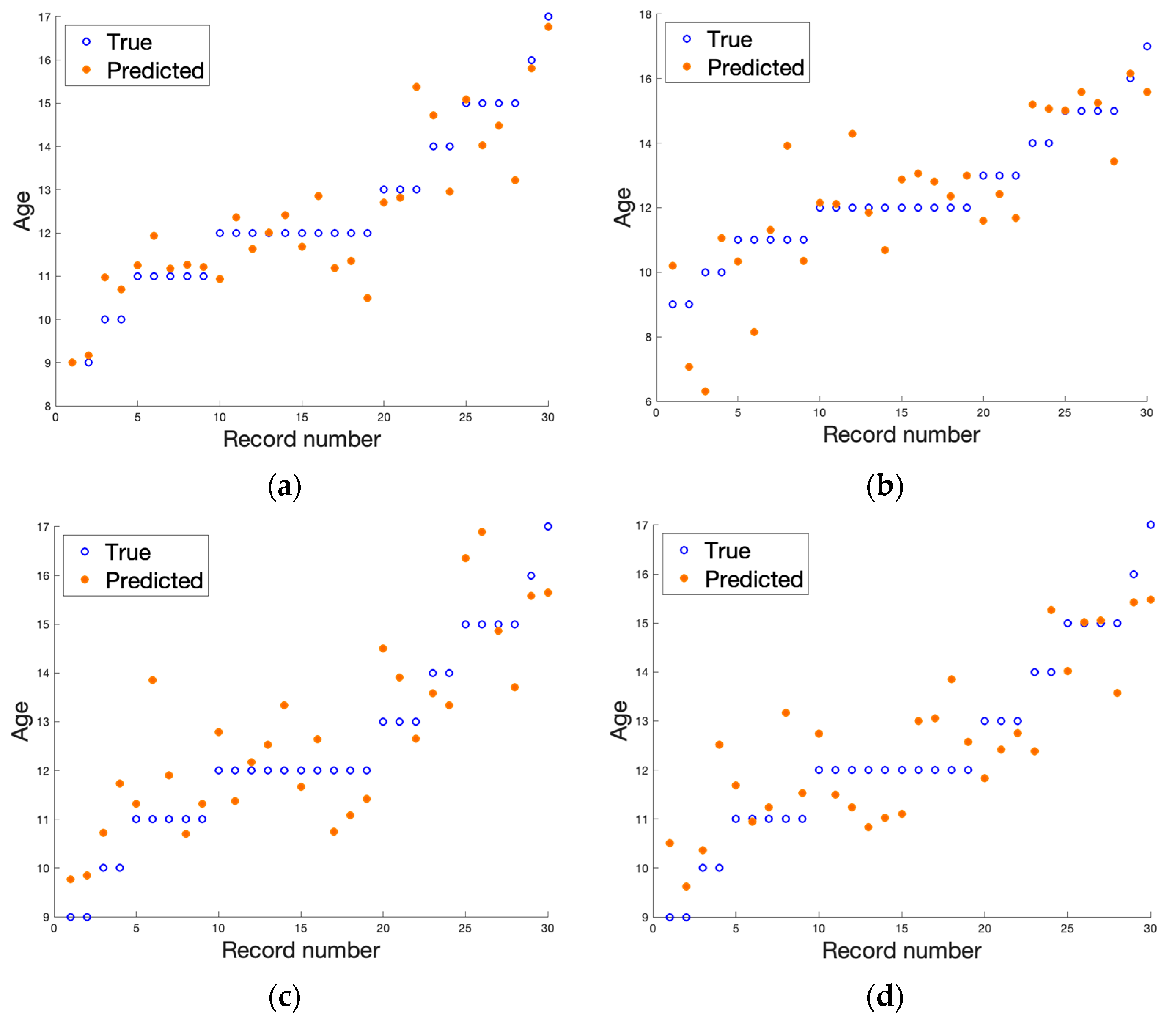
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- 1.
- First-order features
| Feature Name | Formulae | |
|---|---|---|
| Mean | (A1) | |
| Variance | (A2) | |
| Skewness | (A3) | |
| Kurtosis | (A4) | |
| Percentile | (A5) |
- 2.
- Gray-level co-occurrence matrix [27]
| Feature Name | Formulae | |
|---|---|---|
| Contrast | (A6) | |
| Correlation | where µi is average and δi is standard deviation for pi | (A7) |
| Homogeneity | (A8) | |
| Entropy | (A9) | |
| Angular second moment | (A10) | |
| Sum average | (A11) | |
| Sum variance | (A12) | |
| Difference variance | (A13) | |
| Difference entropy | (A14) | |
| Sum entropy | (A15) | |
| Sum of squares | (A16) |
- 3.
- Run-length matrix [55]
| Feature Name | Formulae | |
|---|---|---|
| Short run emphasis | (A17) | |
| Long run emphasis | (A18) | |
| Gray-level non-uniformity | (A19) | |
| Run-length non-uniformity | (A20) | |
| Run percent | (A21) |
- 4.
- Gradient matrix [27]
- 5.
- First order autoregressive model [56]
- 6.
- Haar wavelet transform [57]
- 7.
- Gabor transform
- 8.
- Histogram of oriented gradients [58]
References
- Schmitt, A. Forensic Anthropology and Medicine: Complementary Sciences from Recovery to Cause of Death; Humana: Paramus, NJ, USA, 2006; pp. 212–219. [Google Scholar]
- Abdelbary, M.H.; Abdelkawi, M.M.; Nasr, M.A. Age determination by MR imaging of the wrist in Egyptian male foot ballplayers How far is it reliable? Egypt. J. Radiol. Nucl. Med. 2018, 49, 146–151. [Google Scholar] [CrossRef]
- Dekhne, M.S.; Kocher, I.D.; Hussain, Z.B.; Feroe, A.G.; Sankarankutty, S.; Williams, K.A.; Heyworth, B.E.; Milewski, M.D.; Kocher, M.S. Tibial tubercle apophyseal stage to determine skeletal age in pediatric patients undergoing ACL Reconstruction: A validation and reliability study. Orthop. J. Sports Med. 2021, 9, 23259671211036897. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, S.; Koch, B.; Schulz, R.; Reisinger, W.; Schmeling, A. Studiesin use of the Greulich–Pyle skeletal age method to assess criminal liability. Legal Med. 2008, 10, 190–195. [Google Scholar] [CrossRef]
- Malina, R.M. Skeletal age and age verification in youth sport. Sports Med. 2011, 41, 925–947. [Google Scholar] [CrossRef] [PubMed]
- Schmeling, A.; Reisinger, W.; Geserick, G.; Olze, A. Age estimation of unaccompanied minors: Part I. General considerations. Forensic Sci. Int. 2006, 159, S61–S64. [Google Scholar] [CrossRef] [PubMed]
- Menjívar, C.; Perreira, K.M. Undocumented and unaccompanied: Children of migration in the European Union and the United States. J. Ethn. Migr. Stud. 2019, 45, 197–217. [Google Scholar] [CrossRef] [PubMed]
- Reinehr, T.; de Sousa, G.; Wabitsch, M. Relationships of IGF-I and androgens to skeletal maturation in obese children and adolescents. J. Pediatr. Endocrinol. Metab. 2006, 19, 1133–1140. [Google Scholar] [CrossRef] [PubMed]
- Phillip, M.; Moran, O.; Lazar, L. Growth without growth hormone. J. Pediatr. Endocrinol. Metab. 2002, 15, 1267–1272. [Google Scholar] [PubMed]
- Cox, L.A. The biology of bone maturation and ageing. Acta Paediatr. Suppl. 1997, 423, 107–108. [Google Scholar] [CrossRef]
- Kaplowitz, P.; Srinivasan, S.; He, J.; McCarter, R.; Hayeri, M.R.; Sze, R. Comparison of bone age readings by pediatric endocrinologists and pediatric radiologists using two bone age atlases. Pediatr. Radiol. 2010, 41, 690–693. [Google Scholar] [CrossRef]
- Greulich, W.W.; Pyle, S.I. Radiographic Atlas of Skeletal Development of the Hand and Wrist, 2nd ed.; Stanford University Press: Stanford, CA, USA, 1959. [Google Scholar]
- Tanner, J.M.; Whitehouse, R.H.; Healy, M. A New System for Estimating Skeletal Maturity from the Hand and Wrist with Standards Derived from a Study of 2600 Healthy British Children; Centre International de L’enfance: Paris, France, 1962. [Google Scholar]
- Alshamrani, K.; Messina, F.; Offiah, A.C. Is the Greulich and Pyle atlas applicable to all ethnicities? A systematic review and meta-analysis. Eur. Radiol. 2019, 29, 2910–2923. [Google Scholar] [PubMed]
- Alshamrani, K.; Offiah, A.C. Applicability of two commonly used bone age assessment methods to twenty-first century UK children. Diag. Interv. Radiol. 2020, 30, 504–513. [Google Scholar] [CrossRef]
- van Rijn, R.R.; Lequin, M.H.; Robben, S.G.; Hop, W.C.; van Kuijk, C. Is the Greulich and Pyle atlas still valid for Dutch Caucasian children today. Pediatr. Radiol. 2021, 31, 748–752. [Google Scholar] [CrossRef]
- Cantekin, K.; Celikoglu, M.; Miloglu, O.; Dane, A.; Erdem, A. Bone age assessment: The applicability of the Greulich-Pyle method in eastern Turkish children. J. Forensic Sci. 2012, 57, 679–682. [Google Scholar] [CrossRef] [PubMed]
- Dembetembe, K.A.; Morris, A.G. Is Greulich-Pyle age estimation applicable for determining maturation in male Africans. South Afr. Sci. Suid-Afrik. Wet. 2012, 108, 1–6. [Google Scholar] [CrossRef]
- Mentzel, H.-J.; Vilser, C.; Eulenstein, M.; Schwartz, T.; Vogt, S.; Böttcher, J.; Yaniv, I.; Tsoref, L.; Kauf, E.; Kaiser, W.A. Assessment of skeletal age at the wrist in children with a new ultrasound device. Pediatr. Radiol. 2005, 35, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.M.; Miller, B.S.; Hoggard, E.; Somani, A.; Sarafoglou, K. Application of ultrasound for bone age estimation in clinical practice. J. Pediatr. 2009, 154, 243–247. [Google Scholar] [CrossRef]
- Bilgili, Y.; Hizel, S.; Kara, S.A.; Sanli, C.; Erdal, H.H.; Altinok, D. Accuracy of skeletal age assessment in children from birth to 6 years of age with the ultrasonographic version of the Greulich-Pyle atlas. J. Ultrasound Med. 2003, 22, 683–690. [Google Scholar] [CrossRef]
- Dvorak, J.; George, J.; Junge, A.; Hodler, J. Age determination by magnetic resonance imaging of the wrist in adolescent male football players. Br. J. Sports Med. 2007, 41, 45–52. [Google Scholar] [CrossRef]
- Terada, Y.; Kono, S.; Tamada, D.; Uchiumi, T.; Kose, K.; Miyagi, R.; Yamabe, E.; Yoshioka, H. Skeletal age assessment in children using an open compact MRI system. Magn. Reson. Med. 2013, 69, 1697–1702. [Google Scholar] [CrossRef]
- Terada, Y.; Kono, S.; Uchiumi, T.; Kose, K.; Miyagi, R.; Yamabe, E.; Fujinaga, Y.; Yoshioka, H. Improved reliability in skeletal age assessment using a pediatric hand MR scanner with a 0. 3T permanent magnet. Magn. Reson. Med. Sci. 2014, 13, 215–219. [Google Scholar] [CrossRef] [PubMed]
- Tomei, E.; Sartori, A.; Nissman, D.; Al Ansari, N.; Battisti, S.; Rubini, A.; Stagnitti, A.; Martino, M.; Marini, M.; Barbato, E.; et al. Value of MRI of the hand and the wrist in evaluation of bone age: Preliminary results. J. Magn. Reson. Imaging 2014, 39, 1198–1205. [Google Scholar] [CrossRef] [PubMed]
- Hojreh, A.; Gamper, J.; Schmook, M.T.; Weber, M.; Prayer, D.; Herold, C.J.; Noebauer-Huhmann, I.M. Hand MRI and the Greulich-Pyle atlas in skeletal age estimation in adolescents. Skelet. Radiol. 2018, 47, 963–971. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man. Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Kociołek, M.; Strzelecki, M.; Klepaczko, A. Functional kidney analysis based on textured DCE-MRI images, In Advances in Intelligent Systems and Computing; Piętka, E., Badura, P., Kawa, J., Wieclawek, W., Eds.; Springer Verlag: Berlin/Heidelberg, Germany, 2019; pp. 38–49. [Google Scholar]
- Szczypiński, P.M.; Strzelecki, M.; Materka, A.; Klepaczko, A. MaZda—The software package for textural analysis of biomedical images. Adv. Intell. Soft Comput. 2009, 65, 73–84. [Google Scholar]
- Materka, A. Texture analysis methodologies for magnetic resonance imaging. Dialogues Clin. Neurosci. 2022, 6, 243–250. [Google Scholar] [CrossRef]
- Chrzanowski, L.; Drozdz, J.; Strzelecki, M.; Krzeminska-Pakula, M.; Jedrzejewski, K.; Kasprzak, J. Application of neural networks for the analysis of histological and ultrasonic aortic wall appearance—An in-vitro tissue characterization study. Ultrasound Med. Biol. 2008, 34, 103–113. [Google Scholar] [CrossRef]
- Obuchowicz, R.; Kruszyńska, J.; Strzelecki, M. Classifying median nerves in carpal tunnel syndrome: Ultrasound image analysis. Biocybern. Biomed. Eng. 2021, 41, 335–351. [Google Scholar] [CrossRef]
- Hochberg, Z. Clinical physiology and pathology of the growth plate. Best Pract. Res. Clin. Endocrinol. Metab. 2002, 16, 399–419. [Google Scholar] [CrossRef]
- Jaramillo, D.; Laor, T.; Zaleske, D.J. Indirect trauma to the growth plate: Results of MR imaging after epiphyseal and metaphyseal injury in rabbits. Radiology 1993, 187, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Wilsman, N.J.; Farnum, C.E.; Green, E.M.; Lieferman, E.M.; Clayton, M.K. Cell cycle analysis of proliferative zone chondrocytes in growth plates elongating at different rates. J. Orthop. Res. 1996, 14, 562–572. [Google Scholar] [CrossRef] [PubMed]
- Burdiles, A.; Babyn, P.S. Pediatric bone marrow MR imaging. Magn. Reson. Imaging Clin. N Am. 2009, 17, 391–409. [Google Scholar] [CrossRef]
- Chan, B.Y.; Gill, K.G.; Rebsamen, S.L.; Nguyen, J.C. MR Imaging of Pediatric Bone Marrow. Radiographics 2016, 36, 1911–1930. [Google Scholar] [CrossRef] [PubMed]
- Iglovikov, V.I.; Rakhlin, A.; Kalinin, A.A.; Shvets, A.A. Pediatric bone age assessment using deep convolutional neural networks. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2018; pp. 300–308. [Google Scholar]
- Salim, I.; Hamza, A.B. Ridge regression neural network for pediatric bone age assessment. Multimed. Tools Appl. 2021, 80, 30461–30478. [Google Scholar] [CrossRef]
- Marouf, M.; Siddiqi, R.; Bashir, F.; Vohra, B. Automated hand X-ray based gender classification and bone age assessment using convolutional neural network. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; pp. 1–5. [Google Scholar]
- Liu, B.; Zhang, Y.; Chu, M.; Bai, X.; Zhou, F. Bone age assessment based on rank-monotonicity enhanced ranking CNN. IEEE Access 2019, 7, 120976–120983. [Google Scholar] [CrossRef]
- Zulkifley, M.A.; Mohamed, N.A.; Abdani, S.R.; Kamari, N.A.M.; Moubark, A.M.; Ibrahim, A.A. Intelligent bone age assessment: An automated system to detect a bone growth problem using convolutional neural networks with attention mechanism. Diagnostics 2021, 11, 765. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Tajmir, S.; Lee, J.; Zissen, M.; Yeshiwas, B.A.; Alkasab, T.K.; Choy, G.; Do, S. Fully automated deep learning system for bone age assessment. J. Digit. Imaging 2017, 30, 427–441. [Google Scholar] [CrossRef]
- Castillo, J.; Tong, Y.; Zhao, J.; Zhu, F. RSNA Bone-Age Detection Using Transfer Learning and Attention Mapping. In ECE228 and SIO209 Machine Learning for Physical Applications; 2018; pp. 1–5. Available online: http://noiselab.ucsd.edu/ECE228_2018/Reports/Report6.pdf (accessed on 1 February 2020).
- Karargyris, A.; Kashyap, S.; Wu, J.T.; Sharma, A.; Moradi, M.; Syeda-Mahmood, T. Age prediction using a large chest X-ray dataset. In Proceedings of the Medical Imaging 2019: Computer-Aided Diagnosis, San Diego, CA, USA, 16–21 February 2019; p. 10950. [Google Scholar]
- Nguyen, H.; Soohyung, K. Automatic whole-body bone age assessment using deep hierarchical features. arXiv 2019, arXiv:1901.10237. [Google Scholar]
- Janczyk, K.; Rumiński, J.; Neumann, T.; Głowacka, N.; Wiśniewski, P. Age prediction from low resolution, dual-energy X-ray images using convolutional neural networks. Appl. Sci. 2022, 12, 6608. [Google Scholar] [CrossRef]
- Castillo, R.F.; Ruiz, M.D.C.L. Assessment of age and sex by means of DXA bone densitometry: Application in forensic anthropology. Forensic Sci. Int. 2011, 209, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Navega, D.; Coelho, J.D.O.; Cunha, E.; Curate, F. DXAGE: A new method for age at death estimation based on femoral bone mineral density and artificial neural networks. J. Forensic Sci. 2017, 63, 497–503. [Google Scholar] [CrossRef] [PubMed]
- Pietka, B.E.; Pośpiech, S.; Gertych, A.; Cao, F.; Huang, H.K.; Gilsanz, V. Computer automated approach to the extraction of epiphyseal regions in hand radiographs. J Digit Imaging. 2001, 14, 165–172. [Google Scholar]
- Pietka, E.; Gertych, A.; Pospiech-Kurkowska, S.; Cao, F.; Huang, H.K.; Gilzanz, V. Computer assisted bone age assessment: Graphical user interface for image processing and comparison. J. Digit. Imaging 2004, 17, 175–188. [Google Scholar] [CrossRef] [PubMed]
- Gertych, A.; Piętka, E.; Liu, B.J. Segmentation of regions of interest and post-segmentation edge location improvement in computer-aided bone age assessment. Pattern Anal. Appl. 2007, 10, 115. [Google Scholar] [CrossRef]
- Szczypinski, P.M.; Klepaczko, A.; Kociolek, M. QMaZda—Software tools for image analysis and pattern recognition. In Proceedings of the 2017 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 20–22 September 2017; pp. 217–221. [Google Scholar]
- Galloway, M.M. Texture analysis using grey level run lengths. Comput. Graph. Image Process. 1975, 4, 172–179. [Google Scholar] [CrossRef]
- Kashyap, R.; Chellappa, R. Estimation and choice of neighbors in spatial-interaction models of images. IEEE Trans. Inf. Theory 1983, 29, 60–72. [Google Scholar] [CrossRef]
- Porter, R.; Canagarajah, N. Rotation invariant texture classification schemes using GMRFs and wavelets. In Proceedings of the Proceedings IWISP’96, Manchester, UK, 4–7 November 1996; pp. 183–186. [Google Scholar]
- Pierzchała, M.; Obuchowicz, R.; Guz, W.; Piórkowski, A. Correlation of the results of textural analysis of wrist MRI images with age in boys aged 9–17. Bio-Algorithms Med-Syst. 2021, 17, eA18–eA19. [Google Scholar]
- Hu, J.; Wang, Y.; Guo, D.; Qu, Z.; Sui, C.h.; He, G.; Wang, S.; Chen, X.; Wang, C.h.; Liu, X. Diagnostic performance of magnetic resonance imaging–based machine learning in Alzheimer’s disease detection: A meta-analysis. Neuroradiology 2023, 65, 513–527. [Google Scholar] [CrossRef]
- Snider, E.J.; Hernandez-Torres, S.I.; Hennessey, R. Using ultrasound image augmentation and ensemble predictions to prevent machine-learning model overfitting. Diagnostics 2023, 13, 417. [Google Scholar] [CrossRef]
- Shao, Y.; Hashemi, H.S.; Gordon, P.; Warren, L.; Wang, J.; Rohling, R.; Salcudean, S. Breast cancer detection using multimodal time series features from ultrasound shear wave absolute vibro-elastography. IEEE J. Biomed. Health Inform. 2022, 26, 704–714. [Google Scholar] [CrossRef] [PubMed]
- d’Este, S.H.; Nielsen, M.B.; Hansen, A.E. Visualizing glioma infiltration by the combination of multimodality imaging and artificial Intelligence, a systematic review of the literature. Diagnostics 2021, 11, 592. [Google Scholar] [CrossRef] [PubMed]
- Hoar, D.; Lee, P.Q.; Guida, A.; Patterson, S.; Bowen, C.V.; Merrimen, J.; Wang, C.; Rendon, R.; Beyea, S.D.; Clarke, S.E. Combined transfer learning and test-time augmentation improves convolutional neural network-based semantic segmentation of prostate cancer from multi-parametric MR images. Comput. Methods Programs Biomed. 2021, 210, 106375. [Google Scholar] [CrossRef] [PubMed]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 886–893. [Google Scholar] [CrossRef]
- Kreitner, K.F.; Schweden, F.J.; Riepert, T.; Nafe, B.; Thelen, M. Bone age determination based on the study of the medial extremity of the clavicle. Eur. Radiol. 1998, 8, 1116–1122. [Google Scholar] [CrossRef]
- Charles, Y.P.; Dimeglio, A.; Canavese, F.; Daures, J.-P. Skeletal age assessment from the olecranon for idiopathic scoliosis at Risser grade 0. J. Bone Joint Surg. Am. 2007, 89, 2737–2744. [Google Scholar] [CrossRef] [PubMed]
- Risser, J.C. The Iliac apophysis; an invaluable sign in the management of scoliosis. Clin. Orthop. 1958, 11, 111–119. [Google Scholar] [CrossRef]
- Little, D.G.; Sussman, M.D. The Risser sign: A critical analysis. J. Pediatr. Orthop. 1994, 14, 569–575. [Google Scholar] [CrossRef]
- Li, D.T.; Cui, J.J.; DeVries, S.; Nicholson, A.D.; Li, E.; Petit, L.; Kahan, J.B.; Sanders, J.O.; Liu, R.W.; Cooperman, D.R.; et al. Humeral head ossification predicts peak height velocity timing and percentage of growth remaining in children. J. Pediatr. Orthop. 2018, 38, E546–E550. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, A.D.; Liu, R.W.; Sanders, J.O.; Cooperman, D.R. Relationship of calcaneal and iliac apophyseal ossification to peak height velocity timing in children. J. Bone Joint Surg. Am. 2015, 97, 147–154. [Google Scholar] [CrossRef]
- Li, S.Q.; Nicholson, A.D.; Cooperman, D.R.; Liu, R.W. Applicability of the calcaneal apophysis ossification staging system to the modern pediatric population. J. Pediatr. Orthop. 2019, 39, 46–50. [Google Scholar] [CrossRef]
- Demirjian, A.; Goldstein, H.; Tanner, J.M. A new system of dental age assessment. Hum. Biol. 1973, 45, 211–227. [Google Scholar] [PubMed]
- Sehrawat, J.S.; Singh, M. Willems method of dental age estimation in children: A systematic review and meta-analysis. J. Forensic Leg. Med. 2017, 52, 122–129. [Google Scholar] [CrossRef] [PubMed]
- Malik, P.; Saha, R.; Agarwal, A. Applicability of Demirjian’s method of age assessment in a North Indian female population. Eur. J. Paediatr. Dent. 2012, 13, 133–135. [Google Scholar]
- Heyworth, B.E.; Osei, D.A.; Fabricant, P.D.; Schneider, R.; Doyle, S.h.M.; Green, D.W.; Widmann, R.F.; Lyman, S.; Burke, S.W.; Scher, D.M. The shorthand bone age assessment: A simpler alternative to current methods. J. Pediatr. Orthop. 2013, 33, 569–574. [Google Scholar] [CrossRef]
- Thodberg, H.H.; Kreiborg, S.; Juul, A.; Pedersen, K.D. The BoneXpert method for automated determination of skeletal maturity. IEEE Trans. Med. Imaging 2009, 28, 52–66. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Gu, X.; Chen, S.; Liu, Y.; Shen, Q.; Pan, H.; Shi, L.; Jin, Z. Artificial intelligence system can achieve comparable results to experts for bone age assessment of Chinese children with abnormal growth and development. PeerJ 2020, 8, e8854. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, C.; Cheng, J.; Chen, X.; Wang, Z.J. A multi-scale data fusion framework for bone age assessment with convolutional neural networks. Comput. Biol. Med. 2019, 108, 161–173. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Li, T.; Yang, X.; Wang, S.; Ahmad, S.; Xiang, L.; Stone, S.R.; Li, L.; Zhan, Y.; Shen, D.; et al. Regression convolutional neural network for automated pediatric bone age assessment from hand radiograph. IEEE J. Biomed. Health Inform. 2019, 23, 2030–2038. [Google Scholar] [CrossRef]
- Tong, C.; Liang, B.; Li, J.; Zheng, Z. A Deep Automated Skeletal Bone Age Assessment Model with Heterogeneous Features Learning. J. Med. Syst. 2018, 42, 249. [Google Scholar] [CrossRef]
- Mettler, F.A.; Huda, W.; Yoshizumi, T.T.; Mahesh, M. Effective doses in radiology and diagnostic nuclear medicine: A catalog 1. Radiology 2008, 248, 254–263. [Google Scholar] [CrossRef]
- Xu, H.; Shao, H.; Wang, L.; Jin, J.; Wang, J. A Methodological comparison between ultrasound and X-ray evaluations of bone age. J. Sports Sci. 2008, 6, 27. [Google Scholar]
- Stern, D.; Ebner, T.; Bischof, H.; Grassegger, S.; Ehammer, T.; Urschler, M. Fully automatic bone age estimation from left hand MR images. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2014; Golland, P., Hata, N., Barillot, C., Hornegger, J., Howe, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8674. [Google Scholar]
- Qasim, M.S.h.; Abdullateef, A.; Mohammed, A.l.-H.; Najah, R.R. Magnetic resonance imaging of the left wrist: Assessment of the bone age in a sample of healthy Iraqi adolescent males. J. Fac. Med. 2015, 57, 22–26. [Google Scholar]
- Ecklund, K.; Jaramillo, D. Patterns of premature physeal arrest: MR imaging of 111 children. AJR Am. J. Roentgenol. 2002, 178, 967–972. [Google Scholar] [CrossRef] [PubMed]
- Ballock, R.T.; O'Keefe, R.J. The biology of the growth plate. J. Bone Joint Surg. Am. 2003, 85, 715–726. [Google Scholar] [CrossRef]
- Breur, G.J.; van Enkevort, B.A.; Farnum, C.E.; Wilsman, N.J. Linear relationship between the volume of hypertrophic chondrocytes and the rate of longitudinal bone growth in growth plates. J. Orthop. Res. 1991, 9, 348–359. [Google Scholar] [CrossRef]
- Yun, H.H.; Kim, H.J.; Jeong, M.S.; Choi, Y.S.; Seo, J.Y. Changes of the growth plate in children: 3-dimensional magnetic resonance imaging analysis. Korean. J. Pediatr. 2018, 61, 226–230. [Google Scholar] [CrossRef]
- Craig, J.G.; Cody, D.D.; van Holsbeeck, M. The distal femoral and proximal tibial growth plates: MR imaging, three-dimensional modeling and estimation of area and volume. Skelet. Radiol. 2004, 33, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Stokes, I.A. Growth plate mechanics and mechanobiology. A survey of present understanding. J. Biomech. 2009, 42, 1793–1803. [Google Scholar]
- Mitchell, D.G.; Kim, I.; Chang, T.S.; Vinitski, S.; Consigny, P.M.; Saponaro, S.A.; Ehrlich, S.M.; Rifkin, M.D.; Rubin, R. Fatty liver: Chemical shift phase-difference and suppression magnetic resonance imaging techniques in animals, phantoms, and humans. Invest. Radiol. 1991, 26, 1041–1052. [Google Scholar] [CrossRef]
- Bley, T.A.; Wieben, O.; François, C.J.; Brittain, J.H.; Reeder, S.B. Fat and water magnetic resonance imaging. J. Magn. Reson. Imaging 2010, 31, 4–18. [Google Scholar] [CrossRef]
- Moon, W.J.; Lee, M.H.; Chung, E.C. Diffusion-weighted imaging with sensitivity encoding (SENSE) for detecting cranial bone marrow metastases: Comparison with T1-weighted images. Korean J. Radiol. 2007, 8, 185–191. [Google Scholar] [CrossRef]
- Bzowski, P.; Borys, D.; Guz, W.; Obuchowicz, R.; Piórkowski, A. Evaluation of the MRI Images Matching Using Normalized Mutual Information Method and Preprocessing Techniques. Adv. Intell. Syst. Comput. 2020, 1062, 92–100. [Google Scholar] [CrossRef]
- Wennmann, M.; Klein, A.; Bauer, F.; Chmelik, J.; Grözinger, M.; Uhlenbrock, C.; Lochner, J.; Nonnenmacher, T.; Rotkopf, L.T.; Sauer, S.; et al. Combining deep learning and radiomics for automated, objective, comprehensive bone marrow characterization from whole-body MRI. A multicentric feasibility study. Invest. Radiol. 2022, 57, 752–763. [Google Scholar] [CrossRef] [PubMed]
- Wennmann, M.; Neher, P.; Stanczyk, N.; Kahl, K.C.; Kächele, J.; Weru, V.; Hielscher, T.; Grözinger, M.; Chmelik, J.; Zhang, K.S.; et al. Deep learning for automatic bone marrow apparent diffusion coefficient measurements from whole-body magnetic resonance imaging in patients with multiple myeloma: A retrospective multicenter study. Invest. Radiol. 2023, 58, 273–282. [Google Scholar] [CrossRef] [PubMed]
- Wennmann, M.; Bauer, F.; Klein, A.; Chmelik, J.; Grözinger, M.; Rotkopf, L.T.; Neher, P.; Gnirs, R.; Kurz, F.T.; Nonnenmacher, T.; et al. In vivo repeatability and multiscanner reproducibility of MRI radiomics features in patients with monoclonal plasma cell disorders: A prospective bi-institutional study. Invest Radiol. 2023, 58, 253–264. [Google Scholar] [CrossRef] [PubMed]
- Wennmann, M.; Thierjung, H.; Bauer, F.; Weru, V.; Hielscher, T.; Grözinger, M.; Gnirs, R.; Sauer, S.; Goldschmidt, H.; Weinhold, N.; et al. Repeatability and Reproducibility of ADC Measurements and MRI Signal Intensity Measurements of Bone Marrow in Monoclonal Plasma Cell Disorders: A Prospective Bi-institutional Multiscanner.; Multiprotocol Study. Invest. Radiol. 2022, 57, 272–281. [Google Scholar] [CrossRef]
| Parameter | T1-Weighted | T2-Weighted |
|---|---|---|
| Slice thickness | 3 mm | 3 mm |
| Repetition Time | 435 ms | 2749 ms |
| Echo Time | 16 ms | 106 ms |
| Number of averages | 2 | 2 |
| Spacing | 3.5 mm | 3.5 mm |
| Echo train length | 23 | 23 |
| Bandwidth | 81 MHz | 97 MHz |
| Data | R2 | RMSE | MSE | MAE |
|---|---|---|---|---|
| DICOM T1-weighted | 0.9383 | 0.4584 | 0.2101 | 0.3300 |
| DICOM T2-weighted | 0.7510 | 0.8365 | 0.6997 | 0.6229 |
| PNG T1-weighted | 0.7283 | 0.9344 | 0.8732 | 0.6922 |
| PNG T2-weighted | 0.8711 | 0.5731 | 0.3284 | 0.4429 |
| Data | R2 | RMSE | MSE | MAE |
|---|---|---|---|---|
| DICOM T1-weighted | 0.8041 | 0.8194 | 0.6714 | 0.6142 |
| DICOM T2-weighted | 0.6621 | 1.4104 | 1.9892 | 1.0969 |
| PNG T1-weighted | 0.6743 | 1.0550 | 1.1130 | 0.8740 |
| PNG T2-weighted | 0.5216 | 1.1058 | 1.2228 | 0.9228 |
| References | MAE (Months) |
|---|---|
| Liu et al. [42] | 6.01 |
| Iglovikov et al. [39] | 6.10 |
| Salim and Hamza [40] | 6.38 |
| Zulkifley et al. [43] | 7.70 |
| MAE (years) | |
| Nguyen et al. [47] | 4.856 |
| Our method | 0.330 (T1 DICOM), 0.692 (T1 PNG) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obuchowicz, R.; Nurzynska, K.; Pierzchala, M.; Piorkowski, A.; Strzelecki, M. Texture Analysis for the Bone Age Assessment from MRI Images of Adolescent Wrists in Boys. J. Clin. Med. 2023, 12, 2762. https://doi.org/10.3390/jcm12082762
Obuchowicz R, Nurzynska K, Pierzchala M, Piorkowski A, Strzelecki M. Texture Analysis for the Bone Age Assessment from MRI Images of Adolescent Wrists in Boys. Journal of Clinical Medicine. 2023; 12(8):2762. https://doi.org/10.3390/jcm12082762
Chicago/Turabian StyleObuchowicz, Rafal, Karolina Nurzynska, Monika Pierzchala, Adam Piorkowski, and Michal Strzelecki. 2023. "Texture Analysis for the Bone Age Assessment from MRI Images of Adolescent Wrists in Boys" Journal of Clinical Medicine 12, no. 8: 2762. https://doi.org/10.3390/jcm12082762
APA StyleObuchowicz, R., Nurzynska, K., Pierzchala, M., Piorkowski, A., & Strzelecki, M. (2023). Texture Analysis for the Bone Age Assessment from MRI Images of Adolescent Wrists in Boys. Journal of Clinical Medicine, 12(8), 2762. https://doi.org/10.3390/jcm12082762









