Influence of Cross-Section and Pitch on the Mechanical Response of NiTi Endodontic Files under Bending and Torsional Conditions—A Finite Element Analysis
Abstract
1. Introduction
2. Materials and Methods
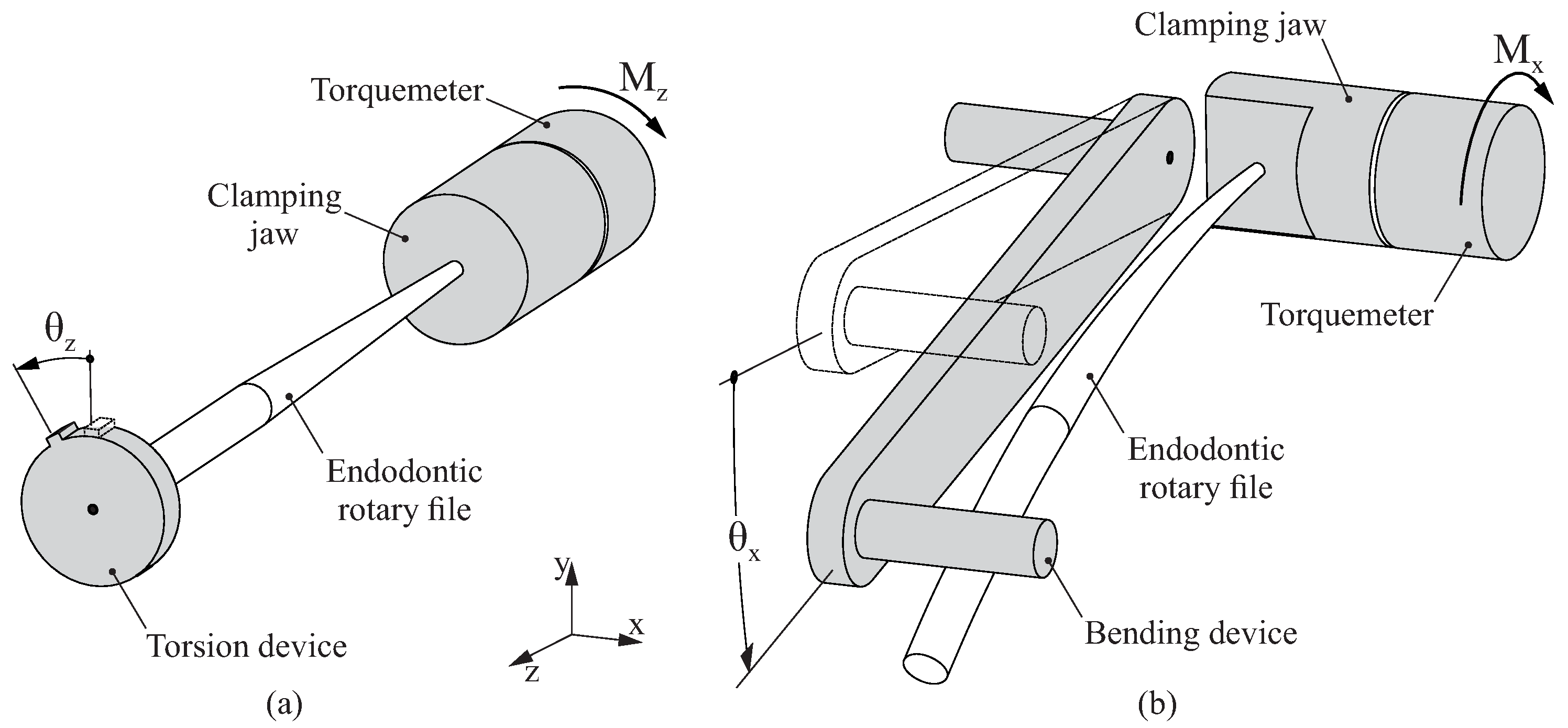
2.1. Devices for Experimental Bending and Torsion Analysis
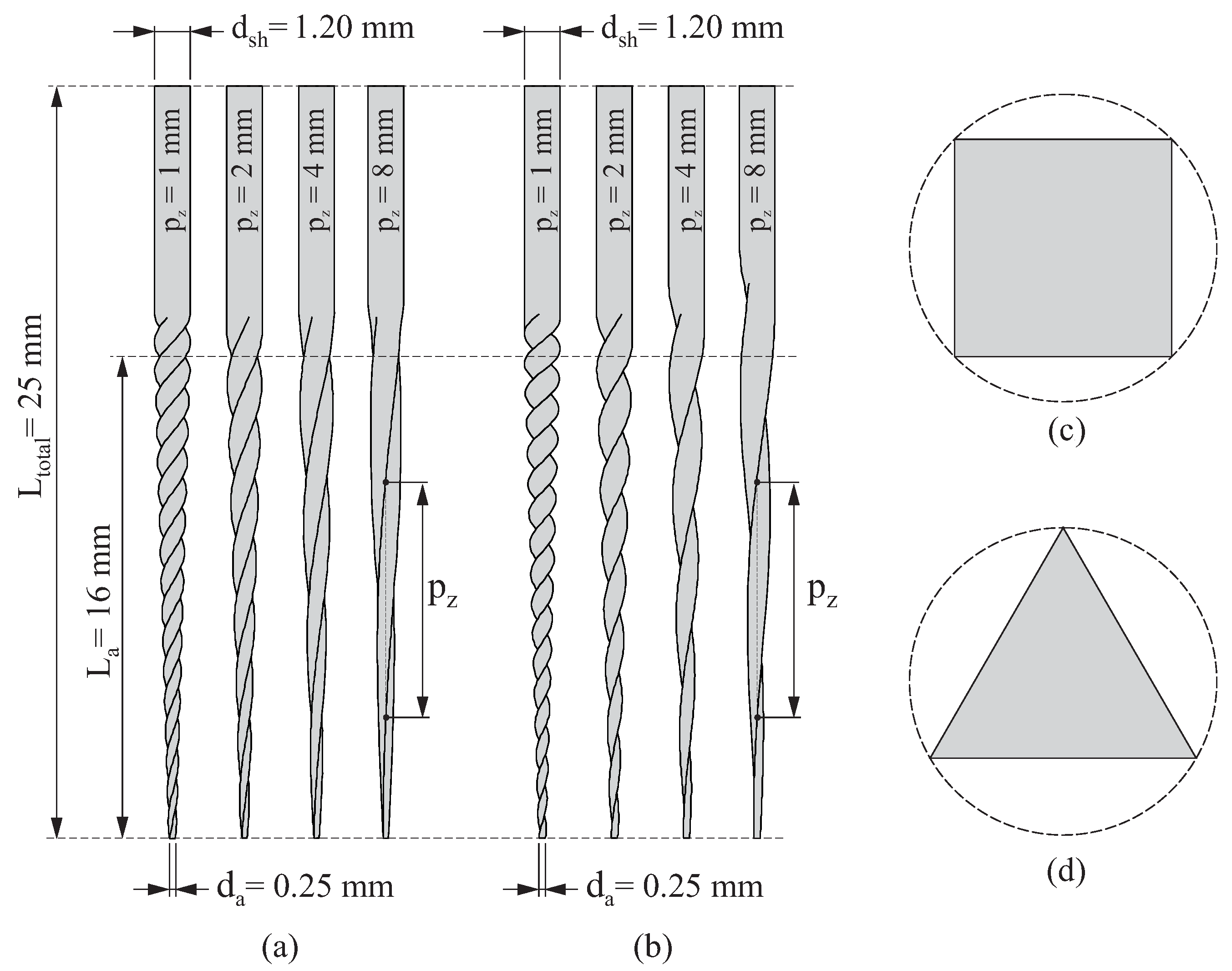
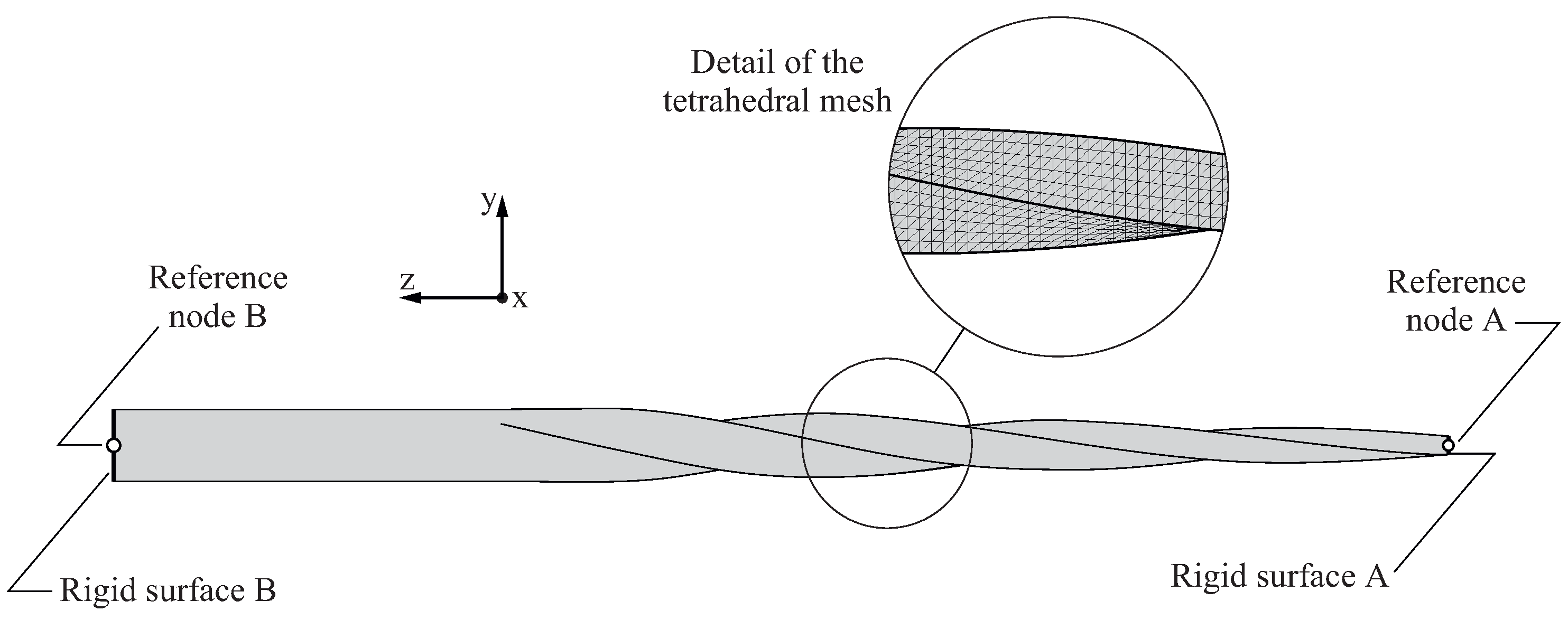
2.2. Definition of the Finite Element Model for the NiTi Endodontic File
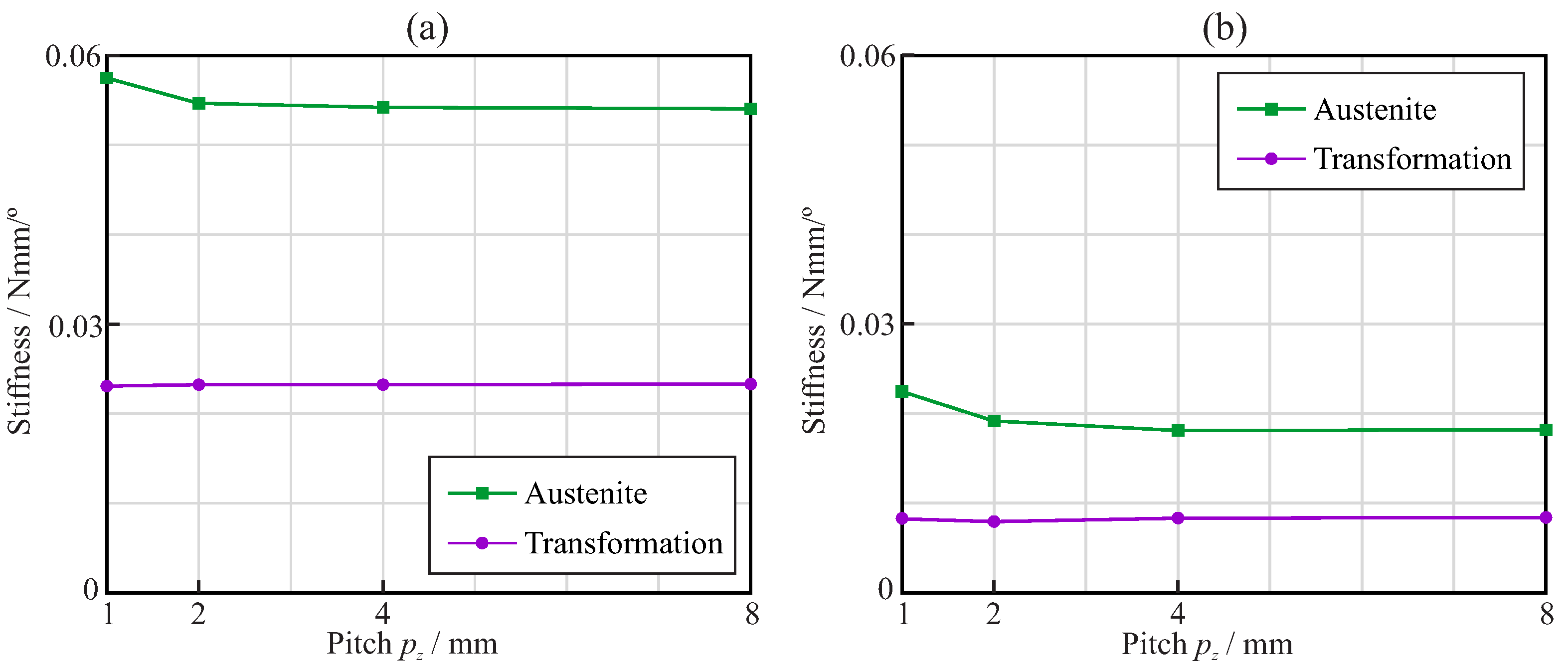
- In the bending analysis, an increasing displacement was imposed at reference node B in the negative direction of the y-axis, until the maximum von Mises stress along the endodontic file reached the end of the martensitic elastic regime. As the results of the bending analyses are sensitive to the orientation of the endodontic file with respect to the bending direction, the analysis was conducted in 24 different angular positions, given by a rotation of the endodontic file with respect to the z-axis.
- In the torsional analysis, an increasing rotation was imposed at reference node B along the positive direction of z-axis, until the maximum von Mises stress along the endodontic file reached the end of the martensitic elastic regime. Here, the results of the analysis do not depend on the orientation of the file.
3. Results
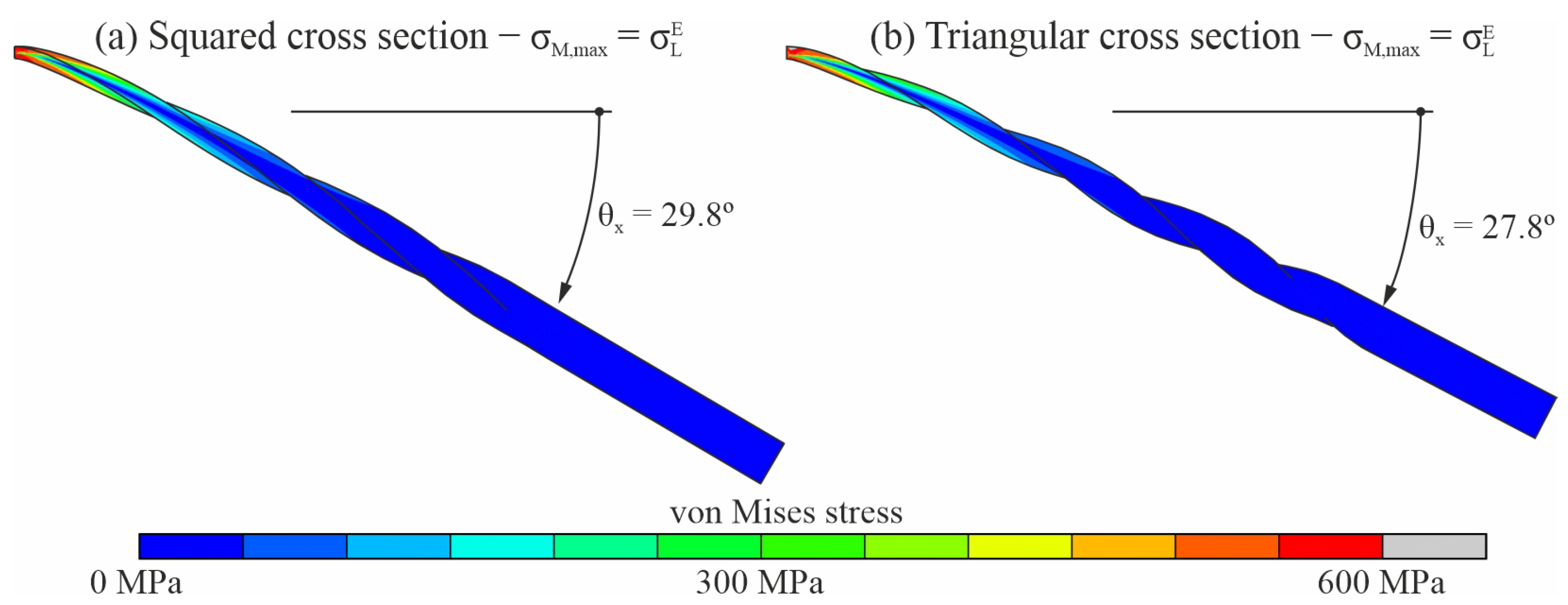
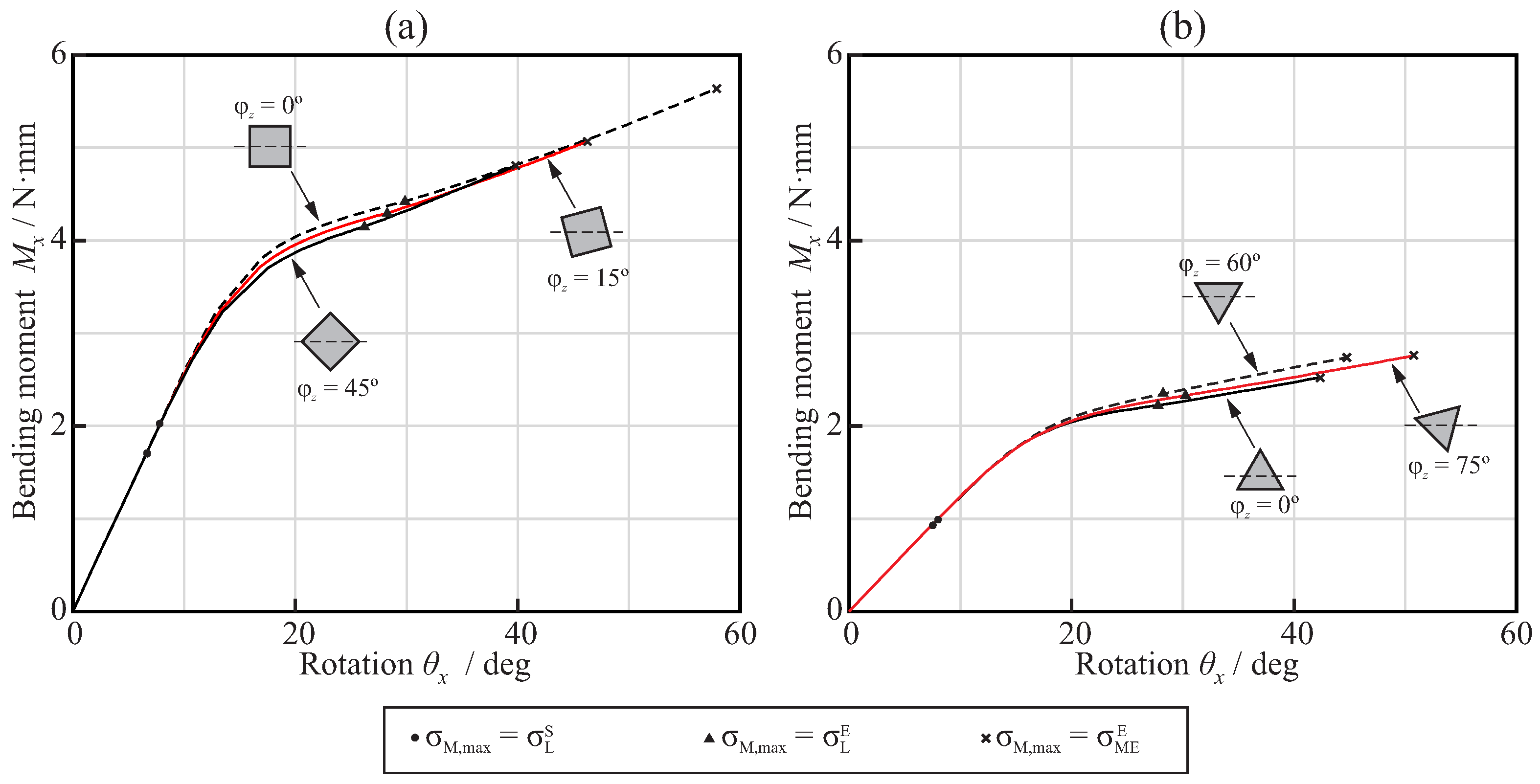
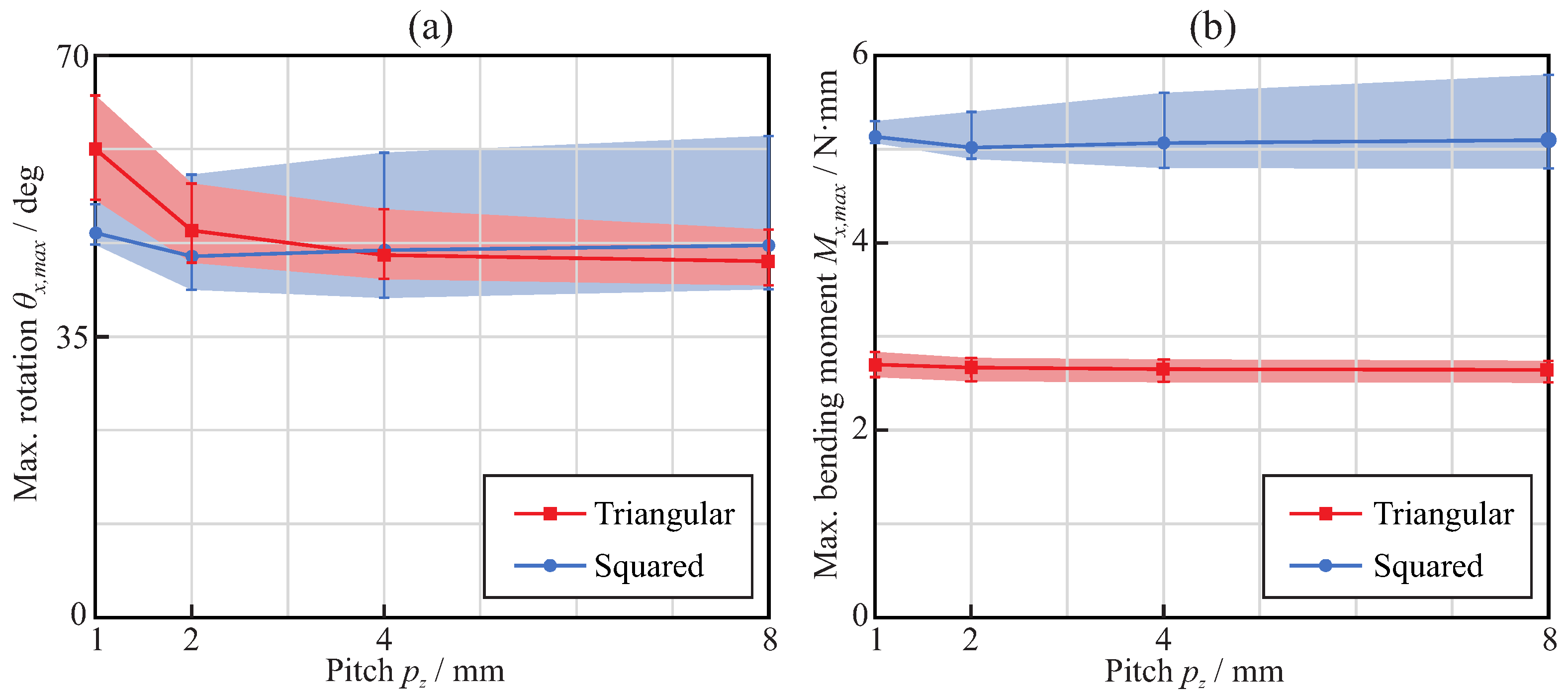
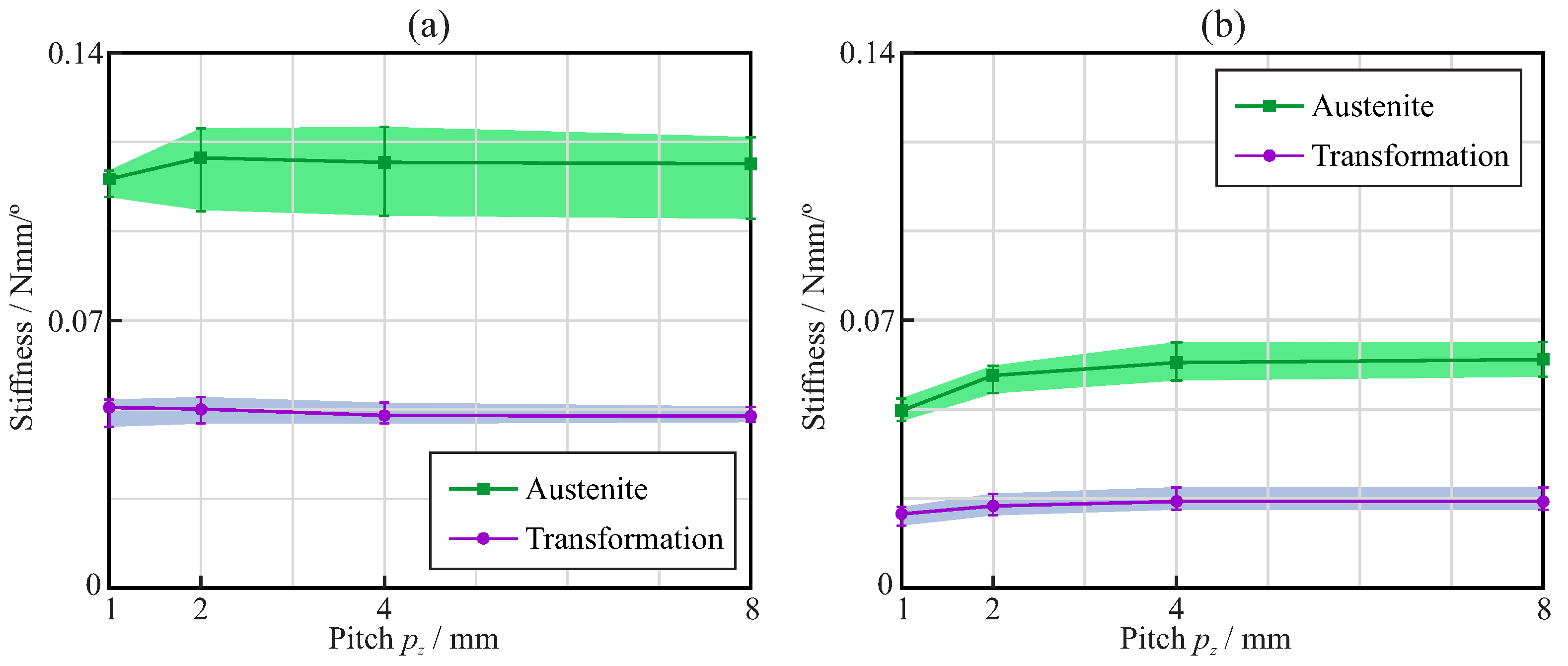
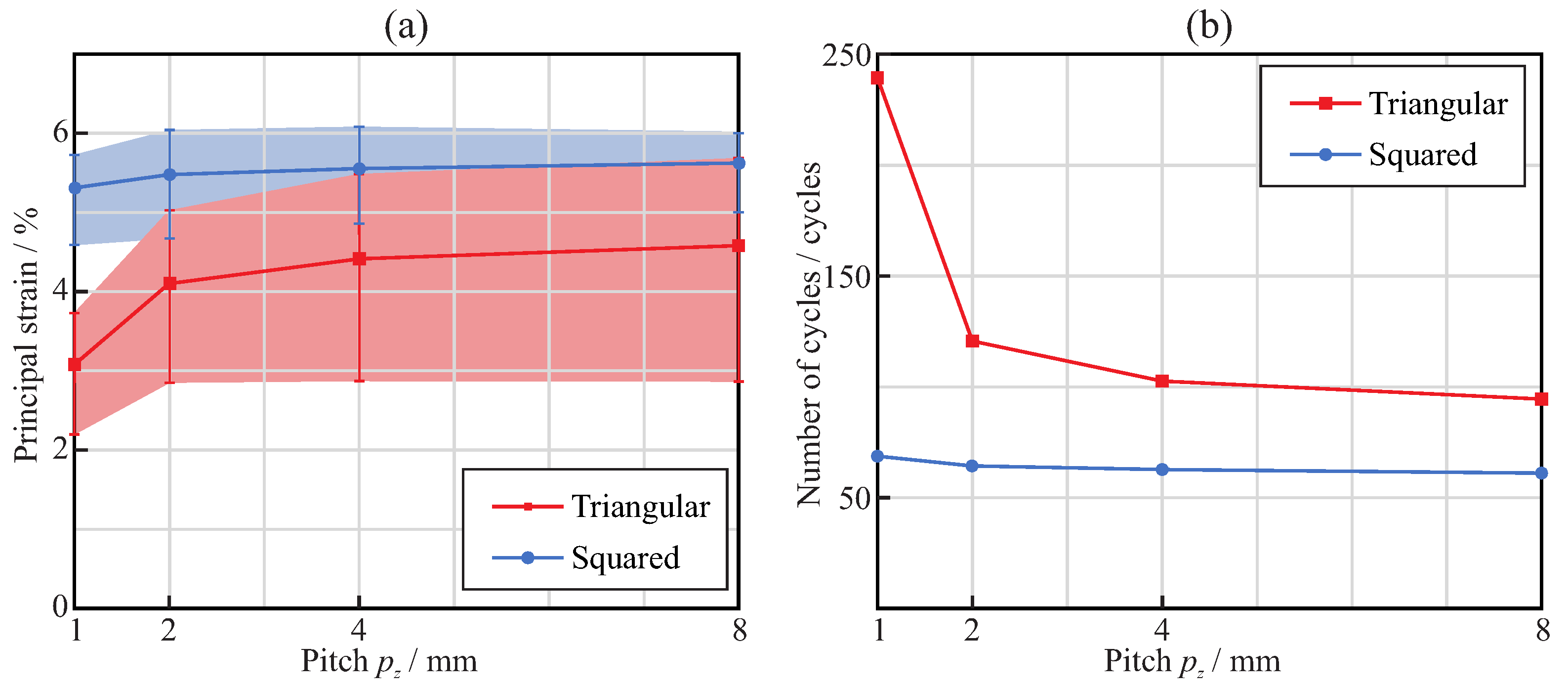
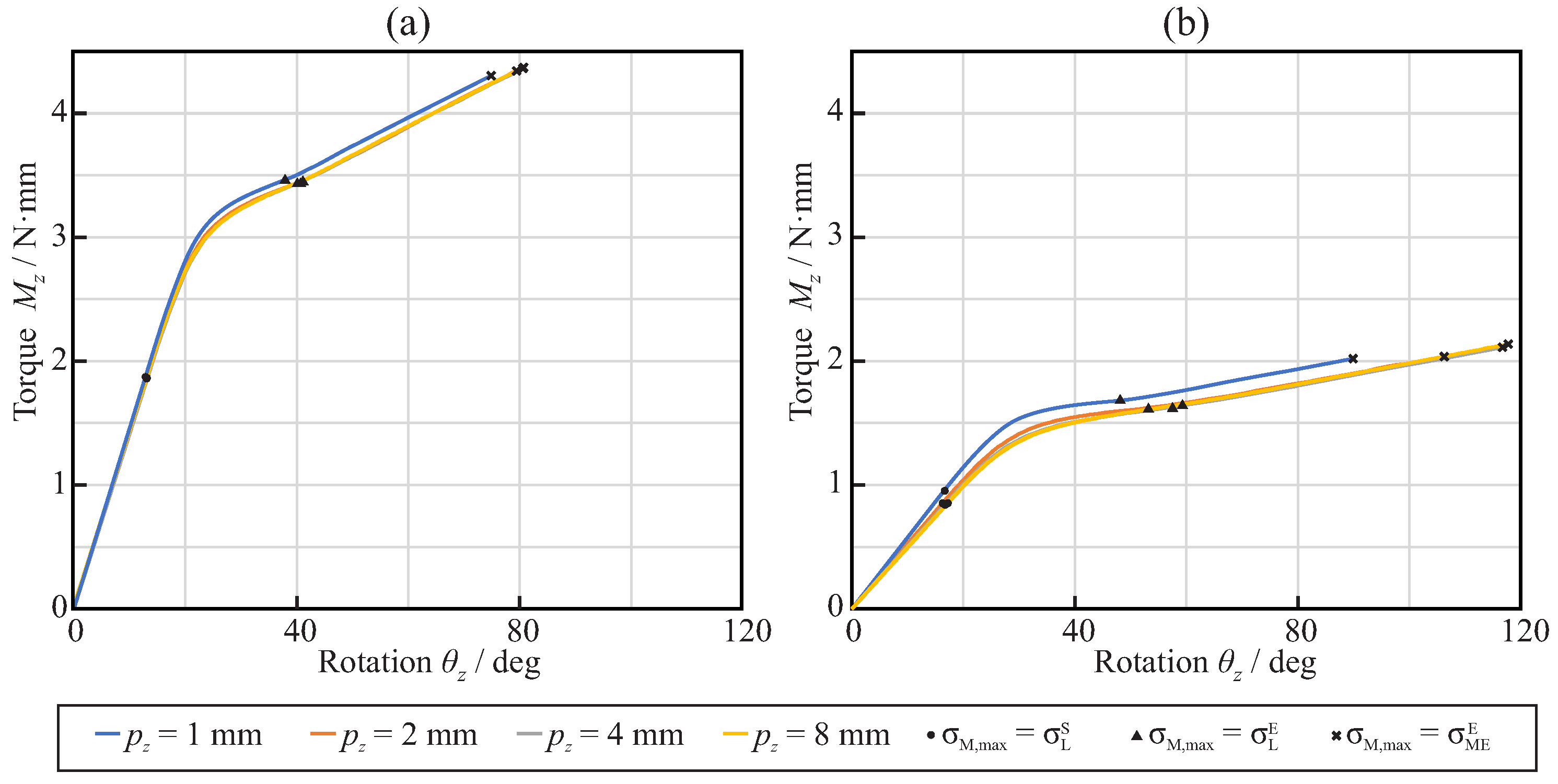
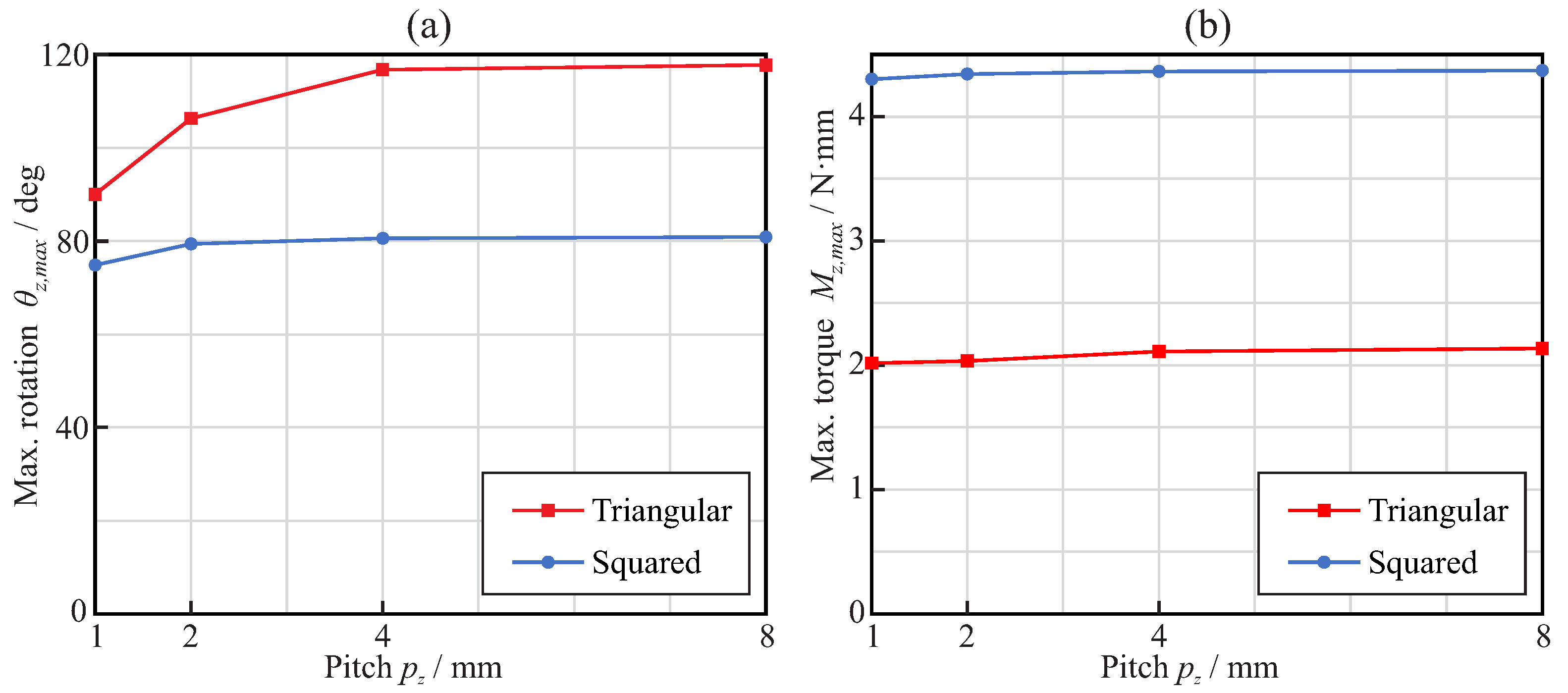
3.1. Bending Analysis
3.2. Torsional Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Post-Processing of the Finite Element Analysis Results
Appendix A.1. Assessment of the Maximum von Mises Stress and Maximum Principal Strain Values in the Endodontic File
- Let refer to each of the tetrahedral finite elements in the model, and refer to the integration points in each tetrahedral element. The von Mises stress at a given element and integration point is denoted as , and the volume associated with each integration point is denoted as (where is the volume of element i).
- The von Mises stress and the volume at each integration point of the model are retrieved and stored in an array with rows. Each row m in contains the von Mises stress and the volume associated with a given integration point, with the shape
- The rows in are rearranged in such a way that the von Mises stresses are sorted in descending order. Then, the algorithm shown in Figure A1 is applied to determine the maximum von Mises stress in the analysis frame.
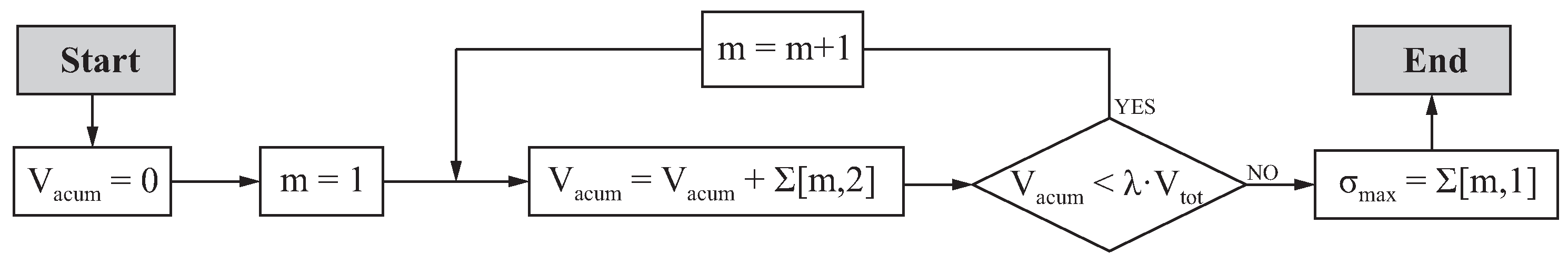
Appendix A.2. Determination of Bending Fatigue Life of the NiTi Endodontic Files
- On one hand, the Coffin–Manson relation is based on a uni-axial strain, but the strain results obtained from the finite element model correspond to a multi-axial strain state. Thus, a criterion to reduce the obtained multi-axial strain state to an equivalent uni-axial strain condition is required.
- On the other hand, the bending analysis conducted using the proposed finite element model does not represent the actual strain history of the endodontic file when it is rotating inside the root canal, as bending is applied in just one direction (uni-directional fatigue). Thus, a conversion method must be proposed to convert the obtained strains into a purely reversed fatigue phenomenon.
Appendix B. Literature Review
| Source | Section Type | Tip Diameter; Taper | Pitch (mm) | Material Model and Parameters | FE Code; Model Type | Boundary Conditions; Number of Nodes/Elements | Conclusions | Limitations |
|---|---|---|---|---|---|---|---|---|
| Xu et al., 2006 [32] | 6 shapes (ProTaper, Hero642, Mtwo, ProFile, Quantec, NiTiflex) | 0.4 mm, | 3.6 | Multi-linear kinematic hardening plastic model = 34.3 GPa, = 0.33, = 480 MPa, = 755 MPa | N/A, Static | Loads: progressive 0–2.5 Nmm torsion in shank, Constraints: fixed at tip, # nodes: Not available. # elements: Not available. | (1) Sections with higher core area show lower stresses for the same torque | (1) Sections analyzed have different total areas |
| Kim et al., 2009 [34] | 4 shapes (ProFile, HeroShaper, Mtwo, NRT) | 0.3 mm; | Several, N/A | = 36 GPa, = 0.3, = 504 MPa, = 755 MPa | ABAQUS; Static (cases I to IV) Dynamic (case V): Simulated shaping | Case I (or II), Load: 1 N (or 2 mm) bending in tip Constraint: shank fixed Case II (or III), Load: 2.5 Nmm (or 10°) torsion in shank Constraint: fixed at 4 mm from tip Case V, Constraint: shank rotation 240 rpm, file introduction in simulated root canal; # nodes: 7018–18,214 # elements: 5300–9440 | (1) Rectangle-based sections have lower expected fatigue life than triangle-based sections | (1) Material model not clearly defined |
| Baek et al., 2011 [36] | 4 theoretical shapes (triangle, slender rectangle, rectangle, square) | 0.3 mm; | 3.2, 1.6, 1.1 | = 36 GPa, = 0.3 | ABAQUS; Static | Load: 20° torsion in shank Constraint: fixed at 4 mm from tip; # nodes: Not available. # elements: Not available. | (1) Rectangle-based sections, even with smaller areas, have higher torsional stiffness than triangular section; (2) Reduction in pitch increases torsional stiffness | (1) Linear material model; (2) Mesh quality not provided |
| Arbab-Chirani et al., 2011 [35] | 5 shapes (Hero, Hero Shaper, Mtwo, ProFile, ProTaper F1) | 0.2mm; | Several, N/A | SMA material model, = 47 GPa, = 0.3 = 505 MPa | Cast3M; Static | Case 1: Load: bending at tip 3.8 mm, Constraint: shank fixed Case 2: Load: torsion at tip 22°, Constraint: shank fixed; # nodes: 66,023–73,561 # elements: 14,100–16,200 | (1) ProTaper F1, Hero Shaper, and Hero are stiffer than Mtwo and ProFile; (2) Maximum stresses near the tip for both cases and similar for all the files | (1) Different pitch among files; (2) Deformations applied are low to extend martensitic transformation to a significant part of the file |
| Versluis et al., 2012 [33] | 4 theoretical shapes (triangle, slender rectangle, rectangle, square) | 0.3 mm; | 3.2, 1.6, 1.1 | SMA material model, = 36 GPa, = 0.3 = 504 MPa, = 600 MPa | MSC.Marc; Static | Load: bending at tip 5 mm (all possible orientations with respect to the cross-section), Constraint: shank axis orientation and shank end location fixed; # nodes: Not available. # elements: Not available. | (1) Flexural stiffness and stress decreases with decreasing pitch; (2) Decreasing the pitch reduces the oscillation of stress when the file rotates; (3) Flexural stiffness and stress correlates with center-core area; (4) Effect of section greater than that of pitch; (5) Maximum stress is affected by bending orientation for rectangular section | (1) Deformations applied are low to extend martensitic transformation to a significant part of the file (max. stresses below 504 MPa) |
| De Arruda et al., 2014 [10] | 3 shapes (Mtwo, RaCe, PTU F1) | 0.25 mm; | Several (Not available) | Shape-memory alloy material model implemented as ABAQUS sub-routine, = 42.53 GPa, = 0.33 = 492 MPa, = 630 MPa | ABAQUS; Static | Case 1: Load: bending in shank from 0° to 45° (two perpendicular orientations), Constraint: fixed at 3 mm from tip Case 2: Load: 3 Nmm torsion in shank, Constraint: fixed at 3 mm from tip; # nodes: 84,126–91,372 # elements: 48,460–55,009 | (1) Finite element analysis results agree with experimental results; (2) RaCe and Mtwo are more flexible than PTU F1 in bending and torsion; (3) Shape of the section affects the maximum stress and the variation in stress with bending orientation | (1) Only three section geometries and two orientations for bending considered; (2) Different pitch among files |
| Ha et al., 2015 [37] | 4 theoretical shapes (triangle, slender rectangle, rectangle, square) | 0.3 mm; | 3.2, 1.6, 1.1 | = 26 GPa, = 0.3 | ABAQUS; Not available. | Load: Prescribed rotation inside the root canal, Constraint: Contact with friction in 3 simulated root canal (15°, 30°, 45° curvature), shank axis orientation & shank end location fixed; # nodes: 10,230–18,042 # elements: 8325–15,540 | (1) The square cross-section shows the highest ‘screw-in’ force and reaction torque; (2) ‘Screw-in’ force and reaction torque are higher for greater pitch and higher root canal curvature | (1) Linear material model; (2) Very low friction coefficient (0.1) considered between file and root canal; (3) Solid surface used as root canal model; (4) Only 3 root canal geometries considered |
| Basser-Ahamed et al., 2018 [31] | 5 theoretical shapes (triangle T, convex triangle C, concave triangle U, combined CTU, combinedUTC) | 0.25 mm; | 1.6 | File: = 36 GPa, = 0.3 Root canal: E = 18.6 GPa, = 0.3 | ANSYS; Not available. | Load: Torque 2 Nm, Constraint: Contact with simulated root canal (45° curvature), shank axis orientation and shank end location fixed, rotation of 180° at 240 rpm; File: # nodes: 16,750–42,785 # elements: 75,430–152,432 Root canal: # nodes: 3000 # elements: 3500 | (1) A combined section CTU (C coronal third, T middle third, U apical third) presents lower stresses than constant section | (1) Geometry of the root canal not clearly defined defined; (2) Contact and friction conditions undefined; (3) Does not consider changes in dentin properties within the root canal; (4) Effect of pitch not analyzed |
References
- Walia, H.; Brantley, W.; Gerstein, H. An initial investigation of the bending and torsional properties of nitinol root canal files. J. Endod. 1988, 14, 346–351. [Google Scholar] [CrossRef]
- Esposito, P.; Cunningham, C. A comparison of canal preparation with nickel-titanium and stainless steel instruments. J. Endod. 1995, 21, 173–176. [Google Scholar] [CrossRef]
- Bergmans, L.; Van Cleynenbreugel, J.; Wevers, M.; Lambrechts, P. Mechanical root canal preparation with NiTi rotary instruments: Rationale, performance and safety. Status Report for the American Journal of Dentistry. Am. J. Dent. 2001, 14, 324–333. [Google Scholar] [PubMed]
- Parashos, P.; Gordon, I.; Messer, H. Factors influencing defects of rotary nickel-titanium endodontic instruments after clinical use. J. Endod. 2004, 30, 722–725. [Google Scholar] [CrossRef] [PubMed]
- Spili, P.; Parashos, P.; Messer, H. The impact of instrument fracture on outcome of endodontic treatment. J. Endod. 2005, 31, 845–850. [Google Scholar] [CrossRef]
- Plotino, G.; Grande, N.M.; Cordaro, M.; Testarelli, L.; Gambarini, G. A Review of Cyclic Fatigue Testing of Nickel-Titanium Rotary Instruments. J. Endod. 2009, 35, 1469–1476. [Google Scholar] [CrossRef]
- Scattina, A.; Alovisi, M.; Paolino, D.S.; Pasqualini, D.; Scotti, N.; Chiandussi, G.; Berutti, E. Prediction of cyclic fatigue life of nickel-titanium rotary files by virtual modeling and finite elements analysis. J. Endod. 2015, 41, 1867–1870. [Google Scholar] [CrossRef]
- Peters, O.; Barbakow, F. Dynamic torque and apical forces of ProFile .04 rotary instruments during preparation of curved canals. Int. Endod. J. 2002, 35, 379–389. [Google Scholar] [CrossRef]
- Kuhn, G.; Tavernier, B.; Jordan, L. Influence of structure on nickel-titanium endodontic instruments failure. J. Endod. 2001, 27, 516–520. [Google Scholar] [CrossRef]
- De Arruda Santos, L.; López, J.; De Las Casas, E.; De Azevedo Bahia, M.; Buono, V. Mechanical behavior of three nickel-titanium rotary files: A comparison of numerical simulation with bending and torsion tests. Mater. Sci. Eng. C 2014, 37, 258–263. [Google Scholar] [CrossRef]
- Pruett, J.; Clement, D.; Carnes, D., Jr. Cyclic fatigue testing of nickel-titanium endodontic instruments. J. Endod. 1997, 23, 77–85. [Google Scholar] [CrossRef]
- Parashos, P.; Messer, H. Rotary NiTi Instrument Fracture and its Consequences. J. Endod. 2006, 32, 1031–1043. [Google Scholar] [CrossRef] [PubMed]
- Topçuoğlu, H.; Topçuoğlu, G. Cyclic Fatigue Resistance of Reciproc Blue and Reciproc Files in an S-shaped Canal. J. Endod. 2017, 43, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Siqueira, J., Jr.; Rôças, I. Polymerase chain reaction-based analysis of microorganisms associated with failed endodontic treatment. Oral Surgery Oral Med. Oral Pathol. Oral Radiol. Endod. 2004, 97, 85–94. [Google Scholar] [CrossRef]
- Strindberg, L. The Dependence of the Results of Pulp Therapy on Certain Factors: An Analytic Study Based on Radiographic and Clinical Follow-Up Examinations. Acta Odontol. Scand. 1956, 14, 1–175. [Google Scholar]
- Yang, Q.; Shen, Y.; Huang, D.; Zhou, X.; Gao, Y.; Haapasalo, M. Evaluation of Two Trephine Techniques for Removal of Fractured Rotary Nickel-titanium Instruments from Root Canals. J. Endod. 2017, 43, 116–120. [Google Scholar] [CrossRef]
- Fu, M.; Zhang, Z.; Hou, B. Removal of broken files from root canals by using ultrasonic techniques combined with dental microscope: A retrospective analysis of treatment outcome. J. Endod. 2011, 37, 619–622. [Google Scholar] [CrossRef]
- Ruiz-Sánchez, C.; Faus-Llacer, V.; Faus-Matoses, I.; Zubizarreta-Macho, A.; Sauro, S.; Faus-Matoses, V. The influence of niti alloy on the cyclic fatigue resistance of endodontic files. J. Clin. Med. 2020, 9, 3755. [Google Scholar] [CrossRef]
- Zupanc, J.; Vahdat-Pajouh, N.; Schäfer, E. New thermomechanically treated NiTi alloys—A review. Int. Endod. J. 2018, 51, 1088–1103. [Google Scholar] [CrossRef]
- Faus-Llacer, V.; Kharrat, N.; Ruiz-Sanchez, C.; Faus-Matoses, I.; Zubizarreta-Macho, A.; Faus-Matoses, V. The effect of taper and apical diameter on the cyclic fatigue resistance of rotary endodontic files using an experimental electronic device. Appl. Sci. 2021, 11, 863. [Google Scholar] [CrossRef]
- Turpin, Y.; Chagneau, F.; Vulcain, J. Impact of two theoretical cross-sections on torsional and bending stresses of nickel-titanium root canal instrument models. J. Endod. 2000, 26, 414–417. [Google Scholar] [CrossRef] [PubMed]
- Sekar, V.; Kumar, R.; Nandini, S.; Ballal, S.; Velmurugan, N. Assessment of the role of cross section on fatigue resistance of rotary files when used in reciprocation. Eur. J. Dent. 2016, 10, 541–545. [Google Scholar] [CrossRef] [PubMed]
- Kwak, S.; Ha, J.H.; Lee, C.J.; El Abed, R.; Abu-Tahun, I.; Kim, H.C. Effects of Pitch Length and Heat Treatment on the Mechanical Properties of the Glide Path Preparation Instruments. J. Endod. 2016, 42, 788–792. [Google Scholar] [CrossRef]
- ISO 3630-1:2008; Dentistry—Root-Canal Instruments—Part 1: General Requirements and Test Methods. International Organization for Standardization: Geneva, Switzerland, 2008.
- Zhang, E.; Cheung, G.; Zheng, Y. A mathematical model for describing the mechanical behaviour of root canal instruments. Int. Endod. J. 2011, 44, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Tsao, C.; Liou, J.; Wen, P.; Peng, C.; Liu, T. Study on bending behaviour of nickel-titanium rotary endodontic instruments by analytical and numerical analyses. Int. Endod. J. 2013, 46, 379–388. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.H.; Versluis, A.; Kim, B.M.; Lee, C.J.; Hur, B.; Kim, H.C. Correlation between experimental cyclic fatigue resistance and numerical stress analysis for nickel-titanium rotary files. J. Endod. 2011, 37, 1152–1157. [Google Scholar] [CrossRef] [PubMed]
- Montalvão, D.; Shengwen, Q.; Freitas, M. A study on the influence of Ni-Ti M-Wire in the flexural fatigue life of endodontic rotary files by using Finite Element Analysis. Mater. Sci. Eng. C 2014, 40, 172–179. [Google Scholar] [CrossRef]
- Bonessio, N.; Pereira, E.; Lomiento, G.; Arias, A.; Bahia, M.; Buono, V.; Peters, O. Validated finite element analyses of WaveOne Endodontic Instruments: A comparison between M-Wire and NiTi alloys. Int. Endod. J. 2015, 48, 441–450. [Google Scholar] [CrossRef]
- Chien, P.Y.; Walsh, L.J.; Peters, O.A. Finite element analysis of rotary nickel-titanium endodontic instruments: A critical review of the methodology. Eur. J. Oral Sci. 2021, 129, e12802. [Google Scholar] [CrossRef]
- Basheer Ahamed, S.; Vanajassun, P.; Rajkumar, K.; Mahalaxmi, S. Comparative Evaluation of Stress Distribution in Experimentally Designed Nickel-titanium Rotary Files with Varying Cross Sections: A Finite Element Analysis. J. Endod. 2018, 44, 654–658. [Google Scholar] [CrossRef]
- Xu, X.; Eng, M.; Zheng, Y.; Eng, D. Comparative study of torsional and bending properties for six models of nickel-titanium root canal instruments with different cross-sections. J. Endod. 2006, 32, 372–375. [Google Scholar] [CrossRef] [PubMed]
- Versluis, A.; Kim, H.C.; Lee, W.; Kim, B.M.; Lee, C.J. Flexural stiffness and stresses in nickel-titanium rotary files for various pitch and cross-sectional geometries. J. Endod. 2012, 38, 1399–1403. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kim, H.; Lee, C.; Kim, B.; Park, J.; Versluis, A. Mechanical response of nickel-titanium instruments with different cross-sectional designs during shaping of simulated curved canals. Int. Endod. J. 2009, 42, 593–602. [Google Scholar] [CrossRef] [PubMed]
- Arbab-Chirani, R.; Chevalier, V.; Arbab-Chirani, S.; Calloch, S. Comparative analysis of torsional and bending behavior through finite-element models of 5 Ni-Ti endodontic instruments. Oral Surgery Oral Med. Oral Pathol. Oral Radiol. Endod. 2011, 111, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.H.; Lee, C.J.; Versluis, A.; Kim, B.M.; Lee, W.; Kim, H.C. Comparison of torsional stiffness of nickel-titanium rotary files with different geometric characteristics. J. Endod. 2011, 37, 1283–1286. [Google Scholar] [CrossRef]
- Ha, J.H.; Cheung, G.S.; Versluis, A.; Lee, C.J.; Kwak, S.W.; Kim, H.C. ‘Screw-in’ tendency of rotary nickel-titanium files due to design geometry. Int. Endod. J. 2015, 48, 666–672. [Google Scholar] [CrossRef]
- Roda-Casanova, V.; Zubizarreta-Macho, A.; Sanchez-Marin, F.; Ezpeleta, O.; Martínez, A.; Catalán, A. Computerized generation and finite element stress analysis of endodontic rotary files. Appl. Sci. 2021, 11, 4329. [Google Scholar] [CrossRef]
- Auricchio, F.; Petrini, L. A three-dimensional model describing stress-temperature induced solid phase transformations: Solution algorithm and boundary value problems. Int. J. Numer. Methods Eng. 2004, 61, 807–836. [Google Scholar] [CrossRef]
- El-Anwar, M.I.; Mandorah, A.O.; Yousief, S.A.; Soliman, T.A.; Abd El-Wahab, T.M. A finite element study on the mechanical behavior of reciprocating endodontic files. Braz. J. Oral Sci. 2015, 14, 52–59. [Google Scholar] [CrossRef][Green Version]
- Stolk, J.; Verdonschot, N.; Huiskes, R. Management of stress fields around singular points in a finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2001, 3, 57–62. [Google Scholar]
- Chen, G.; Pettet, G.; Pearcy, M.; McElwain, D. Comparison of two numerical approaches for bone remodelling. Med. Eng. Phys. 2007, 29, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Żmudzki, J.; Chladek, W. Stress present in bone surrounding dental implants in FEM model experiments. J. Achiev. Mater. Manuf. Eng. 2008, 27, 71–74. [Google Scholar]
- Roda-Casanova, V.; Pérez-González, A.; Zubizarreta-Macho, Á.; Faus-Matoses, V. Fatigue Analysis of NiTi Rotary Endodontic Files through Finite Element Simulation: Effect of Root Canal Geometry on Fatigue Life. J. Clin. Med. 2021, 10, 5692. [Google Scholar] [CrossRef] [PubMed]
- Cheung, G.S.; Darvell, B.W. Fatigue testing of a NiTi rotary instrument. Part 1: Strain-life relationship. Int. Endod. J. 2007, 40, 612–618. [Google Scholar] [CrossRef]
- Figueiredo, A.M.; Modenesi, P.; Buono, V. Low-cycle fatigue life of superelastic NiTi wires. Int. J. Fatigue 2009, 31, 751–758. [Google Scholar] [CrossRef]
- Maletta, C.; Sgambitterra, E.; Furgiuele, F.; Casati, R.; Tuissi, A. Fatigue properties of a pseudoelastic NiTi alloy: Strain ratcheting and hysteresis under cyclic tensile loading. Int. J. Fatigue 2014, 66, 78–85. [Google Scholar] [CrossRef]
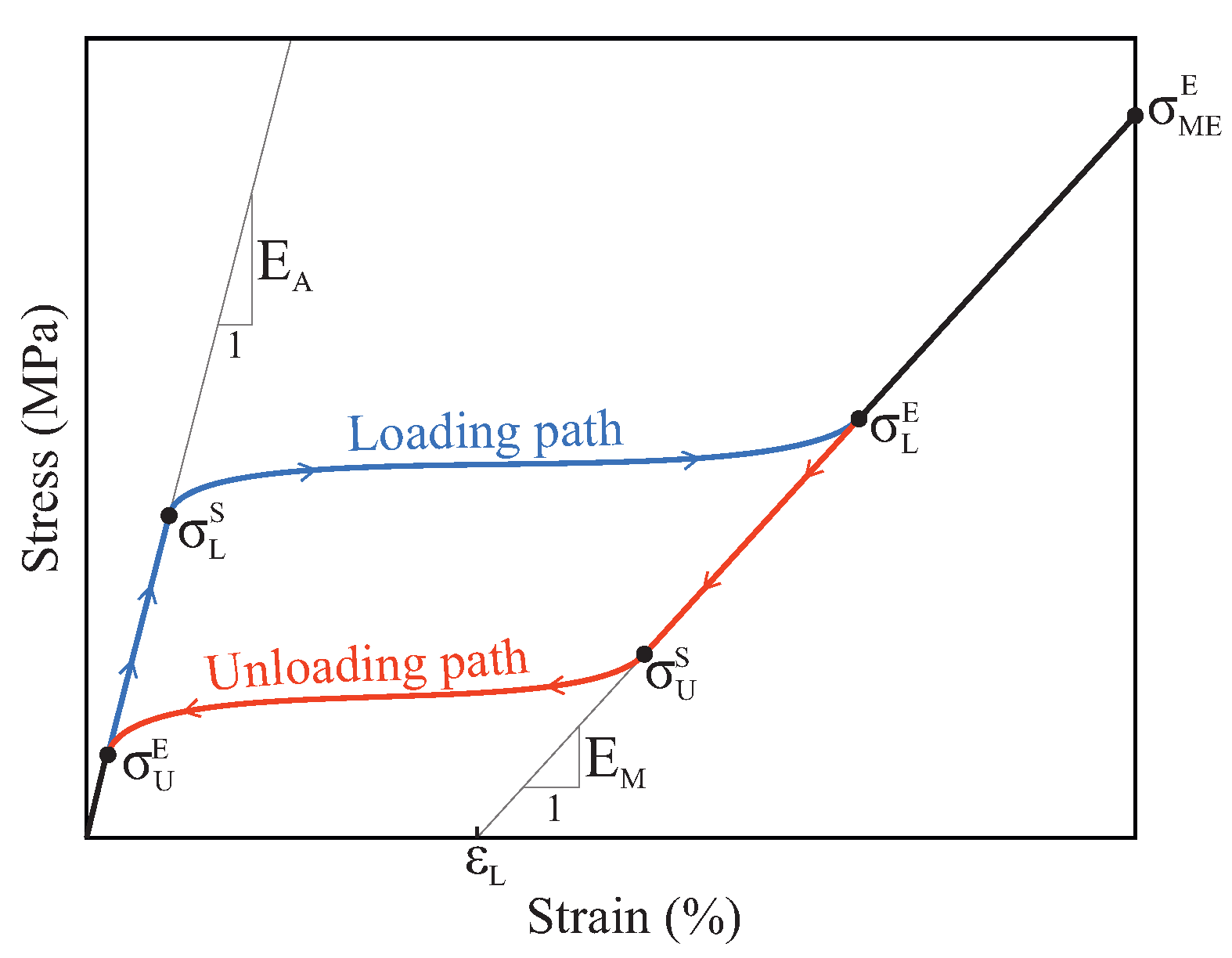

| Parameter | Variable | Magnitude |
|---|---|---|
| Young’s modulus of austenite | 42,530 MPa | |
| Austenite Poisson’s ratio | 0.33 | |
| Young’s modulus of martensite | 12,828 MPa | |
| Martensite Poisson’s ratio | ||
| Uni-axial transformation strain | ||
| Slope of the stress–temperature curve for loading | ||
| Start of transformation loading | ||
| End of transformation loading | ||
| Reference temperature | 22 C | |
| Slope of the stress–temperature curve for unloading | ||
| Start of transformation unloading | ||
| End of transformation unloading | ||
| End of martensitic elastic regime |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roda-Casanova, V.; Pérez-González, A.; Zubizarreta-Macho, A.; Faus-Matoses, V. Influence of Cross-Section and Pitch on the Mechanical Response of NiTi Endodontic Files under Bending and Torsional Conditions—A Finite Element Analysis. J. Clin. Med. 2022, 11, 2642. https://doi.org/10.3390/jcm11092642
Roda-Casanova V, Pérez-González A, Zubizarreta-Macho A, Faus-Matoses V. Influence of Cross-Section and Pitch on the Mechanical Response of NiTi Endodontic Files under Bending and Torsional Conditions—A Finite Element Analysis. Journal of Clinical Medicine. 2022; 11(9):2642. https://doi.org/10.3390/jcm11092642
Chicago/Turabian StyleRoda-Casanova, Victor, Antonio Pérez-González, Alvaro Zubizarreta-Macho, and Vicente Faus-Matoses. 2022. "Influence of Cross-Section and Pitch on the Mechanical Response of NiTi Endodontic Files under Bending and Torsional Conditions—A Finite Element Analysis" Journal of Clinical Medicine 11, no. 9: 2642. https://doi.org/10.3390/jcm11092642
APA StyleRoda-Casanova, V., Pérez-González, A., Zubizarreta-Macho, A., & Faus-Matoses, V. (2022). Influence of Cross-Section and Pitch on the Mechanical Response of NiTi Endodontic Files under Bending and Torsional Conditions—A Finite Element Analysis. Journal of Clinical Medicine, 11(9), 2642. https://doi.org/10.3390/jcm11092642







