IOL Power Calculations and Cataract Surgery in Eyes with Previous Small Incision Lenticule Extraction
Abstract
1. Introduction
2. Materials and Methods
2.1. SMILE Surgery
2.2. Cataract Surgery and IOL Implantation
2.3. Subjective Refraction
2.4. Post-hoc IOL Power Calculation
2.5. Statistical Analysis
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoffer, K.J. Intraocular lens power calculation after previous laser refractive surgery. J. Cataract. Refract. Surg. 2009, 354, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Booth, M.A.; Koch, D.D. Comparison of intraocular lens power calculation methods in eyes that have undergone LASIK. Ophthalmology 2004, 11110, 1825–1831. [Google Scholar] [CrossRef] [PubMed]
- Mackool, R.J.; Ko, W.; Mackool, R. Intraocular lens power calculation after laser in situ keratomileusis: Aphakic refraction technique. J. Cataract Refract. Surg. 2006, 323, 435–437. [Google Scholar] [CrossRef] [PubMed]
- Borasio, E.; Stevens, J.; Smith, G.T. Estimation of true corneal power after keratorefractive surgery in eyes requiring cataract surgery: BESSt formula. J. Cataract Refract. Surg. 2006, 3212, 2004–2014. [Google Scholar] [CrossRef]
- Jin, H.; Rabsilber, T.; Ehmer, A.; Borkenstein, A.F.; Limberger, I.-J.; Guo, H.; Auffarth, G.U. Comparison of ray-tracing method and thin-lens formula in intraocular lens power calculations. J. Cataract Refract. Surg. 2009, 354, 650–662. [Google Scholar] [CrossRef]
- Abulafia, A.; Hill, W.E.; Koch, D.D.; Wang, L.; Barrett, G.D. Accuracy of the Barrett True-K formula for intraocular lens power prediction after laser in situ keratomileusis or photorefractive keratectomy for myopia. J. Cataract Refract. Surg. 2016, 423, 363–369. [Google Scholar] [CrossRef]
- Wang, L.; Tang, M.; Huang, D.; Weikert, M.P.; Koch, D.D. Comparison of Newer Intraocular Lens Power Calculation Methods for Eyes after Corneal Refractive Surgery. Ophthalmology 2015, 12212, 2443–2449. [Google Scholar] [CrossRef]
- Fram, N.R.; Masket, S.; Wang, L. Comparison of Intraoperative Aberrometry, OCT-Based IOL Formula, Haigis-L, and Masket Formulae for IOL Power Calculation after Laser Vision Correction. Ophthalmology 2015, 1226, 1096–1101. [Google Scholar] [CrossRef]
- Canto, A.P.; Chhadva, P.; Cabot, F.; Galor, A.; Yoo, S.H.; Vaddavalli, P.K.; Culbertson, W.W. Comparison of IOL power calculation methods and intraoperative wavefront aberrometer in eyes after refractive surgery. J. Refract. Surg. 2013, 297, 484–489. [Google Scholar] [CrossRef]
- Lischke, R.; Mayer, W.J.; Feucht, N.; Siedlecki, J.; Wiltfang, R.; Kook, D.; Priglinger, S.G.; Luft, N. Total keratometry for determination of true corneal power after myopic small-incision lenticule extraction. J. Cataract Refract. Surg. 2021, 4710, 1285–1289. [Google Scholar] [CrossRef]
- Masket, S.; Masket, S.E. Simple regression formula for intraocular lens power adjustment in eyes requiring cataract surgery after excimer laser photoablation. J. Cataract Refract. Surg. 2006, 323, 430–434. [Google Scholar] [CrossRef]
- Shammas, H.J.; Shammas, M.C. No-history method of intraocular lens power calculation for cataract surgery after myopic laser in situ keratomileusis. J. Cataract Refract. Surg. 2007, 331, 31–36. [Google Scholar] [CrossRef]
- Potvin, R.; Hill, W. New algorithm for intraocular lens power calculations after myopic laser in situ keratomileusis based on rotating Scheimpflug camera data. J. Cataract Refract. Surg. 2015, 412, 339–347. [Google Scholar] [CrossRef]
- Haigis, W. Intraocular lens calculation after refractive surgery for myopia: Haigis-L formula. J. Cataract Refract. Surg. 2008, 3410, 1658–1663. [Google Scholar] [CrossRef]
- Rabsilber, T.M.; Reuland, A.J.; Holzer, M.P.; Auffarth, G.U. Intraocular lens power calculation using ray tracing following excimer laser surgery. Eye 2007, 216, 697–701. [Google Scholar] [CrossRef]
- Savini, G.; Bedei, A.; Barboni, P.; Ducoli, P.; Hoffer, K.J. Intraocular lens power calculation by ray-tracing after myopic excimer laser surgery. Am. J. Ophthalmol. 2014, 1571, 150–153.e151. [Google Scholar] [CrossRef]
- Savini, G.; Calossi, A.; Camellin, M.; Carones, F.; Fantozzi, M.; Hoffer, K.J. Corneal ray tracing versus simulated keratometry for estimating corneal power changes after excimer laser surgery. J. Cataract Refract. Surg. 2014, 407, 1109–1115. [Google Scholar] [CrossRef]
- Saiki, M.; Negishi, K.; Kato, N.; Torii, H.; Dogru, M.; Tsubota, K. Ray tracing software for intraocular lens power calculation after corneal excimer laser surgery. Jpn J. Ophthalmol. 2014, 583, 276–281. [Google Scholar] [CrossRef]
- Preussner, P.R.; Wahl, J.; Lahdo, H.; Dick, B.; Findl, O. Ray tracing for intraocular lens calculation. J. Cataract Refract. Surg. 2002, 288, 1412–1419. [Google Scholar] [CrossRef]
- Canovas, C.; van der Mooren, M.; Rosén, R.; Piers, P.A.; Wang, L.; Koch, D.D.; Artal, P. Effect of the equivalent refractive index on intraocular lens power prediction with ray tracing after myopic laser in situ keratomileusis. J. Cataract Refract. Surg. 2015, 415, 1030–1037. [Google Scholar] [CrossRef]
- Hoffmann, P.; Wahl, J.; Preussner, P.R. Accuracy of intraocular lens calculation with ray tracing. J. Refract. Surg. 2012, 289, 650–655. [Google Scholar] [CrossRef] [PubMed]
- Ghoreyshi, M.; Khalilian, A.; Peyman, M.; Mohammadinia, M.; Peyman, A. Comparison of OKULIX ray-tracing software with SRK-T and Hoffer-Q formula in intraocular lens power calculation. J. Curr. Ophthalmol. 2018, 301, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Ganesh, S.; Brar, S.; Sriprakash, K. Post-small incision lenticule extraction phacoemulsification with multifocal IOL implantation: A case report. Indian J. Ophthalmol. 2019, 678, 1353–1356. [Google Scholar]
- Gyldenkerne, A.; Ivarsen, A.; Hjortdal, J. Comparison of corneal shape changes and aberrations induced By FS-LASIK and SMILE for myopia. J. Refract. Surg. 2015, 314, 223–229. [Google Scholar] [CrossRef]
- Lazaridis, A.; Spiru, B.; Giallouros, E.; Droutsas, K.; Messerschmidt-Roth, A.; Sekundo, W. Corneal Remodeling After Myopic SMILE Versus FS-LASIK. Cornea 2021, 41, 826–832. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Cao, L.J.; Chen, H.W.; Xu, X.H.; Li, Z.N.; Liu, L. Comparison of changes in refractive error and corneal curvature following small-incision lenticule extraction and femtosecond laser-assisted in situ keratomileusis surgery. Indian J. Ophthalmol. 2018, 66, 1562–1567. [Google Scholar] [CrossRef]
- Sekundo, W.; Kunert, K.S.; Blum, M. Small incision corneal refractive surgery using the small incision lenticule extraction (SMILE) procedure for the correction of myopia and myopic astigmatism: Results of a 6 month prospective study. Br. J. Ophthalmol. 2011, 953, 335–339. [Google Scholar] [CrossRef]
- Hoffer, K.J.; Savini, G. Update on Intraocular Lens Power Calculation Study Protocols: The Better Way to Design and Report Clinical Trials. Ophthalmology 2021, 12811, e115–e120. [Google Scholar] [CrossRef]
- Hoffer, K.J.; Aramberri, J.; Haigis, W.; Olsen, T.; Savini, G.; Shammas, H.J.; Bentow, S. Protocols for studies of intraocular lens formula accuracy. Am. J. Ophthalmol. 2015, 1603, 403–405.e401. [Google Scholar] [CrossRef]
- Patel, P.; Ashena, Z.; Vasavada, V.; Vasavada, S.; Vasavada, V.; Sudhalkar, A.; Nanavaty, M. Comparison of intraocular lens calculation methods after myopic laser-assisted in situ keratomileusis and radial keratotomy without prior refractive data. Br. J. Ophthalmol. 2020, 106, 47–53. [Google Scholar] [CrossRef]
- Lazaridis, A.; Schraml, F.; Preussner, P.R.; Sekundo, W. Predictability of intraocular lens power calculation after small-incision lenticule extraction for myopia. J. Cataract Refract. Surg. 2021, 473, 304–310. [Google Scholar] [CrossRef]
- Luft, N.; Siedlecki, J.; Schworm, B.; Kreutzer, T.C.; Mayer, W.J.; Priglinger, S.G.; Dirisamer, M. Intraocular Lens Power Calculation after Small Incision Lenticule Extraction. Sci. Rep. 2020, 101, 5982. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, F.J.; Li, Y.; Song, Y.Z. Stability of the Barrett True-K formula for intraocular lens power calculation after SMILE in Chinese myopic eyes. Int. J. Ophthalmol. 2020, 134, 560–566. [Google Scholar] [CrossRef]

| Eye ID | Patient ID | Implanted IOL Model | Manufacturer | IOL Power (Spherical Equivalent, Diopters) | IOL-Power Calculation Formula Used | Prediction Error (Spherical Equivalent, Diopters) |
|---|---|---|---|---|---|---|
| 1 | 1 | CT Lucia 601PY | Carl Zeiss Meditec AG (Jena, Germany) | 18.5 | Haigis-L | 0.68 |
| 2 | 1 | CT Lucia 601PY | Carl Zeiss Meditec AG (Jena, Germany) | 16.5 | Haigis-L | −0.67 |
| 3 | 2 | CT Lucia 601PY | Carl Zeiss Meditec AG (Jena, Germany) | 21.0 | Haigis-L | 1.17 |
| 4 | 3 | CT Lucia 611 PY | Carl Zeiss Meditec AG (Jena, Germany) | 22.5 | Haigis-L | −1.27 |
| 5 | 4 | AcrySof IQ Toric SN6AT2/3 | Alcon GmbH (Freiburg, Swiss) | 25.0 | Haigis-L | −0.51 |
| 6 | 4 | AcrySof IQ Toric SN6AT2/3 | Alcon GmbH (Freiburg, Swiss) | 24.75 | Haigis-L | −0.35 |
| 7 | 5 | Lentis Comfort LS-313 MF15 | Oculentis GmbH (Berlin, Germany) | 21.0 | Haigis-L | −0.84 |
| 8 | 5 | Lentis Comfort LS-313 MF15 | Oculentis GmbH (Berlin, Germany) | 19.0 | Haigis-L | −0.58 |
| 9 | 6 | Polylens Y 50 P | Polytech-Domilens GmbH (Roßdorf, Germany) | 19.5 | Haigis-L | −3.76 |
| 10 | 6 | Polylens Y 50 P | Polytech-Domilens GmbH (Roßdorf, Germany) | 18.5 | Haigis-L | −1.77 |
| 11 | 7 | CT Asphina 409 MP | Carl Zeiss Meditec AG (Jena, Germany) | 22.0 | Ray tracing | −0.62 |
| Parameter | Mean | Median | SD | Range | ||
|---|---|---|---|---|---|---|
| Age at SMILE (years) | 46.43 | 46 | 6.75 | 37 to 55 | ||
| Age at cataract surgery (years) | 49.45 | 49 | 7.31 | 38 to 59 | ||
| SMILE | Preoperative Manifest Refraction (D) | |||||
| Sphere | −4.86 | −5.25 | 1.30 | −6.50 to −2.75 | ||
| Cylinder | −0.57 | −0.50 | 0.23 | −1.00 to −0.25 | ||
| Spherical Equivalent | −5.15 | −5.38 | 1.31 | −7.00 to −3.00 | ||
| Postoperative Manifest Refraction (D) | ||||||
| Sphere | −0.34 | −0.5 | 0.5 | −1.75 to 0.50 | ||
| Cylinder | −0.27 | −0.25 | 0.24 | −0.75 to 0.00 | ||
| Spherical Equivalent | −0.48 | −0.50 | 0.57 | −1.63 to 0.38 | ||
| Cataract surgery | Preoperative Manifest Refraction (D) | |||||
| Sphere | −2.00 | −1.5 | 2.49 | −7.00 to 1.25 | ||
| Cylinder | −0.89 | −1.00 | 0.58 | −2.00 to −0.25 | ||
| Spherical Equivalent | −2.44 | −2.25 | 2.48 | −7.63 to 0.63 | ||
| Postoperative Manifest Refraction (D) | ||||||
| Sphere | −0.45 | 0.00 | 0.72 | −2.00 to 0.25 | ||
| Cylinder | −0.45 | −0.5 | 0.4 | −1.25 to 0.00 | ||
| Spherical Equivalent | −0.68 | −0.63 | 0.65 | −2.00 to 0.00 | ||
| Formula | Prediction Error (D) | Absolute Error (D) | % of Eyes within PE Range Indicated | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Range | Variance (D2) | Mean | Median | ±0.5 D | ±1.0 D | ±1.5 D | ±2.0 D | ||
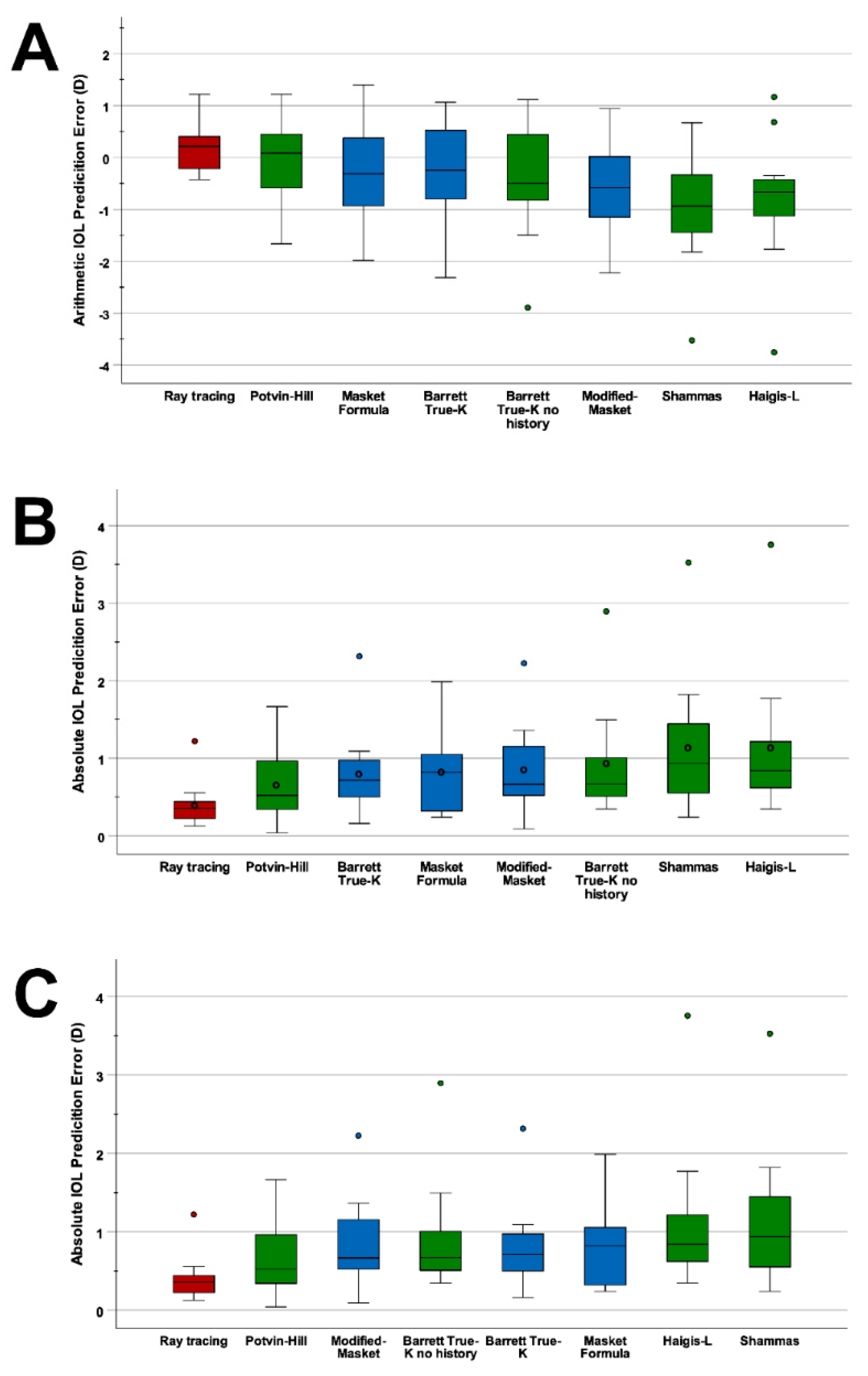
| Ray tracing | 0.18 | 0.48 | −0.43 to 1.22 | 0.23 | 0.4 | 0.36 | 82 | 91 | 100 | 100 | |
| Using prior data | Masket | −0.25 | 0.98 | −1.99 to 1.4 | 0.95 | 0.81 | 0.82 | 36 | 64 | 91 | 100 |
| Modified-Masket | −0.55 | 0.91 | −2.23 to 0.94 | 0.83 | 0.85 | 0.67 | 27 | 64 | 91 | 91 | |
| Barret True-K | −0.27 | 0.98 | −2.32 to 1.07 | 0.96 | 0.80 | 0.72 | 27 | 73 | 91 | 91 | |
| Using no prior data | Shammas | −0.96 | 1.14 | −2.53 to 0.67 | 1.3 | 1.14 | 0.94 | 27 | 55 | 73 | 91 |
| Haigis-L | −0.81 | 1.28 | −3.76 to 1.17 | 1.63 | 1.14 | 0.84 | 9 | 64 | 82 | 91 | |
| Potvin-Hill | −0.06 | 0.86 | −1.67 to 1.22 | 0.74 | 0.66 | 0.52 | 45 | 73 | 91 | 100 | |
| Barrett True K no history | −0.44 | 1.13 | −2.90 to 1.12 | 1.27 | 0.93 | 0.67 | 27 | 73 | 91 | 91 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lischke, R.; Sekundo, W.; Wiltfang, R.; Bechmann, M.; Kreutzer, T.C.; Priglinger, S.G.; Dirisamer, M.; Luft, N. IOL Power Calculations and Cataract Surgery in Eyes with Previous Small Incision Lenticule Extraction. J. Clin. Med. 2022, 11, 4418. https://doi.org/10.3390/jcm11154418
Lischke R, Sekundo W, Wiltfang R, Bechmann M, Kreutzer TC, Priglinger SG, Dirisamer M, Luft N. IOL Power Calculations and Cataract Surgery in Eyes with Previous Small Incision Lenticule Extraction. Journal of Clinical Medicine. 2022; 11(15):4418. https://doi.org/10.3390/jcm11154418
Chicago/Turabian StyleLischke, Roman, Walter Sekundo, Rainer Wiltfang, Martin Bechmann, Thomas C. Kreutzer, Siegfried G. Priglinger, Martin Dirisamer, and Nikolaus Luft. 2022. "IOL Power Calculations and Cataract Surgery in Eyes with Previous Small Incision Lenticule Extraction" Journal of Clinical Medicine 11, no. 15: 4418. https://doi.org/10.3390/jcm11154418
APA StyleLischke, R., Sekundo, W., Wiltfang, R., Bechmann, M., Kreutzer, T. C., Priglinger, S. G., Dirisamer, M., & Luft, N. (2022). IOL Power Calculations and Cataract Surgery in Eyes with Previous Small Incision Lenticule Extraction. Journal of Clinical Medicine, 11(15), 4418. https://doi.org/10.3390/jcm11154418






