Osteolytic vs. Osteoblastic Metastatic Lesion: Computational Modeling of the Mechanical Behavior in the Human Vertebra after Screws Fixation Procedure
Abstract
1. Introduction
2. Materials and Methods
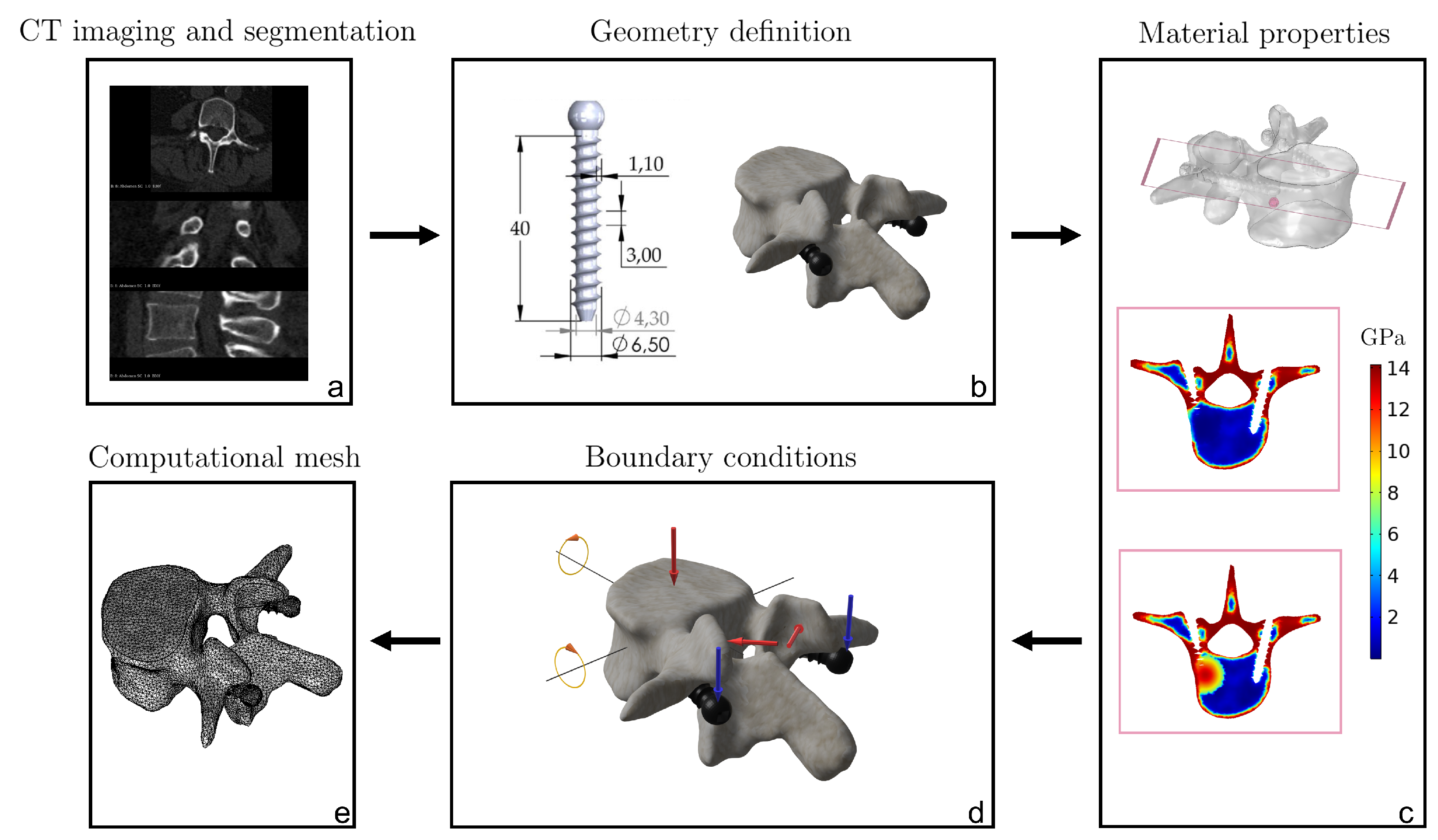
2.1. Imaging and FE Geometric Reconstruction of the Screws-Vertebra Model
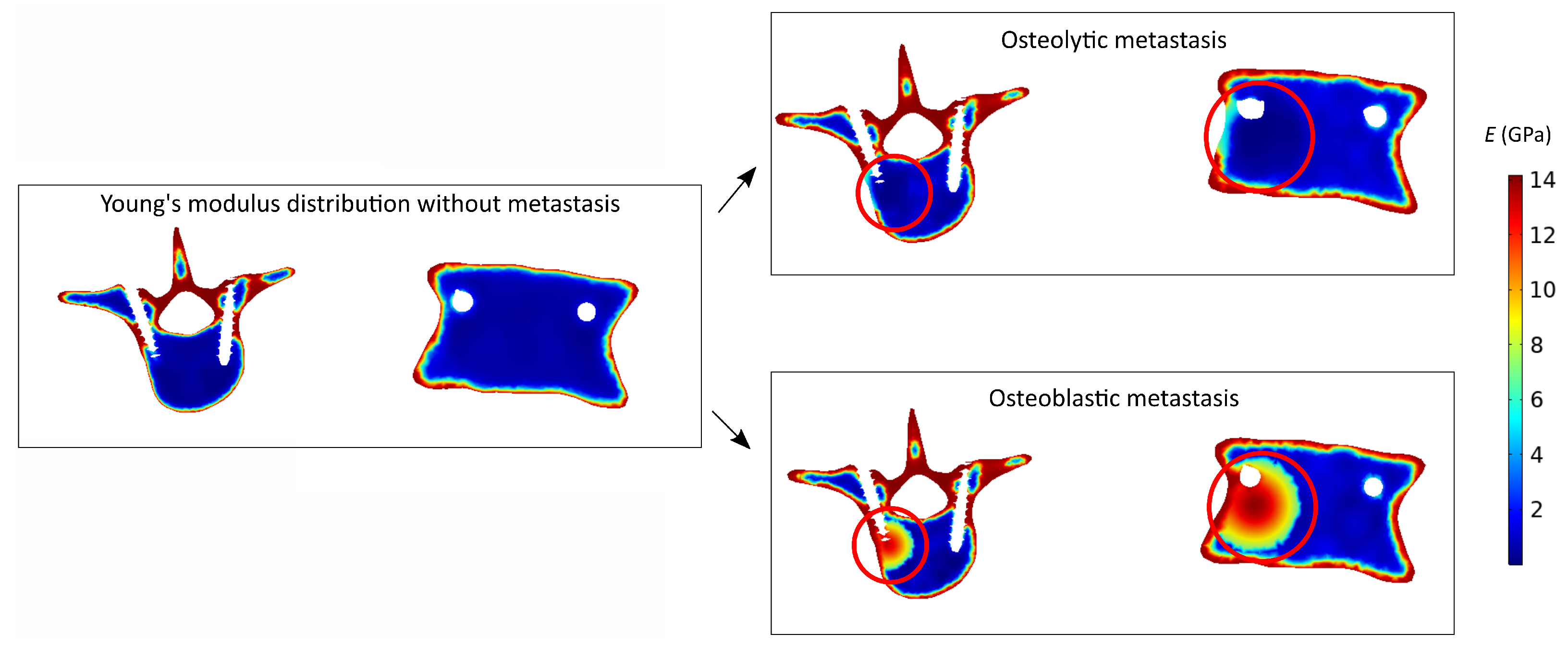
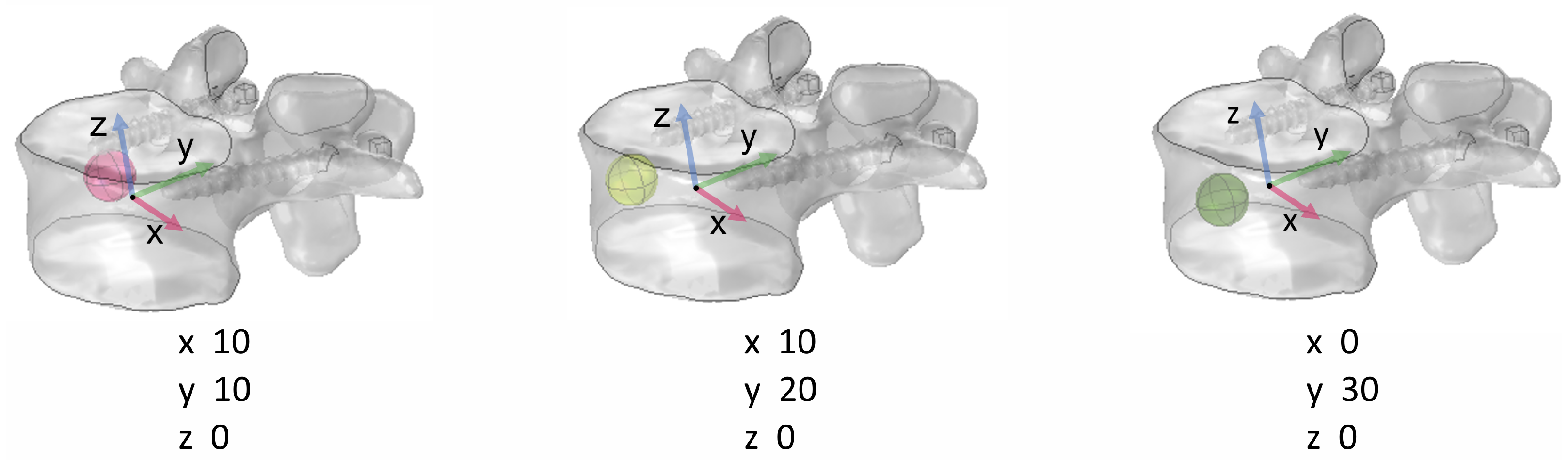
2.2. Simulated Metastasis Description
2.3. Constitutive Modeling
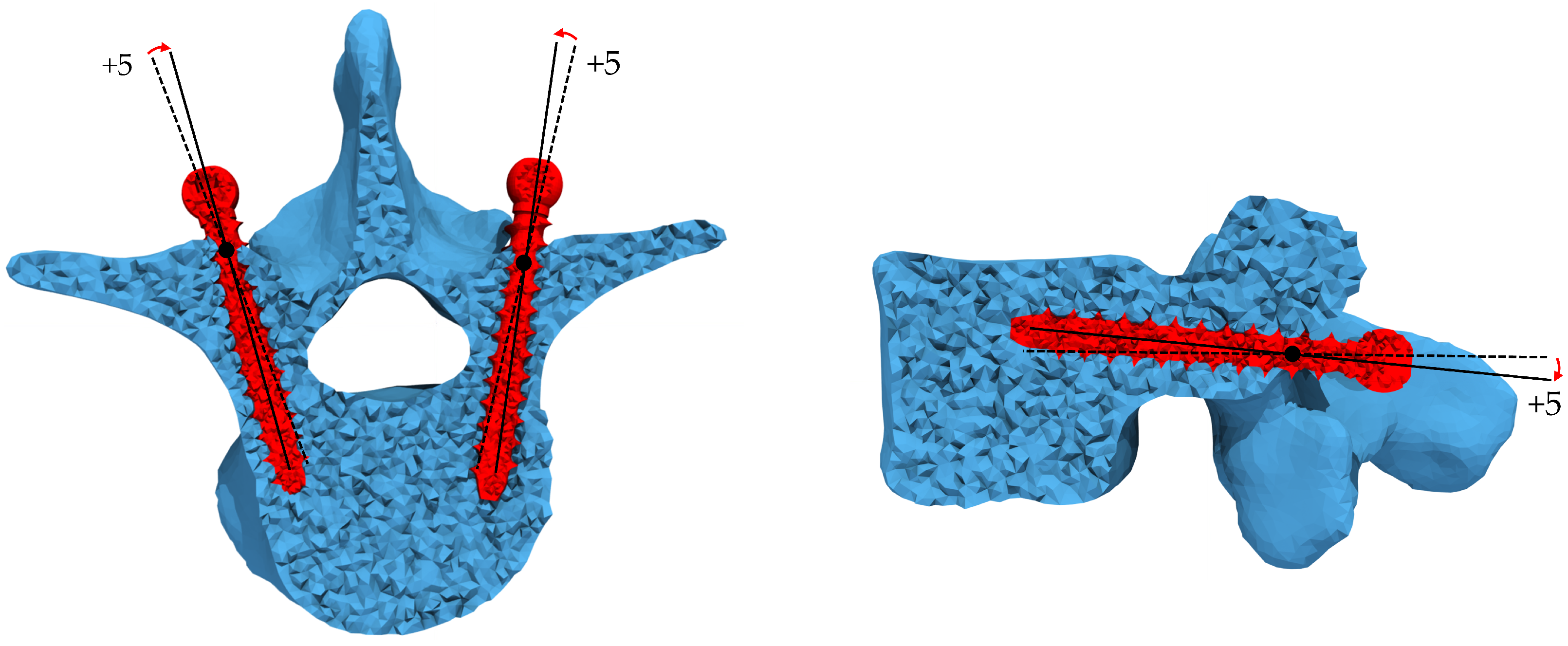
2.4. Loading and Boundary Conditions
2.5. Failure Criteria
2.6. Numerical Procedure
2.7. Parametric Analysis
3. Results
3.1. Fracture Load
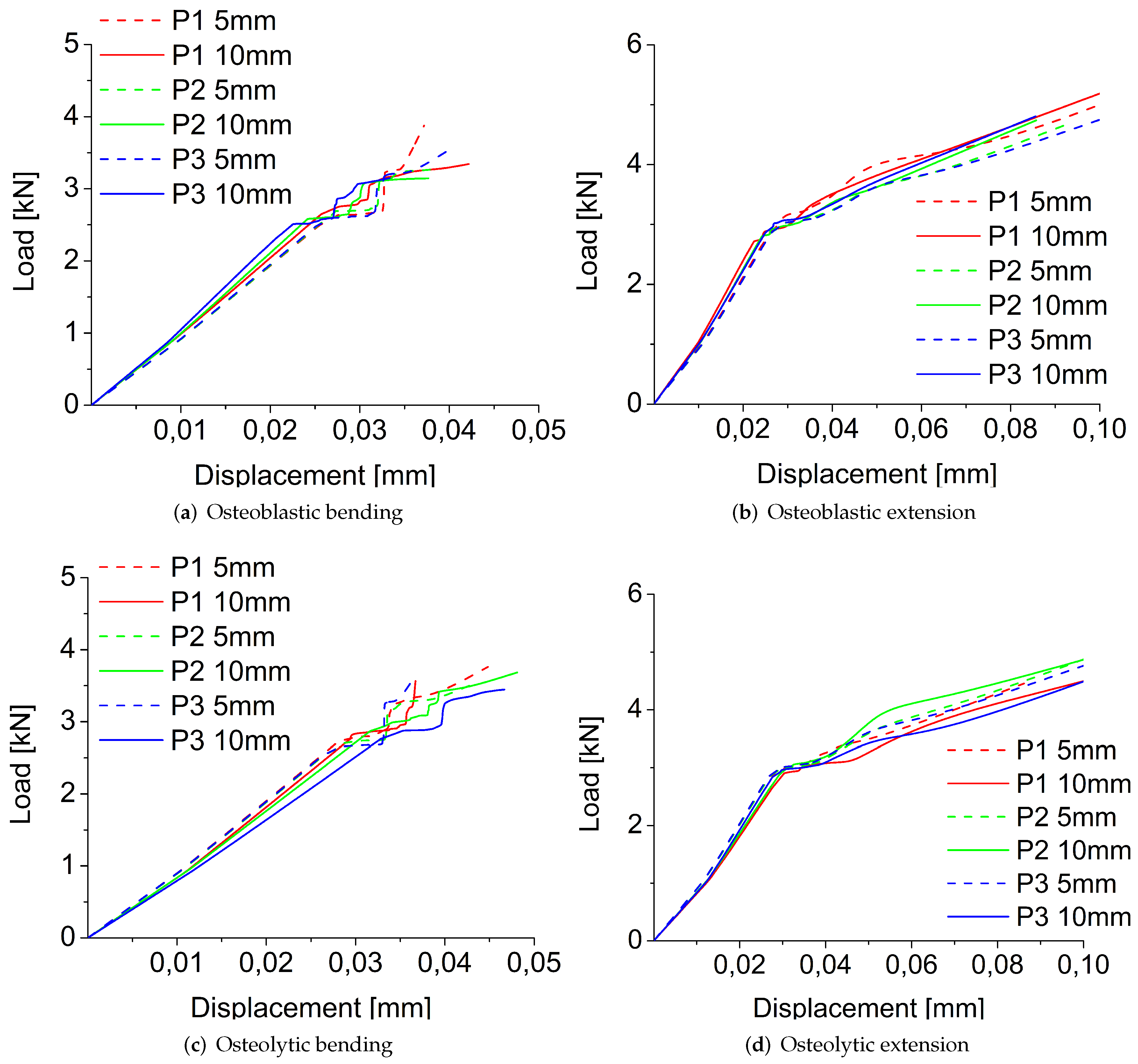
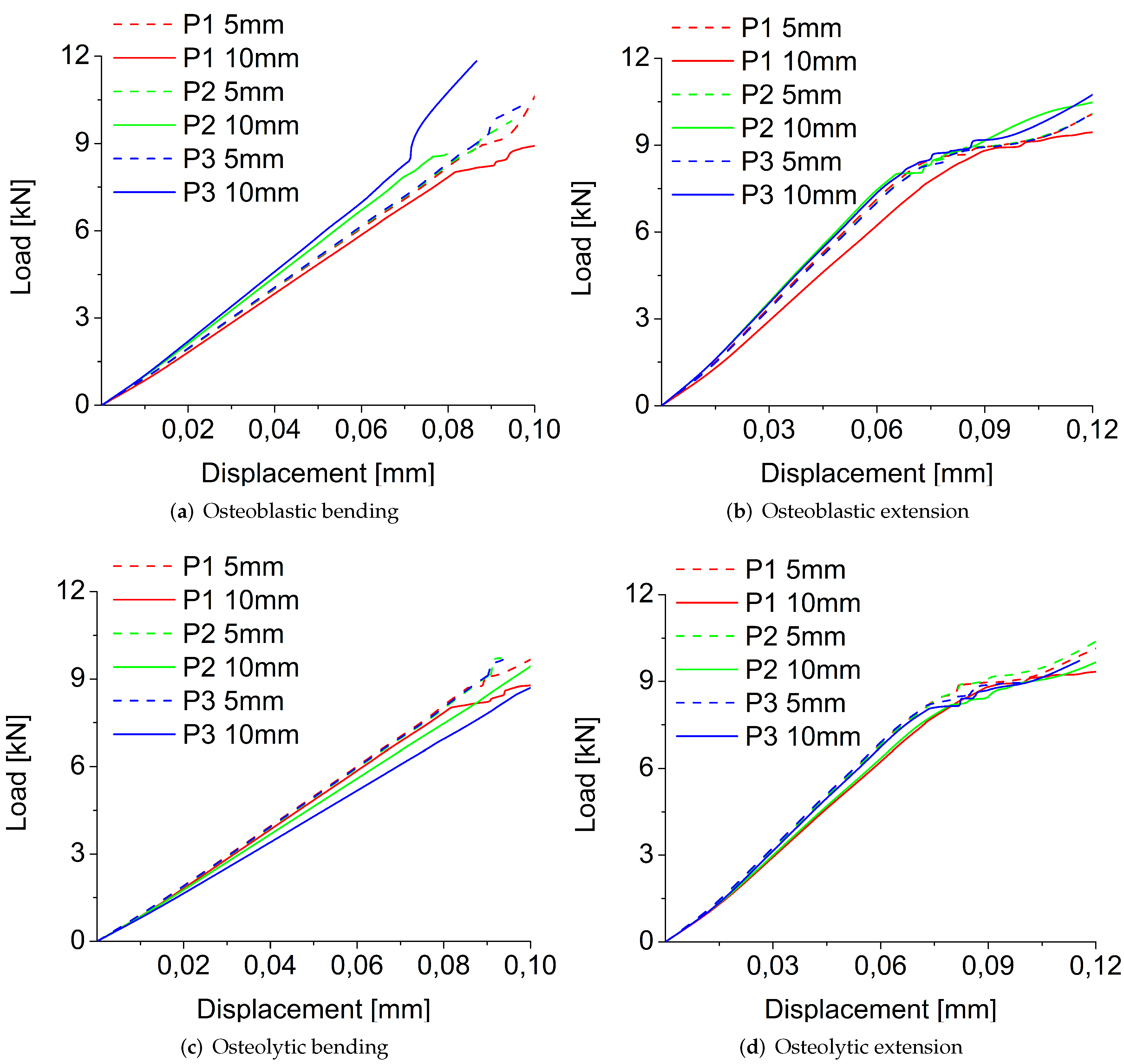
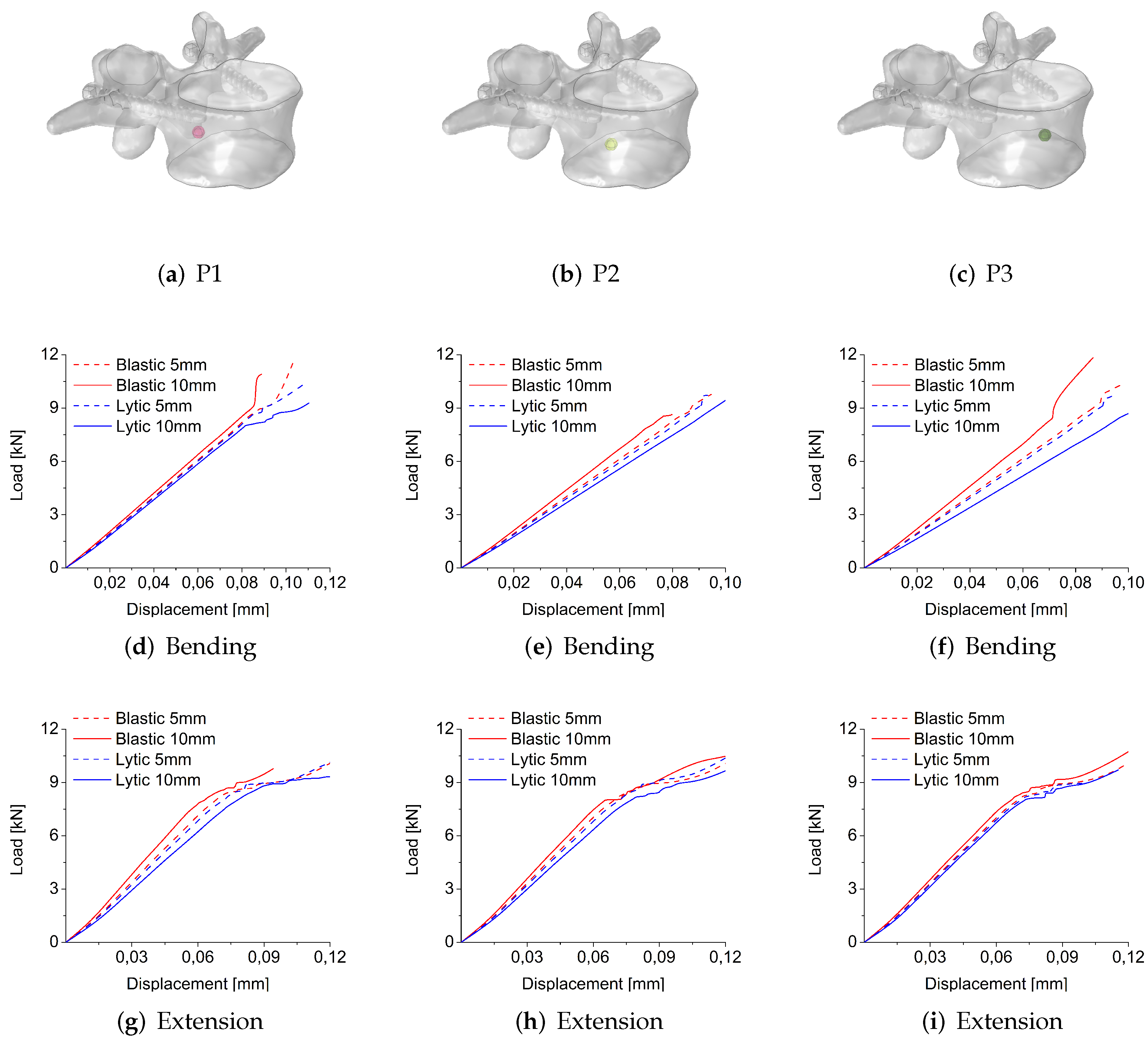
3.1.1. Size, Position, and Shape Effects
3.1.2. Comparison between Osteoblastic and Osteolytic Metastases
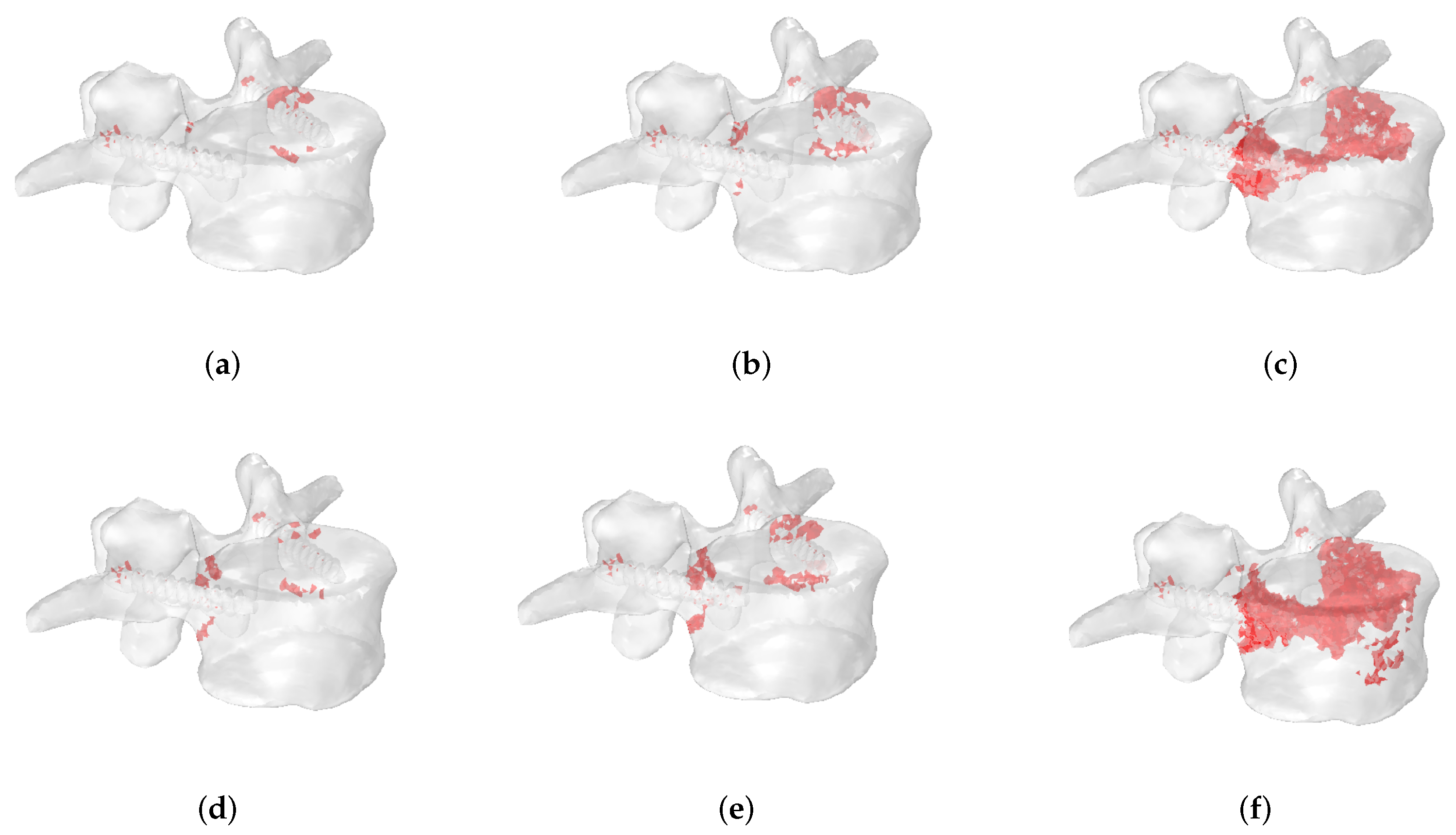
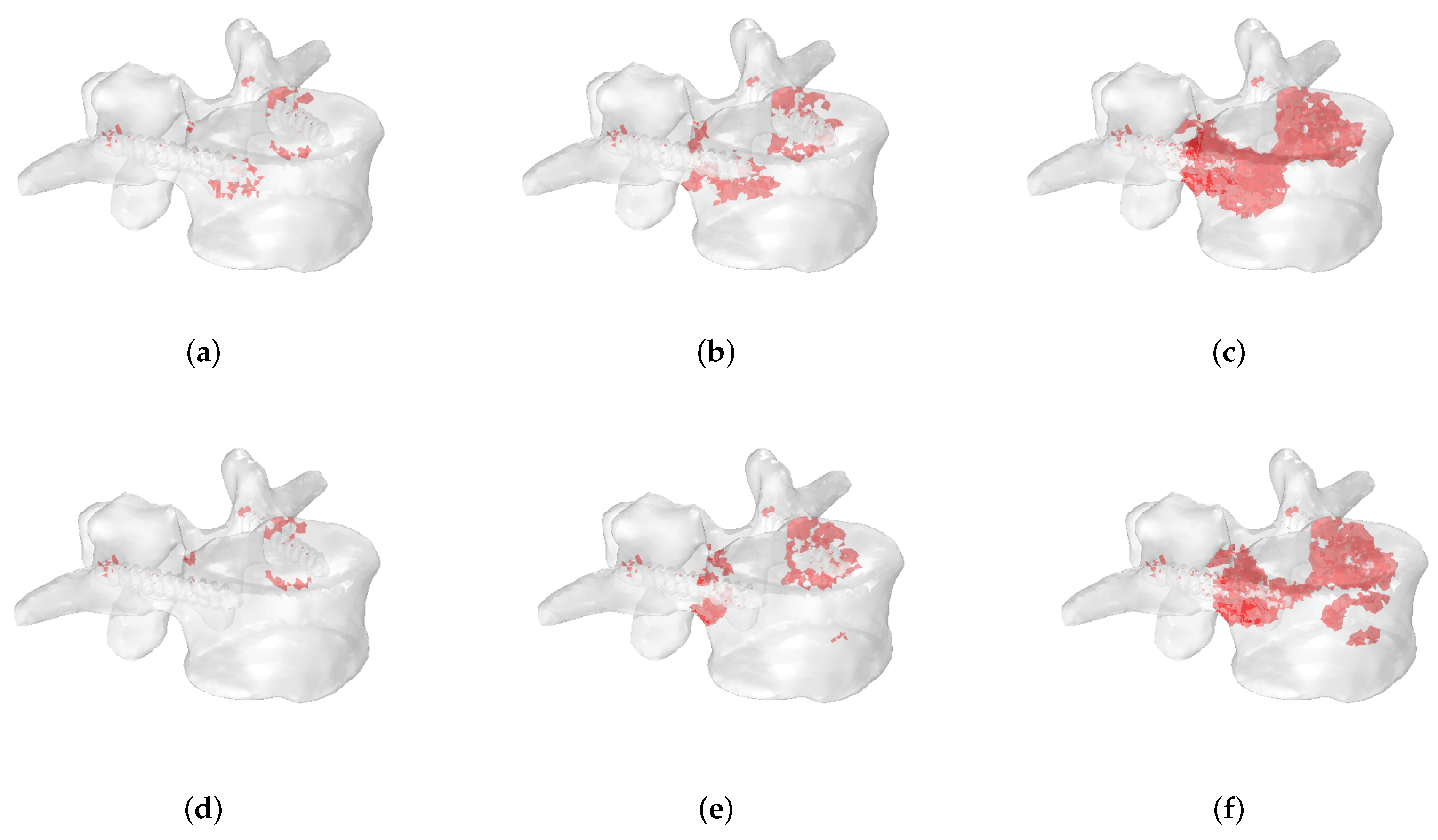
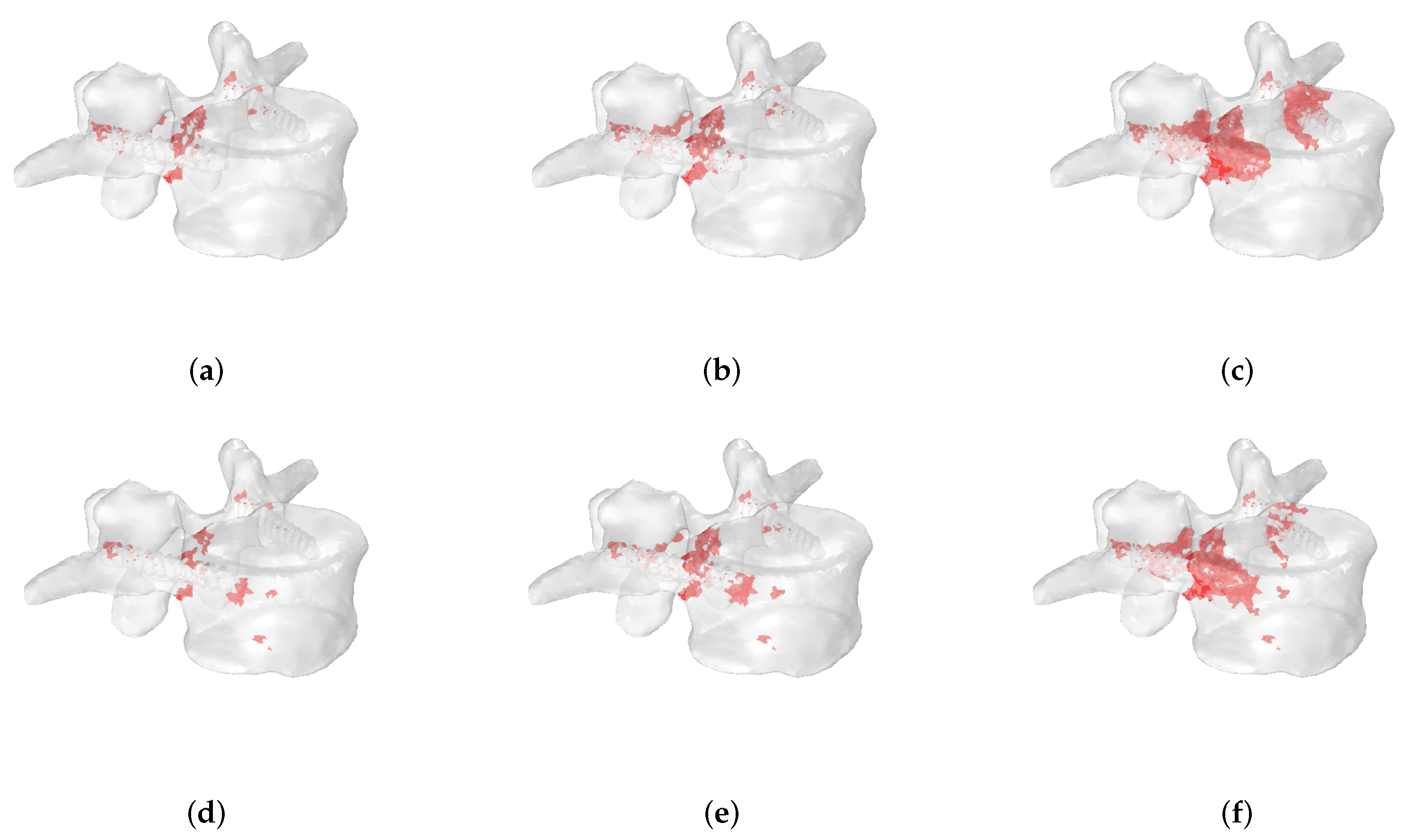
3.2. Fracture Patterns
4. Discussion
Limitations and Perspectives
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gasbarrini, A.; Boriani, S.; Capanna, R.; Casadei, R.; Di Martino, A.; Spinelli, M.S.; Papapietro, N.; Piccioli, A. The Italian Orthopaedic Society Bone Metastasis Study Group Management of patients with metastasis to the vertebrae: Recommendations from the Italian Orthopaedic Society (SIOT) Bone Metastasis Study Group. Expert Rev. Anticancer. Ther. 2014, 14, 143–150. [Google Scholar] [CrossRef] [PubMed]
- Salvatore, G.; Berton, A.; Giambini, H.; Ciuffreda, M.; Florio, P.; Longo, U.G.; Denaro, V.; Thoreson, A.; An, K.N. Biomechanical effects of metastasis in the osteoporotic lumbar spine: A Finite Element Analysis. BMC Musculoskelet. Disord. 2018, 19, 38. [Google Scholar] [CrossRef] [PubMed]
- Denaro, V.; Di Martino, A.; Papalia, R.; Denaro, L. Patients with Cervical Metastasis and Neoplastic Pachymeningitis are Less Likely to Improve Neurologically After Surgery. Clin. Orthop. Relat. Res. 2011, 469, 708–714. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Confavreux, C.B.; Follet, H.; Mitton, D.; Pialat, J.B.; Clezardin, P. Fracture Risk Evaluation of Bone Metastases: A Burning Issue. Cancers 2021, 13, 5711. [Google Scholar] [CrossRef] [PubMed]
- Whyne, C.M.; Ferguson, D.; Clement, A.; Rangrez, M.; Hardisty, M. Biomechanical Properties of Metastatically Involved Osteolytic Bone. Curr. Osteoporos. Rep. 2020, 18, 705–715. [Google Scholar] [CrossRef] [PubMed]
- Bouxsein, M.L. Determinants of skeletal fragility. Best Pract. Res. Clin. Rheumatol. 2005, 19, 897–911. [Google Scholar] [CrossRef]
- Campbell, G.M.; Pena, J.A.; Giravent, S.; Thomsen, F.; Damm, T.; Gluer, C.C.; Borggrefe, J. Assessment of Bone Fragility in Patients With Multiple Myeloma Using QCT-Based Finite Element Modeling. J. Bone Miner. Res. 2017, 32, 151–156. [Google Scholar] [CrossRef]
- Anitha, D.; Baum, T.; Kirschke, J.; Subburaj, K. Risk of vertebral compression fractures in multiple myeloma patients A finite-element study. Medicine 2017, 96, e5825. [Google Scholar] [CrossRef]
- Costa, M.C.; Eltes, P.; Lazary, A.; Varga, P.P.; Viceconti, M.; Dall’Ara, E. Biomechanical assessment of vertebrae with lytic metastases with subject-specific finite element models. J. Mech. Behav. Biomed. Mater. 2019, 98, 268–290. [Google Scholar] [CrossRef]
- Stadelmann, M.A.; Schenk, D.E.; Maquer, G.; Lenherr, C.; Buck, F.M.; Bosshardt, D.D.; Hoppe, S.; Theumann, N.; Alkalay, R.N.; Zysset, P.K. Conventional finite element models estimate the strength of metastatic human vertebrae despite alterations of the bone’s tissue and structure. Bone 2020, 141, 115598. [Google Scholar] [CrossRef]
- Whyne, C.M.; Hu, S.S.; Lotz, J.C. Parametric finite element analysis of vertebral bodies affected by tumors. J. Biomech. 2001, 34, 1317–1324. [Google Scholar] [CrossRef]
- Tschirhart, C.E.; Nagpurkar, A.; Whyne, C.M. Effects of tumor location, shape and surface serration on burst fracture riskin the metastatic spine. J. Biomech. 2004, 37, 653–660. [Google Scholar] [CrossRef] [PubMed]
- Galbusera, F.; Qian, Z.; Casaroli, G.; Bassani, T.; Costa, F.; Schlager, B.; Wilke, H.J. The role of the size and location of the tumors and of the vertebral anatomy in determining the structural stability of the metastatically involved spine: A finite element study. Transl. Oncol. 2018, 11, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.C.; Bresani Campello, L.B.; Ryan, M.; Rochester, J.; Viceconti, M.; Dall’Ara, E. Effect of size and location of simulated lytic lesions on the structural properties of human vertebral bodies, a micro-finite element study. Bone Rep. 2020, 12, 100257. [Google Scholar] [CrossRef] [PubMed]
- Alkalay, R.N. Effect of the metastatic defect on the structural response and failure process of human vertebrae: An experimental study. Clin. Biomech. 2015, 30, 121–128. [Google Scholar] [CrossRef]
- Alkalay, R.N.; Harrigan, T.P. Mechanical assessment of the effects of metastatic lytic defect on the structural response of human thoracolumbar spine. J. Orthop. Res. 2016, 34, 1808–1819. [Google Scholar] [CrossRef]
- Palanca, M.; Brodano Barbanti, G.; Cristofolini, L. The size of simulated lytic metastases affects the strain distribution on the anterior surface of the vertebra. J. Biomech. Eng. 2018, 140, 111005. [Google Scholar] [CrossRef]
- Moussazadeh, N.; Rubin, D.G.; McLaughlin, L.; Lis, E.; Bilsky, M.H.; Laufer, I. Short-segment percutaneous pedicle screw fixation with cement augmentation for tumor-induced spinal instability. Spine J. 2015, 15, 1609–1617. [Google Scholar] [CrossRef]
- Kim, P.; Kim, S.W. Bone cement-augmented percutaneous screw fixation for malignant spinal metastases: Is it feasible? J. Korean Neurosurg. Soc. 2017, 60, 189–194. [Google Scholar] [CrossRef]
- Di Martino, A.; Vincenzi, B.; Denaro, L.; Barnaba, S.A.; Papalia, R.; Santini, D.; Tonini, G.; Denaro, V. Internal bracing’ surgery in the management of solid tumor metastases of the thoracic and lumbar spine. Oncol. Rep. 2009, 21, 431–435. [Google Scholar] [CrossRef]
- Veersteg, A.L.; Verlaan, J.J.; de Baat, P.; Jiya, T.U.; Stadhouder, A.; Diekerhof, C.H.; van Solinge, G.B.; Oner, F.C. Complications After Percutaneous Pedicle Screw Fixation for the Treatment of Unstable Spinal Metastases. Ann. Surg. Oncol. 2016, 23, 2043–2049. [Google Scholar] [CrossRef] [PubMed]
- Di Martino, A.; Caldaria, A.; De Vivo, V.; Denaro, V. Metastatic epidural spinal cord compression. Expert Rev. Anticancer. Ther. 2016, 16, 1189–1198. [Google Scholar] [CrossRef] [PubMed]
- Dea, N.; Versteeg, A.; Fisher, C.; Kelly, A.; Hartig, D.; Boyd, M.; Paquette, S.; Kwon, B.K.; Dvorak, M.; Street, J. Adverse events in emergency oncological spine surgery: A prospective analysis. J. Neurosurg. Spine 2014, 21, 698–703. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A.; Haag, E.; Joerger, A.K.; Jost, P.; Combs, S.E.; Wostrack, M.; Gempt, J.; Meyer, B. Comprehensive surgical treatment strategy for spinal metastases. Sci. Rep. 2021, 11, 7988. [Google Scholar] [CrossRef]
- Molinari, L.; Falcinelli, C.; Gizzi, A.; Di Martino, A. Effect of pedicle screw angles on the fracture risk of the human vertebra: A patient-specific computational model. J. Mech. Behav. Biomed. Mater. 2021, 116, 104359. [Google Scholar] [CrossRef]
- Molinari, L.; Falcinelli, C.; Gizzi, A.; Di Martino, A. Biomechanical modeling of metal screw loadings on the human vertebra. Acta. Mech. Sin. 2021, 37, 307–320. [Google Scholar] [CrossRef]
- Falcinelli, C.; Di Martino, A.; Gizzi, A.; Vairo, G.; Denaro, V. Mechanical behavior of metastatic femurs through patient-specific computational models accounting for bone-metastasis interaction. J. Mech. Behav. Biomed. Mater. 2019, 93, 9–22. [Google Scholar] [CrossRef]
- Falcinelli, C.; Di Martino, A.; Gizzi, A.; Vairo, G.; Denaro, V. Fracture risk assessment in metastatic femurs: A patient- specific CT-based finite-element approac. Meccanica 2020, 55, 861–881. [Google Scholar] [CrossRef]
- Chappard, D.; Bouvard, B.; Basle, M.F.; Legrand, E.; Audran, M. Bone metastasis: Histological changes and pathophysiological mechanisms in osteolytic or osteosclerotic localizations. A review. Morphologie 2011, 95, 65–75. [Google Scholar] [CrossRef]
- Ford, C.; Keaveny, T.; Hayes, W. The effect of impact direction on the structural capacity of the proximal femur during falls. J. Bone Miner. Res. 1996, 11, 377–383. [Google Scholar] [CrossRef]
- Taddei, F.; Pancanti, A.; Viceconti, M. An improved method for the automatic mapping of computed tomography numbers onto finite element models. Med. Eng. Phys. 2004, 26, 61–69. [Google Scholar] [CrossRef]
- Lee, D.C.; Hoffmann, P.F.; Kopperdahl, D.L.; Keaveny, T.M. Phantomless calibration of CT scans for measurement of BMD and bone strength—Inter-operator reanalysis precision. Bone 2017, 103, 325–333. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.H.; Kim, J.J.; Jang, I.G. Patient-specific phantomless estimation of bone mineral density and its effects on finite element analysis results: A feasibility study. Comput. Math. Methods Med. 2019, 2019, 4102410. [Google Scholar] [CrossRef] [PubMed]
- Eggermont, F.; Verdonschot, N.; van der Linden, Y.; Tanck, E. Calibration with or without phantom for fracture risk prediction in cancer patients with femoral bone metastases using CT-based finite element models. PLoS ONE 2019, 14, e0220564. [Google Scholar] [CrossRef]
- Morgan, E.F.; Bayraktar, H.H.; Keaveny, T.M. Trabecular bone modulus–density relationships depend on anatomic site. J. Biomech. 2003, 36, 897–904. [Google Scholar] [CrossRef]
- Fields, A.J.; Lee, G.L.; Keaveny, T.M. Mechanisms of initial endplate failure in the human vertebral body. J. Biomech. 2010, 43, 3126–3131. [Google Scholar] [CrossRef]
- Eggermont, F.; Derikx, L.C.; Verdonschot, N.; van der Geest, I.C.M.; de Jong, M.A.A.; Snyers, A.; van der Linden, Y.M.; Tanck, E. Can patient-specific finite element models better predict fractures in metastatic bone disease than experienced clinicians? Bone Joint Res. 2018, 7, 430–439. [Google Scholar] [CrossRef]
- Bailey, S.; Hackney, D.; Vashishth, D.; Alkalay, R.N. The effects of metastatic lesion on the structural determinants of bone: Current clinical and experimental approaches. Bone 2020, 138, 115159. [Google Scholar] [CrossRef]
- Ulano, A.; Bredella, M.A.; Burke, P.; Chebib, I.; Simeone, F.J.; Huang, A.J.; Torriani, M.; Chang, C.Y. Distinguishing Untreated Osteoblastic Metastases From Enostoses Using CT Attenuation Measurements. AJR Am. J. Roentgenol. 2016, 207, 362–368. [Google Scholar] [CrossRef]
- Hipp, J.A.; Rosenberg, A.E.; Hayes, W.C. Mechanical properties of trabecular bone within and adjacent to osseous metastases. JBMR 1992, 7, 1165–1171. [Google Scholar] [CrossRef]
- Keyak, J.H.; Lee, I.Y.; Skinner, H.B. Correlations between orthogonal mechanical properties and density of trabecular bone: Use of different densitometric measures. J. Biomed. Mater. Res. 1994, 28, 1329–1336. [Google Scholar] [CrossRef] [PubMed]
- Keller, T.S. Predicting the compressive mechanical behavior of bone. J. Biomech. 1994, 27, 1159–1168. [Google Scholar] [CrossRef]
- Bayraktar, H.H.; Morgan, E.F.; Niebur, G.L.; Morris, G.E.; Wong, E.K.; Keaveny, T.M. Comparison of the elastic and yield properties of human femoral trabecular and cortical bone tissue. J. Biomech. 2004, 37, 27–35. [Google Scholar] [CrossRef]
- Algra, P.R.; Heimans, J.J.; Valk, J.; Nauta, J.J.; Lachniet, M.; Van Kooten, B. Do metastases in vertebrae begin in the body or the pedicles? Imaging study in 45 patients. AJR Am. J. Roentgenol. 1992, 158, 1275–1279. [Google Scholar] [CrossRef] [PubMed]
- Whealan, K.M.; Kwak, S.D.; Tedrow, J.R.; Inoue, K.; Snyder, B.D. Noninvasive Imaging Predicts Failure Load of the Spine with Simulated Osteolytic Defects. JBJS 2000, 82, 1240–1251. [Google Scholar] [CrossRef] [PubMed]
- Palanca, M.; De Donno, G.; Dall’Ara, E. A novel approach to evaluate the effects of artificial bone focal lesion on the threedimensional strain distributions within the vertebral body. PLoS ONE 2021, 16, e0251873. [Google Scholar] [CrossRef] [PubMed]
- Tschirhart, C.E.; Finkelstein, J.A.; Whyne, C.M. Biomechanics of vertebral level, geometry, and transcortical tumors in the metastatic spine. J. Biomech. 2007, 40, 46–54. [Google Scholar] [CrossRef]
- Palanca, M.; Barbanti-Brodano, G.; Marras, D.; Marciante, M.; Serra, M.; Gasbarrini, A.; Dall’Ara, E.; Cristofolini, L. Type, size, and position of metastatic lesions explain the deformation of the vertebrae under complex loading conditions. Bone 2021, 151, 116028. [Google Scholar] [CrossRef]
- Hipp, J.; Katz, G.; Hayes, W. Local Demineralization as a Model for Bone Strength Reductions in Lytic Transcortical Metastatic Lesions. Invest. Radiol. 1991, 26, 934–938. [Google Scholar] [CrossRef]
- Malandrino, A.; Kamm, R.D.; Moeendarbary, E. In Vitro Modeling of Mechanics in Cancer Metastasis. ACS Biomater. Sci. Eng. 2018, 4, 294–301. [Google Scholar] [CrossRef]
- Whyne, C.M.; Hu, S.S.; Workman, K.L.; Lotz, J.C. Biphasic material properties of lytic bone metastases. Ann. Biomed. Eng. 2000, 28, 1154–1158. [Google Scholar] [CrossRef] [PubMed]
- Tanck, E.; van Aken, J.B.; van der Linden, Y.M.; Bart Schreuder, H.W.; Binkowski, M.; Huizenga, H.; Verdonschot, N. Pathological fracture prediction in patients with metastatic lesions can be improved with quantitative computed tomography based computer models. Bone 2009, 45, 777–783. [Google Scholar] [CrossRef] [PubMed]
- Goodheart, J.R.; Cleary, R.J.; Damron, T.A.; Mann, K.A. Simulating activities of daily living with finite element analysis improves fracture prediction for patients with metastatic femoral lesions. J. Orthop. Res. 2015, 33, 1226–1234. [Google Scholar] [CrossRef] [PubMed]
- Derikx, L.C.; Verdonschot, N.; Tanck, E. Towards clinical application of biomechanical tools for the prediction of fracture risk i nmetastatic bone disease. J. Biomech. 2015, 48, 761–766. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sciumè, G.; Shelton, S.; Gray, W.G.; Miller, C.T.; Hussain, F.; Ferrari, M.; Decuzzi, P.; Schrefler, B.A. A multiphase model for three-dimensional tumor growth. New. J. Phys. 2013, 15, 015005. [Google Scholar] [CrossRef] [PubMed]
- Sciumè, G.; Gray, W.G.; Ferrari, M.; Decuzzi, P.; Schrefler, B.A. On computational modeling in tumor growth. Arch. Comput. Methods Eng. 2013, 20, 327–352. [Google Scholar] [CrossRef]
- Sciumè, G.; Santagiuliana, R.; Ferrari, M.; Decuzzi, P.; Schrefler, B.A. A tumor growth model with deformable ECM. Phys. Biol. 2014, 11, 065004. [Google Scholar] [CrossRef]
- Katsamba, I.; Evangelidis, P.; Voutouri, C.; Tsamis, A.; Vavourakis, V.; Stylianopoulos, T. Biomechanical modelling of spinal tumour anisotropic growth. Proc. R. Soc. A 2020, 476, 20190364. [Google Scholar] [CrossRef]
- Gu, Y.; Dong, J.; Jiang, X.; Wang, Y. Minimally invasive pedicle screws fixation and percutaneous vertebroplasty for the surgical treatment of thoracic metastatic tumors with neurologic compression. Spine 2016, 41, B14–B22. [Google Scholar] [CrossRef]
- Hsieh, Y.Y.; Kuo, Y.J.; Chen, C.H.; Wu, L.C.; Chiang, C.J.; Lin, C.L. Biomechanical assessment of vertebroplasty combined with cement-augmented screw fixation for lumbar burst fractures: A finite element analysis. Appl. Sci. 2020, 10, 2133. [Google Scholar] [CrossRef]



| Metastasis | Radius | EXT | LLB | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | ||
| FL | FL | FL | FL | FL | FL | FL | FL | FL | FL | FL | FL | ||
| Osteoblastic | 4467 | 4709 | 4751 | 10,388 | 9775 | 9602 | 3877 | 3269 | 3543 | 11,704 | 9773 | 10,368 | |
| 5570 | 4741 | 4809 | 9781 | 10,402 | 11,905 | 3343 | 3145 | 3148 | 10,907 | 8632 | 11,829 | ||
| Osteolytic | 4456 | 4111 | 4788 | 10,138 | 10,811 | 8947 | 3763 | 3508 | 3581 | 10,466 | 9713 | 9678 | |
| 4045 | 4253 | 4659 | 9449 | 9402 | 9711 | 3565 | 3685 | 3446 | 9284 | 9645 | 8937 | ||
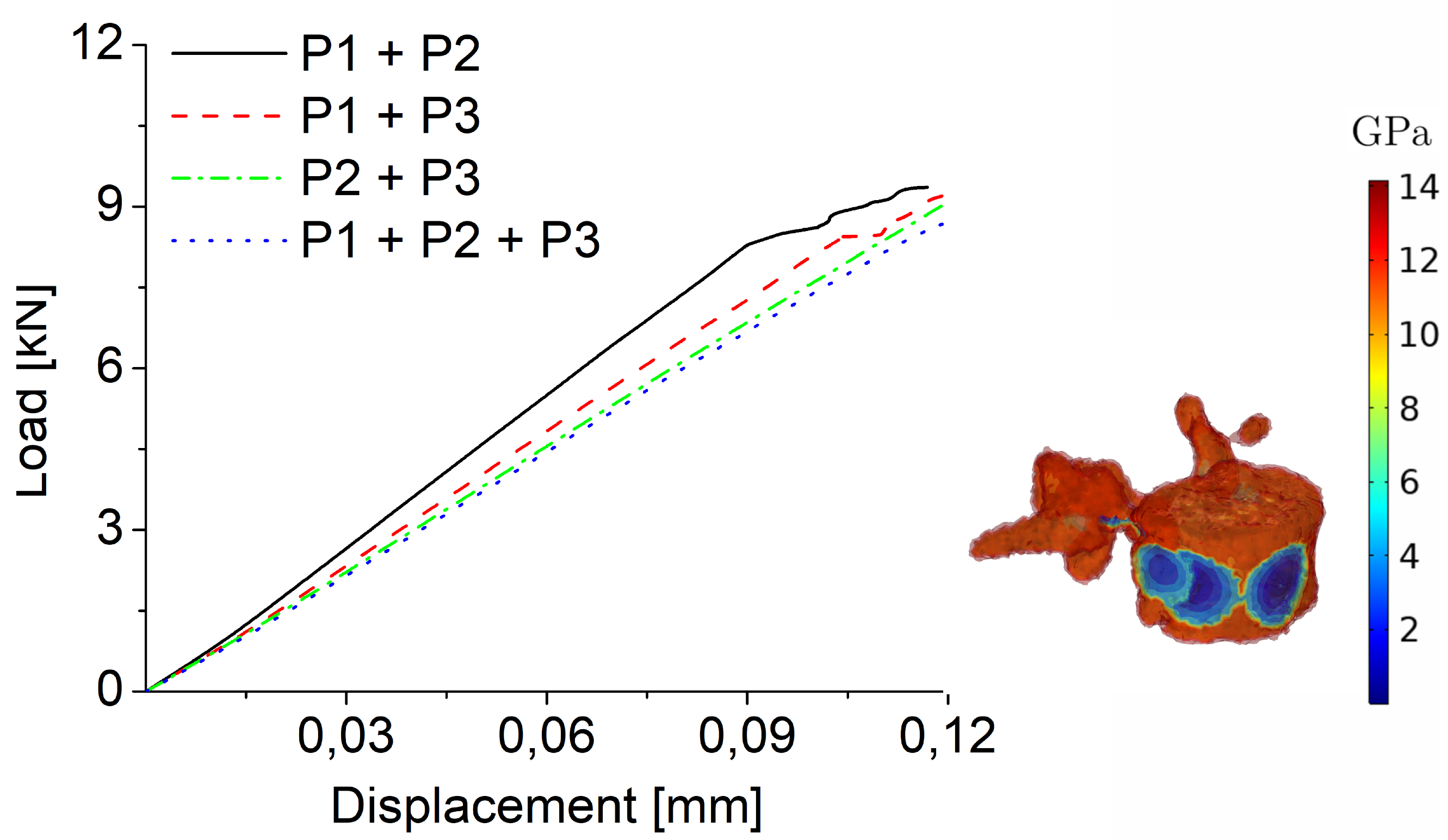
| Metastasis | Radius | LLB | |||
|---|---|---|---|---|---|
| P1+P2 | P1+P3 | P2+P3 | P1+P2+P3 | ||
| FL | FL | FL | FL | ||
| Osteolytic | 9359 | 9362 | 9373 | 9024 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchi, D.; Falcinelli, C.; Molinari, L.; Gizzi, A.; Di Martino, A. Osteolytic vs. Osteoblastic Metastatic Lesion: Computational Modeling of the Mechanical Behavior in the Human Vertebra after Screws Fixation Procedure. J. Clin. Med. 2022, 11, 2850. https://doi.org/10.3390/jcm11102850
Bianchi D, Falcinelli C, Molinari L, Gizzi A, Di Martino A. Osteolytic vs. Osteoblastic Metastatic Lesion: Computational Modeling of the Mechanical Behavior in the Human Vertebra after Screws Fixation Procedure. Journal of Clinical Medicine. 2022; 11(10):2850. https://doi.org/10.3390/jcm11102850
Chicago/Turabian StyleBianchi, Daniele, Cristina Falcinelli, Leonardo Molinari, Alessio Gizzi, and Alberto Di Martino. 2022. "Osteolytic vs. Osteoblastic Metastatic Lesion: Computational Modeling of the Mechanical Behavior in the Human Vertebra after Screws Fixation Procedure" Journal of Clinical Medicine 11, no. 10: 2850. https://doi.org/10.3390/jcm11102850
APA StyleBianchi, D., Falcinelli, C., Molinari, L., Gizzi, A., & Di Martino, A. (2022). Osteolytic vs. Osteoblastic Metastatic Lesion: Computational Modeling of the Mechanical Behavior in the Human Vertebra after Screws Fixation Procedure. Journal of Clinical Medicine, 11(10), 2850. https://doi.org/10.3390/jcm11102850








