Hybrid Forward Osmosis–Nanofiltration for Wastewater Reuse: System Design
Abstract
:1. Introduction
2. Materials and Methods
2.1. FO Fouling Tests
2.1.1. Lab Unit, Membranes, and Draw Solutes
2.1.2. Wastewater Samples and Fouling Experiment Protocol
2.2. Modeling of the Forward Osmosis–Nanofiltration Fluxes
2.2.1. Case 1: Simulation of the Water Flux across the FO Membrane during Fouling Experiments
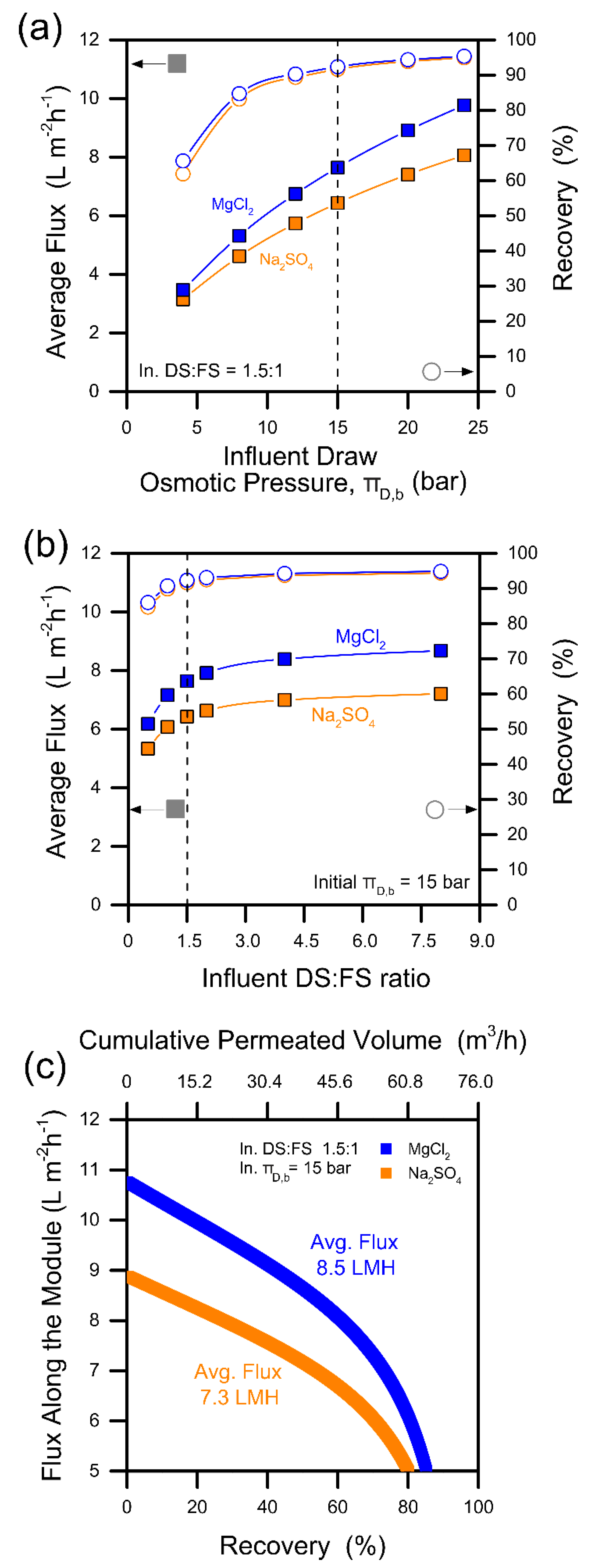
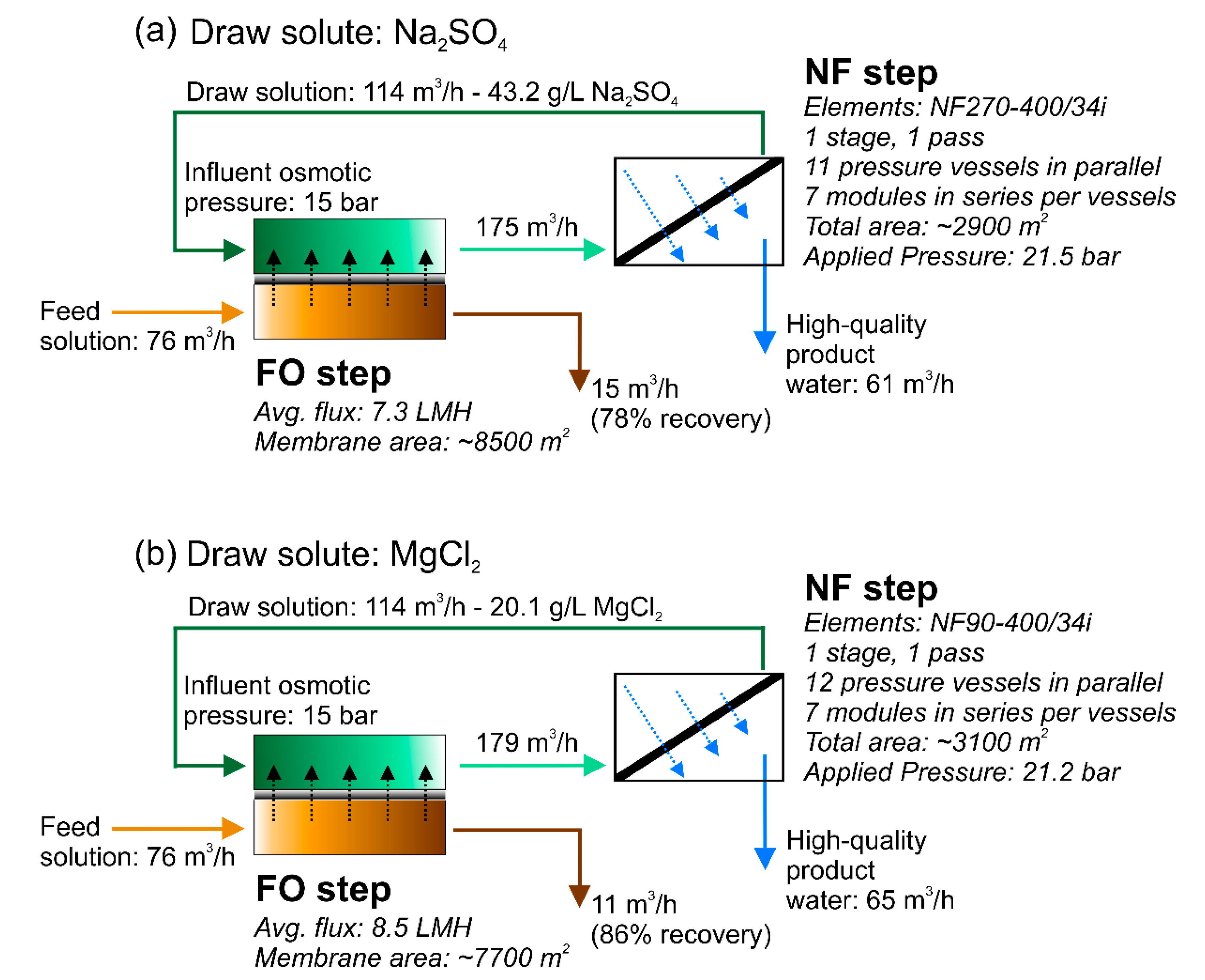
2.2.2. Case 2: System-Scale Analysis and Design of the Forward-Osmosis Nanofiltration System
3. Results and Discussion
3.1. Design of the Forward Osmosis–Nanofiltration Hybrid System
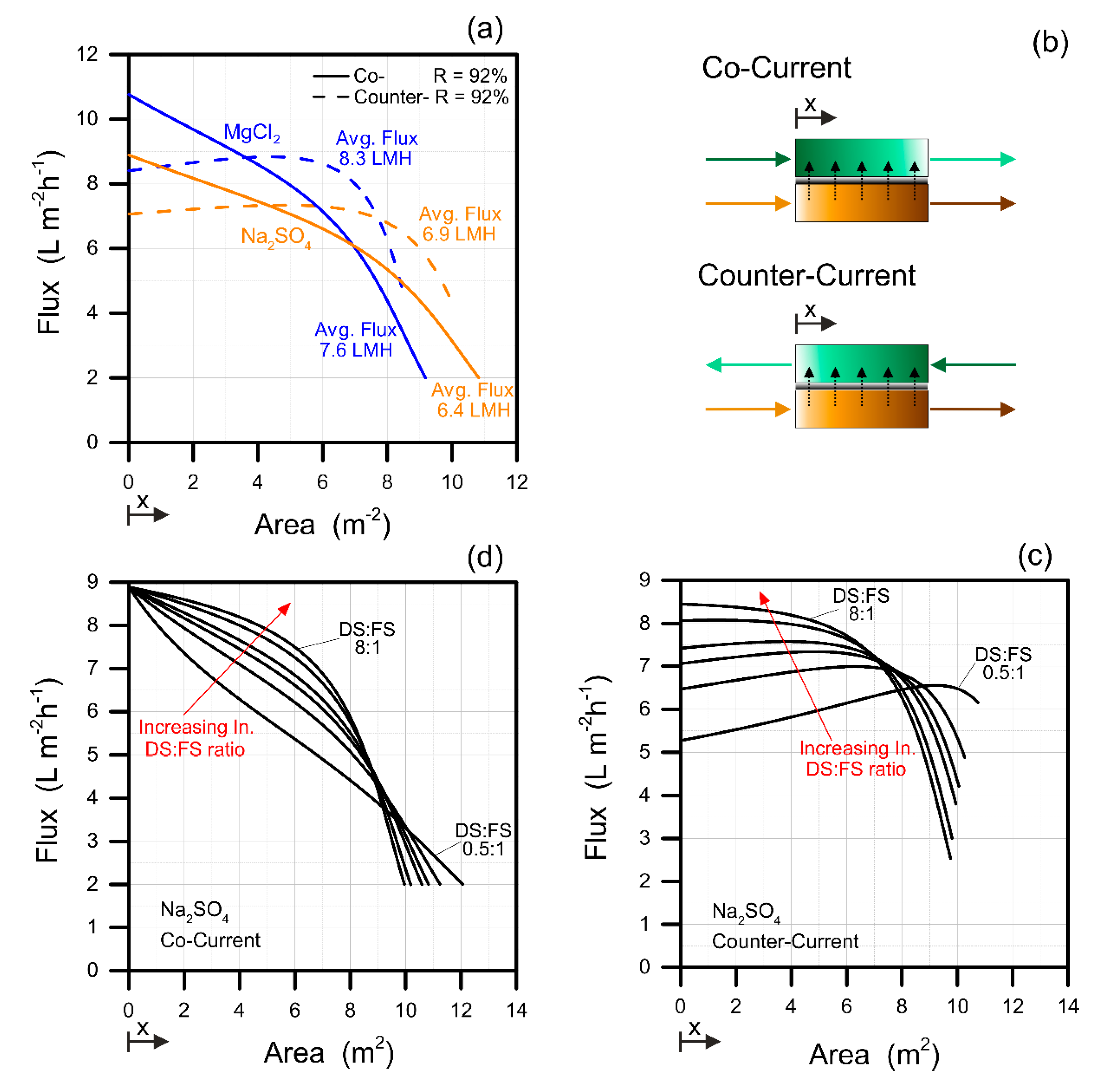
3.2. Cocurrent versus Counter-Current Configuration
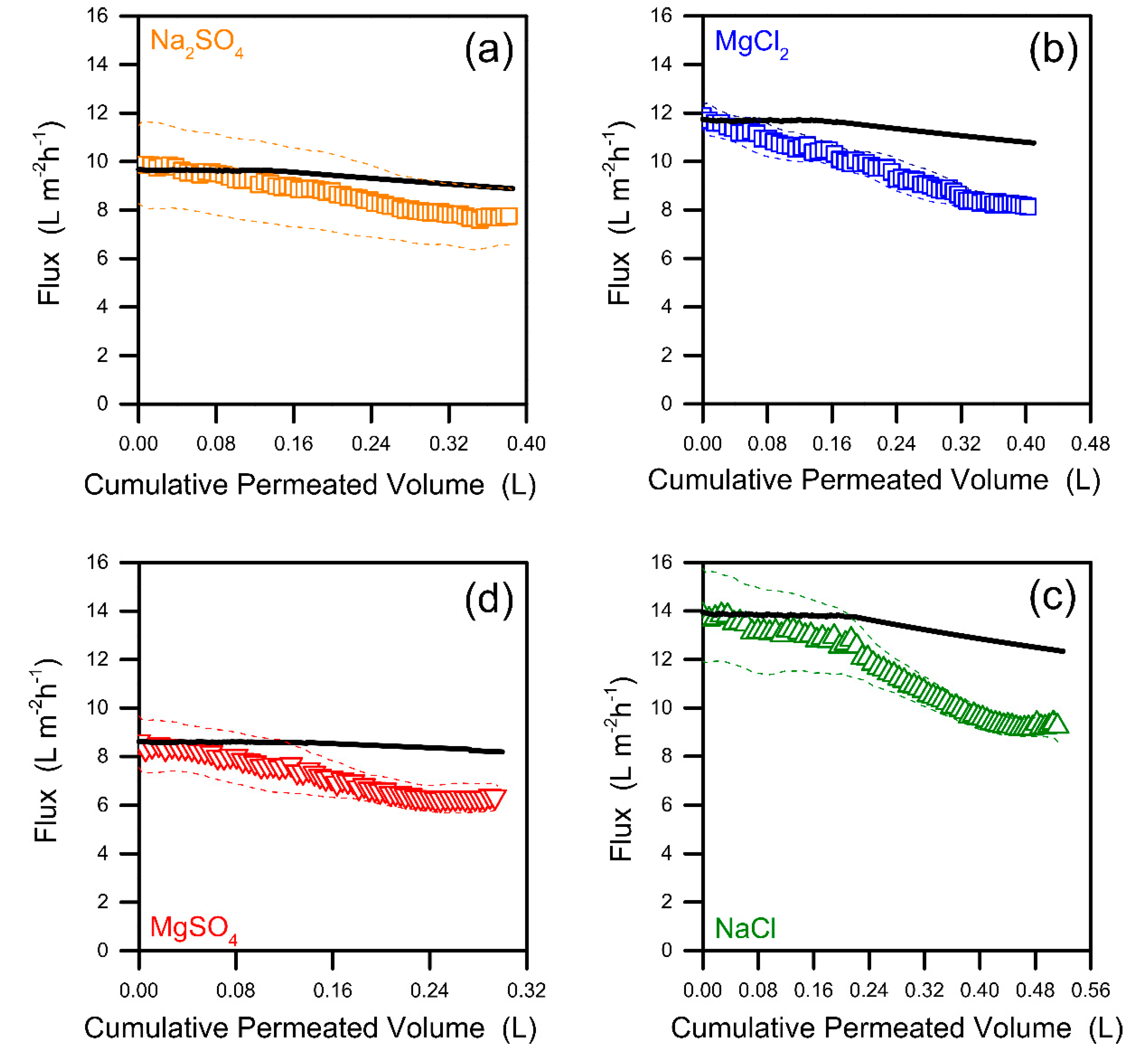
3.3. Fouling Propensity and Behavior
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, S.F.; Zou, L.; Tang, C.Y.Y.; Mulcahy, D. Recent Developments in Forward Osmosis: Opportunities and Challenges. J. Membr. Sci. 2012, 396, 1–21. [Google Scholar] [CrossRef]
- Shaffer, D.L.; Werber, J.R.; Jaramillo, H.; Lin, S.H.; Elimelech, M. Forward Osmosis: Where Are We Now? Desalination 2015, 356, 271–284. [Google Scholar] [CrossRef]
- Petrotos, K.B.; Lazarides, H.N. Osmotic Concentration of Liquid Foods. J. Food Eng. 2001, 49, 201–206. [Google Scholar] [CrossRef]
- Cath, T.Y.; Childress, A.E.; Elimelech, M. Forward Osmosis: Principles, Applications, and Recent Developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- McGinnis, R.L.; Elimelech, M. Global Challenges in Energy and Water Supply: The Promise of Engineered Osmosis. Environ. Sci. Technol. 2008, 42, 8625–8629. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Castello, E.M.; McCutcheon, J.R.; Elimelech, M. Performance Evaluation of Sucrose Concentration Using Forward Osmosis. J. Membr. Sci. 2009, 338, 61–66. [Google Scholar] [CrossRef]
- Giagnorio, M.; Ricceri, F.; Tiraferri, A. Desalination of Brackish Groundwater and Reuse of Wastewater by Forward Osmosis Coupled with Nanofiltration for Draw Solution Recovery. Water Res. 2019, 153, 134–143. [Google Scholar] [CrossRef] [PubMed]
- Phuntsho, S.; Shon, H.K.; Majeed, T.; El Saliby, I.; Vigneswaran, S.; Kandasamy, J.; Hong, S.; Lee, S. Blended Fertilizers as Draw Solutions for Fertilizer-Drawn Forward Osmosis Desalination. Environ. Sci. Technol. 2012, 46, 4567–4575. [Google Scholar] [CrossRef]
- Achilli, A.; Cath, T.Y.; Childress, A.E. Selection of Inorganic-Based Draw Solutions for Forward Osmosis Applications. J. Membr. Sci. 2010, 364, 233–241. [Google Scholar] [CrossRef]
- Phuntsho, S.; Shon, H.K.; Hong, S.; Lee, S.; Vigneswaran, S.; Kandasamy, J. Fertiliser Drawn Forward Osmosis Desalination: The Concept, Performance and Limitations for Fertigation. Rev. Environ. Sci. Bio-Technol. 2012, 11, 147–168. [Google Scholar] [CrossRef]
- McGinnis, R.L.; Hancock, N.T.; Nowosielski-Slepowron, M.S.; McGurgan, G.D. Pilot Demonstration of the Nh3/Co2 Forward Osmosis Desalination Process on High Salinity Brines. Desalination 2013, 312, 67–74. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; McGinnis, R.L.; Elimelech, M. A Novel Ammonia-Carbon Dioxide Forward (Direct) Osmosis Desalination Process. Desalination 2005, 174, 1–11. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, S.; McCutcheon, J.R.; Rahaman, M.S. Treatment of Fracking Wastewaters Via Forward Osmosis: Evaluation of Suitable Organic Draw Solutions. Desalination 2019, 452, 149–158. [Google Scholar] [CrossRef]
- Yip, N.Y.; Tiraferri, A.; Phillip, W.A.; Schiffman, J.D.; Elimelech, M. High Performance Thin-Film Composite Forward Osmosis Membrane. Environ. Sci. Technol. 2010, 44, 3812–3818. [Google Scholar] [CrossRef] [PubMed]
- Tiraferri, A.; Yip, N.Y.; Phillip, W.A.; Schiffman, J.D.; Elimelech, M. Relating Performance of Thin-Film Composite Forward Osmosis Membranes to Support Layer Formation and Structure. J. Membr. Sci. 2011, 367, 340–352. [Google Scholar] [CrossRef]
- Tiraferri, A.; Kang, Y.; Giannelis, E.P.; Elimelech, M. Highly Hydrophilic Thin-Film Composite Forward Osmosis Membranes Functionalized with Surface-Tailored Nanoparticles. ACS Appl. Mater. Interfaces 2012, 4, 5044–5053. [Google Scholar] [CrossRef] [PubMed]
- Faria, A.F.; Liu, C.H.; Xie, M.; Perreault, F.; Nghiem, L.D.; Ma, J.; Elimelech, M. Thin-Film Composite Forward Osmosis Membranes Functionalized with Graphene Oxide-Silver Nanocomposites for Biofouling Control. J. Membr. Sci. 2017, 525, 146–156. [Google Scholar] [CrossRef]
- Zhao, S.F.; Zou, L.D.; Mulcahy, D. Brackish Water Desalination by a Hybrid Forward Osmosis-Nanofiltration System Using Divalent Draw Solute. Desalination 2012, 284, 175–181. [Google Scholar] [CrossRef]
- Linares, R.V.; Li, Z.; Yangali-Quintanilla, V.; Ghaffour, N.; Amy, G.; Leiknes, T.; Vrouwenvelder, J.S. Life Cycle Cost of a Hybrid Forward Osmosis Low Pressure Reverse Osmosis System for Seawater Desalination and Wastewater Recovery. Water Res. 2016, 88, 225–234. [Google Scholar] [CrossRef]
- Xie, M.; Nghiem, L.D.; Price, W.E.; Elimelech, M. Toward Resource Recovery from Wastewater: Extraction of Phosphorus from Digested Sludge Using a Hybrid Forward Osmosis-Membrane Distillation Process. Environ. Sci. Technol. Lett. 2014, 1, 191–195. [Google Scholar] [CrossRef]
- Dutta, S.; Nath, K. Prospect of Ionic Liquids and Deep Eutectic Solvents as New Generation Draw Solution in Forward Osmosis Process. J. Water Process Eng. 2018, 21, 163–176. [Google Scholar] [CrossRef]
- Corzo, B.; de la Torre, T.; Sans, C.; Escorihuela, R.; Navea, S.; Malfeito, J.J. Long-Term Evaluation of a Forward Osmosis-Nanofiltration Demonstration Plant for Wastewater Reuse in Agriculture. Chem. Eng. J. 2018, 338, 383–391. [Google Scholar] [CrossRef]
- Deshmukh, A.; Yip, N.Y.; Lin, S.H.; Elimelech, M. Desalination by Forward Osmosis: Identifying Performance Limiting Parameters through Module-Scale Modeling. J. Membr. Sci. 2015, 491, 159–167. [Google Scholar] [CrossRef]
- Mondal, S.; Field, R.W.; Wu, J.J. Novel Approach for Sizing Forward Osmosis Membrane Systems. J. Membr. Sci. 2017, 541, 321–328. [Google Scholar] [CrossRef]
- Banchik, L.D.; Weiner, A.M.; Al-Anzi, B.; Lienhard, J.H. System Scale Analytical Modeling of Forward and Assisted Forward Osmosis Mass Exchangers with a Case Study on Fertigation. J. Membr. Sci. 2016, 510, 533–545. [Google Scholar] [CrossRef]
- Attarde, D.; Jain, M.; Gupta, S.K. Modeling of a Forward Osmosis and a Pressure-Retarded Osmosis Spiral Wound Module Using the Spiegler-Kedem Model and Experimental Validation. Sep. Purif. Technol. 2016, 164, 182–197. [Google Scholar] [CrossRef]
- Ali, S.M.; Kim, J.E.; Phuntsho, S.; Jang, A.; Choi, J.Y.; Shon, H.K. Forward Osmosis System Analysis for Optimum Design and Operating Conditions. Water Res. 2018, 145, 429–441. [Google Scholar] [CrossRef]
- Xiao, D.Z.; Li, W.Y.; Chou, S.R.; Wang, R.; Tang, C.Y.Y. A Modeling Investigation on Optimizing the Design of Forward Osmosis Hollow Fiber Modules. J. Membr. Sci. 2012, 392, 76–87. [Google Scholar] [CrossRef]
- Tiraferri, A.; Yip, N.Y.; Straub, A.P.; Castrillon, S.R.V.; Elimelech, M. A Method for the Simultaneous Determination of Transport and Structural Parameters of Forward Osmosis Membranes. J. Membr. Sci. 2013, 444, 523–538. [Google Scholar] [CrossRef]
- Hoek, E.M.V.; Kim, A.S.; Elimelech, M. Influence of Crossflow Membrane Filter Geometry and Shear Rate on Colloidal Fouling in Reverse Osmosis and Nanofiltration Separations. Environ. Sci. Technol. 2002, 19, 357–372. [Google Scholar] [CrossRef]
- Giagnorio, M.; Ruffino, B.; Grinic, D.; Steffenino, S.; Meucci, L.; Zanetti, M.C.; Tiraferri, A. Achieving Low Concentrations of Chromium in Drinking Water by Nanofiltration: Membrane Performance and Selection. Environ. Sci. Pollut. Res. 2018, 25, 25294–25305. [Google Scholar] [CrossRef]
- Lee, J.; Kim, B.; Hong, S. Fouling Distribution in Forward Osmosis Membrane Process. J. Environ. Sci. 2014, 26, 1348–1354. [Google Scholar] [CrossRef]
- Ge, Q.C.; Ling, M.M.; Chung, T.S. Draw Solutions for Forward Osmosis Processes: Developments, Challenges, and Prospects for the Future. J. Membr. Sci. 2013, 442, 225–237. [Google Scholar] [CrossRef]
- Hoek, E.M.V.; Elimelech, M. Cake-Enhanced Concentration Polarization: A New Fouling Mechanism for Salt-Rejecting Membranes. Environ. Sci. Technol. 2003, 37, 5581–5588. [Google Scholar] [CrossRef]
- Zou, S.; Gu, Y.S.; Xiao, D.Z.; Tang, C.Y.Y. The Role of Physical and Chemical Parameters on Forward Osmosis Membrane Fouling During Algae Separation. J. Membr. Sci. 2011, 366, 356–362. [Google Scholar] [CrossRef]
- Zou, S.; Wang, Y.N.; Wicaksana, F.; Aung, T.; Wong, P.C.Y.; Fane, A.G.; Tang, C.Y. Direct Microscopic Observation of Forward Osmosis Membrane Fouling by Microalgae: Critical Flux and the Role of Operational Conditions. J. Membr. Sci. 2013, 436, 174–185. [Google Scholar] [CrossRef]
- Mo, H.; Tay, K.G.; Ng, H.Y. Fouling of Reverse Osmosis Membrane by Protein (Bsa): Effects of Ph, Calcium, Magnesium, Ionic Strength and Temperature. J. Membr. Sci. 2008, 315, 28–35. [Google Scholar] [CrossRef]
- Jin, X.; Huang, X.F.; Hoek, E.M.V. Role of Specific Ion Interactions in Seawater Ro Membrane Fouling by Alginic Acid. Environ. Sci. Technol. 2009, 43, 3580–3587. [Google Scholar] [CrossRef]
- Lay, W.C.L.; Chong, T.H.; Tang, C.Y.Y.; Fane, A.G.; Zhang, J.S.; Liu, Y. Fouling Propensity of Forward Osmosis: Investigation of the Slower Flux Decline Phenomenon. Water Sci. Technol. 2010, 61, 927–936. [Google Scholar] [CrossRef]
- Wang, Y.N.; Wicaksana, F.; Tang, C.Y.; Fane, A.G. Direct Microscopic Observation of Forward Osmosis Membrane Fouling. Environ. Sci. Technol. 2010, 44, 7102–7109. [Google Scholar] [CrossRef]
- Zhao, S.F.; Zou, L.D.; Mulcahy, D. Effects of Membrane Orientation on Process Performance in Forward Osmosis Applications. J. Membr. Sci. 2011, 382, 308–315. [Google Scholar] [CrossRef]
- Diagne, N.W.; Rabiller-Baudry, M.; Paugam, L. On the Actual Cleanability of Polyethersulfone Membrane Fouled by Proteins at Critical or Limiting Flux. J. Membr. Sci. 2013, 425, 40–47. [Google Scholar] [CrossRef]
- Field, R.W.; Pearce, G.K. Critical, Sustainable and Threshold Fluxes for Membrane Filtration with Water Industry Applications. Adv. Colloid Interface Sci. 2011, 164, 38–44. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Dissolved organic carbon (mg/L) | 22 |
| pH | 8.0 |
| Cl‒ (mg/L) | 100 |
| F‒ (mg/L) | 0.1 |
| PO43‒ (mg/L) | 1.5 |
| NO3‒ (mg/L) | 2.2 |
| SO42‒ (mg/L) | 250 |
| N-NH4 (mg/L) | 0.004 |
| Ca2+ (mg/L) | 31 |
| Mg2+ (mg/L) | 13 |
| K+ (mg/L) | 15 |
| Na+ (mg/L) | 120 |
| Al (µg/L) | 70 |
| As (µg/L) | 4.2 |
| Cr (µg/L) | 1.3 |
| Fe (µg/L) | 16 |
| Ni (µg/L) | 3.7 |
| Conductivity (µS/cm) | 1100 |
| Total dissolved solids (TDS) (mg/L) | 540 |
| Osmotic pressure (bar) | 0.5 |
| Draw Solute | B (LMH) | D (m2/s) |
|---|---|---|
| Na2SO4 | 0.06 | 7.6 × 10−10 |
| MgCl2 | 0.07 | 1.1 × 10−9 |
| NaCl | 0.94 | 1.5 × 10−9 |
| MgSO4 | 0.39 | 4.3 × 10−10 |
| CaCl2 | 0.16 | 1.1 × 10−9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giagnorio, M.; Ricceri, F.; Tagliabue, M.; Zaninetta, L.; Tiraferri, A. Hybrid Forward Osmosis–Nanofiltration for Wastewater Reuse: System Design. Membranes 2019, 9, 61. https://doi.org/10.3390/membranes9050061
Giagnorio M, Ricceri F, Tagliabue M, Zaninetta L, Tiraferri A. Hybrid Forward Osmosis–Nanofiltration for Wastewater Reuse: System Design. Membranes. 2019; 9(5):61. https://doi.org/10.3390/membranes9050061
Chicago/Turabian StyleGiagnorio, Mattia, Francesco Ricceri, Marco Tagliabue, Luciano Zaninetta, and Alberto Tiraferri. 2019. "Hybrid Forward Osmosis–Nanofiltration for Wastewater Reuse: System Design" Membranes 9, no. 5: 61. https://doi.org/10.3390/membranes9050061
APA StyleGiagnorio, M., Ricceri, F., Tagliabue, M., Zaninetta, L., & Tiraferri, A. (2019). Hybrid Forward Osmosis–Nanofiltration for Wastewater Reuse: System Design. Membranes, 9(5), 61. https://doi.org/10.3390/membranes9050061







