Influence of Hydraulic Pressure on Performance Deterioration of Direct Contact Membrane Distillation (DCMD) Process
Abstract
:1. Introduction
2. Theory
2.1. Mass and Heat Transfer in Direct Contact Membrane Distillation (DCMD)
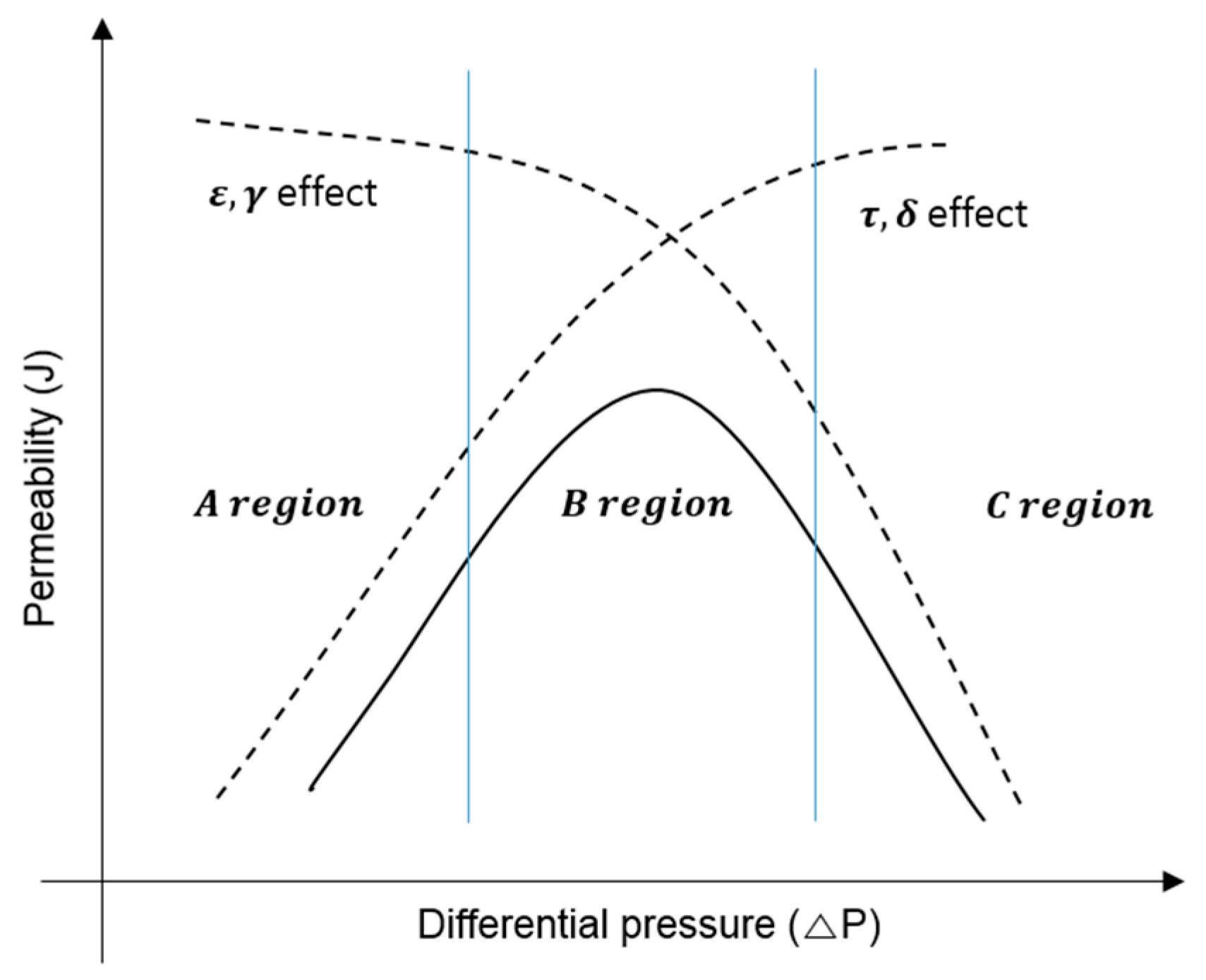
2.2. Membrane Compaction
3. Materials and Methods
3.1. Membrane Characterization
3.1.1. Membrane Thickness and Pore Area
3.1.2. Contact Angle Measurement
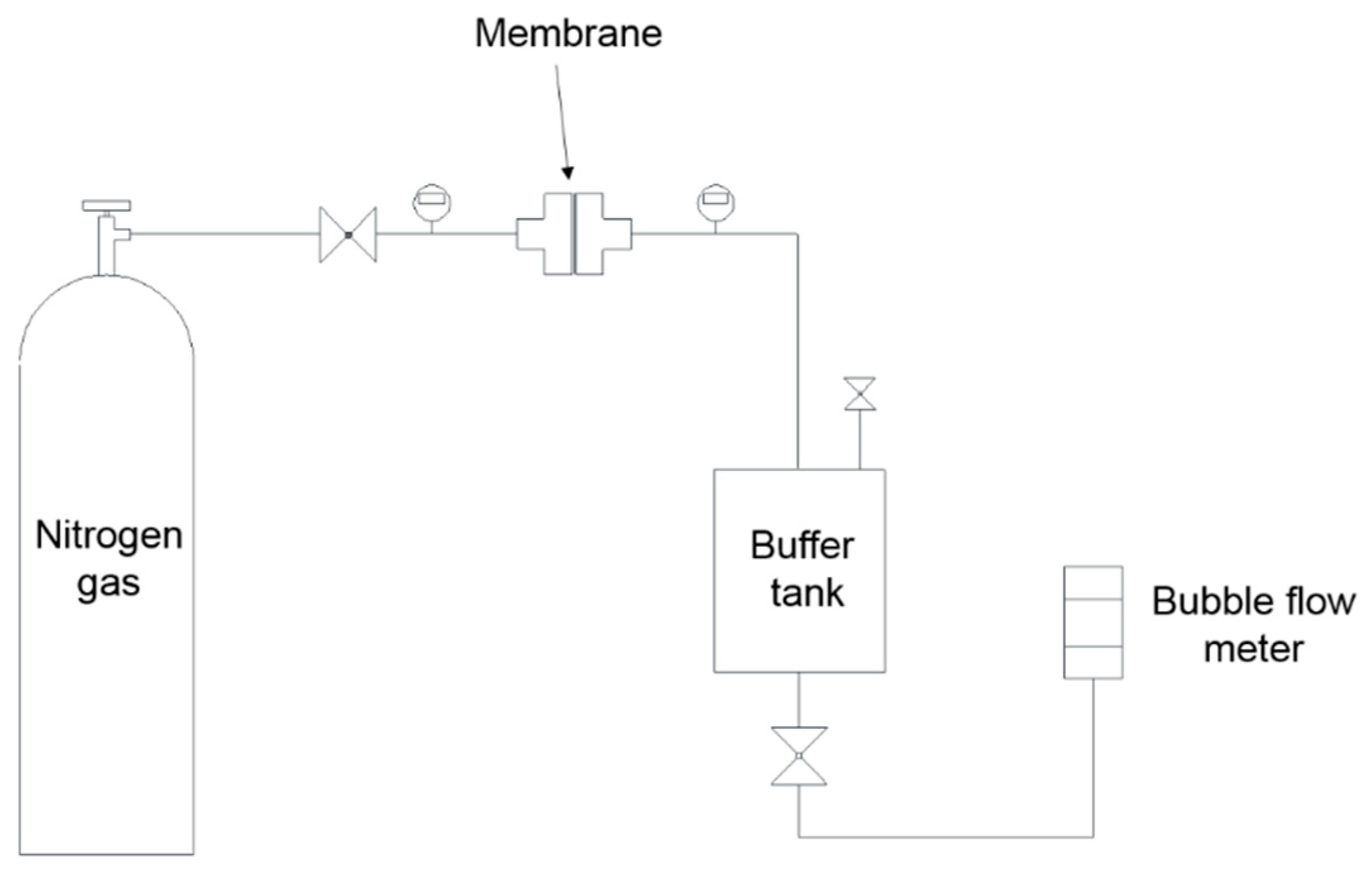
3.2. Gas Permeability Measurements
3.2.1. Gas Permeability Measurements at Low Pressure (Δp = 1 kPa)
- Each membrane was placed into the module of the gas permeability device.
- Then, feed pressure (Pm) was adjusted with the regulator of the membrane module and permeate pressure was allowed to come to a steady state and the buffer tank allowed the permeate-side pressure. This created a pressure difference between the membranes.
3.2.2. Gas Permeability Measurements at High Pressure (Δp = 30 kPa)
3.3. DCMD Experiments
4. Results and Discussion
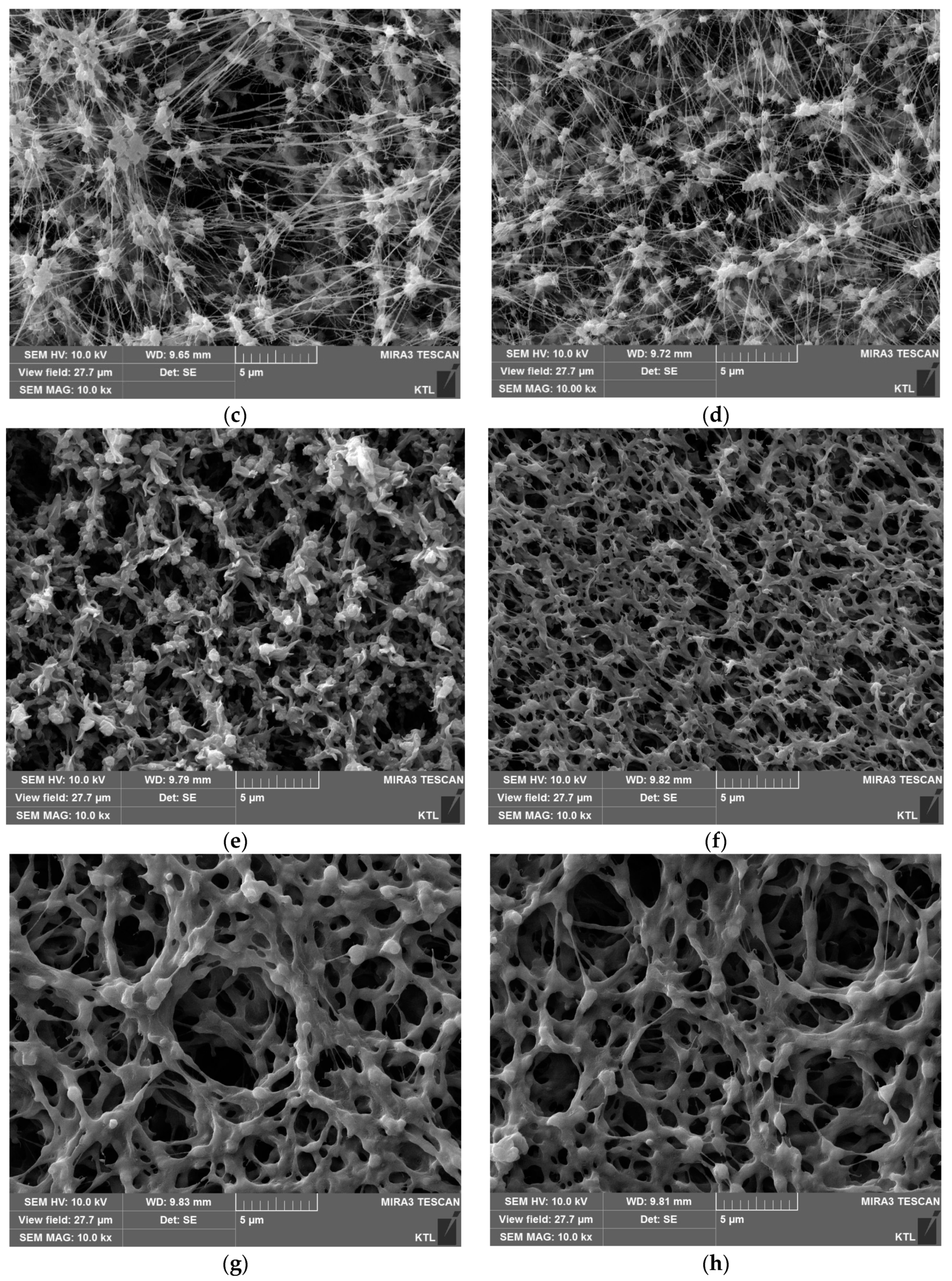
4.1. Scanning Electron Microscopy (SEM) Analysis
4.2. Gas Permeability Measurements
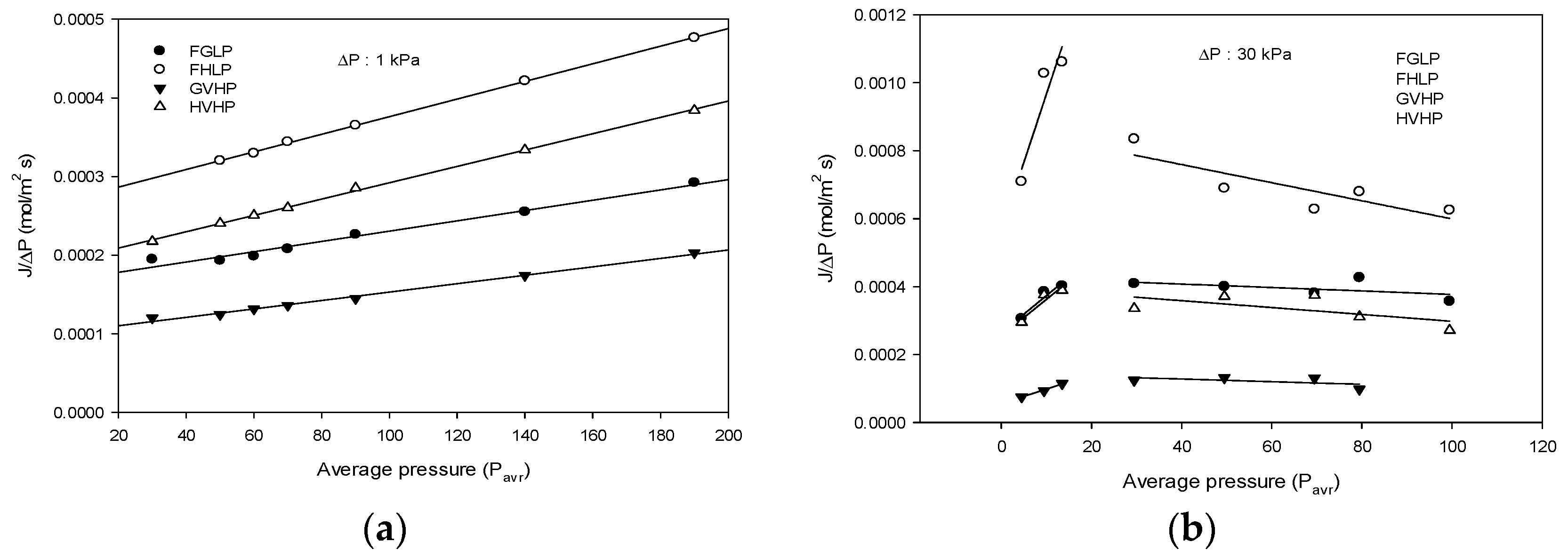
4.2.1. Gas Permeability Measurements at Low Pressure (Δp = 1 kPa)
4.2.2. Gas Permeability Measurements at High Pressure (Δp = 30 kPa)
4.3. DCMD Experiments
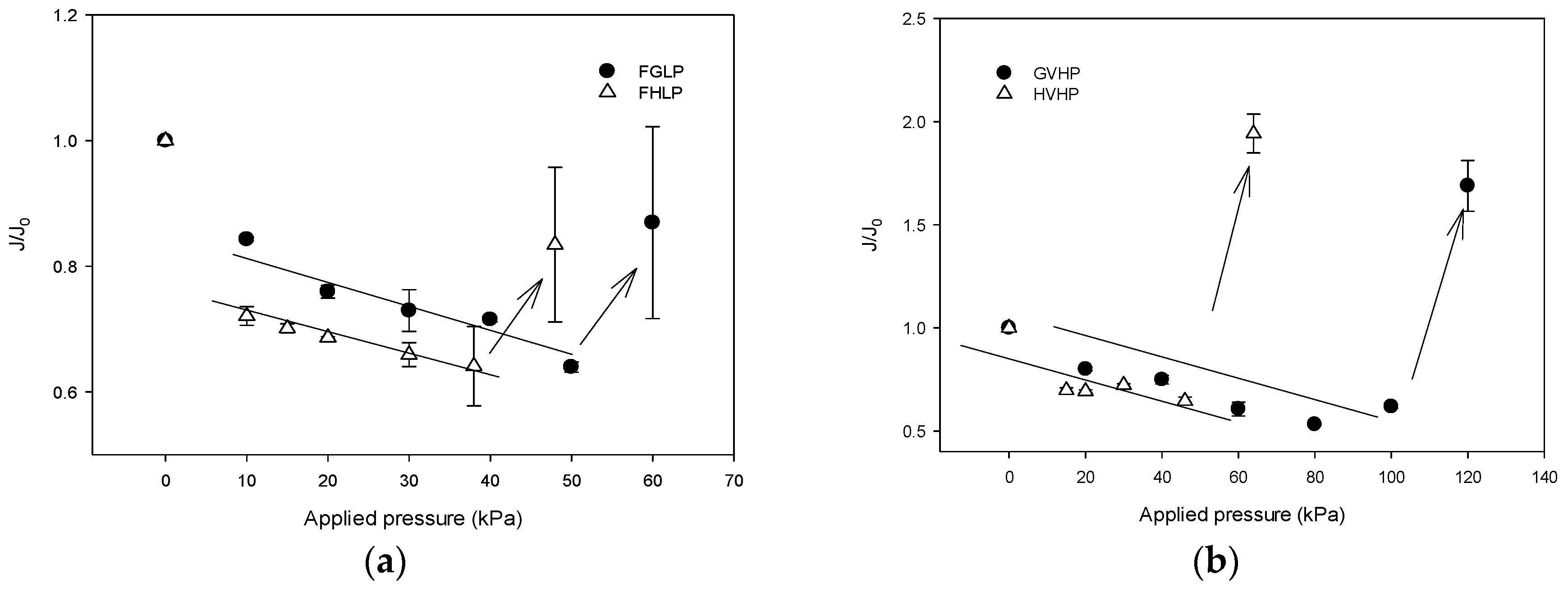
4.3.1. Effect of Applied Pressure (Δp) on Flux
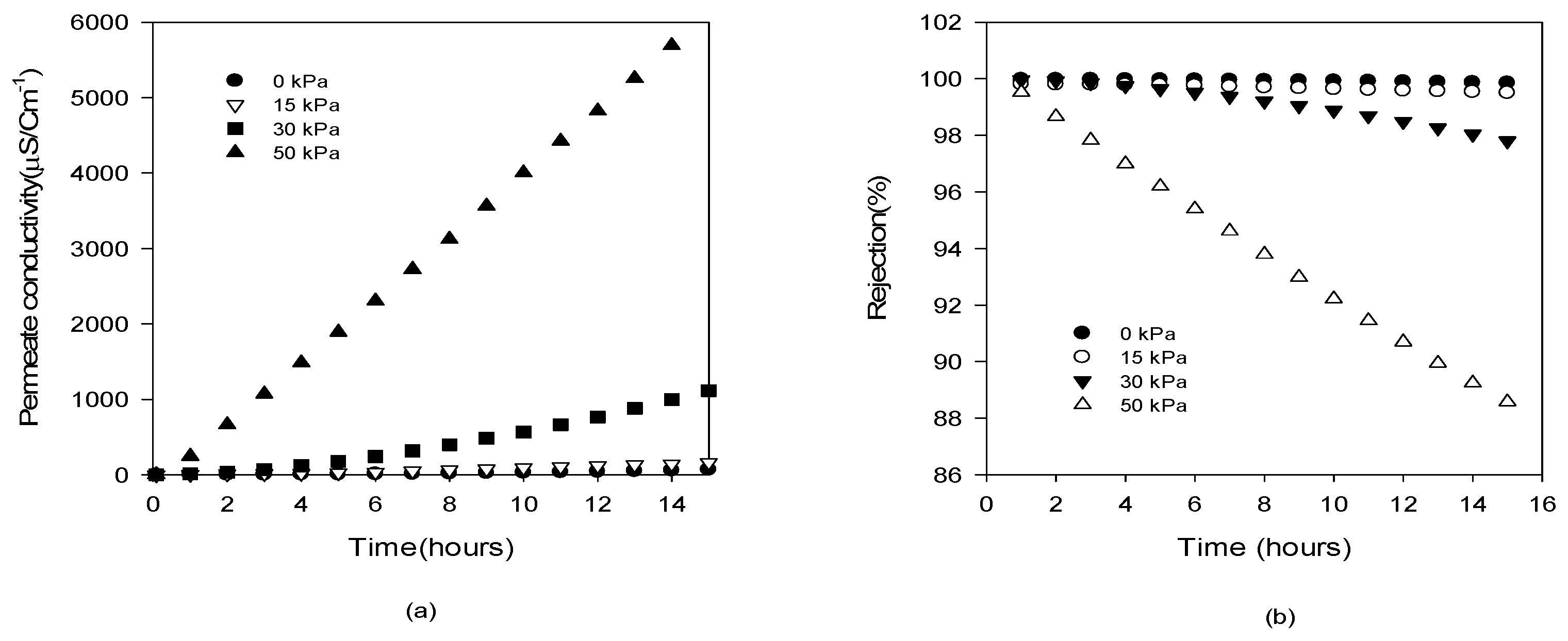
4.3.2. Effect of Δp on Salt Rejection
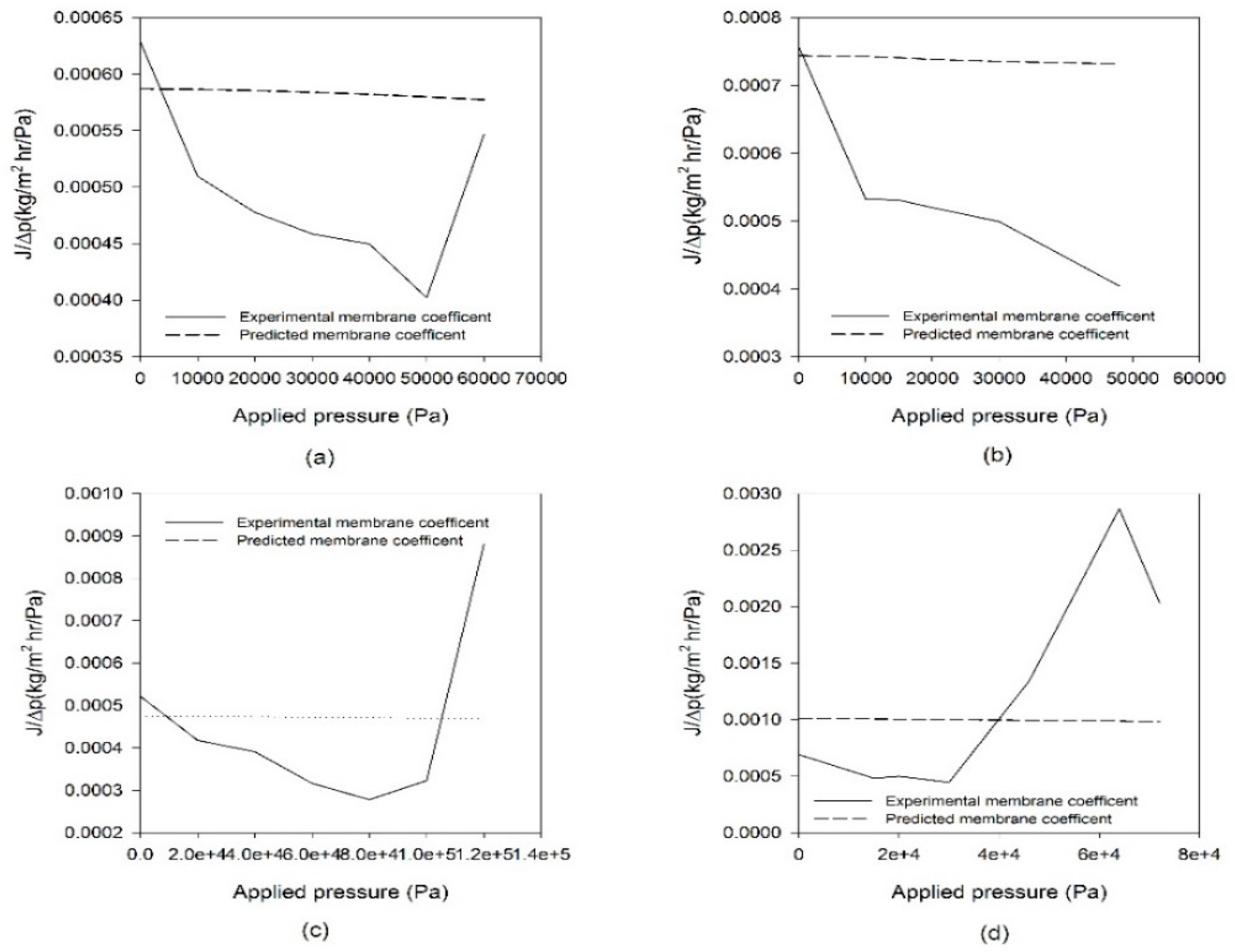
4.4. Comparison of Mass Transfer Coefficients
5. Conclusions
- The results of SEM analysis indicate that the MD membranes are deformed by applying the hydraulic pressure across the membrane. The thickness, pore size, and porosity of the membranes were found to be reduced.
- The gas permeabilities of the membranes were significantly reduced under high Δp conditions. This is attributed to the deformation or compaction of the membrane structures.
- A set of DCMD experiments was carried out by adjusting Δp. The membrane permeability decreases with an increase in Δp, which is attributed to the compaction of the membrane. When Δp exceeds critical values, however, the membrane permeability abruptly increases, which results from partial wetting of the membranes.
- Initially, the J/J0 decreases with Δp, suggesting that the membrane permeability is reduced by the applied pressure. The water permeabilities for FGLP and FHLP membranes was reduced by up to 15% and 25%, respectively. Above certain ΔP values (50 kPa for FGLP and 60 kPa for FHLP), however, the J/J0 suddenly increases, indicating the wetting of the membranes. The partial wetting phenomena were also confirmed by monitoring the solute rejection by the membranes under various Δp.
- Under various Δp conditions, the mass transfer coefficients determined from model equations were compared with those obtained from the experimental data. The model predictions failed to match the experimental results. This suggests that the current MD models cannot properly reflect the effect of Δp on its performance.
- Based on above results, it can be concluded that the control of feed pressure and transmembrane pressure are important not only in pressure-driven membrane processes but also thermal membrane processes such as DCMD. In fact, the MD pilot plant operated at about 30 to 70 kPa (Pilot Plant in Korea). Based on the results of this study, it is desirable to design the MD system to operate at 30 kPa or less.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Membrane Area |
| A0 | Knudsen flux coefficient |
| B0 | viscous flux coefficient |
| DAB | diffusivity of water vapor |
| ε | membrane porosity |
| Kb | Botzmann constant |
| σ | collision diameter |
| p | Mean pressure |
| JK | Vapor flux in the membrane resulting from Knudsen diffusion |
| R | universal gas constant |
| τ | Average tortuosity |
| T | Average temperature in the membrane pores |
| JM | Vapor flux in the membrane resulting from molecular diffusion |
| ya | mole fraction of the water vapor |
| initial membrane thickness | |
| uncompacted membrane thickness | |
| compaction coefficient | |
| η | gas viscosity |
References
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Membrane distillation: A comprehensive review. Desalination 2012, 287, 2–18. [Google Scholar] [CrossRef]
- Khayet, M. Membranes and theoretical modeling of membrane distillation: A review. Adv. Colloid Interface Sci. 2011, 164, 56–88. [Google Scholar] [CrossRef] [PubMed]
- Song, K.K.S.A.L. Pilot-Scale Studies for Direct Contact Membrane Distillation-Based Desalination Process; DWPR Report No. 134; U.S Department of the Interior Bureau of Reclamation: Washington, DC, USA, 2009.
- Gryta, M. Fouling in direct contact membrane distillation process. J. Membr. Sci. 2008, 325, 383–394. [Google Scholar] [CrossRef]
- Hitsov, I.; Maere, T.; de Sitter, K.; Dotremont, C.; Nopens, I. Modelling approaches in membrane distillation: A critical review. Sep. Purif. Technol. 2015, 142, 48–64. [Google Scholar] [CrossRef]
- Noever, D.A. Diffusive slip and surface transport properties. J. Colloid Interface Sci. 1991, 147, 186–191. [Google Scholar] [CrossRef]
- Winter, D.; Koschikowski, J.; Wieghaus, M. Desalination using membrane distillation: Experimental studies on full scale spiral wound modules. J. Membr. Sci. 2011, 375, 104–112. [Google Scholar] [CrossRef]
- Song, L.; Li, B.; Sirkar, K.K.; Gilron, J.L. Direct Contact Membrane Distillation-Based Desalination: Novel Membranes, Devices, Larger-Scale Studies, and a Model. Ind. Eng. Chem. Res. 2007, 46, 2307–2323. [Google Scholar] [CrossRef]
- Dumée, L.; Germain, V.; Sears, K.; Schütz, J.; Finn, N.; Duke, M.; Cerneaux, S.; Cornu, D.; Gray, S. Enhanced durability and hydrophobicity of carbon nanotube bucky paper membranes in membrane distillation. J. Membr. Sci. 2011, 376, 241–246. [Google Scholar] [CrossRef]
- Rezaei, M.; Warsinger, D.M.; Lienhard V, J.H.; Duke, M.C.; Matsuura, T.; Samhaber, W.M. Wetting phenomena in membrane distillation: Mechanisms, reversal, and prevention. Water Res. 2018, 139, 329–352. [Google Scholar] [CrossRef] [PubMed]
- Goh, S.; Zhang, J.; Liu, Y.; Fane, A.G. Fouling and wetting in membrane distillation (MD) and MD-bioreactor (MDBR) for wastewater reclamation. Desalination 2013, 323, 39–47. [Google Scholar] [CrossRef]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of membrane distillation in seawater desalination: Thermal efficiency, sensitivity study and cost estimation. Adv. Colloid Interface Sci. 2008, 323, 85–98. [Google Scholar]
- Kesieme, U.K.; Milne, N.; Aral, H.; Cheng, C.Y.; Duke, M. Economic analysis of desalination technologies in the context of carbon pricing, and opportunities for membrane distillation. Desalination 2013, 323, 66–74. [Google Scholar] [CrossRef]
- Alklaibi, A.M.; Lior, N. Membrane-distillation desalination: Status and potential. Desalination 2005, 171, 111–131. [Google Scholar] [CrossRef]
- Andrjesdóttir, Ó.; Ong, C.L.; Nabavi, M.; Paredes, S.; Khalil, A.S.G.; Michel, B.; Poulikakos, D. An experimentally optimizedmodel for heat and mass transfer in direct contactmembrane distillation. Int. J. Heat Mass Transf. 2013, 66, 855–867. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.-D.; Duke, M.; Xie, Z.; Gray, S. Performance of asymmetric hollow fibre membranes in membrane distillation under various configurations and vacuum enhancement. J. Membr. Sci. 2010, 362, 517–528. [Google Scholar] [CrossRef]
- Drioli, E.; Curcio, E.; di Profio, G.; Macedonio, F.; Criscuoli, A. Integrating Membrane Contactors Technology and Pressure-Driven Membrane Operations for Seawater Desalination. Chem. Eng. Res. Des. 2006, 84, 209–220. [Google Scholar] [CrossRef]
- Lalia, B.S.; Guillen-Burrieza, E.; Arafat, H.A.; Hashaikeh, R. Fabrication and characterization of polyvinylidenefluoride-co-hexafluoropropylene (PVDF-HFP) electrospun membranes for direct contact membrane distillation. J. Membr. Sci. 2013, 428, 104–115. [Google Scholar] [CrossRef]
- Bonyadi, S.; Chung, T.S. Flux enhancement in membrane distillation by fabrication of dual layer hydrophilic–hydrophobic hollow fiber membranes. J. Membr. Sci. 2007, 306, 134–146. [Google Scholar] [CrossRef]
- Lawson, K.W.; Hall, M.S.; Lloyd, D.R. Compaction of microporous membranes used in membrane distillation. I. Effect on gas permeability. J. Membr. Sci. 1995, 101, 99–108. [Google Scholar] [CrossRef]
- Lei, B.C.Z.; Ding, Z. Special Distillation Processes; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D. Gas and vapor transport through microporous membranes I: Knudsen Poiseuille transition. J. Membr. Sci. 1990, 53, 159–171. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Chen, G.; You, W.; Jiang, Y.; Sun, W. Experimental Study of Mass Transfer in Membrane Absorption Process Using Membranes with Different Porosities. Ind. Eng. Chem. Res. 2010, 49, 6641–6648. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.-D.; Gray, S. Effect of applied pressure on performance of PTFE membrane in DCMD. J. Membr. Sci. 2011, 369, 514–525. [Google Scholar] [CrossRef]
- Laganà, F.; Barbieri, G.; Drioli, E. Direct contact membrane distillation: Modelling and concentration experiments. J. Membr. Sci. 2000, 166, 1–11. [Google Scholar] [CrossRef]
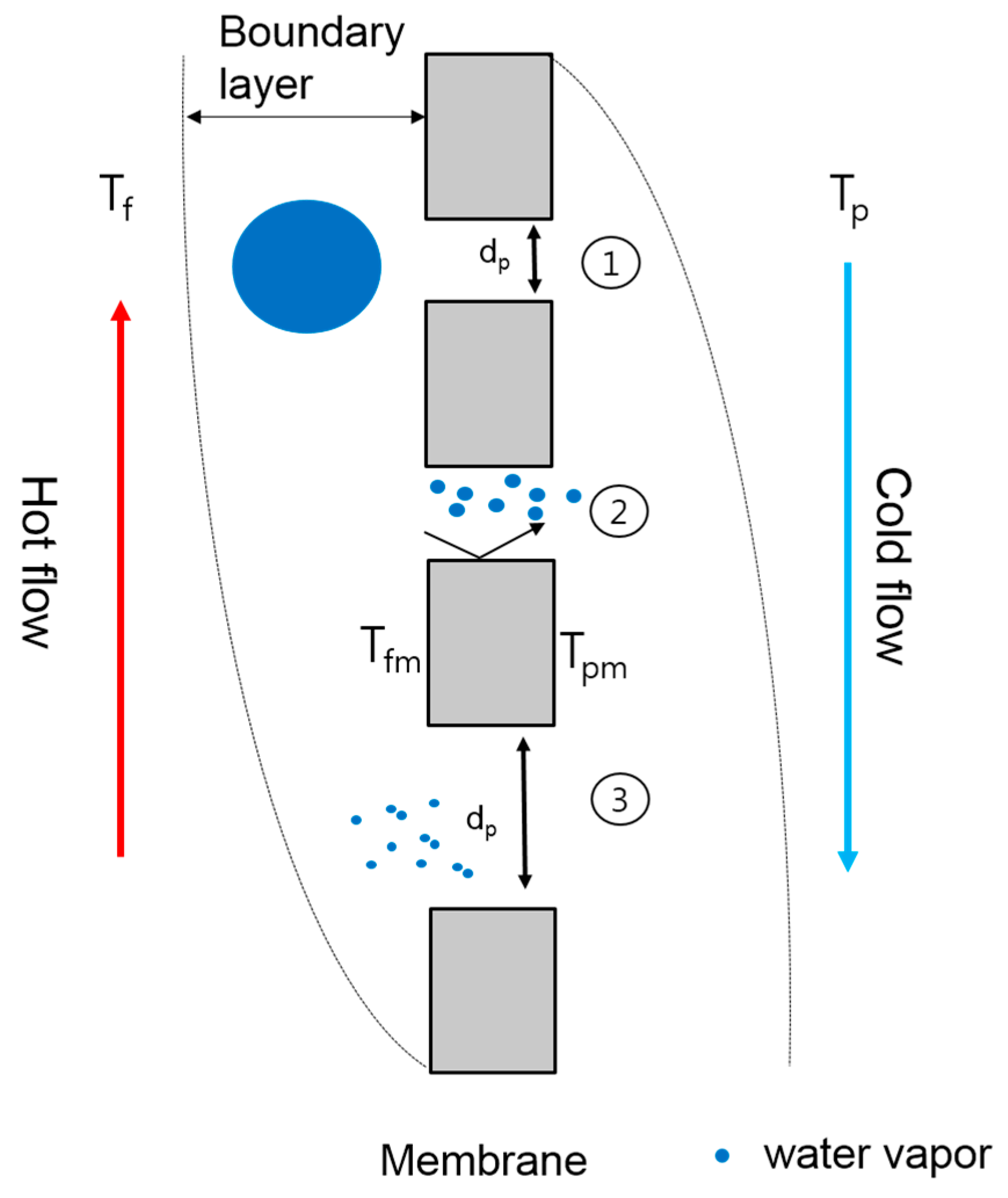




| Continuum Region | Transition Region | Knudsen Region |
|---|---|---|
| Kn < 0.01 or dp > 100λ | 0.01 < Kn < 1 or λ < dp < 100λ | Kn > 1 or dp < λ |
| Membrane Trade Name | Material | δ (μm) | rp (μm) | εa | (M−1) | K1 () | LEPw (kPa) a |
|---|---|---|---|---|---|---|---|
| GVHP | PVDF | 112 | 0.120 c | 0.75 | 2930 ± 20 b | 1520 ± 10 b | 204 |
| HVHP | PVDF | 130 | 0.240 c | 0.75 | 6130 ± 50 b | 2080 ± 20 b | 105 |
| FGLP | PTFE/PE | 130 a | 0.145 c | 0.70 | 7930 ± 50 b | 560 ± 6 b | 208 |
| FHLP | PTFE/PE | 175 a | 0.210 c | 0.85 | 10,880 ± 80 b | 1170 ± 10 b | 124 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-M.; Lee, S. Influence of Hydraulic Pressure on Performance Deterioration of Direct Contact Membrane Distillation (DCMD) Process. Membranes 2019, 9, 37. https://doi.org/10.3390/membranes9030037
Park S-M, Lee S. Influence of Hydraulic Pressure on Performance Deterioration of Direct Contact Membrane Distillation (DCMD) Process. Membranes. 2019; 9(3):37. https://doi.org/10.3390/membranes9030037
Chicago/Turabian StylePark, Seung-Min, and Sangho Lee. 2019. "Influence of Hydraulic Pressure on Performance Deterioration of Direct Contact Membrane Distillation (DCMD) Process" Membranes 9, no. 3: 37. https://doi.org/10.3390/membranes9030037
APA StylePark, S.-M., & Lee, S. (2019). Influence of Hydraulic Pressure on Performance Deterioration of Direct Contact Membrane Distillation (DCMD) Process. Membranes, 9(3), 37. https://doi.org/10.3390/membranes9030037






