Factors Limiting the Apparent Hydrogen Flux in Asymmetric Tubular Cercer Membranes Based on La27W3.5Mo1.5O55.5−δ and La0.87Sr0.13CrO3−δ
Abstract
:1. Introduction
2. Materials and Methods
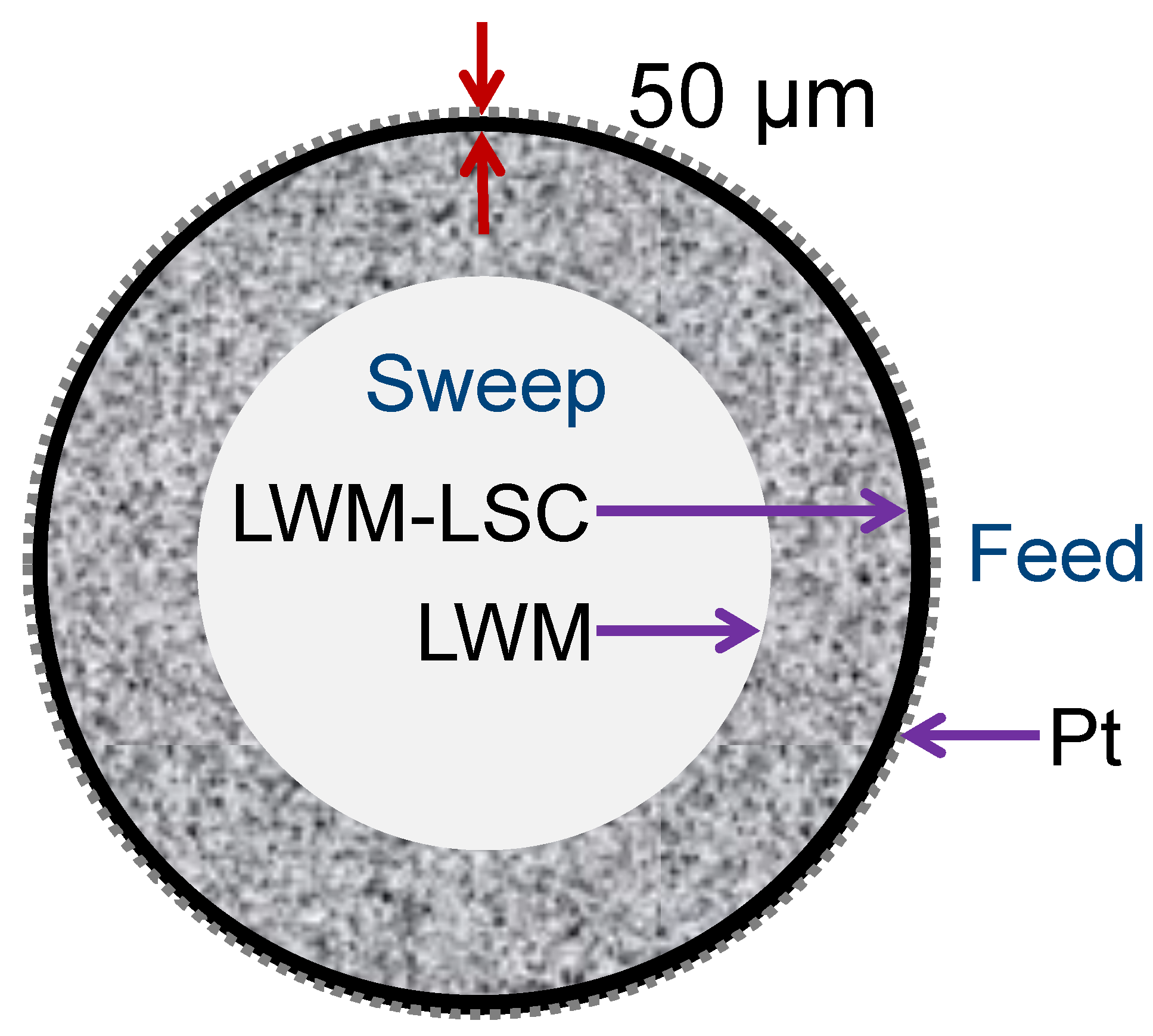
2.1. Fabrication of Asymmetric LWM–LSC Tubular Membranes
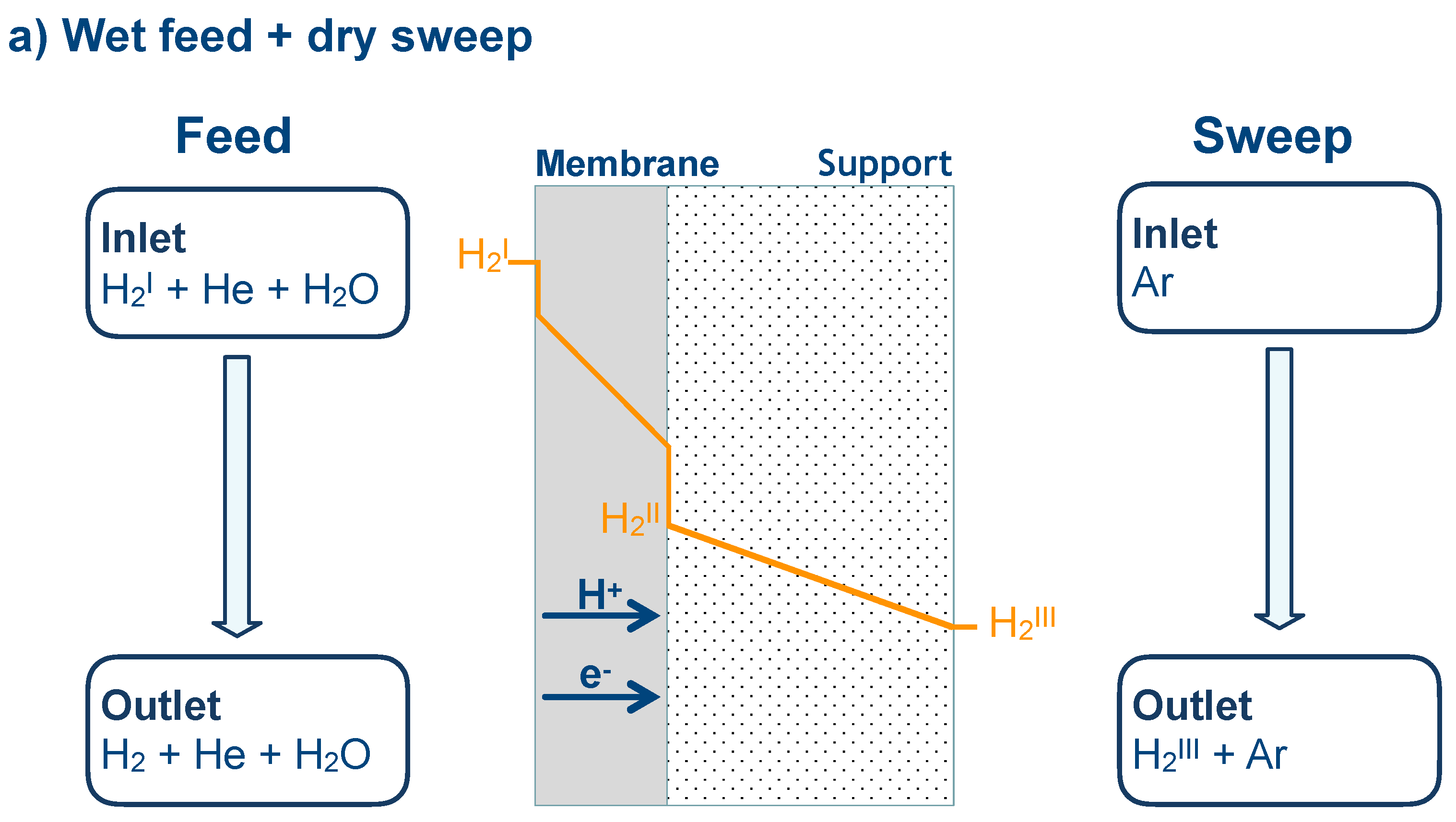
2.2. Hydrogen Permeation Measurements
2.3. Numerical Modeling for Gas Transport in Porous Support
3. Results and Discussion
3.1. Characterization of Tubular Membranes
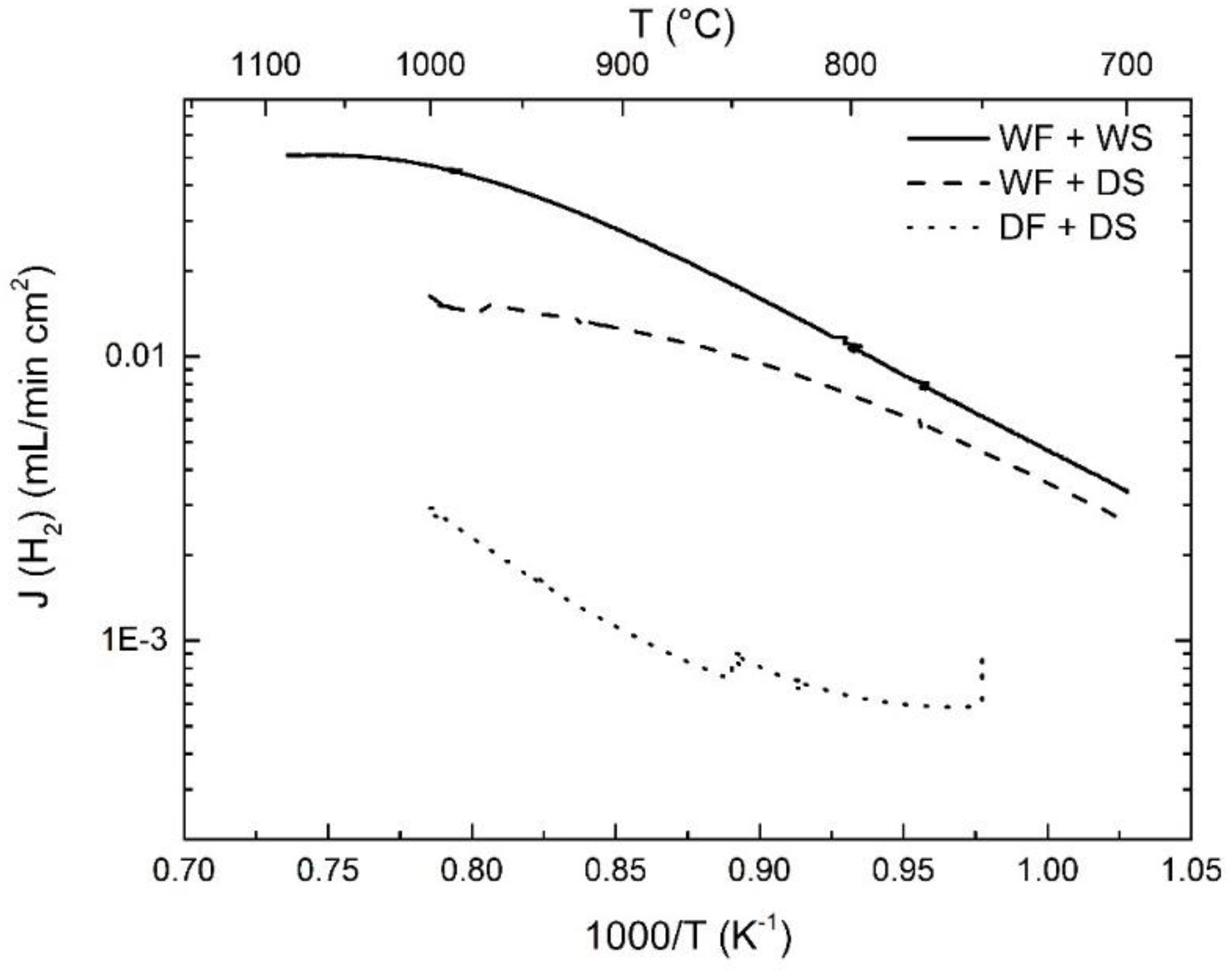
3.2. Hydrogen Permeation
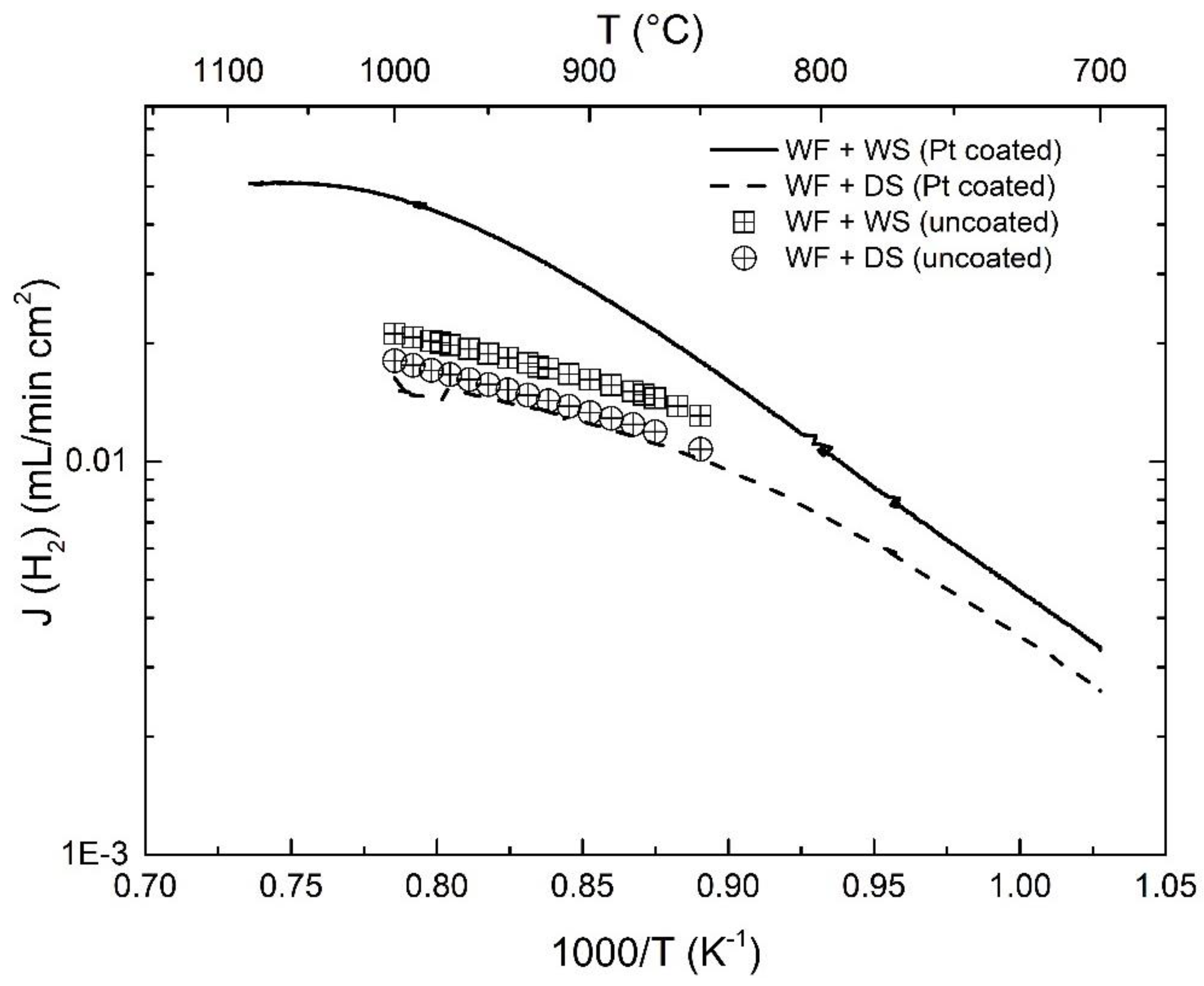
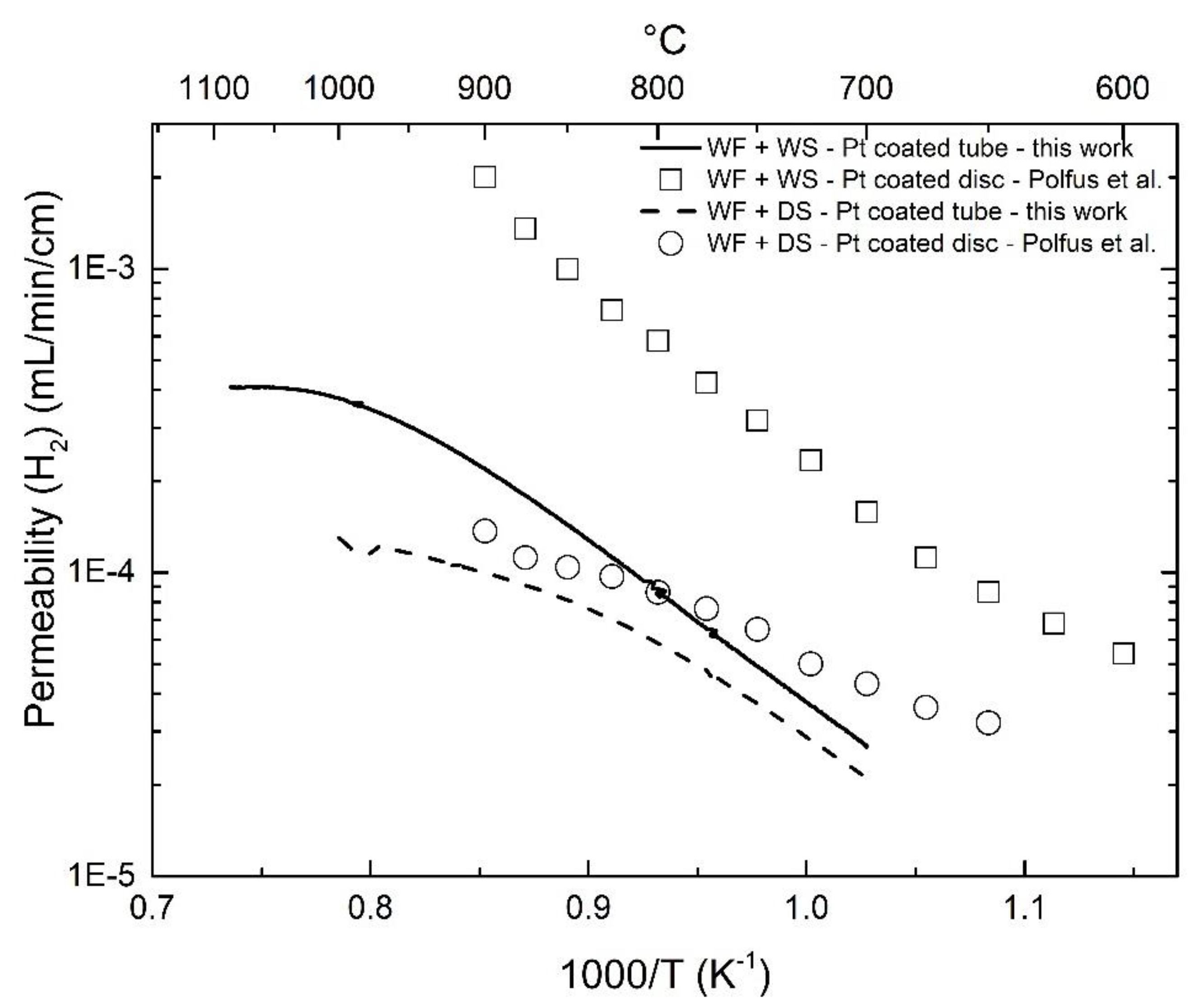
3.3. Effect of Pt-Coating and Comparison with Disc-Shaped Membranes
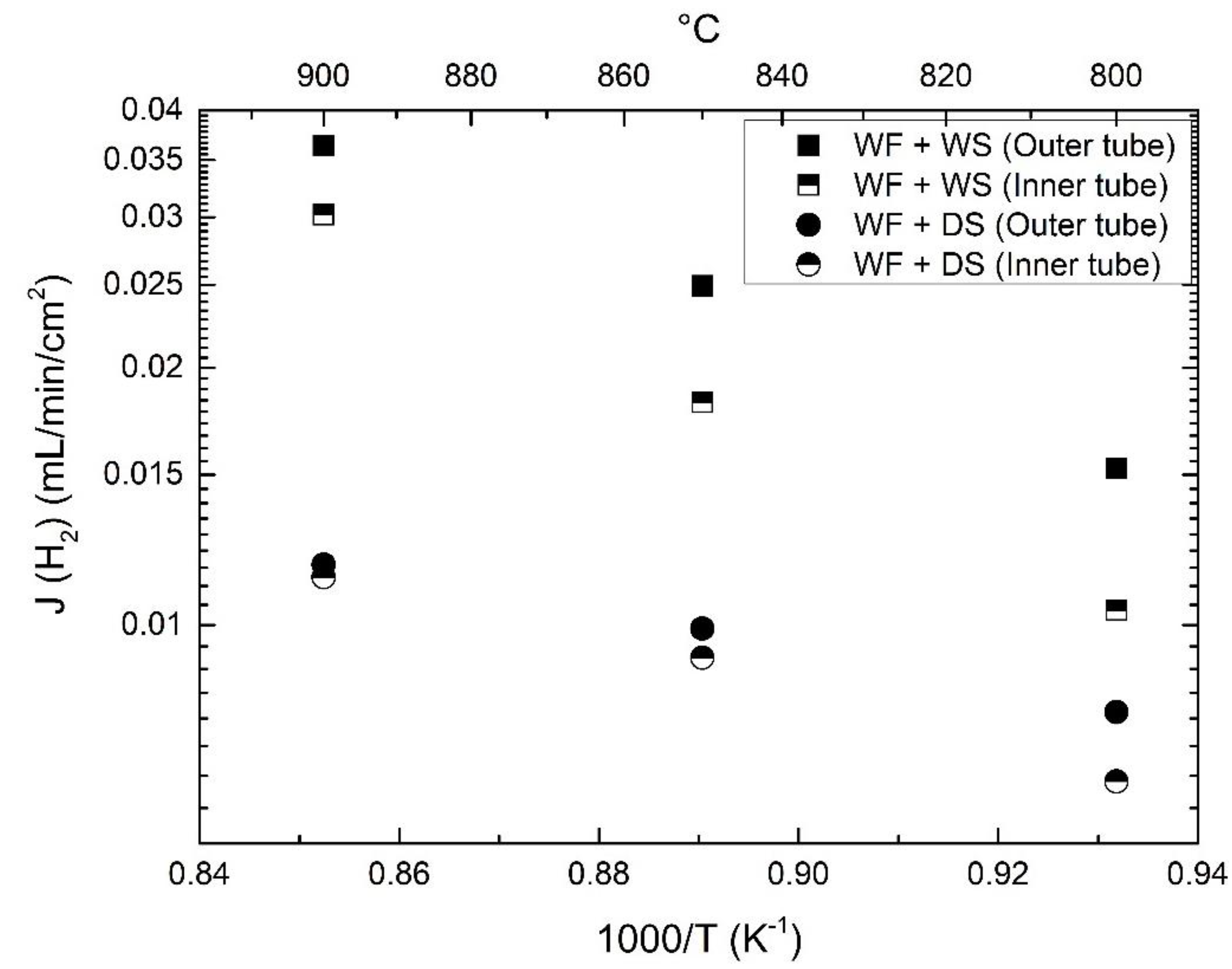
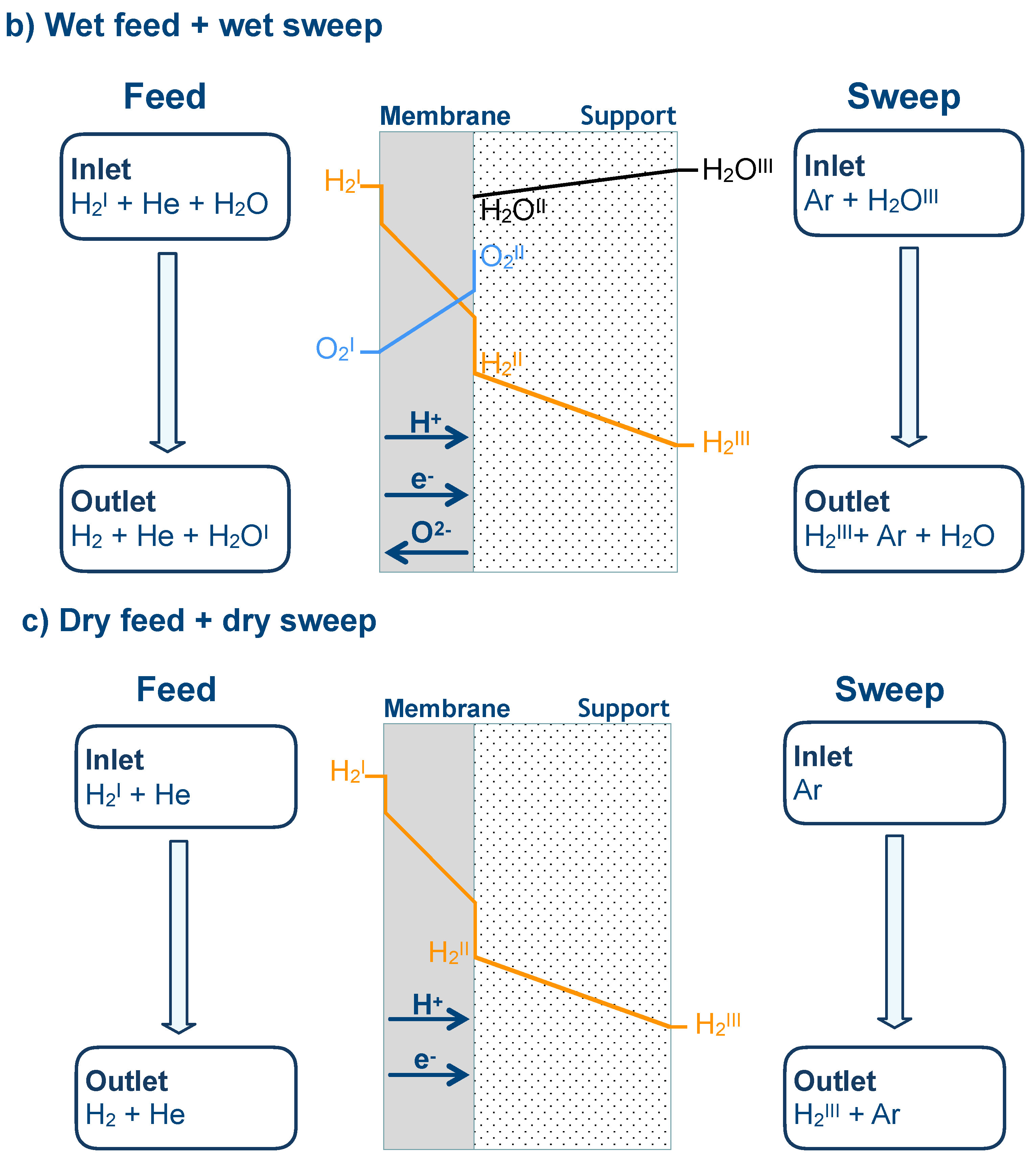
3.4. Effects of Water Splitting
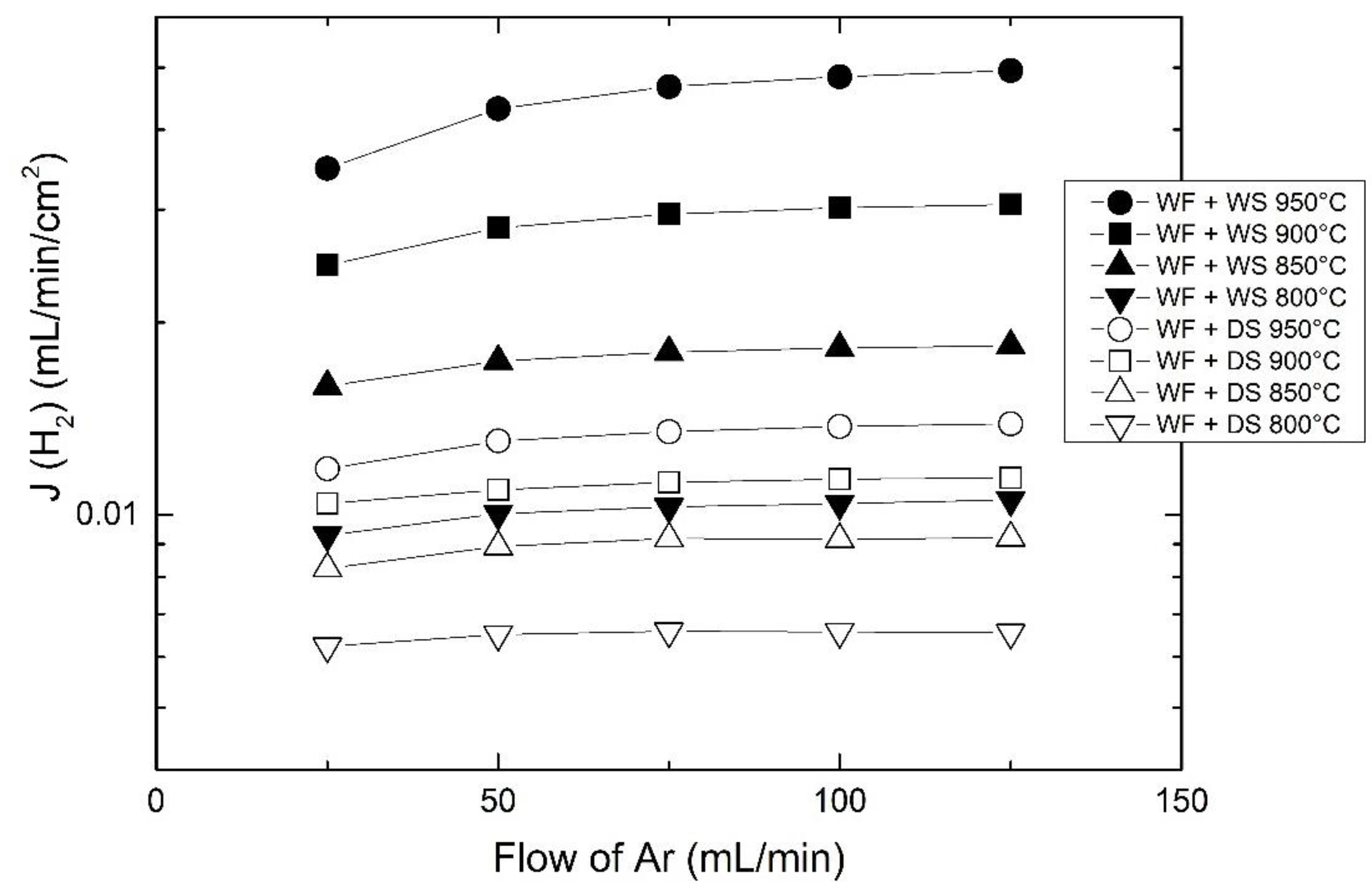
3.5. Effects of Flow and Porous Support
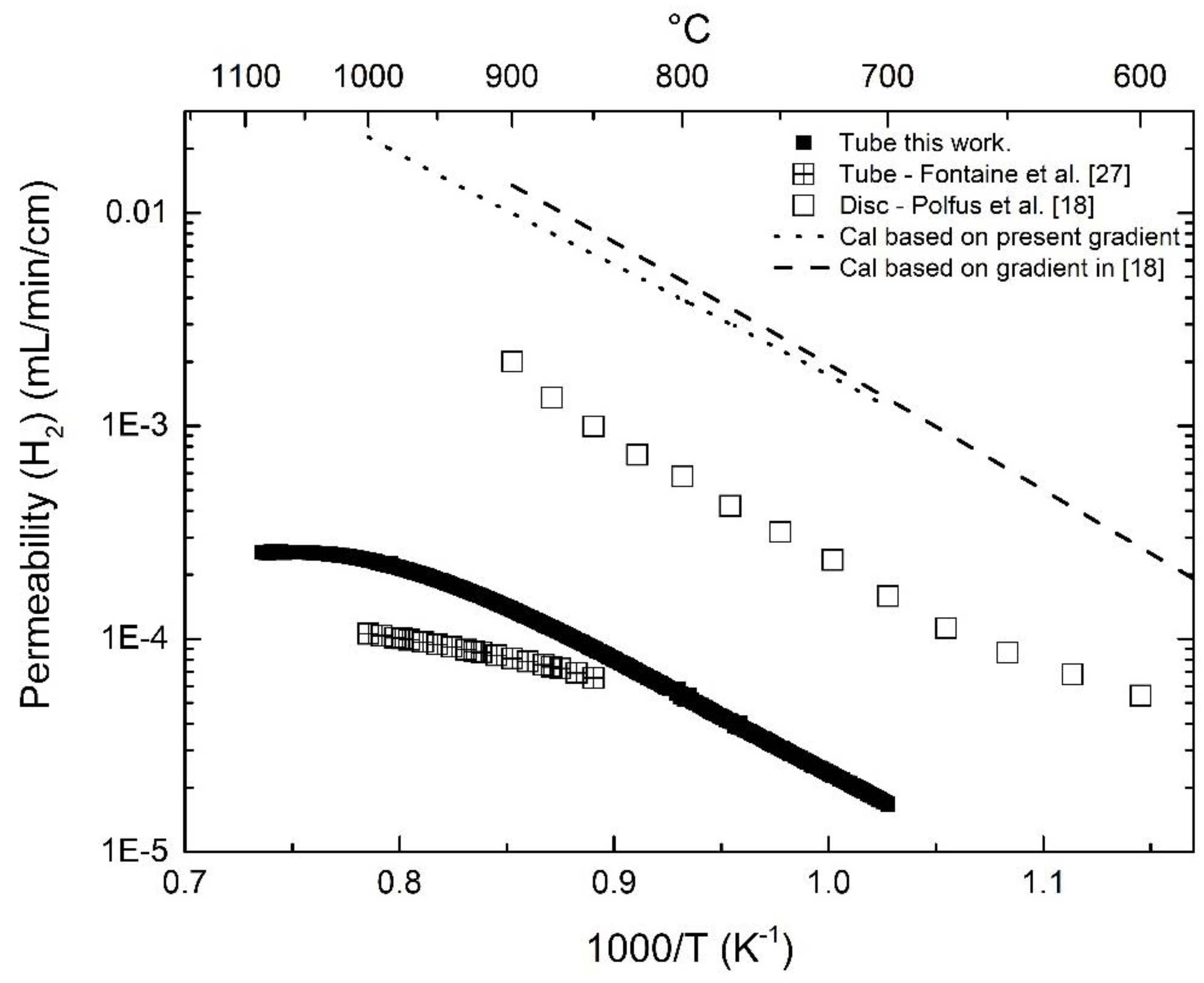
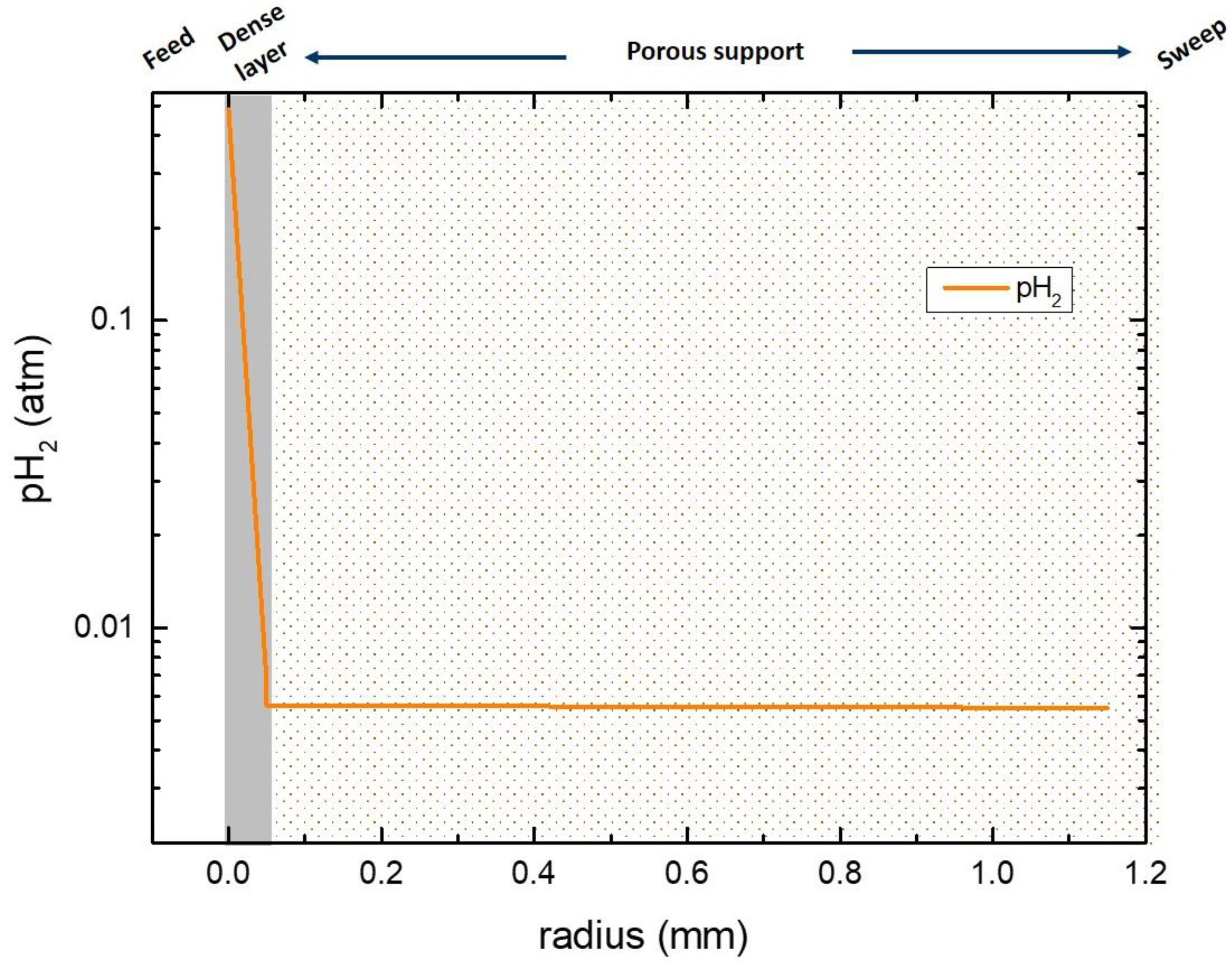
3.6. Numerical Simulation of Gas Transport Across the Membrane
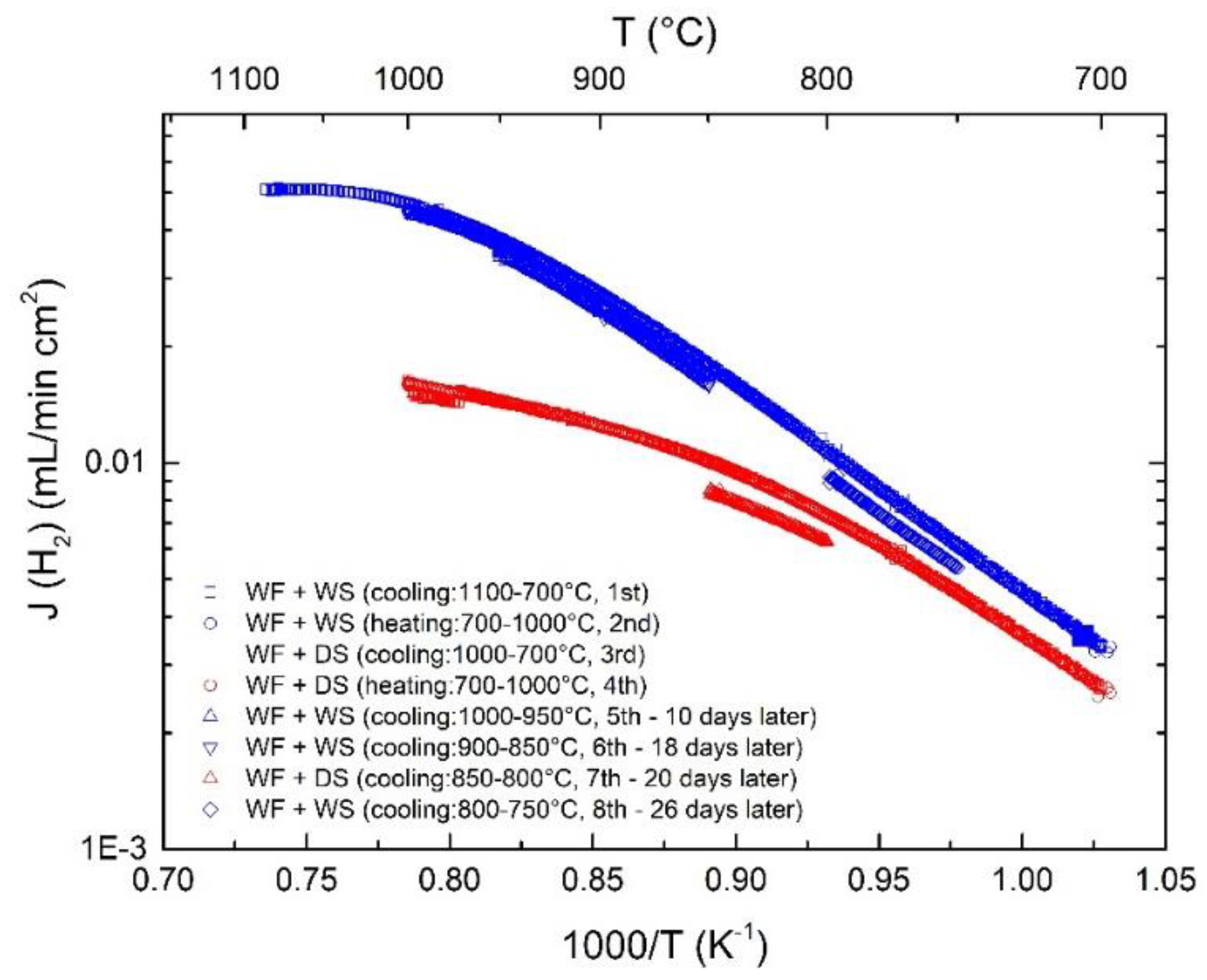
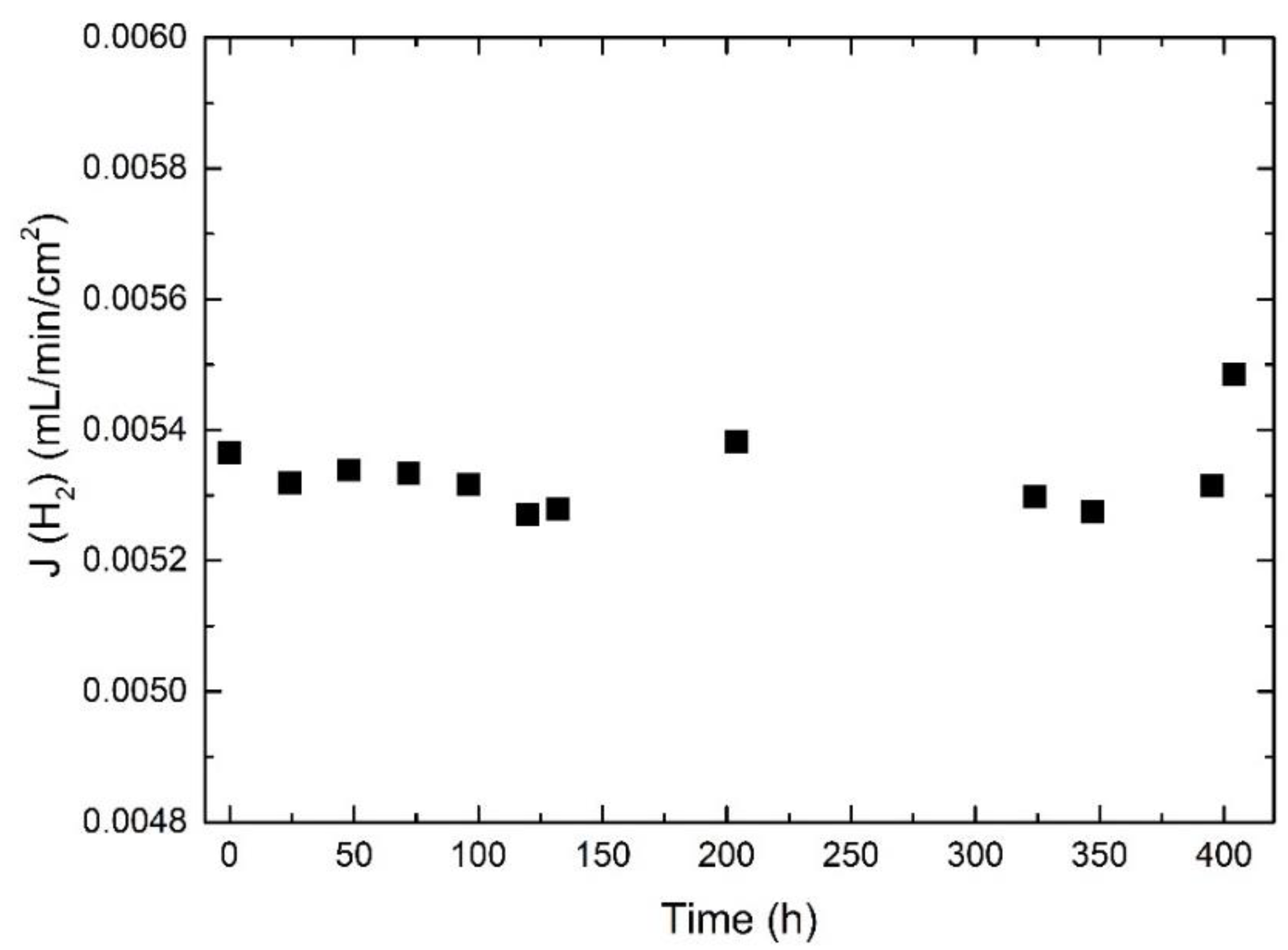
3.7. Long-Term Stability
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, J.; Yoon, H.; Oh, T.K.; Wachsman, E.D. High temperature SrCe0.9Eu0.1O3−δ proton conducting membrane reactor for H2 production using the water–gas shift reaction. Appl. Catal. B Environ. 2009, 92, 234–239. [Google Scholar]
- Li, L.; Borry, R.W.; Iglesia, E. Reaction-transport simulations of non-oxidative methane conversion with continuous hydrogen removal—Homogeneous–Heterogeneous reaction pathways. Chem. Eng. Sci. 2001, 56, 1869–1881. [Google Scholar] [CrossRef]
- Deibert, W.; Ivanova, M.E.; Baumanna, S.; Guillon, O.; Meulenberg, W.A. Ion-conducting ceramic membrane reactors for high-temperature applications. J. Membr. Sci. 2017, 543, 79–97. [Google Scholar] [CrossRef]
- Ockwig, N.W.; Nenoff, T.M. Membranes for hydrogen separation. Chem. Rev. 2007, 107, 4078–4110. [Google Scholar] [CrossRef] [PubMed]
- Peters, T.A.; Kaleta, T.; Stange, M.; Bredesen, R. Hydrogen transport through a selection of thin Pd-alloy membranes: Membrane stability, H2S inhibition, and flux recovery in hydrogen and simulated WGS mixtures. Catal. Today 2012, 193, 8–19. [Google Scholar] [CrossRef]
- Norby, T.; Haugsrud, R. Membranes for Energy Conversion; John Wiley & Sons: Weinheim, Germany, 2008; pp. 169–216. [Google Scholar]
- Ivanova, M.E.; Deibert, W.; Marcano, D.; Escolástico, S.; Mauer, G.; Meulenberg, W.A.; Bram, M.; Serra, J.M.; Vassen, R.; Guillon, O. Lanthanum tungstate membranes for H2 extraction and CO2 utilization: Fabrication strategies based on sequential tape casting and plasma-spray physical vapor deposition. Sep. Purif. Technol. 2019, 219, 100–112. [Google Scholar] [CrossRef]
- Mather, G.C.; Islam, M.S. Defect and dopant properties of the SrCeO3-based proton conductor. Chem. Mater. 2005, 17, 1736–1744. [Google Scholar] [CrossRef]
- Iwahara, H.; Yajima, T.; Hibino, T.; Ushida, H. Performance of Solid Oxide Fuel Cell Using Proton and Oxide Ion Mixed Conductors Based on BaCe1−xSmxO3−α. J. Electrochem. Soc. 1993, 140, 1687–1691. [Google Scholar] [CrossRef]
- Zuo, C.; Lee, T.H.; Dorris, S.E.; Balachandran, U.; Liu, M. Composite Ni–Ba (Zr0.1Ce0.7Y0.2) O3 membrane for hydrogen separation. J. Power Sour. 2006, 159, 1291–1295. [Google Scholar] [CrossRef]
- Zhang, G.; Dorris, S.E.; Balachandran, U.; Liu, M. Interfacial resistances of Ni–BCY mixed-conducting membranes for hydrogen separation. Solid State Ionics 2003, 159, 121–134. [Google Scholar] [CrossRef]
- Weirich, M.; Gurauskis, J.; Gil, V.; Wiik, K.; Einarsrud, M. Preparation of lanthanum tungstate membranes by tape casting technique. Int. J. Hydrogen Energy 2012, 37, 8056–8061. [Google Scholar] [CrossRef]
- Deibert, W.; Ivanova, M.E.; Meulenberg, W.A.; Vaßen, R.; Guillon, O. Preparation and sintering behaviour of La5.4WO12−δ asymmetric membranes with optimised microstructure for hydrogen separation. J. Membr. Sci. 2015, 492, 439–451. [Google Scholar] [CrossRef]
- Escolástico, S.; Stournari, V.; Malzbender, J.; Haas-Santo, K.; Dittmeyer, R.; Serra, J.M. Chemical stability in H2S and creep characterization of the mixed protonic conductor Nd5.5WO11.25-δ. Int. J. Hydrogen Energy 2018, 43, 8342–8354. [Google Scholar] [CrossRef]
- Haugsrud, R. Defects and transport properties in Ln6WO12 (Ln= La, Nd, Gd, Er). Solid State Ionics 2007, 178, 555–560. [Google Scholar] [CrossRef]
- Amsif, M.; Magrasό, A.; Marrero-Lόpez, D.; Ruiz-Morales, J.C.; Canales-Vάzquez, J.; Núnez, P. Mo-Substituted Lanthanum Tungstate La28–yW4+ yO54+δ: A Competitive Mixed Electron–Proton Conductor for Gas Separation Membrane Applications. Chem. Mater. 2012, 24, 3868–3877. [Google Scholar] [CrossRef]
- Escolastico, S.; Seeger, J.; Roitsch, S.; Ivanova, M.; Meulenberg, W.A.; Serra, J. Enhanced H2 separation through mixed proton–electron conducting membranes based on La5.5W0.8M0.2O11.25−δ. ChemSusChem 2013, 6, 1523–1532. [Google Scholar] [CrossRef] [PubMed]
- Polfus, J.M.; Xing, W.; Fontaine, M.; Denonville, C.; Henriksen, P.P.; Bredesen, R. Hydrogen separation membranes based on dense ceramic composites in the La27W5O55 5–LaCrO3 system. J. Memb. Sci. 2015, 479, 39–45. [Google Scholar] [CrossRef]
- Escolastico, S.; Cecilia, S.; Kjølseth, C.; Serra, J.M. Outstanding hydrogen permeation through CO2-stable dual-phase ceramic membranes. Energy Environ. Sci. 2014, 7, 3736–3746. [Google Scholar] [CrossRef]
- Larring, Y.; Vigen, C.; Ahouanto, F.; Fontaine, M.L.; Peters, T.; Smith, J.B.; Norby, T.; Bredesen, R. Investigation of La1−xSrxCrO3−∂(x~0.1) as membrane for hydrogen production. Membranes 2012, 2, 665–686. [Google Scholar] [CrossRef] [PubMed]
- Vøllestad, E.; Vigen, C.K.; Magrasó, A.; Haugsrud, R. Hydrogen permeation characteristics of La27Mo1.5W3.5O55.5. J. Membr. Sci. 2014, 461, 81–88. [Google Scholar] [CrossRef]
- Li, Z.; Kjølseth, C.; Haugsrud, R. Hydrogen permeation, water splitting and hydration kinetics in Nd5.4Mo0.3W0.7O12−δ. J. Membr. Sci. 2015, 476, 105–111. [Google Scholar] [CrossRef]
- Polfus, J.M.; Li, Z.; Xing, W.; Sunding, M.F.; Walmsley, J.C.; Fontaine, M.; Henriksen, P.P.; Bredesen, R. Chemical stability and H2 flux degradation of cercer membranes based on lanthanum tungstate and lanthanum chromite. J. Memb. Sci. 2016, 503, 42–47. [Google Scholar] [CrossRef]
- Deibert, W.; Schulze-Küppers, F.; Forster, E.; Ivanova, M.E.; Müller, M.; Meulenberg, W.A. Stability and sintering of MgO as a substrate material for Lanthanum Tungstate membranes. J. Eur. Ceram. Soc. 2017, 37, 671–677. [Google Scholar] [CrossRef]
- Gellings, P.J.; Bouwmeester, H.J.M. The CRC Handbook of Solid State Electrochemistry; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Xing, W.; Fontaine, M.L.Z.; Polfus, J.M.; Larring, Y.; Denonville, C.; Nonnet, E.; Stevenson, A.; Henriksen, P.P.; Bredesen, R. Asymmetric tubular CaTi0 6Fe0.15Mn0.25O3-δ membranes: Membrane architecture and long-term stability. J. Memb. Sci. 2018, 548, 372–379. [Google Scholar] [CrossRef]
- Fontaine, M.; Denonville, C.; Li, Z.; Xing, W.; Polfus, J.M.; Kvello, J.; Graff, J.S.; Dahl, P.I.; Henriksen, P.P.; Bredesen, R. Fabrication and H2 flux measurement of asymmetric La27W3.5Mo1.5O55.5-δ−La0.87Sr0.13CrO3- membranes. J. Eur. Ceram. Soc. 2018, 38, 1695–1701. [Google Scholar] [CrossRef]
- Mason, E. Malinauskas, Gas Transport in Porous Media: The Dusty-Gas Model; American Elsevier: New York, NY, USA, 1983. [Google Scholar]
- Zhu, H.; Kee, R.; Janardhanan, V.; Deutschmann, O.; Goodwin, D. Modeling elementary heterogeneous chemistry and electrochemistry in solid-oxide fuel cells. J. Electrochem. Soc. 2005, 152, A2427–A2440. [Google Scholar] [CrossRef]

| Name | Value |
|---|---|
| Length of the support (mm) | 1.1 |
| Porosity | 0.46 |
| Tortuosity | 3 |
| Pore size (µm) | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Polfus, J.M.; Xing, W.; Denonville, C.; Fontaine, M.-L.; Bredesen, R. Factors Limiting the Apparent Hydrogen Flux in Asymmetric Tubular Cercer Membranes Based on La27W3.5Mo1.5O55.5−δ and La0.87Sr0.13CrO3−δ. Membranes 2019, 9, 126. https://doi.org/10.3390/membranes9100126
Li Z, Polfus JM, Xing W, Denonville C, Fontaine M-L, Bredesen R. Factors Limiting the Apparent Hydrogen Flux in Asymmetric Tubular Cercer Membranes Based on La27W3.5Mo1.5O55.5−δ and La0.87Sr0.13CrO3−δ. Membranes. 2019; 9(10):126. https://doi.org/10.3390/membranes9100126
Chicago/Turabian StyleLi, Zuoan, Jonathan M. Polfus, Wen Xing, Christelle Denonville, Marie-Laure Fontaine, and Rune Bredesen. 2019. "Factors Limiting the Apparent Hydrogen Flux in Asymmetric Tubular Cercer Membranes Based on La27W3.5Mo1.5O55.5−δ and La0.87Sr0.13CrO3−δ" Membranes 9, no. 10: 126. https://doi.org/10.3390/membranes9100126
APA StyleLi, Z., Polfus, J. M., Xing, W., Denonville, C., Fontaine, M.-L., & Bredesen, R. (2019). Factors Limiting the Apparent Hydrogen Flux in Asymmetric Tubular Cercer Membranes Based on La27W3.5Mo1.5O55.5−δ and La0.87Sr0.13CrO3−δ. Membranes, 9(10), 126. https://doi.org/10.3390/membranes9100126






