Modeling Fixed Bed Membrane Reactors for Hydrogen Production through Steam Reforming Reactions: A Critical Analysis
Abstract
1. Introduction
- Momentum transport
- Mass transport by convection, dispersion and permeation across the membrane of different components which are produced/consumed by chemical reactions
- Energy transport by convection, conduction, exchange between permeate and retentate, and exchange between the reactor and its wall, as well as the heat generation due to the chemical reactions
- a top-down approach, where the complete model is gradually simplified by removing the description of all phenomena that can be considered to be unimportant
- a bottom-up approach, in which the most simple model is initially considered, and all the significant phenomena are gradually added
- the transport phenomena described (e.g., isothermal vs. non-isothermal models)
- the dimension of the problem (e.g., 1D vs. 2D models)
- the transport mechanisms considered (e.g., neglecting dispersion with respect to convection)
- the detail used in the description of each mechanism (e.g., assuming the same diffusion coefficient for all components vs. accounting for differences in diffusion coefficient values)
2. Reactor Configurations
- lower pressure drops due to a void fraction that is almost twice the value achieved in traditional packed beds;
- high surface area to volume ratios, leading to enhanced rates of heat and mass transfer and therefore higher reactions effectiveness factors;
- increased turbulence and convective heat transfer
3. Description of Reactor Performance
- Reactant conversion: as in the case of traditional reactors, this parameter measures the extent of completion of the reaction. In the case of membrane reactors, their efficiency may be quantified by determining the excess conversion with respect to the equilibrium value that one would obtain from the feed at the same temperature and pressure conditions, as was done, for example, in [23].
- Permeate flow rate: this is a measure of the amount of pure hydrogen produced and is often the design parameter. The value of the total permeate flow rate intrinisically accounts for the efficiency of both the separation and the reaction, albeit without providing information on the relative importance of the two.
- Yield: the yield is generally defined as the ratio between the amount of pure hydrogen produced, i.e., the permeate, and the reactant feed flow rate. Its significance is esentially the same as that of the permeate flow rate with the additional advantage that it allows an easier comparison of systems characterized by different feed flow rates. The maximum value that it may reach is the stoichiometric ratio between hydrogen and the reference reactant.
- Recovery: the recovery is defined as the ratio between the amount of pure hydrogen permeating across the membrane and the amount of hydrogen produced by the reaction. This parameter is, in effect, a measure of the efficiency of the membrane separation in that it provides no information on the extent of reaction completion. Its upperbound is 1 if no hydrogen is present in the feed.
- Separator-based yield: This parameter has been introduced in [54,55] and is defined as the ratio between the hydrogen permeate flow rate and the inlet hydrogen flow rate. Naturally, this parameter can only be defined if hydrogen is already present in the feed and is particularly significant if the feed is the product of a pre-reactor in which equilibrium conditions have been reached. Under these conditions, its maximum value is the inverse of the equilibrium conversion of the reactant. This parameter is particularly interesting because, similarly to the permeate flow rate or yield, it provides information on the efficiency of both reaction and separation, while giving some insight into the relative weight of the two. In the absence of a reaction its maximum value would be equal to 1, and the degree with which it exceeds the value of 1 is indicative of the extent of the reaction.
4. Equations of Change
- The momentum balance may be described through the modified Navier–Stokes equation for a fixed bed porous medium. The terms on the r.h.s. of Equation (1) refer to (a) pressure gradients, (b) bed permeability and inertial losses, (c) viscous and inertial drag forces imposed by catalyst pore walls on the fluid, and (d) volumetric forces acting on the fluid. The friction coefficient, , is given by Equation (2) and the stress term is given by Newton’s Equation (3) for a compressible fluid. At the steady state, the momentum balance may simplify to Darcy’s law with the bed permeability expressed through the Kozeny–Carman equation. Works on membrane reactor modeling have adopted both approaches, with a majority resorting to the former (see [1,56,57] and other works by the same authors) rather than the latter (see [7,58,59] and other works by the same authors).
- Mass balance equations are reported in terms of mass units, in order to simplify the coupling with momentum equation. Sometimes, these equations are written assuming the product to be constant. Indeed, the values of the terms and , appearing in the dispersion tensor, depend on the molecular diffusion coefficient, the gas velocity and the characteristics of the packed bed, while varies as discussed in detail below. A thorough review of transversal and longitudinal dispersion in packed beds is presented in the work of Delgado [60]. As for the boundary conditions, at the reactor inlet two choices are possible: the Danckwerts condition, which meets the requirement of flux continuity, or the condition of concentration continuity. The consensus is larger for the outlet boundary condition, where a purely convective flux is assumed. The radial boundary conditions are of impermeability on one of the walls and hydrogen permeation on the other. For all other components, impermeability is imposed on both walls, assuming that the membrane presents infinite selectivity towards hydrogen. The different forms in which the hydrogen permeating flux may be described are discussed in greater detail in Section 7.2.
- Some authors have proposed the use of a Stefan–Maxwell-like expression to describe the dispersive flux [21], thereby making the implicit assumption that the balance of forces on gas molecules, from which this expression derives, applies to dispersion as well as molecular diffusion. However, it is worth observing that existing theoretical approaches quantifying dispersion in periodic and disordered media are grounded on a diluted assumption for the transported species [61,62,63]. Since semi-empirical correlations used to interpret experimental data are implicitly or explicitly based on these theoretical results, the validity of the Stefan–Maxwell constitutive equation at the Darcy scale should be further investigated.
- In many cases, mass balance equations are written in molar units, as reported in Table 3. It is worth noting that in this case, the mass balance equation may be simplified by assuming to be constant, provided that isothermal conditions can be assumed; furthermore from a rigorous point of view, should be the molar average velocity of the gas mixture, which is, in general, different from the mass average velocity used in the momentum equation. Even if the difference between the velocity may be significant for mixtures containing components with large differences in the molecular weight (in our systems carbon dioxide (MW 44) and hydrogen (MW 2)), it is likely that the errors are of the same order of magnitude of the uncertainties in the evaluation of the dispersion coefficients.
- The reaction rates inserted in the mass balance equation must be intended as effective reaction rates per unit volume of the catalyst bed. Therefore, in the presence of significant intraparticle or interparticle mass or heat transport limitations, a reduction of the efficiency factor must be accounted for. The efficiency factor is explicitly accounted for in some models (see for example [64]). It is worth noting that the characteristic dimension of the catalyst strongly affects the transport limitations, as well as affecting the pressure drop in the catalytic bed, which in turn results in a reduction of the driving force for hydrogen permeation. More specifically, large catalyst sizes result in a low efficiency factor, but also in low head losses in the packed bed.
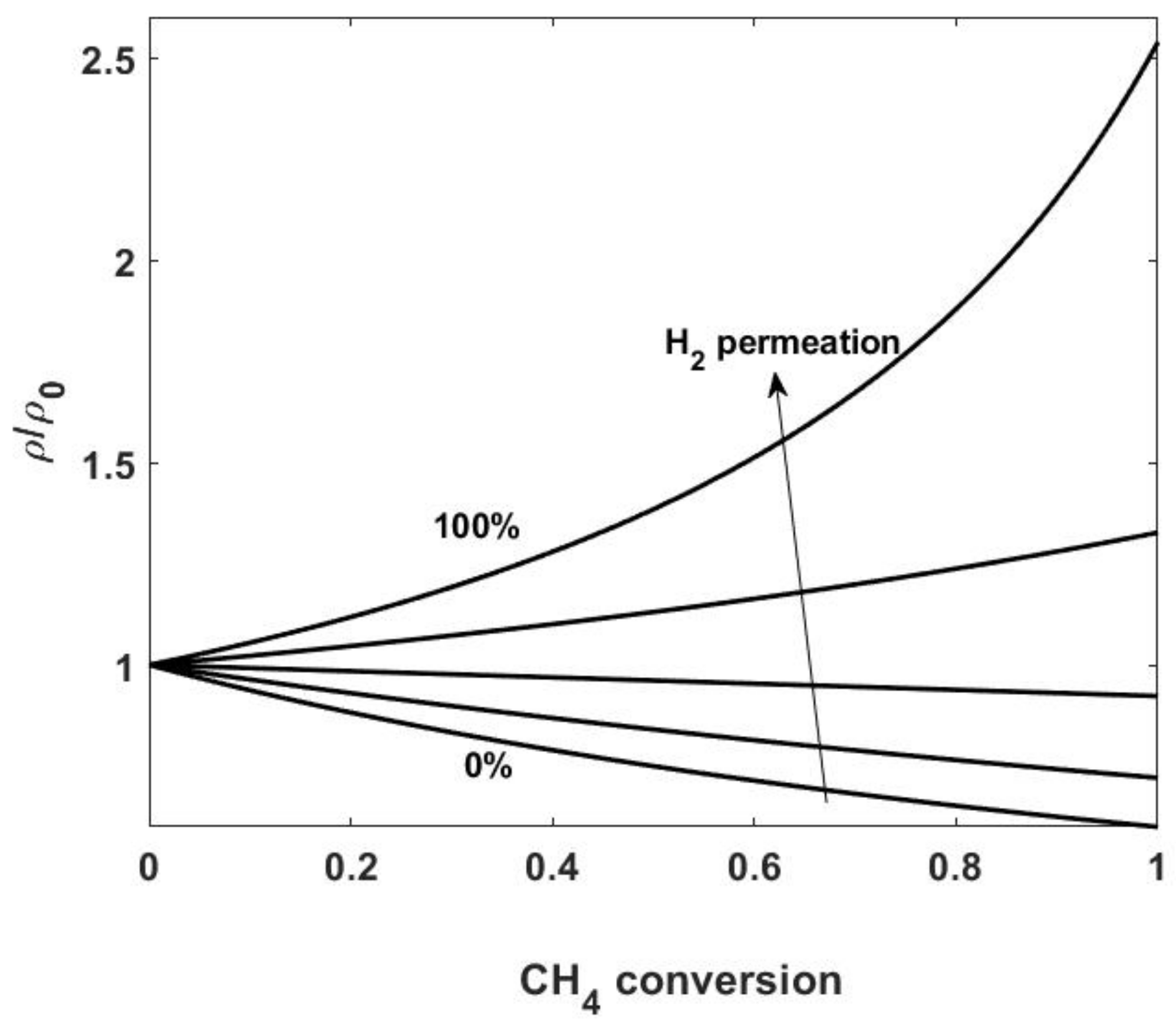
- To evaluate the possibility of simplifying the mass balance equations, it is useful to discuss how the mass or molar density varies along the reactor, depending on changes in pressure, temperature and gas composition. Usually, in such a reactor, no large head losses occur and pressure is almost constant. Therefore, the molar density, c, only depends on temperature changes; in other words, in isothermal or almost isothermal conditions, c can be assumed to be constant. As for the mass density, , changes in gas composition result in its variation, even under constant pressure and temperature conditions. These variations can be significant, especially in the reforming process, where low molecular weight compounds (hydrogen) are obtained. We also remark that the situation is completely different for conventional and membrane reactors: in fact, if the hydrogen produced by the reforming remains in the reactor, mass density decreases as the reaction proceeds; on the other hand, in a membrane reactor, where hydrogen is continuously removed as the current flows downstream the reactor, a significant increase in the mass density may be observed (see Figure 2 for methane reforming). Note that in the evaluation of integral quantities, changes in the mass density with composition generally have a negligible effect. On the other hand, by neglecting density changes, the resulting concentration profiles may suffer from inaccuracies that do not enable a correct quantification of effects such as concentration polarization and membrane inhibition (see Section 7.2). The choice of accounting for density changes therefore depends on the scope of the study and should be made on a case-by-case basis.
- As regards the energy transport equation, reported in Table 4, we only remark that terms related to the change of pressure, to the viscous effects, and to the dispersive fluxes are neglected. Values of the effective heat conductivity and of the heat transfer coefficients (appearing in and ) depend on the properties of the gas and of the catalyst bed, and change sizeably depending on whether the catalyst is supported on pellets or solid foams. Several correlations have been reported in the literature [49,65,66] and are discussed more thoroughly in Section 7.3.
5. 1D Models
6. 2D Models
7. Constitutive Equations
7.1. Reaction Rate Expressions
7.1.1. Methane Steam Reforming
7.1.2. Ethanol Steam Reforming
7.1.3. Methanol Steam Reforming
7.2. Hydrogen Permeating Flux
7.3. Heat Exchange with the Reactor Wall and Permeate
8. Some Literature 1D Models
9. Some Literature 2D Models
- negligible pressure drops
- negligible axial dispersion
- negligible radial convective mass transfer
- negligible heat and mass transfer resistances between the gas and catalyst
10. Models with Different Degrees of Complexity
- Equilibrium composition of the inlet feed
- Zero hydrogen partial pressure in the permeate
- Uniform temperature
- Negligible membrane inhibition
- Infinitely fast reaction (i.e., ) and hydrogen permeation limited by transport across the membrane (case 1)
- Infinitely fast reaction and hydrogen permeation limited by transport in the packed bed (case 2)
- Infinitely slow reaction (i.e., ) and hydrogen permeation limited by transport across the membrane (case 3)
- Infinitely slow reaction and hydrogen permeation limited by transport in the packed bed (case 4)
- Determine the value of the dimensionless groups (, , );
- Evaluate the permeate flow rate as a function of pressure with Equation (113) (membrane-controlled regime);
- Evaluate the permeate flow rate as a function of pressure with Equation (122) (transport-controlled regime);
- Draw on the same graph the curves depicting the permeate flow rate as a function of pressure obtained in steps 2 and 3;
- The “actual” permeate flow rate will be given, for any pressure value, by the lowest of the two curves
11. Concluding Remarks and Directions of Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| geometric ratio | |
| specific heat or | |
| d | characteristic dimension of packed bed particles |
| radial dispersion coefficient | |
| axial dispersion coefficient | |
| diffusion coefficient | |
| effective dispersion tensor | |
| f | average molar weight |
| hydrogen mass flux through the membrane | |
| hydrogen molar flux through the membrane | |
| k | reaction rate constant |
| effective heat conductivity | |
| equilibrium constant | |
| L | reactor length |
| unit vector normal to the membrane surface | |
| P | pressure |
| partial pressure of the i-th component | |
| outlet pressure | |
| reference pressure | |
| membrane permeability | |
| heat flux between catalyst and reactor wall | |
| heat flux between catalyst and permeate | |
| r | radial coordinate |
| volume-specific mass rate of production of the i-th component | |
| gas constant | |
| inner reactor radius | |
| outer reactor radius | |
| volume-specific molar rate of methane consumption | |
| T | temperature |
| U | inlet gas velocity |
| heat transfer coefficient between permeate and retentate | |
| heat transfer coefficient between wall and retentate | |
| mass average velocity | |
| molar average velocity | |
| molar weight of the i-th component | |
| z | axial coordinate |
| Greek symbols | |
| dimensionless outlet pressure | |
| ratio between characteristic and inlet velocities | |
| dimensionless permeability parameter | |
| membrane thickness | |
| proximity to reaction equilibrium | |
| packed bed permeability | |
| gas viscosity | |
| dimensionless permeate flow rate | |
| gas density | |
| density of the i-th component | |
| geometric ratio, | |
| packed bed tortuosity factor | |
| stoichiometric coefficient of the i-th component | |
| intrinsic membrane permeability | |
| mass fraction of the i-th component | |
| linear combination of hydrogen and methane densities | |
| hydrogen recovery (permeated hydrogen/produced hydrogen) | |
| separator-base yield (permeated hydrogen/inlet hydrogen) | |
| inhibition factor | |
| Dimensionless parameters | |
| Damkholer number | |
| modified Damkholer number | |
| dimensionless radial dispersion | |
| dimensionless dispersion tensor | |
| characteristic length of permeation | |
| Peclet number | |
| molecular Peclet number | |
| effective radial Peclet number | |
| effective axial Peclet number | |
| Reynolds number | |
| Schmidt number | |
| Subscripts | |
| c | carbon dioxide |
| h | hydrogen |
| m | methane |
| w | water |
| i | i-th component |
References
- Castro-Dominguez, B.; Mardilovich, I.; Ma, L.; Ma, R.; Dixon, A.; Kazantzis, N.; Ma, Y. Integration of methane steam reforming and water gas shift reaction in a Pd/Au/Pd-based catalytic membrane reactor for process intensification. Membranes 2016, 6, 44. [Google Scholar] [CrossRef] [PubMed]
- Roses, L.; Manzolini, G.; Campanari, S.; De Wit, E.; Walter, M. Techno-economic Assessment of Membrane Reactor Technologies for Pure Hydrogen Production for Fuel Cell Vehicle Fleets. Energy Fuels 2013, 27, 4423–4431. [Google Scholar] [CrossRef]
- Brunetti, A.; Barbieri, G.; Drioli, E. Integrated membrane system for pure hydrogen production: A Pd-Ag membrane reactor and a PEMFC. Fuel Process. Technol. 2011, 92, 166–174. [Google Scholar] [CrossRef]
- Mori, N.; Nakamura, T.; Noda, K.-I.; Sakai, O.; Takahashi, A.; Ogawa, N.; Sakai, H.; Iwamoto, Y.; Hattori, T. Reactor configuration and concentration polarization in methane steam reforming by a membrane reactor with a highly hydrogen-permeable membrane. Ind. Eng. Chem. Res. 2007, 46, 1952–1958. [Google Scholar] [CrossRef]
- Patrascu, M.; Sheintuch, M. On-site pure hydrogen production by methane steam reforming in high flux membrane reactor: Experimental validation, model predictions and membrane inhibition. Chem. Eng. J. 2015, 262, 862–874. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Sosio, F.; Manzolini, G.; Campanari, S. Fixed bed membrane reactor for hydrogen production from steam methane reforming: Experimental and modeling approach. Int. J. Hydrogen Energy 2015, 40, 7559–7567. [Google Scholar] [CrossRef]
- Kyriakides, A.S.; Voutetakis, S.; Papadopoulou, S.; Seferlis, P. Optimization of an experimental membrane reactor for low-temperature methane steam reforming. Clean Technol. Environ. Policy 2016, 18, 2065–2075. [Google Scholar] [CrossRef]
- Kyriakides, A.-S.; Ipsakis, D.; Voutetakis, S.; Papadopoulou, S.; Seferlis, P. Modelling and simulation of a membrane reactor for the low temperature methane steam reforming. Chem. Eng. Trans. 2013, 35, 109–114. [Google Scholar]
- Simakov, D.; Sheintuch, M. Experimental optimization of an autonomous scaled-down methane membrane reformer for hydrogen generation. Ind. Eng. Chem. Res. 2010, 49, 1123–1129. [Google Scholar] [CrossRef]
- Said, S.; Simakov, D.; Mokheimer, E.; Habib, M.; Ahmed, S.; Waseeuddin, M.; Roman-Leshkov, Y. Computational fluid dynamics study of hydrogen generation by low temperature methane reforming in a membrane reactor. Int. J. Hydrogen Energy 2015, 40, 3158–3169. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Xu, H.; Xiong, G. Hydrogen production capacity of membrane reformer for methane steam reforming near practical working conditions. J. Membrane Sci. 2008, 322, 453–459. [Google Scholar] [CrossRef]
- Lin, Y.-M.; Liu, S.-L.; Chuang, C.-H.; Chu, Y.-T. Effect of incipient removal of hydrogen through palladium membrane on the conversion of methane steam reforming: Experimental and modeling. Catal. Today 2003, 82, 127–139. [Google Scholar] [CrossRef]
- Dittmar, B.; Behrens, A.; Schödel, N.; Rüttinger, M.; Franco, T.; Straczewski, G.; Dittmeyer, R. Methane steam reforming operation and thermal stability of new porous metal supported tubular palladium composite membranes. Int. J. Hydrogen Energy 2013, 38, 8759–8771. [Google Scholar] [CrossRef]
- Kim, C.; Han, J.; Kim, S.; Lee, B.; Lim, H.; Lee, K.; Ryi, S. Hydrogen production by steam methane reforming in a membrane reactor equipped with a Pd composite membrane deposited on a porous stainless steel. Int. J. Hydrogen Energy 2018, 43, 7684–7692. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Andalib, E.; Basile, A. Evaluation of dense Pd-Ag membrane reactor performance during methanol steam reforming in comparison with autothermal reforming using CFD analysis. Int. J. Hydrogen Energy 2016, 41, 8745–8754. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Moorrone, P.; Babalou, A.; Basile, A. A simulation study on methanol steam reforming in the silica membrane reactor for hydrogen production. Int. J. Hydrogen Energy 2015, 40, 3909–3918. [Google Scholar] [CrossRef]
- Lee, D.; Park, S.; Yu, C.; Ihm, S.; Lee, K. Study on methanol reforming-inorganic membrane reactors combined with water-gas shift reaction and relationship between membrane performance and methanol conversion. J. Membrane Sci. 2008, 316, 63–72. [Google Scholar] [CrossRef]
- Liguori, S.; Iulianelli, A.; Dalena, F.; Piemonte, V.; Huang, Y.; Basile, A. Methanol steam reforming in an Al2O3 supported thin Pd-layer membrane reactor over Cu/ZnO/Al2O3 catalyst. Int. J. Hydrogen Energy 2014, 39, 18702–18710. [Google Scholar] [CrossRef]
- Saidi, M. Performance assessment and evaluation of catalytic membrane reactor for pure hydrogen production via steam reforming of methanol. Int. J. Hydrogen Energy 2017, 42, 16170–16185. [Google Scholar] [CrossRef]
- Israni, S.H.; Harold, M.P. Methanol steam reforming in Pd- Ag membrane reactors: Effects of reaction system species on transmembrane hydrogen flux. Ind. Eng. Chem. Res. 2010, 49, 10242–10250. [Google Scholar] [CrossRef]
- Israni, S.H.; Harold, M.P. Methanol steam reforming in single-fiber packed bed Pd–Ag membrane reactor: Experiments and modeling. J. Membrane Sci. 2011, 369, 375–387. [Google Scholar] [CrossRef]
- Seelam, P.; Liguori, S.; Iulianelli, A.; Pinacci, P.; Calabro, V.; Huuhtanen, M.; Piemonte, P.; Tosti, S.; De Falco, M.; Basile, A. Hydrogen production from bio-ethanol steam reforming reaction in a Pd/PSS membrane reactor. Catal. Today 2012, 193, 42–48. [Google Scholar] [CrossRef]
- Murmura, M.A.; Patrascu, M.; Annesini, M.C.; Palma, V.; Ruocco, C.; Sheintuch, M. Directing selectivity of ethanol steam reforming in membrane reactors. Int. J. Hydrogen Energy 2015, 40, 5837–5848. [Google Scholar] [CrossRef]
- Ma, R.; Castro-Dominguez, B.; Mardilovich, I.; Dixon, A.; Ma, Y. Experimental and simulation studied of the production of renewable hydrogen through ethanol steam reforming in a large-scale catalytic membrane reactor. Chem. Eng. J. 2016, 303, 302–313. [Google Scholar] [CrossRef]
- Ma, R.; Castro-Dominguez, B.; Dixon, A.; Ma, Y. CFD study of heat and mass transfer in ethanol steam reforming in a catalytic membrane reactor. Int. J. Hydrogen Energy 2018, 43, 7662–7674. [Google Scholar] [CrossRef]
- Gallucci, F.; De Falco, M.; Tosti, S.; Marrelli, L.; Basile, A. Ethanol steam reforming in a dense Pd-Ag membrane reactor: A modelling work. Comparison with the traditional system. Int. J. Hydrogen Energy 2008, 33, 644–651. [Google Scholar] [CrossRef]
- Domínguez, M.; Taboada, E.; Molins, E.; Llorca, J. Ethanol steam reforming at very low temperature over cobalt talc in a membrane reactor. Catal. Today 2012, 193, 101–106. [Google Scholar] [CrossRef]
- Vasquez Castillo, J.M.; Sato, T.; Itoh, N. Effect of temperature and pressure on hydrogen production from steam reforming of biogas with Pd-Ag membrane reactor. Int. J. Hydrogen Energy 2015, 40, 3582–3591. [Google Scholar] [CrossRef]
- Iulianelli, A.; Liguori, S.; Huang, Y.; Basile, A. Model biogas steam reforming in a thin Pd-supported membrane reactor to generate clean hydrogen for fuel cells. J. Power Sources 2015, 273, 25–32. [Google Scholar] [CrossRef]
- Lin, K.; Lin, W.; Hsiao, C.; Chang, H.; Chang, A. Hydrogen production in steam reforming of glycerol by conventional and membrane reactors. Int. J. Hydrogen Energy 2012, 37, 13770–13776. [Google Scholar] [CrossRef]
- Iulianelli, A.; Longo, T.; Liguori, S.; Basile, A. Production of hydrogen via glycerol steam reforming in a Pd–Ag membrane reactor over Co–Al2O3 catalyst. Asia-Pac. J. Chem. Eng. 2010, 5, 138–145. [Google Scholar] [CrossRef]
- Shoham Patrascu, M.; Sheintuch, M. Multi-fuel scaled-down autothermal pure H2 generator: Design and proof of concept. AIChE J. 2016, 62, 2112–2125. [Google Scholar] [CrossRef]
- Barbieri, G.; Brunetti, A.; Tricoli, G.; Drioli, E. An innovative configuration of a Pd-based membrane reactor for the production of pure hydrogen: Experimental analysis of water gas shift. J. Power Sources 2008, 182, 160–167. [Google Scholar] [CrossRef]
- Mendes, D.; Sá, S.; Tosti, S.; Sousa, J.M.; Madeira, L.M.; Mendes, A. Experimental and modeling studies on the low-temperature water-gas shift reaction in a dense Pd–Ag packed-bed membrane reactor. Chem. Eng. Sci. 2011, 66, 2356–2367. [Google Scholar] [CrossRef]
- Chein, R.; Chen, Y.; Chung, J. Sweep gas flow effect on membrane reactor performance for hydrogen production from high-temperature water-gas shift reaction. J. Membrane Sci. 2015, 475, 193–203. [Google Scholar] [CrossRef]
- Morpeth, L.; Dolan, M. Modelling and experimental studies of a water-gas shift catalytic membrane reactor. Chem. Eng. J. 2015, 276, 289–302. [Google Scholar]
- Augustine, A.S.; Ma, Y.H.; Kazantzis, N. High pressure palladium membrane reactor for the high temperature water–gas shift reaction. Int. J. Hydrogen Energy 2011, 36, 5350–5360. [Google Scholar] [CrossRef]
- Kim, S.-J.; Xu, Z.; Reddy, G.; Smirniotis, P.; Dong, J. Effect of pressure on high-temperature water gas shift reaction in microporous zeolite membrane reactor. Ind. Eng. Chem. Res. 2012, 51, 1364–1375. [Google Scholar] [CrossRef]
- Itoh, N.; Oshima, A.; Suga, E.; Sato, T. Kinetic enhancement of ammonia decomposition as a chemical hydrogen carrier in palladium membrane reactor. Catal. Today 2014, 236, 70–76. [Google Scholar] [CrossRef]
- Rizzuto, E.; Palange, P.; Del Prete, Z. Characterization of an ammonia decomposition process by means of a multifunctional catalytic membrane reactor. Int. J. Hydrogen Energy 2014, 39, 11403–11410. [Google Scholar] [CrossRef]
- Choi, S.; Jones, C.; Nair, S.; Sholl, D.; Moore, J.; Liu, Y.; Dixit, R.; Pendergast, J. Material properties and operating configurations of membrane reactors for propane dehydrogenation. AIChE J. 2015, 61, 922–935. [Google Scholar] [CrossRef]
- Jin, Y.; Meng, X.; Bo, M.; Yang, N.; Sunarso, J.; Liu, S. Parametric modeling study of oxidative dehydrogenation of propane in La0.6Sr0.4Co0.2Fe0.8O3−δ hollow fiber membrane reactor. Catal. Today 2018. [Google Scholar] [CrossRef]
- Ahn, S.; Yun, G.; Takagaki, A.; Kikuchi, R.; Oyama, S. Effects of pressure, contact time, permeance, and selectivity in membrane reactors: The case of the dehydrogenation of ethane. Sep. Purif. Technol. 2018, 194, 197–206. [Google Scholar] [CrossRef]
- Peters, T.; Liron, O.; Tschentscher, R.; Sheintuch, M.; Bredesen, R. Investigation of Pd-based membranes in propane dehydrogenation (PDH) processes. Chem. Eng. J. 2016, 305, 191–200. [Google Scholar] [CrossRef]
- Lee, D.; Nam, S.; Sea, B.; Ihm, B.; Lee, K. Preparation of Pt-loaded hydrogen selective membranes for methanol reforming. Catal. Today 2006, 118, 198–204. [Google Scholar] [CrossRef]
- Vigneault, A.; Grace, J.R. Hydrogen production in multi-channel membrane reactor via steam methane reforming and methane catalytic combustion. Int. J. Hydrogen Energy 2015, 40, 233–243. [Google Scholar] [CrossRef]
- Boeltken, T.; Wunsch, A.; Gietzelt, T.; Pfeifer, P.; Dittmeyer, R. Ultra-compact microstructured methane steam reformer with integrated Palladium membrane for on-site production of pure hydrogen: Experimental demonstration. Int. J. Hydrogen Energy 2014, 39, 18058–18068. [Google Scholar] [CrossRef]
- Singh, A.P.; Singh, S.; Ganguly, S.; Patwardhan, A.V. Steam reforming of methane and methanol in simulated macro & micro-scale membrane reactors: Selective separation of hydrogen for optimum conversion. J. Nat. Gas Sci. Eng. 2014, 18, 286–295. [Google Scholar]
- Richardson, J.; Remue, D.; Hung, J.K. Properties of ceramic foam catalyst supports: Mass and heat transfer. Appl. Catal. A Gen. 2003, 250, 319–329. [Google Scholar] [CrossRef]
- Giaconia, A.; Monteleone, G.; Morico, B.; Salladini, A.; Shabtai, K.; Sheintuch, M.; Boettge, D.; Adles, J.; Palma, V.; Voutetakis, S.; et al. Multi-fuelled solar steam reforming for pure hydrogen production using solar salts as heat transfer fluid. Energy Procedia 2015, 69, 1750–1758. [Google Scholar] [CrossRef]
- Twigg, M.; Richardson, J. Fundamentals and applications of structured ceramic foam catalysts. Ind. Eng. Chem. Res. 2007, 46, 4166–4177. [Google Scholar] [CrossRef]
- Twigg, M.; Richardson, J. Theory and applications of ceramic foam catalysts. Chem. Eng. Res. Design 2002, 80, 183–189. [Google Scholar] [CrossRef]
- Roses, L.; Gallucci, F.; Manzolini, G.; Campanari, S.; van Sint Annaland, M. Comparison between fixed bed and fluidized bed membrane reactor configurations for PEM based micro-cogeneration systems. Chem. Eng. J. 2011, 171, 1415–1427. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Turchetti, L.; Annesini, M.C. Transport-permeation regimes in an annular membrane separator for hydrogen purification. J. Membrane Sci. 2016, 503, 199–211. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Designing the optimal geometry of a membrane reactor for hydrogen production froma a pre-reformed gas mixture based on the extent of the reaction boundary layer. Chem. Eng. Process. Process Intensif. 2017, 120, 148–160. [Google Scholar] [CrossRef]
- Tiemersma, T.P.; Patil, C.S.; Annaland, M.; Kuipers, J.A.M. Modelling of packed bed membrane reactors for autothermal production of ultrapure hydrogen. Chem. Eng. Sci. 2006, 61, 1602–1616. [Google Scholar] [CrossRef]
- Said, S.A.; Simakov, D.S.; Waseeuddin, M.; Román-Leshkov, Y. Solar molten salt heated membrane reformer for natural gas upgrading and hydrogen generation: A CFD model. Solar Energy 2016, 124, 163–176. [Google Scholar] [CrossRef]
- Murmura, M.A.; Diana, M.; Spera, R.; Annesini, M.C. Modeling of autothermal methane steam reforming: Comparison of reactor configurations. Chem. Eng. Process. Process Intensif. 2016, 109, 125–135. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Transport-reaction-permeation regimes in catalytic membrane reactors for hydrogen production: Steam reforming of methane as a case study. Chem. Eng. Sci. 2017, 162, 88–103. [Google Scholar] [CrossRef]
- Delgado, J. A critical review of dispersion in packed beds. Heat Mass Transf. 2006, 42, 279–310. [Google Scholar] [CrossRef]
- Mauri, R. Heat and mass transport in random velocity field with application to dispersion in porous media. J. Eng. Math. 1995, 29, 77–89. [Google Scholar] [CrossRef]
- Brenner, H.; Edwards, D. Macrotransport Processes; Butterworth-Heinemann: Oxford, UK, 1993. [Google Scholar]
- Giona, A.; Adrover, A.; Cerbelli, S.; Garofalo, F. Laminar dispersin at high peclet numbers in finite length-channels: Effects of the near-wall velocity profile and connection with the generalized leveque problem. Phys. Fluids 2009, 21, 123601. [Google Scholar] [CrossRef]
- Marin, P.; Patino, Y.; Diez, F.; Ordonez, S. Modelling of hydrogen perm-selective membrane reactors for catalytic methane steam reforming. Int. J. Hydrogen Energy 2012, 37, 18433–18445. [Google Scholar] [CrossRef]
- Tsotsas, E.; Martin, H. Thermal conductivity of packed beds: A review. Chem. Eng. Process. Process Intensif. 1987, 22, 19–37. [Google Scholar] [CrossRef]
- Peng, Y.; Richardson, J. Properties of ceramic foam catalyst supports: one-dimensional and two-dimensional heat transfer correlations. Appl. Catal. A Gen. 2004, 266, 235–244. [Google Scholar] [CrossRef]
- Boon, J.; Li, H.; Dijkstra, J.W.; Pieterse, J.A.Z. 2-dimensional membrane separator modelling: Mass transfer by convection and diffusion. Energy Procedia 2011, 4, 699–706. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. An equilibrium theory for catalytic steam reforming in membrane reactors. Chem. Eng. Sci. 2017, 160, 291–303. [Google Scholar] [CrossRef]
- Nekhamkina, O.; Sheintuch, M. Effective approximations for concentration-polarization in Pd-membrane separators. Chem. Eng. J. 2015, 260, 835–845. [Google Scholar] [CrossRef]
- Wei, J.; Iglesia, E. Isotopic and kinetic assessment of the mechanism of reactions of CH4 with CO2 or H2O to form synthesis gas and carbon on nickel catalysts. J. Catal. 2004, 224, 370–383. [Google Scholar] [CrossRef]
- Godini, H.; Xiao, S.; Kim, M.; Holst, N.; Jaso, S.; Gorke, O.; Steinbach, J.; Wozny, G. Experimental and model-based analysis of membrane reactor performance for methane oxidative coupling: Effect of radial heat and mass transfer. J. Ind. Eng. Chem. 2014, 20, 1993–2202. [Google Scholar] [CrossRef]
- Holst, N.; Jaso, S.; Godini, H.; Gloser, S.; Arellano-Garcia, H.; Wozny, G.; Steinback, J. Two-dimensionals model for oxidative coupling of methane in a packed bed membrane reactor. Chem. Eng. Technol. 2012, 35, 294–301. [Google Scholar] [CrossRef]
- Jin, W.; Gux, X.; Li, S.; Huang, P.; Xu, N.; Shi, J. Experimental and simulation study on a catalyst packed tubular dense membrane reactor for partial oxidation of methane to syngas. Chem. Eng. Sci. 2000, 55, 2617–2625. [Google Scholar] [CrossRef]
- Oyama, S.; Hacariloglu, P. The boundary between simple and complex descriptions of membrane reactors: The transition between 1-D and 2-D analysis. J. Membrane Sci. 2009, 337, 188–199. [Google Scholar] [CrossRef]
- Murmura, M.A.; Turchetti, L.; Augelletti, R.; Annesini, M.C.; Cerbelli, S. How does radial convection influence the performance of membrane module for gas separation processes. Chem. Eng. Trans. 2015, 43, 1063–1068. [Google Scholar]
- Sheintuch, M. Pure hydrogen production in a membrane reformer: Demonstration, macro-scale and atomic scale modeling. Chem. Eng. J. 2015, 278, 363–373. [Google Scholar] [CrossRef]
- Turchetti, L.; Murmura, M.A.; Monteleone, G.; Giaconia, A.; Lemonidou, A.; Angeli, S.; Palma, V.; Ruocco, C.; Annesini, M.C. Kinetic assessment of Ni-based catalysts in low-temperature methane/biogas steam reforming. Int. J. Hydrogen Energy 2016, 41, 16865–16877. [Google Scholar] [CrossRef]
- Lao, L.; Aguirre, A.; Tran, A.; Wu, Z.; Durand, H.; Christofides, P. CFD modeling and control of a steam methane reforming reactor. Chem. Eng. Sci. 2016, 148, 78–92. [Google Scholar] [CrossRef]
- Iulianelli, A.; Manzolini, G.; De Falco, M.; Campanari, S.; Longo, T.; Liguori, S.; Basile, A. H2 production by low pressure methane steam reforming in Pd-Ag membrane reactor over a Ni-based catalyst: Experimental and modeling. Int. J. Hydrogen Energy 2010, 35, 11514–11524. [Google Scholar] [CrossRef]
- Kyriakides, A.; Rodriguez-Garcia, L.; Voutetakis, S.; Ipsakis, D.; Seferlis, P.; Papadopoulou, S. Enhancement of pure hydrogen production through the use of a membrane reactor. Int. J. Hydrogen Energy 2014, 39, 4749–4760. [Google Scholar] [CrossRef]
- Xu, J.; Froment, G. Methane steam reforming, methanation and water-gas shift: I. intrinsic kinetics. AIChE J. 1989, 35, 88–96. [Google Scholar] [CrossRef]
- Hou, K.; Hughes, R. The kinetics of methane steam reforming over a Ni/α-Al2O catalyst. Chem. Eng. J. 2001, 82, 311–328. [Google Scholar] [CrossRef]
- Soria, M.; Mateos-Pedrero, C.; Marin, P.; Ordonez, S.; Gerrero-Ruiz, A.; Rodriguez-Ramos, I. Kinetic analysis of the Ru/SiO2-catalyzed low temperatrue methane steam reforming. Appl. Catal. A 2012, 414, 366–374. [Google Scholar] [CrossRef]
- Pieterse, J.; Boon, J.; van Delft, Y.; Dijkstra, J.; van den Brink, R. On the potential of nickel catalysts for steam reforming in membrane reactors. Catal. Today 2010, 156, 153–164. [Google Scholar] [CrossRef]
- Numaguchi, T.; Kikuchi, K. Intrinsic kinetics design simulation in a complex reaction network; steam-methane reforming. Chem. Eng. Sci. 1988, 43, 2295–2301. [Google Scholar] [CrossRef]
- Angeli, S.D.; Monteleone, G.; Giaconia, A.; Lemonidou, A.A. State-of-the-art catalysts for CH4 steam reforming at low temperature. Int. J. Hydrogen Energy 2014, 39, 1979–1997. [Google Scholar] [CrossRef]
- Sprung, C.; Arstad, B.; Olsbye, U. Metahne steam reforming over a Ni/NiAl2O4 model catalyst - Kinetics. ChemCatChem 2014, 7, 1969–1982. [Google Scholar] [CrossRef]
- Palma, V.; Castaldo, F.; Ciambelli, P.; Iaquaniello, G. CeO2-supported Pt/Ni catalyst for the renewable and clean H2 production via ethanol steam reforming. Appl. Catal. B Environ. 2014, 145, 73–84. [Google Scholar] [CrossRef]
- Sahoo, D.; Vajpai, S.; Pater, S.; Pant, K. Kinetic modeling of steam reforming of ethanol for the production of hydrogen over Co/Al2O3 catalyst. Chem. Eng. J. 2007, 125, 139–147. [Google Scholar] [CrossRef]
- Contreras, J.L.; Salmones, J.; Colin-Luna, J.A.; Nuno, L.; Quintana, B.; Cordova, I.; Zeiferst, B.; Tapia, C.; Fuentes, G.A. Catalysts for H2 production using ethanol steam reforming (a review). Int. J. Hydrogen Energy 2014, 39, 18835–18853. [Google Scholar] [CrossRef]
- Lee, J.; Ko, J.; Kim, D. Methanol steam reforming over Cu/ZnO/Al2o3 catalyst: Kinetics and effectiveness factor. Appl. Catal. A 2004, 278, 25–35. [Google Scholar] [CrossRef]
- Patel, S.; Pant, K. Experimental study and mechanistic kinetic modeling for selective production of hydrogen via catalytic steam reforming of methanol. Chem. Eng. Sci. 2007, 62, 5425–5435. [Google Scholar] [CrossRef]
- Samms, S.; Savinelli, R. Kinetics of methano-steam reformation in an internal reforming fuel cell. J. Power Sources 2002, 112, 13–29. [Google Scholar] [CrossRef]
- Tesser, R.; Di Serio, M.; Santacesaria, E. Methanol steam reforming: A comparison of different kinetics in the simulation of a packed bed reactor. Chem. Eng. J. 2009, 154, 69–75. [Google Scholar] [CrossRef]
- Peppley, B.; Amphlett, J.; Kearns, L.; Mann, R. Methanol-steam reforming on Cu/Zno/Al2O3 catalysts. part II. A comprehensive kinetic model. Appl. Catal. A Gen. 1999, 179, 31–49. [Google Scholar] [CrossRef]
- Sa, S.; Sousa, J.M.; Mendes, A. Steam reforming of methanol over a CuO/Zno/Al2O3 catalyst part II: A carbon membrane reactor. Chem. Eng. Sci. 2011, 66, 5523–5530. [Google Scholar] [CrossRef]
- Sa, S.; Sousa, J.; Mendes, A. Steam reforming of methanol over a CuO/Zno/Al2O3 catalyst, part I: Kinetic modelling. Chem. Eng. Sci. 2011, 66, 4913–4921. [Google Scholar] [CrossRef]
- Conde, J.J.; Maroño, M.; Sánchez-Hervás, J.M. Pd-Based Membranes for Hydrogen Separation: Review of Alloying Elements and Their Influence on Membrane Properties. Sep. Purif. Rev. 2017, 46, 152–177. [Google Scholar] [CrossRef]
- Al-Mufachi, N.A.; Rees, N.V.; Steinberger-Wilkens, R. Hydrogen selective membranes: A review of palladium-based dense metal membranes. Renew. Sustain. Energy Rev. 2015, 47, 540–551. [Google Scholar] [CrossRef]
- Yun, S.; Oyama, S.T. Correlations in palladium membranes for hydrogen separation: A review. J. Membrane Sci. 2011, 375, 28–45. [Google Scholar] [CrossRef]
- Peters, T.; Stange, M.; Klette, H.; Bredesen, R. High pressure performance of this Pd-23%Ag/stainless steel composite membranes in water gas shift mixtures; influence of dilution, mass transfer and surface effects on the hydrogen flux. J. Membrane Sci. 2008, 316, 119–127. [Google Scholar] [CrossRef]
- Abir, H.; Sheintuch, M. Modeling H2 transport through a Pd/Ag membrane, and its inhibition by co-adsorbates, from first principles. J. Membrane Sci. 2014, 466, 58–69. [Google Scholar] [CrossRef]
- Carvella, A.; Scura, F.; Barbieri, G.; Drioli, E. Inhibition by CO and polarization in Pd-based membranes: A novel permeation reduction coefficient. J. Phys. Chem. B 2010, 114, 12264–12276. [Google Scholar] [CrossRef] [PubMed]
- Unemoto, A.; Kaimai, A.; Sato, K.; Ota, T.; Yashiro, K.; Mizusaki, J.; Kawada, T.; Tsuneki, T.; Shirasaki, Y.; Yasuda, I. The effect of co-existing gases from the process of steam reforming reaction on hydrogen permeability of palladium alloy membrane at high temperatures. Int. J. Hydrogen Energy 2007, 32, 2881–2887. [Google Scholar] [CrossRef]
- Mejdell, A.; Jondahl, M.; Peters, T.; Bredesen, R.; Venvik, H. Effects of CO and CO2 on hydrogen permeation through a ∼3 μm Pd/Ag 23 wt.% membrane emplyed in a microchannel membrane configuration. Sep. Purif. Technol. 2009, 68, 178–184. [Google Scholar] [CrossRef]
- Peters, T.; Polfus, J.; Stange, M.; Veenstra, P.; Nijmeijer, A.; Bredesen, R. H2 flux inhibition and stability of Pd-Ag membranes under exposure to trace amounts of NH3. Fuel Process. Technol. 2016, 152, 259–265. [Google Scholar] [CrossRef]
- Mundschau, M.; Xie, X.; Evenso, C.; Sammells, A. Dense inorganic membrane for production of hydrogen form methane and coal with carbon dioxide sequestration. Catal. Today 2006, 118, 12–23. [Google Scholar] [CrossRef]
- Peters, T.; Kaleta, T.; Stange, M.; Bredesen, R. Hydrogen transport through a selection of thin Pd-alloy membranes: Membrane stability, H2S inhibition, and flux recovery in hydrogen and simulated WGS mixtures. Catal. Today 2012, 193, 8–19. [Google Scholar] [CrossRef]
- O’Brien, C.; Howard, B.; Miller, J.; Morreale, B.; Gellman, A. Inhibition of hydrogen transport through Pd and Pd47Cu53 membranes by H2S. J. Membrane Sci. 2010, 349, 380–384. [Google Scholar] [CrossRef]
- Chen, C.; Ma, Y. The effect of H2S on the performance of Pd and Pd/Au composite membrane. J. Membrane Sci. 2010, 362, 535–544. [Google Scholar] [CrossRef]
- Kurokawa, H.; Yakabe, H.; Yasuda, I.; Peters, T.; Bredesen, R. Inhibition effect of CO on hydrogen permeability of Pd-Ag membrane applied in a microchannel module configuration. Int. J. Hydrogen Energy 2014, 39, 17201–17209. [Google Scholar] [CrossRef]
- Boon, J.; Pieterse, J.; Van Berke, F.; Vand Delft, Y.; van Sint Annaland, M. Hydrogen permeation through palladium membranes and inhibition by carbon monoxide, carbon dioxide, and steam. J. Membrane Sci. 2015, 496, 344–358. [Google Scholar] [CrossRef]
- Scura, F.; Barbieri, G.; De Luca, G.; Drioli, E. The influence of the CO inhibition effect on the estimation of the H2 purification unit surface. Int. J. Hydrogen Energy 2008, 33, 4183–4192. [Google Scholar] [CrossRef]
- Catalano, J.; Giacinti Baschetti, M.; Sarti, G. Hydrogen permeation in palladium-based membranes in the presence of carbon monoxide. J. Membrane Sci. 2010, 362, 221–233. [Google Scholar] [CrossRef]
- Barbieri, G.; Scura, F.; Lentini, F.; De Luca, G.; Drioli, E. A novel model equation for the permeation of hydrogen in mixture with carbon monoxide through Pd-Ag membranes. Sep. Purif. Technol. 2008, 61, 217–224. [Google Scholar] [CrossRef]
- Murmura, M.A.; Sheintuch, M. Permeance inhibition of Pd-based membranes by competitive adsorption of CO: Membrane size effects and first principles predictions. Chem. Eng. J. 2018, 347, 301–312. [Google Scholar] [CrossRef]
- Conrad, H.; Ertl, G.; Koch, J.; Latta, E. Adsorption of CO on Pd single crystal surfaces. Surf. Sci. 1973, 43, 462–489. [Google Scholar] [CrossRef]
- Gan, L.; Zhang, Y.; Zhao, Y. Comparison of S poisoning effects on CO adsorption on Pd, Au, and bimetallic PdAu (111) surfaces. J. Phys. Chem. C 2010, 114, 996–1003. [Google Scholar] [CrossRef]
- Gonzales, S.; Illas, F. CO adsorption on monometallic Pd, Rh, Cu and bimetallic PdCu and RhCu monolayers supported on ru(0001). Surf. Sci. 2005, 598, 144–155. [Google Scholar] [CrossRef]
- Neurock, M. First-principles analysis of the hydrogenation of carbon monoxide over palladium. Top. Catal. 1999, 9, 135–152. [Google Scholar] [CrossRef]
- Wang, W.; Thomas, S.; Zhang, X.; Pan, X.; Yang, W.; Xiong, G. H2/N2 gaseous mixture separation in dense Pd/α-Al2O3 hollow fiber membranes: Experimental and simulation studies. Sep. Purif. Technol. 2006, 52, 177–185. [Google Scholar] [CrossRef]
- Guazzone, F.; Engwall, E.E.; Ma, Y.H. Effects of surface activity, defects and mass transfer on hydrogen permeance and n-value in composite palladium-porous stainless steel membranes. Catal. Today 2006, 118, 24–31. [Google Scholar] [CrossRef]
- Mourgues, A.; Sanchez, J. Theoretical analysis of concentration polarization in membrane modules for gas separation with feed inside the hollow-fibers. J. Membrane Sci. 2005, 252, 133–144. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, D.; He, M.; Xu, H.; Li, W. Experimental and simulation studies on concentration polarization in H2 enrichment by highly permeable and selective pd membranes. J. Membrane Sci. 2006, 274, 83–91. [Google Scholar] [CrossRef]
- Catalano, J.; Baschetti, M.G.; Sarti, G.C. Influence of the gas phase resistance on hydrogen flux through thin palladium–silver membranes. J. Membrane Sci. 2009, 339, 57–67. [Google Scholar] [CrossRef]
- Bey, O.; Eigenberger, G. Gas flow and heat transfer through catalyst filled tubes. Int. J. Therm. Sci. 2001, 40, 152–164. [Google Scholar] [CrossRef]
- Demirel, Y.; Sharma, R.; Al-Ali, H. On the effective heat transfer parameters in a packed bed. Int. J. Heat Mass Transf. 2000, 43, 327–332. [Google Scholar] [CrossRef]
- Li, C.; Finlayson, B. Heat transfer in packed bed—A reevaluation. Chem. Eng. Sci. 1977, 32, 1055–1066. [Google Scholar] [CrossRef]
- de Wasch, A.; Froment, G. Heat transfer in packed beds. Chem. Eng. Sci. 1972, 27, 567–576. [Google Scholar] [CrossRef]
- Calderbank, P.H.; Pogorski, L.A. Heat transfer in packed beds. Trans. Inst. Chem. Eng. 1957, 35, 195–207. [Google Scholar]
- Yagi, A.; Kunii, D. Studies on heat transfer near wall surface in packed beds. AIChE J. 1960, 6, 97–104. [Google Scholar] [CrossRef]
- Busse, C.; Freund, H.; Schwieger, W. Intensification of heat transfer in catalytic reactors by additively manufactured periodic open cellular structures (POCS). Chem. Eng. Process. Process Intensif. 2018, 124, 199–214. [Google Scholar] [CrossRef]
- Bianchi, E.; Heidig, T.; Visconti, C.; Groppi, G.; Freund, H.; Tronconi, E. Heat transfer properties of metal foam supports for structured catalysts: Wall heat transfer coefficient. Catal. Today 2013, 216, 121–134. [Google Scholar] [CrossRef]
- Dietrich, B. Heat transfer coefficients for solid ceramic sponges - experimental results and correlation. Int. J. Heat Mass Transf. 2013, 61, 627–637. [Google Scholar] [CrossRef]
- Xia, X.; Chen, X.; Sun, C.; Li, A.; Liu, B. Experiment on the convective heat transfer from airflow to skeleton in open-cell foams. Int. J. Heat Mass Transf. 2017, 106, 83–90. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Modelling and optimization of hydrogen yield in membrane steam reforming reactors. Can. J. Chem. Eng. 2017, 95, 1676–1682. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Progress on modeling and design of membrane reactors for hydrogen production. Chem. Eng. Trans. 2017, 57, 919–924. [Google Scholar]
- Piemonte, V.; De Falco, M.; Favetta, B.; Basile, A. Counter-current membrane reactor for WGS process: Membrane design. Int. J. Hydrogen Energy 2010, 35, 12609–12617. [Google Scholar] [CrossRef]
- Giaconia, A.; de Falco, M.; Caputo, G.; Grena, R.; Tarquini, P.; Marrelli, L. Solar steam reforming of natural gas for hydrogen production using molten salt heat carriers. AIChE J. 2008, 54, 1932–1944. [Google Scholar] [CrossRef]
- Murmura, M.A.; Annesini, M.C.; Sheintuch, M. Bistability in membrane reactors due to membrane inhibition by competitive adsorption of reactants. Chem. Eng. J. 2018, 334, 1594–1604. [Google Scholar] [CrossRef]
- Ozisik, M.N. Heat Conduction; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Bogert, B. Some roots of an equation involving Bessel functions. J. Math. Phys. 1951, 30, 102–105. [Google Scholar] [CrossRef]
- Hutter, C.; Zenklusen, A.; Lang, R.; von Rohr, P.R. Axial dispersion in metal foams and streamwise-periodic porous media. Chem. Eng. Sci. 2011, 66, 1132–1141. [Google Scholar] [CrossRef]
- Zuercher, S.; Pabst, K.; Schaub, G. Ceramic foams as structured catalyst inserts in gas–particle filters for gas reactions—Effect of backmixing. Appl. Catal. A Gen. 2009, 357, 85–92. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Kyriakides, A.; Voutetakis, S.; Seferlis, P.; Papadopoulou, S.; Annesini, M.C. Hydrogen production in a packed bed membrane reactor: A preliminary analysis of mass dispersion in solid foams. In Proceedings of the ISCRE, Florence, Italy, 20–23 May 2018. [Google Scholar]


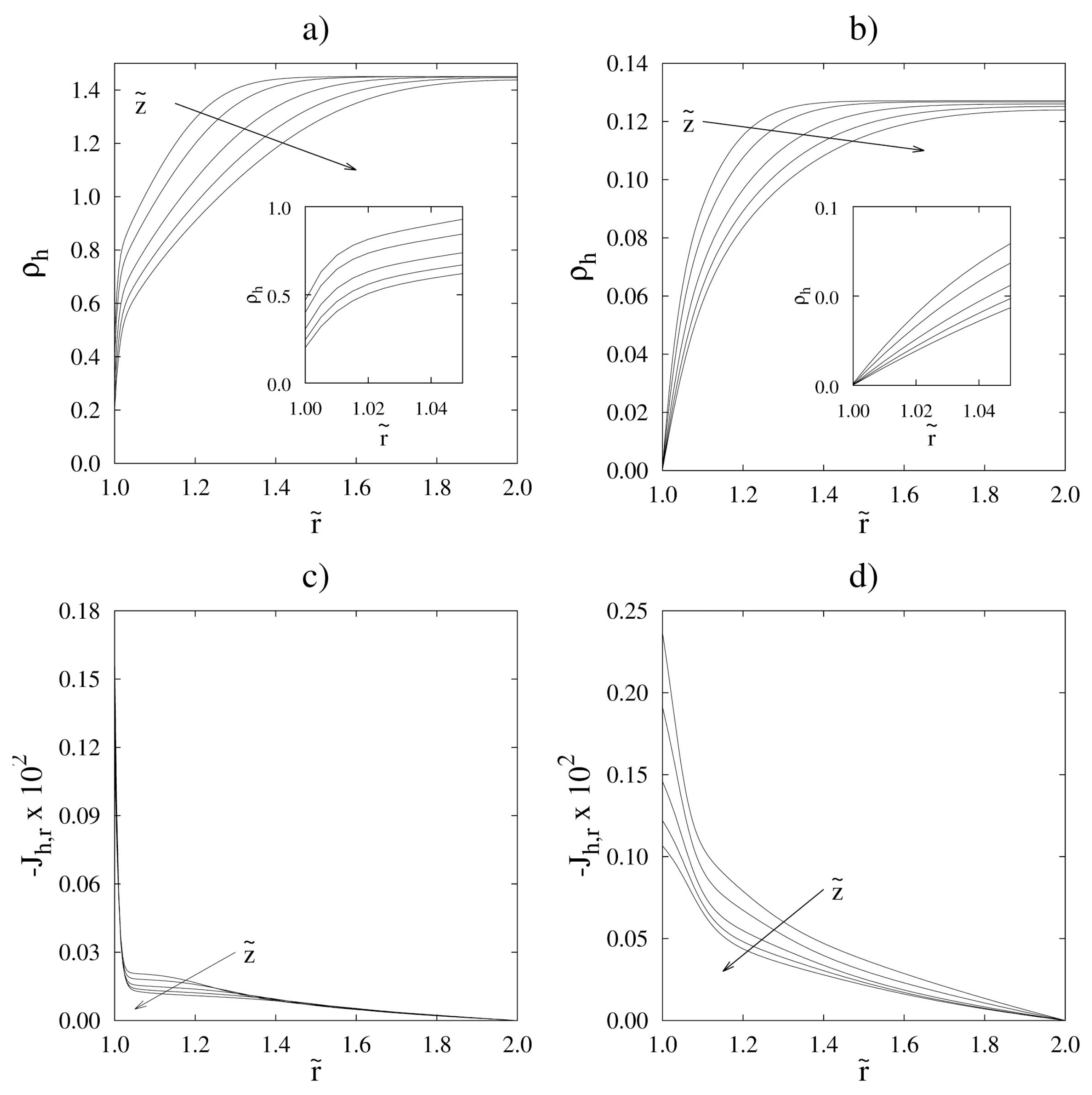
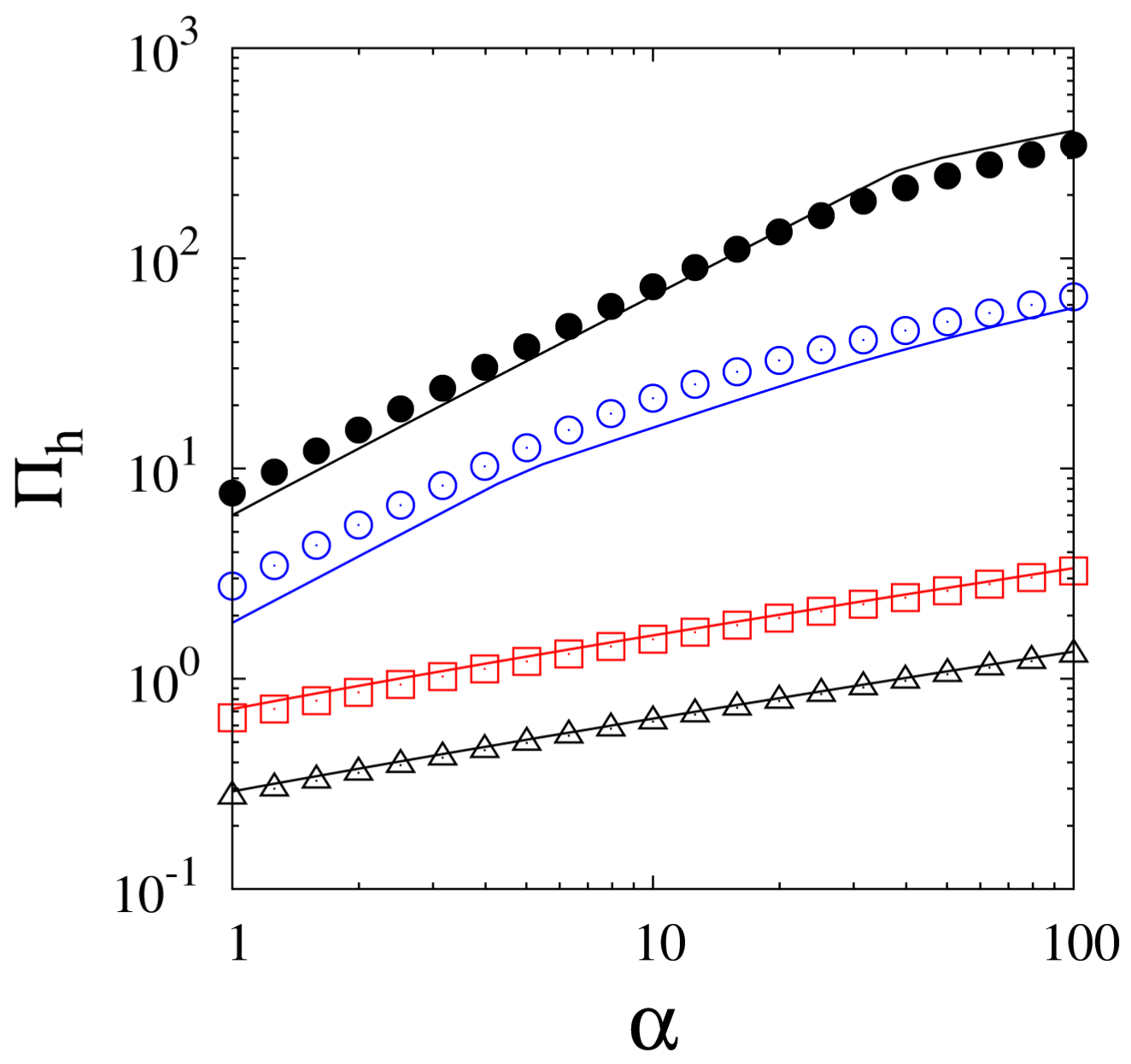
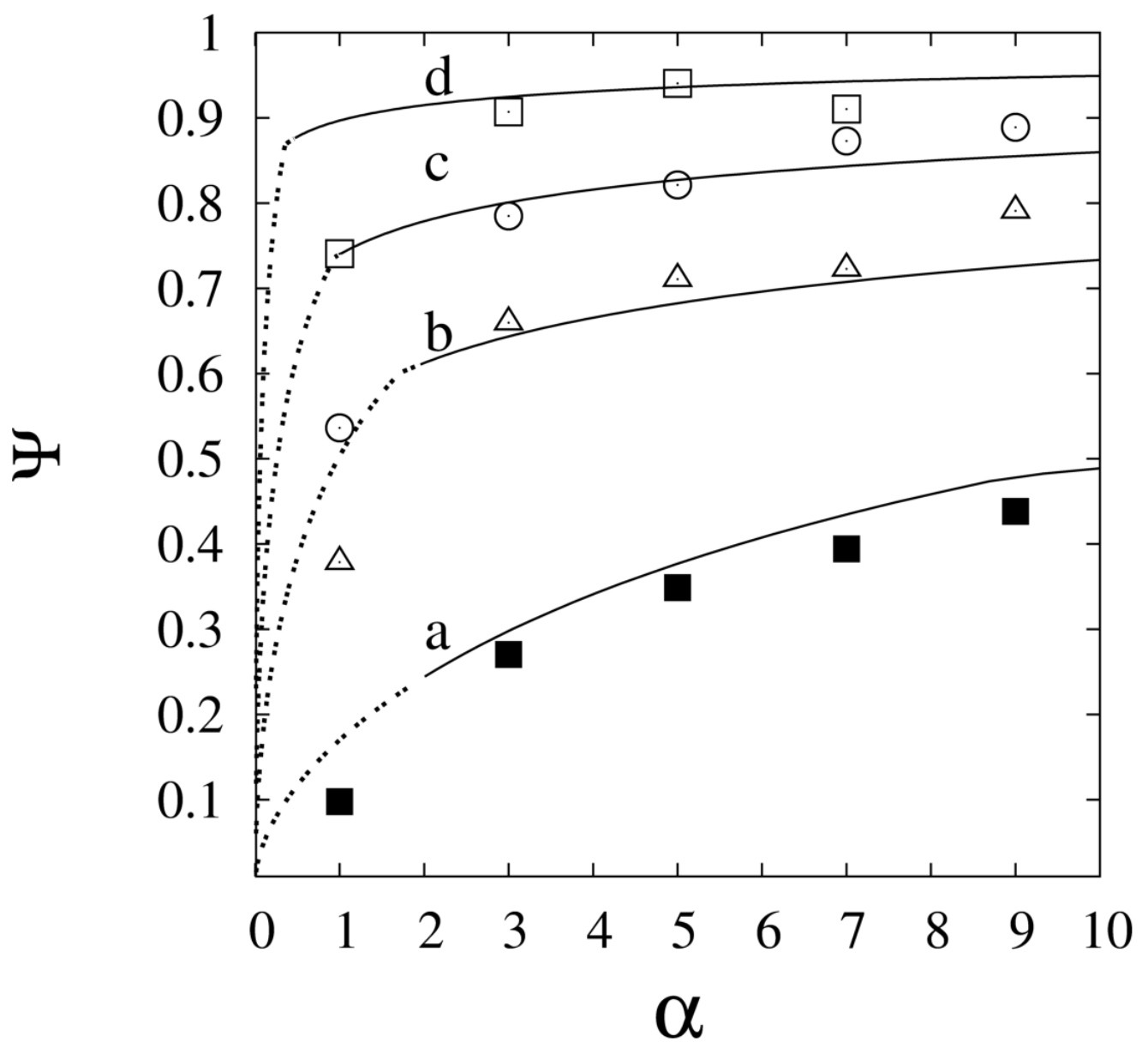
| or: |
| Boundary conditions |
| Boundary conditions |
| Boundary conditions |
| Boundary conditions |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Modeling Fixed Bed Membrane Reactors for Hydrogen Production through Steam Reforming Reactions: A Critical Analysis. Membranes 2018, 8, 34. https://doi.org/10.3390/membranes8020034
Murmura MA, Cerbelli S, Annesini MC. Modeling Fixed Bed Membrane Reactors for Hydrogen Production through Steam Reforming Reactions: A Critical Analysis. Membranes. 2018; 8(2):34. https://doi.org/10.3390/membranes8020034
Chicago/Turabian StyleMurmura, Maria Anna, Stefano Cerbelli, and Maria Cristina Annesini. 2018. "Modeling Fixed Bed Membrane Reactors for Hydrogen Production through Steam Reforming Reactions: A Critical Analysis" Membranes 8, no. 2: 34. https://doi.org/10.3390/membranes8020034
APA StyleMurmura, M. A., Cerbelli, S., & Annesini, M. C. (2018). Modeling Fixed Bed Membrane Reactors for Hydrogen Production through Steam Reforming Reactions: A Critical Analysis. Membranes, 8(2), 34. https://doi.org/10.3390/membranes8020034






