Development and Testing of a Fully Adaptable Membrane Bioreactor Fouling Model for a Sidestream Configuration System
Abstract
:1. Introduction
1.1. Previous Modelling Studies of MBR Fouling—Sub-Critical to Supra-Critical Flux Ranges
1.2. Some Problems of Using Phenomenological Membrane Fouling Models for Plant Design, Operation and Control
- As membrane fouling is in reality a very complex and very little understood process at this moment in time, it is difficult to make a generalised mechanistic fouling model that can adequately address all issues and specific nuances involved.
- Ideally fouling models of this type need to be made bespoke for each individual filtration system on a case-by-case basis. This is especially true for the hydrodynamics of the process (e.g., type of sparging system or membrane scour system in use), and the membrane operational regime (e.g., submerged or sidestream or vertical air-lift).
- The models are often highly dimensional and contain numerous parameters that need determination by specific plant data sets, specific process operations (i.e., flux stepping trials) and with the use of extended specialist laboratory experiments (e.g., specific cake resistance tests). Thus the models, themselves, can be over-parameterised with too many degrees of freedom.
- Parameter estimation and optimisation can prove to be a convoluted and complex procedure requiring expert knowledge and extensive experience.
- For many applications insufficient data is available to allow a full model calibration and validation, and thus the verified model is not omnipotent for every situation.
- The general application of such complex models, which in themselves require considerable calibration experience to give sufficient predictive accuracy, means their take up for process control and the development of future operational strategies will always prove limited [20].
2. Description of Model Used—Duclos-Orsello

2.1. Practical Limitations of the Duclos-Orsello Approach
- Since Duclos-Orsello [19] uses solutions from solved differential equations when calculating the flow through the unblocked membrane area, the state variables in the study must remain constant during any simulation. In a real life plant this is not the case, with say the MLSS concentration which is analogous to the Cb parameter (bulk concentration) in this model, often changing significantly in time. So any altered model formulation procedure must allow for this fact.
- Since Duclos-Orsello [19] uses an integral expression to calculate the flow through the blocked membrane area, the initial conditions in this study must remain fixed in any simulation, and any simulation must always commence from this point. In any useful simulation model, the user must be able to state different and varied initial conditions, and also be able to start a simulation from any point in time. So any altered model formulation must cater for this modelling issue.
- The integral expression means the TMP is kept constant during the simulation, and therefore the mathematical formulation of this model cannot be used for varying TMP situations which occur in many real life plant scenarios.
- This model formulation assumes pore constriction stops as soon as pore blockage occurs. This may not be the case as experienced in real life membrane fouling within a MBR system.
2.2. Initial Improvements to Duclos-Orsello’s Approach










2.3. Using SIMULINK© Genetic Algorithm Toolbox to Optimise Model Parameters Using Duclos-Orsello’s Original Data
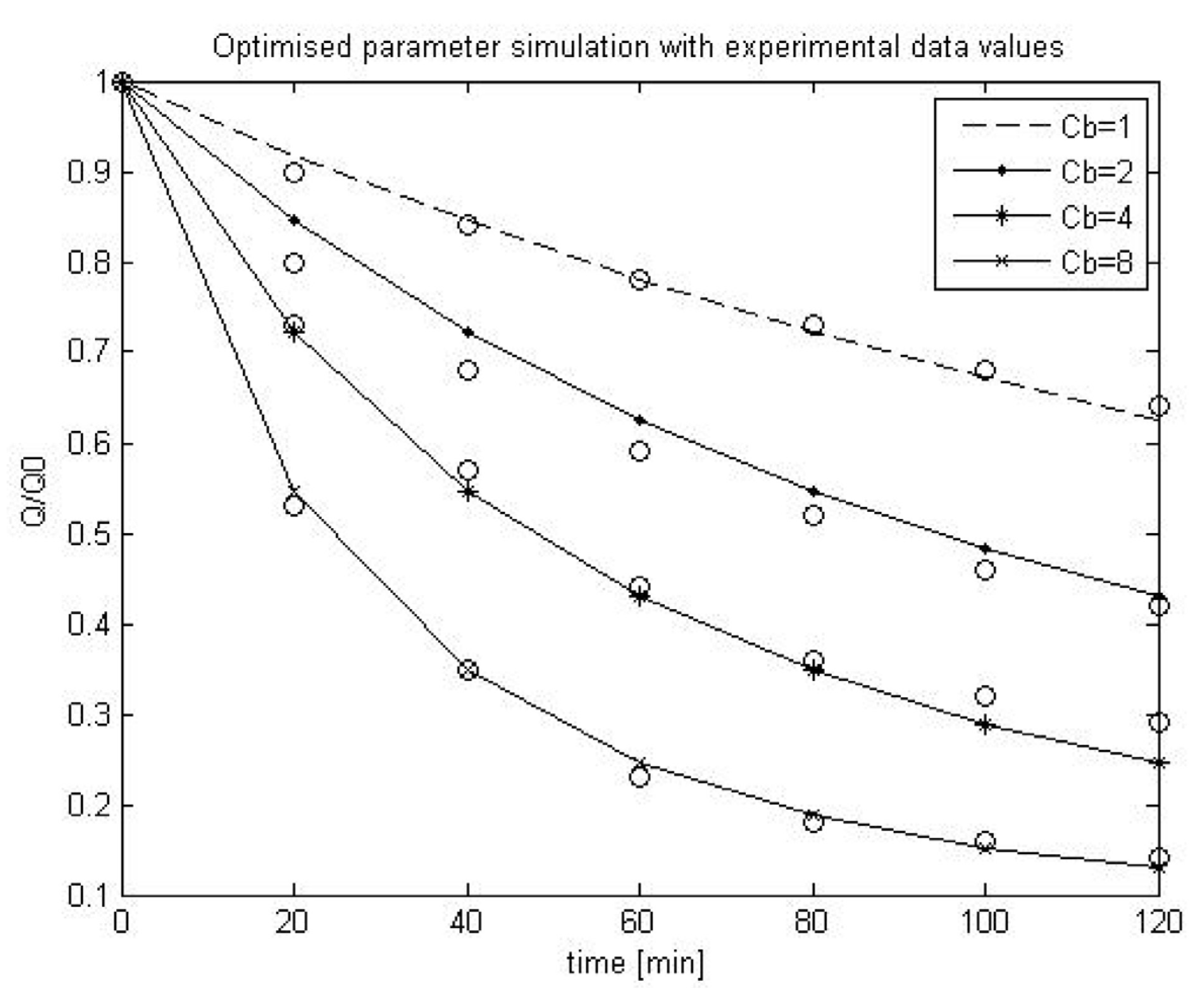
2.4. Scenario Analysis of Model Parameters using Duclos-Orsello’s Original Data
| Simulation No. | α | β | f′R′ | Rp0/Rm |
|---|---|---|---|---|
| 1. equivalent to: normal MBR operation conditions | 0.0001 | 0.1 | 4 × 109 | 0.5 |
| 2. equivalent to: SMP formation conditions | 0.1 | 10 | 4 × 1010 | 0.7 |
| 3. equivalent to: Extreme lab SMP formation conditions | 10 | 300 | 4 × 1011 | 0.9 |
3. Reformulation of Duclos-Orsello Model for Specific MBR Plant Layouts
3.1. Further Modifications to Duclos-Orsello Model
- Membrane surface scour which occurs in both submerged and cross flow sidestream MBR plant. In submerged plant this is usually a constant air scouring and sparging by coarse bubble aeration. For cross flow sidestream plant this membrane scouring is induced by applying a constant cross flow velocity which is developed from continuous recirculation of mixed liquors from the bioreactor (as is the case with the pilot MBR plant described further below). Thus a membrane scour term needs to be added to the model formulation.
- A backwash mode which is used to remove material accumulated within the membrane by reversing the permeate flow rate. This is usually for a fixed periodic interval of constant duration and intensity (as is the case with the pilot membrane filtration unit described further below). Hence a backwash mode with clean membrane area reset should form part of the model.
- As mentioned already, most researchers agree that the pore constriction mechanisms within a MBR are probably due to the building up of SMP [21]. This correlation can be catered for in this model by replacing the bulk concentration term, Cb, with a new term, SSMP, which relates solely to SMP effects.
- One final reformulation of the model needs to be done to allow the model to be used for varying TMP operational conditions such as occurred with pilot membrane filtration unit mentioned later on in this work.
3.2. Membrane Surface Scour Effects Inclusion



3.3. Backwashing


3.4. SMP Effects Inclusion

3.5. Total Flow through Membrane for Constant Flux/Varying TMP Operation





4. Model Calibration and Validation—Pilot MBR Plant and Pilot Membrane Filtration Unit
4.1. Pilot MBR Plant
| Aquabio Pilot MBR Plant-sidestream cross flow configuration | |
|---|---|
| Membrane type and area | Vertical “Berghof” tubular; PVC-C 0.02 μm pore size; 4.1 m2 |
| Membrane data | 55 tubes each of 8 mm ℘; outer diameter of module is 90 mm |
| Membrane feed flow (m3/h) | 10 × ν where cross flow velocity is ν (m/s) |
| Feed-Permeate differential pressure | −30 to +600 kPa |
| Pressure drop along module (kPa) | 2.1 × ν × L where module length is L(m) = 3010 mm |
| Backwash/cleaning regime | Automated backflush possible of varying length (but in flux stepping tests a manual backflush of 120 s was used); periodic hypochlorite clean every few weeks |
| Biological feed data | COD ~ 700 mg O2/L; TSS ~ 50 mg/L |
| Bioreactor operational data | MLSS ~ 7,000–12,000 mg/L; SMP ~ 500 mg/L |
4.2. Pilot Membrane Filtration Unit
| ITT Sanitaire membrane filtration unit (without bioreactor) | |
|---|---|
| Membrane type and area | Horizontal “Kolon” fibres; PVDF 0.1 μm pore size; 20 m2 |
| Recirculation flow; permeate flow; backwash | 1–2.4 m3/h; 0.6–1 m3/h; 1.2–1.8 m3/h |
| Backwash interval & duration | Every 4 min with 30 s ON |
| TMP | 300–500 mbar |
| Aeration rate | 13 N m3/h from coarse bubble tube diffuser |
| Cleaning regime | hypochlorite dosed 4 times daily into permeate tank |
| Feed flow biological data | COD concentration 50 mg O2/L; TSS concentration 25 mg/L |
| Indicative feed flow SMP data | Measured glucose concentration 5 mg/L; measured protein concentration 100 mg/L |
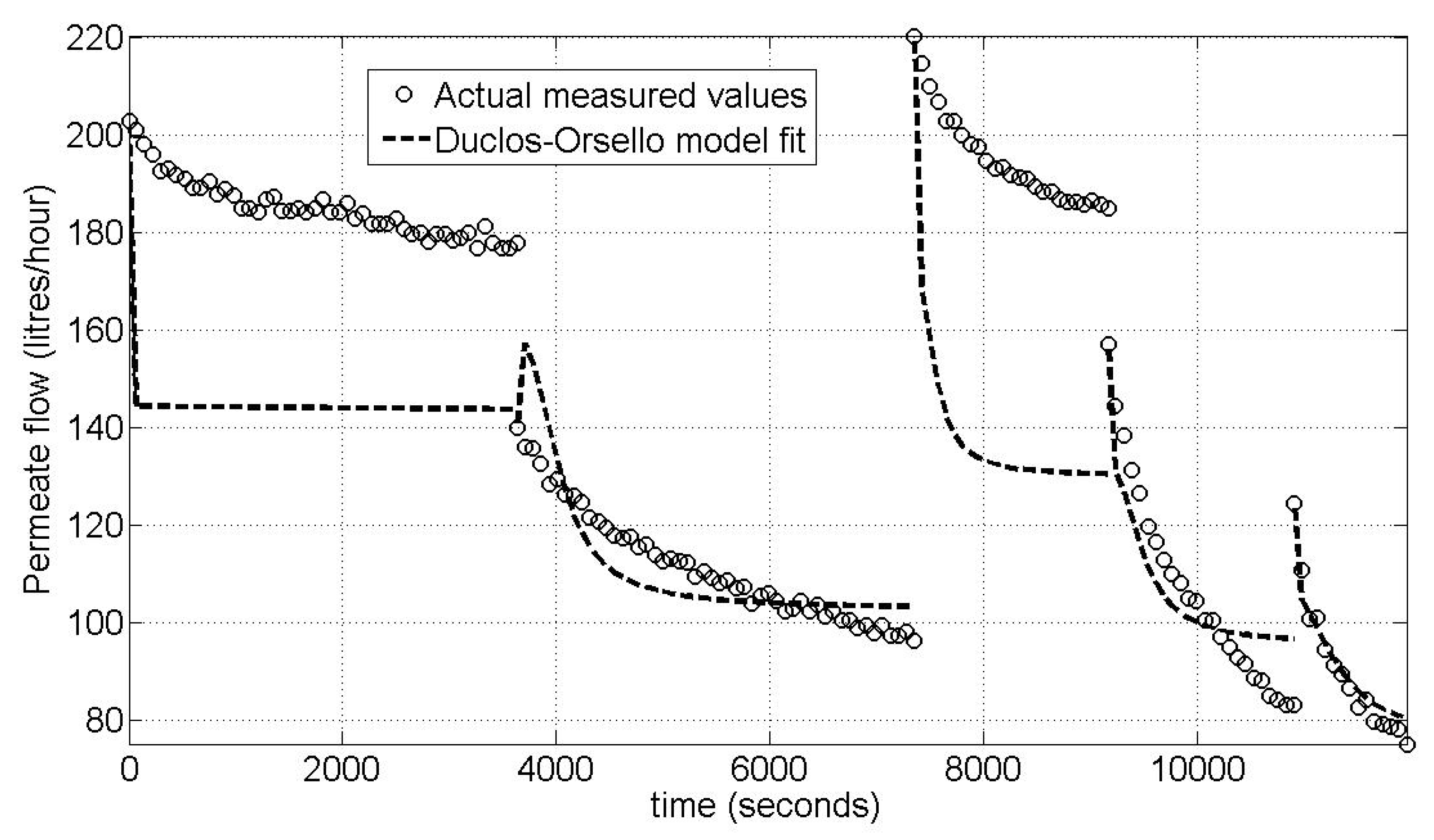
4.3. Model Calibration Results for Pilot MBR Plant—Fit for 5 Flux Steps at Constant TMP/Varying Flux Regime
4.4. Model Calibration Results for Pilot MBR Plant—Fit for Single Flux Step at Constant TMP/Varying Flux Regime

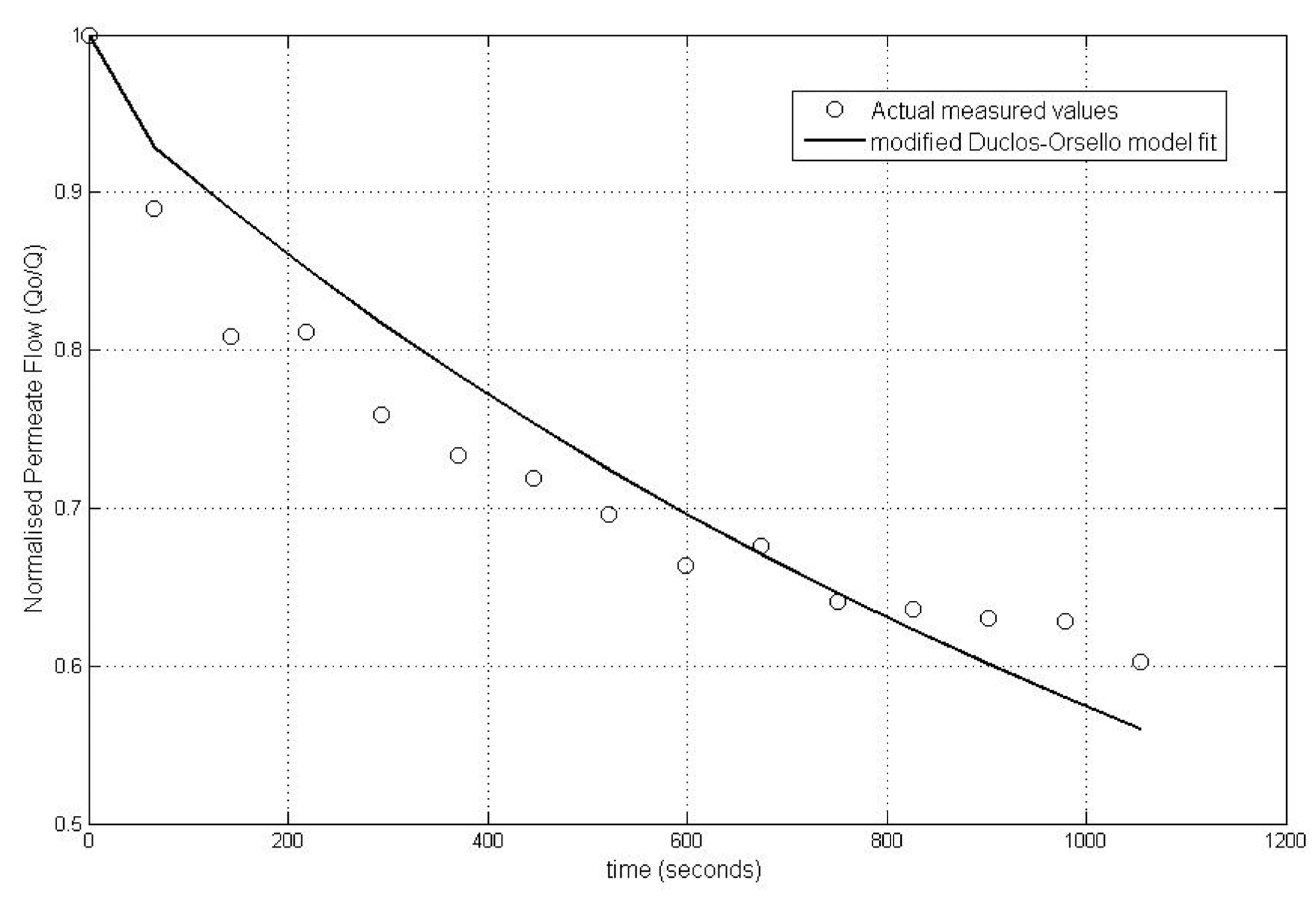
4.5. Model Validation Results for Pilot MBR Plant—Fit for Single Flux Step at Constant TMP/Varying Flux Regime
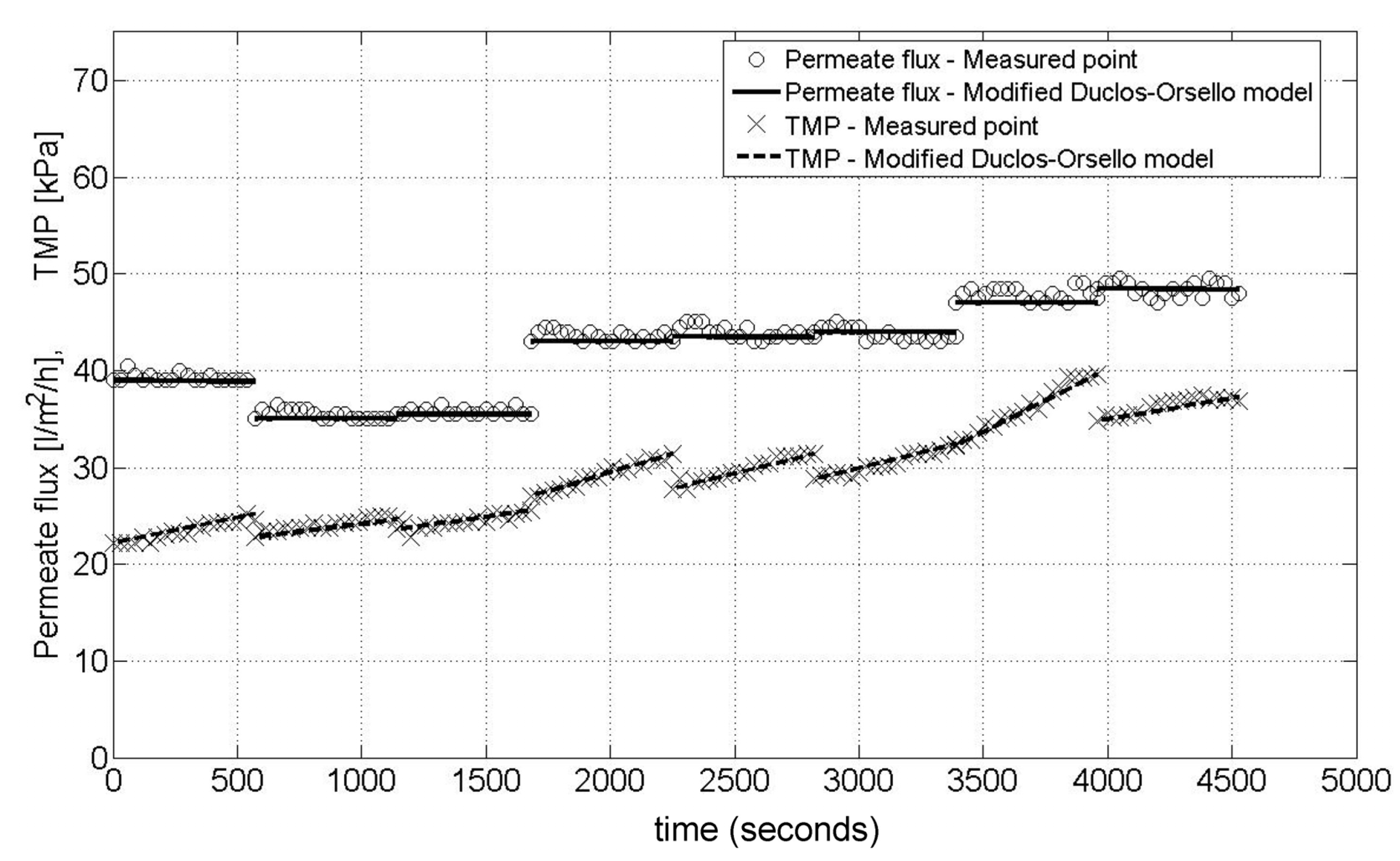
4.6. Pilot Membrane Filtration Unit—Fit for 8 Flux Steps at Constant Flux/Varying TMP
- -
- The membrane unit has no complex bioreactor (i.e., no significant biological and biochemical variations to be considered).
- -
- Very low mixed liquor concentrations and subsequent very low SMP levels gave an extremely consistent membrane performance.
- -
- The plant flow train is simple. Also the entire flux stepping procedure is automated including the backwash procedure, meaning it is less prone to human error as compared to manually altering a throttle valve setting.
- -
- Other factors that influenced these exceptional results are this was a constant flux operation giving simpler hydrodynamics with no discontinuities in time between flux steps.
- -
- Also the plant had been operating consistently over a long period of time unlike the Aquabio pilot MBR plant. Further, the flux stepping tests all occurred on the same day, and also the air sparging procedure used to clean the membrane was at a very high rate (i.e., much higher than for a full size commercial unit) and occurred continuously even during the backwashes. This meant extreme membrane clogging was very unlikely.
4.7. Summarising Model Fitting Results for Both Sets of Data from the Pilot Units
| Plant type and flux step combo | Best GA fit | Mean GA fit |
|---|---|---|
| Aquabio—all 5 flux steps | 72.1059 | 75.9315 |
| Aquabio—single flux step | 1.9425 | 2.2955 |
| ITT pilot unit Cardiff—all 8 flux steps | 0.037944 | 1.0377 |
| Plant type and flux step combo | α | β | f′R′ | Rp0/Rm | kp | kb | frp | frAU |
|---|---|---|---|---|---|---|---|---|
| Aquabio—all 5 flux steps | 6934 | 0.07 | 9184 | 0.17 | 43.50 | 12.50 | 0.98 | 0.013 |
| Aquabio—single flux step | 5237 | 1.80 | 6909 | 0.66 | 83.94 | 359 | 0.53 | 0.73 |
| ITT pilot unit Cardiff—all 8 flux steps | 3469 | 0.14 | 8079 | 0.56 | 183 | 694 | 0.97 | 0.26 |
5. Conclusions
Acknowledgments
Nomenclature
| Cb | Bulk concentration (g/L) |
| f′ | Fractional amount of total foulant contributing to deposit growth |
| J0 | Initial flux rate of clean membrane (m/s) |
| Qt | Total volumetric flow rate (m3/s) |
| Q0 | Initial volumetric flow rate (m3/s) |
| Rm | Resistance of the clean membrane (m−1) |
| Rp0 | Original resistance of the deposit (m−1) |
| R′ | Specific protein layer resistance (m/kg) |
| Rp | Resistance of the deposit (m−1) |
| t | Filtration time (s) |
| tp | Filtration time after initial membrane blocking occurs(s) |
| Δp | Constant total trans-membrane pressure (Pa) |
Greek letters
| a | Pore blockage parameter (m2/kg) |
| β | Pore constriction parameter (kg) |
Membrane surface scour terms
| kp | Membrane surface scour constant term related to cake resistance |
| kb | Membrane surface scour constant term related to unblocked area |
| A0(afterBW) | Original unblocked area after backwash interval (m2) |
Backwash mode terms
| Rp(afterBW) | Cake resistance after backwash interval (m−1) |
| Rp(beforeBW) | Cake resistance before backwash interval (m−1) |
| frp | Cake resistance recovery constant term |
| A0 | Original area before backwash commences (m2) |
| AU(beforeBW) | Unblocked area before backwash interval (m2) |
| frAU | Unblocked area recovery constant term |
SMP term
| SSMP | Concentration of SMP in the sludge water (g/L) |
Variable TMP term
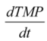 | Rate of change of Δp |
Liang membrane fouling model
| Rr | Reversible (cake) resistance (m−1) |
| a | Specific cake resistance (m/kg) |
| kr | Fouling strength factor (m/kg) |
References
- Le-Clech, P.; Chen, V.; Fane, A.G. Fouling in membrane bioreactors used in wastewater treatment. J. Membr. Sci. 2006, 284, 17–53. [Google Scholar] [CrossRef]
- Cho, B.D.; Fane, A.G. Fouling transients in nominally sub-critical flux operation of a membrane bioreactor. J. Membr. Sci. 2002, 209, 391–403. [Google Scholar] [CrossRef]
- Ye, Y.; Le-Clech, P.; Chen, V.; Fane, A.G.; Jefferson, B. Fouling mechanisms of alginate solutions as model extracellular polymeric substances. Desalination 2005, 175, 7–20. [Google Scholar] [CrossRef]
- Chang, S.; Fane, T.G.; Waite, T.D. Effect of coagulation within the cake layer on fouling transitions with dead-end hollow fiber membranes. In Proceedings of the International Congress on Membranes and Membrane Processes (ICOM), Seoul, Korea, 21–26 August 2005.
- Hermanowicz, S.W. Membrane filtration of biological solids: a unified framework and its applications to MBR. In Proceedings of the Water Environment-Membrane Technology Conference, Seoul, Korea, 7–10 June 2004.
- Kim, J.; DiGiano, F.A. Fouling models for low-pressure membrane systems. Sep. Purif. Technol. 2009, 68, 293–304. [Google Scholar] [CrossRef]
- Ng, A.; Albert, N.L.; Kim, S. A mini-review of modeling studies on membrane bioreactor (MBR) treatment for municipal wastewaters. Desalination 2007, 212, 261–281. [Google Scholar] [CrossRef]
- Broeckmann, A.; Busch, J.; Wintgens, T.; Marquardt, W. Modeling of pore blocking and cake layer formation in membrane filtration for wastewater treatment. Desalination 2006, 189, 97–109. [Google Scholar] [CrossRef]
- Busch, J.; Cruse, A.; Marquardt, W. Modeling submerged hollow-fiber membrane filtration for wastewater treatment. J. Membr. Sci. 2007, 288, 94–111. [Google Scholar] [CrossRef]
- Gehlert, G.; Abdulkadir, M.; Fuhrmann, J.; Hapke, J. Dynamic modeling of an ultrafiltration module for use in a membrane bioreactor. J. Membr. Sci. 2005, 248, 63–71. [Google Scholar] [CrossRef]
- Zarragoitia-Gonzalez, A.; Schetrite, S.; Alliet, M.; Jauregui-Haza, U.; Albasi, C. Modelling of submerged membrane bioreactor: Conceptual study about link between activated sludge biokinetics, aeration and fouling process. J. Membr. Sci. 2008, 325, 612–624. [Google Scholar] [CrossRef]
- Lee, Y.; Cho, J.; Seo, Y.; Lee, J.W.; Ahn, K.H. Modeling of submerged membrane bioreactor process for wastewater treatment. Desalination 2002, 146, 451–457. [Google Scholar] [CrossRef]
- Wintgens, T.; Rosen, J.; Melin, T.; Brepols, C.; Drensla, K.; Engelhardt, N. Modelling of a membrane bioreactor system for municipal wastewater treatment. J. Membr. Sci. 2003, 216, 55–65. [Google Scholar] [CrossRef]
- Ognier, S.; Wisniewski, C.; Grasmick, A. Membrane bioreactor fouling in sub-critical filtration conditions: a local critical flux concept. J. Membr. Sci. 2004, 229, 171–177. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, V.; Fane, A.G. Modeling long-term subcritical filtration of model EPS solutions. Desalination 2006, 191, 318–327. [Google Scholar] [CrossRef]
- Psoch, C.; Schiewer, S. Resistance analysis for enhanced wastewater membrane filtration. J. Membr. Sci. 2006, 280, 284–297. [Google Scholar] [CrossRef]
- Hermia, J. Constant pressure blocking filtration law: Application to power law non-Newtonian fluids. Trans. Inst. Chem. Eng. 1982, 60, 183–187. [Google Scholar]
- Ho, C.C.; Zydney, A.L. A combined pore blockage and cake filtration model for protein fouling during microfiltration. J. Colloid Interface Sci. 2000, 232, 389–399. [Google Scholar]
- Duclos-Orsello, C.; Li, W.; Ho, C. A three mechanism model to describe fouling of microfiltration membranes. J. Membr. Sci. 2006, 280, 856–866. [Google Scholar] [CrossRef]
- Yoo, C.K.; Vanrolleghem, P.A.; In-Beum, L. Nonlinear modeling and adaptive monitoring with fuzzy and multivariate statistical methods in biological wastewater treatment plants. J. Biotechnol. 2003, 105, 135–163. [Google Scholar]
- Drews, A.; Mante, J.; Iversen, V.; Vocks, M.; Lesjean, B.; Kraume, M. Does fouling in MBRs depend on SMP? Desalination 2008, 231, 141–149. [Google Scholar] [CrossRef]
- Paul, P.; Ulanicki, B.; Lueder, F. Development of a microfiltration fouling model to be linked to the biology of an MBR system. In Proceedings of the 7th Aachen Membranes and Water Conference, Aachen, Germany, 30–31 October 2007.
- Paul, P. Using Traditional Modelling Approaches for a MBR System to Investigate Alternate Approaches based on System Identification Procedures for Improved Design and Control of a Wastewater Treatment Process. Ph.D. Thesis, Department of Engineering, Faculty of Technology, De Montfort University, Leicester, UK, September 2011. [Google Scholar]
- Liang, S.; Song, L.; Tao, G.; Kekre, K.A.; Seah, H. A modeling study of fouling development in membrane bioreactors for wastewater treatment. Water Environ. Res. 2006, 78, 857–863. [Google Scholar] [CrossRef]
- Janus, T.; Paul, P.; Ulanicki, B. Modelling and simulation of short and long term membrane filtration experiments. Desalin. Water Treat. 2009, 8, 37–47. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Paul, P. Development and Testing of a Fully Adaptable Membrane Bioreactor Fouling Model for a Sidestream Configuration System. Membranes 2013, 3, 24-43. https://doi.org/10.3390/membranes3020024
Paul P. Development and Testing of a Fully Adaptable Membrane Bioreactor Fouling Model for a Sidestream Configuration System. Membranes. 2013; 3(2):24-43. https://doi.org/10.3390/membranes3020024
Chicago/Turabian StylePaul, Parneet. 2013. "Development and Testing of a Fully Adaptable Membrane Bioreactor Fouling Model for a Sidestream Configuration System" Membranes 3, no. 2: 24-43. https://doi.org/10.3390/membranes3020024
APA StylePaul, P. (2013). Development and Testing of a Fully Adaptable Membrane Bioreactor Fouling Model for a Sidestream Configuration System. Membranes, 3(2), 24-43. https://doi.org/10.3390/membranes3020024




