Research Progress of Computational Fluid Dynamics in Mixed Ionic–Electronic Conducting Oxygen-Permeable Membranes
Abstract
1. Introduction
2. Fundamentals of MIEC Oxygen-Permeable Membranes
- (1)
- Feed-side convection and diffusion: Oxygen molecules undergo physical adsorption onto membrane surfaces at the feed side through interactions with active surface sites, where adsorption efficiency is determined by binding energy and surface chemical characteristics.
- (2)
- Feed-side surface exchange: Adsorbed oxygen molecules dissociate into atomic oxygen species via surface catalytic reactions. This energy-intensive process requires overcoming activation barriers, typically achieved through thermal activation or catalytic mediation.
- (3)
- Bulk-phase diffusion: Dissociated oxygen atoms are incorporated into the crystal lattice as ionic species through coordination with metal cations, concurrently generating oxygen vacancies that serve as migration pathways. This step involves electron liberation and initiates oxygen ion migration through vacancy-mediated hopping mechanisms.
- (4)
- Permeate-side surface exchange: Migrated oxygen ions recombine into molecular oxygen at the permeate side under partial pressure gradients. The desorption process necessitates overcoming specific energy thresholds to complete the net oxygen transfer across the membrane.
- (5)
- Permeate-side convection and diffusion: Liberated oxygen molecules desorb from the membrane surface and diffuse into the low-oxygen partial pressure gas phase, completing the transmembrane transport cycle.
3. CFD Modeling of MIEC Oxygen-Permeable Membranes
3.1. Mathematical Models
3.1.1. Oxygen Permeation Models

3.1.2. Mass Conservation
3.1.3. Momentum Conservation
3.1.4. Energy Balance
3.1.5. Component Transport
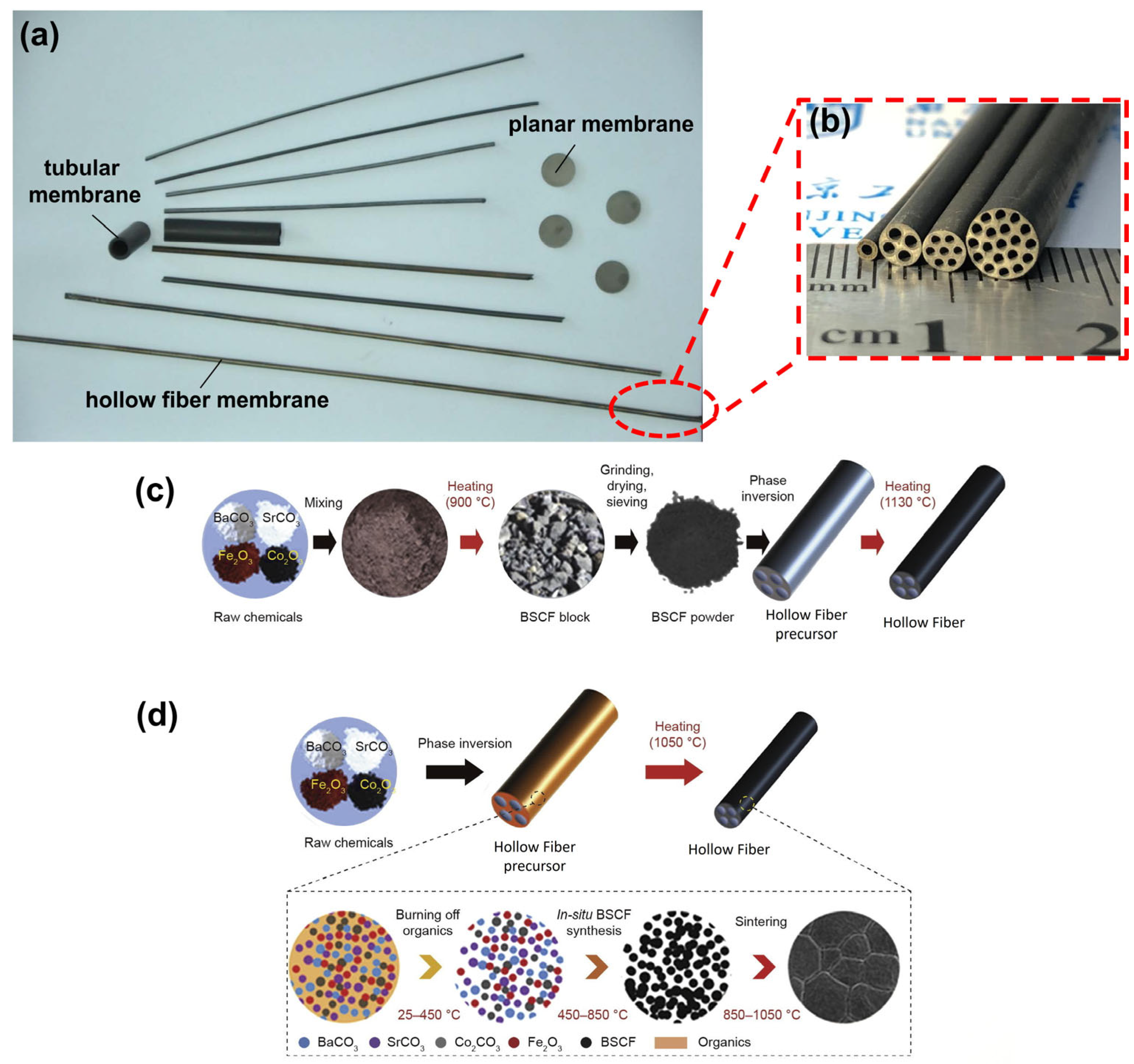
3.2. Geometric Models

4. Application of CFD in MIEC Oxygen-Permeable Membranes
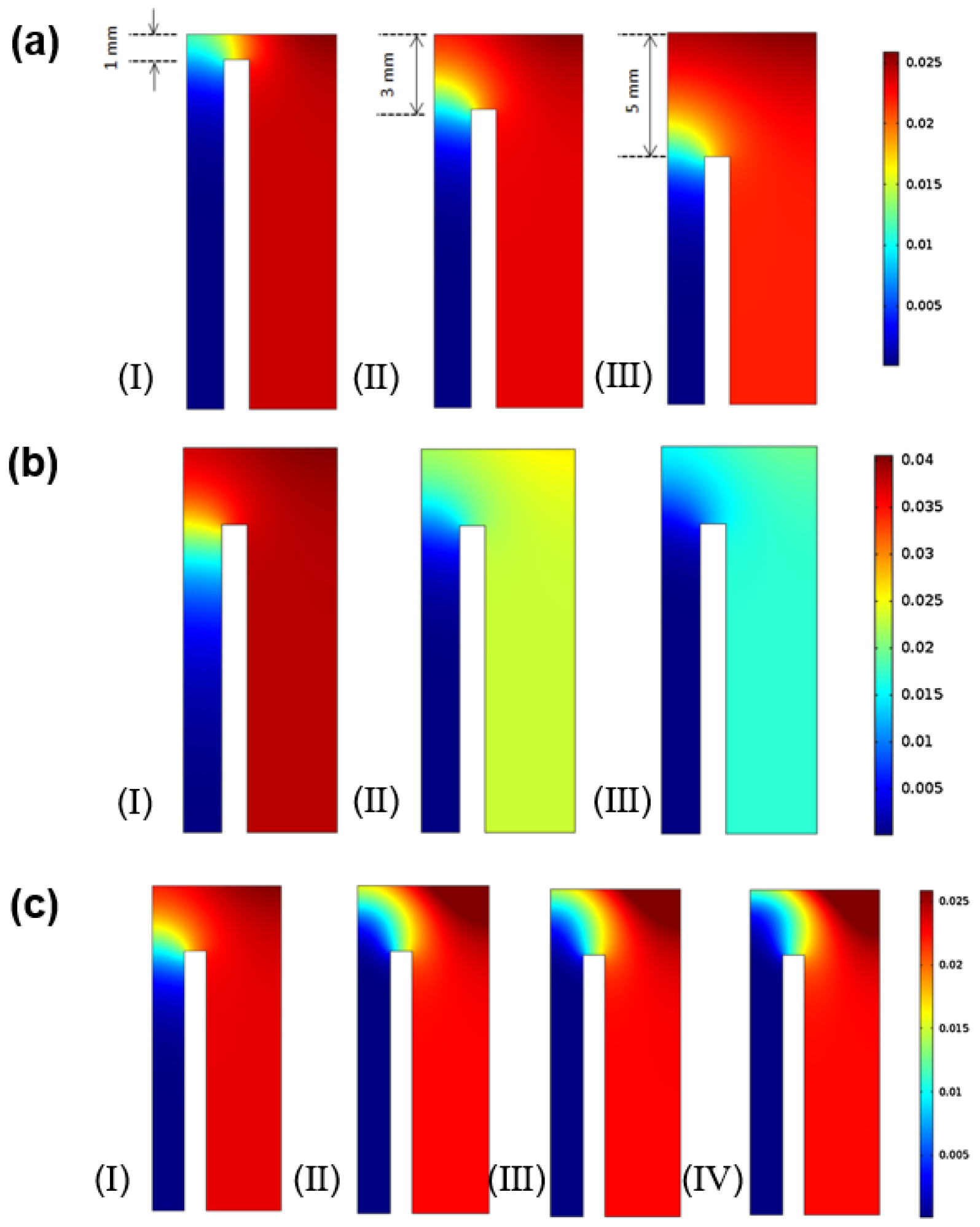
4.1. CFD Studies of Heat and Mass Transfer Phenomena
4.2. CFD Studies of Membrane Reactor Design
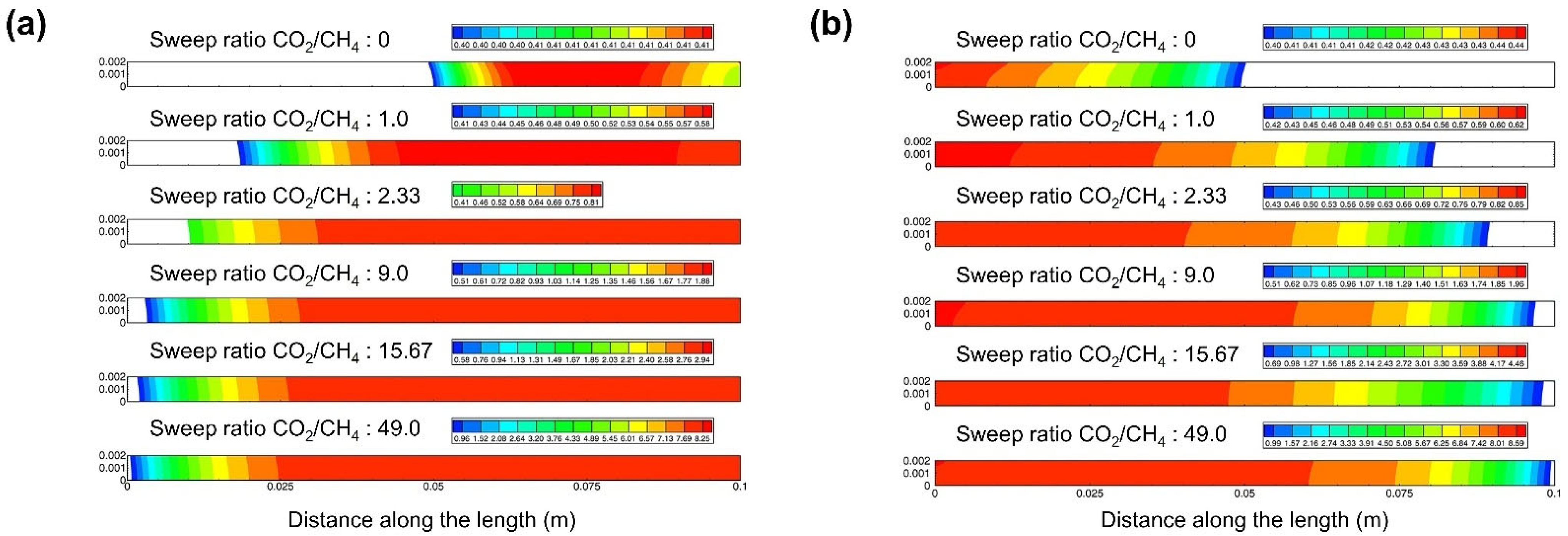
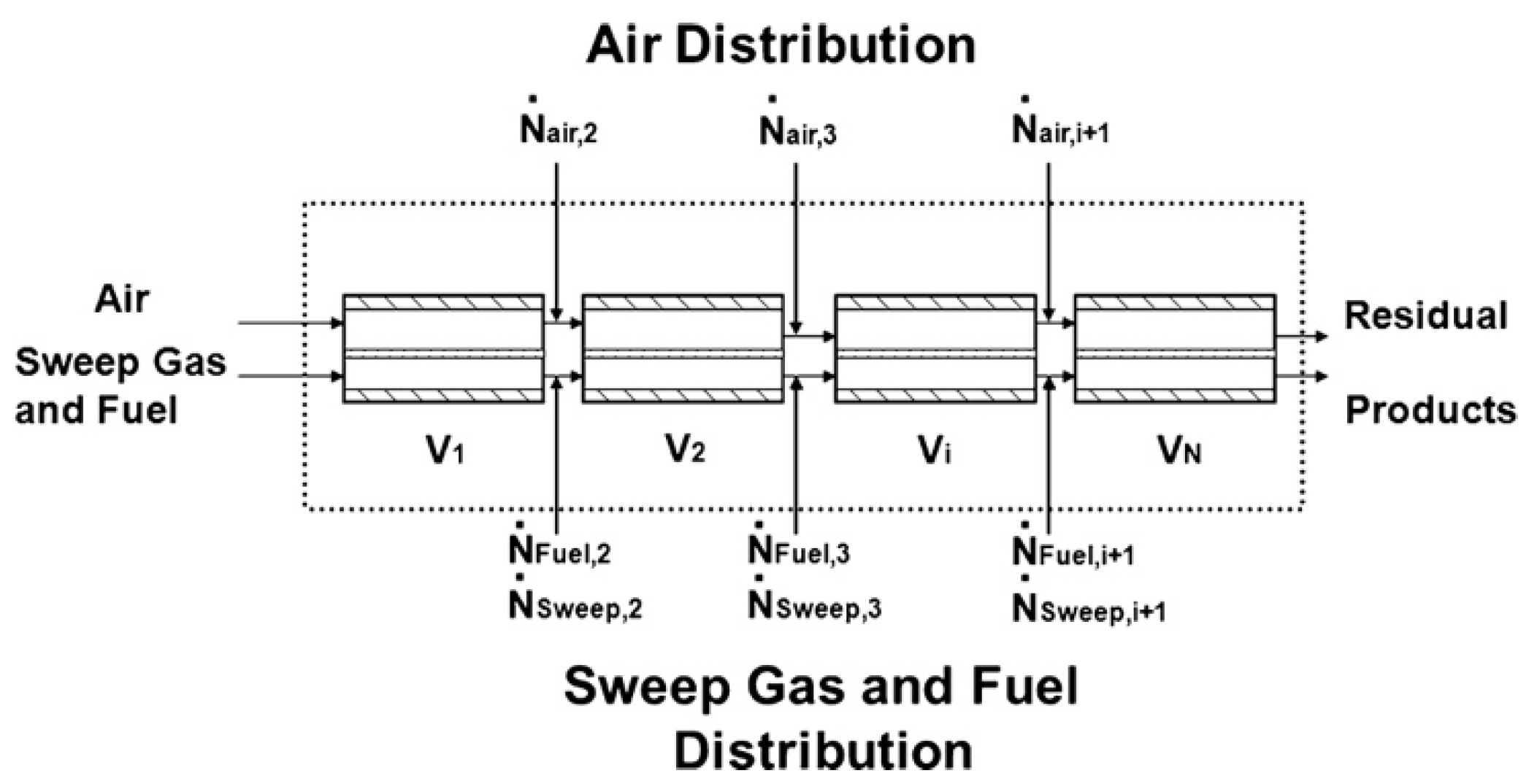
4.3. CFD Studies of Membrane Module Design
5. Challenges and Prospects of CFD in MIEC Oxygen-Permeable Membranes
5.1. Challenges
5.2. Prospects
5.2.1. ML in CFD-Based Membrane Design
5.2.2. DTs in CFD-Based Membrane Design
5.2.3. MD in CFD-Based Membrane Design
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, W.S.; Wang, H.H.; Zhu, X.F.; Liu, L.W. Development and application of oxygen permeable membrane in selective oxidation of light alkanes. Top. Catal. 2005, 35, 155–167. [Google Scholar] [CrossRef]
- Sunarso, J.; Hashim, S.S.; Zhu, N.; Zhou, W. Perovskite oxides applications in high temperature oxygen separation, solid oxide fuel cell and membrane reactor: A review. Prog. Energy Combust. Sci. 2017, 61, 57–77. [Google Scholar] [CrossRef]
- Zhang, C.; Sunarso, J.; Liu, S.M. Designing CO2-resistant oxygen-selective mixed ionic-electronic conducting membranes: Guidelines, recent advances, and forward directions. Chem. Soc. Rev. 2017, 46, 2941–3005. [Google Scholar] [CrossRef]
- Thursfield, A.; Murugan, A.; Franca, R.; Metcalfe, I.S. Chemical looping and oxygen permeable ceramic membranes for hydrogen production-a review. Energy Environ. Sci. 2012, 5, 7421–7459. [Google Scholar] [CrossRef]
- Zhu, X.F.; Yang, W.S. Microstructural and Interfacial Designs of Oxygen-Permeable Membranes for Oxygen Separation and Reaction-Separation Coupling. Adv. Mater. 2019, 31, 1902547. [Google Scholar] [CrossRef]
- Serrano, J.R.; Martín, J.; Gomez-Soriano, J.; Raggi, R. Theoretical and experimental evaluation of the spark-ignition premixed oxy-fuel combustion concept for future CO2 captive powerplants. Energy Convers. Manag. 2021, 244, 114498. [Google Scholar] [CrossRef]
- Serrano, J.R.; Bracho, G.; Gomez-Soriano, J.; Fernandes, C. Development of an Oxy-Fuel Combustion System in a Compression-Ignition Engine for Ultra-Low Emissions Powerplants Using CFD and Evolutionary Algorithms. Appl. Sci. 2022, 12, 7104. [Google Scholar] [CrossRef]
- Arnau, F.J.; Bracho, G.; García-Cuevas, L.M.; Farias, V.H. A strategy to extend load operation map range in oxy-fuel compression ignition engines with oxygen separation membranes. Appl. Therm. Eng. 2023, 226, 120268. [Google Scholar] [CrossRef]
- Serrano, J.R.; Arnau, F.J.; Calvo, A.; Burgos, R. Modeling and Evaluation of Oxy-Combustion and In Situ Oxygen Production in a Two-Stroke Marine Engine. Appl. Sci. 2023, 13, 10350. [Google Scholar] [CrossRef]
- Ishihara, T.; Takita, Y. Partial oxidation of methane into syngas with oxygen permeating ceramic membrane reactors. Catal. Surv. Jpn. 2000, 4, 125–133. [Google Scholar] [CrossRef]
- Elbadawi, A.H.; Ge, L.; Li, Z.H.; Liu, S.M.; Wang, S.B.; Zhu, Z.H. Catalytic partial oxidation of methane to syngas: Review of perovskite catalysts and membrane reactors. Catal. Rev. 2021, 63, 1–67. [Google Scholar] [CrossRef]
- Geffroy, P.M.; Fouletier, J.; Richet, N.; Chartier, T. Rational selection of MIEC materials in energy production processes. Chem. Eng. Sci. 2013, 87, 408–433. [Google Scholar] [CrossRef]
- Li, W.P.; Cao, Z.W.; Zhu, X.F.; Yang, W.S. High-Rate Hydrogen Separation Using an MIEC Oxygen Permeable Membrane Reactor. AIChE J. 2017, 63, 1278–1286. [Google Scholar] [CrossRef]
- Wu, X.-Y.; Chang, L.; Uddi, M.; Kirchen, P.; Ghoniem, A.F. Toward enhanced hydrogen generation from water using oxygen permeating LCF membranes. Phys. Chem. Chem. Phys. 2015, 17, 10093–10107. [Google Scholar] [CrossRef]
- Spallina, V.; Melchiori, T.; Gallucci, F.; Annaland, M. Auto-Thermal Reforming Using Mixed Ion-Electronic Conducting Ceramic Membranes for a Small-Scale H2 Production Plant. Molecules 2015, 20, 4998–5023. [Google Scholar] [CrossRef]
- Li, W.P.; Zhu, X.F.; Cao, Z.W.; Wang, W.P.; Yang, W.S. Mixed ionic-electronic conducting (MIEC) membranes for hydrogen production from water splitting. Int. J. Hydrogen Energy 2015, 40, 3452–3461. [Google Scholar] [CrossRef]
- Ghidossi, R.; Veyret, D.; Moulin, P. Computational fluid dynamics applied to membranes: State of the art and opportunities. Chem. Eng. Process 2006, 45, 437–454. [Google Scholar] [CrossRef]
- Keir, G.; Jegatheesan, V. A review of computational fluid dynamics applications in pressure-driven membrane filtration. Rev. Environ. Sci. Bio. 2014, 13, 183–201. [Google Scholar] [CrossRef]
- Shirazi, M.M.A.; Kargari, A.; Ismail, A.F.; Matsuura, T. Computational Fluid Dynamic (CFD) opportunities applied to the membrane distillation process: State-of-the-art and perspectives. Desalination 2016, 377, 73–90. [Google Scholar] [CrossRef]
- Toh, K.Y.; Liang, Y.Y.; Lau, W.J.; Weihs, F.; Gustavo, A. A Review of CFD Modelling and Performance Metrics for Osmotic Membrane Processes. Membranes 2020, 10, 285. [Google Scholar] [CrossRef]
- Foo, K.; Liang, Y.Y.; Goh, P.S.; Fletcher, D.F. Computational fluid dynamics simulations of membrane gas separation: Overview, challenges and future perspectives. Chem. Eng. Res. Des. 2023, 191, 127–140. [Google Scholar] [CrossRef]
- Ma, L.; Ingham, D.B.; Pourkashanian, M.; Carcadea, E. Review of the computational fluid dynamics modeling of fuel cells. J. Fuel. Cell Sci. Technol. 2005, 2, 246–257. [Google Scholar] [CrossRef]
- Janardhanan, V.M.; Deutschmann, O. Modeling of solid-oxide fuel cells. Z. Phys. Chem. 2007, 221, 443–478. [Google Scholar] [CrossRef]
- Dhanasekaran, A.; Subramanian, Y.; Omeiza, L.A.; Raj, V.; Yassin, H.P.H.M.; Sa, M.A.; Azad, A.K.K. Computational Fluid Dynamics for Protonic Ceramic Fuel Cell Stack Modeling: A Brief Review. Energies 2023, 16, 208. [Google Scholar] [CrossRef]
- Chen, G.X.; Feldhoff, A.; Weidenkaff, A.; Li, C.; Liu, S.M.; Zhu, X.F.; Sunarso, J.; Huang, K.; Wu, X.; Choniem, A.F.; et al. Roadmap on Sustainable Mixed Ionic-Electronic Conducting Membranes. Adv. Funct. Mater. 2022, 32, 2105702. [Google Scholar] [CrossRef]
- Sunarso, J.; Baumann, S.; Serra, J.M.; Meulenberg, W.A.; Liu, S.; Lin, Y.S.; da Costa, J.C.D. Mixed ionic-electronic conducting (MIEC) ceramic-based membranes for oxygen separation. J. Membr. Sci. 2008, 320, 13–41. [Google Scholar] [CrossRef]
- Sahini, M.G.; Mwankemwa, B.S.; Kanas, N. BaxSr1−xCoyFe1−yO3−δ (BSCF) mixed ionic-electronic conducting (MIEC) materials for oxygen separation membrane and SOFC applications: Insights into processing, stability, and functional properties. Ceram. Int. 2022, 48, 2948–2964. [Google Scholar] [CrossRef]
- Schlehuber, D.; Wessel, E.; Singheiser, L.; Markus, T. Long-term operation of a La0.58Sr0.4Co0.2Fe0.8O3−δ-membrane for oxygen separation. J. Membr. Sci. 2010, 351, 16–20. [Google Scholar] [CrossRef]
- Jin, W.Q.; Xu, N.P. Mixed–Conducting Oxygen–Permeation Materials (Book); Science Press: Beijing, China, 2013. [Google Scholar]
- Zhang, C.; Xu, Z.; Chang, X.F.; Zhang, Z.C.; Jin, W.Q. Preparation and characterization of mixed-conducting thin tubular membrane. J. Membr. Sci. 2007, 299, 261–267. [Google Scholar] [CrossRef]
- Wang, H.H.; Cong, Y.; Yang, W.S. Oxygen permeation study in a tubular Ba0.5Sr0.5Co0.8Fe0.2O3−δ oxygen permeable membrane. J. Membr. Sci. 2002, 210, 259–271. [Google Scholar] [CrossRef]
- Shubnikova, E.V.; Popov, M.P.; Bychkov, S.F.; Chizhik, S.A.; Nemudry, A.P. The modeling of oxygen transport in MIEC oxide hollow fiber membranes. Chem. Eng. Sci. 2019, 372, 251–259. [Google Scholar] [CrossRef]
- Gao, J.; Lun, Y.T.; Hu, Y.D.; You, Z.J.; Tan, X.Y.; Wang, S.B.; Sunarso, J.; Liu, S.M. The effect of A-site element on CO2 resistance of O2-selective La-based perovskite hollow fibers. J. Ind. Eng. Chem. 2017, 53, 276–284. [Google Scholar] [CrossRef]
- Zhu, J.W.; Zhang, G.R.; Liu, G.P.; Liu, Z.K.; Jin, W.Q.; Xu, N.P. Perovskite Hollow Fibers with Precisely Controlled Cation Stoichiometry via One-Step Thermal Processing. Adv. Mater. 2017, 29, 1606377. [Google Scholar] [CrossRef]
- Wang, T.L.; Fan, Z.; Wang, S.F.; Zheng, Q.K.; Tan, J.K.; Liu, Z.K.; Zhang, G.R.; Jin, W.Q. One-step thermal processing of BaCe0.8Y0.2O3−δ hydrogen permeable multichannel hollow fiber membrane. AIChE J. 2022, 68, e17607. [Google Scholar] [CrossRef]
- Wang, T.L.; Liu, Z.K.; Xu, X.L.; Zhu, J.W.; Zhang, G.R.; Jin, W.Q. Insights into the design of nineteen-channel perovskite hollow fiber membrane and its oxygen transport behaviour. J. Membr. Sci. 2020, 595, 117600. [Google Scholar] [CrossRef]
- Han, N.; Zhang, W.; Guo, W.; Xie, S.J.; Zhang, C.; Zhang, X.; Fransaer, J.; Liu, S.M. Novel oxygen permeable hollow fiber perovskite membrane with surface wrinkles. Sep. Purif. Technol. 2021, 261, 118295. [Google Scholar] [CrossRef]
- Manning, P.S.; Sirman, J.D.; Kilner, J.A. Oxygen self-diffusion and surface exchange studies of oxide electrolytes having the fluorite structure. Solid State Ion. 1996, 93, 125–132. [Google Scholar] [CrossRef]
- Ishihara, T.; Kilner, J.A.; Honda, M.; Sakai, N.; Yokokawa, H.; Takita, Y. Oxygen surface exchange and diffusion in LaGaO3 based perovskite type oxides. Solid State Ion. 1998, 113, 593–600. [Google Scholar] [CrossRef]
- Ruiz-Trejo, E.; Sirman, J.D.; Baikov, Y.M.; Kilner, J.A. Oxygen ion diffusivity, surface exchange and ionic conductivity in single crystal Gadolinia doped Ceria. Solid State Ion. 1998, 113, 565–569. [Google Scholar] [CrossRef]
- Lane, J.A.; Kilner, J.A. Oxygen surface exchange on gadolinia doped ceria. Solid State Ion. 2000, 136, 927–932. [Google Scholar] [CrossRef]
- Li, C.D.; Chew, J.J.; Mahmoud, A.; Liu, S.M.; Sunarso, J. Modelling of oxygen transport through mixed ionic-electronic conducting (MIEC) ceramic-based membranes: An overview. J. Membr. Sci. 2018, 567, 228–260. [Google Scholar] [CrossRef]
- Niehoff, P.; Baumann, S.; Schulze-Küppers, F.; Bradley, R.S.; Shapiro, I.; Meulenberg, W.A.; Withers, P.J.; Vassen, R. Oxygen transport through supported Ba0.5Sr0.5Co0.8Fe0.2O3−δ membranes. Sep. Purif. Technol. 2014, 121, 60–67. [Google Scholar] [CrossRef]
- Xu, S.J.; Thomson, W.J. Oxygen permeation rates through ion-conducting perovskite membranes. Chem. Eng. Sci. 1999, 54, 3839–3850. [Google Scholar] [CrossRef]
- Lin, Y.S.; Wang, W.J.; Han, J.H. Oxygen Permeation Through Thin Mixed-Conducting Solid Oxide Membranes. AIChE J. 1994, 40, 786–798. [Google Scholar] [CrossRef]
- Kim, S.; Yang, Y.L.; Jacobson, A.J.; Abeles, B. Oxygen surface exchange in mixed ionic electronic conductor membranes. Solid State Ion. 1999, 121, 31–36. [Google Scholar] [CrossRef]
- Tan, X.Y.; Li, K. Modeling of air separation in a LSCF hollow-fiber membrane module. AIChE J. 2002, 48, 1469–1477. [Google Scholar] [CrossRef]
- Zhu, X.F.; Liu, H.Y.; Cong, Y.; Yang, W.S. Permeation model and experimental investigation of mixed conducting membranes. AIChE J. 2012, 58, 1744–1754. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, W.P.; Liu, Y.; Zhu, X.F.; Yang, W.S. Selection of Oxygen Permeation Models for Different Mixed Ionic-Electronic Conducting Membranes. AIChE J. 2017, 63, 4043–4053. [Google Scholar] [CrossRef]
- Liu, S.M.; Gavalas, G.R. Oxygen selective ceramic hollow fiber membranes. J. Membr. Sci. 2005, 246, 103–108. [Google Scholar] [CrossRef]
- Nemitallah, M.A.; Habib, M.A.; Mezghani, K. Experimental and numerical study of oxygen separation and oxy-combustion characteristics inside a button-cell LNO-ITM reactor. Energy 2015, 84, 600–611. [Google Scholar] [CrossRef]
- Gozálvez-Zafrilla, J.M.; Santafé-Moros, A.; Escolástico, S.; Serra, J.M. Fluid dynamic modeling of oxygen permeation through mixed ionic-electronic conducting membranes. J. Membr. Sci. 2011, 378, 290–300. [Google Scholar] [CrossRef]
- Hong, J.; Kirchen, P.; Ghoniem, A.F. Numerical simulation of ion transport membrane reactors: Oxygen permeation and transport and fuel conversion. J. Membr. Sci. 2012, 407, 71–85. [Google Scholar] [CrossRef]
- Engels, S.; Beggel, F.; Modigell, M.; Stadler, H. Simulation of a membrane unit for oxyfuel power plants under consideration of realistic BSCF membrane properties. J. Membr. Sci. 2010, 359, 93–101. [Google Scholar] [CrossRef]
- Tan, X.Y.; Li, K.; Thursfield, A.; Metcalfe, I.S. Oxyfuel combustion using a catalytic ceramic membrane reactor. Catal. Today 2008, 131, 292–304. [Google Scholar] [CrossRef]
- Balachandran, U.; Dusek, J.T.; Mieville, R.L.; Poeppel, R.B.; Kleefisch, M.S.; Pei, S.; Kobylinski, T.P.; Udovich, C.A.; Bose, A.C. Dense ceramic membranes for partial oxidation of methane to syngas. Appl. Catal. A-Gen. 1995, 133, 19–29. [Google Scholar] [CrossRef]
- Bouwmeester, H.J.M. Dense ceramic membranes for methane conversion. Catal. Today 2003, 82, 141–150. [Google Scholar] [CrossRef]
- Jin, W.Q.; Li, S.G.; Huang, P.; Xu, N.P.; Shi, J.; Lin, Y.S. Tubular lanthanum cobaltite perovskite-type membrane reactors for partial oxidation of methane to syngas. J. Membr. Sci. 2000, 166, 13–22. [Google Scholar] [CrossRef]
- Smit, J.; Zhang, W.X.; Annaland, M.V.; Kuipers, J.A.M. Feasibility study of a novel membrane reactor for syngas production Part 2: Adiabatic reactor simulations. J. Membr. Sci. 2007, 291, 33–45. [Google Scholar] [CrossRef]
- Tan, X.Y.; Li, K. Design of Mixed Conducting Ceramic Membranes/Reactors for the Partial Oxidation of Methane to Syngas. AIChE J. 2009, 55, 2675–2685. [Google Scholar] [CrossRef]
- Wang, W.; Lin, Y.S. Analysis of oxidative coupling of methane in dense oxide membrane reactors. J. Membr. Sci. 1995, 103, 219–233. [Google Scholar] [CrossRef]
- Tenelshof, J.E.; Bouwmeester, H.J.M.; Verweij, H. Oxidative coupling of methane in a mixed-conducting perovskite membrane reactor. Appl. Catal. A-Gen. 1995, 130, 195–212. [Google Scholar] [CrossRef]
- Jin, W.Q.; Zhang, C.; Zhang, P.; Fan, Y.Q.; Xu, N.P. Thermal decomposition of carbon dioxide coupled with POM in a membrane reactor. AIChE J. 2006, 52, 2545–2550. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, W.Q.; Yang, C.; Xu, N.P. Decomposition of CO2 coupled with POM in a thin tubular oxygen-permeable membrane reactor. Catal. Today 2009, 148, 298–302. [Google Scholar] [CrossRef]
- Wu, X.Y.; Ghoniem, A.F.; Uddi, M. Enhancing co-production of H2 and syngas via water splitting and POM on surface-modified oxygen permeable membranes. AIChE J. 2016, 62, 4427–4435. [Google Scholar] [CrossRef]
- Wu, X.Y.; Ghoniem, A.F. CO2 reduction and methane partial oxidation on surface catalyzed La0.9Ca0.1FeO3−δ oxygen transport membranes. Proc. Combust. Inst. 2019, 37, 5517–5524. [Google Scholar] [CrossRef]
- Hunt, A.; Dimitrakopoulos, G.; Kirchen, P.; Ghoniem, A.F. Measuring the oxygen profile and permeation flux across an ion transport (La0.9Ca0.1FeO3−δ) membrane and the development and validation of a multistep surface exchange model. J. Membr. Sci. 2014, 468, 62–72. [Google Scholar] [CrossRef]
- Farooqui, A.E.; Badr, H.M.; Habib, M.A.; Ben-Mansour, R. Numerical investigation of combustion characteristics in an oxygen transport reactor. Int. J. Energy Res. 2014, 38, 638–651. [Google Scholar] [CrossRef]
- Tan, X.Y.; Liu, Y.T.; Li, K. Mixed conducting ceramic hollow-fiber membranes for air separation. AIChE J. 2005, 51, 1991–2000. [Google Scholar] [CrossRef]
- Farooqui, A.E.; Habib, M.A.; Badr, H.M.; Ben-Mansour, R. Modeling of ion transport reactor for oxy-fuel combustion. Int. J. Energy Res. 2013, 37, 1265–1279. [Google Scholar] [CrossRef]
- Coroneo, M.; Montante, G.; Baschetti, M.G.; Paglianti, A. CFD modelling of inorganic membrane modules for gas mixture separation. Chem. Eng. Sci. 2009, 64, 1085–1094. [Google Scholar] [CrossRef]
- Coroneo, M.; Montante, G.; Catalano, J.; Paglianti, A. Modelling the effect of operating conditions on hydrodynamics and mass transfer in a Pd-Ag membrane module for H2 purification. J. Membr. Sci. 2009, 343, 34–41. [Google Scholar] [CrossRef]
- Catálan-Martínez, D.; Santafé-Moros, A.; Gozálvez-Zafrilla, J.M.; García-Fayos, J.; Serra, J.M. Characterization of oxygen transport phenomena on BSCF membranes assisted by fluid dynamic simulations including surface exchange. Chem. Eng. J. 2020, 387, 124069. [Google Scholar] [CrossRef]
- Abdolahimansoorkhani, H.; Xue, X.J. Computational thermal fluid enabled multi-physics transport processes analysis of ceramic hollow fiber membrane for oxygen separation. Energy 2024, 306, 132552. [Google Scholar] [CrossRef]
- Habib, M.A.; Ahmed, P.; Ben-Mansour, R.; Mezghani, K.; Alam, Z.; Shao-Horn, Y.; Ghoniem, A.F. Experimental and Numerical Investigation of La2NiO4 Membranes for Oxygen Separation: Geometry Optimization and Model Validation. J. Energy Resour. Technol. 2015, 137, 031102. [Google Scholar] [CrossRef]
- Ahmed, P.; Habib, M.A.; Ben-Mansour, R.; Jamal, A. Investigation of oxygen permeation through disc-shaped BSCF ion transport membrane under reactive conditions. Int. J. Energy Res. 2017, 41, 1049–1062. [Google Scholar] [CrossRef]
- Chen, W.; Nauels, N.; Bouwmeester, H.J.M.; Nijmeijer, A.; Winnubst, L. An accurate way to determine the ionic conductivity of mixed ionic-electronic conducting (MIEC) ceramics. J. Eur. Ceram. Soc. 2015, 35, 3075–3083. [Google Scholar] [CrossRef]
- Adler, S.B. Chemical expansivity of electrochemical ceramics. J. Am. Ceram. Soc. 2001, 84, 2117–2119. [Google Scholar] [CrossRef]
- Kharton, V.V.; Yaremchenko, A.A.; Patrakeev, M.V.; Naumovich, E.N.; Marques, F.M.B. Thermal and chemical induced expansion of La0.3Sr0.7(Fe, Ga)O3−δ ceramics. J. Eur. Ceram. Soc. 2003, 23, 1417–1426. [Google Scholar] [CrossRef]
- Park, C.Y.; Jacobson, A.J. Thermal and chemical expansion properties of La0.2Sr0.8Fe0.55Ti0.45O3−x. Solid State Ion. 2005, 176, 2671–2676. [Google Scholar] [CrossRef]
- Chen, X.Y.; Yu, J.S.; Adler, S.B. Thermal and chemical expansion of Sr-doped lanthanum cobalt oxide (La1−xSrxCoO3−δ). Chem. Mater. 2005, 17, 4537–4546. [Google Scholar] [CrossRef]
- McIntosh, S.; Vente, J.F.; Haije, W.G.; Blank, D.H.A.; Bouwmeester, H.J.M. Oxygen stoichiometry and chemical expansion of Ba0.5Sr0.5Co0.8Fe0.2O3−δ measured by in situ neutron diffraction. Chem. Mater. 2006, 18, 2187–2193. [Google Scholar] [CrossRef]
- Zolochevsky, A.; Grabovskiy, A.V.; Parkhomenko, L.; Lin, Y.S. Coupling effects of oxygen surface exchange kinetics and membrane thickness on chemically induced stresses in perovskite-type membranes. Solid State Ion. 2012, 212, 55–65. [Google Scholar] [CrossRef]
- Bai, W.; Feng, J.X.; Fan, H.B.; Zhao, Y.J. Effect of fluid dynamics conditions and combustion reactions on the performance and heat and mass transfer distribution of dual-phase oxygen transport membranes. Therm. Sci. 2023, 27, 2751–2762. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Habib, M.A.; Badr, H.M.; Azharuddin; Nemitallah, M. Characteristics of Oxy-fuel Combustion in an Oxygen Transport Reactor. Energy Fuel. 2012, 26, 4599–4606. [Google Scholar] [CrossRef]
- Mancini, N.D.; Gunasekaran, S.; Mitsos, A. A Multiple-Compartment Ion-Transport-Membrane Reactive Oxygen Separator. Ind. Eng. Chem. Res. 2012, 51, 7988–7997. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Adebiyi, A.A.; Habib, M.A. Investigation of performance of fire-tube boilers integrated with ion transport membrane for oxy-fuel combustion. Int. J. Energy Res. 2016, 40, 1673–1687. [Google Scholar] [CrossRef]
- Mansir, I.B.; Ben-Mansour, R.; Habib, M.A. Numerical modeling of heat transfer characteristics in a two-pass oxygen transport reactor for fire tube boilers under oxy-fuel combustion. Appl. Therm. Eng. 2021, 195, 117248. [Google Scholar] [CrossRef]
- Mansir, I.B.; Ben-Mansour, R.; Habib, M.A. Oxy-fuel combustion in a two-pass oxygen transport reactor for fire tube boiler application. Appl. Energy 2018, 229, 828–840. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, C.S.; Ye, H. CFD Simulation of Syngas Combustion in a Two-Pass Oxygen Transport Membrane Reactor for Fire Tube Boiler Application. Energies 2021, 14, 7348. [Google Scholar] [CrossRef]
- Jin, W.Q.; Gu, X.H.; Li, S.G.; Huang, P.; Xu, N.P.; Shi, J. Experimental and simulation study on a catalyst packed tubular dense membrane reactor for partial oxidation of methane to syngas. Chem. Eng. Sci. 2000, 55, 2617–2625. [Google Scholar] [CrossRef]
- Zhang, W.X.; Smit, J.; Annaland, M.V.; Kuipers, J.A.M. Feasibility study of a novel membrane reactor for syngas production Part 1: Experimental study of O2 permeation through perovskite membranes under reducing and non-reducing atmospheres. J. Membr. Sci. 2007, 291, 19–32. [Google Scholar] [CrossRef]
- Habib, M.A.; Ben-Mansour, R.; Nemit-allah, M.A. Modeling of oxygen permeation through a LSCF ion transport membrane. Comput. Fluids 2013, 76, 1–10. [Google Scholar] [CrossRef]
- Glarborg, P.; Bentzen, L.L.B. Chemical effects of a high CO2 concentration in oxy-fuel combustion of methane. Energy Fuel. 2008, 22, 291–296. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Simplified Reaction Mechanisms for the Oxidation of Hydrocarbon Fuels in Flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Andersen, J.; Rasmussen, C.L.; Giselsson, T.; Glarborg, P. Global Combustion Mechanisms for Use in CFD Modeling under Oxy-Fuel Conditions. Energy Fuel. 2009, 23, 1379–1389. [Google Scholar] [CrossRef]
- Nemitallah, M.A.; Habib, M.A.; Ben-Mansour, R. Investigations of oxy-fuel combustion and oxygen permeation in an ITM reactor using a two-step oxy-combustion reaction kinetics model. J. Membr. Sci. 2013, 432, 1–12. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Nemitallah, M.A.; Habib, M.A. Numerical investigation of oxygen permeation and methane oxy-combustion in a stagnation flow ion transport membrane reactor. Energy 2013, 54, 322–332. [Google Scholar] [CrossRef]
- Nemitallah, M.A. A study of methane oxy-combustion characteristics inside a modified design button-cell membrane reactor utilizing a modified oxygen permeation model for reacting flows. J. Nat. Gas Sci. Eng. 2016, 28, 61–73. [Google Scholar] [CrossRef]
- Ahmed, P.; Habib, M.A.; Ben-Mansour, R.; Kirchen, P.; Ghoniem, A.F. CFD (computational fluid dynamics) analysis of a novel reactor design using ion transport membranes for oxy-fuel combustion. Energy 2014, 77, 932–944. [Google Scholar] [CrossRef]
- Habib, M.A.; Ahmed, P.; Ben-Mansour, R.; Badr, H.M.; Kirchen, P.; Ghoniem, A.F. Modeling of a combined ion transport and porous membrane reactor for oxy-combustion. J. Membr. Sci. 2013, 446, 230–243. [Google Scholar] [CrossRef]
- Nemitallah, M.A.; Mansir, I.B.; Habib, M.A. Experimental and numerical study of oxy-methane flames in a porous-plate reactor mimicking membrane reactor operation. Int. J. Energy Res. 2019, 43, 7040–7057. [Google Scholar] [CrossRef]
- Tahir, F.; Imteyaz, B.; Yasir, M.; Al-Ghamdi, S.G. Oxy-methane combustion characteristics in a vertical porous plate reactor. Energy Rep. 2023, 9, 2900–2910. [Google Scholar] [CrossRef]
- Kirchen, P.; Apo, D.J.; Hunt, A.; Ghoniem, A.F. A novel ion transport membrane reactor for fundamental investigations of oxygen permeation and oxy-combustion under reactive flow conditions. Proc. Combust. Inst. 2013, 34, 3463–3470. [Google Scholar] [CrossRef]
- Habib, M.A.; Salaudeen, S.A.; Nemitallah, M.A.; Ben-Mansour, R.; Mokheimer, E.M.A. Numerical investigation of syngas oxy-combustion inside a LSCF-6428 oxygen transport membrane reactor. Energy 2016, 96, 654–665. [Google Scholar] [CrossRef]
- Nemitallah, M.A. Characteristics of Oxygen Permeation and Partial Oxidation of Methane in a Catalytic Membrane Reactor for Syngas Production. Energy Fuel. 2020, 34, 7522–7532. [Google Scholar] [CrossRef]
- Sommer, D.E.; Kirchen, P. Towards improved partial oxidation product yield in mixed ionic-electronic membrane reactors using CSTR and CFD modelling. Chem. Eng. Sci. 2019, 195, 11–22. [Google Scholar] [CrossRef]
- Wang, B.; Li, T.; Wang, Z.G.; Othman, M.H.D.; Liu, S.M.; Xiao, R. A review of water splitting via mixed ionic-electronic conducting (MIEC) membrane reactors. Green Chem. 2023, 25, 6930–6948. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, C.S.; Ye, H. CFD Simulation of Hydrogen Generation and Methane Combustion Inside a Water Splitting Membrane Reactor. Energies 2021, 14, 7175. [Google Scholar] [CrossRef]
- Bittner, K.; Margaritis, N.; Schulze-Küppers, F.; Wolters, J.; Natour, G. Computational Fluid Dynamics Modelling of Hydrogen Production via Water Splitting in Oxygen Membrane Reactors. Membranes 2024, 14, 219. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Ahmed, P.; Habib, M.A.; Jamal, A. Oxy-combustion of liquid fuel in an ion transport membrane reactor. Int. J. Energy Environ. Eng. 2018, 9, 21–37. [Google Scholar] [CrossRef]
- Habib, M.A.; Nemitallah, M.A.; Afaneh, D.A. Numerical investigation of a hybrid polymeric-ceramic membrane unit for carbon-free oxy-combustion applications. Energy 2018, 147, 362–376. [Google Scholar] [CrossRef]
- Feng, B.; Song, J.; Wang, Z.G.; Dewangan, N.; Kawi, S.; Tan, X.Y. CFD modeling of the perovskite hollow fiber membrane modules for oxygen separation. Chem. Eng. Sci. 2021, 230, 116214. [Google Scholar] [CrossRef]
- Abdolahimansoorkhani, H.; Xue, X.J. CFD simulation and design of ceramic hollow fiber membrane stack for oxygen separation. Chem. Eng. Sci. 2024, 298, 120437. [Google Scholar] [CrossRef]
- Nauels, N.; Herzog, S.; Modigell, M.; Broeckmann, C. Membrane module for pilot scale oxygen production. J. Membr. Sci. 2019, 574, 252–261. [Google Scholar] [CrossRef]
- Schulze-Küppersa, F.; Drago, F.; Ferravante, L.; Herzog, S.; Baumann, S.; Pinacci, P.; Meulenberg, W.A. Design and fabrication of large-sized planar oxygen transport membrane components for direct integration in oxy-combustion processes. Sep. Purif. Technol. 2019, 220, 89–101. [Google Scholar] [CrossRef]
- Yuan, S.; Ajam, H.; Sinnah, Z.A.B.; Altalbawy, F.M.A.; Ameer, S.A.A.; Husain, A.; Al Mashhadani, Z.I.; Alkhayyat, A.; Alsalamy, A.; Zubaid, R.A.; et al. The roles of artificial intelligence techniques for increasing the prediction performance of important parameters and their optimization in membrane processes: A systematic review. Ecotox. Environ. Saf. 2023, 260, 115066. [Google Scholar] [CrossRef]
- Wei, Y.F. Development of novel computational models based on artificial intelligence technique to predict liquids mixtures separation via vacuum membrane distillation. Sci. Rep. 2024, 14, 24121. [Google Scholar] [CrossRef]
- Sousa, P.; Rodrigues, C.V.; Afonso, A. Enhancing CFD solver with Machine Learning techniques. Comput. Methods Appl. Mech. Eng. 2024, 429, 117133. [Google Scholar] [CrossRef]
- Sun, X.X.; Cao, W.B.; Shan, X.L.; Liu, Y.L.; Zhang, W.W. A generalized framework for integrating machine learning into computational fluid dynamics. J. Comput. Sci. 2024, 82, 102404. [Google Scholar] [CrossRef]
- Paternina-Verona, D.A.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Saba, M.; Ramos, H.M. Digital Twin Based on CFD modelling for analysis of two-phase flows during pipeline Filling-Emptying procedures. Appl. Sci. 2025, 15, 2643. [Google Scholar] [CrossRef]
- Tognia, M.; Hou, M.J.; Dong, X.Y.; Li, L.; Wang, H.; Wang, T.H. Integrated molecular and computational fluid dynamics study of CO2 mass transport mechanisms in carbon molecular sieve membranes. Sep. Purif. Technol. 2025, 363, 132068. [Google Scholar] [CrossRef]
- Bayat, G.; Saghatchi, R.; Azamat, J.; Khataee, A. Separation of methane from different gas mixtures using modified silicon carbide nanosheet: Micro and macro scale numerical studies. Chin. J. Chem. Eng. 2020, 28, 1268–1276. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Li, D.; Huang, Z.G.; Bi, C.H. Computational simulation of mass transfer in membranes using hybrid machine learning models and computational fluid dynamics. Case Stud. Therm. Eng. 2023, 47, 103086. [Google Scholar] [CrossRef]
- Thajudeen, K.Y.; Ahmed, M.M.; Alshehri, S.A. Integration of machine learning and CFD for modeling mass transfer in water treatment using membrane separation process. Sci. Rep. 2024, 14, 23970. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; Baumann, A.; Ryan, E.M. Using Machine-Learning-aided Computational Fluid Dynamics to facilitate design of experiments. Ind. Eng. Chem. Res. 2024, 63, 21444–21454. [Google Scholar] [CrossRef]
- Vinuesa, R.; Brunton, S.L. Enhancing computational fluid dynamics with machine learning. Nat. Comput. Sci. 2022, 2, 358–366. [Google Scholar] [CrossRef]
- Schlenz, H.; Baumann, S.; Meulenberg, W.A.; Guillon, O. The development of eew perovskite-type oxygen transport membranes using Machine Learning. Crystals 2022, 12, 947. [Google Scholar] [CrossRef]
- Wang, T.Y.; Zhong, W.Q.; Chen, X.; Ma, Q.L.; Gu, Y.H.; Dong, W.L.; Pan, Z.C. A self-calibrating digital twin approach by integrating CFD and sensor data for coal-fired boiler water wall temperature. J. Therm. Sci. 2025, 34, 738–755. [Google Scholar] [CrossRef]
- Hossain, M.A.; Morse, A.; Hernandez, I.; Quintana, J.; Choudhuri, A. Liquid rocket engine performance characterization using computational modeling: Preliminary analysis and validation. Aerospace 2024, 11, 824. [Google Scholar] [CrossRef]
- Aláez, D.; Prieto, M.; Villadangos, J.; Astrain, J.J. On constructing efficient uav aerodynamic surrogate models for digital twins. IEEE Trans. Ind. Inform. 2024, 20, 13181–13189. [Google Scholar] [CrossRef]
- Dasgupta, D.; Pal, P.; Torelli, R.; Som, S.; Paulson, N.; Libera, J.; Stan, M. Computational fluid dynamics modeling and analysis of silica nanoparticle synthesis in a flame spray pyrolysis reactor. Combust. Flame 2022, 236, 111789. [Google Scholar] [CrossRef]




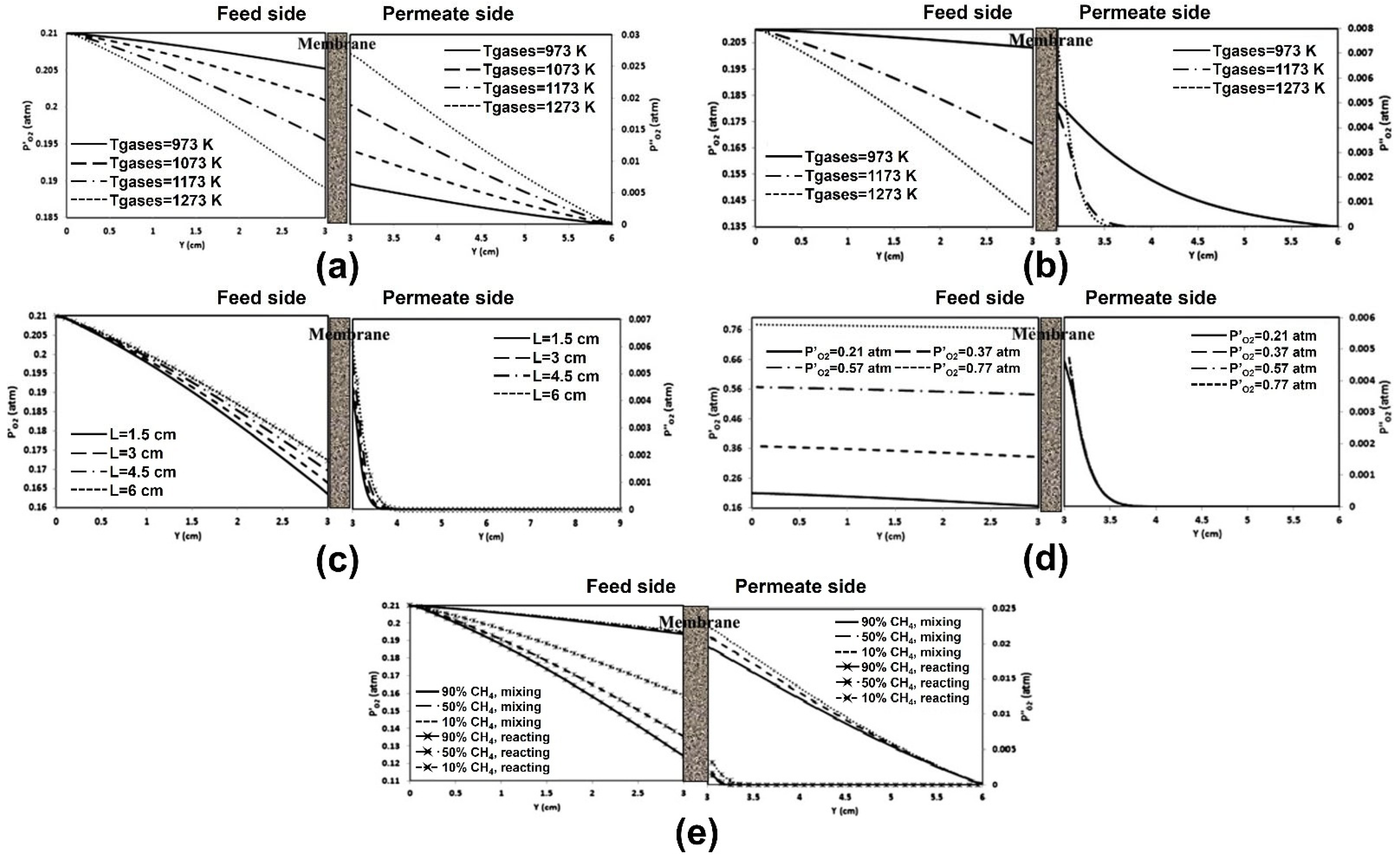
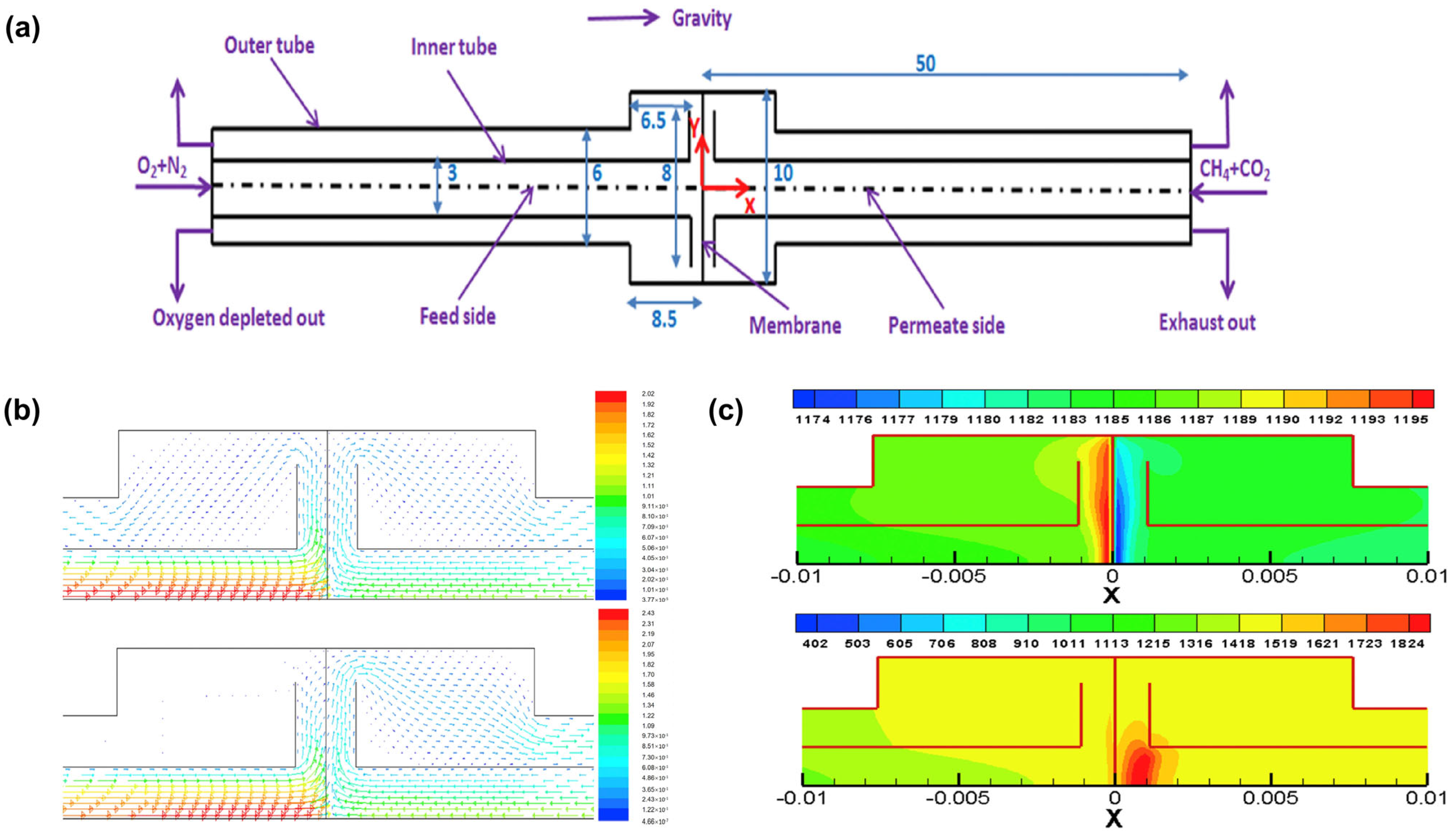
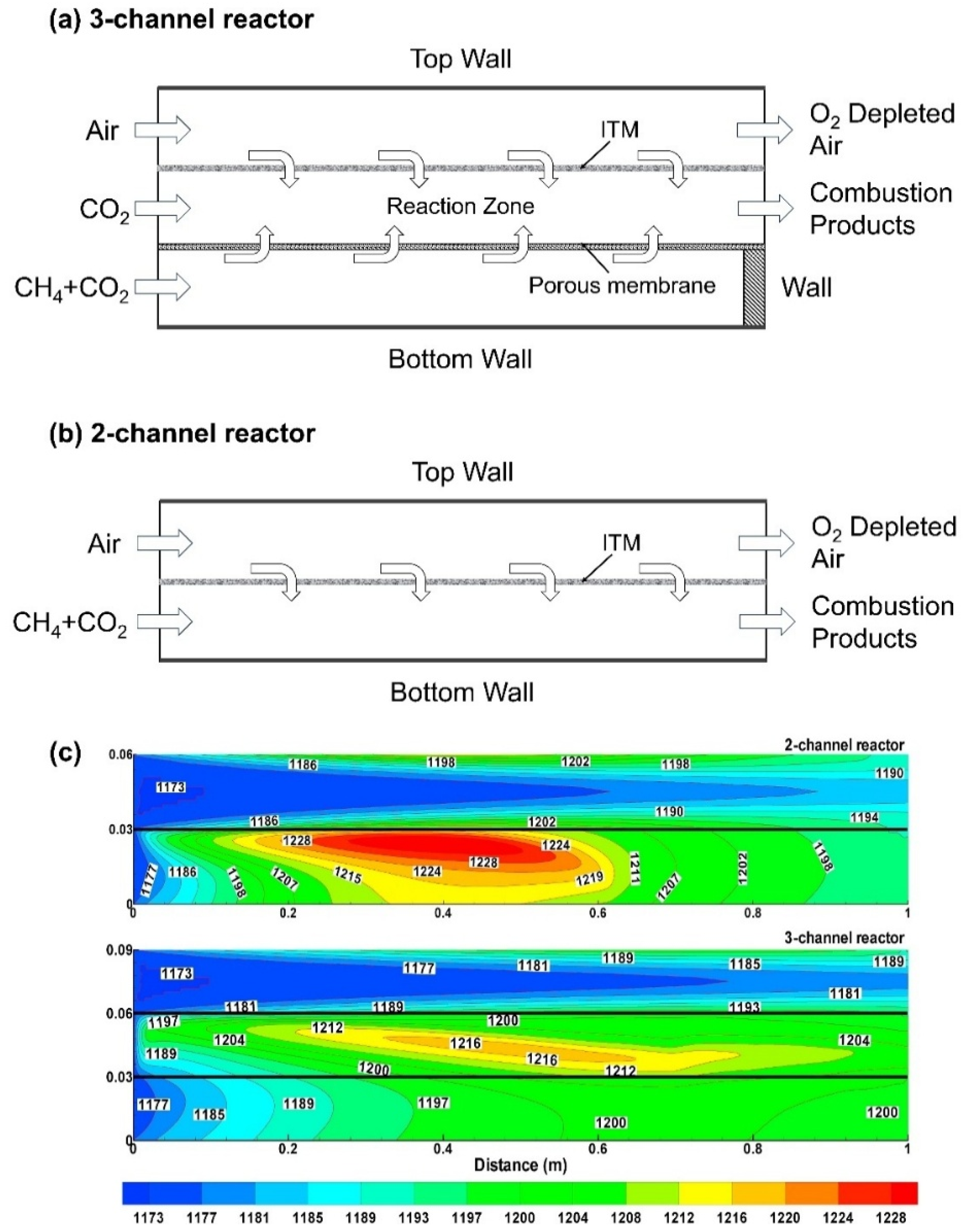
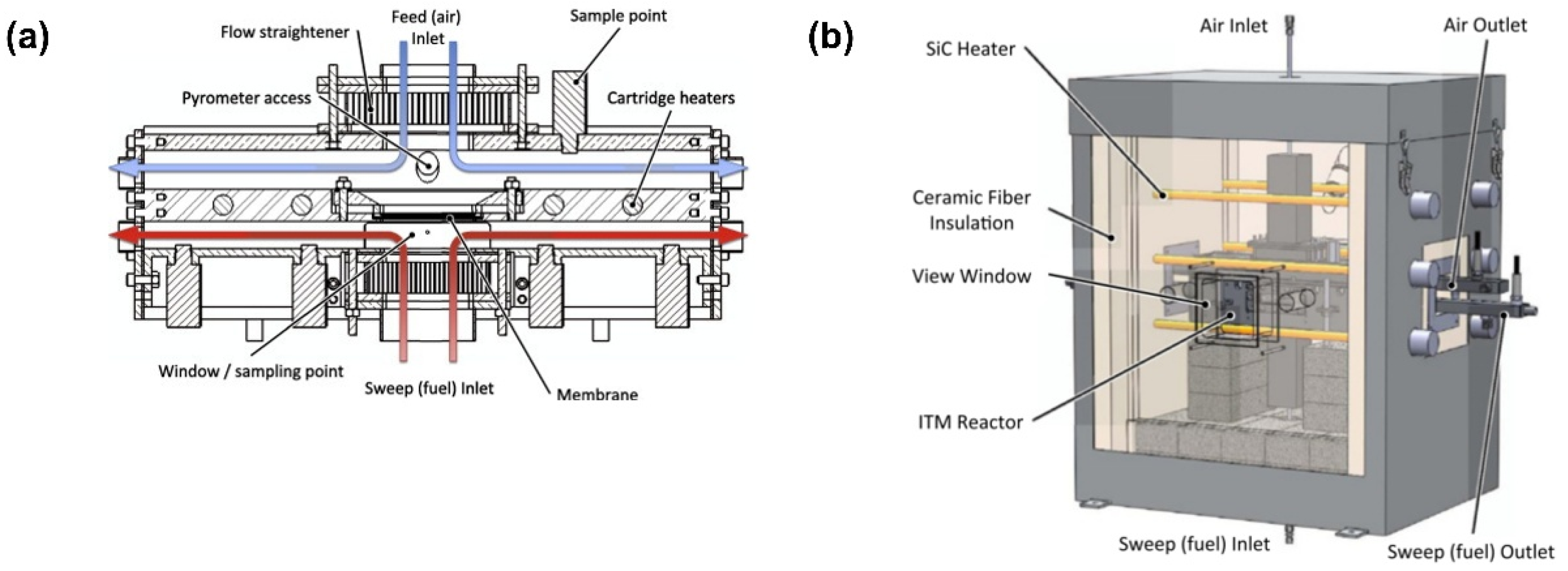
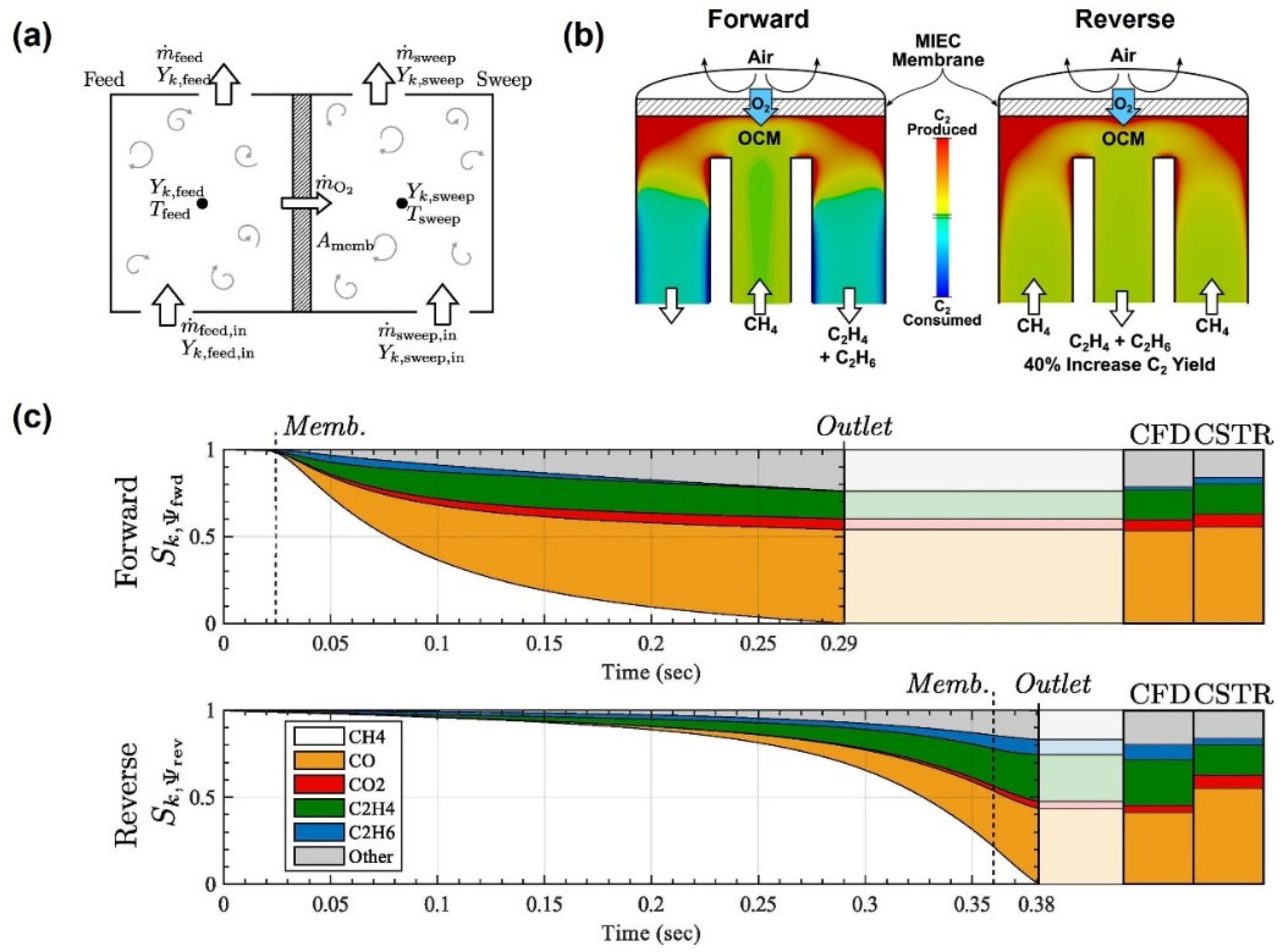
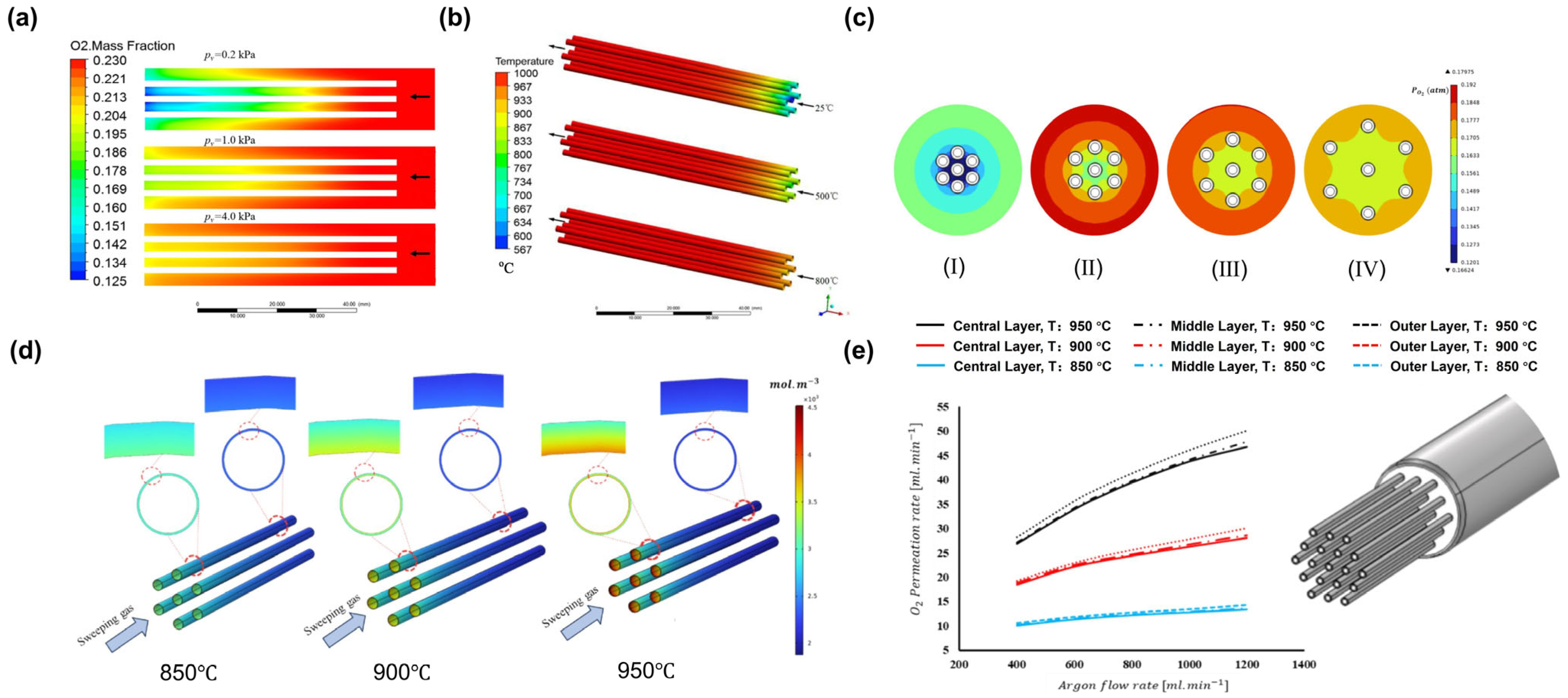
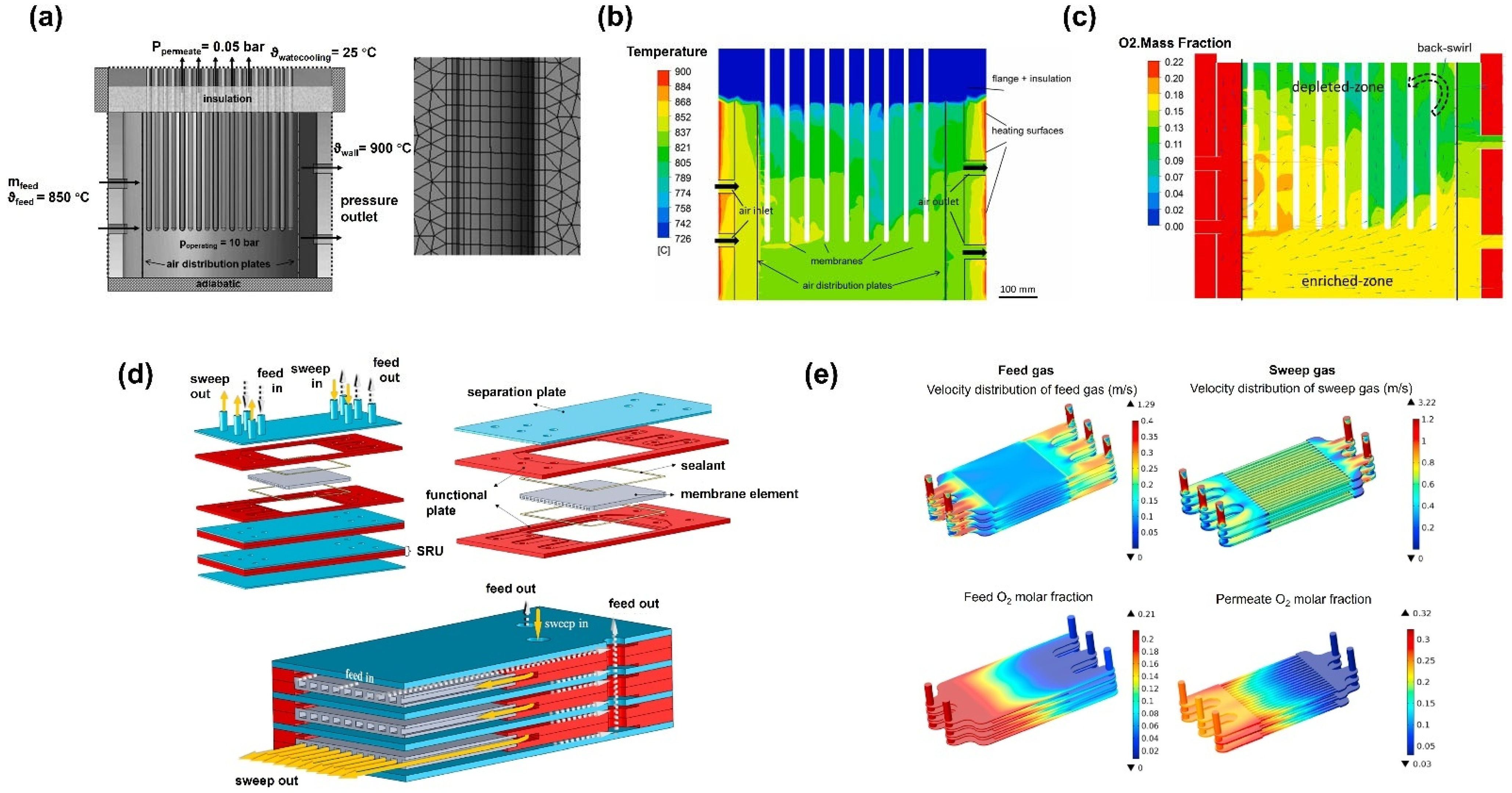
| Mathematical Model | Model Equation | Application Scenarios |
|---|---|---|
| Wagner theory model [43] (2014) | This model is suitable for thick membranes, single-phase MIEC membranes, and steady-state high-temperature operations. | |
| Xu–Thomson model [44] (1999) | This model is suitable for studies where variations in the oxygen vacancy concentration depend on the oxygen partial pressure. | |
| Kim model [46] (1999) | This model is suitable for disc membranes, assuming that the oxygen vacancy density at the membrane interface does not significantly vary with the oxygen partial pressure. | |
| Kim model [46] (1999) | This model is suitable for tubular membranes, assuming that the oxygen vacancy density at the membrane interface does not significantly vary with the oxygen partial pressure. | |
| Tan and Li model [47] (2002) | This model is suitable for hollow fiber membranes. | |
| Zhu model [48] (2012) | This model is suitable for single- and dual-phase disc membranes, where both surface exchange reactions and bulk diffusion limit the process. | |
| Liu model [50] (2005) | (n < 1) (n > 0) | This model is suitable for making quick predictions of oxygen permeation performance, particularly for preliminary studies in large-scale industrial applications. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhao, J.; Liu, Y.; Zhu, Y.; Zhou, W.; Gu, Z.; Zhang, G.; Liu, Z. Research Progress of Computational Fluid Dynamics in Mixed Ionic–Electronic Conducting Oxygen-Permeable Membranes. Membranes 2025, 15, 193. https://doi.org/10.3390/membranes15070193
Liu J, Zhao J, Liu Y, Zhu Y, Zhou W, Gu Z, Zhang G, Liu Z. Research Progress of Computational Fluid Dynamics in Mixed Ionic–Electronic Conducting Oxygen-Permeable Membranes. Membranes. 2025; 15(7):193. https://doi.org/10.3390/membranes15070193
Chicago/Turabian StyleLiu, Jun, Jing Zhao, Yulu Liu, Yongfan Zhu, Wanglin Zhou, Zhenbin Gu, Guangru Zhang, and Zhengkun Liu. 2025. "Research Progress of Computational Fluid Dynamics in Mixed Ionic–Electronic Conducting Oxygen-Permeable Membranes" Membranes 15, no. 7: 193. https://doi.org/10.3390/membranes15070193
APA StyleLiu, J., Zhao, J., Liu, Y., Zhu, Y., Zhou, W., Gu, Z., Zhang, G., & Liu, Z. (2025). Research Progress of Computational Fluid Dynamics in Mixed Ionic–Electronic Conducting Oxygen-Permeable Membranes. Membranes, 15(7), 193. https://doi.org/10.3390/membranes15070193







