Hydrogen and Ammonia Co-Adsorption on M(1 1 1) and Pd3M(1 1 1) (M = Pd, Ru, Ag, Au, Cu) Surfaces
Abstract
:1. Introduction
2. Methods
2.1. DFT Calculations
2.2. Thermodynamic Modelling
3. Results and Discussion
3.1. M(1 1 1) Surfaces
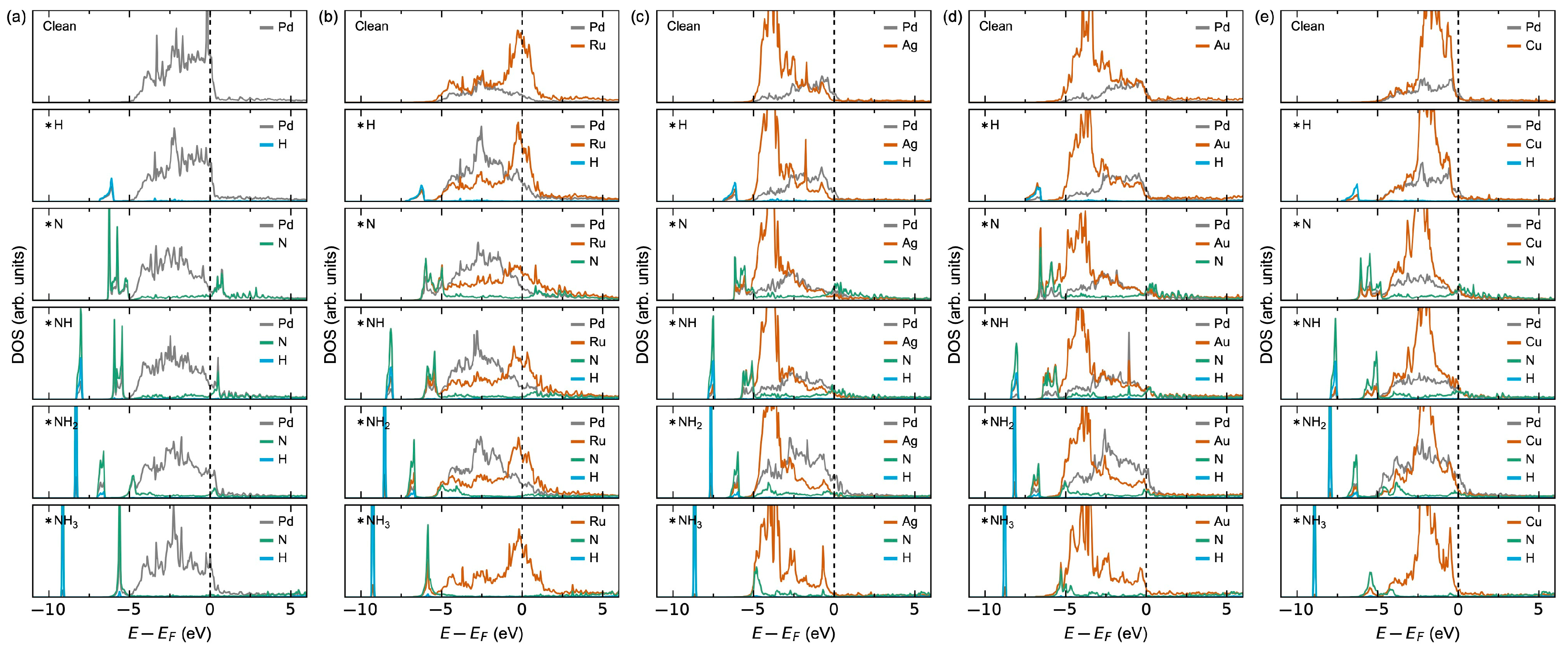
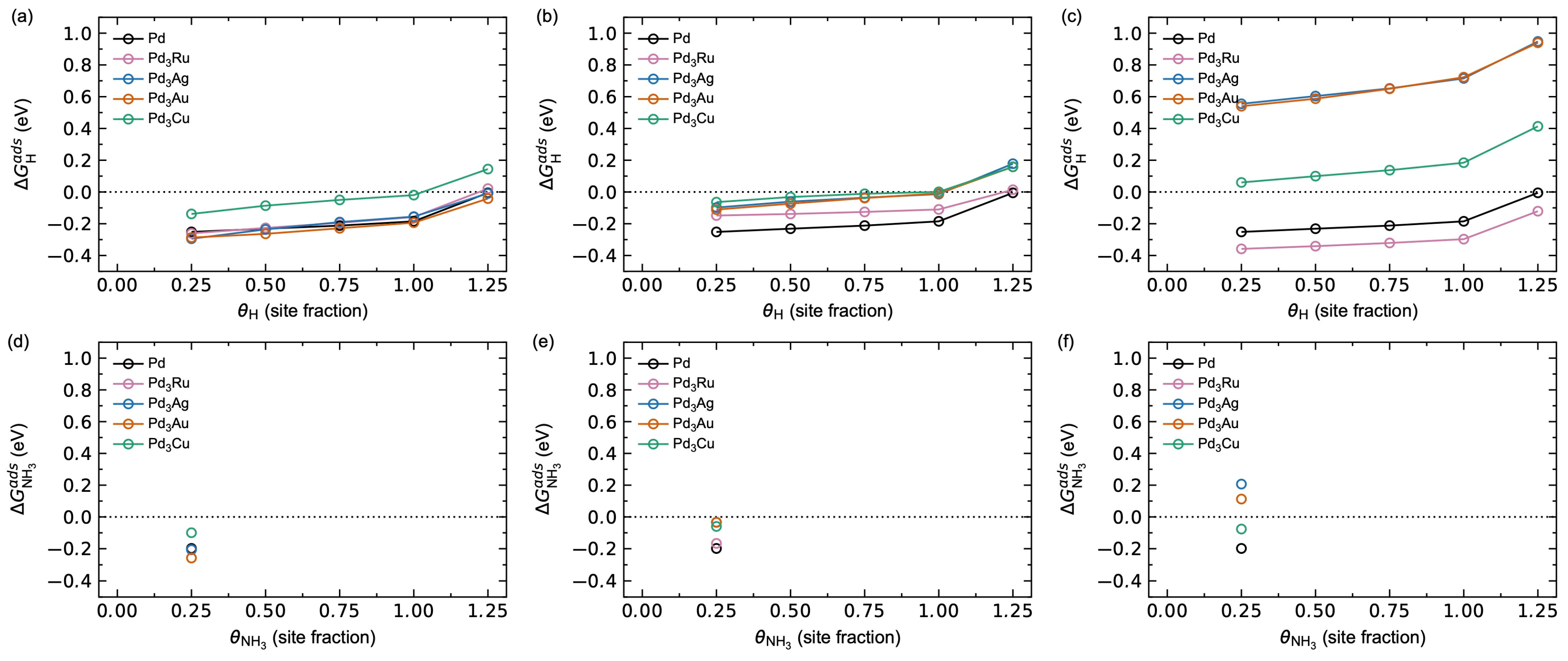
3.1.1. Adsorption Thermodynamics
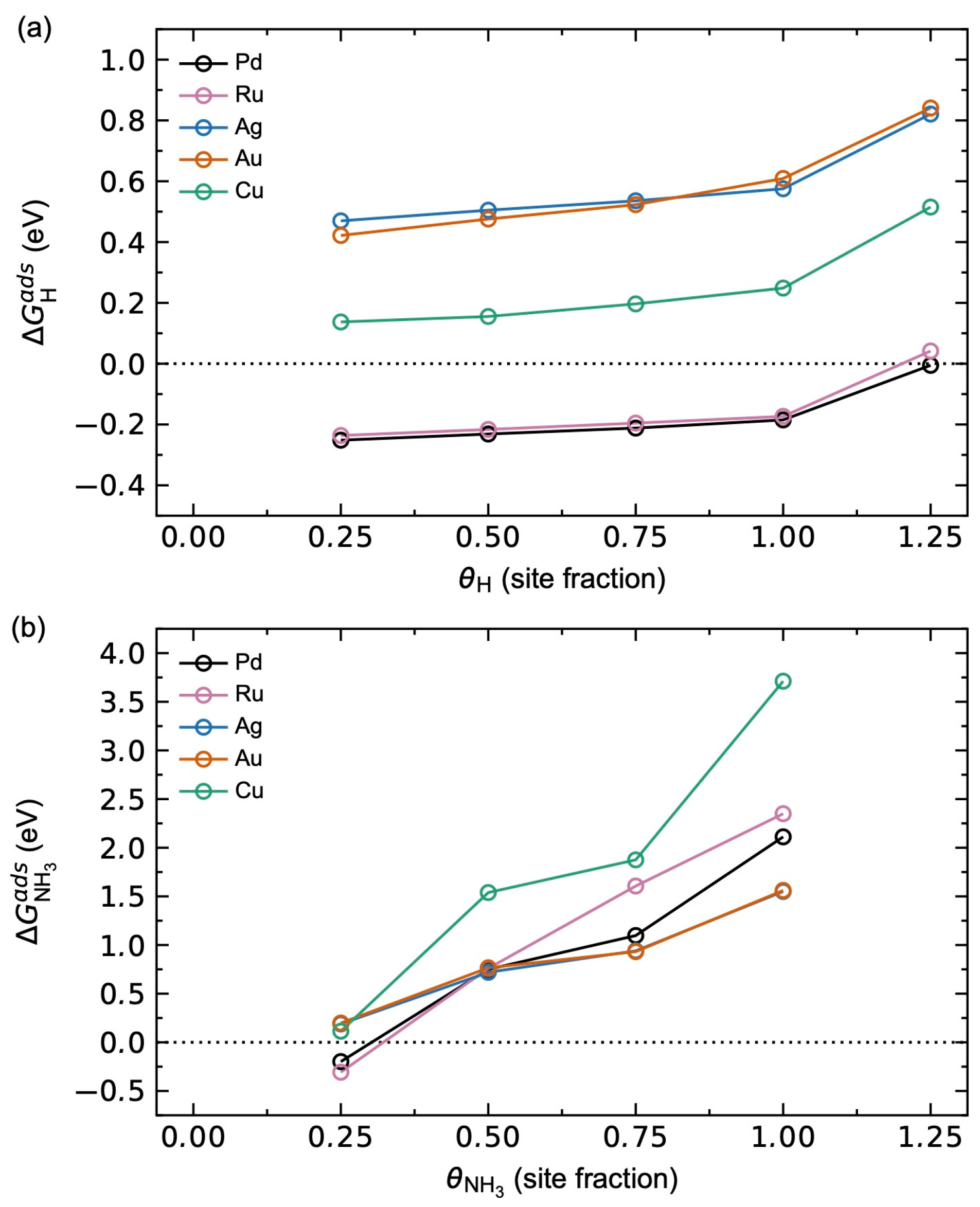
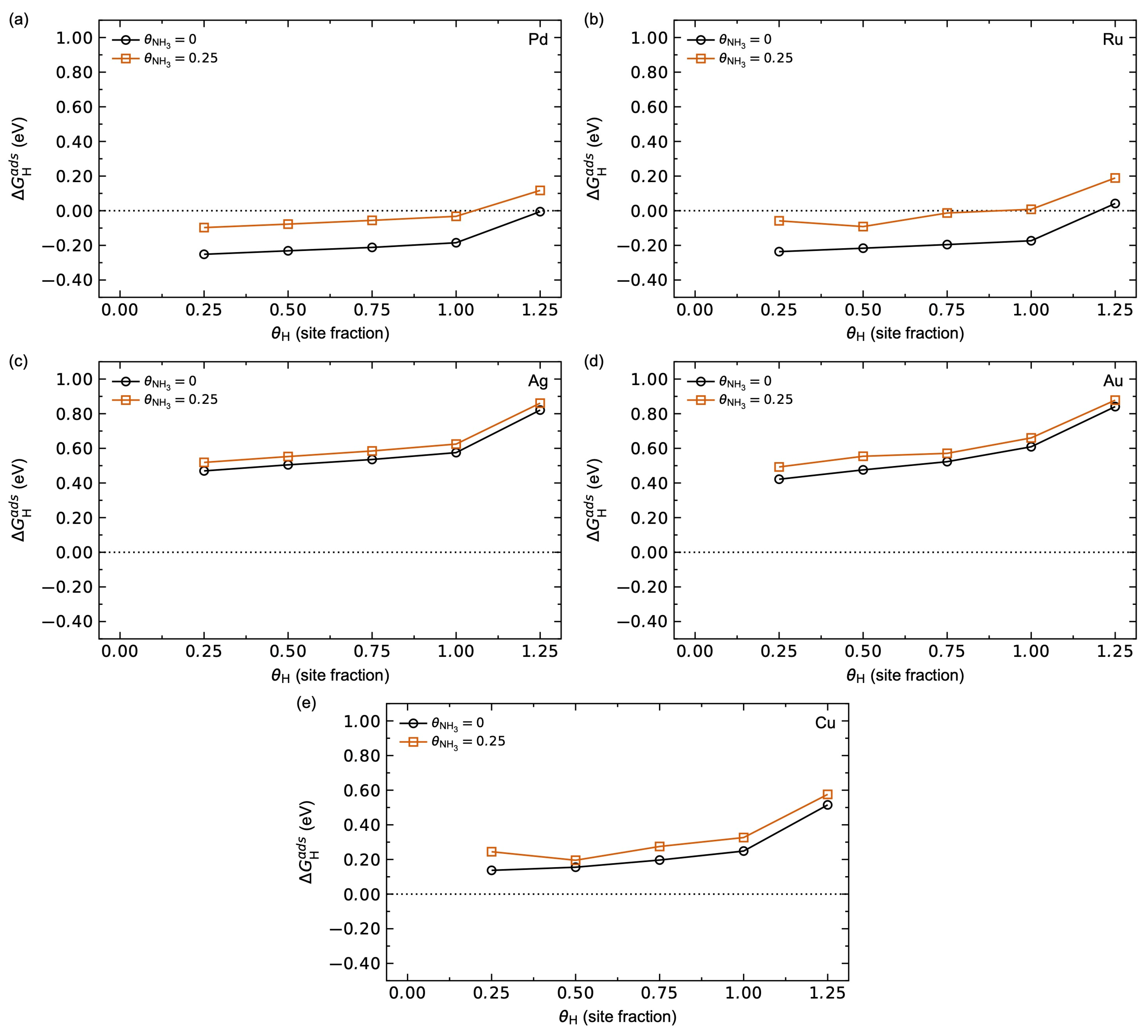
3.1.2. Adsorbate–Adsorbate Interactions and Co-Adsorption Energetics
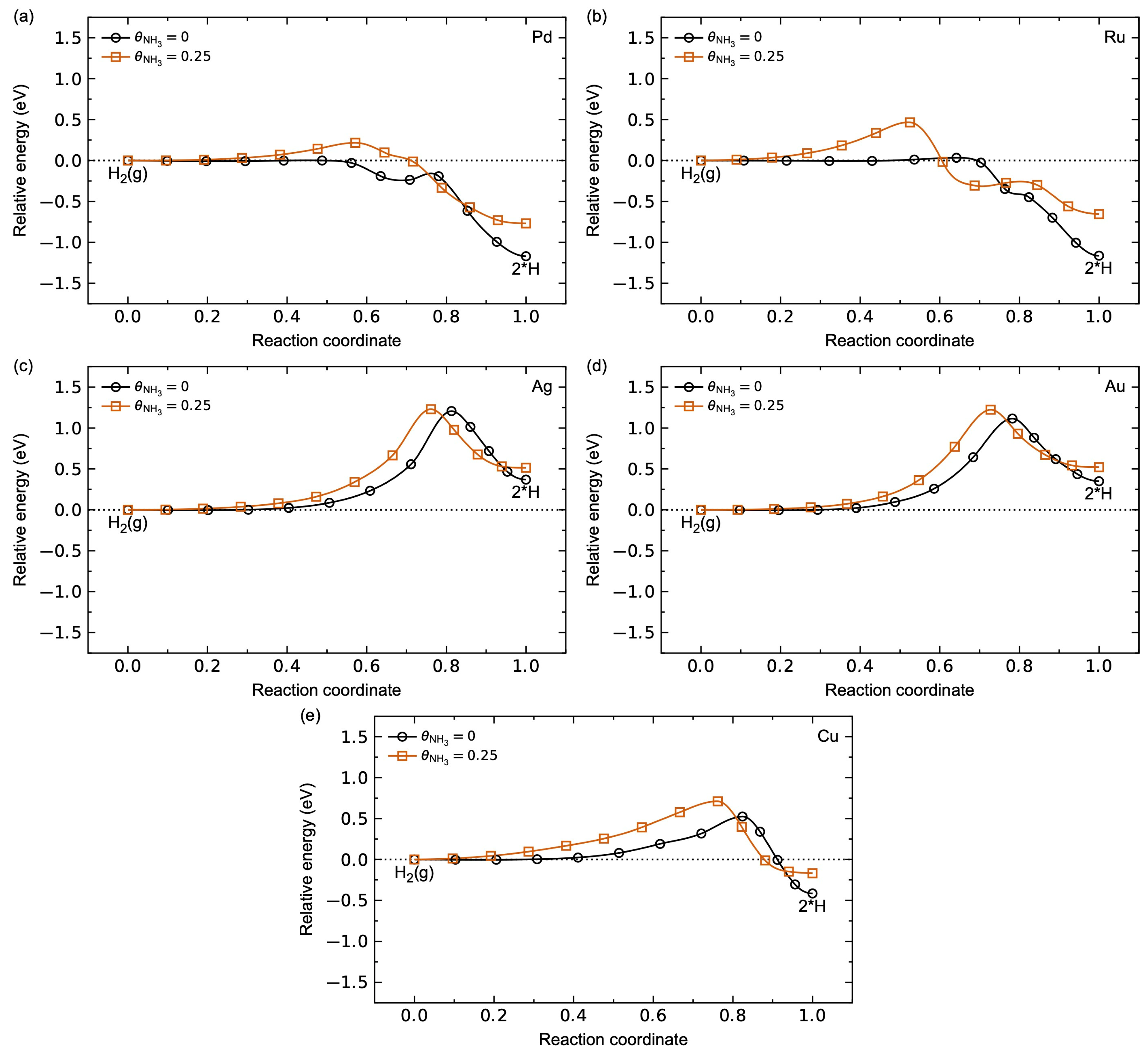
3.1.3. Hydrogen Diffusion Energetics
3.2. Pd3M Alloys
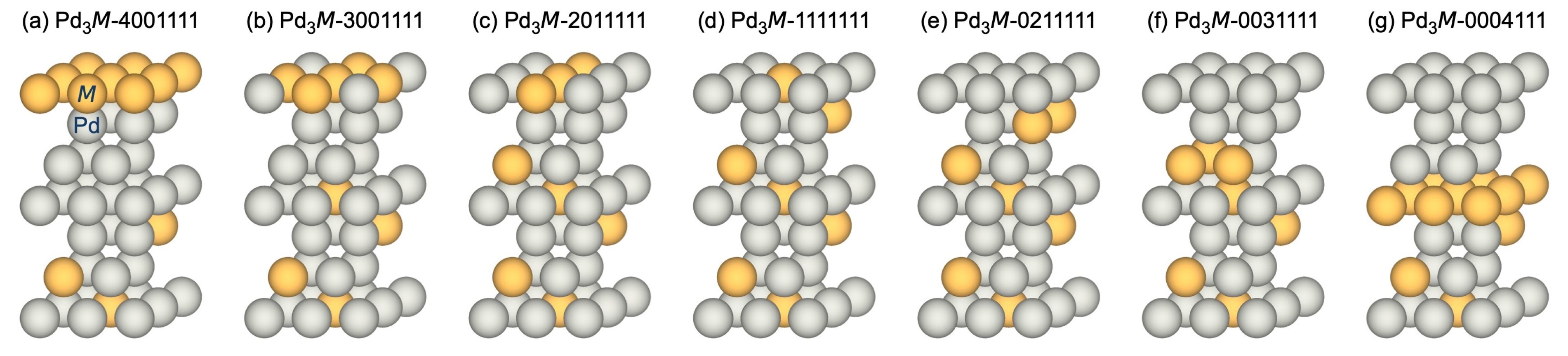
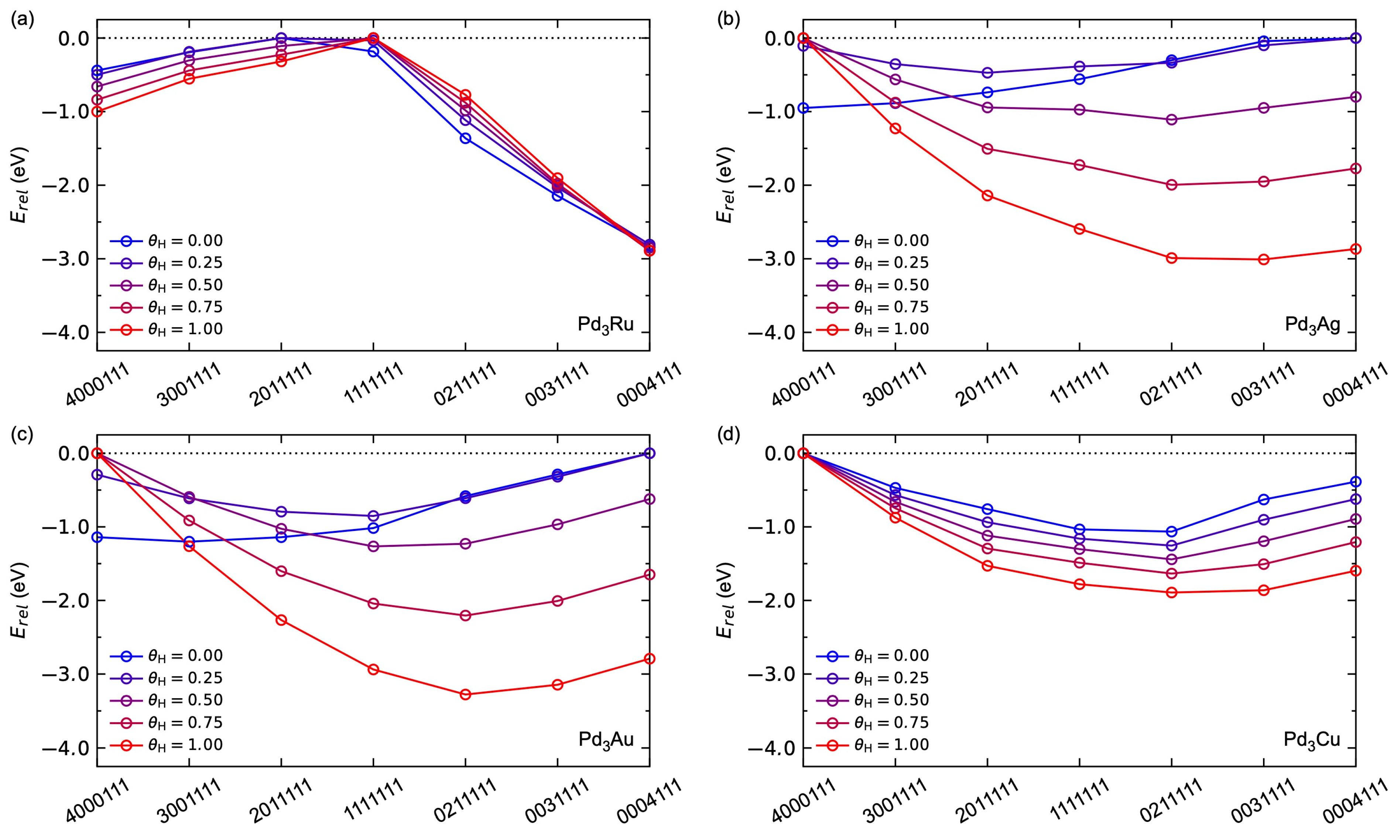
3.2.1. Adsorption-Induced Surface Segregation for Pd3M(1 1 1)
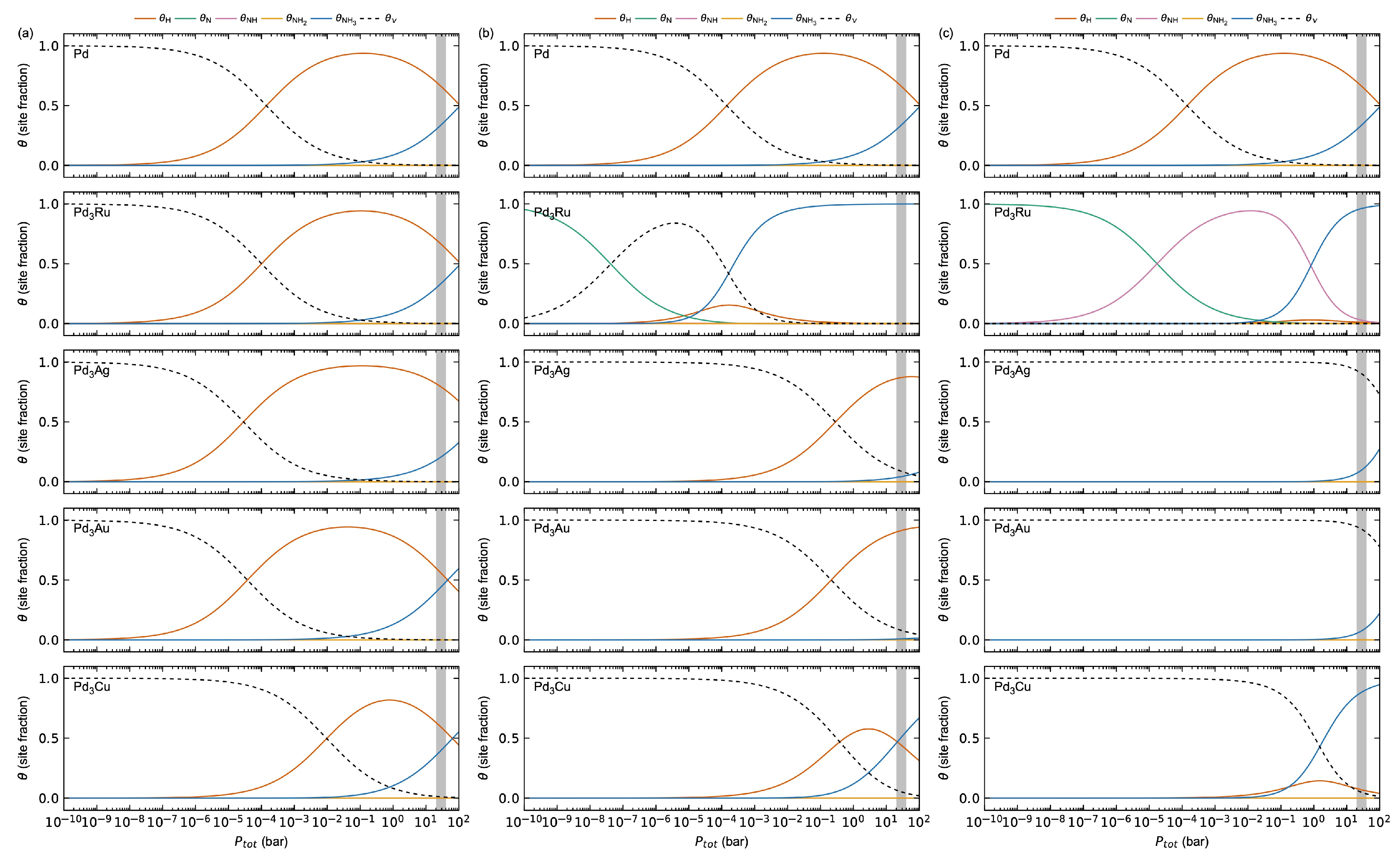
3.2.2. Adsorption Thermodynamics
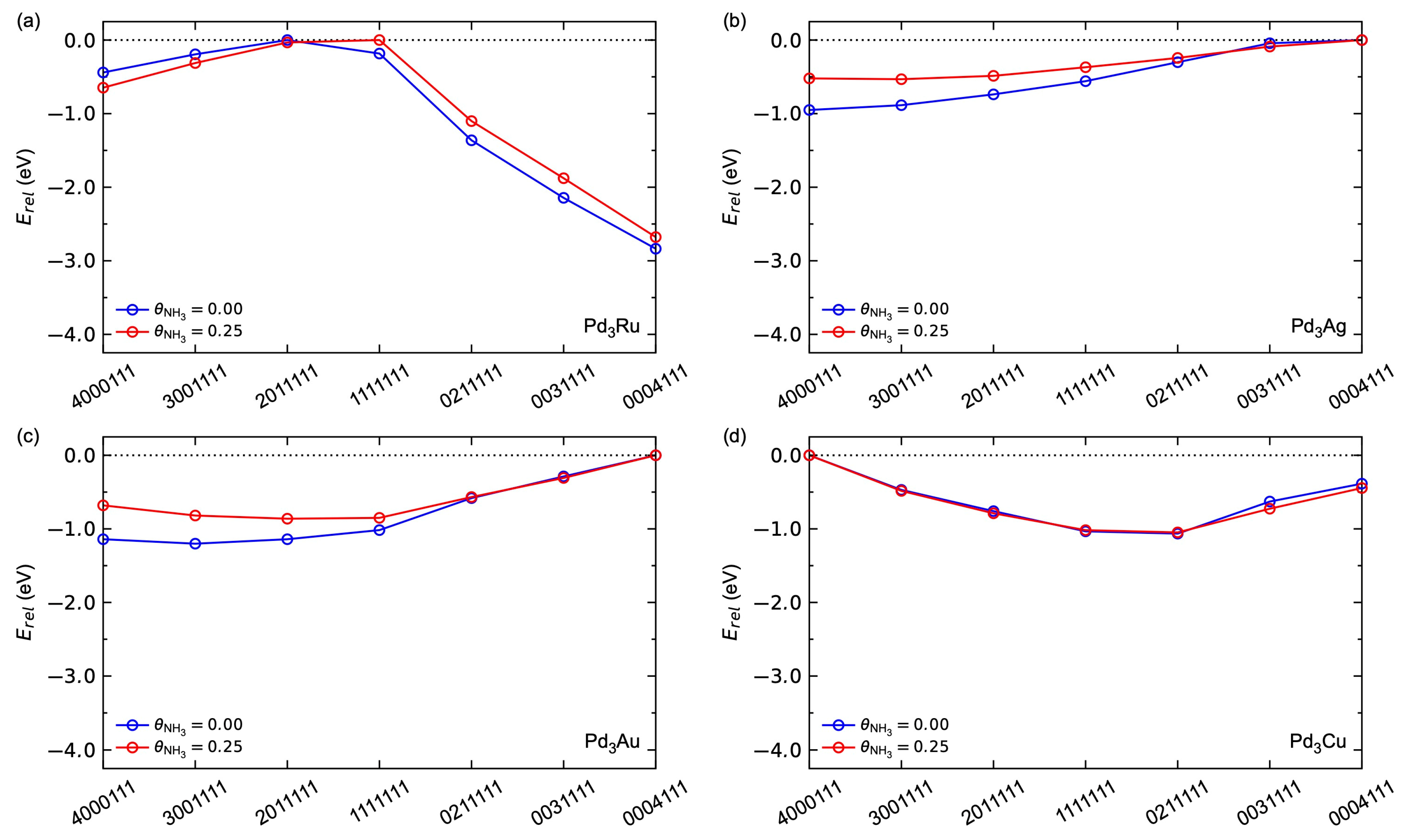
3.2.3. Adsorbate–Adsorbate Interactions and Co-Adsorption
3.2.4. Hydrogen Dissociation Energetics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kurien, C.; Mittal, M. Utilization of green ammonia as a hydrogen energy carrier for decarbonization in spark ignition engines. Int. J. Hydrogen Energy 2023, 48, 28803–28823. [Google Scholar] [CrossRef]
- Langella, G.; De Joannon, M.; Sabia, P.; Iodice, P.; Amoresano, A. Ammonia as a fuel for internal combustion engines: Latest advances and future challenges. J. Phys. Conf. Ser. 2022, 2385, 012036. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, W.; Liu, S.; Wang, W.; Peng, Y.; Wang, Z. A review on ammonia-hydrogen fueled internal combustion engines. eTransportation 2023, 18, 100288. [Google Scholar] [CrossRef]
- Tornatore, C.; Marchitto, L.; Sabia, P.; De Joannon, M. Ammonia as Green Fuel in Internal Combustion Engines: State-of-the-Art and Future Perspectives. Front. Mech. Eng. 2022, 8, 944201. [Google Scholar] [CrossRef]
- Valera-Medina, A.; Amer-Hatem, F.; Azad, A.K.; Dedoussi, I.C.; De Joannon, M.; Fernandes, R.X.; Glarborg, P.; Hashemi, H.; He, X.; Mashruk, S.; et al. Review on Ammonia as a Potential Fuel: From Synthesis to Economics. Energy Fuels 2021, 35, 6964–7029. [Google Scholar] [CrossRef]
- Rathore, S.S.; Biswas, S.; Fini, D.; Kulkarni, A.P.; Giddey, S. Direct ammonia solid-oxide fuel cells: A review of progress and prospects. Int. J. Hydrogen Energy 2021, 46, 35365–35384. [Google Scholar] [CrossRef]
- Dhawale, D.S.; Biswas, S.; Kaur, G.; Giddey, S. Challenges and advancement in direct ammonia solid oxide fuel cells: A review. Inorg. Chem. Front. 2023, 10, 6176–6192. [Google Scholar] [CrossRef]
- Cheliotis, M.; Boulougouris, E.; Trivyza, N.L.; Theotokatos, G.; Livanos, G.; Mantalos, G.; Stubos, A.; Stamatakis, E.; Venetsanos, A. Review on the Safe Use of Ammonia Fuel Cells in the Maritime Industry. Energies 2021, 14, 3023. [Google Scholar] [CrossRef]
- Dimitriou, P.; Javaid, R. A review of ammonia as a compression ignition engine fuel. Int. J. Hydrogen Energy 2020, 45, 7098–7118. [Google Scholar] [CrossRef]
- Keller, M.; Koshi, M.; Otomo, J.; Iwasaki, H.; Mitsumori, T.; Yamada, K. Thermodynamic evaluation of an ammonia-fueled combined-cycle gas turbine process operated under fuel-rich conditions. Energy 2020, 194, 116894. [Google Scholar] [CrossRef]
- Jeerh, G.; Zhang, M.; Tao, S. Recent progress in ammonia fuel cells and their potential applications. J. Mater. Chem. A 2021, 9, 727–752. [Google Scholar] [CrossRef]
- Miyaoka, H.; Miyaoka, H.; Ichikawa, T.; Ichikawa, T.; Kojima, Y. Highly purified hydrogen production from ammonia for PEM fuel cell. Int. J. Hydrogen Energy 2018, 43, 14486–14492. [Google Scholar] [CrossRef]
- Okanishi, T.; Okura, K.; Srifa, A.; Muroyama, H.; Matsui, T.; Kishimoto, M.; Saito, M.; Iwai, H.; Yoshida, H.; Saito, M.; et al. Comparative Study of Ammonia-fueled Solid Oxide Fuel Cell Systems. Fuel Cells 2017, 17, 383–390. [Google Scholar] [CrossRef]
- García-García, F.R.; Ma, Y.H.; Rodríguez-Ramos, I.; Guerrero-Ruiz, A. High purity hydrogen production by low temperature catalytic ammonia decomposition in a multifunctional membrane reactor. Catal. Commun. 2008, 9, 482–486. [Google Scholar] [CrossRef]
- Collins, J.P.; Way, J.D. Catalytic decomposition of ammonia in a membrane reactor. J. Membr. Sci. 1994, 96, 259–274. [Google Scholar] [CrossRef]
- Itoh, N.; Oshima, A.; Suga, E.; Sato, T. Kinetic enhancement of ammonia decomposition as a chemical hydrogen carrier in palladium membrane reactor. Catal. Today 2014, 236, 70–76. [Google Scholar] [CrossRef]
- Cechetto, V.; Di Felice, L.; Medrano, J.A.; Makhloufi, C.; Zuniga, J.; Gallucci, F. H2 production via ammonia decomposition in a catalytic membrane reactor. Fuel Process. Technol. 2021, 216, 106772. [Google Scholar] [CrossRef]
- Cechetto, V.; Agnolin, S.; Di Felice, L.; Pacheco Tanaka, A.; Llosa Tanco, M.; Gallucci, F. Metallic Supported Pd-Ag Membranes for Simultaneous Ammonia Decomposition and H2 Separation in a Membrane Reactor: Experimental Proof of Concept. Catalysts 2023, 13, 920. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, H.; Li, W. High-purity COx-free H2 generation from NH3 via the ultra permeable and highly selective Pd membranes. J. Membr. Sci. 2006, 277, 85–93. [Google Scholar] [CrossRef]
- Peters, T.A.; Polfus, J.M.; Stange, M.; Veenstra, P.; Nijmeijer, A.; Bredesen, R. H 2 flux inhibition and stability of Pd-Ag membranes under exposure to trace amounts of NH 3. Fuel Process. Technol. 2016, 152, 259–265. [Google Scholar] [CrossRef]
- Zhang, Z.; Liguori, S.; Fuerst, T.F.; Way, J.D.; Wolden, C.A. Efficient Ammonia Decomposition in a Catalytic Membrane Reactor To Enable Hydrogen Storage and Utilization. ACS Sustain. Chem. Eng. 2019, 7, 5975–5985. [Google Scholar] [CrossRef]
- Cechetto, V.; Di Felice, L.; Gallucci, F. Advances and Perspectives of H2 Production from NH3 Decomposition in Membrane Reactors. Energy Fuels 2023, 37, 10775–10798. [Google Scholar] [CrossRef] [PubMed]
- Clark, D.; Malerød-Fjeld, H.; Budd, M.; Yuste-Tirados, I.; Beeaff, D.; Aamodt, S.; Nguyen, K.; Ansaloni, L.; Peters, T.; Vestre, P.K.; et al. Single-step hydrogen production from NH3, CH4, and biogas in stacked proton ceramic reactors. Science 2022, 376, 390–393. [Google Scholar] [CrossRef]
- Peters, T.A.; Polfus, J.M.; van Berkel, F.P.F.; Bredesen, R. Interplay between propylene and H2S co-adsorption on the H2 flux characteristics of Pd-alloy membranes employed in propane dehydrogenation (PDH) processes. Chem. Eng. J. 2016, 304, 134–140. [Google Scholar] [CrossRef]
- Svenum, I.-H.; Herron, J.A.; Mavrikakis, M.; Venvik, H.J. Pd3Ag(111) as a Model System for Hydrogen Separation Membranes: Combined Effects of CO Adsorption and Surface Termination on the Activation of Molecular Hydrogen. Top. Catal. 2020, 63, 750–761. [Google Scholar] [CrossRef]
- Svenum, I.-H.; Herron, J.A.; Mavrikakis, M.; Venvik, H.J. Adsorbate-induced segregation in a PdAg membrane model system: Pd3Ag(111). Catal. Today 2012, 193, 111–119. [Google Scholar] [CrossRef]
- Småbråten, D.R.; Strømsheim, M.D.; Peters, T. Hydrogen and NH3 co-adsorption on Pd–Ag membranes. Int. J. Hydrogen Energy 2024, 72, 475–484. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Henkelman, G.; Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
- Chase, M.W., Jr. NIST-JANAF Thermochemical Tables, Fourth Edition. J. Phys. Chem. Ref. Data Monogr. 1998, 9, 1–1951. [Google Scholar]
- Campbell, C.T.; Sellers, J.R.V. The Entropies of Adsorbed Molecules. J. Am. Chem. Soc. 2012, 134, 18109–18115. [Google Scholar] [CrossRef]
- Carabineiro, S.A.C.; Matveev, A.V.; Gorodetskii, V.V.; Nieuwenhuys, B.E. Selective oxidation of ammonia over Ru(0001). Surf. Sci. 2004, 555, 83–93. [Google Scholar] [CrossRef]
- Danielson, L.R.; Dresser, M.J.; Donaldson, E.E.; Dickinson, J.T. Adsorption and desorption of ammonia, hydrogen, and nitrogen on ruthenium (0001). Surf. Sci. 1978, 71, 599–614. [Google Scholar] [CrossRef]
- Liu, R.; Shen, W.; Zhang, J.; Li, M. Adsorption and dissociation of ammonia on Au(111) surface: A density functional theory study. Appl. Surf. Sci. 2008, 254, 5706–5710. [Google Scholar] [CrossRef]
- Jiang, Z.; Qin, P.; Fang, T. Mechanism of ammonia decomposition on clean and oxygen-covered Cu (1 1 1) surface: A DFT study. Chem. Phys. 2014, 445, 59–67. [Google Scholar] [CrossRef]
- Kulkarni, S.R.; Realpe, N.; Yerrayya, A.; Velisoju, V.K.; Sayas, S.; Morlanes, N.; Cerillo, J.; Katikaneni, S.P.; Paglieri, S.N.; Solami, B.; et al. Elucidating the rate-determining step of ammonia decomposition on Ru-based catalysts using ab initio-grounded microkinetic modeling. Catal. Sci. Technol. 2023, 13, 2026–2037. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Furness, J.W.; Kaplan, A.D.; Ning, J.; Perdew, J.P.; Sun, J. Accurate and Numerically Efficient r2 SCAN Meta-Generalized Gradient Approximation. J. Phys. Chem. Lett. 2020, 11, 8208–8215. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Hamada, I. Van der Waals density functional made accurate. Phys. Rev. B Condens. Matter Mater. Phys. 2014, 89, 121103. [Google Scholar] [CrossRef]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 2010, 22, 022201. [Google Scholar] [CrossRef] [PubMed]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar] [CrossRef]
- Polfus, J.M.; Peters, T.; Bredesen, R.; Løvvik, O.M. Vacancy diffusion in palladium hydrides. Phys. Chem. Chem. Phys. 2021, 23, 13680–13686. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Theoretical surface science and catalysis—Calculations and concepts. In Advances in Catalysis; Impact of Surface Science on Catalysis; Academic Press: Cambridge, MA, USA, 2000; Volume 45, pp. 71–129. [Google Scholar]
- Karimadom, B.R.; Sermiagin, A.; Meyerstein, D.; Zidki, T.; Mizrahi, A.; Bar-Ziv, R.; Kornweitz, H. Hydrogen adsorption on various transition metal (111) surfaces in water: A DFT forecast. Phys. Chem. Chem. Phys. 2024, 26, 7647–7657. [Google Scholar] [CrossRef]
- Dong, W.; Hafner, J. H2 dissociative adsorption on Pd(111). Phys. Rev. B 1997, 56, 15396–15403. [Google Scholar] [CrossRef]
- Dipojono, H.K.; Padama, A.A.B.; Ozawa, N.; Nakanishi, H.; Kasai, H. A First Principles Study on Dissociation and Adsorption Processes of H2 on Pd3Ag(111) Surface. Jpn. J. Appl. Phys. 2010, 49, 115702. [Google Scholar] [CrossRef]
- Peters, T.A.; Kaleta, T.; Stange, M.; Bredesen, R. Development of thin binary and ternary Pd-based alloy membranes for use in hydrogen production. J. Membr. Sci. 2011, 383, 124–134. [Google Scholar] [CrossRef]
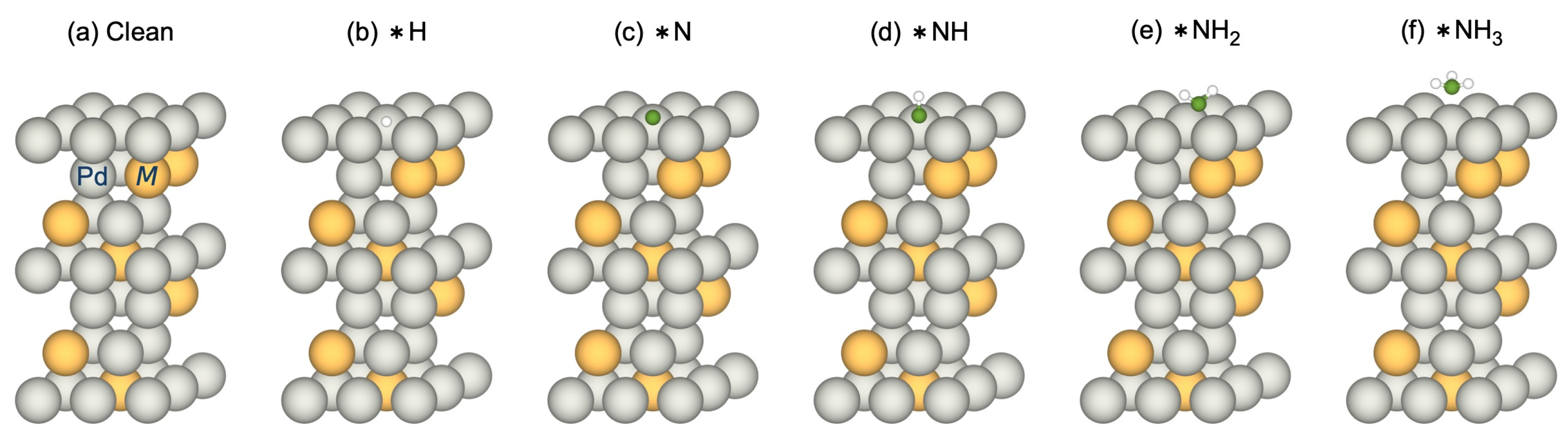

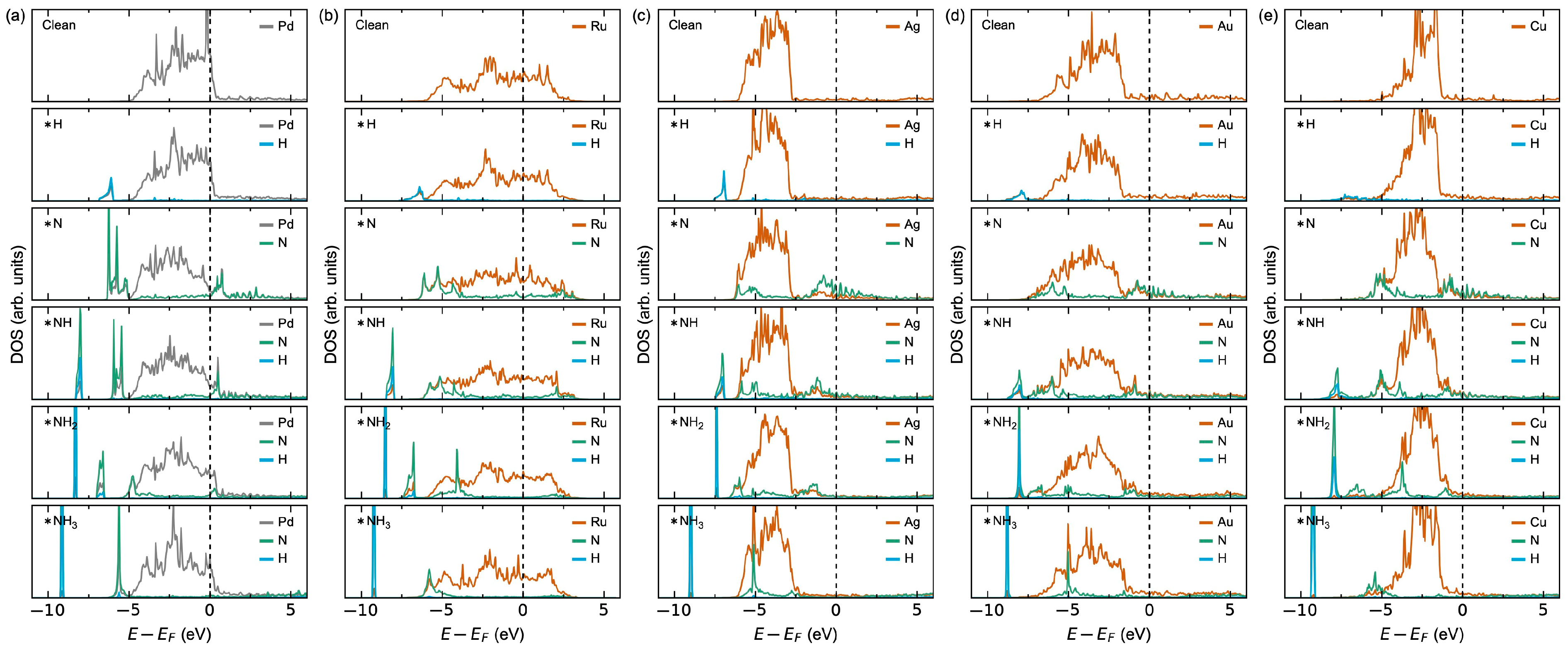


| Species | Site | (eV) | (eV) | (eV) | (cm−1) |
|---|---|---|---|---|---|
| Pd | |||||
| H | fcc | −0.67 | −0.42 | −0.25 | 964, 841, 841 |
| N | fcc | 1.47 | 0.18 | 1.28 | 503, 494, 493 |
| NH | fcc | 0.60 | −0.23 | 0.84 | 3377, 714, 714, 503, 437, 437 |
| NH2 | bridge | 0.11 | −0.59 | 0.70 | 3478, 3374, 1449, 673, 637, 575, 435, 320, 161 |
| NH3 | top | −0.84 | −0.61 * | −0.20 | - |
| Ru | |||||
| H | fcc | −0.66 | −0.42 | −0.24 | 1122, 823, 818 |
| N | fcc | 0.68 | 0.21 | 0.47 | 514, 384, 384 |
| NH | fcc | −0.20 | −0.22 | 0.01 | 3431, 693, 687, 572, 370, 368 |
| NH2 | bridge | −0.44 | −0.59 | 0.15 | 3452, 3364, 1488, 674, 628, 620, 460, 307, 155 |
| NH3 | top | −0.92 | −0.61 | −0.31 | - |
| Ag | |||||
| H | fcc | 0.07 | −0.40 | 0.47 | 799, 771, 771 |
| N | fcc | 3.97 | 0.22 | 3.75 | 396, 396, 395 |
| NH | fcc | 2.23 | −0.18 | 2.41 | 3427, 555, 555, 398, 354, 354 |
| NH2 | bridge | 0.81 | −0.51 | 1.33 | 3511, 3409, 1481, 527, 502, 490, 350, 242, 112 |
| NH3 | top | −0.42 | −0.61 * | 0.19 | - |
| Au | |||||
| H | fcc | 0.03 | −0.39 | 0.42 | 825, 678, 678 |
| N | fcc | 3.65 | 0.20 | 3.45 | 454, 454, 424 |
| NH | fcc | 2.20 | −0.23 | 2.43 | 3445, 759, 759, 455, 455, 422 |
| NH2 | bridge | 1.04 | −0.57 | 1.61 | 3537, 3425, 1468, 693, 633, 582, 366, 282, 156 |
| NH3 | top | −0.41 | −0.61 * | 0.20 | - |
| Cu | |||||
| H | fcc | −0.29 | −0.42 | 0.14 | 1042, 854, 854 |
| N | fcc | 2.42 | 0.18 | 2.23 | 508, 482, 482 |
| NH | fcc | 0.99 | −0.21 | 1.20 | 3449, 608, 607, 513, 408, 407 |
| NH2 | bridge | 0.27 | −0.55 | 0.82 | 3496, 3404, 1496, 575, 559, 552, 419, 287, 127 |
| NH3 | top | −0.49 | −0.61 * | 0.11 | - |
| Species | Site | (eV) | (eV) | (eV) | (cm−1) |
|---|---|---|---|---|---|
| Pd3Ru | |||||
| H | fcc | −0.61 | −0.41 | −0.19 | 1076, 1074, 431 |
| N | fcc | 0.62 | 0.21 | 0.41 | 566, 531, 134 |
| NH | fcc | 0.01 | −0.21 | 0.23 | 3375, 725, 538, 488, 442, 281 |
| NH2 | bridge | −0.42 | −0.59 | 0.17 | 3493, 3385, 1447, 647, 564, 430, 426, 209, 119 |
| NH3 | top | −1.16 | −0.61 | −0.56 | - |
| Pd3Ag | |||||
| H | fcc | −0.45 | −0.40 | −0.05 | 1076, 1074, 431 |
| N | fcc | 2.53 | 0.24 | 2.29 | 566, 531, 134 |
| NH | fcc | 1.43 | −0.20 | 1.63 | 3375, 725, 538, 488, 442, 281 |
| NH2 | bridge | 0.63 | −0.53 | 1.16 | 3493, 3385, 1447, 647, 564, 430, 426, 209, 119 |
| NH3 | top | −0.48 | −0.61 | 0.13 | - |
| Pd3Au | |||||
| H | fcc | −0.47 | −0.41 | −0.06 | 964, 920, 662 |
| N | fcc | 2.36 | 0.19 | 2.17 | 511, 502, 378 |
| NH | fcc | 1.36 | −0.22 | 1.58 | 3390, 715, 684, 479, 430, 396 |
| NH2 | bridge | 0.67 | −0.57 | 1.23 | 3508, 3398, 1446, 627, 607, 568, 411, 271, 146 |
| NH3 | top | −0.39 | −0.61 | 0.22 | - |
| Pd3Cu | |||||
| H | fcc | −0.46 | −0.42 | −0.04 | 1045, 898, 740 |
| N | fcc | 2.23 | 0.19 | 2.04 | 517, 492, 419 |
| NH | fcc | 1.05 | −0.22 | 1.27 | 3393, 701, 665, 490, 425, 403 |
| NH2 | bridge | 0.36 | −0.57 | 0.93 | 3478, 3379, 1462, 603, 590, 526, 415, 300, 149 |
| NH3 | top | −0.64 | −0.61 | −0.03 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Småbråten, D.R.; Strømsheim, M.D.; Peters, T.A. Hydrogen and Ammonia Co-Adsorption on M(1 1 1) and Pd3M(1 1 1) (M = Pd, Ru, Ag, Au, Cu) Surfaces. Membranes 2025, 15, 135. https://doi.org/10.3390/membranes15050135
Småbråten DR, Strømsheim MD, Peters TA. Hydrogen and Ammonia Co-Adsorption on M(1 1 1) and Pd3M(1 1 1) (M = Pd, Ru, Ag, Au, Cu) Surfaces. Membranes. 2025; 15(5):135. https://doi.org/10.3390/membranes15050135
Chicago/Turabian StyleSmåbråten, Didrik R., Marie D. Strømsheim, and Thijs A. Peters. 2025. "Hydrogen and Ammonia Co-Adsorption on M(1 1 1) and Pd3M(1 1 1) (M = Pd, Ru, Ag, Au, Cu) Surfaces" Membranes 15, no. 5: 135. https://doi.org/10.3390/membranes15050135
APA StyleSmåbråten, D. R., Strømsheim, M. D., & Peters, T. A. (2025). Hydrogen and Ammonia Co-Adsorption on M(1 1 1) and Pd3M(1 1 1) (M = Pd, Ru, Ag, Au, Cu) Surfaces. Membranes, 15(5), 135. https://doi.org/10.3390/membranes15050135







