Boundary Flow-Induced Membrane Tubulation Under Turgor Pressures
Abstract
1. Introduction
2. Model and Methods
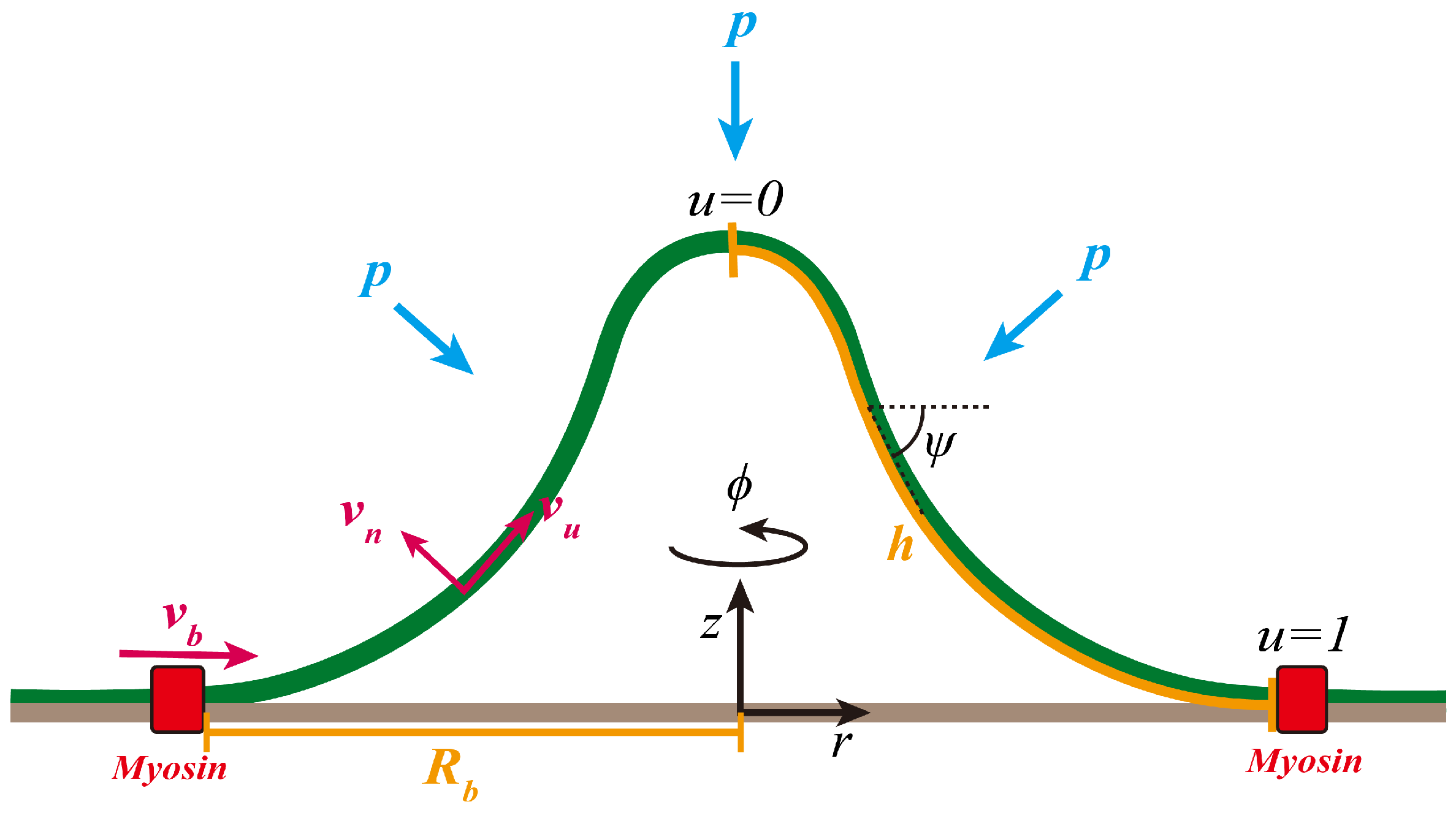
2.1. Geometry of the Membrane Surface
2.2. Flow Field on the Membrane Surface
2.3. Variational Formulation of the Dynamic Membrane Shape Equations
2.4. Non-Dimensionalization and Choice of Parameters
3. Results
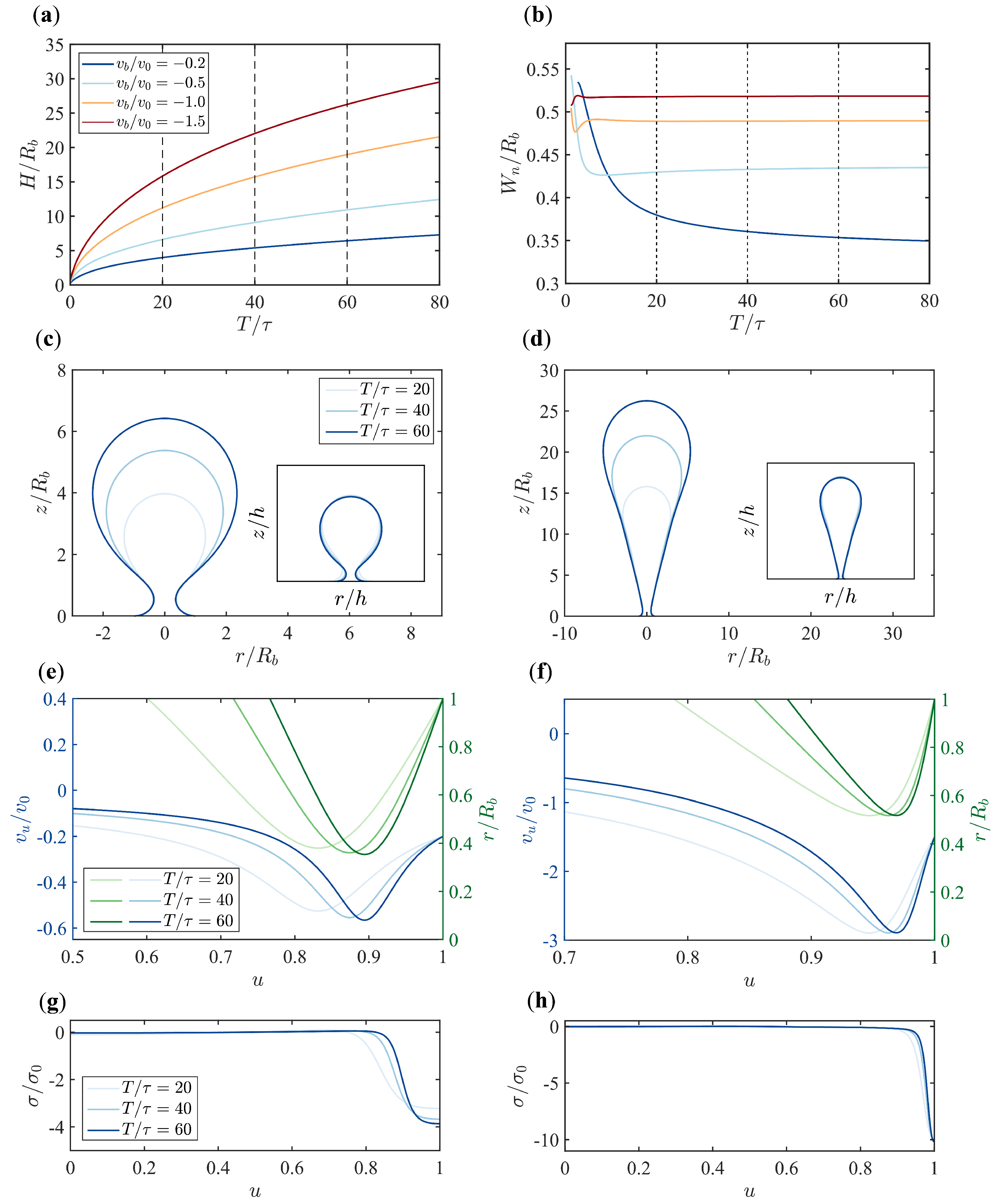
3.1. Different Boundary Flow Velocities Induce Various Vesicle Morphologies
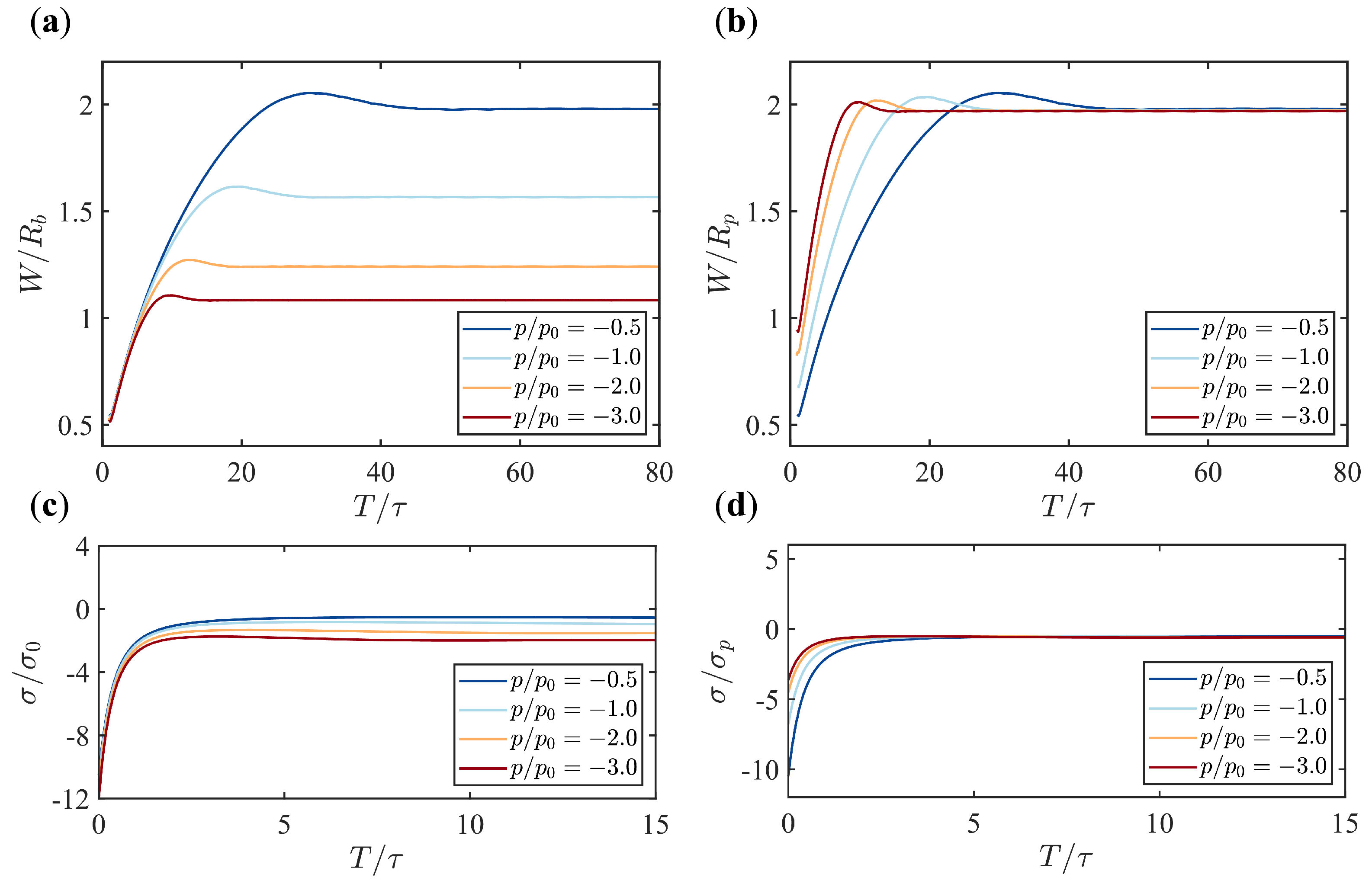
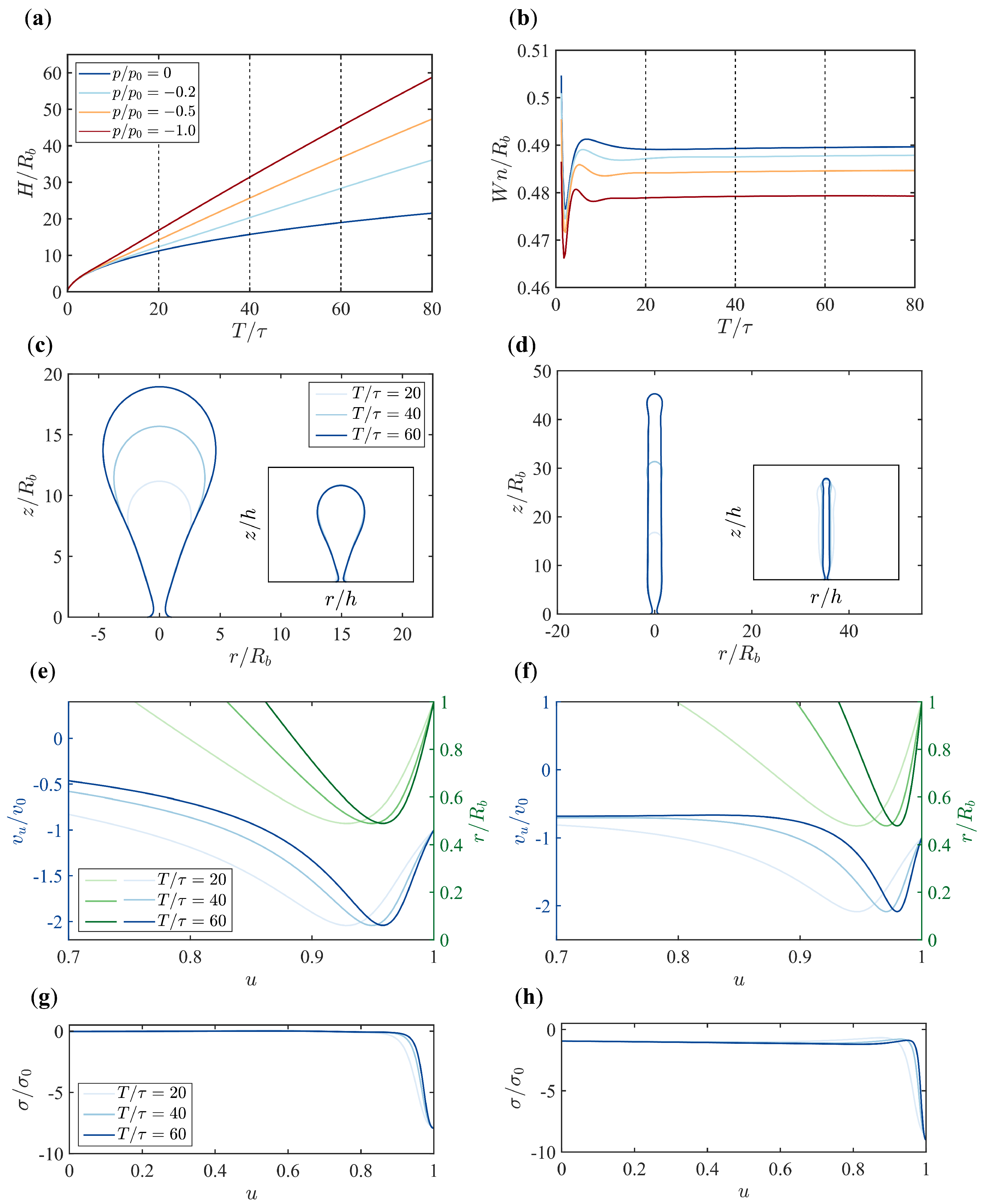
3.2. Pressure Makes a Dramatic Difference in Membrane Morphology and Growth Dynamics
3.3. The Scaling Behavior Between the Width of the Tubular Membrane and the Pressure
3.4. The Scaling Behavior Between the Membrane Tension and the Pressure
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Description of the Variational Formulation
Appendix A.1. Energy Dissipation Rate
Appendix A.2. Free Energy Change Rate
Appendix A.3. Work per Unit Time Exerted by the External Force
Appendix A.4. Incompressibility Condition and Coordinate Constraint
Appendix A.5. Derivation of the Variational Equations
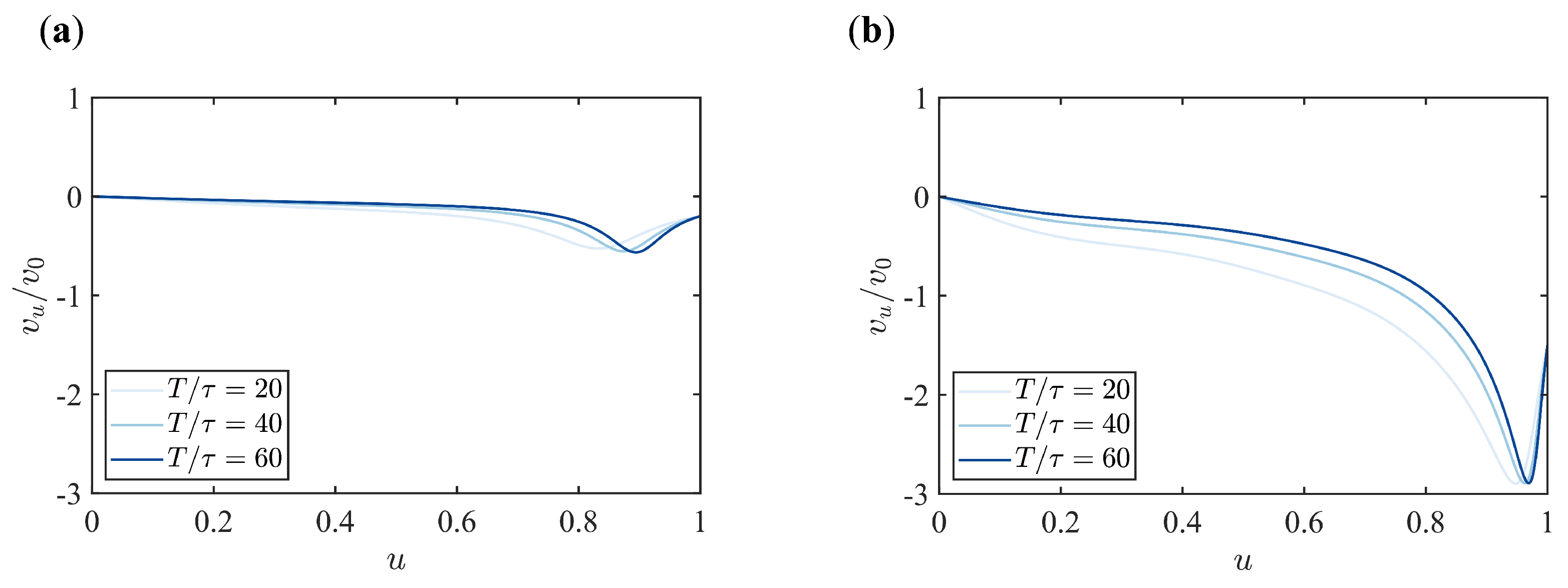
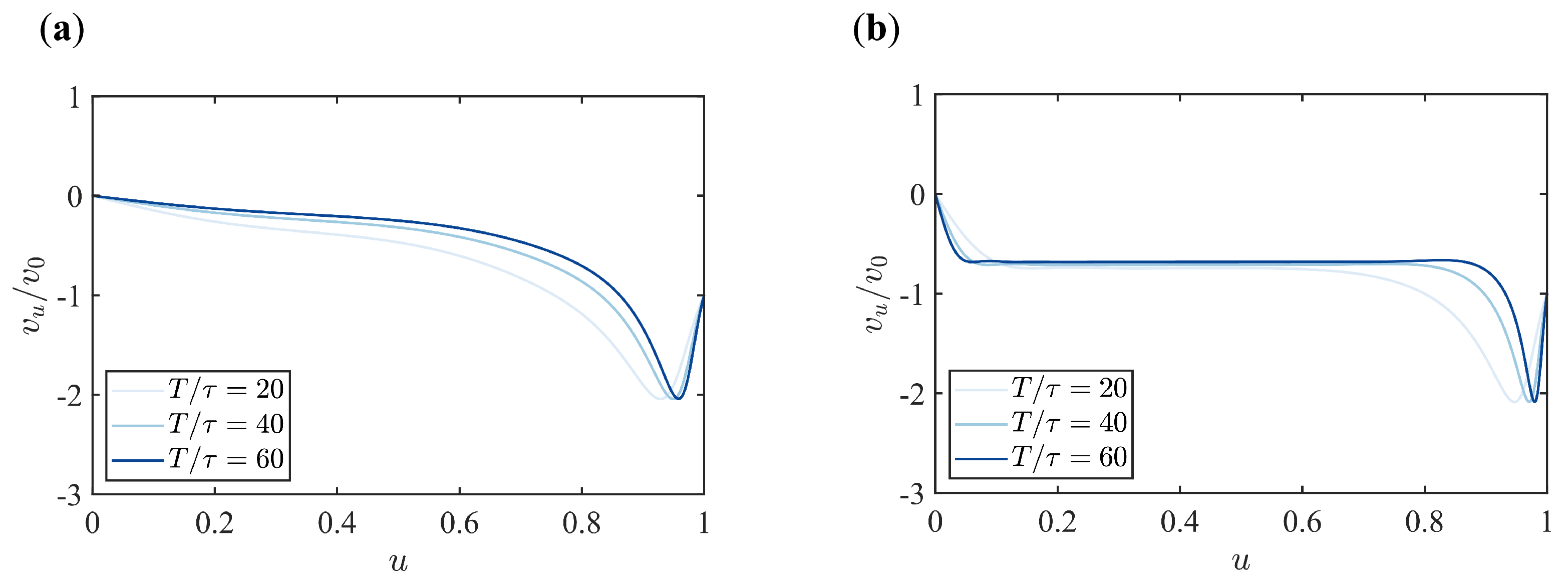
Appendix B. Supplementary Figures

References
- Kaksonen, M.; Roux, A. Mechanisms of clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2018, 19, 313–326. [Google Scholar] [PubMed]
- McMahon, H.T.; Boucrot, E. Molecular mechanism and physiological functions of clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2011, 12, 517–533. [Google Scholar] [PubMed]
- Kirchhausen, T. Three ways to make a vesicle. Nat. Rev. Mol. Cell Biol. 2000, 1, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Doherty, G.J.; McMahon, H.T. Mechanisms of endocytosis. Annu. Rev. Biochem. 2009, 78, 857–902. [Google Scholar]
- Schmid, S.L. Clathrin-coated vesicle formation and protein sorting: An integrated process. Annu. Rev. Biochem. 1997, 66, 511–548. [Google Scholar]
- Mettlen, M.; Chen, P.H.; Srinivasan, S.; Danuser, G.; Schmid, S.L. Regulation of clathrin-mediated endocytosis. Annu. Rev. Biochem. 2018, 87, 871–896. [Google Scholar]
- Kukulski, W.; Schorb, M.; Kaksonen, M.; Briggs, J.A. Plasma membrane reshaping during endocytosis is revealed by time-resolved electron tomography. Cell 2012, 150, 508–520. [Google Scholar]
- Boulant, S.; Kural, C.; Zeeh, J.C.; Ubelmann, F.; Kirchhausen, T. Actin dynamics counteract membrane tension during clathrin-mediated endocytosis. Nat. Cell Biol. 2011, 13, 1124–1131. [Google Scholar]
- Aghamohammadzadeh, S.; Ayscough, K.R. Differential requirements for actin during yeast and mammalian endocytosis. Nat. Cell Biol. 2009, 11, 1039–1042. [Google Scholar]
- Basu, R.; Munteanu, E.L.; Chang, F. Role of turgor pressure in endocytosis in fission yeast. Mol. Biol. Cell 2014, 25, 679–687. [Google Scholar]
- Minc, N.; Boudaoud, A.; Chang, F. Mechanical forces of fission yeast growth. Curr. Biol. 2009, 19, 1096–1101. [Google Scholar] [CrossRef]
- Atilgan, E.; Magidson, V.; Khodjakov, A.; Chang, F. Morphogenesis of the fission yeast cell through cell wall expansion. Curr. Biol. 2015, 25, 2150–2157. [Google Scholar] [CrossRef] [PubMed]
- Avinoam, O.; Schorb, M.; Beese, C.J.; Briggs, J.A.; Kaksonen, M. Endocytic sites mature by continuous bending and remodeling of the clathrin coat. Science 2015, 348, 1369–1372. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Steigmann, D.J. Modeling protein-mediated morphology in biomembranes. Biomech. Model. Mechanobiol. 2009, 8, 371–379. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, N.J.; Nukpezah, J.; Radhakrishnan, R. Minimal mesoscale model for protein-mediated vesiculation in clathrin-dependent endocytosis. PLoS Comput. Biol. 2010, 6, e1000926. [Google Scholar] [CrossRef] [PubMed]
- Walani, N.; Torres, J.; Agrawal, A. Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc. Natl. Acad. Sci. USA 2015, 112, E1423–E1432. [Google Scholar] [CrossRef]
- Dmitrieff, S.; Nédélec, F. Membrane mechanics of endocytosis in cells with turgor. PLoS Comput. Biol. 2015, 11, e1004538. [Google Scholar] [CrossRef]
- Hassinger, J.; Oster, G.; Drubin, D.; Rangamani, P. Design principles for robust vesiculation in clathrin-mediated endocytosis. Biophys. J. 2017, 112, 310a. [Google Scholar] [CrossRef]
- Tweten, D.; Bayly, P.; Carlsson, A. Actin growth profile in clathrin-mediated endocytosis. Phys. Rev. E 2017, 95, 052414. [Google Scholar] [CrossRef]
- Alimohamadi, H.; Vasan, R.; Hassinger, J.; Stachowiak, J.; Rangamani, P. The role of traction in membrane curvature generation. Biophys. J. 2018, 114, 600a. [Google Scholar] [CrossRef]
- Napoli, G.; Goriely, A. Elastocytosis. J. Mech. Phys. Solids 2020, 145, 104133. [Google Scholar]
- Ma, R.; Berro, J. Endocytosis against high turgor pressure is made easier by partial coating and freely rotating base. Biophys. J. 2021, 120, 1625–1640. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, A.E.; Bayly, P.V. Force generation by endocytic actin patches in budding yeast. Biophys. J. 2014, 106, 1596–1606. [Google Scholar] [PubMed]
- Wang, X.; Galletta, B.J.; Cooper, J.A.; Carlsson, A.E. Actin-regulator feedback interactions during endocytosis. Biophys. J. 2016, 110, 1430–1443. [Google Scholar]
- Lacy, M.M.; Ma, R.; Ravindra, N.G.; Berro, J. Molecular mechanisms of force production in clathrin-mediated endocytosis. FEBS Lett. 2018, 592, 3586–3605. [Google Scholar]
- Mund, M.; van Der Beek, J.A.; Deschamps, J.; Dmitrieff, S.; Hoess, P.; Monster, J.L.; Picco, A.; Nédélec, F.; Kaksonen, M.; Ries, J. Systematic nanoscale analysis of endocytosis links efficient vesicle formation to patterned actin nucleation. Cell 2018, 174, 884–896. [Google Scholar] [CrossRef]
- Sirotkin, V.; Berro, J.; Macmillan, K.; Zhao, L.; Pollard, T.D. Quantitative analysis of the mechanism of endocytic actin patch assembly and disassembly in fission yeast. Mol. Biol. Cell 2010, 21, 2894–2904. [Google Scholar]
- Footer, M.J.; Kerssemakers, J.W.; Theriot, J.A.; Dogterom, M. Direct measurement of force generation by actin filament polymerization using an optical trap. Proc. Natl. Acad. Sci. USA 2007, 104, 2181–2186. [Google Scholar] [CrossRef]
- Hartman, M.A.; Spudich, J.A. The myosin superfamily at a glance. J. Cell Sci. 2012, 125, 1627–1632. [Google Scholar]
- Pollard, T.D. Mechanics of cytokinesis in eukaryotes. Curr. Opin. Cell Biol. 2010, 22, 50–56. [Google Scholar]
- Buss, F.; Kendrick-Jones, J. How are the cellular functions of myosin VI regulated within the cell? Biochem. Biophys. Res. Commun. 2008, 369, 165–175. [Google Scholar] [PubMed]
- Pedersen, R.T.; Drubin, D.G. Type I myosins anchor actin assembly to the plasma membrane during clathrin-mediated endocytosis. J. Cell Biol. 2019, 218, 1138–1147. [Google Scholar] [PubMed]
- Pedersen, R.T.; Snoberger, A.; Pyrpassopoulos, S.; Safer, D.; Drubin, D.G.; Ostap, E.M. Endocytic myosin-1 is a force-insensitive, power-generating motor. J. Cell Biol. 2023, 222, e202303095. [Google Scholar]
- Seifert, U.; Berndl, K.; Lipowsky, R. Shape transformations of vesicles: Phase diagram for spontaneous-curvature and bilayer-coupling models. Phys. Rev. A 1991, 44, 1182. [Google Scholar]
- Jülicher, F.; Seifert, U. Shape equations for axisymmetric vesicles: A clarification. Phys. Rev. E 1994, 49, 4728. [Google Scholar]
- Mietke, A.; Jülicher, F.; Sbalzarini, I.F. Self-organized shape dynamics of active surfaces. Proc. Natl. Acad. Sci. USA 2019, 116, 29–34. [Google Scholar]
- Torres-Sánchez, A.; Millán, D.; Arroyo, M. Modelling fluid deformable surfaces with an emphasis on biological interfaces. J. Fluid Mech. 2019, 872, 218–271. [Google Scholar] [CrossRef]
- Gao, D.; Sun, H.; Ma, R.; Mietke, A. Self-organised dynamics and emergent shape spaces of active isotropic fluid surfaces. arXiv 2025, arXiv:2501.17849. [Google Scholar]
- Arroyo, M.; DeSimone, A. Relaxation dynamics of fluid membranes. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2009, 79, 031915. [Google Scholar]
- Jin, A.J.; Prasad, K.; Smith, P.D.; Lafer, E.M.; Nossal, R. Measuring the elasticity of clathrin-coated vesicles via atomic force microscopy. Biophys. J. 2006, 90, 3333–3344. [Google Scholar]
- Borja da Rocha, H.; Bleyer, J.; Turlier, H. A viscous active shell theory of the cell cortex. J. Mech. Phys. Solids 2022, 164, 104876. [Google Scholar] [CrossRef]
- Mietke, A.; Jemseena, V.; Kumar, K.V.; Sbalzarini, I.F.; Jülicher, F. Minimal model of cellular symmetry breaking. Phys. Rev. Lett. 2019, 123, 188101. [Google Scholar] [PubMed]
- Bois, J.S.; Jülicher, F.; Grill, S.W. Pattern formation in active fluids. Biophys. J. 2011, 100, 445a. [Google Scholar]
- Kumar, K.V.; Bois, J.S.; Jülicher, F.; Grill, S.W. Pulsatory patterns in active fluids. Phys. Rev. Lett. 2014, 112, 208101. [Google Scholar]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Für Naturforschung C 1973, 28, 693–703. [Google Scholar]
- Zhong-Can, O.Y.; Helfrich, W. Instability and deformation of a spherical vesicle by pressure. Phys. Rev. Lett. 1987, 59, 2486. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, H.; Ma, R. Boundary Flow-Induced Membrane Tubulation Under Turgor Pressures. Membranes 2025, 15, 106. https://doi.org/10.3390/membranes15040106
Xue H, Ma R. Boundary Flow-Induced Membrane Tubulation Under Turgor Pressures. Membranes. 2025; 15(4):106. https://doi.org/10.3390/membranes15040106
Chicago/Turabian StyleXue, Hao, and Rui Ma. 2025. "Boundary Flow-Induced Membrane Tubulation Under Turgor Pressures" Membranes 15, no. 4: 106. https://doi.org/10.3390/membranes15040106
APA StyleXue, H., & Ma, R. (2025). Boundary Flow-Induced Membrane Tubulation Under Turgor Pressures. Membranes, 15(4), 106. https://doi.org/10.3390/membranes15040106





