Formation of Multispheres and Myelin Based on Multiple Solutions of Membrane Shape Equation
Abstract
1. Introduction
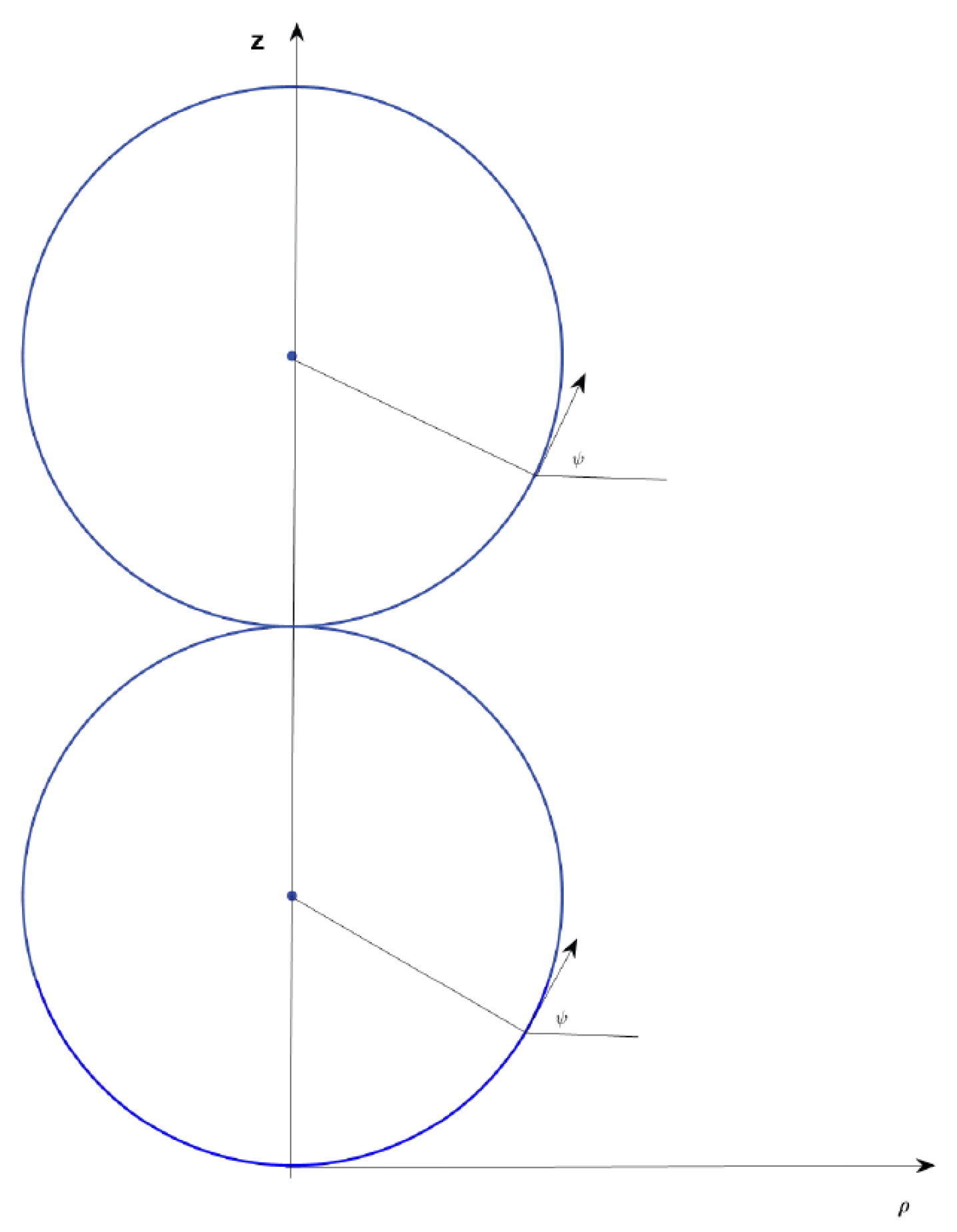
2. Membrane Shape Equation
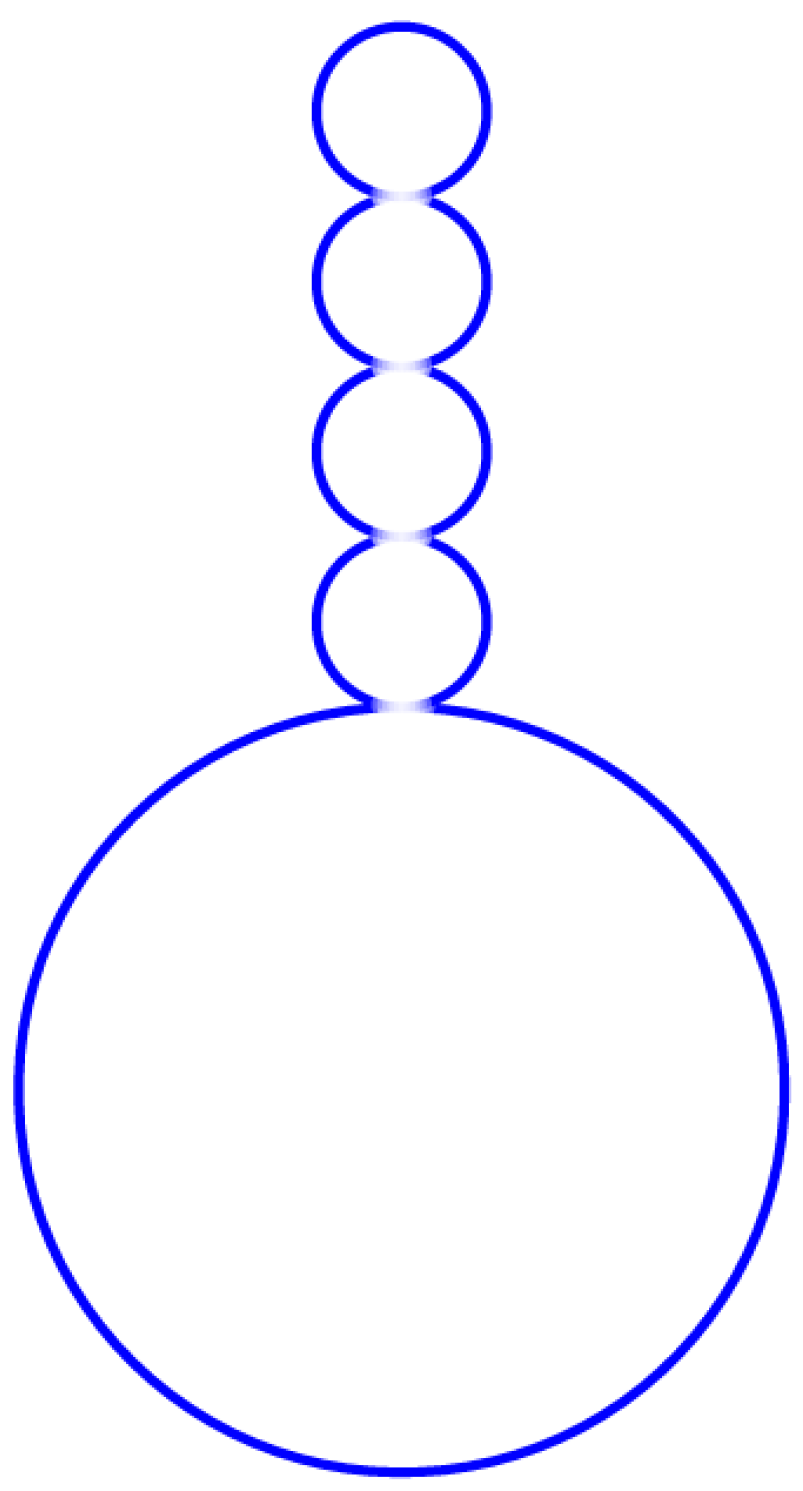
3. Multisphere Solution
4. Multisphere Formation in GUV Experiments
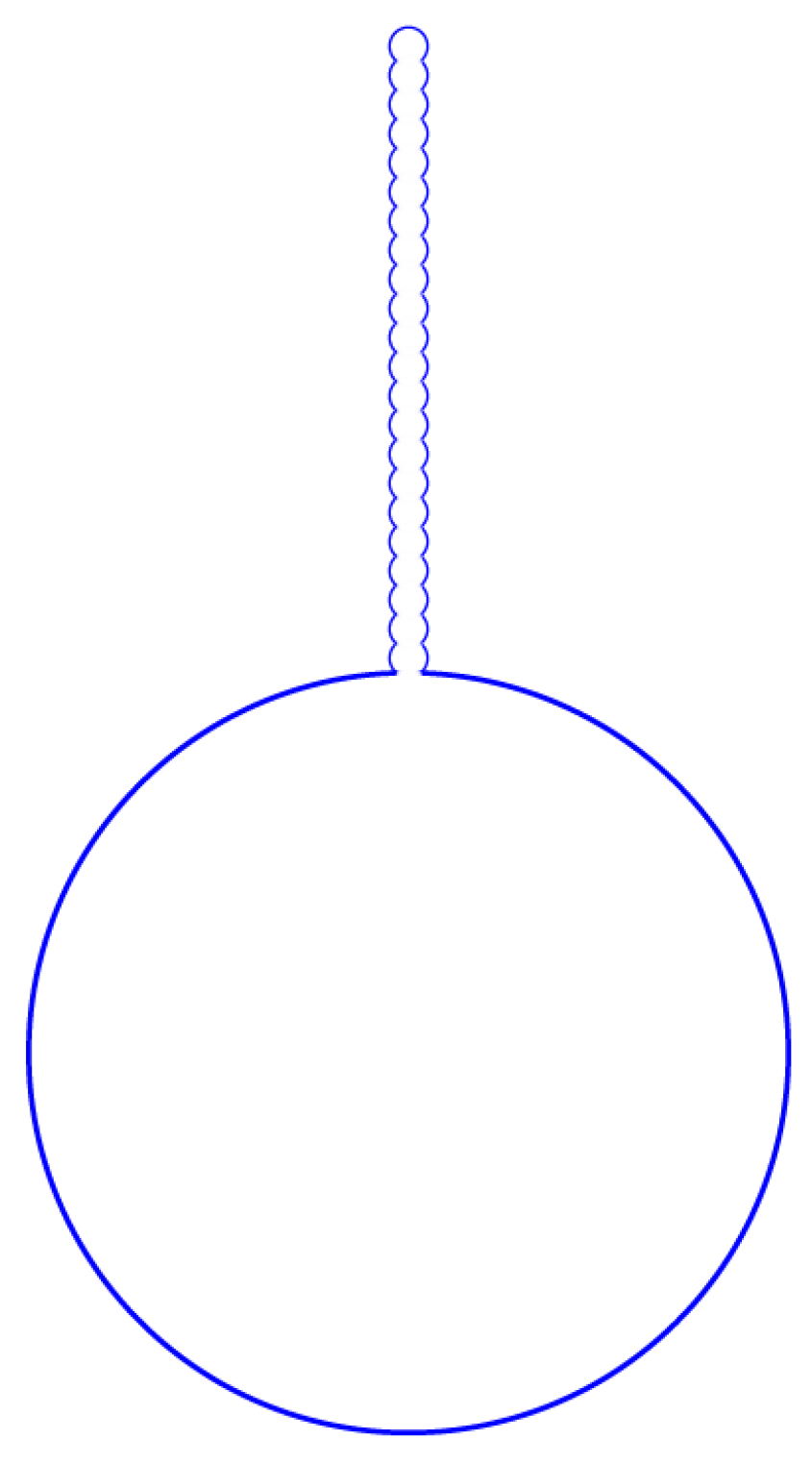
5. Myelin Formation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lberts, B.A.; Bray, D.; Lewis, J.; Raff, M.; Roberts, K.; Watson, J.D. Molecular Biology of the Cell, 2nd ed.; Garland Science Press: New York, NY, USA, 1989. [Google Scholar]
- Svoboda, K.; Schmdt, C.E.; Branton, D.; Block, S.M. Conformation and elasticity of the isolated red blood cell membrane skeleton. Biophys. J. 1992, 63, 784–793. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, C.E.; Svoboda, K.; Lei, N.; Petsche, I.B.; Berman, I.E.; Safinya, C.R.; Grest, G.S. Existence of a flat phase in red cell membrane skeletons. Science 1993, 259, 952–955. [Google Scholar] [CrossRef]
- Pond, E.; Pond, R.V. Observations quantitatives sur la production de formes myeliniques par les stromas de globules rouges. Nouv. Rev. Fr. Hemat. 1963, 3, 553. [Google Scholar]
- Bessis, M. Living Blood Cells and Their Ultrastructure; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Evans, E.; Rawicz, W. Entropy-Driven Tension and Bending Elasticity in Condensed-Fluid Membranes. Phys. Rev. Lett. 1990, 64, 2094. [Google Scholar] [CrossRef]
- Evans, E.; Needham, D. Physical properties of surfactant bilayer membranes: Thermal transitions, elasticity, rigidity, cohesion, and colloidal interactions. J. Phys. Chem. 1987, 91, 4219–4228. [Google Scholar] [CrossRef]
- Evans, E. Adhesion of surfactant-membrane covered droplets: Special features and curvature elasticity effects. Colloids Surf. 1990, 43, 327–347. [Google Scholar] [CrossRef]
- Bo, L.; Waugh, R. Determination of bilayer membrane bending stiffness by tether formation from giant, thin-walled vesicles. Biophys. J. 1989, 55, 509–517. [Google Scholar] [CrossRef] [PubMed]
- Ou-Yang, Z.-C.; Helfrich, W. Instability and deformation of a spherical vesicle by pressure. Phys. Rev. Lett. 1987, 59, 2486. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C 1973, 28, 693–703. [Google Scholar] [CrossRef]
- Naito, H.; Okuda, M.; Ou-Yang, Z.-C. Counterexample to some shape equations for axisymmetric vesicles. Phys. Rev. E 1995, 52, 2095. [Google Scholar] [CrossRef]
- Ou-Yang, Z.-C.; Helfrich, W. Bending energy of vesicle membranes: General expressions for the first, second and third variation of the shape energy and applications to spheres and cylinders. Phys. Rev. A 1989, 39, 5280. [Google Scholar] [CrossRef]
- Naito, H.; Okuda, M.; Ou-Yang, Z.-C. New solutions to the Helfrich variation problem for the spheres of lipid bilayer vesicles: Beyond Delaunays’s surface. Phys. Rev. Lett. 1995, 74, 4345. [Google Scholar] [CrossRef]
- Hu, J.G.; Ou-Yang, Z.C. Shape equations of the axisymmetric vesicles. Phys. Rev. E 1993, 47, 461. [Google Scholar] [CrossRef]
- Zheng, W.M.; Liu, J.X. Helfrich shape equation for axisymmetric vesicles as a first integral. Phys. Rev. E 1993, 48, 2856–2860. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, J.L.; Anderson, W.R.G.; Brown, M.S. Coated pits, coated vesicles, and receptor-mediated endocytosis. Nature 1979, 279, 679–685. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, J.; Drubin, D.G. Clathrin-mediated endo cytosis in budding yeast. Trends Cell Biol. 2012, 22, 1–13. [Google Scholar] [CrossRef]
- Sutton, R.B.; Fasshauer, D.; Jahn, R.; Brunger, A.T. Crystal structure of a snare complex involved in synaptic exocytosis at 2.4 A resolution. Nature 1998, 395, 347–353. [Google Scholar] [CrossRef]
- Giraudo, C.G.; Eng, W.S.; Melia, T.J.; Rothman, J.E. Aclamping mechanism involved in snare-dependent exocytosis. Science 2006, 313, 676–680. [Google Scholar] [CrossRef] [PubMed]
- Rothman, J.E.; Wieland, F.T. Protein sorting by trans port vesicles. Science 1996, 272, 227–234. [Google Scholar] [CrossRef]
- Mathivanan, S.; Ji, H.; Simpson, R.J. Exosomes: Extra cellular organelles important in intercellular communica tion. J. Proteom. 2010, 73, 1907–1920. [Google Scholar] [CrossRef]
- Takeshige, K.; Baba, M.; Tsuboi, S.; Noda, T.; Ohsumi, Y. Autophagy in yeast demonstrated with proteins-deficient mutants and conditions for its induction. J. Cell Biol. 1992, 119, 301–311. [Google Scholar] [CrossRef]
- Ou-Yang, Z.C. The study of complex shapes of fluid membrane, the Helfrich variation model and new application. In Proceedings of the Conference of Soft Matter, Xiamen, China, 5–8 July 2025. [Google Scholar]
- Olver, P.J. Application of Lie Groups to Different Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Xu, T. The classification of axisymmetric membrane shape equation. Commu. Math. Phys. 2025, submitted.
- Bhatia, T.; Christ, S.; Steinkuhler, J.; Dimova, R.; Lipowsky, R. Simple sugars shape giant vesicles into multispheres with many membrane necks. Soft Matter 2020, 16, 1246–1258. [Google Scholar] [CrossRef]
- Lipowsky, R. Understanding Giant Vesicles: A Theoretical Perspective; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Macia, E.; Ehrlich, M.; Massol, R.; Boucrot, E.; Brunner, C.; Kirchhausen, T. Dynasore, a cell-permeable inhibitor of dynamin. Dev. Cell 2006, 10, 839–850. [Google Scholar] [CrossRef]
- Boucrot, E.; Pick, A.; Camdere, G.; Liska, N.; Evergren, E.; McMahon, H.; Kozlov, M.M. Membrane fission is promoted by insertion of amphipathic helices and is restricted by crescent bar domains. Cell 2012, 149, 124–136. [Google Scholar] [CrossRef]
- Hurley, J.H.; Hanson, P.I. Membrane budding and scission by the escrt machinery: It’s all in the neck. Nat. Rev. Mol. Cell Biol. 2010, 11, 556–566. [Google Scholar] [CrossRef]
- Ramirez-Diaz, D.A.; Merino-Salomon, A.; Heymann, M.; Schwille, P. Bidirectional ftsz filament treadmilling promotes membrane constriction via torsional stress. bioRxiv 2019. [Google Scholar] [CrossRef]
- Ford, M.G.J.; Jenni, S.; Nunnari, J. The crystal structure of dynamin. Nature 2011, 477, 561–566. [Google Scholar] [CrossRef] [PubMed]
- Guizetti, J.; Schermelleh, L.; Mantler, J.; Maar, S.; Poser, I.; Leonhardt, H.; Muller-Reichert, T.; Gerlich, D.W. Cortical constriction during abscission involves helices of escrt-iii dependent filaments. Science 2011, 331, 1616–1620. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Kaksonen, M.; Drubin, D.G.; Oster, G. Endocytic vesicle scission by lipid phase boundary forces. Proc. Natl. Acad. Sci. USA 2006, 103, 10277–10282. [Google Scholar] [CrossRef]
- Vasan, R.; Rudraraju, S.; Akamatsu, M.; Garikipati, K.; Rangamani, P. A mechanical model reveals that non-axisymmetric buckling lowers the energy barrier associated with membrane neck constriction. Soft Matter 2020, 16, 784–797. [Google Scholar] [CrossRef]
- Tu, Z.C.; Ou-Yang, Z.C.; Liu, J.X.; Xie, Y.Z. Geometric Methods in Elastic Theory of Membranes in Liquid Crystal Phases; Peking University Press: Beijing, China, 2014. [Google Scholar]
- Kas, J.; Sackmann, E. Shape transitions and shape stability of giant phospholipid vesicles in pure water induced by area-to-volume changes. Biophys. J. 1991, 60, 825–844. [Google Scholar] [CrossRef]
- Berndl, K.; Kas, J.; Lipowsky, R.; Sackmann, E.; Seifert, U. Shape transformations of giant vesicles: Extreme sensitivity to bilayer asymmetry. Europhys. Lett. 1990, 13, 659. [Google Scholar] [CrossRef]
- Dobereiner, H.G.; Evans, E.; Seifert, O.; Wortis, M. Spinodal fluctuations of budding vesicles. Phys. Rev. Lett. 1995, 75, 3360. [Google Scholar] [CrossRef]
- Frolov, V.A.; Lizunov, V.A.; Dunina-Barkovskaya, A.Y.; Samsonov, A.V.; Zimmerberg, J. Shape bistability of a membrane neck: A toggle switch to control vesicle content release. Proc. Natl. Acad. Sci. USA 2003, 100, 8698–8703. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Bowman, H.; Leung, A.; Needham, D.; Tirrell, D. Biomembrane templates for nanoscale conduits and networks. Science 1996, 273, 933–935. [Google Scholar] [CrossRef] [PubMed]
- Waugh, R.E.; Hochmuth, R.M. Mechanical equilibrium of thick, hollow, liquid, membrane cylinders. Biophys. J. 1987, 52, 391–400. [Google Scholar] [CrossRef]
- Boroske, E.; Elwenspoek, M.; Helfrich, W. Osmotic shrinkage of giant egg-lecithin vesicles. Biophys. J. 1981, 34, 95–109. [Google Scholar] [CrossRef]
- Wennerstrom, H.; Sparr, E.; Stenhammar, J. Thermal fluctuations and osmotic stability of lipid vesicles. Phys. Rev. E 2022, 106, 064607. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, R.; Miettinen, M.S.; Fricke, N.; Dimova, R. The glycolipid GM1 reshapes asymmetric biomembranes and giant vesicles by curvature generation. Proc. Natl. Acad. Sci. USA 2018, 115, 5756–5761. [Google Scholar] [CrossRef]
- Come, B.; Donato, M.; Potenza, L.F.; Mariani, P.; Itri, R.; Spinozzi, F. The intriguing role of rhamnolipids on plasma membrane remodelling: From lipid rafts to membrane budding. J. Colloid Interface Sci. B 2021, 582, 669–677. [Google Scholar] [CrossRef]
- Holopainen, J.M.; Angelova, M.I.; Kinnunen, P.K. Vectorial budding of vesicles by asymmetrical enzymatic formation of ceramide in giant liposomes. Biophys. J. 2000, 78, 830–838. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Peng, Y.X.; Wang, P.; Jiang, Z.Y.; Zhao, X.J.; Zhu, T. Membrane inward/outward budding and transition pathway induced by the asymmetric solutions. Colloids Surf. A 2023, 675, 132111. [Google Scholar] [CrossRef]
- Liu, X.Y.; Stenhammar, J.; Wennerstrom, H.; Sparr, E. Vesicles Balance Osmotic stress with bending energy that can be released to form daughter vesicles. Phys. Chem. Lett. 2022, 13, 498–507. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997, 46, 13–137. [Google Scholar] [CrossRef]
- Fischer, T.M. Bending stiffness of lipid bilayers. V. Comparison of two formulations. J. Phys. H Fr. 1993, 3, 1795–1805. [Google Scholar]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics with Special Applications to Particulate Media; Martinus Nijhoff Publishes: Boston, MA, USA, 1983. [Google Scholar]
- Deuling, H.J.; Helfrich, W. Red blood cell shapes as explained on the basis of curvature elasticity. Biophys. J. 1976, 16, 861–868. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Ou-Yang, Z.-C. Formation of Multispheres and Myelin Based on Multiple Solutions of Membrane Shape Equation. Membranes 2025, 15, 319. https://doi.org/10.3390/membranes15100319
Xu T, Ou-Yang Z-C. Formation of Multispheres and Myelin Based on Multiple Solutions of Membrane Shape Equation. Membranes. 2025; 15(10):319. https://doi.org/10.3390/membranes15100319
Chicago/Turabian StyleXu, Tao, and Zhong-Can Ou-Yang. 2025. "Formation of Multispheres and Myelin Based on Multiple Solutions of Membrane Shape Equation" Membranes 15, no. 10: 319. https://doi.org/10.3390/membranes15100319
APA StyleXu, T., & Ou-Yang, Z.-C. (2025). Formation of Multispheres and Myelin Based on Multiple Solutions of Membrane Shape Equation. Membranes, 15(10), 319. https://doi.org/10.3390/membranes15100319





