Modelling the Performance of Electrically Conductive Nanofiltration Membranes
Abstract
1. Introduction
2. Model Description
2.1. Problem Statement

2.2. Governing Equations
2.3. Boundary Conditions
2.4. Concentration Polarization
2.5. Numerical Implementation
3. Results and Discussion
3.1. Physical Parameters
3.2. The Influence of Electronic Charge
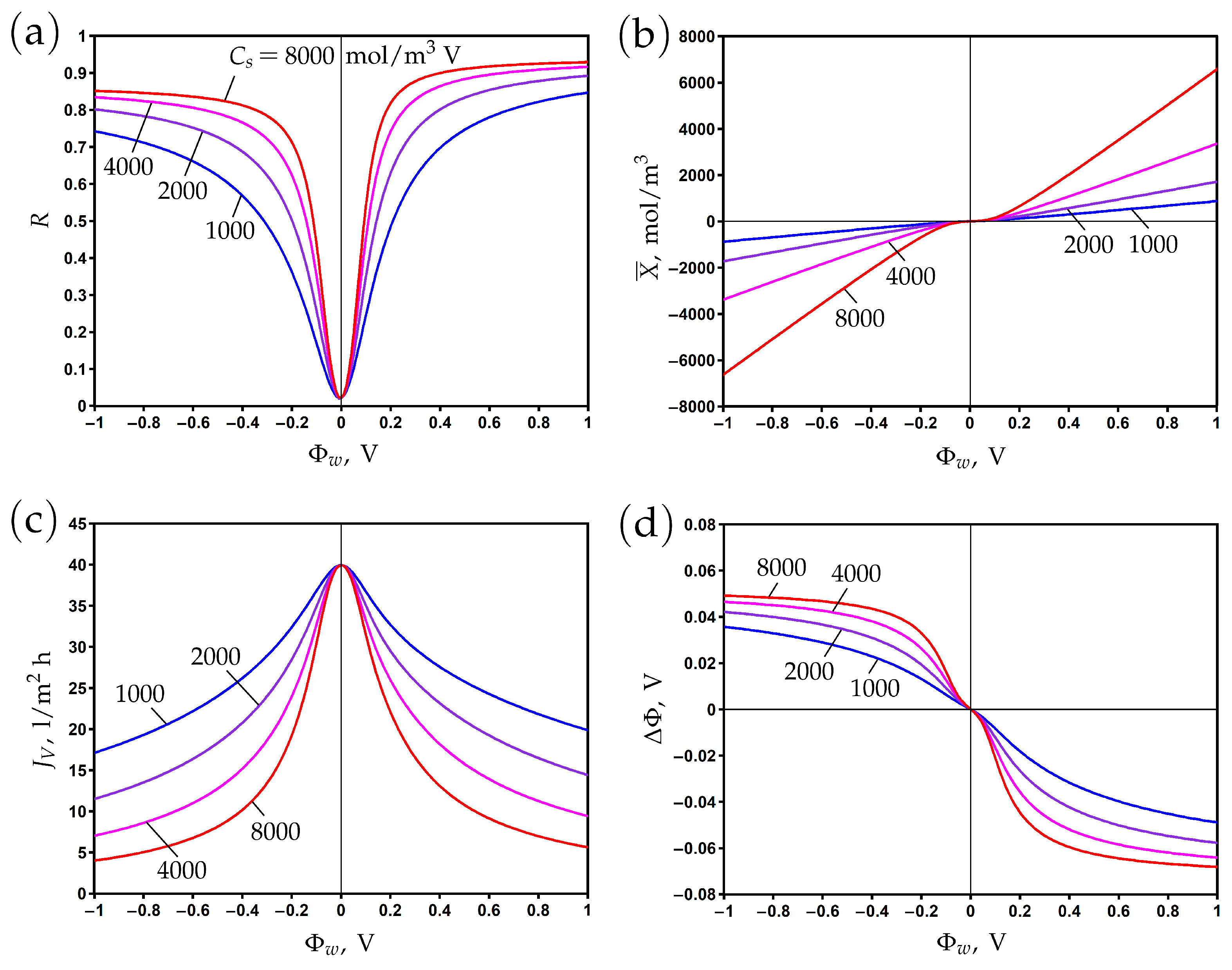
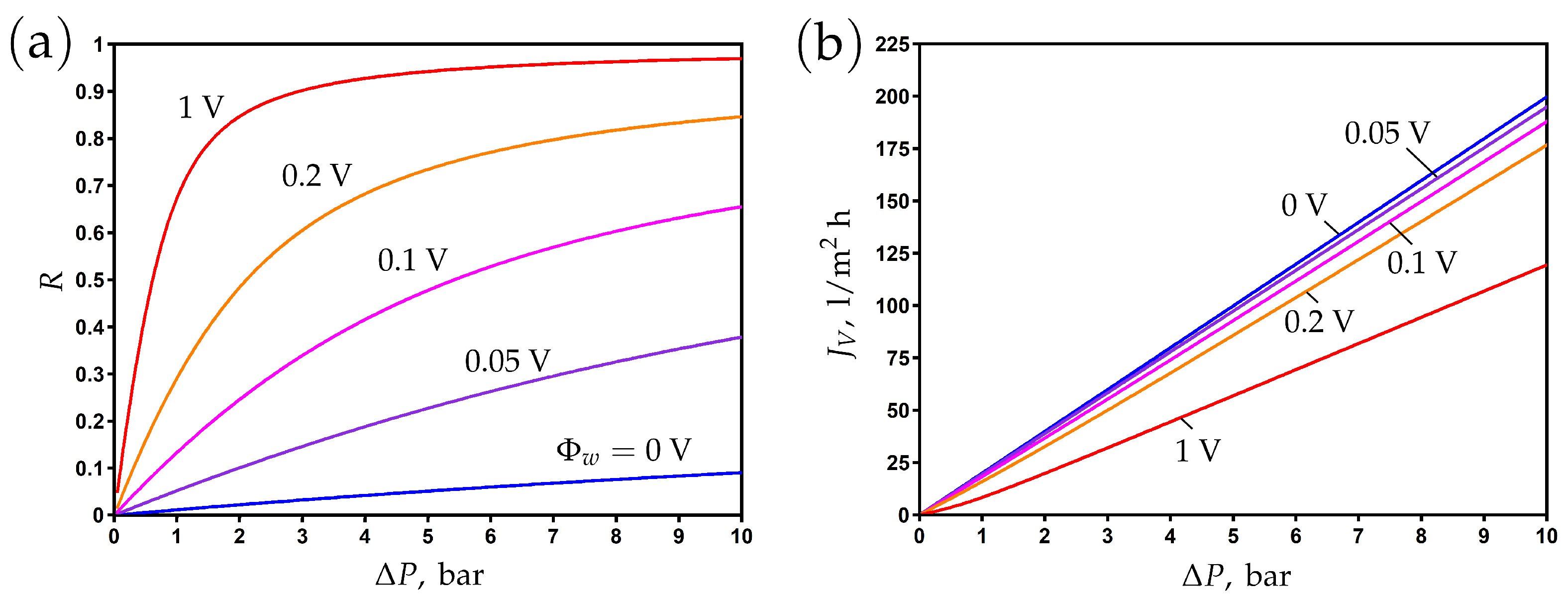
3.3. The Influence of Pressure Difference
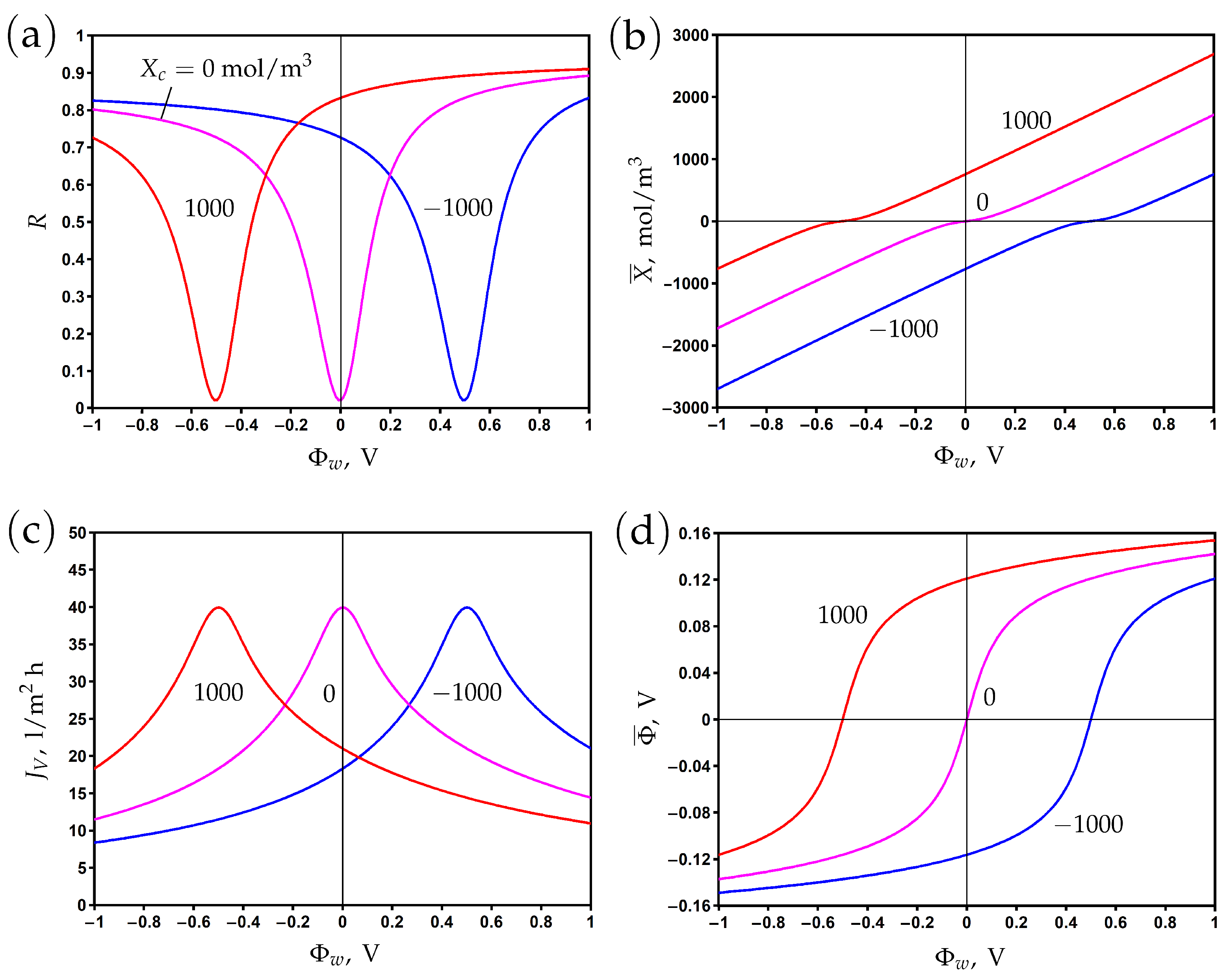
3.4. The Influence of Chemical Charge
3.5. The Influence of Other Factors
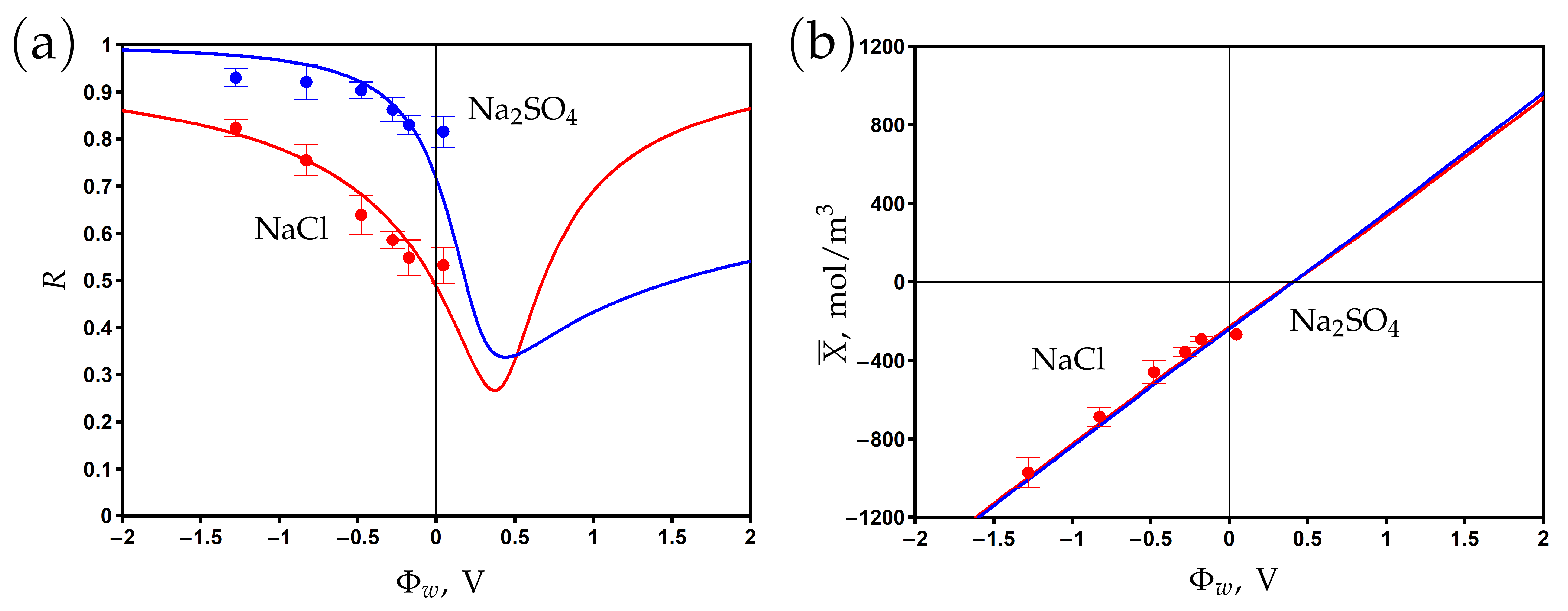
3.6. Comparison with Experimental Results: PANi–PSS/CNT Membranes
3.7. Comparison with Experimental Results: MXene/CNT Membranes
| Parameter | Dimension | Value |
|---|---|---|
| Membrane properties | ||
| Average pore size | nm | 2 |
| Thickness L | m | 0.502 |
| Permeability A for MO | L/m h bar | 27 |
| Permeability A for OG | L/m h bar | 25 |
| Porosity | − | 0.2 |
| Parameters of filtration experiments | ||
| Temperature T | K | 298.15 |
| Pressure difference | bar | 1 |
| MO feed concentration | mol/m | 0.0611 |
| OG feed concentration | mol/m | 0.0884 |
| Surface potential | V | −1.6...0 |
| Ion properties | ||
| Na radius | nm | 0.095 |
| Na diffusion coefficient | m/s | 1.33 |
| MO anion radius | nm | 0.420 |
| OG anion radius | nm | 0.550 |
| MO anion charge number | − | −1 |
| OG anion charge number | − | −2 |
| MO anion diffusion coefficient | m/s | 0.91 |
| OG anion diffusion coefficient | m/s | 0.70 |
| Model parameters | ||
| Stern layer thickness | nm | 0.5 |
| Stern layer volume capacitance | mol/m V | 700 |
| Volume chemical charge density | mol/m | −200 |
| Friction factor | − | 0.18 |
| Charge reduction factor | − | 8.03·10 |
| Mass transfer coefficient | L/m h | 100 |
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| r | Transversal coordinate, m |
| z | Longitudinal coordinate, m |
| R | Pore radius or half-width, m |
| L | Pore length/selective layer thickness, m |
| Cation/anion charge number | |
| Cation/anion radius, m | |
| Concentration of cations/anions, mol/m | |
| Cation/anion flux, mol/m s | |
| Cation/anion diffusion coefficient, m/s | |
| Friction factor | |
| Steric factor | |
| D | Salt diffusion coefficient, m/s |
| Solvent flux, m/m s | |
| Electrical potential, V | |
| Surface potential, V | |
| P | Pressure, Pa |
| Pressure difference, Pa | |
| Total surface charge density, C/m | |
| Electronic surface charge density, C/m | |
| Chemical surface charge density, C/m | |
| X | Total volume charge density, mol/m |
| Volume chemical charge density, mol/m | |
| Stern layer capacitance, F/m | |
| Stern layer volume capacitance, mol/m V | |
| Stern layer thickness, m | |
| Dielectric constant, F/m | |
| Stern layer relative permittivity | |
| Membrane porosity | |
| T | Temperature, K |
| Universal gas constant, J/kg·K | |
| F | Faraday constant, C/mol |
| A | Membrane permittivity, m/m h bar |
| Solvent dynamic viscosity, Pa·s | |
| Mass transfer coefficient, m/m h | |
| u | Cross-flow velocity, m/s |
| H | Gap height in a cross-flow cell, m |
| Gap length in a cross-flow cell, m | |
| Concentration polarization layer thickness, m | |
| R | Aspect ratio of the gap |
| Peclet number | |
| Sherwood number | |
| Indices | |
| f | feed |
| p | permeate |
References
- Strathmann, H. Introduction to Membrane Science and Technology; Wiley–VCH: Weinheim, Germany, 2011. [Google Scholar]
- Mohammad, A.W.; Teow, Y.H.; Ang, W.L.; Chung, Y.T.; Oatley–Radcliffe, D.L.; Hilal, N. Nanofiltration membranes review: Recent advances and future prospects. Desalination 2015, 356, 226–254. [Google Scholar] [CrossRef]
- Volkov, V.V.; Mchedlishvili, B.V.; Roldugin, V.I.; Ivanchev, S.S.; Yaroslavtsev, A.B. Membranes and nanotechnologies. Nanotech. Russia 2008, 3, 656–687. [Google Scholar] [CrossRef]
- Zhang, H.; He, Q.; Luo, J.; Wan, Y.; Darling, S.B. Sharpening nanofiltration: Strategies for enhanced membrane selectivity. ACS Appl. Mater. Interfaces 2020, 12, 39948–39966. [Google Scholar] [CrossRef]
- Schoch, R.B.; Han, J.; Renaud, P. Transport phenomena in nanofluidics. Rev. Mod. Phys. 2008, 80, 839–883. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, G.; Li, Y.; Chen, X.; Yao, Y.; Ren, S.; Li, M.; Wu, Y.; An, C. Electrically conductive inorganic membranes: A review on principles, characteristics and applications. Chem. Eng. J. 2022, 427, 131987. [Google Scholar] [CrossRef]
- Alayande, A.B.; Goh, K.; Son, M.; Kim, C.M.; Chae, K.J.; Kang, Y.; Jang, J.; Kim, I.S.; Yang, E. Recent progress in one– and two–dimensional nanomaterial–based electro–responsive membranes: Versatile and smart applications from fouling mitigation to tuning mass transport. Membranes 2021, 11, 5. [Google Scholar] [CrossRef]
- Larocque, M.J.; Gelb, A.; Latulippe, D.R.; Lannoy, C.F. Meta–analysis of electrically conductive membranes: A comparative review of their materials, applications, and performance. Sep. Purif. Technol. 2022, 287, 120482. [Google Scholar] [CrossRef]
- Barbhuiya, N.H.; Misra, U.; Singh, S.P. Synthesis, fabrication, and mechanism of action of electrically conductive membranes: A review. Environ. Sci. Water Res. Technol. 2021, 7, 671–705. [Google Scholar] [CrossRef]
- Fan, X.; Wei, G.; Quan, X. Carbon nanomaterial–based membranes for water and wastewater treatment under electrochemical assistance. Environ. Sci. Nano 2023, 10, 11–40. [Google Scholar] [CrossRef]
- Duval, J.; Lyklema, J.; Kleijn, J.M.; Leeuwen, H.P. Amphifunctionally electrified interfaces: Coupling of electronic and ionic surface–charging processes. Langmuir 2001, 17, 7573–7581. [Google Scholar] [CrossRef]
- Duval, J.; Kleijn, J.M.; Lyklema, J.; Leeuwen, H.P. Double layers at amphifunctionally electrified interfaces in the presence of electrolytes containing specifically adsorbing ions. J. Electroanal. Chem. 2002, 532, 337–352. [Google Scholar] [CrossRef]
- Formoso, P.; Pantuso, E.; Filpo, G.; Nicoletta, F.P. Electro–conductive membranes for permeation enhancement and fouling mitigation: A Short review. Membranes 2017, 7, 39. [Google Scholar] [CrossRef]
- Nishizawa, M.; Menon, V.P.; Martint, C.R. Metal Nanotubule membranes with electrochemically switchable ion–transport selectivity. Science 1995, 268, 700–702. [Google Scholar] [CrossRef]
- Martin, C.R.; Nishizawa, M.; Jirage, K.; Kang, M.; Lee, S.B. Controlling ion–transport selectivity in gold nanotubule membranes. Adv. Mater. 2001, 13, 1351–1362. [Google Scholar] [CrossRef]
- Kang, M.S.; Martin, C.R. Investigations of potential–dependent fluxes of ionic permeates in gold nanotubule membranes prepared via the template method. Langmuir 2001, 17, 2753–2759. [Google Scholar] [CrossRef]
- Surwade, S.P.; Chai, S.H.; Choi, J.P.; Wang, X.; Lee, J.S.; Vlassiouk, I.V.; Mahurin, S.M.; Dai, S. Electrochemical control of ion transport through a Mesoporous Carbon Membrane. Langmuir 2014, 30, 3606–3611. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Cha, C.S.; Lu, J.; Zhuang, L. Ionic conductivity of pure water in charged porous matrix. ChemPhysChem 2012, 13, 514–519. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Martin, C.R. Voltage charging enhances ionic conductivity in gold nanotube membranes. ACS Nano 2014, 8, 8266–8272. [Google Scholar] [CrossRef]
- Ryzhkov, I.I.; Lebedev, D.V.; Solodovnichenko, V.S.; Minakov, A.V.; Simunin, M.M. On the origin of membrane potential in membranes with polarizable nanopores. J. Membr. Sci. 2018, 549, 616–630. [Google Scholar] [CrossRef]
- Lebedev, D.V.; Solodovnichenko, V.S.; Simunin, M.M.; Ryzhkov, I.I. Effect of electric field on ion transport in nanoporous membranes with conductive surface. Petrol. Chem. 2018, 58, 474–481. [Google Scholar] [CrossRef]
- Ryzhkov, I.I.; Shchurkina, M.A.; Mikhlina, E.V.; Simunin, M.M.; Nemtsev, I.V. Switchable ionic selectivity of membranes with electrically conductive surface: Theory and experiment. Electrochim. Acta 2021, 375, 137970. [Google Scholar] [CrossRef]
- Zhang, H.; Quan, X.; Fan, X.; Yi, G.; Chen, S.; Yu, H.; Chen, Y. Improving ion rejection of conductive nanofiltration membrane through electrically enhanced surface charge density. Environ. Sci. Technol. 2019, 53, 868–877. [Google Scholar] [CrossRef]
- Hu, C.; Liu, Z.; Lu, X.; Sun, J.; Liu, H.; Qu, J. Enhancement of the Donnan effect through capacitive ion increase using an electroconductive rGO–CNT nanofiltration membrane. J. Mater. Chem. A 2018, 6, 4737–4745. [Google Scholar] [CrossRef]
- Yi, G.; Du, L.; Wei, G.; Zhang, H.; Yu, H.; Quan, X.; Chen, S. Selective molecular separation with conductive MXene/CNT nanofiltration membranes under electrochemical assistance. J. Membr. Sci. 2022, 658, 120719. [Google Scholar] [CrossRef]
- Sun, J.; Hu, C.; Wu, B.; Liu, H.; Qu, J. Improving ion rejection of graphene oxide conductive membranes by applying electric field. J. Membr. Sci. 2020, 604, 118077. [Google Scholar] [CrossRef]
- Fan, X.; Zhao, H.; Liu, Y.; Quan, X.; Yu, H.; Chen, S. Enhanced permeability, selectivity, and antifouling ability of CNTs/Al2O3 membrane under electrochemical assistance. Environ. Sci. Technol. 2015, 49, 2293–2300. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Wang, G.; Li, S.; Li, X.; Yu, H.; Quan, X. Porous carbon membrane with enhanced selectivity and antifouling capability for water treatment under electrochemical assistance. J. Colloid Int. Sci. 2020, 560, 59–68. [Google Scholar] [CrossRef]
- Yaroshchuk, A.; Bruening, M.; Zholkovskiy, E. Modelling nanofiltration of electrolyte solutions. Adv. Colloid Int. Sci. 2019, 268, 39–63. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Lin, S. Pore model for nanofiltration: History, theoretical framework, key predictions, limitations, and prospects. J. Membr. Sci. 2021, 620, 118809. [Google Scholar] [CrossRef]
- Mareev, S.; Gorobchenko, A.; Ivanov, D.; Anokhin, D.; Nikonenko, V. Ion and water transport in ion–exchange membranes for power generation systems: Guidelines for modeling. Int. J. Mol. Sci. 2023, 24, 34. [Google Scholar] [CrossRef]
- Spiegler, K.S.; Kedem, O. Thermodynamics of hyperfiltration (reverse osmosis): Criteria for efficient membranes. Desalination 1966, 1, 311–326. [Google Scholar] [CrossRef]
- Jacazio, G.; Probstein, R.F.; Sonin, A.A.; Yung, D. Electrokinetic salt rejection in hyperfiltration through porous materials. Theory and experiment. J. Phys. Chem. 1972, 76, 4015–4023. [Google Scholar] [CrossRef]
- Probstein, R.F.; Sonin, A.A.; Yung, D. Brackish water salt rejection by porous hyperfiltration membranes. Desalination 1973, 13, 303–316. [Google Scholar] [CrossRef]
- Wang, X.L.; Tsuru, T.; Nakao, S.I.; Kimura, S. Electrolyte transport through nanofiltration membranes by the space–charge model and the comparison with Teorell–Meyer–Sievers model. J. Membr. Sci. 1995, 103, 117–133. [Google Scholar] [CrossRef]
- Bowen, W.R.; Mohammad, A.W.; Hilai, N. Characterisation of nanofiltration membranes for predictive purposes—Use of salts, uncharged solutes, and atomic force microscopy. J. Membr. Sci. 1997, 126, 91–105. [Google Scholar] [CrossRef]
- Bowen, W.R.; Welfoot, J.S. Modelling the performance of membrane nanofiltration—Critical assessment and model development. Chem. Eng. Sci. 2002, 57, 1121–1137. [Google Scholar] [CrossRef]
- Bandini, S.; Vezzani, D. Nanofiltration modeling: The role of dielectric exclusion in membrane characterization. Chem. Eng. Sci. 2003, 58, 3303–3326. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Chen, J.C.; Elimelech, M. Coupled model of concentration polarization and pore transport in crossflow nanofiltration. AIChE J. 2001, 47, 2733–2745. [Google Scholar] [CrossRef]
- Ryzhkov, I.I.; Minakov, A.V. Theoretical study of electrolyte transport in nanofiltration membranes with constant surface potential/charge density. J. Membr. Sci. 2016, 520, 515–528. [Google Scholar] [CrossRef]
- Ryzhkov, I.I.; Minakov, A.V. Finite ion size effects on electrolyte transport in nanofiltration membranes. J. SibFU Math. Phys. 2017, 10, 186–198. [Google Scholar] [CrossRef]
- Ryzhkov, I.I.; Lebedev, D.V.; Solodovnichenko, V.S.; Shiverskiy, A.V.; Simunin, M.M. Induced–charge enhancement of the diffusion potential in membranes with polarizable nanopores. Phys. Rev. Lett. 2017, 119, 226001. [Google Scholar] [CrossRef]
- Yaroshchuk, A.; Zholkovskiy, E. Streaming potential with ideally polarizable electron–conducting substrates. Langmuir 2022, 38, 9974–9980. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Biesheuvel, P.M.; Ryzhkov, I.I. Theory of ion and water transport in electron–conducting membrane pores with pH–dependent chemical charge. Phys. Rev. Appl. 2019, 12, 014039. [Google Scholar] [CrossRef]
- Ryzhkov, I.I.; Vyatkin, A.S.; Mikhlina, E.V. Modelling of conductive nanoporous membranes with switchable ionic selectivity. Membr. Membr. Technol. 2020, 2, 10–19. [Google Scholar] [CrossRef]
- Krom, A.I.; Ryzhkov, I.I. Ionic conductivity of nanopores with electrically conductive surface: Comparison between 1D and 2D models. Adv. Theory Simul. 2021, 4, 2100174. [Google Scholar] [CrossRef]
- Brown, M.A.; Abbas, Z.; Kleibert, A.; Green, R.G.; Goel, A.; May, S.; Squires, T.M. Determination of surface potential and electrical double–layer structure at the aqueous electrolyte–nanoparticle interface. Phys. Rev. X 2016, 6, 011007. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Porada, S.; Elimelech, M.; Dykstra, J.E. Tutorial review of reverse osmosis and electrodialysis. J. Membr. Sci. 2022, 647, 120221. [Google Scholar] [CrossRef]
- Kimani, E.; Pranić, M.; Porada, S.; Kemperman, A.J.B.; Ryzhkov, I.I.; Van der Meer, W.G.J.; Biesheuvel, P.M. The influence of feedwater pH on membrane charge ionization and ion rejection by reverse osmosis: An experimental and theoretical study. J. Membr. Sci. 2022, 660, 120800. [Google Scholar] [CrossRef]
- Sablani, S.S.; Goosena, M.F.A.; Al–Belushi, R.; Wilf, M. Concentration polarization in ultrafiltration and reverse osmosis: A critical review. Desalination 2001, 141, 269–289. [Google Scholar] [CrossRef]
- Foo, K.; Liang, Y.Y.; Tan, C.K.; Fimbres Weihs, G.A. Coupled effects of circular and elliptical feed spacers under forced–slip on viscous dissipation and mass transfer enhancement based on CFD. J. Membr. Sci. 2021, 637, 119599. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kim, S.; Hoek, E.M.V. Modeling concentration polarization in reverse osmosis processes. Desalination 2005, 186, 111–128. [Google Scholar] [CrossRef]
- Zhou, Z.; Ling, B.; Battiato, I.; Husson, S.M.; Ladner, D.A. Concentration polarization over reverse osmosis membranes with engineered surface features. J. Membr. Sci. 2021, 617, 118199. [Google Scholar] [CrossRef]
- Hussain, A.A.; Nataraj, S.K.; Abashar, M.E.E.; Al–Mutaz, I.S.; Aminabhavi, T.M. Prediction of physical properties of nanofiltration membranes using experiment and theoretical models. J. Membr. Sci. 2008, 310, 321–336. [Google Scholar] [CrossRef]
- Zhang, H. (Dalian University of Technology, Dalian 116024, China). Personal communication, 2023.
- Osorio, S.C.; Biesheuvel, P.M.; Dykstra, J.E.; Virga, E. Nanofiltration of complex mixtures: The effect of the adsorption of divalent ions on membrane retention. Desalination 2022, 527, 115552. [Google Scholar] [CrossRef]
- Song, S.; Hao, C.; Zhang, X.; Zhang, Q.; Sun, R. Sonocatalytic degradation of methyl orange in aqueous solution using Fe–doped TiO2 nanoparticles under mechanical agitation. Open Chem. 2018, 16, 1283–1296. [Google Scholar] [CrossRef]
- Leaist, G.D. Diffusion with stepwise aggregation in aqueous solutions of the ionic azo dye methyl orange. J. Colloid Int. Sci. 1988, 125, 327–332. [Google Scholar] [CrossRef]
- Farag, A.A.; Sedahmed, G.H.; Farag, H.A.; Nagawi, A.F. Diffusion of some dyes in aqueous polymer solutions. Br. Polym. J. 1976, 8, 54–57. [Google Scholar] [CrossRef]
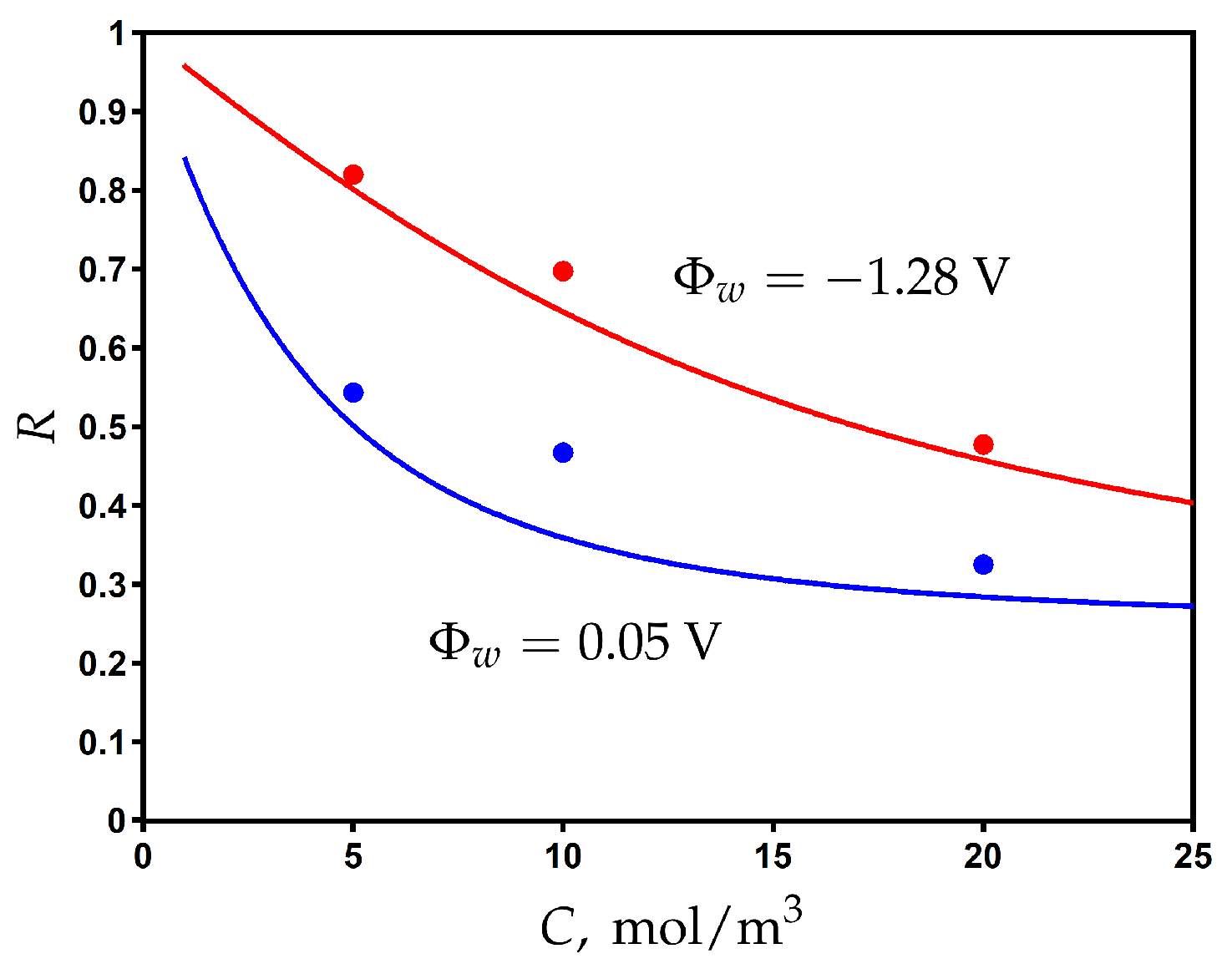
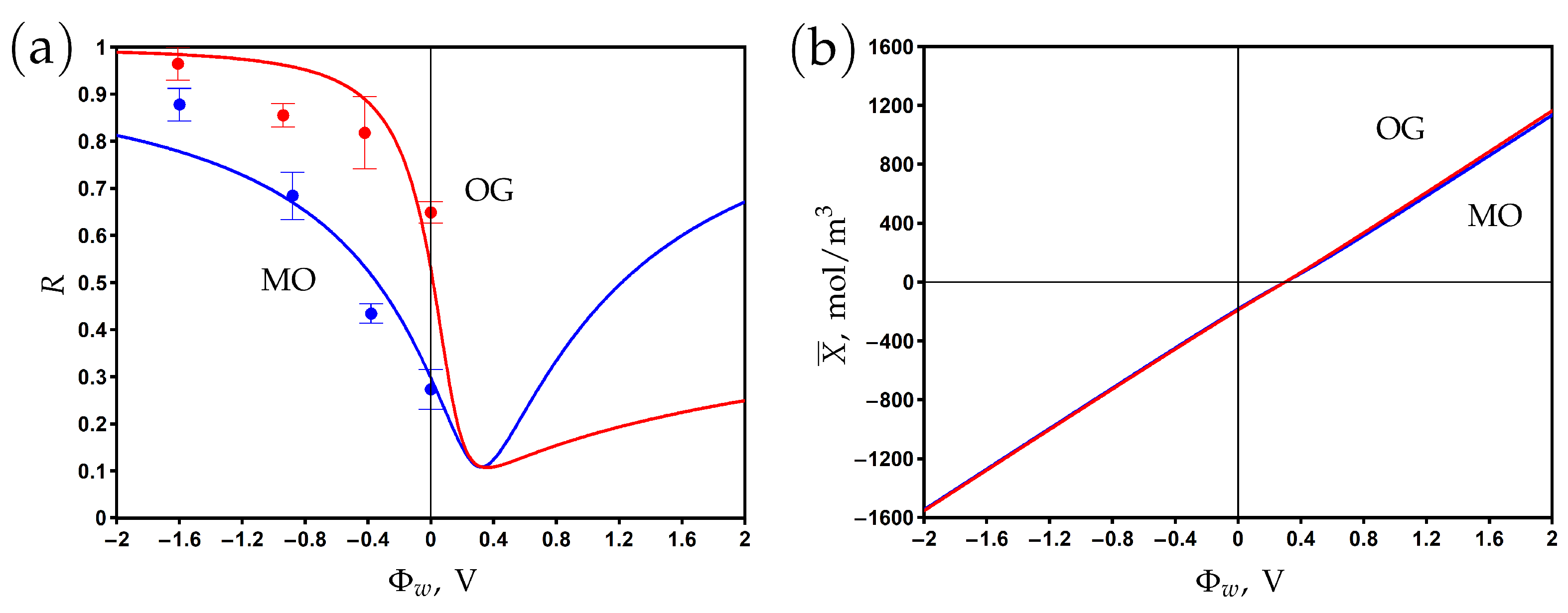
| Parameter | Dimension | Value |
|---|---|---|
| Temperature T | K | 298.15 |
| Pore size | nm | 2 |
| Stern layer thickness | nm | 0.5 |
| Membrane thickness L | m | 2 |
| Membrane permeability A | L/m h bar | 20 |
| Pressure difference | bar | 2 |
| Feed concentration | mol/m | 10 |
| Surface potential | V | 0.1 |
| Stern layer volume capacitance | mol/m V | 2000 |
| Volume chemical charge density | mol/m | 0 |
| Cation charge number | − | +1 |
| Anion charge number | − | −1 |
| Cation radius | nm | 0.095 |
| Anion radius | nm | 0.181 |
| Diffusion coefficient | m/s | 1.33 |
| Diffusion coefficient | m/s | 2.03 |
| Friction factor | − | 1.0 |
| Porosity reduction factor | − | 0.2 |
| Parameter | Dimension | Value |
|---|---|---|
| Membrane properties | ||
| Average pore size | nm | 2 |
| Thickness L | m | 2.8 |
| Permeability A | L/m h bar | 14.5 |
| Porosity | − | 0.2 |
| Parameters of filtration experiments | ||
| Temperature T | K | 298.15 |
| Pressure difference | bar | 2 |
| Feed concentration | mol/m | 5...20 |
| Surface potential | V | −1.28...0.05 |
| Ion properties | ||
| Na radius | nm | 0.095 |
| Cl radius | nm | 0.181 |
| SO radius | nm | 0.290 |
| Na diffusion coefficient | m/s | 1.33 |
| Cl diffusion coefficient | m/s | 2.03 |
| SO diffusion coefficient | m/s | 1.06 |
| Model parameters | ||
| Stern layer thickness | nm | 0.5 |
| Stern layer volume capacitance | mol/m V | 617 |
| Volume chemical charge density | mol/m | −250 |
| Friction factor | − | 0.16 |
| Charge reduction factor | − | 0.079 |
| Mass transfer coefficient | L/m h | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapitonov, A.A.; Ryzhkov, I.I. Modelling the Performance of Electrically Conductive Nanofiltration Membranes. Membranes 2023, 13, 596. https://doi.org/10.3390/membranes13060596
Kapitonov AA, Ryzhkov II. Modelling the Performance of Electrically Conductive Nanofiltration Membranes. Membranes. 2023; 13(6):596. https://doi.org/10.3390/membranes13060596
Chicago/Turabian StyleKapitonov, Alexey A., and Ilya I. Ryzhkov. 2023. "Modelling the Performance of Electrically Conductive Nanofiltration Membranes" Membranes 13, no. 6: 596. https://doi.org/10.3390/membranes13060596
APA StyleKapitonov, A. A., & Ryzhkov, I. I. (2023). Modelling the Performance of Electrically Conductive Nanofiltration Membranes. Membranes, 13(6), 596. https://doi.org/10.3390/membranes13060596






