Using the Log Mean Temperature Difference (LMTD) and ε-NTU Methods to Analyze Heat and Mass Transfer in Direct Contact Membrane Distillation
Abstract
1. Introduction
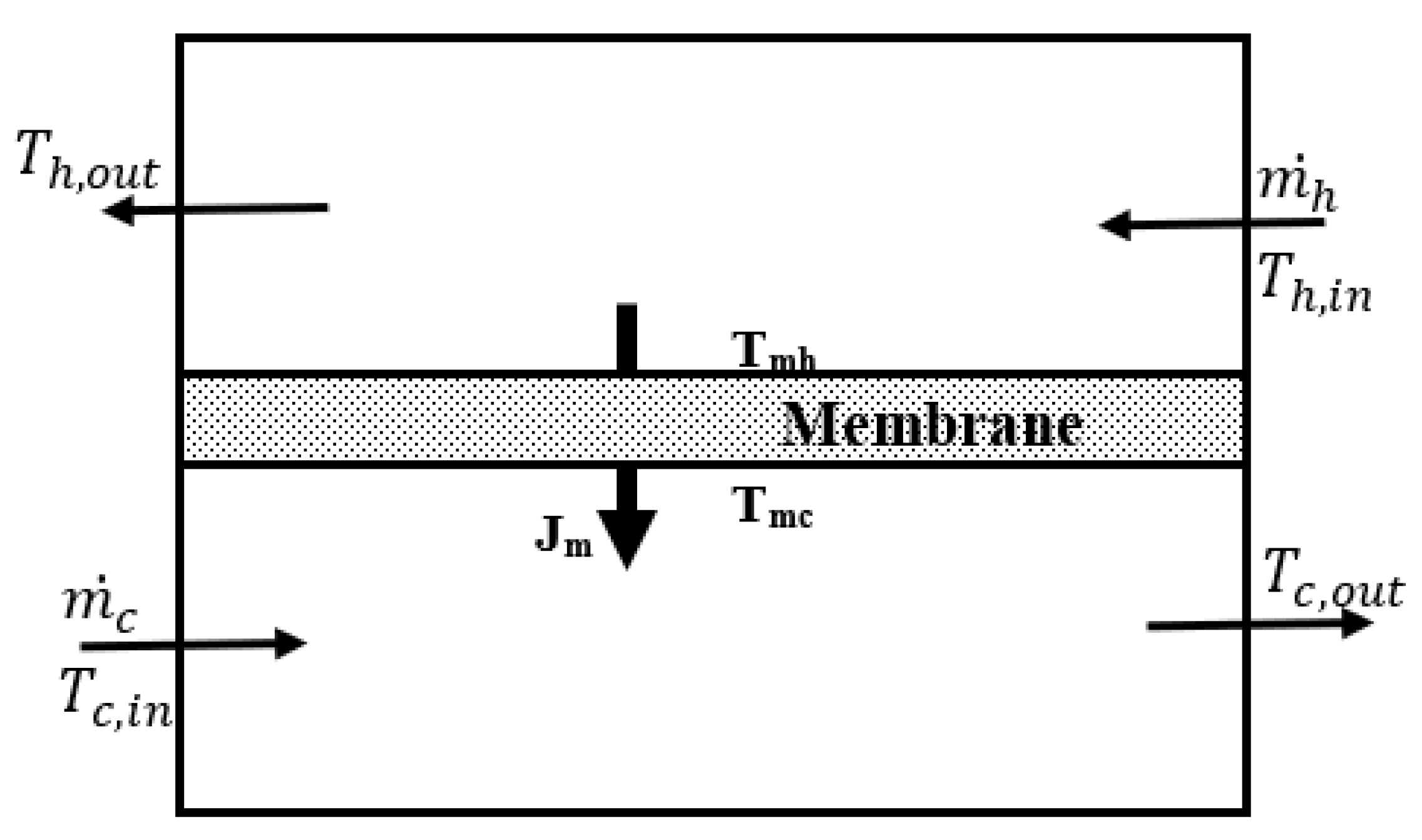
2. Modeling and Configuration Description
2.1. The Heat Transfer Model
2.1.1. The Log Mean Temperature Difference (LMTD) Method
2.1.2. The Effectiveness-NTU Method
2.2. Mass Transfer Model
2.2.1. Relevant Quantities and Relations Involved in Mass Transfer Modeling
2.2.2. Diffusion Coefficient of the Membrane ()
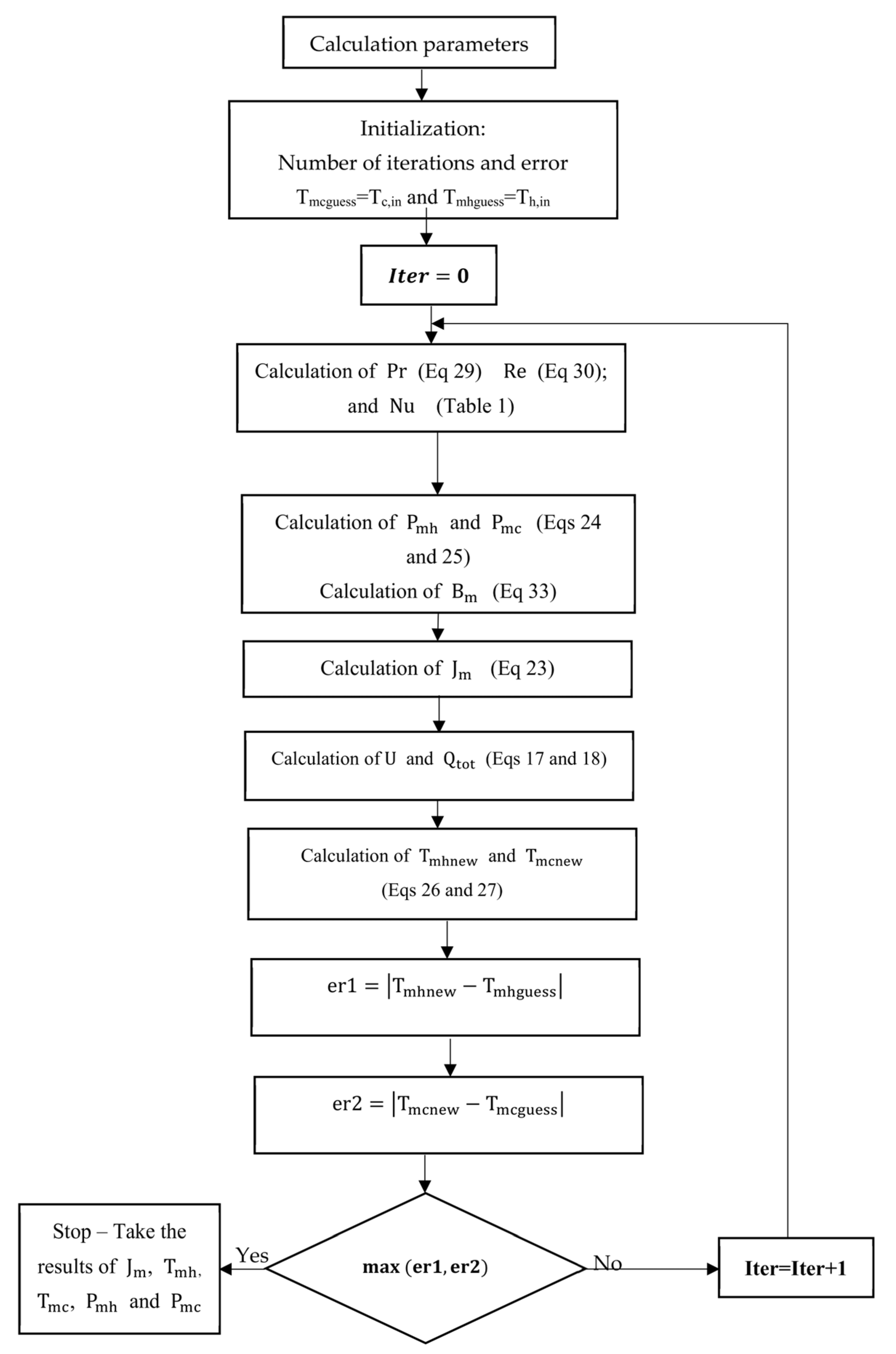
3. Numerical Simulation
4. Results and Discussion
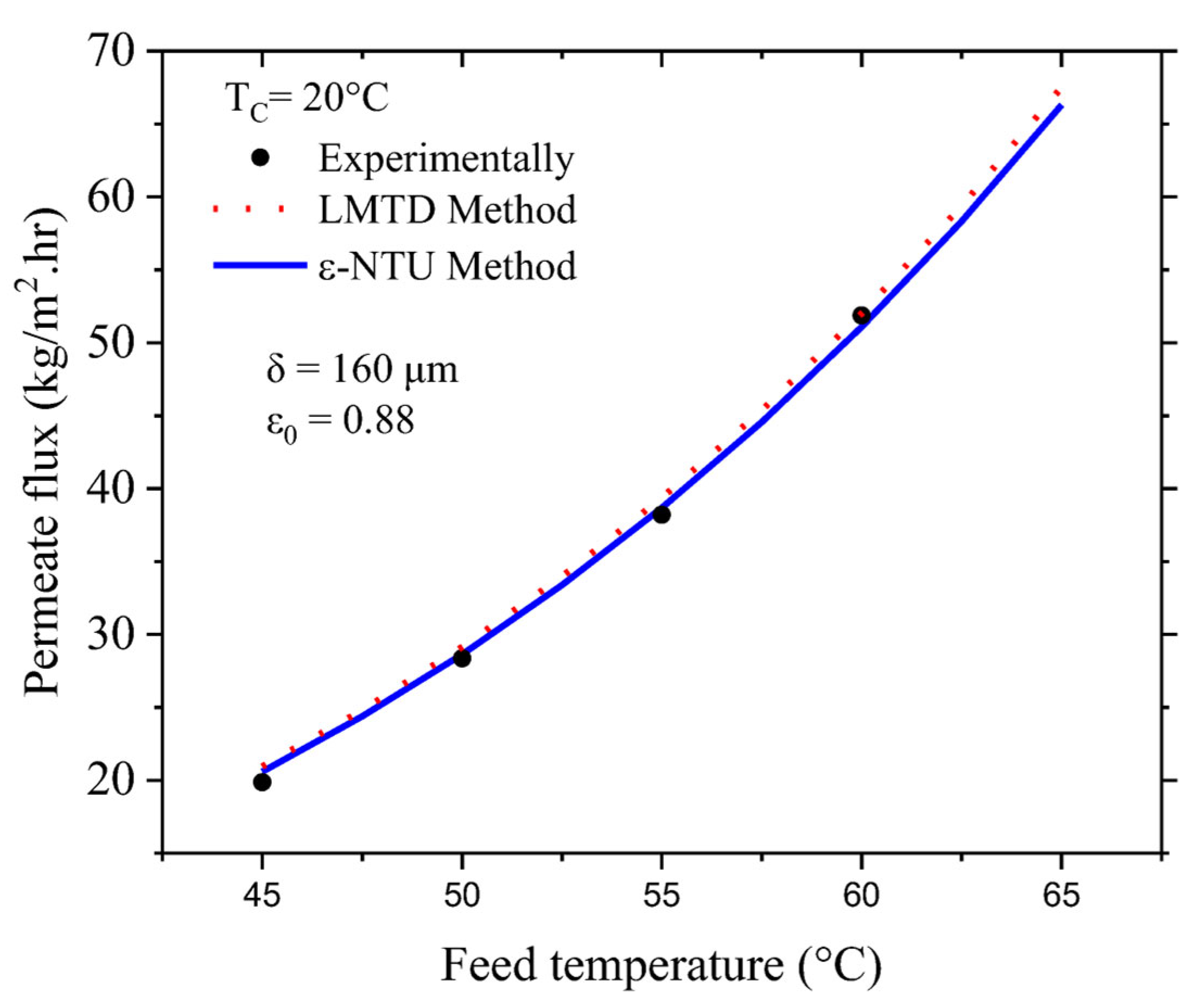
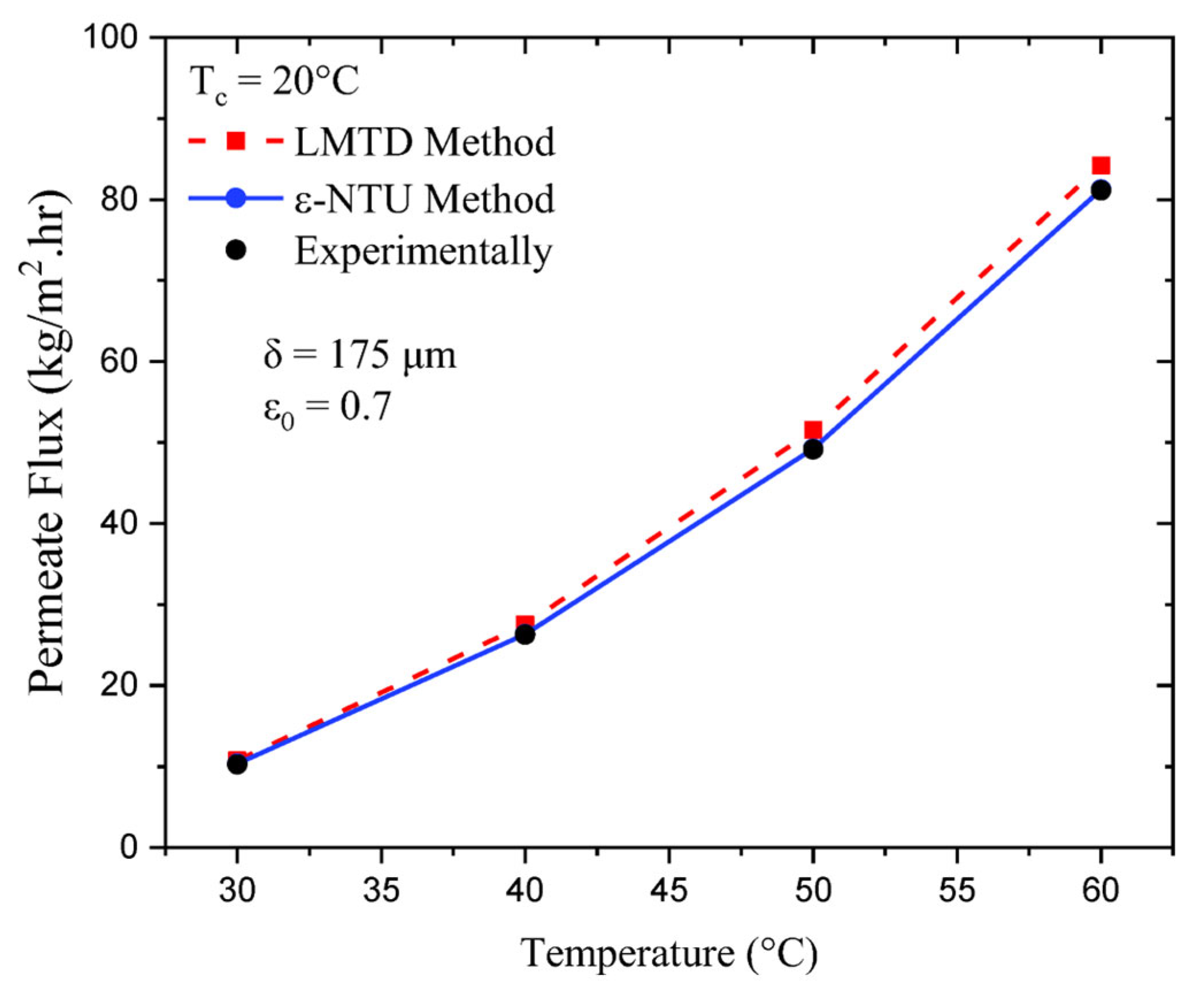
4.1. Model Validation
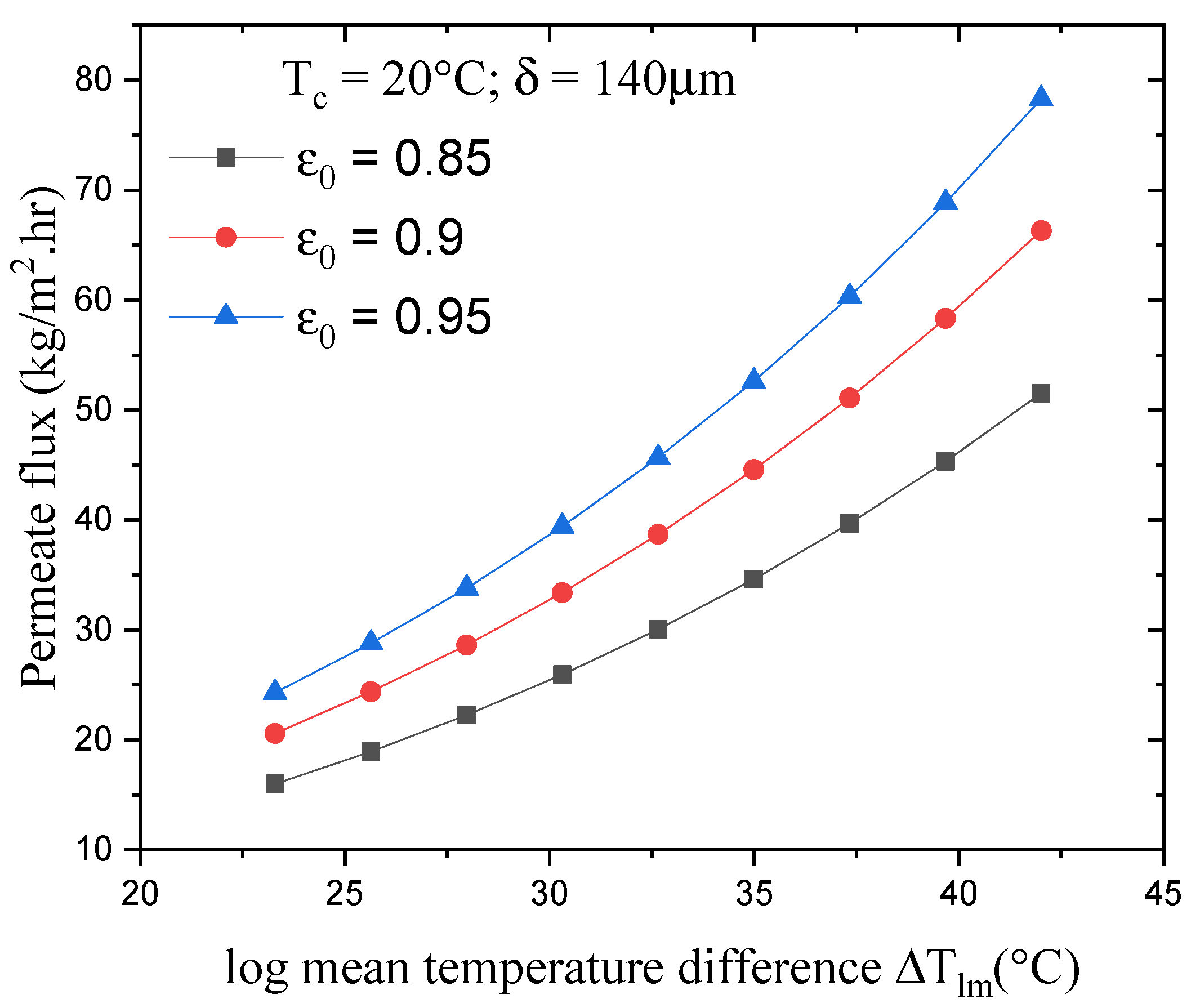
4.2. Effect of Log Mean Temperature on the Permeate Flux
4.3. Effect of the Number of Transfer Units (NTU) on the Permeate Flux
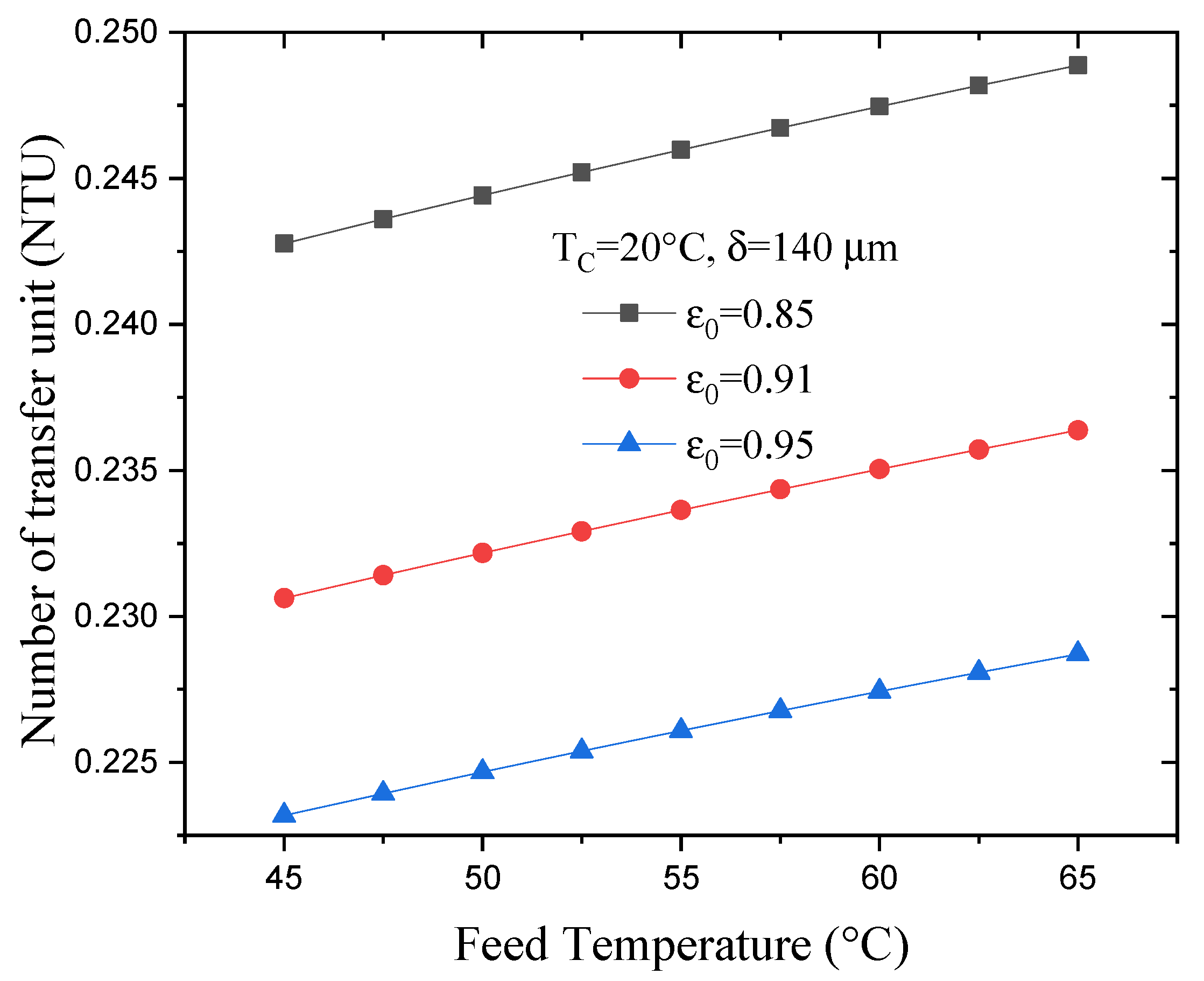
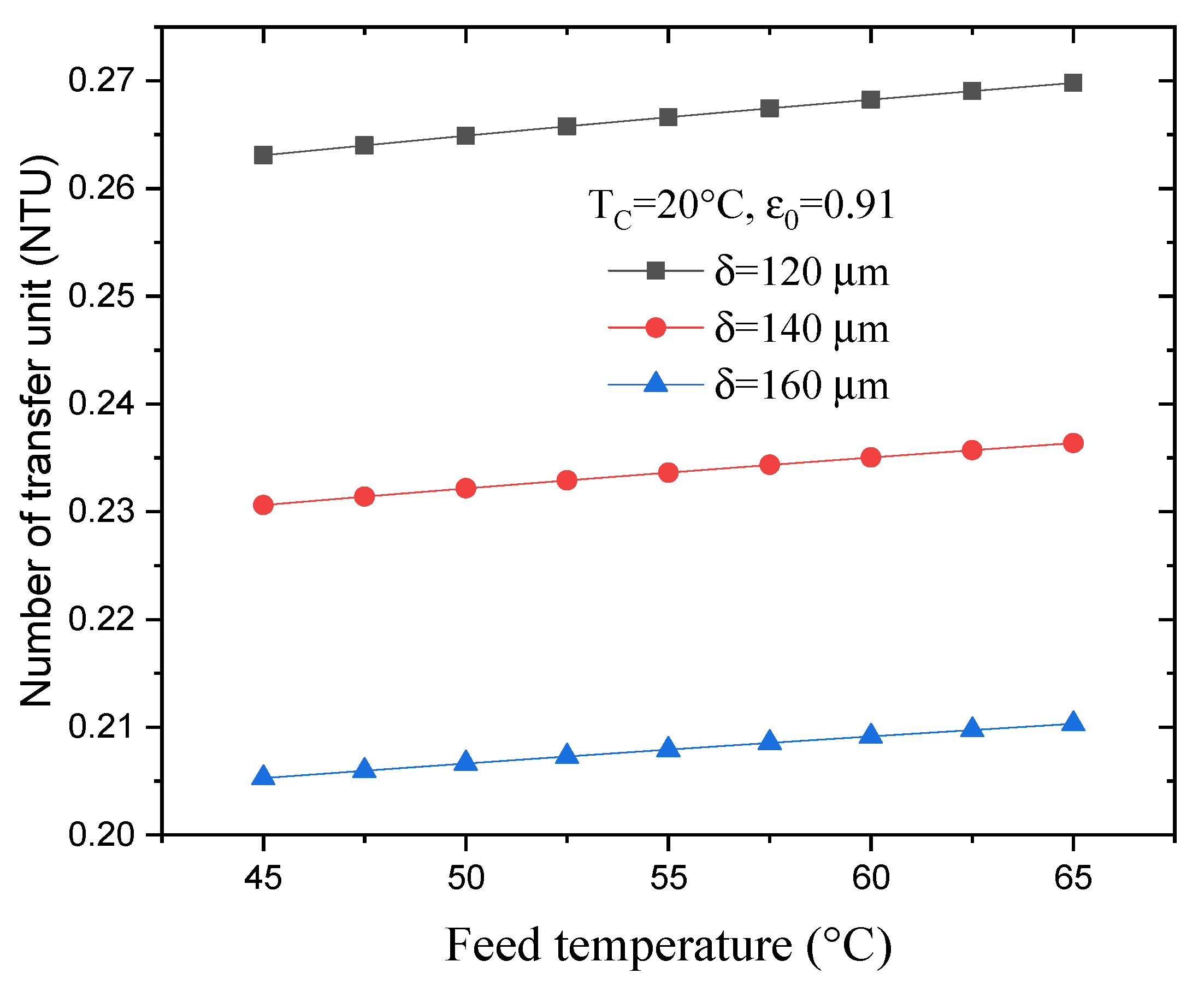
4.4. Effect of Feed Temperature on the NTU
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Bm | Mass transfer coefficient (kg × m−2 × h−1 × Pa−1) |
| Cp | Specific heat of water (J × kg−1 × K−1) |
| Cc | Heat capacity rate for the cold water (W × K−1) |
| Ch | Heat capacity rate for the hot water (W × K−1) |
| Cmin | Min (, ) (W × K−1) |
| Cmax | Max (, ) (W × K−1) |
| C | Capacity ratio () |
| dh | Hydraulic diameter (m) |
| dp | Mean pore diameter of the membrane (m) |
| A | Surface area of the membrane (m2) |
| hc | Heat transfer coefficient of permeate (W × m−2× K−1) |
| hh | Heat transfer coefficient of feed (W × m−2 × K−1) |
| hm | Heat transfer coefficient of the membrane (W × m−2 ×K−1) |
| Jm | Permeate flux (kg × m−2 × h−1) |
| Ki | Mean thermal conductivity (W × m−1 ×K−1) |
| Km | Thermal conductivity of the membrane (W × m−1 × K−1) |
| Kg | Thermal conductivity of the gas filling the membrane pores (W × m−1 × K−1) |
| Kp | Thermal conductivity of the polymer (membrane material) (W × m−1 × K−1) |
| Mw | Molecular weight of water (g × mol−1) |
| Mass flow rate of the cold water (kg × s−1) | |
| Mass flow rate of the hot water (kg × s−1) | |
| Nu | Nusselt number (Dimensionless) |
| Pa | Air pressure inside the membrane pores (Pa) |
| P×D | Diffusion coefficient in the pores (Pa × m2 × s −1) |
| Pmc | Membrane interface partial pressure of water molecule on the permeate side (Pa) |
| Pmh | Membrane interface partial pressure of water molecule on the feed side (Pa) |
| Pr | Prandtl number (Dimensionless) |
| Qtot | Rate of heat transfer between hot and cold fluids (W) |
| Qmax | Maximum possible heat transfer rate (W) |
| R | Universal gas constant (8.314472 J × mol−1 × K−1) |
| Re | Reynolds number (Dimensionless) |
| Tc | Permeate temperature (°C) |
| Th | Feed temperature (°C) |
| Tmc | Membrane interface temperature on permeate side (°C) |
| Tmh | Membrane interface temperature on feed side (°C) |
| Tmav | Mean temperature (Tmav = (Th + Tc)/2) (°C) |
| U | Overall heat transfer coefficient (W × m−2 × K−1) |
| ΔTlm | Log mean temperature difference (°C) |
| ε | Effectiveness |
| NTU | Number of transfer units |
| v | Average velocity (m × s−1) |
| δ | Membrane thickness (m) |
| ε0 | Membrane porosity (%) |
| µ | Dynamic viscosity (Pa × s) |
| ν | Kinematic viscosity (m2 × s−1) |
| ρ | Density (Kg × m−3) |
| τ | Membrane tortuosity |
| Subscripts: | |
| c | cold |
| h | hot |
| m | membrane surface |
| in | inlet |
| out | outlet |
References
- Hasanizadeh, M.; Jafari, P.; Farshighazani, B.; Moraveji, M.K. CFD simulation of heat and mass transport for water transfer through hydrophilic membrane in direct-contact membrane distillation process. Desalin. Water Treat. 2015, 57, 18109–18119. [Google Scholar] [CrossRef]
- Janajreh, I.; Suwwan, D.; Hashaikeh, R. Assessment of direct contact membrane distillation under different configurations, velocities and membrane properties. Appl. Energy 2016, 185, 2058–2073. [Google Scholar] [CrossRef]
- Swaminathan, J.; Chung, H.W.; Warsinger, D.M.; Lienhard, J.V.H. Membrane distillation model based on heat exchanger theory and configuration comparison. Appl. Energy 2016, 184, 491–505. [Google Scholar] [CrossRef]
- Karam, A.M.; Alsaadi, A.S.; Ghaffour, N.; Laleg-Kirati, T.M. Analysis of direct contact membrane distillation based on a lumped-parameter dynamic predictive model. Desalination 2016, 402, 50–61. [Google Scholar] [CrossRef]
- Khalifa, A.; Ahmad, H.; Antar, M.; Laoui, T.; Khayet, M. Experimental and theoretical investigations on water desalination using direct contact membrane distillation. Desalination 2017, 404, 22–34. [Google Scholar] [CrossRef]
- Park, D.J.; Norouzi, E.; Park, C. Experimentally-validated computational simulation of direct contact membrane distillation performance. Int. J. Heat Mass Transf. 2019, 129, 1031–1042. [Google Scholar] [CrossRef]
- Soukane, S.; Naceur, M.W.; Francis, L.; Alsaadi, A.; Ghaffour, N. Effect of feed flow pattern on the distribution of permeate fluxes in desalination by direct contact membrane distillation. Desalination 2017, 418, 43–59. [Google Scholar] [CrossRef]
- Lee, J.-G.; Jeong, S.; Alsaadi, A.S.; Ghaffour, N. Influence of high range of mass transfer coefficient and convection heat transfer on direct contact membrane distillation performance. Desalination 2018, 426, 127–134. [Google Scholar] [CrossRef]
- Long, R.; Lai, X.; Liu, Z.; Liu, W. Direct contact membrane distillation system for waste heat recovery: Modelling and multi-objective optimization. Energy 2018, 148, 1060–1068. [Google Scholar] [CrossRef]
- Perfilov, V.; Ali, A.; Fila, V. A general predictive model for direct contact membrane distillation. Desalination 2018, 445, 181–196. [Google Scholar] [CrossRef]
- Kuang, Z.; Long, R.; Liu, Z.; Liu, W. Analysis of temperature and concentration polarizations for performance improvement in direct contact membrane distillation. Int. J. Heat Mass Transf. 2019, 145, 118724. [Google Scholar] [CrossRef]
- Lou, J.; Vanneste, J.; DeCaluwe, S.C.; Cath, T.Y.; Tilton, N. Computational fluid dynamics simulations of polarization phenomena in direct contact membrane distillation. J. Membr. Sci. 2019, 591, 117150. [Google Scholar] [CrossRef]
- Kim, W.-J.; Campanella, O.; Heldman, D.R. Predicting the performance of direct contact membrane distillation (DCMD): Mathematical determination of appropriate tortuosity based on porosity. J. Food Eng. 2020, 294, 110400. [Google Scholar] [CrossRef]
- Lou, J.; Johnston, J.; Cath, T.Y.; Martinand, D.; Tilton, N. Computational fluid dynamics simulations of unsteady mixing in spacer-filled direct contact membrane distillation channels. J. Membr. Sci. 2021, 622, 118931. [Google Scholar] [CrossRef]
- Lim, J.; Son, K.P.; Kang, S.M.; Park, J.; Min, S.; Cho, H.; Kim, S.-H.; Lee, S.; Chae, S.; Park, P.-K. Correlation between the feed composition and membrane wetting in a direct contact membrane distillation process. Environ. Sci. Water Res. Technol. 2021, 7, 1020–1031. [Google Scholar] [CrossRef]
- Noamani, S.; Niroomand, S.; Rastgar, M.; Azhdarzadeh, M.; Sadrzadeh, M. Modeling of Air-Gap Membrane Distillation and Comparative Study with Direct Contact Membrane Distillation. Ind. Eng. Chem. Res. 2021, 59, 21930–21947. [Google Scholar] [CrossRef]
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook; Phlogiston Press: Cambridge, MA, USA, 2020; pp. 121–127. [Google Scholar]
- Sieder, E.N.; Tate, G.E. Heat transfer and pressure drop of liquid in tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Thomas, L.C. Heat Transfer; Prentice-Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Lawal, D.U.; Khalifa, A.E. Flux Prediction in Direct Contact Membrane Distillation. Int. J. Mater. Mech. Manuf. 2014, 2, 302–308. [Google Scholar] [CrossRef]
- Andrjesdóttir, Ó.; Ong, C.L.; Nabavi, M.; Paredes, S.; Khalil, A.; Michel, B.; Poulikakos, D. An experimentally optimized model for heat and mass transfer in direct contact membrane distillation. Int. J. Heat Mass Transf. 2013, 66, 855–867. [Google Scholar] [CrossRef]
- Cath, T.Y.; Adams, V.D.; Childress, A.E. Experimental study of desalination using direct contact membrane distillation: A new approach to flux enhancement. J. Membr. Sci. 2004, 228, 5–16. [Google Scholar] [CrossRef]
- Nishad, V.; Rajput, M.S. Membrane Distillation for Desalination and Water Treatment. J. Innov. Appl. Res. 2023, 6, 21–33. [Google Scholar] [CrossRef]
- Shirazi, M.M.A.; Kargari, A. A review on application of membrane distillation (MD) process for wastewater treatment A Review on Applications of Membrane Distillation (MD) Process for Wastewater Treatment. J. Memb. Sci. 2015, 1, 101–112. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeshaal, M.A.; Choubani, K. Using the Log Mean Temperature Difference (LMTD) and ε-NTU Methods to Analyze Heat and Mass Transfer in Direct Contact Membrane Distillation. Membranes 2023, 13, 588. https://doi.org/10.3390/membranes13060588
Almeshaal MA, Choubani K. Using the Log Mean Temperature Difference (LMTD) and ε-NTU Methods to Analyze Heat and Mass Transfer in Direct Contact Membrane Distillation. Membranes. 2023; 13(6):588. https://doi.org/10.3390/membranes13060588
Chicago/Turabian StyleAlmeshaal, Mohammed A., and Karim Choubani. 2023. "Using the Log Mean Temperature Difference (LMTD) and ε-NTU Methods to Analyze Heat and Mass Transfer in Direct Contact Membrane Distillation" Membranes 13, no. 6: 588. https://doi.org/10.3390/membranes13060588
APA StyleAlmeshaal, M. A., & Choubani, K. (2023). Using the Log Mean Temperature Difference (LMTD) and ε-NTU Methods to Analyze Heat and Mass Transfer in Direct Contact Membrane Distillation. Membranes, 13(6), 588. https://doi.org/10.3390/membranes13060588








