Real Space and Time Imaging of Collective Headgroup Dipole Motions in Zwitterionic Lipid Bilayers
Abstract
1. Introduction
2. Materials and Methods
2.1. Coarse-Grained Molecular Dynamics (MD) Simulations
2.2. 3D, 2D, 1D Van Hove Correlation Functions
3. Results
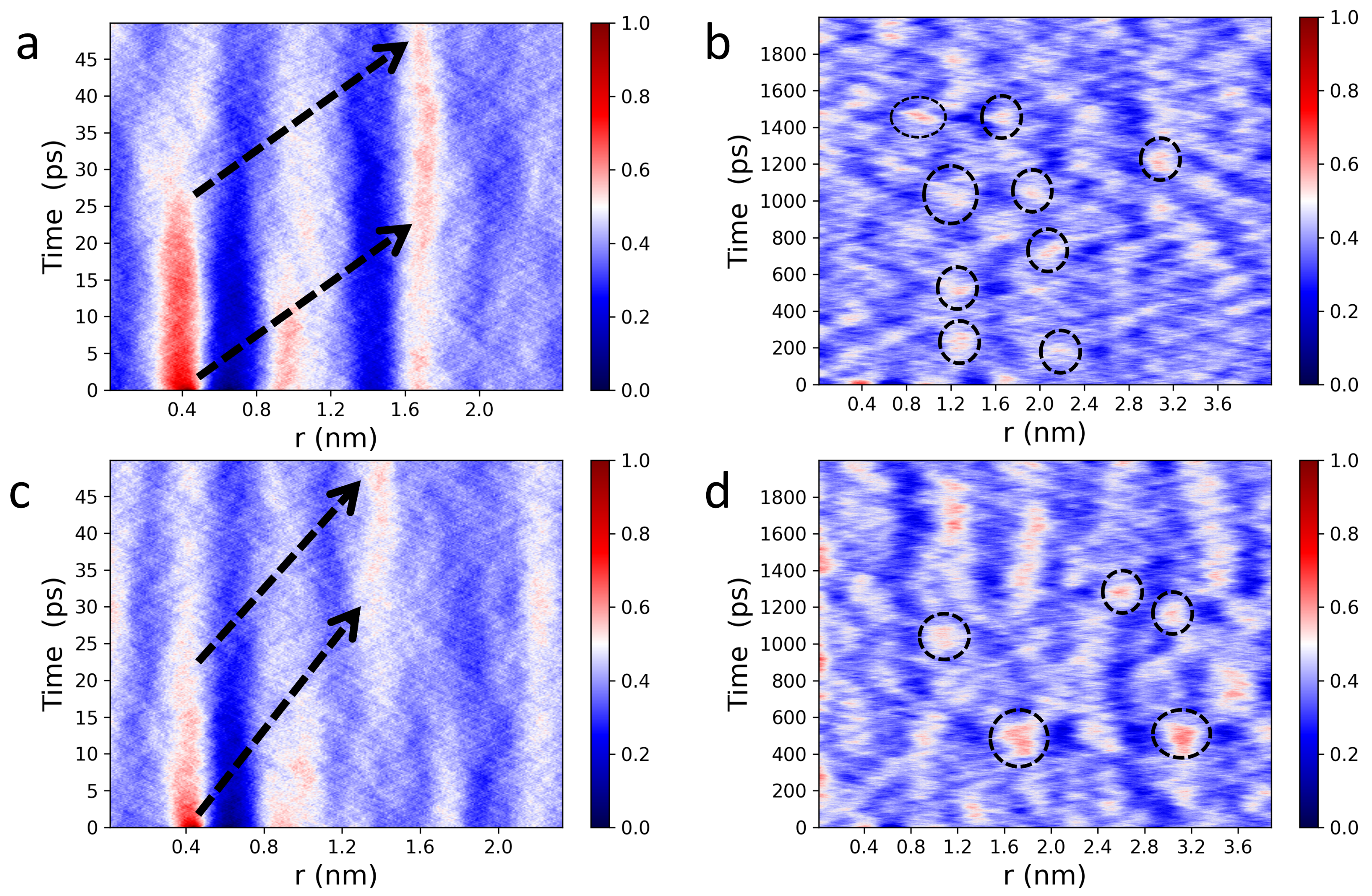
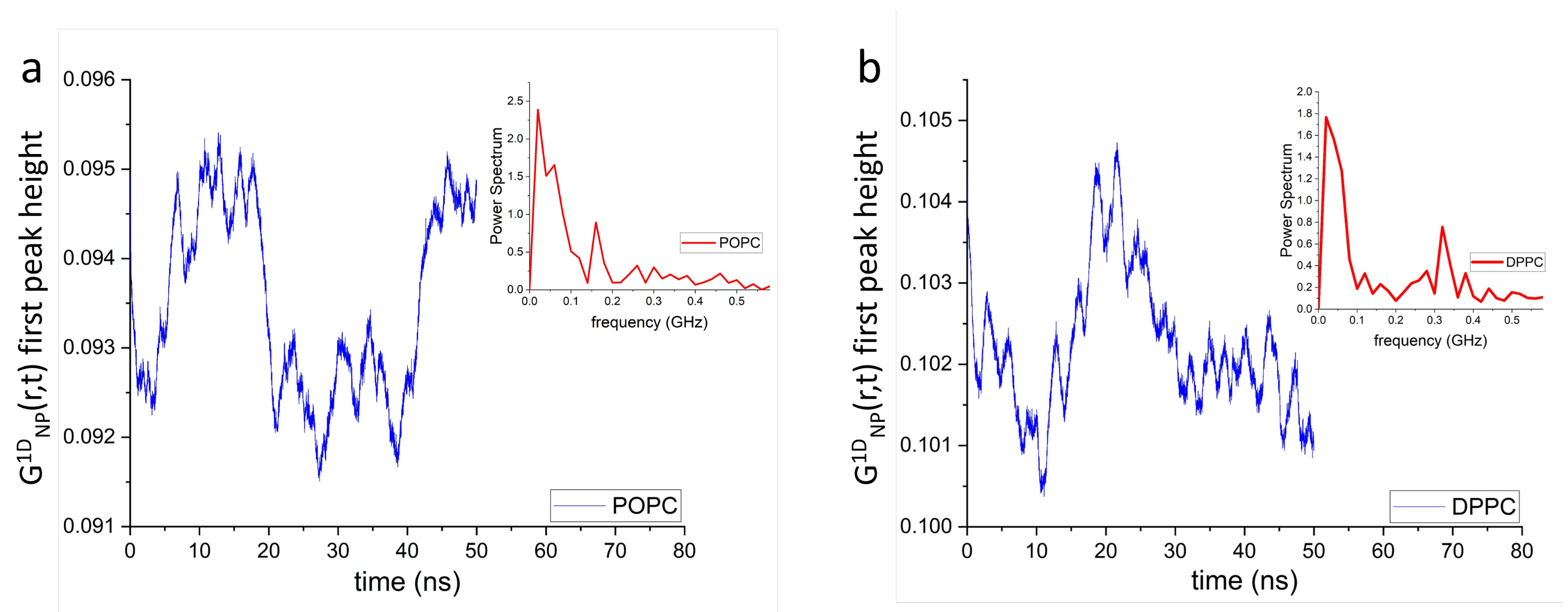
3.1. Spatiotemporal Imaging of Collective Headgroup Dipole Motions and Relaxation Processes in Hydrated Phospholipid Bilayers
3.2. Dipole-Dipole Interactions in Lipid Bilayers
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Luyet, C.; Elvati, P.; Vinh, J.; Violi, A. Low-THz Vibrations of Biological Membranes. Membranes 2023, 13, 139. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Ashkar, R. The dynamic face of lipid membranes. Soft Matter 2021, 17, 6910–6928. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, D.; Thompson, K.C.; García Sakai, V.; Schweins, R.; Moulin, M.; Haertlein, M.; Strohmeier, G.A.; Pichler, H.; Forsyth, V.T.; Barlow, D.J.; et al. Nanoscale structure and dynamics of model membrane lipid raft systems, studied by neutron scattering methods. Front. Phys. 2022, 10, 326. [Google Scholar] [CrossRef]
- D’Angelo, G.; Nibali, V.C.; Wanderlingh, U.; Branca, C.; De Francesco, A.; Sacchetti, F.; Petrillo, C.; Paciaroni, A. Multiple interacting collective modes and phonon gap in phospholipid membranes. J. Phys. Chem. Lett. 2018, 9, 4367–4372. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Mamontov, E. Multiscale lipid membrane dynamics as revealed by neutron spectroscopy. Prog. Lipid Res. 2022, 87, 101179. [Google Scholar] [CrossRef] [PubMed]
- Surovtsev, N.; Adichtchev, S. Dynamic response on a nanometer scale of binary phospholipid-cholesterol vesicles: Low-frequency Raman scattering insight. Phys. Rev. E 2021, 104, 054406. [Google Scholar] [CrossRef] [PubMed]
- Soloviov, D.; Cai, Y.Q.; Bolmatov, D.; Suvorov, A.; Zhernenkov, K.; Zav’yalov, D.; Bosak, A.; Uchiyama, H.; Zhernenkov, M. Functional lipid pairs as building blocks of phase-separated membranes. Proc. Natl. Acad. Sci. USA 2020, 117, 4749–4757. [Google Scholar] [CrossRef]
- Anishkin, A.; Loukin, S.H.; Teng, J.; Kung, C. Feeling the hidden mechanical forces in lipid bilayer is an original sense. Proc. Natl. Acad. Sci. USA 2014, 111, 7898–7905. [Google Scholar] [CrossRef]
- Aponte-Santamaría, C.; Brunken, J.; Gräter, F. Stress propagation through biological lipid bilayers in silico. J. Am. Chem. Soc. 2017, 139, 13588–13591. [Google Scholar] [CrossRef]
- Bolmatov, D.; Kinnun, J.J.; Katsaras, J.; Lavrentovich, M.O. Phonon-mediated lipid raft formation in biological membranes. Chem. Phys. Lipids 2020, 232, 104979. [Google Scholar] [CrossRef]
- Mondal, D.; Malik, S.; Banerjee, P.; Kundu, N.; Debnath, A.; Sarkar, N. Modulation of membrane fluidity to control interfacial water structure and dynamics in saturated and unsaturated phospholipid vesicles. Langmuir 2020, 36, 12423–12434. [Google Scholar] [CrossRef] [PubMed]
- Bullerjahn, J.T.; von Bülow, S.; Hummer, G. Optimal estimates of self-diffusion coefficients from molecular dynamics simulations. J. Chem. Phys. 2020, 153, 024116. [Google Scholar] [CrossRef] [PubMed]
- Vorobyov, I.; Olson, T.E.; Kim, J.H.; Koeppe, R.E.; Andersen, O.S.; Allen, T.W. Ion-induced defect permeation of lipid membranes. Biophys. J. 2014, 106, 586–597. [Google Scholar] [CrossRef] [PubMed]
- Eremchev, M.; Roesel, D.; Poojari, C.S.; Roux, A.; Hub, J.S.; Roke, S. Passive transport of Ca2+ ions through lipid bilayers imaged by wide-field second harmonic microscopy. Biophys. J. 2023, 122, 624–631. [Google Scholar] [CrossRef]
- Bolmatov, D.; Carrillo, J.M.Y.; Sumpter, B.G.; Katsaras, J.; Lavrentovich, M.O. Double membrane formation in heterogeneous vesicles. Soft Matter 2020, 16, 8806–8817. [Google Scholar] [CrossRef]
- Baczynski, K.; Markiewicz, M.; Pasenkiewicz-Gierula, M. Is the tilt of the lipid head group correlated with the number of intermolecular interactions at the bilayer interface? FEBS Lett. 2018, 592, 1507–1515. [Google Scholar] [CrossRef]
- Ray, A.; Gräter, F.; Thukral, L. Probing molecular forces in multi-component physiological membranes. Phys. Chem. Chem. Phys. 2018, 20, 2155–2161. [Google Scholar] [CrossRef]
- Friedman, R.; Khalid, S.; Aponte-Santamaría, C.; Arutyunova, E.; Becker, M.; Boyd, K.J.; Christensen, M.; Coimbra, J.T.; Concilio, S.; Daday, C.; et al. Understanding conformational dynamics of complex lipid mixtures relevant to biology. J. Membr. Biol. 2018, 251, 609–631. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y.; Li, G.; Liu, C.; Wang, L.; Zhang, A.; Yan, Z.; Song, C. The push-to-open mechanism of the tethered mechanosensitive ion channel NompC. eLife 2021, 10, e58388. [Google Scholar] [CrossRef]
- Daday, C.; de Groot, B.L. Lipid–protein forces predict conformational changes in a mechanosensitive channel. Eur. Biophys. J. 2021, 50, 181–186. [Google Scholar] [CrossRef]
- Bolmatov, D. The Phonon Theory of Liquids and Biological Fluids: Developments and Applications. J. Phys. Chem. Lett. 2022, 13, 7121–7129. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Zav’yalov, D.; Zhernenkov, M.; Musaev, E.T.; Cai, Y.Q. Unified phonon-based approach to the thermodynamics of solid, liquid and gas states. Ann. Phys. 2015, 363, 221–242. [Google Scholar] [CrossRef]
- Bolmatov, D.; Musaev, E.T.; Trachenko, K. Symmetry breaking gives rise to energy spectra of three states of matter. Sci. Rep. 2013, 3, 2794. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Brazhkin, V.; Trachenko, K. The phonon theory of liquid thermodynamics. Sci. Rep. 2012, 2, 421. [Google Scholar] [CrossRef]
- Javanainen, M.; Melcrová, A.; Magarkar, A.; Jurkiewicz, P.; Hof, M.; Jungwirth, P.; Martinez-Seara, H. Two cations, two mechanisms: Interactions of sodium and calcium with zwitterionic lipid membranes. Chem. Commun. 2017, 53, 5380–5383. [Google Scholar] [CrossRef] [PubMed]
- Melcr, J.; Martinez-Seara, H.; Nencini, R.; Kolafa, J.; Jungwirth, P.; Ollila, O.S. Accurate binding of sodium and calcium to a POPC bilayer by effective inclusion of electronic polarization. J. Phys. Chem. B 2018, 122, 4546–4557. [Google Scholar] [CrossRef]
- McClintic, W.T.; Scott, H.L.; Moore, N.; Farahat, M.; Maxwell, M.; Schuman, C.D.; Bolmatov, D.; Barrera, F.N.; Katsaras, J.; Collier, C.P. Heterosynaptic plasticity in biomembrane memristors controlled by pH. MRS Bulletin 2022, 48, 13–21. [Google Scholar] [CrossRef]
- Deplazes, E.; Tafalla, B.D.; Murphy, C.; White, J.; Cranfield, C.G.; Garcia, A. Calcium ion binding at the lipid–water interface alters the ion permeability of phospholipid bilayers. Langmuir 2021, 37, 14026–14033. [Google Scholar] [CrossRef]
- Shamaeva, D.V.; Okotrub, K.A.; Surovtsev, N.V. Coexistence of lipid phases in multilayer phospholipid films probed by Raman mapping. Analyst 2022, 147, 3748–3755. [Google Scholar] [CrossRef]
- Walde, P.; Ichikawa, S. Lipid vesicles and other polymolecular aggregates-from basic studies of polar lipids to innovative applications. Appl. Sci. 2021, 11, 10345. [Google Scholar] [CrossRef]
- Bolmatov, D.; McClintic, W.T.; Taylor, G.; Stanley, C.B.; Do, C.; Collier, C.P.; Leonenko, Z.; Lavrentovich, M.O.; Katsaras, J. Deciphering melatonin-stabilized phase separation in phospholipid bilayers. Langmuir 2019, 35, 12236–12245. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Jin, J.; Li, S. Role of polyunsaturated phospholipids in liquid-ordered and liquid-disordered phases. RSC Adv. 2021, 11, 27115–27120. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Chen, Y.; Yang, L.; Bie, M.; Wang, B. Role of lipid rafts in persistent Helicobacter pylori infection: A narrative review. Ann. Transl. Med. 2022, 10, 376. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Lavrentovich, M.; Reiter, R.J. Molecular interactions of melatonin with lipid rafts. Mel. Res. 2022, 5, 101–113. [Google Scholar] [CrossRef]
- Karathanou, K.; Bondar, A.N. Dynamic water hydrogen-bond networks at the interface of a lipid membrane containing palmitoyl-oleoyl phosphatidylglycerol. J. Membr. Biol. 2018, 251, 461–473. [Google Scholar] [CrossRef]
- Srivastava, A.; Debnath, A. Hydration dynamics of a lipid membrane: Hydrogen bond networks and lipid-lipid associations. J. Chem. Phys. 2018, 148, 094901. [Google Scholar] [CrossRef]
- Conti Nibali, V.; Branca, C.; Wanderlingh, U.; D’Angelo, G. Intermolecular Hydrogen-Bond Interactions in DPPE and DMPC Phospholipid Membranes Revealed by Far-Infrared Spectroscopy. Appl. Sci. 2021, 11, 10038. [Google Scholar] [CrossRef]
- Katsaras, J. X-ray diffraction studies of oriented lipid bilayers. Biochem. Cell Biol. 1995, 73, 209–218. [Google Scholar] [CrossRef]
- Kučerka, N.; Nagle, J.F.; Sachs, J.N.; Feller, S.E.; Pencer, J.; Jackson, A.; Katsaras, J. Lipid bilayer structure determined by the simultaneous analysis of neutron and X-ray scattering data. Biophys. J. 2008, 95, 2356–2367. [Google Scholar] [CrossRef]
- Marquardt, D.; Frontzek, M.D.; Zhao, Y.; Chakoumakos, B.C.; Katsaras, J. Neutron diffraction from aligned stacks of lipid bilayers using the WAND instrument. J. Appl. Crystallogr. 2018, 51, 235–241. [Google Scholar] [CrossRef]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Wu, E.L.; Cheng, X.; Jo, S.; Rui, H.; Song, K.C.; Dávila-Contreras, E.M.; Qi, Y.; Lee, J.; Monje-Galvan, V.; Venable, R.M.; et al. CHARMM-GUI membrane builder toward realistic biological membrane simulations. J. Comput. Chem. 2014, 35, 1997–2004. [Google Scholar] [CrossRef] [PubMed]
- Van Hove, L. Correlations in space and time and Born approximation scattering in systems of interacting particles. Phys. Rev. 1954, 95, 249. [Google Scholar] [CrossRef]
- Egami, T.; Shinohara, Y. Correlated atomic dynamics in liquid seen in real space and time. J. Chem. Phys. 2020, 153, 180902. [Google Scholar] [CrossRef] [PubMed]
- Iwashita, T.; Wu, B.; Chen, W.R.; Tsutsui, S.; Baron, A.Q.; Egami, T. Seeing real-space dynamics of liquid water through inelastic x-ray scattering. Sci. Adv. 2017, 3, e1603079. [Google Scholar] [CrossRef]
- Shinohara, Y.; Osaka, T.; Inoue, I.; Iwashita, T.; Dmowski, W.; Ryu, C.W.; Sarathchandran, Y.; Egami, T. Split-pulse X-ray photon correlation spectroscopy with seeded X-rays from X-ray laser to study atomic-level dynamics. Nat. Commun. 2020, 11, 6213. [Google Scholar] [CrossRef]
- Dmowski, W.; Diallo, S.O.; Lokshin, K.; Ehlers, G.; Ferré, G.; Boronat, J.; Egami, T. Observation of dynamic atom-atom correlation in liquid helium in real space. Nat. Commun. 2017, 8, 15294. [Google Scholar] [CrossRef]
- Shinohara, Y.; Ivanov, A.S.; Maltsev, D.; Granroth, G.E.; Abernathy, D.L.; Dai, S.; Egami, T. Real-Space Local Dynamics of Molten Inorganic Salts Using Van Hove Correlation Function. J. Phys. Chem. Lett. 2022, 13, 5956–5962. [Google Scholar] [CrossRef]
- Katsaras, J.; Tristram-Nagle, S.; Liu, Y.; Headrick, R.; Fontes, E.; Mason, P.; Nagle, J.F. Clarification of the ripple phase of lecithin bilayers using fully hydrated, aligned samples. Phys. Rev. E 2000, 61, 5668. [Google Scholar] [CrossRef]
- Ashcraft, R.; Wang, Z.; Abernathy, D.; Quirinale, D.; Egami, T.; Kelton, K. Experimental determination of the temperature-dependent Van Hove function in a Zr80Pt20 liquid. J. Chem. Phys. 2020, 152, 074506. [Google Scholar] [CrossRef] [PubMed]
- Zhernenkov, M.; Bolmatov, D.; Soloviov, D.; Zhernenkov, K.; Toperverg, B.P.; Cunsolo, A.; Bosak, A.; Cai, Y.Q. Revealing the mechanism of passive transport in lipid bilayers via phonon-mediated nanometre-scale density fluctuations. Nat. Commun. 2016, 7, 11575. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Cai, Y.Q.; Zav’yalov, D.; Zhernenkov, M. Crossover from picosecond collective to single particle dynamics defines the mechanism of lateral lipid diffusion. Biochim. Biophys. Acta (BBA)-Biomembr. 2018, 1860, 2446–2455. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Soloviov, D.; Zhernenkov, M.; Zav’yalov, D.; Mamontov, E.; Suvorov, A.; Cai, Y.Q.; Katsaras, J. Molecular picture of the transient nature of lipid rafts. Langmuir 2020, 36, 4887–4896. [Google Scholar] [CrossRef]
- Bolmatov, D.; Zhernenkov, M.; Zav’yalov, D.; Stoupin, S.; Cai, Y.Q.; Cunsolo, A. Revealing the mechanism of the viscous-to-elastic crossover in liquids. J. Phys. Chem. Lett. 2015, 6, 3048–3053. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Zhernenkov, M.; Zav’yalov, D.; Stoupin, S.; Cunsolo, A.; Cai, Y.Q. Thermally triggered phononic gaps in liquids at THz scale. Sci. Rep. 2016, 6, 19469. [Google Scholar] [CrossRef] [PubMed]
- Sacci, R.L.; Scott, H.L.; Liu, Z.; Bolmatov, D.; Doughty, B.; Katsaras, J.; Collier, C.P. Disentangling memristive and memcapacitive effects in droplet interface bilayers using dynamic impedance spectroscopy. Adv. Electron. Mater. 2022, 8, 2200121. [Google Scholar] [CrossRef]
- Lindahl, E.; Edholm, O. Mesoscopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophys. J. 2000, 79, 426–433. [Google Scholar] [CrossRef]
- Haataja, M.P. Lipid domain co-localization induced by membrane undulations. Biophys. J. 2017, 112, 655–662. [Google Scholar] [CrossRef]
- Monzel, C.; Sengupta, K. Measuring shape fluctuations in biological membranes. J. Phys. D Appl. Phys. 2016, 49, 243002. [Google Scholar] [CrossRef]
- Bradley, R.P.; Radhakrishnan, R. Curvature–undulation coupling as a basis for curvature sensing and generation in bilayer membranes. Proc. Natl. Acad. Sci. USA 2016, 113, E5117–E5124. [Google Scholar] [CrossRef] [PubMed]
- Molaei, M.; Kandy, S.K.; Graber, Z.T.; Baumgart, T.; Radhakrishnan, R.; Crocker, J.C. Probing lipid membrane bending mechanics using gold nanorod tracking. Phys. Rev. Res. 2022, 4, L012027. [Google Scholar] [CrossRef] [PubMed]
- Pinigin, K.V. Determination of Elastic Parameters of Lipid Membranes with Molecular Dynamics: A Review of Approaches and Theoretical Aspects. Membranes 2022, 12, 1149. [Google Scholar] [CrossRef] [PubMed]
- Najem, J.S.; Hasan, M.S.; Williams, R.S.; Weiss, R.J.; Rose, G.S.; Taylor, G.J.; Sarles, S.A.; Collier, C.P. Dynamical nonlinear memory capacitance in biomimetic membranes. Nat. Commun. 2019, 10, 3239. [Google Scholar] [CrossRef]
- Ball, P. Soft learning. Nat. Mater. 2023, 22, 2. [Google Scholar] [CrossRef]
- Xiong, T.; Li, C.; He, X.; Xie, B.; Zong, J.; Jiang, Y.; Ma, W.; Wu, F.; Fei, J.; Yu, P.; et al. Neuromorphic functions with a polyelectrolyte-confined fluidic memristor. Science 2023, 379, 156–161. [Google Scholar] [CrossRef]
- Robin, P.; Emmerich, T.; Ismail, A.; Niguès, A.; You, Y.; Nam, G.H.; Keerthi, A.; Siria, A.; Geim, A.; Radha, B.; et al. Long-term memory and synapse-like dynamics in two-dimensional nanofluidic channels. Science 2023, 379, 161–167. [Google Scholar] [CrossRef]
- Nicoll, R.A. A brief history of long-term potentiation. Neuron 2017, 93, 281–290. [Google Scholar] [CrossRef]
- Scott, H.L.; Bolmatov, D.; Podar, P.T.; Liu, Z.; Kinnun, J.J.; Doughty, B.; Lydic, R.; Sacci, R.L.; Collier, C.P.; Katsaras, J. Evidence for long-term potentiation in phospholipid membranes. Proc. Natl. Acad. Sci. USA 2022, 119, e2212195119. [Google Scholar] [CrossRef]
- Bliss, T.V.; Lømo, T. Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. Physiol. J. 1973, 232, 331–356. [Google Scholar] [CrossRef]
- Harden, J.; Diorio, N.; Petrov, A.G.; Jakli, A. Chirality of lipids makes fluid lamellar phases piezoelectric. Phys. Rev. E 2009, 79, 011701. [Google Scholar] [CrossRef] [PubMed]
- Jákli, A.; Harden, J.; Notz, C.; Bailey, C. Piezoelectricity of phospholipids: A possible mechanism for mechanoreception and magnetoreception in biology. Liq. Cryst. 2008, 35, 395–400. [Google Scholar] [CrossRef]
- Huang, H.; Delikanli, S.; Zeng, H.; Ferkey, D.M.; Pralle, A. Remote control of ion channels and neurons through magnetic-field heating of nanoparticles. Nat. Nanotechnol. 2010, 5, 602–606. [Google Scholar] [CrossRef]
- Mosgaard, L.D.; Zecchi, K.A.; Heimburg, T. Mechano-capacitive properties of polarized membranes. Soft Matter 2015, 11, 7899–7910. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Romero, G.; Christiansen, M.G.; Mohr, A.; Anikeeva, P. Wireless magnetothermal deep brain stimulation. Science 2015, 347, 1477–1480. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, M.G.; Homma, K.; Villarreal, S.; Richter, C.P.; Bezanilla, F. Infrared light excites cells by changing their electrical capacitance. Nat. Commun. 2012, 3, 736. [Google Scholar] [CrossRef] [PubMed]
- Freeman, E.; Najem, J.; Sukharev, S.; Philen, M.; Leo, D. The mechanoelectrical response of droplet interface bilayer membranes. Soft Matter 2016, 12, 3021–3031. [Google Scholar] [CrossRef]
- Bolmatov, D.; Zhernenkov, M.; Sharpnack, L.; Agra-Kooijman, D.M.; Kumar, S.; Suvorov, A.; Pindak, R.; Cai, Y.Q.; Cunsolo, A. Emergent optical phononic modes upon nanoscale mesogenic phase transitions. Nano Lett. 2017, 17, 3870–3876. [Google Scholar] [CrossRef]
- Plaksin, M.; Shapira, E.; Kimmel, E.; Shoham, S. Thermal transients excite neurons through universal intramembrane mechanoelectrical effects. Phys. Rev. X 2018, 8, 011043. [Google Scholar] [CrossRef]
- Bolmatov, D.; Soloviov, D.; Zav’yalov, D.; Sharpnack, L.; Agra-Kooijman, D.M.; Kumar, S.; Zhang, J.; Liu, M.; Katsaras, J. Anomalous nanoscale optoacoustic phonon mixing in nematic mesogens. J. Phys. Chem. Lett. 2018, 9, 2546–2553. [Google Scholar] [CrossRef]
- Thomas, N.; Agrawal, A. Quantification of in-plane flexoelectricity in lipid bilayers. Europhys. Lett. 2021, 134, 68003. [Google Scholar] [CrossRef]
- Kim, T.; Kadji, H.; Whalen, A.J.; Ashourvan, A.; Freeman, E.; Fried, S.I.; Tadigadapa, S.; Schiff, S.J. Thermal effects on neurons during stimulation of the brain. J. Neural Eng. 2022, 19, 056029. [Google Scholar] [CrossRef] [PubMed]
- Thomas, N.; Agrawal, A. A lateral electric field inhibits gel-to-fluid transition in lipid bilayers. Soft Matter 2022, 18, 6437–6442. [Google Scholar] [CrossRef] [PubMed]
- Heimburg, T. The excitable fluid mosaic. Biochim. Biophys. Acta (BBA)-Biomembr. 2023, 1865, 184104. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolmatov, D.; Collier, C.P.; Zav’yalov, D.; Egami, T.; Katsaras, J. Real Space and Time Imaging of Collective Headgroup Dipole Motions in Zwitterionic Lipid Bilayers. Membranes 2023, 13, 442. https://doi.org/10.3390/membranes13040442
Bolmatov D, Collier CP, Zav’yalov D, Egami T, Katsaras J. Real Space and Time Imaging of Collective Headgroup Dipole Motions in Zwitterionic Lipid Bilayers. Membranes. 2023; 13(4):442. https://doi.org/10.3390/membranes13040442
Chicago/Turabian StyleBolmatov, Dima, C. Patrick Collier, Dmitry Zav’yalov, Takeshi Egami, and John Katsaras. 2023. "Real Space and Time Imaging of Collective Headgroup Dipole Motions in Zwitterionic Lipid Bilayers" Membranes 13, no. 4: 442. https://doi.org/10.3390/membranes13040442
APA StyleBolmatov, D., Collier, C. P., Zav’yalov, D., Egami, T., & Katsaras, J. (2023). Real Space and Time Imaging of Collective Headgroup Dipole Motions in Zwitterionic Lipid Bilayers. Membranes, 13(4), 442. https://doi.org/10.3390/membranes13040442







