Numerical Analysis of the Effect of Liquid Water during Switching Mode for Unitised Regenerative Proton Exchange Membrane Fuel Cell
Abstract
1. Introduction
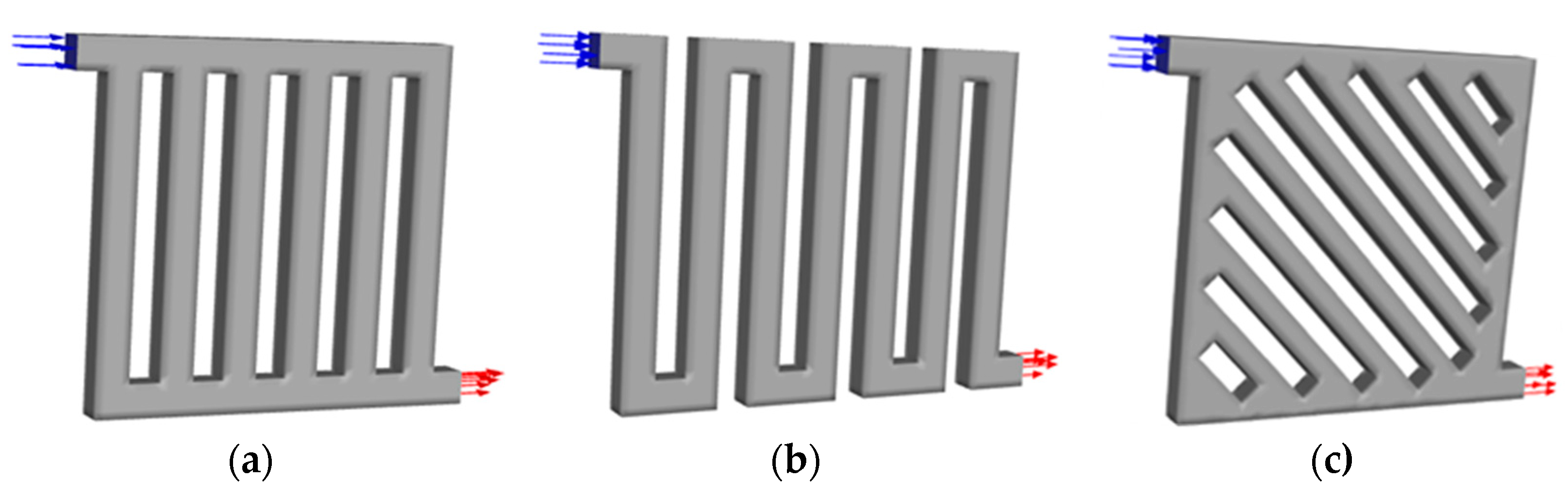
2. Methods
3. Results and Discussion
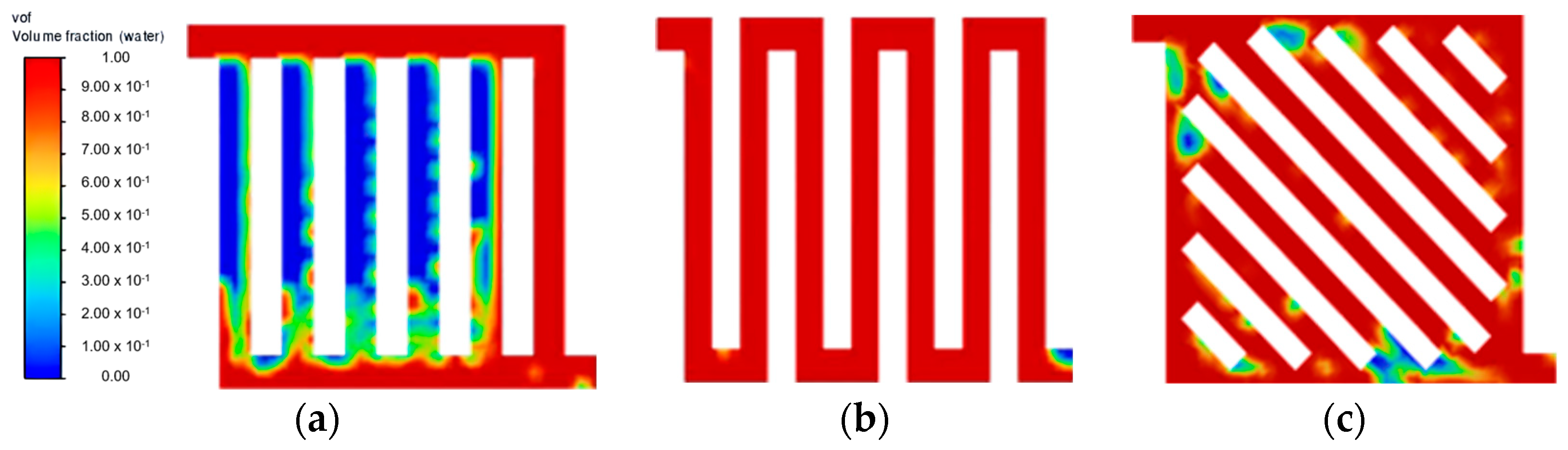
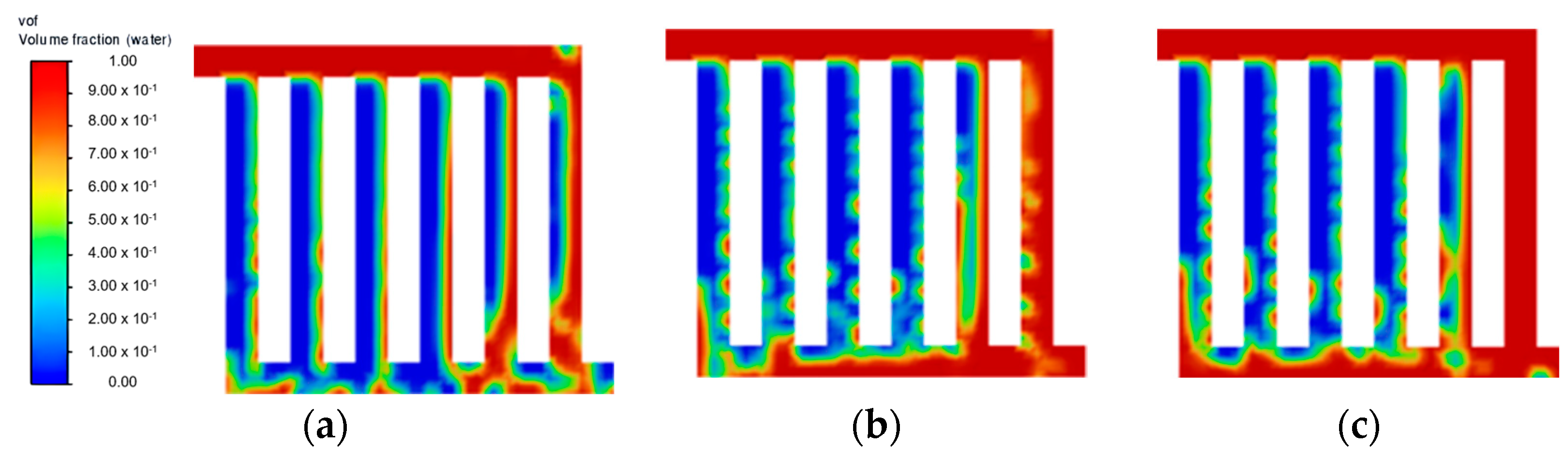
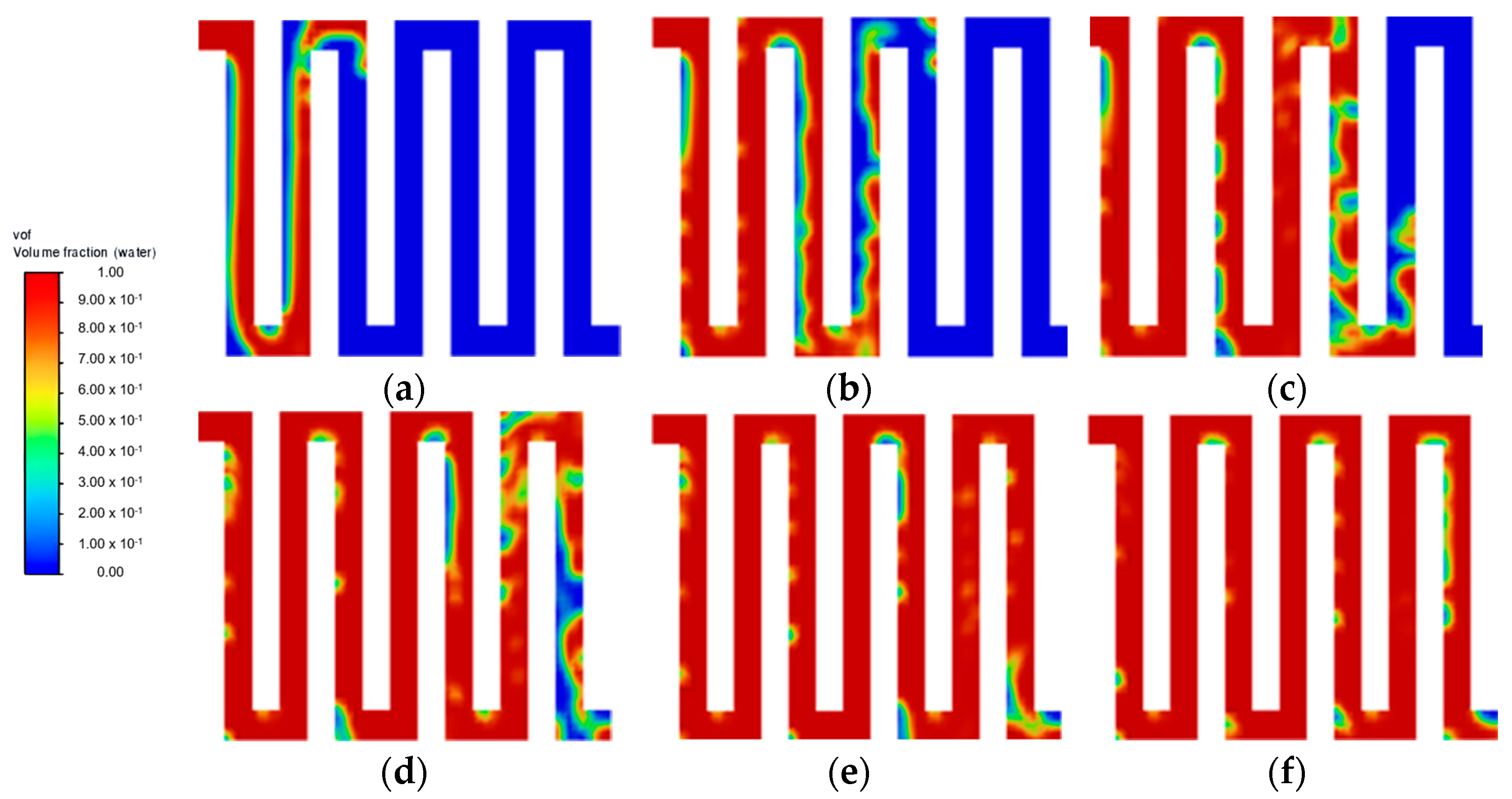
3.1. Water Velocity
3.2. Flow Field Configuration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, X.; Taie, Z.; Liu, J.; Zhang, Y.; Peng, X.; Regmi, Y.N.; Fornaciari, J.C.; Capuano, C.; Binny, D.; Kariuki, N.N.; et al. Hierarchical Electrode Design of Highly Efficient and Stable Unitized Regenerative Fuel Cells (URFCs) for Long-Term Energy Storage. Energy Environ. Sci. 2020, 13, 4872–4881. [Google Scholar] [CrossRef]
- Paul, B.; Andrews, J. PEM Unitised Reversible/Regenerative Hydrogen Fuel Cell Systems: State of the Art and Technical Challenges. Renew. Sustain. Energy Rev. 2017, 79, 585–599. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; He, W.; Zhao, Y.; Wang, X. Lattice Boltzmann Simulation of the Structural Degradation of a Gas Diffusion Layer for a Proton Exchange Membrane Fuel Cell. J. Power Sources 2023, 556, 232452. [Google Scholar] [CrossRef]
- Vincent, I.; Lee, E.-C.; Kim, H.-M. Solutions to the Water Flooding Problem for Unitized Regenerative Fuel Cells: Status and Perspectives. RSC Adv. 2020, 10, 16844–16860. [Google Scholar] [CrossRef]
- Guo, H.; Guo, Q.; Ye, F.; Ma, C.F.; Zhu, X.; Liao, Q. Three-Dimensional Two-Phase Simulation of a Unitized Regenerative Fuel Cell during Mode Switching from Electrolytic Cell to Fuel Cell. Energy Convers. Manag. 2019, 195, 989–1003. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, H.; Ye, F.; Xing, L.; Ma, C.F. A Numerical Study of Dynamic Behaviors of a Unitized Regenerative Fuel Cell during Gas Purging. Int. J. Hydrogen Energy 2022, 47, 22203–22214. [Google Scholar] [CrossRef]
- Yuan, X.M.; Guo, H.; Ye, F.; Ma, C.F. Experimental Study of Gas Purge Effect on Cell Voltage during Mode Switching from Electrolyser to Fuel Cell Mode in a Unitized Regenerative Fuel Cell. Energy Convers. Manag. 2019, 186, 258–266. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, H.; Ye, F.; Ma, C.F.; Liao, Q.; Zhu, X. Heat and Mass Transfer in a Unitized Regenerative Fuel Cell during Mode Switching. Int. J. Energy Res. 2019, 43, 2678–2693. [Google Scholar] [CrossRef]
- Bazarah, A.; Majlan, E.H.; Husaini, T.; Zainoodin, A.M.; Alshami, I.; Goh, J.; Masdar, M.S. Factors Influencing the Performance and Durability of Polymer Electrolyte Membrane Water Electrolyzer: A Review. Int. J. Hydrogen Energy 2022, 47, 35976–35989. [Google Scholar] [CrossRef]
- Yuan, X.M.; Ye, F.; Liu, J.X.; Guo, H.; Ma, C.F. Voltage Response and Two-Phase Flow during Mode Switching from Fuel Cell to Water Electrolyser in a Unitized Regenerative Fuel Cell. Int. J. Hydrogen Energy 2019, 44, 15917–15925. [Google Scholar] [CrossRef]
- Guo, H.; Zhao, Q.; Ye, F. An Experimental Study on Gas and Liquid Two-Phase Flow in Orientated-Type Flow Channels of Proton Exchange Membrane Fuel Cells by Using a Side-View Method. Renew. Energy 2022, 188, 603–618. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, H.; Ye, F.; Ma, C.F. Effect of Liquid Water Accumulation in Electrolytic Cell Mode on Start-up Performance of Fuel Cell Mode of Unitized Regenerative Fuel Cells. Energy Convers. Manag. 2022, 254, 115288. [Google Scholar] [CrossRef]
- Li, H.Y.; Guo, H.; Ye, F.; Ma, C.F. Experimental Investigation on Voltage Response to Operation Parameters of a Unitized Regenerative Fuel Cell during Mode Switching from Fuel Cell to Electrolysis Cell. Int. J. Energy Res. 2018, 42, 3378–3389. [Google Scholar] [CrossRef]
- Ashrafi, M.; Kanani, H.; Shams, M. Numerical and Experimental Study of Two-Phase Flow Uniformity in Channels of Parallel PEM Fuel Cells with Modified Z-Type Flow-Fields. Energy 2018, 147, 317–328. [Google Scholar] [CrossRef]
- Cao, Y.; El-Shorbagy, M.A.; Dahari, M.; Cao, D.N.; Din, E.M.T.E.; Huynh, P.H.; Wae-hayee, M. Examining the Relationship between Gas Channel Dimensions of a Polymer Electrolyte Membrane Fuel Cell with Two-Phase Flow Dynamics in a Flooding Situation Using the Volume of Fluid Method. Energy Rep. 2022, 8, 9420–9430. [Google Scholar] [CrossRef]
- Bao, Z.; Niu, Z.; Jiao, K. Analysis of Single- and Two-Phase Flow Characteristics of 3-D Fine Mesh Flow Field of Proton Exchange Membrane Fuel Cells. J. Power Sources 2019, 438, 226995. [Google Scholar] [CrossRef]
- Guo, H.; Guo, Q.; Ye, F.; Ma, C.; Liao, Q.; Zhu, X. Improving the Electric Performance of a Unitized Regenerative Fuel Cell during Mode Switching through Mass Transfer Enhancement. Energy Convers. Manag. 2019, 188, 27–39. [Google Scholar] [CrossRef]
- Majasan, J.O.; Cho, J.I.S.; Dedigama, I.; Tsaoulidis, D.; Shearing, P.; Brett, D.J.L. Two-Phase Flow Behaviour and Performance of Polymer Electrolyte Membrane Electrolysers: Electrochemical and Optical Characterisation. Int. J. Hydrogen Energy 2018, 43, 15659–15672. [Google Scholar] [CrossRef]
- Wilberforce, T.; El Hassan, Z.; Ogungbemi, E.; Ijaodola, O.; Khatib, F.N.; Durrant, A.; Thompson, J.; Baroutaji, A.; Olabi, A.G. A Comprehensive Study of the Effect of Bipolar Plate (BP) Geometry Design on the Performance of Proton Exchange Membrane (PEM) Fuel Cells. Renew. Sustain. Energy Rev. 2019, 111, 236–260. [Google Scholar] [CrossRef]
- Lim, B.H.; Majlan, E.H.; Daud, W.R.W.; Rosli, M.I.; Husaini, T. Numerical Investigation of the Effect of Three-Dimensional Modified Parallel Flow Field Designs on Proton Exchange Membrane Fuel Cell Performance. Chem. Eng. Sci. 2020, 217, 115499. [Google Scholar] [CrossRef]
- Lim, B.H.; Majlan, E.H.; Daud, W.R.W.; Rosli, M.I.; Husaini, T. Numerical Analysis of Modified Parallel Flow Field Designs for Fuel Cells. Int. J. Hydrogen Energy 2017, 42, 9210–9218. [Google Scholar] [CrossRef]
- Lim, B.H.; Majlan, E.H.; Daud, W.R.W.; Rosli, M.I.; Husaini, T. Numerical Analysis of Flow Distribution Behavior in a Proton Exchange Membrane Fuel Cell. Heliyon 2018, 4, e00845. [Google Scholar] [CrossRef] [PubMed]
- Rosli, M.I.; Lim, B.H.; Majlan, E.H.; Husaini, T.; Daud, W.R.W.; Lim, S.F. Performance Analysis of PEMFC with Single-Channel and Multi-Channels on the Impact of the Geometrical Model. Energies 2022, 15, 7960. [Google Scholar] [CrossRef]
- Lim, B.H.; Majlan, E.H.; Daud, W.R.W.; Husaini, T.; Rosli, M.I. Effects of Flow Field Design on Water Management and Reactant Distribution in PEMFC: A Review. Ionics 2016, 22, 301–316. [Google Scholar] [CrossRef]
- Pamplona Solis, B.; Cruz Argüello, J.C.; Gómez Barba, L.; Gurrola, M.P.; Zarhri, Z.; TrejoArroyo, D.L. Bibliometric Analysis of the Mass Transport in a Gas Diffusion Layer in PEM Fuel Cells. Sustainability 2019, 11, 6682. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Operating temperature (K) | 293.15 |
| Operating pressure (atm) | 1.0 |
| Gravity (m·s−2) | 9.81 |
| Water-liquid Velocity (m·s−1) | 0.25/0.5/0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Low, H.C.; Lim, B.H. Numerical Analysis of the Effect of Liquid Water during Switching Mode for Unitised Regenerative Proton Exchange Membrane Fuel Cell. Membranes 2023, 13, 391. https://doi.org/10.3390/membranes13040391
Low HC, Lim BH. Numerical Analysis of the Effect of Liquid Water during Switching Mode for Unitised Regenerative Proton Exchange Membrane Fuel Cell. Membranes. 2023; 13(4):391. https://doi.org/10.3390/membranes13040391
Chicago/Turabian StyleLow, Hock Chin, and Bee Huah Lim. 2023. "Numerical Analysis of the Effect of Liquid Water during Switching Mode for Unitised Regenerative Proton Exchange Membrane Fuel Cell" Membranes 13, no. 4: 391. https://doi.org/10.3390/membranes13040391
APA StyleLow, H. C., & Lim, B. H. (2023). Numerical Analysis of the Effect of Liquid Water during Switching Mode for Unitised Regenerative Proton Exchange Membrane Fuel Cell. Membranes, 13(4), 391. https://doi.org/10.3390/membranes13040391








