Optimization of Small-Scale Hydrogen Production with Membrane Reactors
Abstract
1. Introduction
2. Methodology
2.1. FBMR Model and KPIs
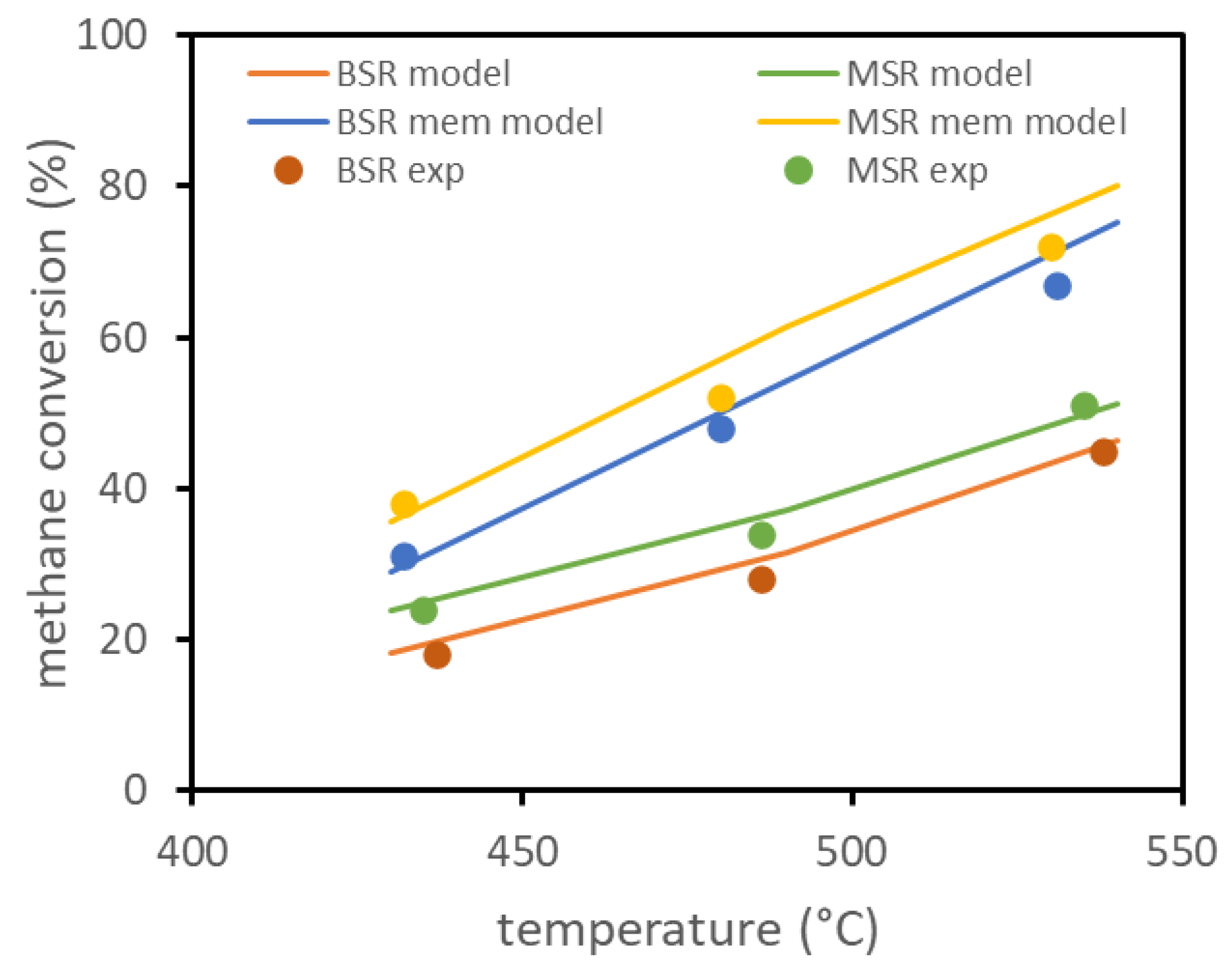
2.2. Model Validation
2.3. Assumptions
3. Reactor Analysis
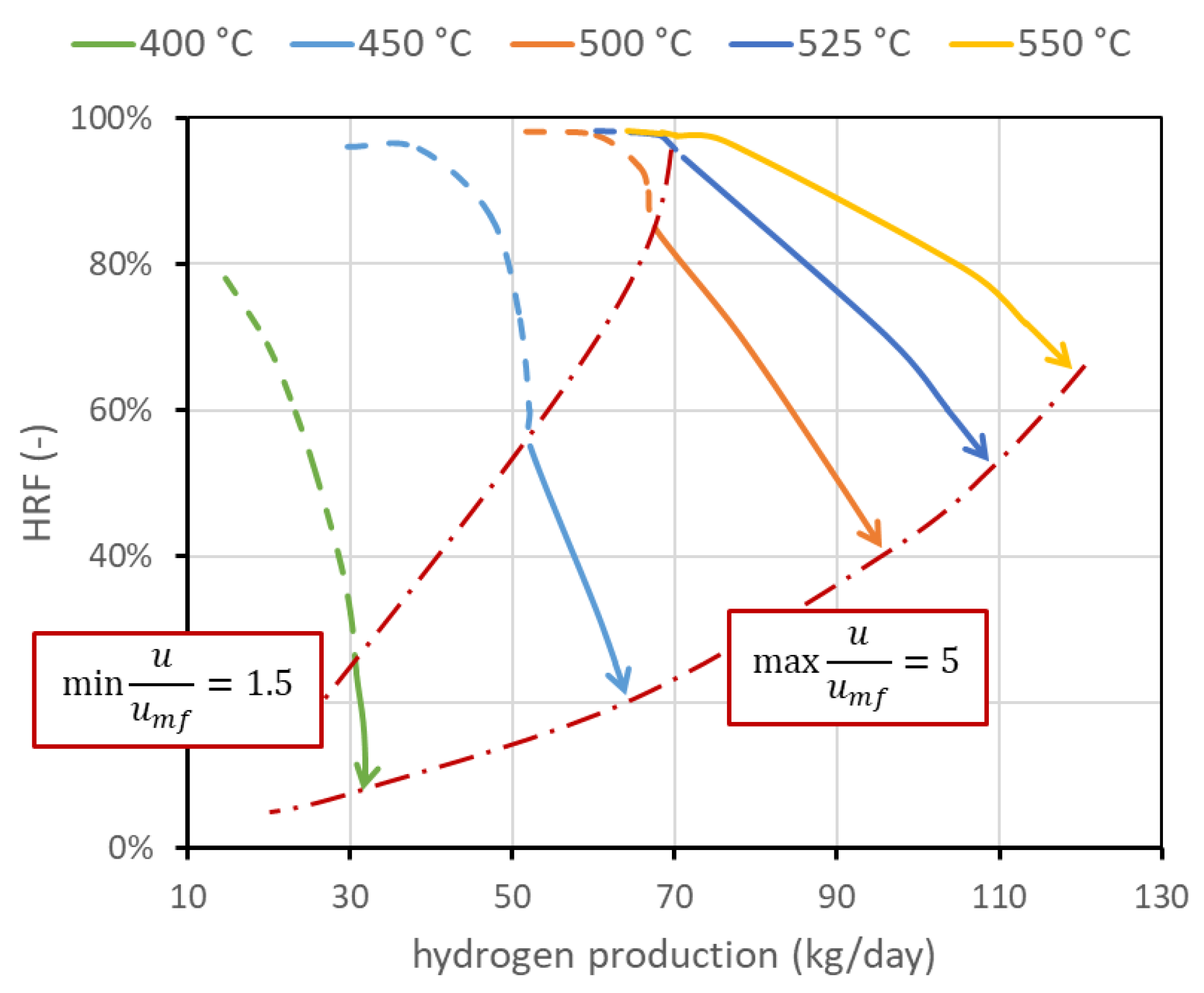
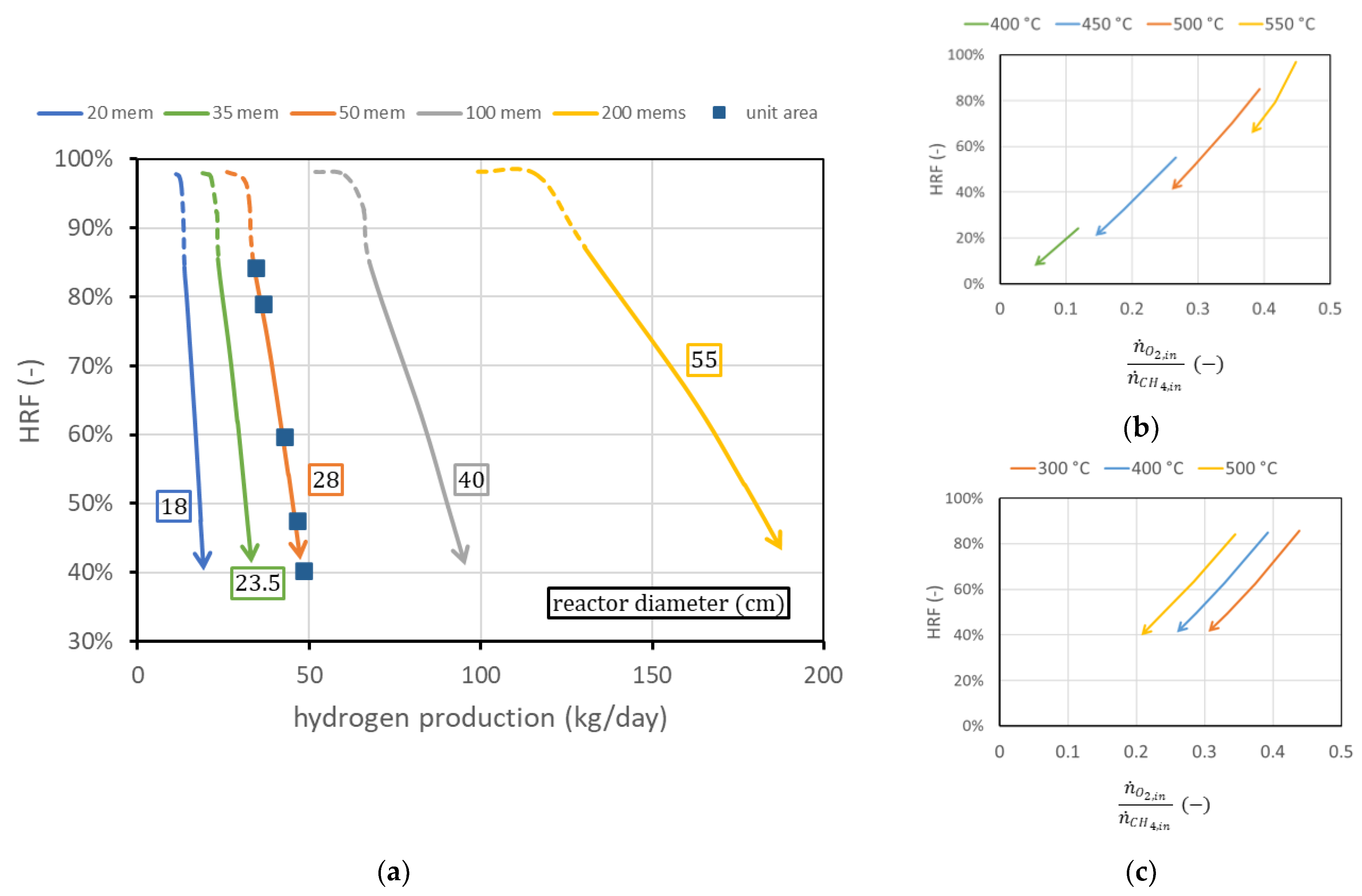
3.1. Performance Charts
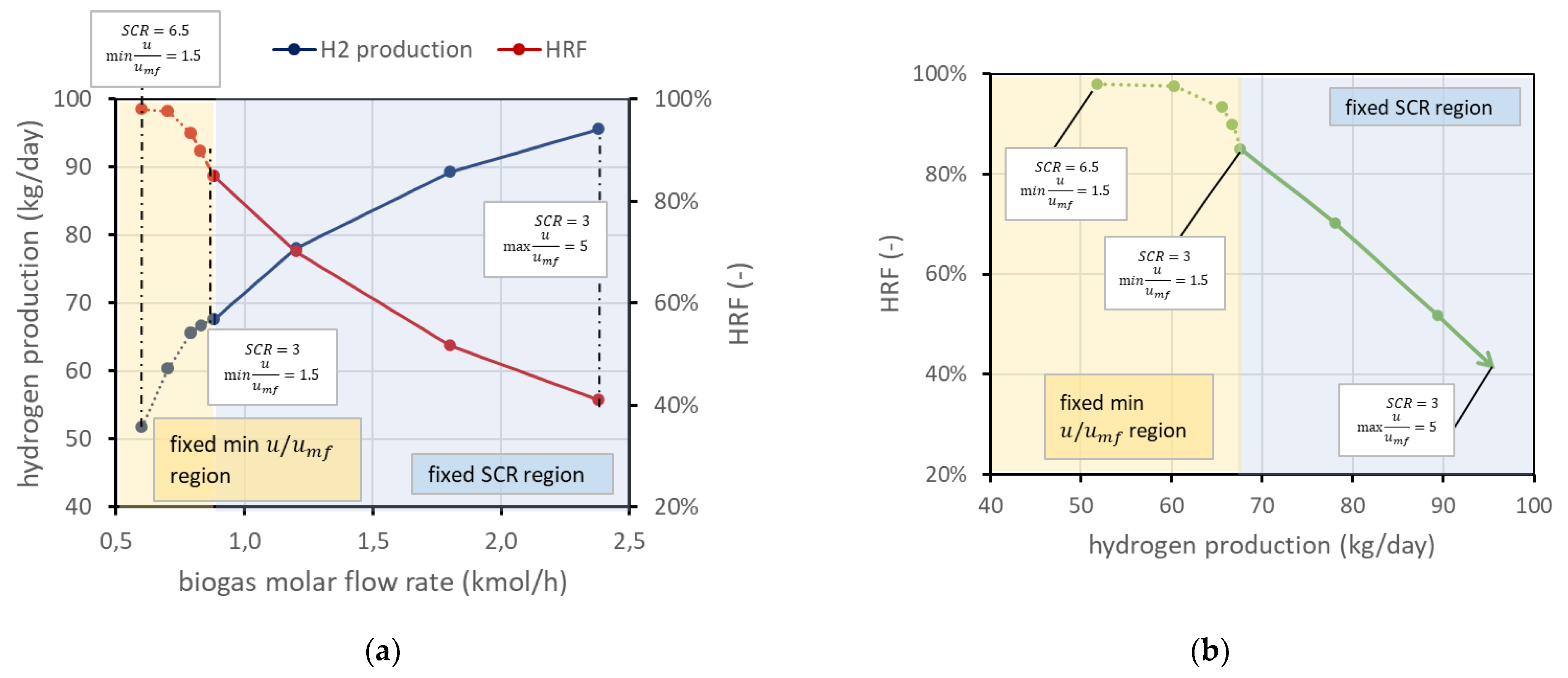
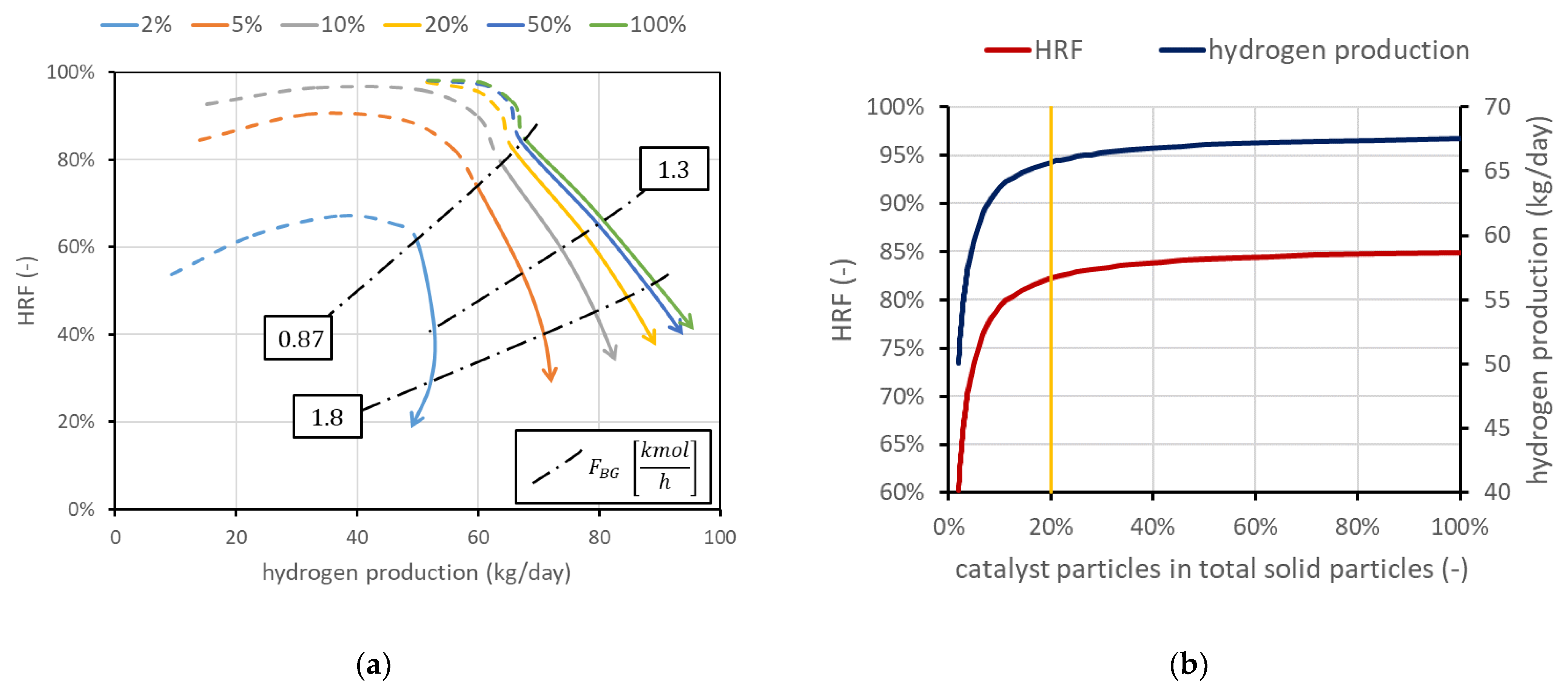
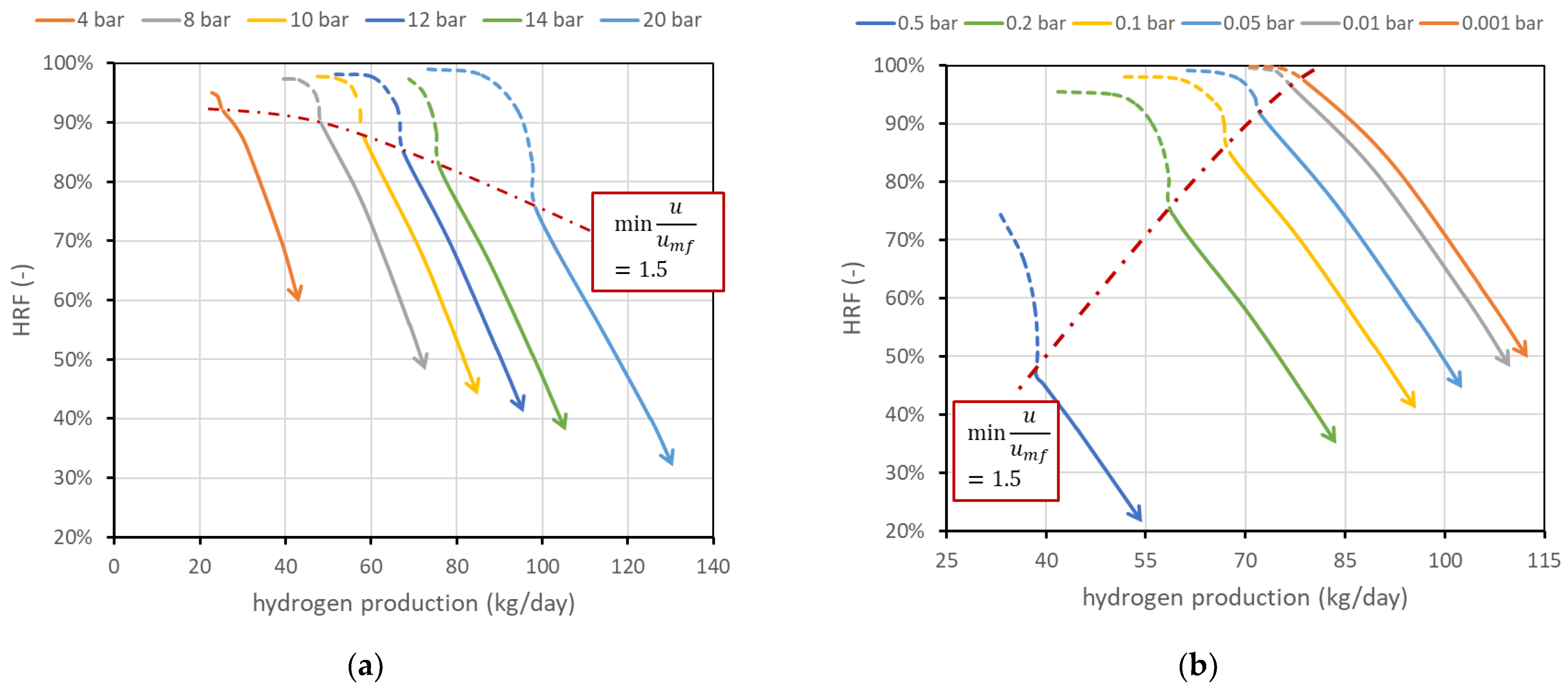
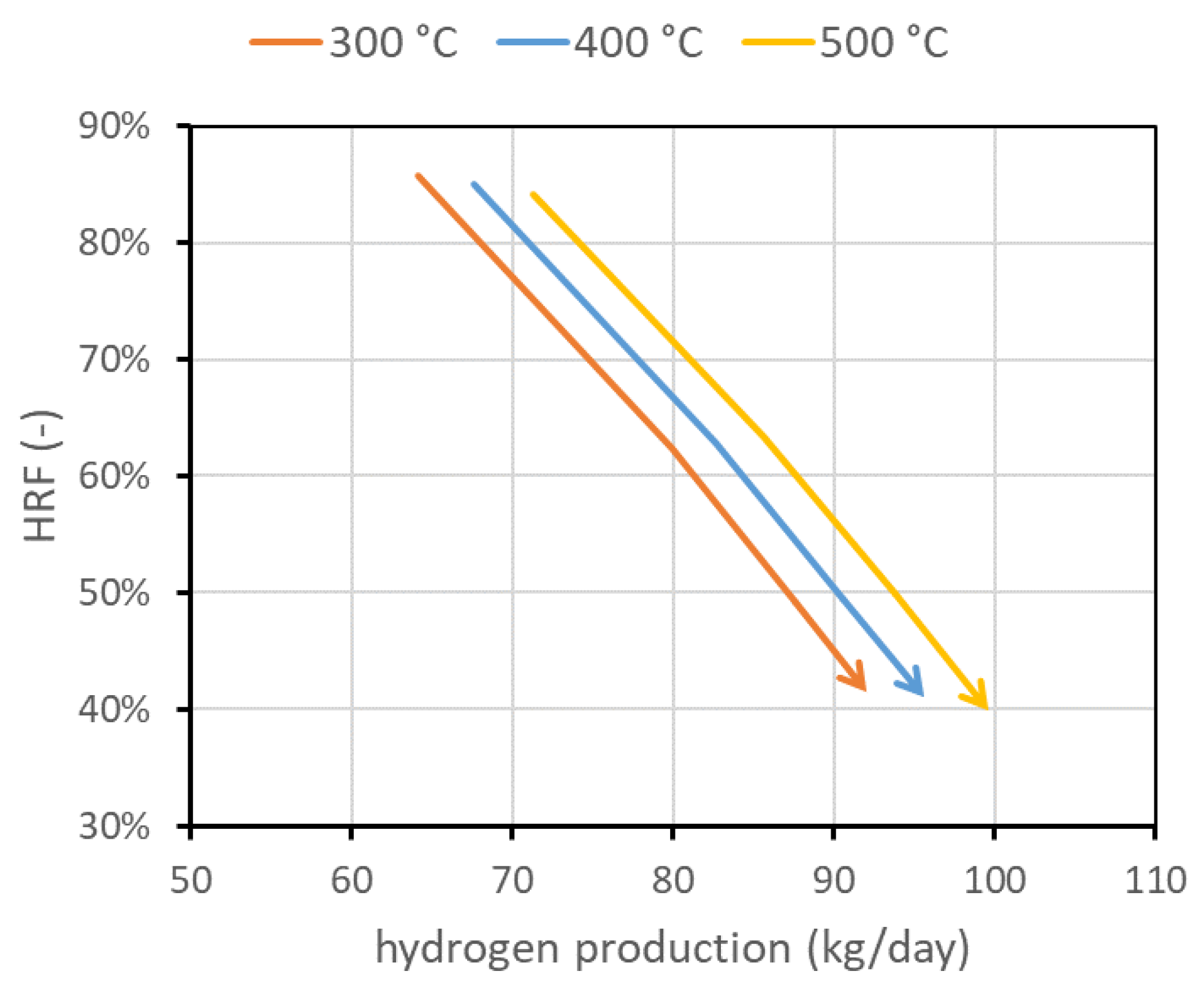
3.2. Influence of Operating Conditions
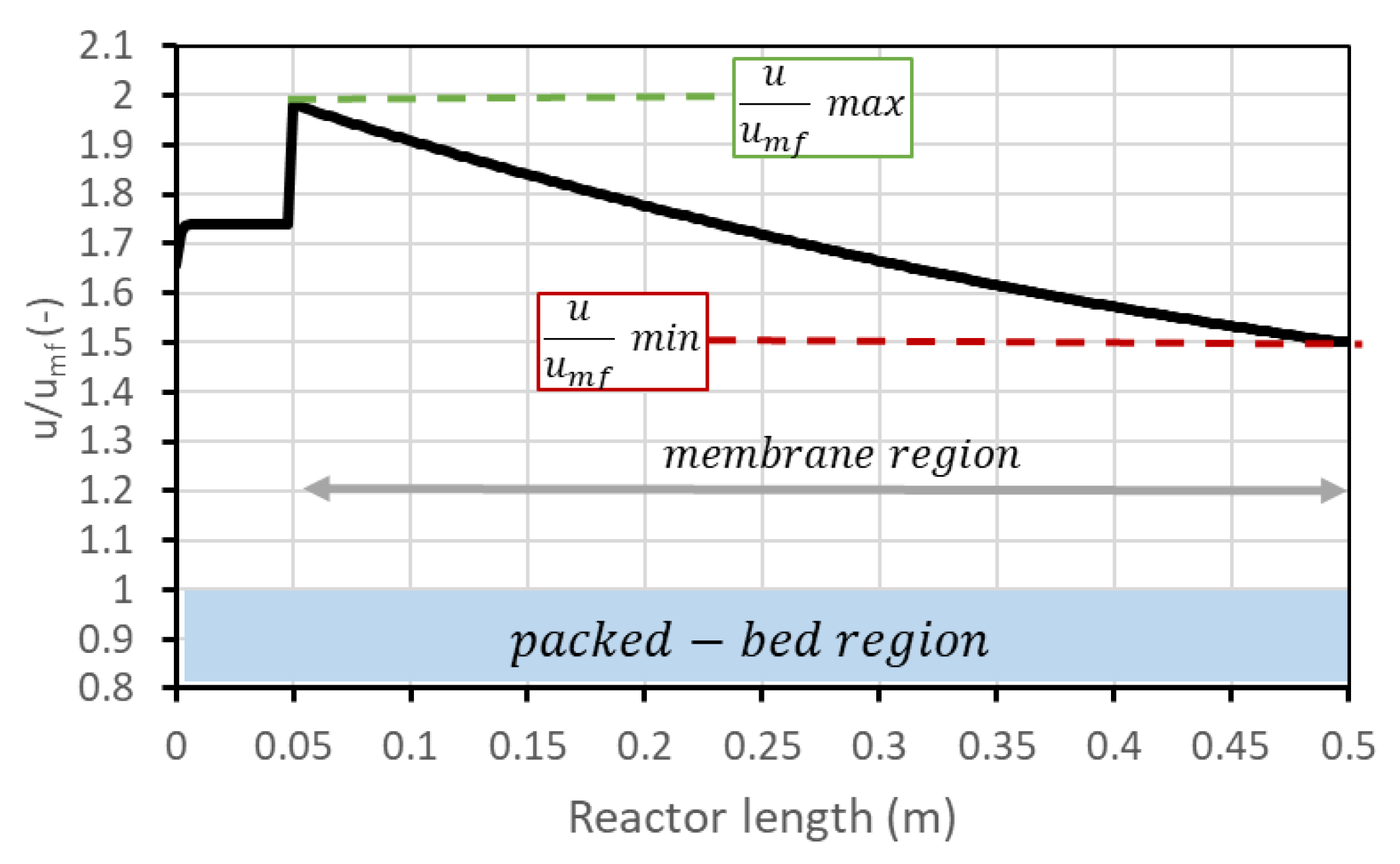
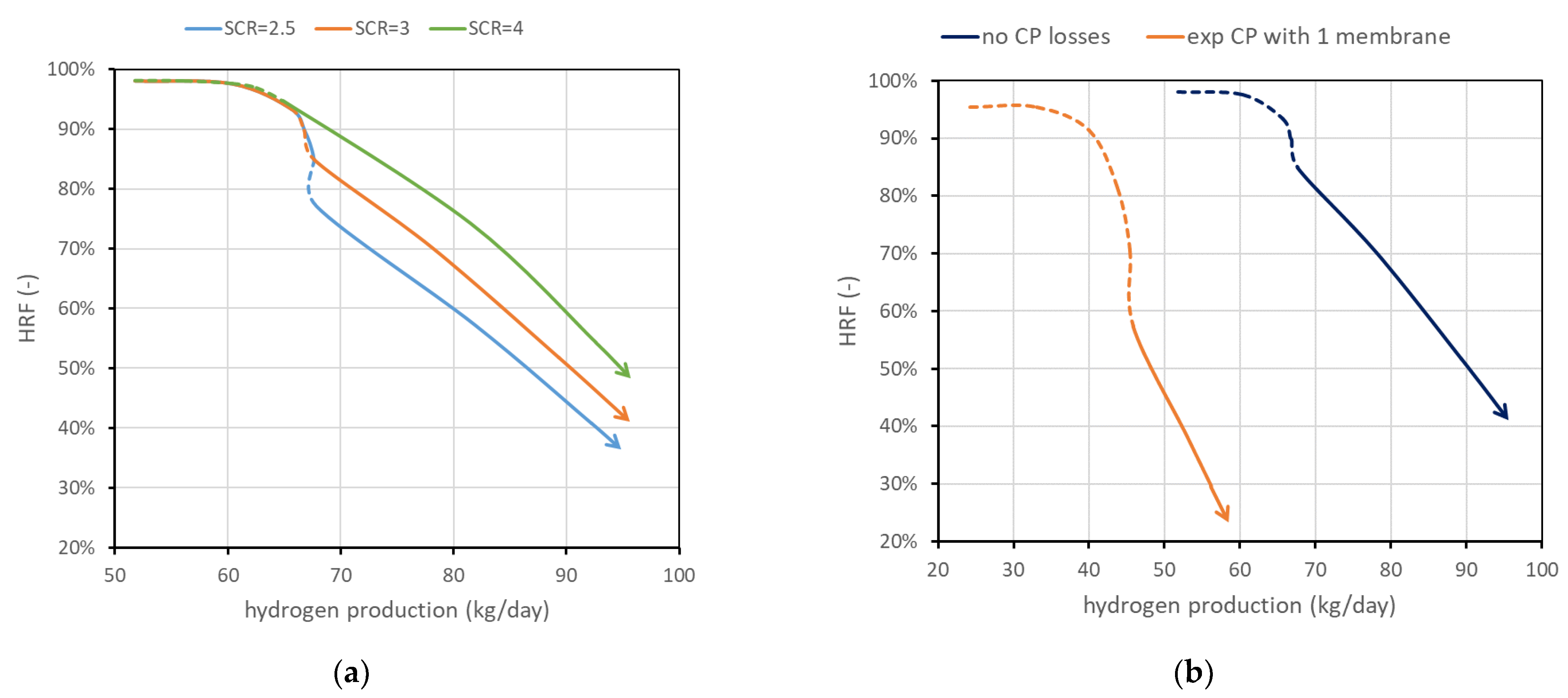
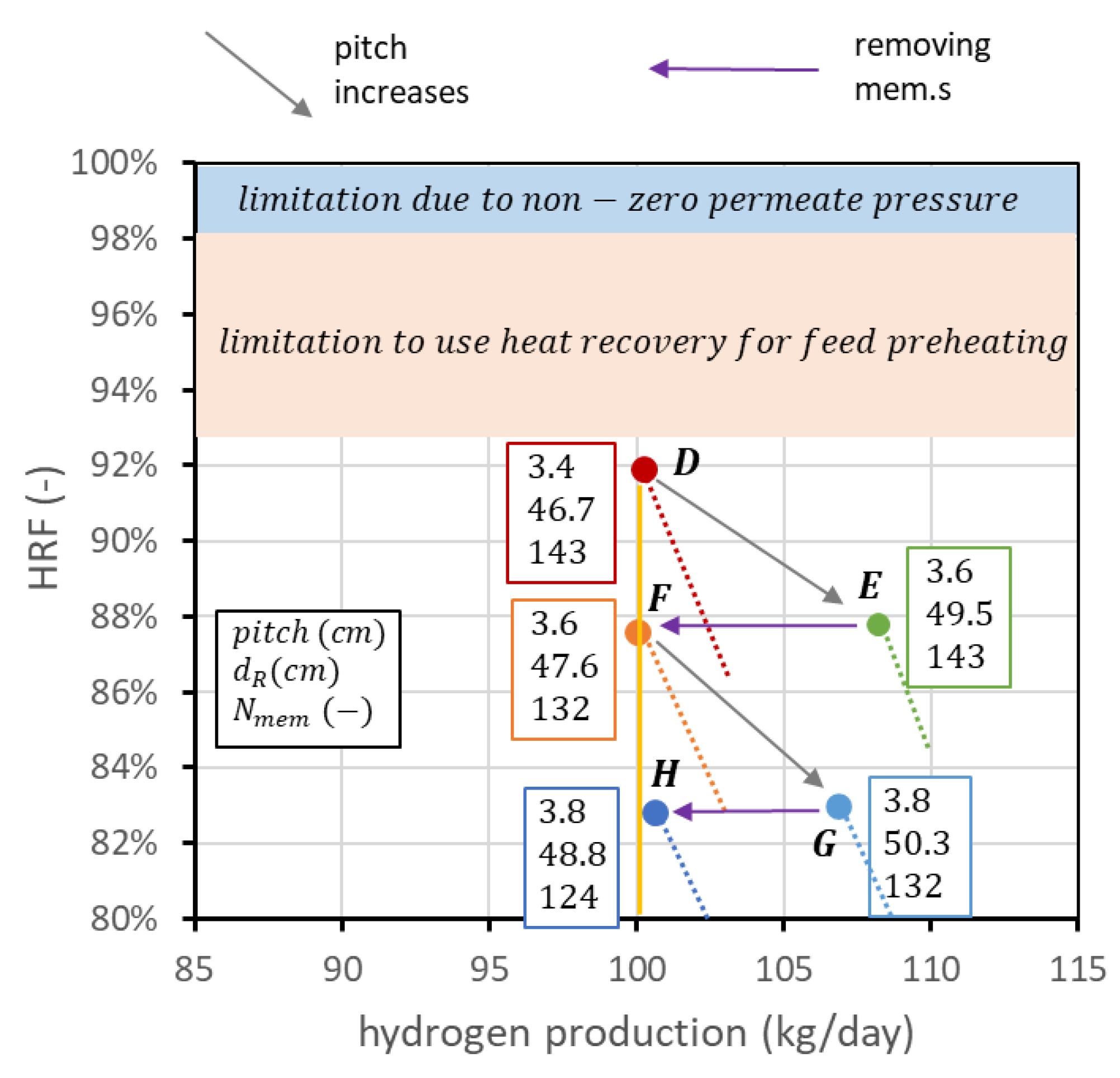
3.3. Geometric Considerations
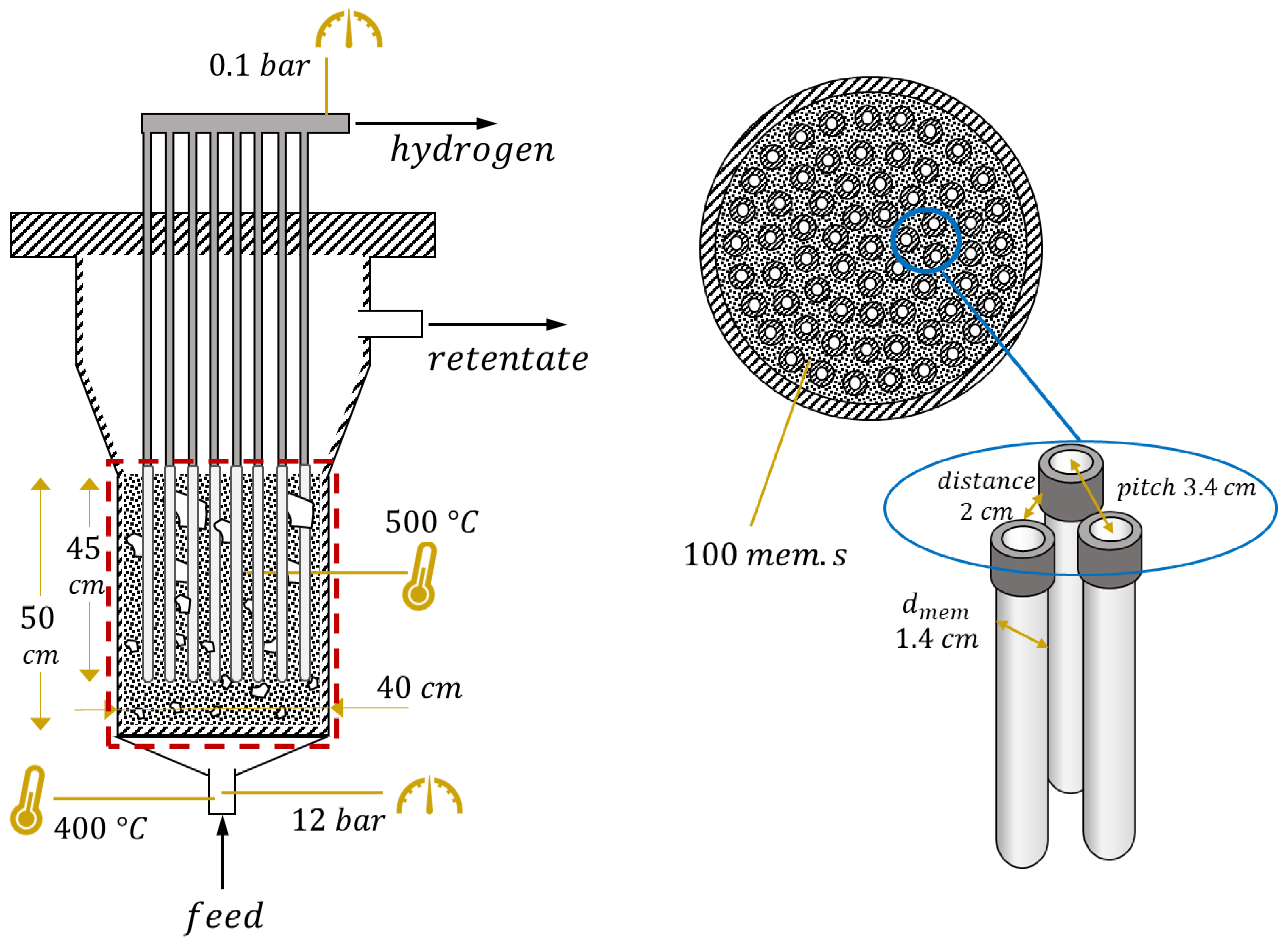
4. Reactor Design
5. Outlooks
6. Conclusions
Author Contributions
Funding

Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameter | Description | Unit |
| Cross-section area | m2 | |
| Archimedes number | - | |
| Membrane pitch | m | |
| Molar concentration | kmol/m3 | |
| Specific heat at constant pressure | kJ/(kmol∙K) | |
| Diameter | m | |
| Diffusivity | m2/s | |
| Activation energy | kJ/mol | |
| Total moles of hydrogen permeated at each axial position | kmol/(h∙m) | |
| g | Gravitational acceleration | m/s2 |
| Molar enthalpy | kJ/kmol | |
| Hydrogen recovery factor | - | |
| Hydrogen flux through the membrane | kmol/(h∙m2) | |
| Mass transfer coefficient in film layer model | m/h | |
| Pre-exponential coefficient in chemical reaction | kmol/(h∙kg∙barx) | |
| Exchange coefficient between FBMR phases | 1/h | |
| Equilibrium constant of chemical reaction | barx | |
| Lower heating value | MJ/kg | |
| Mass flow rate | kg/s | |
| Exponent in hydrogen flux expression | - | |
| molar flow rate | kmol/h | |
| Number of membranes | - | |
| Number of chemical reactions considered | - | |
| Pressure | bara | |
| Partial pressure of component i | bar | |
| Pre-exponential factor of membrane permeability | mol/(s∙m∙bar0.5) | |
| Reaction rate of reaction j | kmol/(h∙kgcat) | |
| Universal gas constant | kJ/(mol∙K) | |
| Ratio between moles of steam and moles of methane fed | - | |
| Thickness | m | |
| Temperature | °C | |
| Velocity | m/s | |
| Total volumetric flow rate of gas through the reactor | m3/h | |
| Molar fraction of hydrogen | - | |
| Axial coordinate along the reactor | m | |
| Greek letter | ||
| Parameter for wake fraction estimation | - | |
| Fraction of phase (wake or emulsion or bubble) | - | |
| Difference | x | |
| Void fraction | - | |
| Stoichiometric coefficient of species i in reaction j | - | |
| Viscosity | Pa∙s | |
| Density | kg/m3 | |
| subscripts | ||
| Reference size or variable at position z=0 in the reactor | ||
| Parameter in bubble phase | ||
| Parameter in emulsion phase | ||
| Parameter valid for the feed stream | ||
| Parameter averaged in gas phase flowing into the reactor | ||
| Parameter valid for chemical component (or species) | ||
| Parameter at the reactor/system inlet | ||
| j | Parameter related to chemical reaction | |
| Parameter related to the membranes | ||
| Parameter calculated at the membrane surface | ||
| In minimum fluidization conditions | ||
| Oxidated | ||
| Parameter of a single catalyst particle | ||
| Pinch-point in heat exchangers | ||
| Related to the permeation process | ||
| Parameter about the permeate stream | ||
| Parameter value for the reactor | ||
| ret | Parameter for the retentate stream | |
| Selective layer of the membrane | ||
| Steam methane reforming reaction | ||
| Parameter in wake phase | ||
| Water gas shift reaction | ||
Acronyms
| 1D | Mono-dimensional |
| ACM | Aspen Custom Modeler |
| ATR | Autothermal reforming |
| BG | Biogas |
| CCUS | Carbon capture, utilization, and storage |
| CP | Concentration polarization |
| EU | European Union |
| FBMR | Fluidized bed membrane reactor |
| HRF | Hydrogen recovery factor |
| KPI | Key performance indicator |
| LHV | Lower heating value |
| MACBETH | Membranes And Catalysts Beyond Economic and Technological Hurdles |
| MR | Membrane reactor |
| SCR | Steam–carbon ratio |
Appendix A. FBMR Model Equations
References
- Gallucci, F.; Tanaka, D.P.; Medrano, J.A.; Sole, J.V. Membrane Reactors Using Metallic Membranes. In Current Trends and Future Developments on (Bio-) Membranes; Elsevier Inc.: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- MACBETH » Macbeth. Available online: https://www.macbeth-project.eu/ (accessed on 1 January 2023).
- Gallucci, F.; Fernandez, E.; Corengia, P.; van Sint Annaland, M. Recent advances on membranes and membrane reactors for hydrogen production. Chem. Eng. Sci. 2013, 92, 40–66. [Google Scholar] [CrossRef]
- Kunii, D.; Levenspiel, O. Fluidization Engineering, 2nd ed.; Butterworth-Heinemann: Stoneham, UK, 1991. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Binotti, M.; Manzolini, G.; Viviente, J.L.; Arratibel, A.; Roses, L.; Gallucci, F. Achievements of European projects on membrane reactor for hydrogen production. J. Clean. Prod. 2017, 161, 1442–1450. [Google Scholar] [CrossRef]
- BIONICO Project. Available online: http://www.bionicoproject.eu/ (accessed on 5 December 2022).
- International Energy Agency. Global Hydrogen Review 2022. 2022. Available online: www.iea.org/t&c/ (accessed on 5 December 2022).
- International Energy Agency. The Future of Hydrogen: Seizing Today’s Opportunities. 2019. Available online: https://www.iea.org/reports/the-future-of-hydrogen (accessed on 11 January 2023).
- Gas for Climate. Market State and Trends in Renewable and Low-Carbon Gases in Europe. 2020. Available online: https://www.europeanbiogas.eu/wp-content/uploads/2020/12/GfC_MSTReport_2020_final.pdf (accessed on 2 December 2022).
- Marra, L.; Wolbers, P.F.; Gallucci, F.; van Sint Annaland, M. Development of a RhZrO2 catalyst for low temperature autothermal reforming of methane in membrane reactors. Catal. Today 2014, 236, 23–33. [Google Scholar] [CrossRef]
- Brencio, C.; Fontein, F.W.A.; Medrano, J.A.; Di Felice, L.; Arratibel, A.; Gallucci, F. Pd-based membranes performance under hydrocarbon exposure for propane dehydrogenation processes: Experimental and modeling. Int. J. Hydrogen Energy 2022, 47, 11369–11384. [Google Scholar] [CrossRef]
- Medrano, J.A.; Tasdemir, M.; Gallucci, F.; van Sint Annaland, M. On the internal solids circulation rates in freely-bubbling gas-solid fluidized beds. Chem. Eng. Sci. 2017, 172, 395–406. [Google Scholar] [CrossRef]
- de Nooijer, N.; Gallucci, F.; Pellizzari, E.; Melendez, J.; Tanaka, D.A.P.; Manzolini, G.; van Sint Annaland, M. On concentration polarisation in a fluidized bed membrane reactor for biogas steam reforming: Modelling and experimental validation. Chem. Eng. J. 2018, 348, 232–243. [Google Scholar] [CrossRef]
- Helmi, A.; Voncken, R.J.W.; Raijmakers, A.J.; Roghair, I.; Gallucci, F.; van Sint Annaland, M. On concentration polarization in fluidized bed membrane reactors. Chem. Eng. J. 2018, 332, 464–478. [Google Scholar] [CrossRef]
- Gallucci, F.; van Sint Annaland, M.; Kuipers, J.A.M. Autothermal Reforming of Methane with Integrated CO2 Capture in a Novel Fluidized Bed Membrane Reactor. Part 2 Comparison of Reactor Configurations Number of CSTRs in the bubble phase N e Number of CSTRs in the emulsion phase. Top. Catal. 2008, 51, 146–157. [Google Scholar] [CrossRef]
- Deshmukh, S.A.R.K.; Laverman, J.A.; Cents, A.H.G.; van Sint Annaland, M.; Kuipers, J.A.M. Development of a Membrane-Assisted Fluidized Bed Reactor. 1. Gas Phase Back-Mixing and Bubble-to-Emulsion Phase Mass Transfer Using Tracer Injection and Ultrasound Experiments. Ind. Eng. Chem. Res. 2005, 44, 5955–5965. [Google Scholar] [CrossRef]
- Brencio, C.; Di Felice, L.; Gallucci, F. Fluidized Bed Membrane Reactor for the Direct Dehydrogenation of Propane: Proof of Concept. Membranes 2022, 12, 1211. [Google Scholar] [CrossRef] [PubMed]
- Foresti, S.; Di Marcoberardino, G.; Manzolini, G.; De Nooijer, N.; Gallucci, F.; van Sint Annaland, M. A comprehensive model of a fluidized bed membrane reactor for small-scale hydrogen production. Chem. Eng. Process.-Process Intensif. 2018, 127, 136–144. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Knijff, J.; Binotti, M.; Gallucci, F.; Manzolini, G. Techno-Economic Assessment in a Fluidized Bed Membrane Reactor for Small-Scale H2 Production: Effect of Membrane Support Thickness. Membranes 2019, 9, 116. [Google Scholar] [CrossRef] [PubMed]
- Di Marcoberardino, G.; Gallucci, F.; Manzolini, G.; van Sint Annaland, M. Definition of validated membrane reactor model for 5 kW power output CHP system for different natural gas compositions. Int. J. Hydrogen Energy 2016, 41, 19141–19153. [Google Scholar] [CrossRef]
- Ongis, M.; Di Marcoberardino, G.; Manzolini, G.; Gallucci, F.; Binotti, M. Membrane reactors for green hydrogen production from biogas and biomethane: A techno-economic assessment. Int. J. Hydrogen Energy 2023. [Google Scholar] [CrossRef]
- Spallina, V.; Pandolfo, D.; Battistella, A.; Romano, M.C.; Annaland, M.V.S.; Gallucci, F. Techno-economic assessment of membrane assisted fluidized bed reactors for pure H2 production with CO2 capture. Energy Convers. Manag. 2016, 120, 257–273. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Foresti, S.; Binotti, M.; Manzolini, G. Potentiality of a biogas membrane reformer for decentralized hydrogen production. Chem. Eng. Process.-Process Intensif. 2018, 129, 131–141. [Google Scholar] [CrossRef]
- Arratibel, A.; Tanaka, A.P.; Laso, I.; van Sint Annaland, M.; Gallucci, F. Development of Pd-based double-skinned membranes for hydrogen production in fluidized bed membrane reactors. J. Memb. Sci. 2018, 550, 536–544. [Google Scholar] [CrossRef]
- Voncken, R.J.W.; Roghair, I.; van Sint Annaland, M. A numerical study on concentration polarization in 3D cylindrical fluidized beds with vertically immersed membranes. Chem. Eng. Sci. 2019, 205, 299–318. [Google Scholar] [CrossRef]
- Smaller Circles within a Larger Circle-Calculator. Available online: https://www.engineeringtoolbox.com/smaller-circles-in-larger-circle-d_1849.html (accessed on 6 February 2023).



| Species | Biogas (%mol) | Air (%mol) |
|---|---|---|
| 58.1 | 0 | |
| 33.9 | 0 | |
| 3.8 | 79 | |
| 1.1 | 21 | |
| 3.1 | 0 |
| Parameter | Value | Units |
|---|---|---|
| 7.81 | kJ/mol | |
| 0.749 | - | |
| 79.2 | m/h |
| Parameter | Value | Units |
|---|---|---|
| 83.6 | kJ/mol | |
| 54.5 | kJ/mol | |
| 2095 | kg/m3 | |
| 475 | 500 | 525 | |
|---|---|---|---|
| 9 | 89.7 | 91.3 | 93.6 |
| 12 | 90.3 | 92.0 | 93.7 |
| 15 | 90.7 | 92.4 | 94.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ongis, M.; Di Marcoberardino, G.; Baiguini, M.; Gallucci, F.; Binotti, M. Optimization of Small-Scale Hydrogen Production with Membrane Reactors. Membranes 2023, 13, 331. https://doi.org/10.3390/membranes13030331
Ongis M, Di Marcoberardino G, Baiguini M, Gallucci F, Binotti M. Optimization of Small-Scale Hydrogen Production with Membrane Reactors. Membranes. 2023; 13(3):331. https://doi.org/10.3390/membranes13030331
Chicago/Turabian StyleOngis, Michele, Gioele Di Marcoberardino, Mattia Baiguini, Fausto Gallucci, and Marco Binotti. 2023. "Optimization of Small-Scale Hydrogen Production with Membrane Reactors" Membranes 13, no. 3: 331. https://doi.org/10.3390/membranes13030331
APA StyleOngis, M., Di Marcoberardino, G., Baiguini, M., Gallucci, F., & Binotti, M. (2023). Optimization of Small-Scale Hydrogen Production with Membrane Reactors. Membranes, 13(3), 331. https://doi.org/10.3390/membranes13030331









