Synchronous Design of Membrane Material and Process for Pre-Combustion CO2 Capture: A Superstructure Method Integrating Membrane Type Selection
Abstract
1. Introduction
1.1. Background
1.2. Research Progress
1.3. Aim and Novelty of This Work
- (1)
- Optimization of two-stage membrane process based on the commercial membrane, aiming at exploring the optimal process, capture cost and operation parameters based on existing commercial membranes through parameter optimization.
- (2)
- Using the H2-selective membrane changes based on the Robeson upper bound and the commercial CO2 membrane, the process optimization of a two-stage membrane aims to explore the potential for the reduction of the capture cost and the change of the best H2-selective membrane performance when the performance of H2-selective membrane changes.
- (3)
- Using the H2-selective membrane and CO2-selective membrane change based on the Robeson upper bound, the optimization of a two-stage membrane process and the comparison of the optimal process of membrane type combination aim at determining the influence of two membrane types on the optimal process and its capture cost; the necessity of using a hybrid membrane is clarified by analyzing the gap between different membrane type combinations.
2. Model and Optimization Method
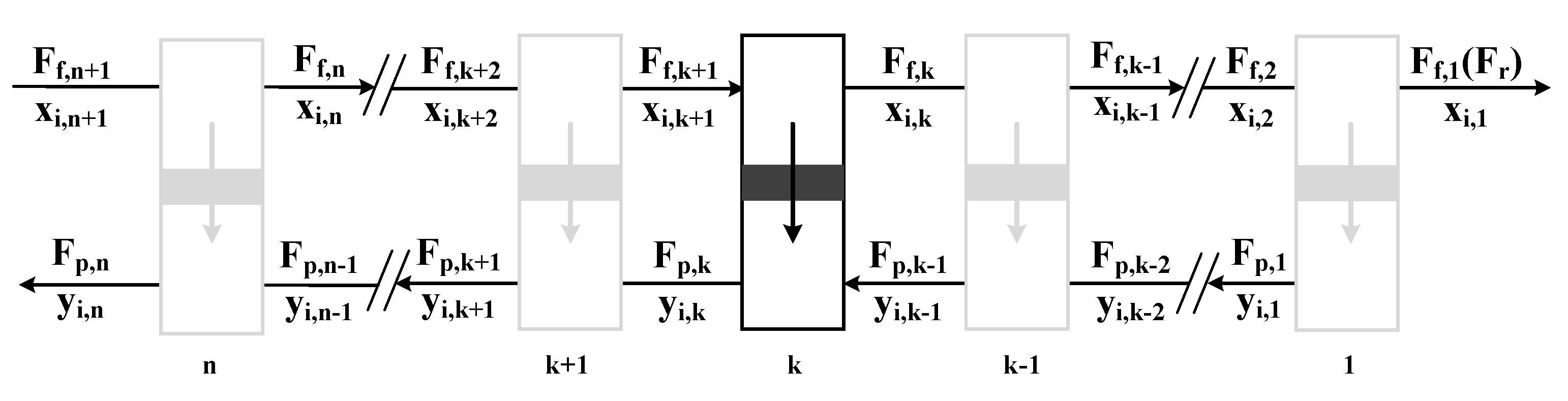
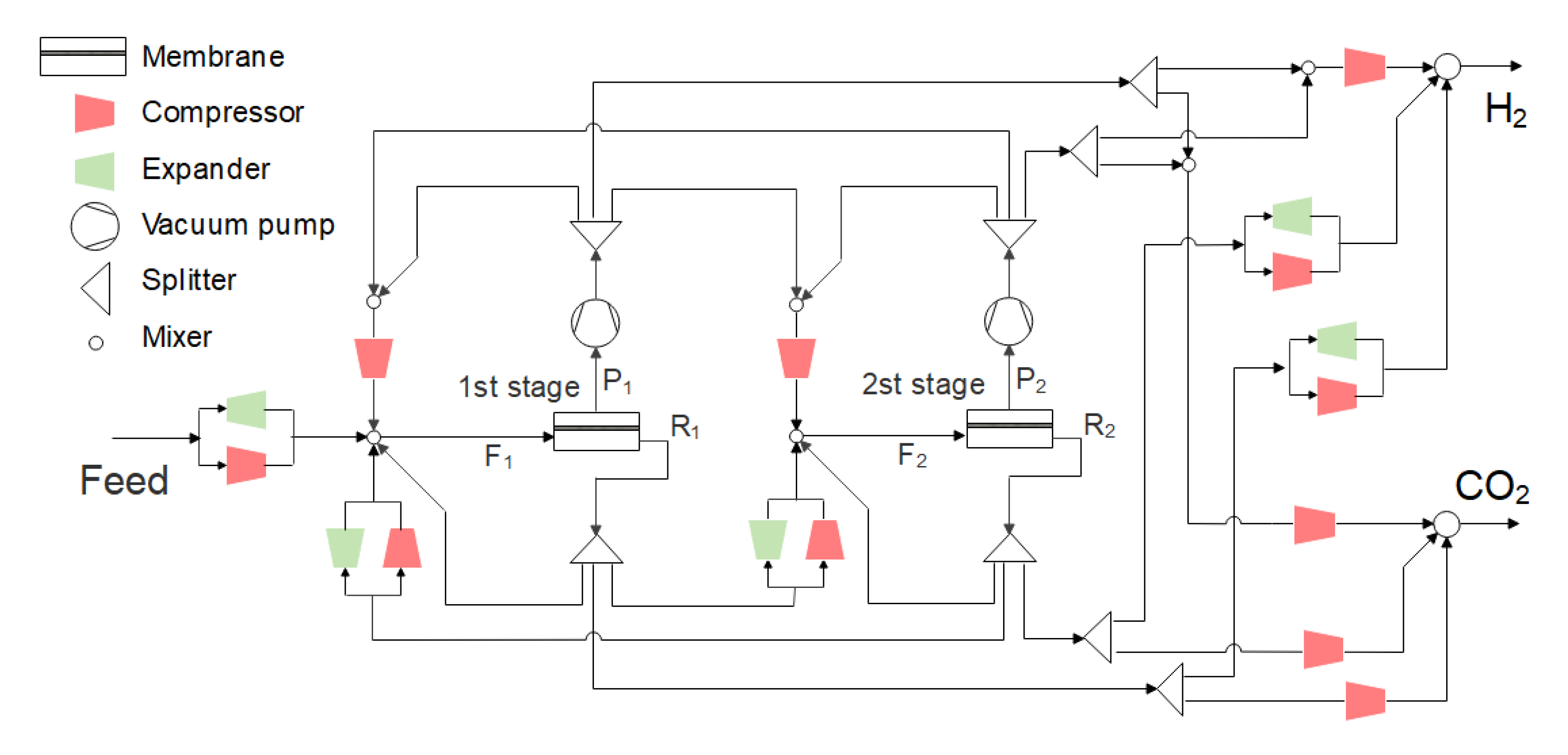
2.1. Problem Formulation
2.2. Mathematical Modeling
- (1)
- (2)
- The membrane is operated at an isothermal temperature [33].
- (3)
- (4)
- (5)
2.3. Superstructure Model and Optimization Method
- (1)
- Avoid the permeate/residue side stream of each stage membrane as the feed gas of another stage membrane at the same time, because this is actually the reverse process of separation [20].
- (2)
- Try to avoid concentration mixing between membrane stages. If both the first-stage and the second-stage membranes are H2-selective or CO2-selective membranes, the stream of the second-stage membrane returning to the first-stage membrane will be opposite to the stream of the first-stage membrane going to the second-stage membrane. If the first-stage and second-stage membranes are different, the stream from the second-stage membrane back to the first-stage membrane must be the same as that from the first-stage membrane to the second-stage membrane.
2.4. Commercial Membrane Performance and its Robeson Upper Bound
2.5. Economic Model and Performance Parameters
3. Results and Discussion
3.1. Feasibility Analysis of Single-Stage Membrane System
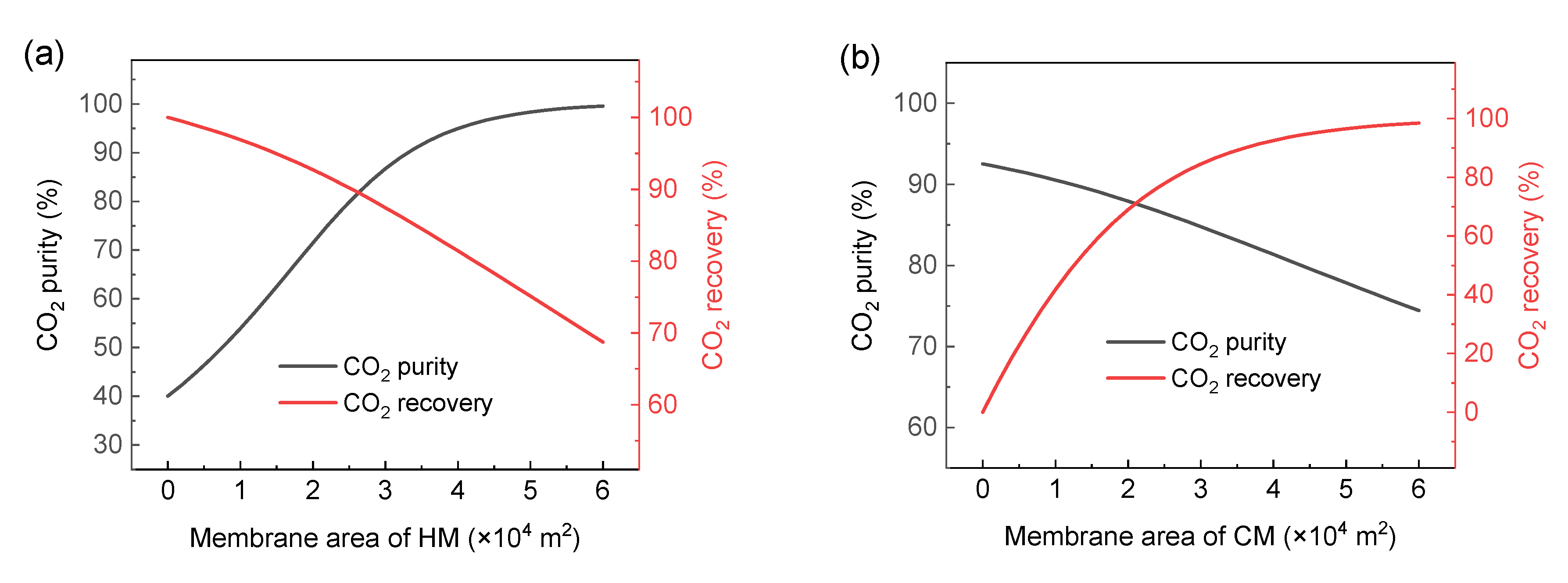
3.2. Optimization of Membrane Process Based on Commercial Membrane
3.2.1. Optimization of Two-Stage Membrane Process Considering Membrane Type Combination When the Operating Pressure of Each Stage Is Fixed
3.2.2. Optimization of Operating Parameters of the Two-Stage Membrane Process
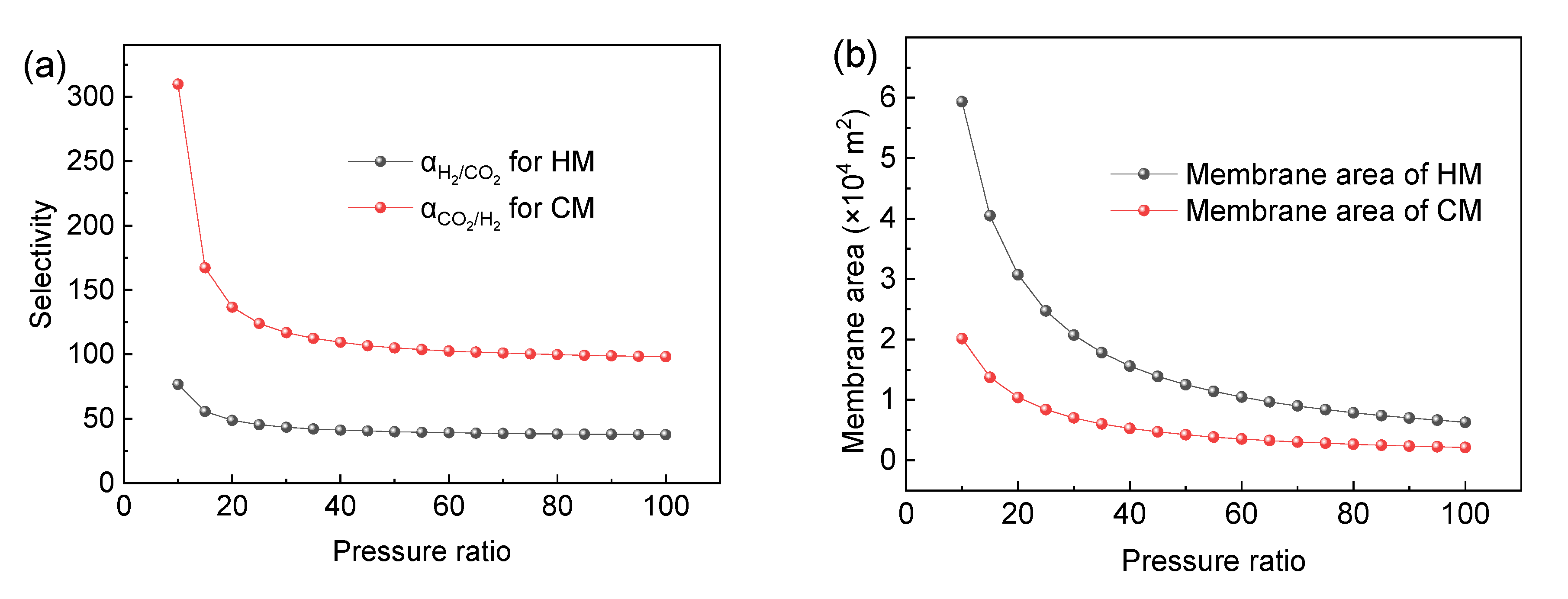
3.3. Optimization of Membrane Process Based on Robeson Upper Bound
3.3.1. Optimization of H2-Selective Membrane Performance
3.3.2. The Performance of H2-Selective Membrane and CO2-Selective Membrane Changing Simultaneously
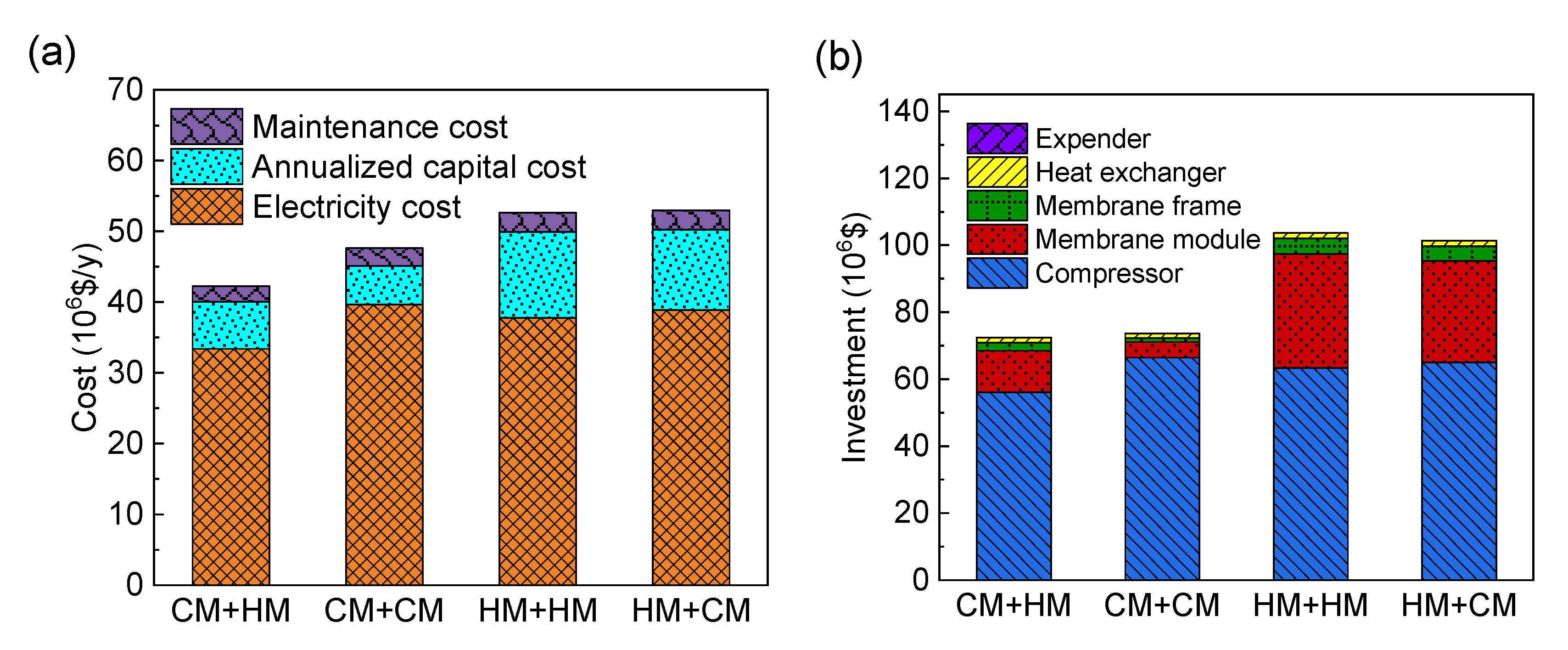
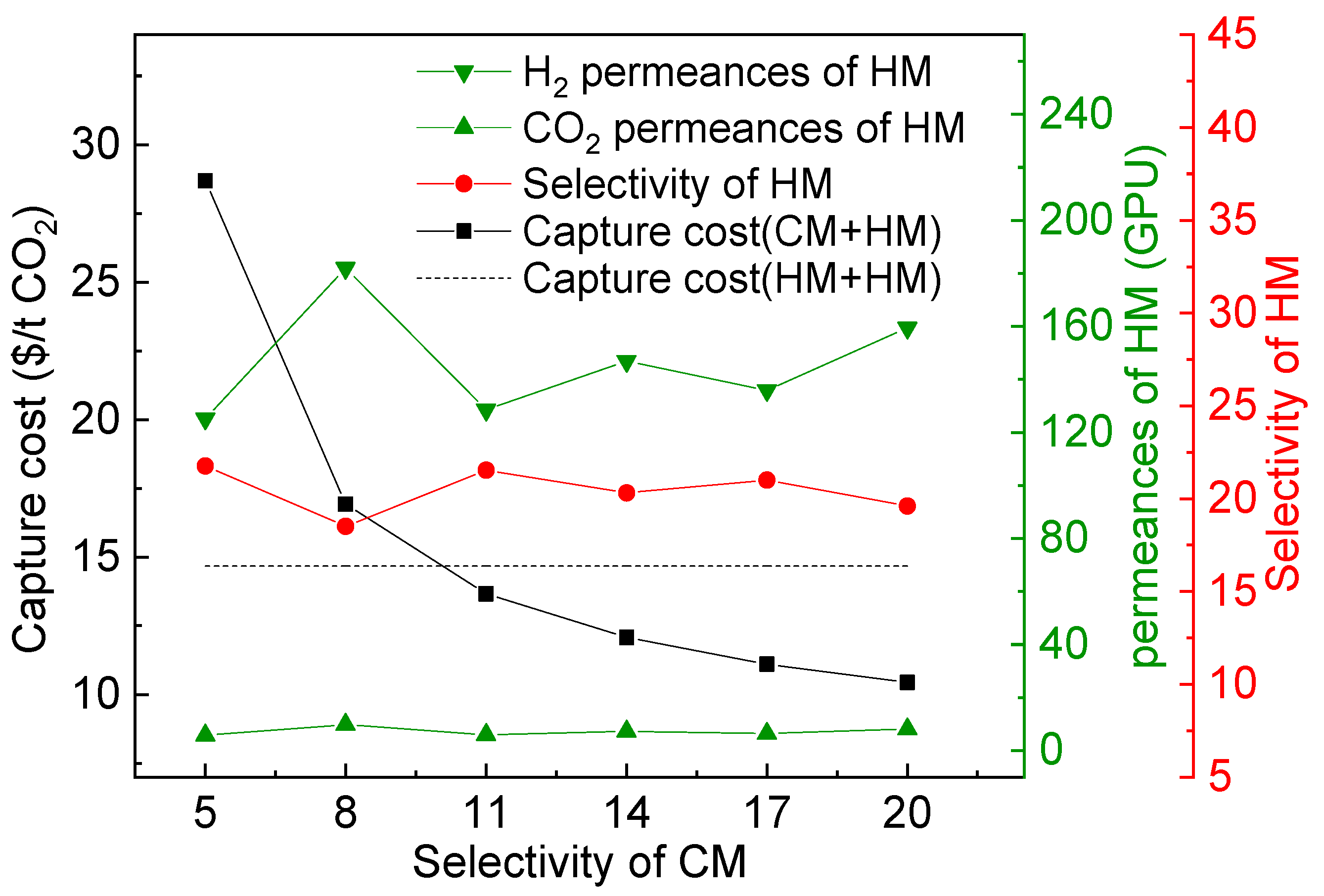
3.4. Influence of the Combination of the Membrane Type
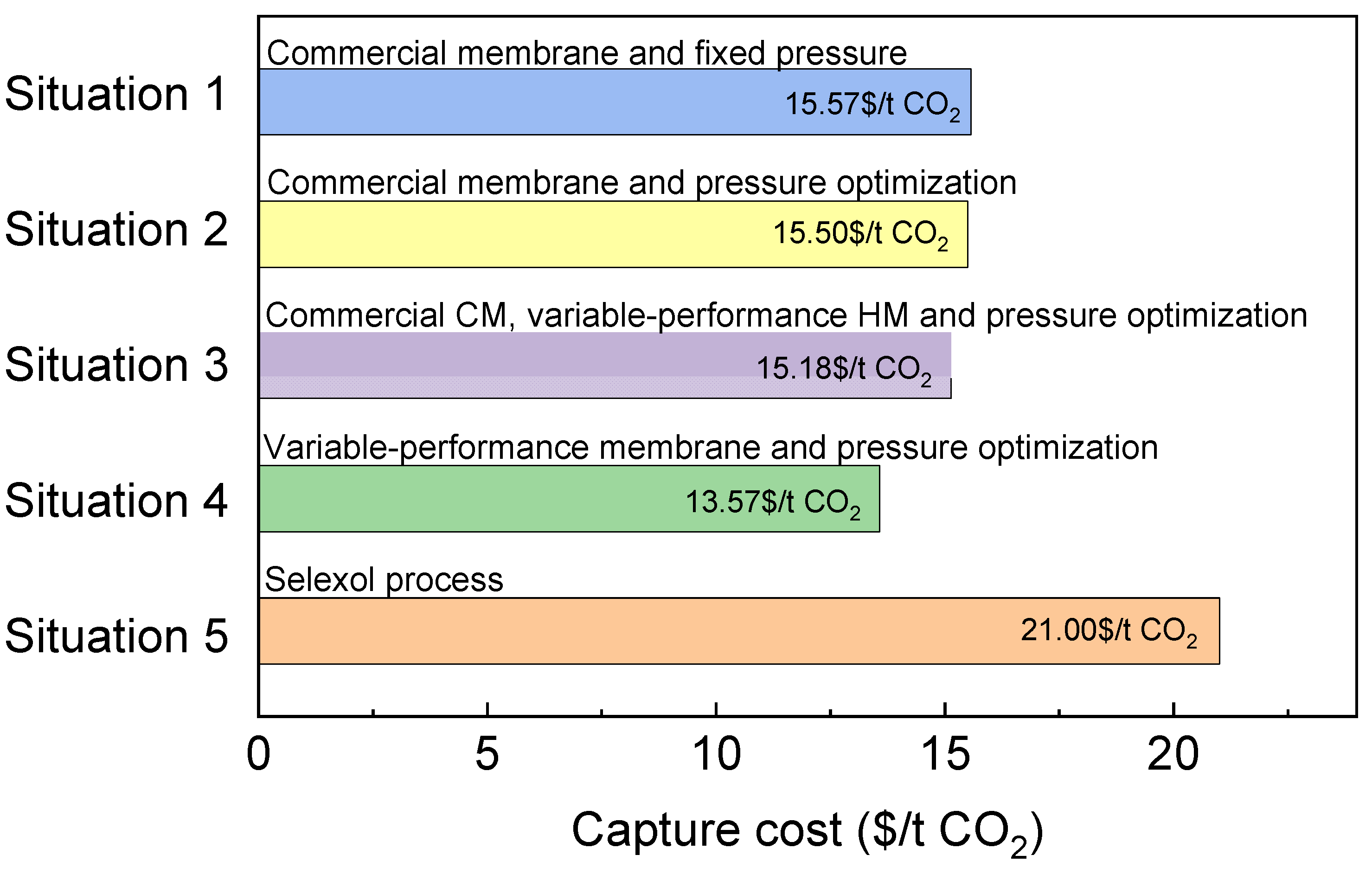
3.5. Comparison of Different Situations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| x | optimization variable |
| α | selectivity |
| Pi | permeability of the fast gas i |
| k | front factor |
| n | slope of the log–log plot of the Robeson upper bound |
| L | flow rate of heat exchange stream |
| r | penalty factor |
| Subscripts | |
| m | membrane |
| mf | membrane frame |
| cp | compressor |
| vp | vacuum pump |
| ex | expander |
| he | heat exchanger |
| acc | annualized capital cost |
| mc | maintenance cost |
| ec | electricity cost |
| spe | specific |
| cap | capture |
| Acronyms | |
| IGCC | integrated gasification combined cycle |
| CM | CO2-selective membrane |
| HM | H2-selective membrane |
| F | feed stream |
| P | permeate side stream |
| R | residue side stream |
| MINLP | mixed-integer nonlinear programming |
| I | investment |
| A | membrane area |
| W | power consumption |
| C | cost |
References
- Song, C.; Liu, Q.; Deng, S.; Li, H.; Kitamura, Y. Cryogenic-based CO2 capture technologies: State-of-the-art developments and current challenges. Renew. Sustain. Energy Rev. 2019, 101, 265–278. [Google Scholar] [CrossRef]
- Ren, L.-X.; Chang, F.-L.; Kang, D.-Y.; Chen, C.-L. Hybrid membrane process for post-combustion CO2 capture from coal-fired power plant. J. Membr. Sci. 2020, 603, 118245. [Google Scholar] [CrossRef]
- Kotowicz, J.; Skorek-osikowska, A.; Janusz-szymańska, K. Membrane separation of carbon dioxide in the integrated gasification combined cycle systems. Arch. Thermodyn. 2010, 31, 145–164. [Google Scholar] [CrossRef]
- Merkel, T.C.; Zhou, M.; Baker, R.W. Carbon dioxide capture with membranes at an IGCC power plant. J. Membr. Sci. 2012, 389, 441–450. [Google Scholar] [CrossRef]
- Ku, A.Y.; Kulkarni, P.; Shisler, R.; Wei, W. Membrane performance requirements for carbon dioxide capture using hydrogen-selective membranes in integrated gasification combined cycle (IGCC) power plants. J. Membr. Sci. 2011, 367, 233–239. [Google Scholar] [CrossRef]
- Picaud-Vannereux, S.; Lutin, F.; Favre, E.; Roizard, D. Energy efficiency of membrane vs hybrid membrane/cryogenic processes for propane recovery from nitrogen purging vents: A simulation study. Sep. Purif. Technol. 2020, 240, 116613. [Google Scholar] [CrossRef]
- Giordano, L.; Roizard, D.; Bounaceur, R.; Favre, E. Evaluating the effects of CO2 capture benchmarks on efficiency and costs of membrane systems for post-combustion capture: A parametric simulation study. Int. J. Greenh. Gas Control 2017, 63, 449–461. [Google Scholar] [CrossRef]
- Dai, Y.; Niu, Z.; Luo, W.; Wang, Y.; Mu, P.; Li, J. A review on the recent advances in composite membranes for CO2 capture processes. Sep. Purif. Technol. 2023, 307, 122752. [Google Scholar] [CrossRef]
- Franz, J.; Scherer, V. An evaluation of CO2 and H2 selective polymeric membranes for CO2 separation in IGCC processes. J. Membr. Sci. 2010, 359, 173–183. [Google Scholar] [CrossRef]
- Vakharia, V.; Ramasubramanian, K.; Winston Ho, W.S. An experimental and modeling study of CO2-selective membranes for IGCC syngas purification. J. Membr. Sci. 2015, 488, 56–66. [Google Scholar] [CrossRef]
- Han, Y.; Ho, W.S.W. Facilitated transport membranes for H2 purification from coal-derived syngas: A techno-economic analysis. J. Membr. Sci. 2021, 636, 119549. [Google Scholar] [CrossRef]
- Lin, H.; He, Z.; Sun, Z.; Kniep, J.; Ng, A.; Baker, R.W.; Merkel, T.C. CO2-selective membranes for hydrogen production and CO2 capture–Part II: Techno-economic analysis. J. Membr. Sci. 2015, 493, 794–806. [Google Scholar] [CrossRef]
- Giordano, L.; Gubis, J.; Bierman, G.; Kapteijn, F. Conceptual design of membrane-based pre-combustion CO2 capture process: Role of permeance and selectivity on performance and costs. J. Membr. Sci. 2019, 575, 229–241. [Google Scholar] [CrossRef]
- Krishnan, G.; Steele, D.; O’Brien, K.; Callahan, R.; Berchtold, K.; Figueroa, J. Simulation of a Process to Capture CO2 From IGCC Syngas Using a High Temperature PBI Membrane. Energy Procedia 2009, 1, 4079–4088. [Google Scholar] [CrossRef]
- Arias, A.M.; Mussati, M.C.; Mores, P.L.; Scenna, N.J.; Caballero, J.A.; Mussati, S.F. Optimization of multi-stage membrane systems for CO 2 capture from flue gas. Int. J. Greenh. Gas Control 2016, 53, 371–390. [Google Scholar] [CrossRef]
- Mores, P.L.; Arias, A.M.; Scenna, N.J.; Mussati, M.C.; Mussati, S.F. Cost-based comparison of multi-stage membrane configurations for carbon capture from flue gas of power plants. Int. J. Greenh. Gas Control 2019, 86, 177–190. [Google Scholar] [CrossRef]
- Chiwaye, N.; Majozi, T.; Daramola, M.O. Optimisation of post-combustion carbon dioxide capture by use of a fixed site carrier membrane. Int. J. Greenh. Gas Control 2021, 104, 103182. [Google Scholar] [CrossRef]
- Roussanaly, S.; Anantharaman, R. Cost-optimal CO 2 capture ratio for membrane-based capture from different CO2 sources. Chem. Eng. J. 2017, 327, 618–628. [Google Scholar] [CrossRef]
- Gabrielli, P.; Gazzani, M.; Mazzotti, M. On the optimal design of membrane-based gas separation processes. J. Membr. Sci. 2017, 526, 118–130. [Google Scholar] [CrossRef]
- Lee, S.; Binns, M.; Kim, J.-K. Automated process design and optimization of membrane-based CO2 capture for a coal-based power plant. J. Membr. Sci. 2018, 563, 820–834. [Google Scholar] [CrossRef]
- Fernández-Barquín, A.; Casado-Coterillo, C.; Irabien, Á. Separation of CO2-N2 gas mixtures: Membrane combination and temperature influence. Sep. Purif. Technol. 2017, 188, 197–205. [Google Scholar] [CrossRef]
- Hussain, A.; Farrukh, S.; Minhas, F.T. Two-Stage Membrane System for Post-combustion CO2 Capture Application. Energy Fuels 2015, 29, 6664–6669. [Google Scholar] [CrossRef]
- Ohs, B.; Lohaus, J.; Wessling, M. Optimization of membrane based nitrogen removal from natural gas. J. Membr. Sci. 2016, 498, 291–301. [Google Scholar] [CrossRef]
- Chiwaye, N.; Majozi, T.; Daramola, M.O. On optimisation of N2 and CO2-selective hybrid membrane process systems for post-combustion CO2 capture from coal-fired power plants. J. Membr. Sci. 2021, 638, 119691. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Zhang, C.; Zhao, S.; Qiao, Z.; Li, P.; Wang, J.; Wang, S. Parametric analysis and potential prediction of membrane processes for hydrogen production and pre-combustion CO2 capture. Chem. Eng. Sci. 2015, 135, 202–216. [Google Scholar] [CrossRef]
- Kazama, S.; Haraya, K. Optimization of CO2 concentration captured by membrane technology-Possibility of reduction in CO2 capture energy and cost. Energy Procedia 2013, 37, 969–975. [Google Scholar] [CrossRef]
- Weller, S.; Steiner, W.A. Separation of Gases by Fractional Permeation through Membranes. J. Appl. Phys. 1950, 21, 279–283. [Google Scholar] [CrossRef]
- Pan, C.Y.; Habgood, H. Gas separation by permeation part I. Calculation methods and parametric analysis. Can. J. Chem. Eng. 1978, 56, 197–209. [Google Scholar] [CrossRef]
- Pan, C.Y.; Habgood, H. Gas separation by permeation Part II: Effect of permeate pressure drop and choice of permeate pressure. Can. J. Chem. Eng. 1978, 56, 210–217. [Google Scholar] [CrossRef]
- Coker, D.; Freeman, B.; Fleming, G. Modeling multicomponent gas separation using hollow-fiber membrane contactors. AIChE J. 1998, 44, 1289–1302. [Google Scholar] [CrossRef]
- Pan, C. Gas separation by permeators with high-flux asymmetric membranes. AIChE J. 1983, 29, 545–552. [Google Scholar] [CrossRef]
- Taifan, G.S.P.; Maravelias, C.T. Generalized optimization-based synthesis of membrane systems for multicomponent gas mixture separation. Chem. Eng. Sci. 2022, 252, 117482. [Google Scholar] [CrossRef]
- Ramírez-Santos, Á.A.; Bozorg, M.; Addis, B.; Piccialli, V.; Castel, C.; Favre, E. Optimization of multistage membrane gas separation processes. Example of application to CO2 capture from blast furnace gas. J. Membr. Sci. 2018, 566, 346–366. [Google Scholar] [CrossRef]
- Hao, J.; Rice, P.A.; Stern, S.A. Upgrading low-quality natural gas with H2S- and CO2-selective polymer membranes. J. Membr. Sci. 2008, 320, 108–122. [Google Scholar] [CrossRef]
- Datta, A.K.; Sen, P.K. Optimization of membrane unit for removing carbon dioxide from natural gas. J. Membr. Sci. 2006, 283, 291–300. [Google Scholar] [CrossRef]
- Scholes, C.A.; Ho, M.T.; Aguiar, A.A.; Wiley, D.E.; Stevens, G.W.; Kentish, S.E. Membrane gas separation processes for CO2 capture from cement kiln flue gas. Int. J. Greenh. Gas Control 2014, 24, 78–86. [Google Scholar] [CrossRef]
- Kim, K.-M.; Lee, J.-W.; Lee, J.-B. No-mixing-loss design of a multistage membrane carbon capture process for off-gas in thermal power plants. J. Membr. Sci. 2020, 598, 117796. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Han, Y.; Ho, W.S.W. Polymeric membranes for CO2 separation and capture. J. Membr. Sci. 2021, 628, 119244. [Google Scholar] [CrossRef]
- He, X.; Lei, L.; Dai, Z. Green hydrogen enrichment with carbon membrane processes: Techno-economic feasibility and sensitivity analysis. Sep. Purif. Technol. 2021, 276, 119346. [Google Scholar] [CrossRef]
- Couling, D.J.; Prakash, K.; Green, W.H. Analysis of Membrane and Adsorbent Processes for Warm Syngas Cleanup in Integrated Gasification Combined-Cycle Power with CO2Capture and Sequestration. Ind. Eng. Chem. Res. 2011, 50, 11313–11336. [Google Scholar] [CrossRef]
- Koutsonikolas, D.E.; Kaldis, S.P.; Pantoleontos, G.T.; Zaspalis, V.T.; Sakellaropoulos, G.P. Techno-economic assessment of polymeric, ceramic and metallic membranes integration in an advanced IGCC process for H2 production and CO2 capture. Chem. Eng. Trans. 2013, 35, 715–720. [Google Scholar]
- Micari, M.; Dakhchoune, M.; Agrawal, K.V. Techno-economic assessment of postcombustion carbon capture using high-performance nanoporous single-layer graphene membranes. J. Membr. Sci. 2021, 624, 119103. [Google Scholar] [CrossRef]
- Ruan, X.; Huo, W.; Wang, J.; Guo, M.; Zheng, W.; Zou, Y.; Huang, A.; Shou, J.; He, G. Multi-technique integration separation frameworks after steam reforming for coal-based hydrogen generation. Chin. J. Chem. Eng. 2021, 35, 163–172. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Qiao, Z.; Wu, H.; Dong, S.; Zhao, S.; Wang, J. Post-combustion CO2 capture with membrane process: Practical membrane performance and appropriate pressure. J. Membr. Sci. 2019, 581, 195–213. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Z.; Wang, J.; Wang, S. Potential of Two-Stage Membrane System with Recycle Stream for CO2 Capture from Postcombustion Gas. Energy Fuels 2009, 23, 4755–4762. [Google Scholar] [CrossRef]
- Havas, D.; Lin, H. Optimal membranes for biogas upgrade by removing CO2: High permeance or high selectivity? Sep. Sci. Technol. 2016, 52, 186–196. [Google Scholar] [CrossRef]
- Scholz, M.; Alders, M.; Lohaus, T.; Wessling, M. Structural optimization of membrane-based biogas upgrading processes. J. Membr. Sci. 2015, 474, 1–10. [Google Scholar] [CrossRef]
- Li, Q.; Wu, H.; Wang, Z.; Wang, J. Analysis and optimal design of membrane processes for flue gas CO2 capture. Sep. Purif. Technol. 2022, 298, 121584. [Google Scholar] [CrossRef]
- Mat, N.C.; Lipscomb, G.G. Membrane process optimization for carbon capture. Int. J. Greenh. Gas Control 2017, 62, 1–12. [Google Scholar] [CrossRef]
- He, X.; Kumakiri, I.; Hillestad, M. Conceptual process design and simulation of membrane systems for integrated natural gas dehydration and sweetening. Sep. Purif. Technol. 2020, 247, 116993. [Google Scholar] [CrossRef]
- Yuan, M.; Narakornpijit, K.; Haghpanah, R.; Wilcox, J. Consideration of a nitrogen-selective membrane for postcombustion carbon capture through process modeling and optimization. J. Membr. Sci. 2014, 465, 177–184. [Google Scholar] [CrossRef]
- Low, B.T.; Zhao, L.; Merkel, T.C.; Weber, M.; Stolten, D. A parametric study of the impact of membrane materials and process operating conditions on carbon capture from humidified flue gas. J. Membr. Sci. 2013, 431, 139–155. [Google Scholar] [CrossRef]
- Lee, W.-S.; Oh, H.-T.; Lee, J.-C.; Oh, M.; Lee, C.-H. Performance analysis and carbon reduction assessment of an integrated syngas purification process for the co-production of hydrogen and power in an integrated gasification combined cycle plant. Energy 2019, 171, 910–927. [Google Scholar] [CrossRef]
- Fisher, K.S.; Beitler, C.; Rueter, C.; Searcy, K.; Rochelle, G.; Jassim, M. Integrating MEA regeneration with CO2 compression and peaking to reduce CO2 capture costs. Trimeric Corp. 2005. [Google Scholar] [CrossRef]






| Control Variable | Variable Type | Range | |
|---|---|---|---|
| Selection and performance of membrane types | 1-stage membrane type selection coefficient x1 | Binary | {0, 1} |
| 2-stage membrane type selection coefficient x2 | Binary | {0, 1} | |
| 1-stage membrane selectivity x3 | Continuous | [2, 30] for HM [5, 15] for CM [2, 30] for HM [5, 15] for CM | |
| 2-stage membrane selectivity x4 | Continuous | ||
| 1-stage membrane area x5 | Continuous | [500, 200,000] | |
| 2-stage membrane area x6 | Continuous | [500, 200,000] | |
| Process structure | 1-stage membrane recycle stream selection coefficient x7 | Binary | {0, 1} |
| 1-stage membrane recycle percentage x8 | Continuous | [0, 100] | |
| 2-stage membrane feed side selection coefficient x9 | Binary | {0, 1} | |
| 2-stage membrane feed percentage x10 | Continuous | [0, 100] | |
| 1-stage membrane feed selection coefficient from 2-stage membrane x11 | Binary | {0, 1} | |
| 1-stage membrane feed percentage from 2-stage membrane x12 | Continuous | [0, 100] | |
| 2-stage membrane recycle stream selection coefficient x13 | Binary | {0, 1} | |
| 2-stage membrane recycle percentage x14 | Continuous | [0, 100] | |
| System parameters | 1-stage membrane inlet pressure x15 | Continuous | [105, 5000] |
| 1-stage membrane outlet pressure x16 | Continuous | [20, 105] | |
| 2-stage membrane inlet pressure x17 | Continuous | [105, 5000] | |
| 2-stage membrane outlet pressure x18 | Continuous | [20, 105] | |
| Membrane Type | Unit | H2 Permeance | CO2 Permeance |
|---|---|---|---|
| H2-selective membrane | GPU | 300 | 20 |
| CO2-selective membrane | GPU | 85 | 1000 |
| Cost Parameter | Unit | Equation | Reference |
|---|---|---|---|
| Membrane module | $ | [44] | |
| Membrane frame | $ | [45] | |
| Compressor | $ | [37] | |
| Vacuum pump | $ | [37] | |
| Expander | $ | [37] | |
| Heat exchanger | $ | [46] | |
| Annualized capital cost | $ | [46] | |
| Depreciation factor of other equipment | d | 0.064 (25 years) | [46] |
| Depreciation factor of membrane | dm | 0.225 (5 years) | [46] |
| Maintenance cost | $ | [46] | |
| Electricity cost | $ | [37] | |
| Total cost | $ | [46] | |
| Cost per ton CO2 | $/t | [46] |
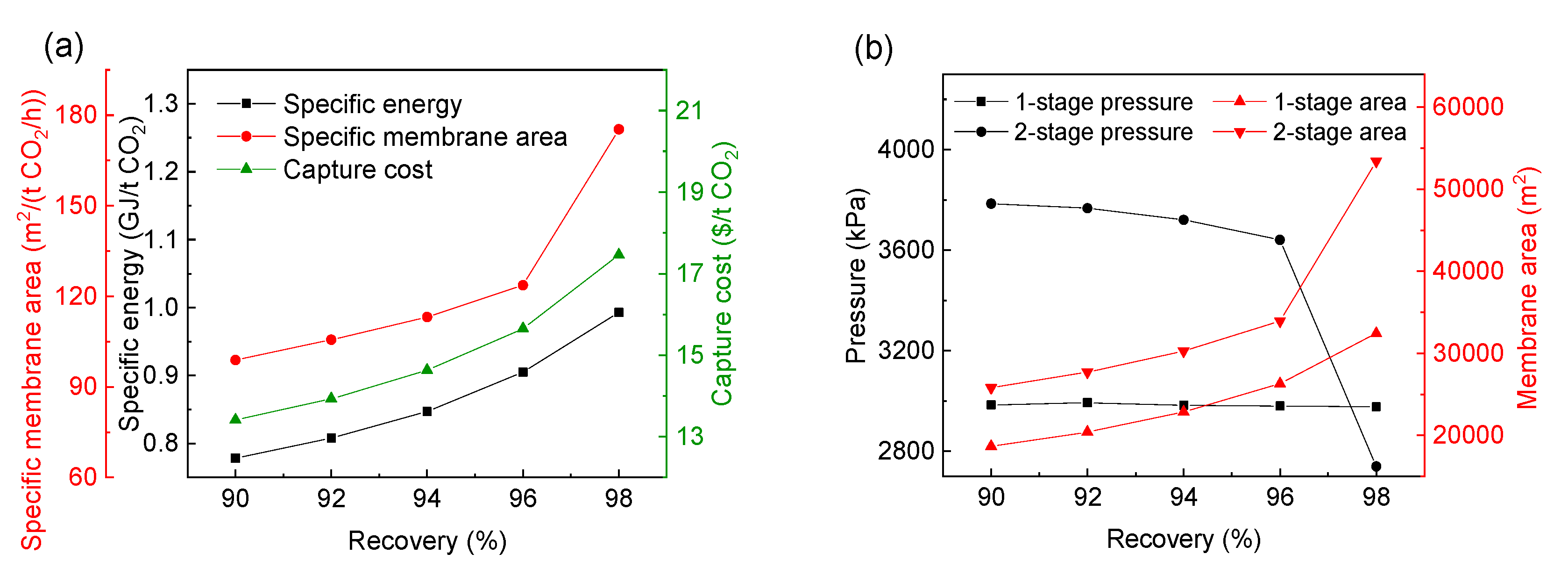
| CO2 Recovery (%) | 90 | 92 | 94 | 96 | 98 |
|---|---|---|---|---|---|
| Optimal selectivity for HM | 19.85 | 20.68 | 20.33 | 19.27 | 18.55 |
| Optimal permeance for HM (GPU) | 154.9 | 141.0 | 146.6 | 165.8 | 181.1 |
| 1-stage pressure (kPa) | 2983 | 2961 | 3001 | 2918 | 2994 |
| 2-stage pressure (kPa) | 3908 | 3919 | 4025 | 3964 | 3796 |
| 1-stage area (m2) | 18,290 | 20,180 | 22,200 | 26,460 | 31,690 |
| 2-stage area (m2) | 47,850 | 55,820 | 56,020 | 55,220 | 60,000 |
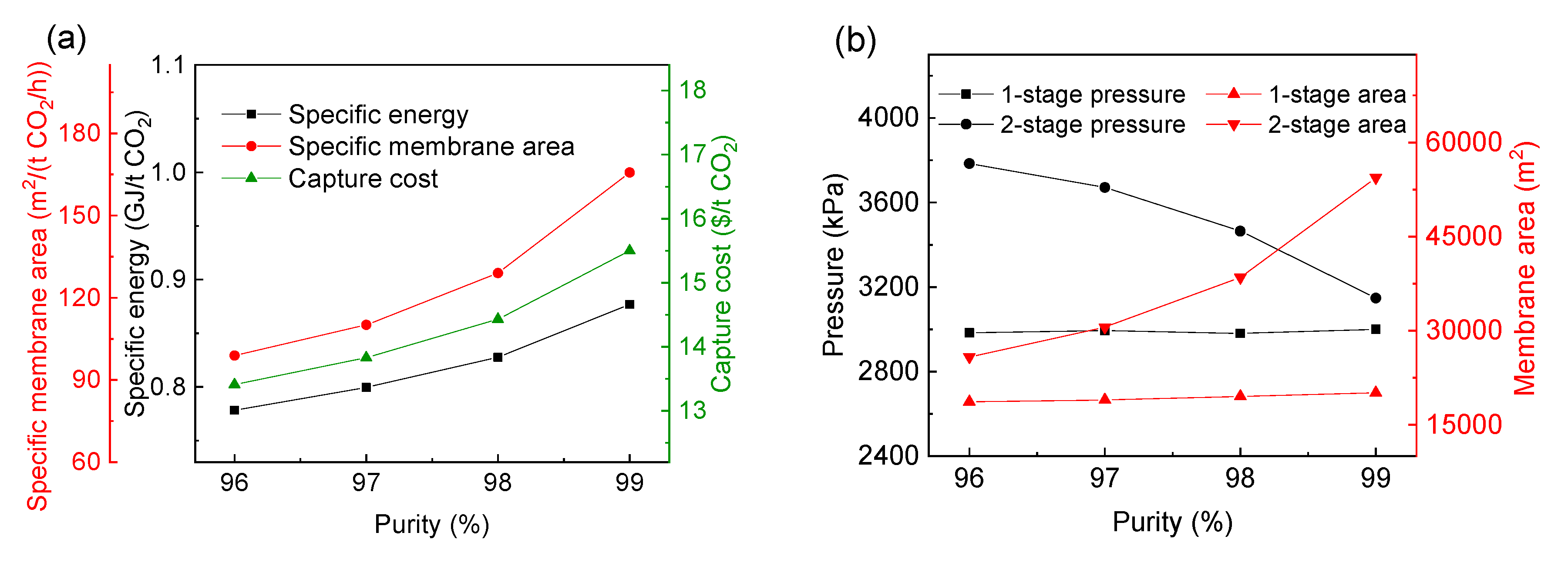
| CO2 Purity (%) | 96 | 97 | 98 | 99 |
|---|---|---|---|---|
| Optimal selectivity for HM | 19.85 | 19.84 | 20.03 | 19.74 |
| Optimal permeance for HM (GPU) | 154.9 | 155.2 | 151.7 | 156.9 |
| 1-stage pressure (kPa) | 2983 | 2982 | 2997 | 2890 |
| 2-stage pressure (kPa) | 3908 | 3975 | 3948 | 4050 |
| 1-stage area (m2) | 18,290 | 18,580 | 18,830 | 20,220 |
| 2-stage area (m2) | 47,850 | 53,500 | 64,790 | 76,510 |
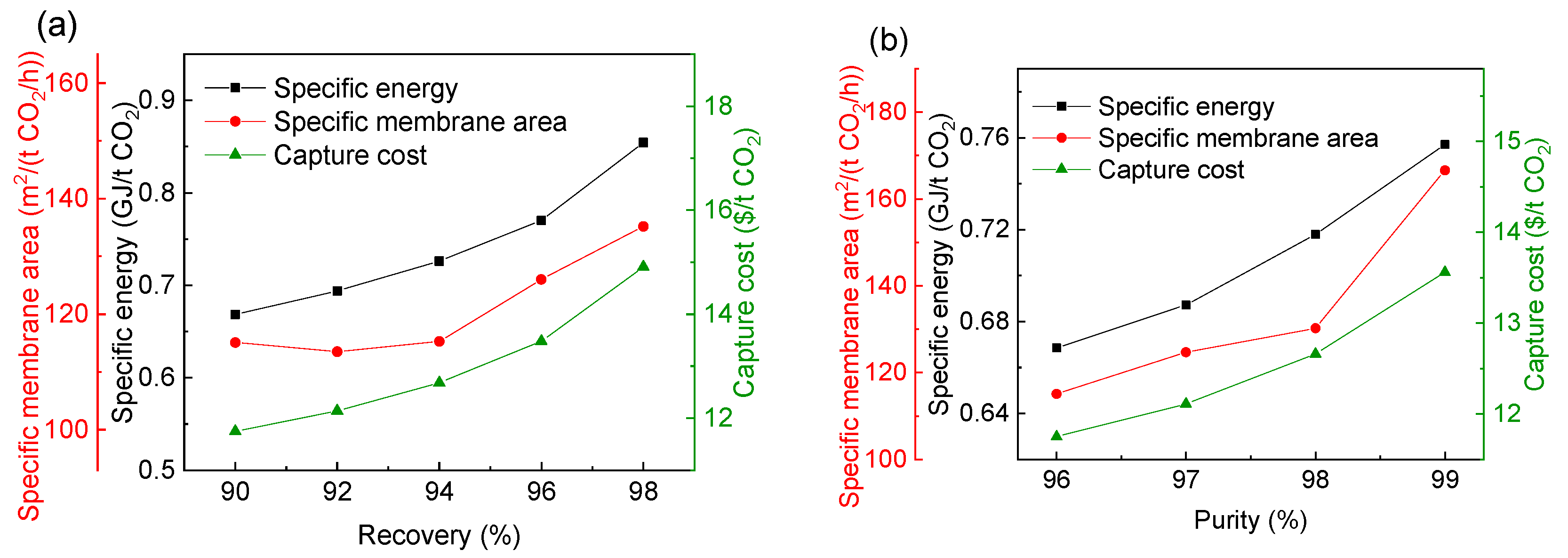
| CO2 Recovery (%) | 90 | 92 | 94 | 96 | 98 |
|---|---|---|---|---|---|
| Optimal selectivity for CM | 15 | 15 | 15 | 15 | 15 |
| Optimal permeance for CM (GPU) | 2643 | 2643 | 2643 | 2643 | 2643 |
| Optimal selectivity for HM | 20.70 | 20.68 | 19.77 | 19.43 | 18.35 |
| Optimal permeance for HM (GPU) | 140.6 | 140.9 | 156.3 | 162.7 | 185.5 |
| 1-stage pressure (kPa) | 2948 | 2995 | 2984 | 2968 | 2995 |
| 2-stage pressure (kPa) | 4001 | 4232 | 4054 | 3878 | 3636 |
| 1-stage area (m2) | 6923 | 7440 | 8347 | 9668 | 11,810 |
| 2-stage area (m2) | 44,840 | 44,750 | 45,810 | 50,800 | 54,390 |
| Specific energy(GJ/tCO2) | 0.6685 | 0.6940 | 0.7261 | 0.7702 | 0.8543 |
| Specific membrane area (m2/(t CO2/h)) | 115.1 | 113.5 | 115.3 | 126.0 | 135.2 |
| Capture cost ($/t CO2) | 11.75 | 12.14 | 12.68 | 13.48 | 14.91 |
| CO2 Recovery (%) | 96 | 97 | 98 | 99 |
|---|---|---|---|---|
| Optimal selectivity for CM | 15 | 15 | 15 | 15 |
| Optimal permeance for CM (GPU) | 2643 | 2643 | 2643 | 2643 |
| Optimal selectivity for HM | 20.70 | 20.43 | 19.31 | 20.18 |
| Optimal permeance for HM (GPU) | 140.6 | 144.9 | 165.0 | 149.2 |
| 1-stage pressure (kPa) | 2948 | 3000 | 2936 | 2938 |
| 2-stage pressure (kPa) | 4001 | 4080 | 4104 | 4363 |
| 1-stage area (m2) | 6923 | 6871 | 7209 | 7376 |
| 2-stage area (m2) | 44,840 | 49,210 | 51,330 | 67,550 |
| Specific energy(GJ/tCO2) | 0.6685 | 0.6872 | 0.7179 | 0.7570 |
| Specific membrane area (m2/(t CO2/h)) | 115.1 | 124.7 | 130.2 | 166.6 |
| Capture cost ($/t CO2) | 11.75 | 12.11 | 12.66 | 13.57 |
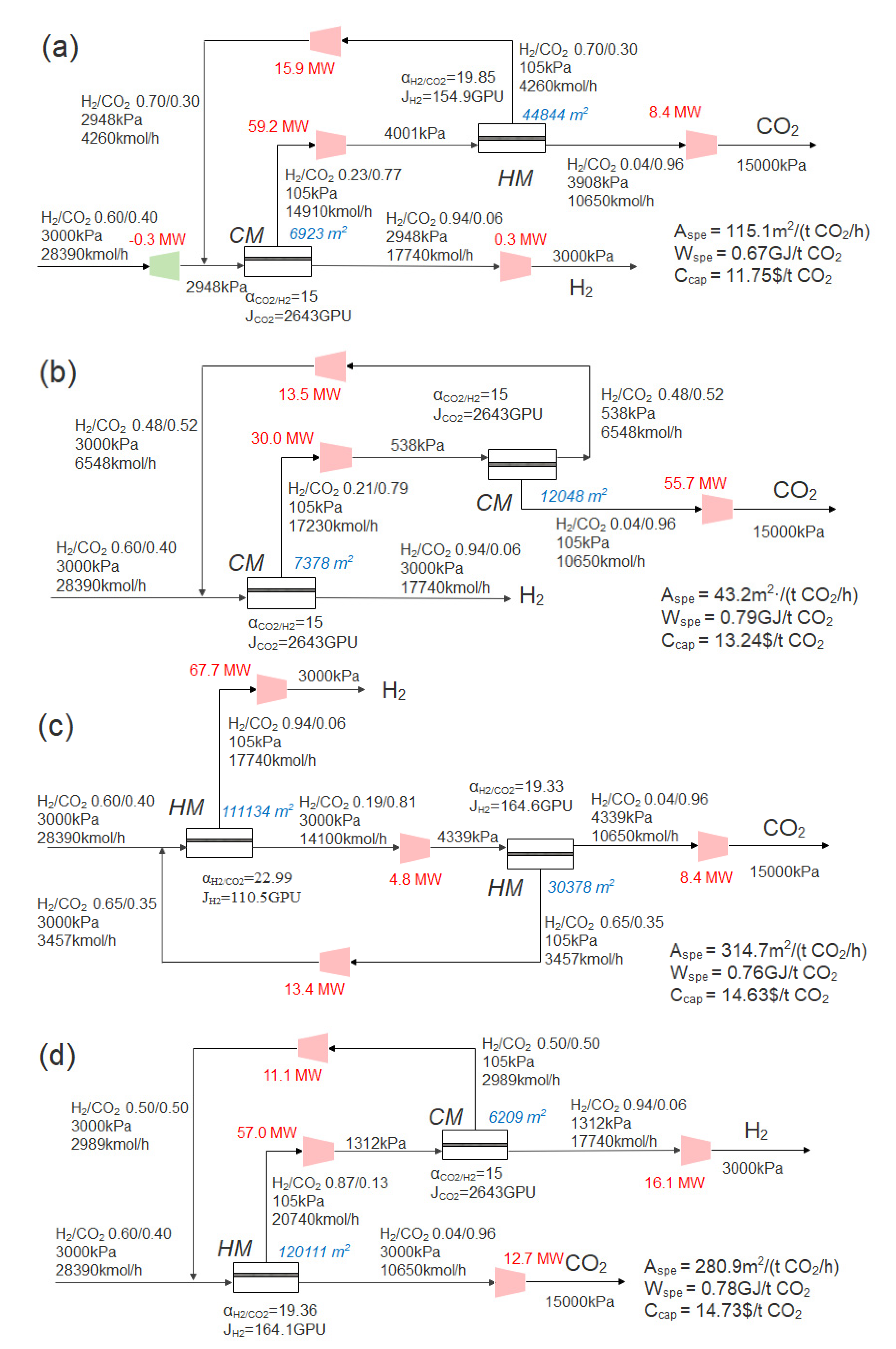
| System Parameter | Situation 1 | Situation 2 | Situation 3 | Situation 4 |
|---|---|---|---|---|
| 1-stage membrane permeance | αCO2/H2 = 11.76 JCO2 = 1000 GPU | αCO2/HF = 11.76 JCO2 = 1000 GPU | αCO2/H2 = 11.76 JCO2 = 1000 GPU | αCO2/H2 = 15.00 JCO2 = 2643 GPU |
| 2-stage membrane permeance | αH2/CO2 = 15 JH2 = 300 GPU | αH2/CO2 = 15 JH2 = 300 GPU | αH2/CO2 = 19.74 JH2 = 156.9 GPU | αH2/CO2 = 20.18 JH2 = 149.2 GPU |
| Number of compressor | 3 | 4 | 4 | 4 |
| Number of expander | 0 | 1 | 1 | 1 |
| Power consumption of compressor (MW) | 109.7 | 110.0 | 104.8 | 94.9 |
| Output power of expander (MW) | 0 | 0.2 | 0.6 | 0.3 |
| Net power consumption (MW) | 109.7 | 109.8 | 104.2 | 94.6 |
| Membrane area (m2) | 77,770 | 71,800 | 96,730 | 74,926 |
| Capture cost ($/t CO2) | 15.57 | 15.50 | 15.18 | 13.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, Z.; Cao, Y.; Zhang, X.; Zhang, N.; Xiao, W.; Bao, J.; He, G. Synchronous Design of Membrane Material and Process for Pre-Combustion CO2 Capture: A Superstructure Method Integrating Membrane Type Selection. Membranes 2023, 13, 318. https://doi.org/10.3390/membranes13030318
Ni Z, Cao Y, Zhang X, Zhang N, Xiao W, Bao J, He G. Synchronous Design of Membrane Material and Process for Pre-Combustion CO2 Capture: A Superstructure Method Integrating Membrane Type Selection. Membranes. 2023; 13(3):318. https://doi.org/10.3390/membranes13030318
Chicago/Turabian StyleNi, Zhiqiang, Yue Cao, Xiaopeng Zhang, Ning Zhang, Wu Xiao, Junjiang Bao, and Gaohong He. 2023. "Synchronous Design of Membrane Material and Process for Pre-Combustion CO2 Capture: A Superstructure Method Integrating Membrane Type Selection" Membranes 13, no. 3: 318. https://doi.org/10.3390/membranes13030318
APA StyleNi, Z., Cao, Y., Zhang, X., Zhang, N., Xiao, W., Bao, J., & He, G. (2023). Synchronous Design of Membrane Material and Process for Pre-Combustion CO2 Capture: A Superstructure Method Integrating Membrane Type Selection. Membranes, 13(3), 318. https://doi.org/10.3390/membranes13030318








