Evaluation of Physicochemical Properties of Sustained-Release Membranes Based on Analytic Hierarchy
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source
2.2. Data Processing and Statistical Analysis
2.3. Steps and Principles of Optimal AHP
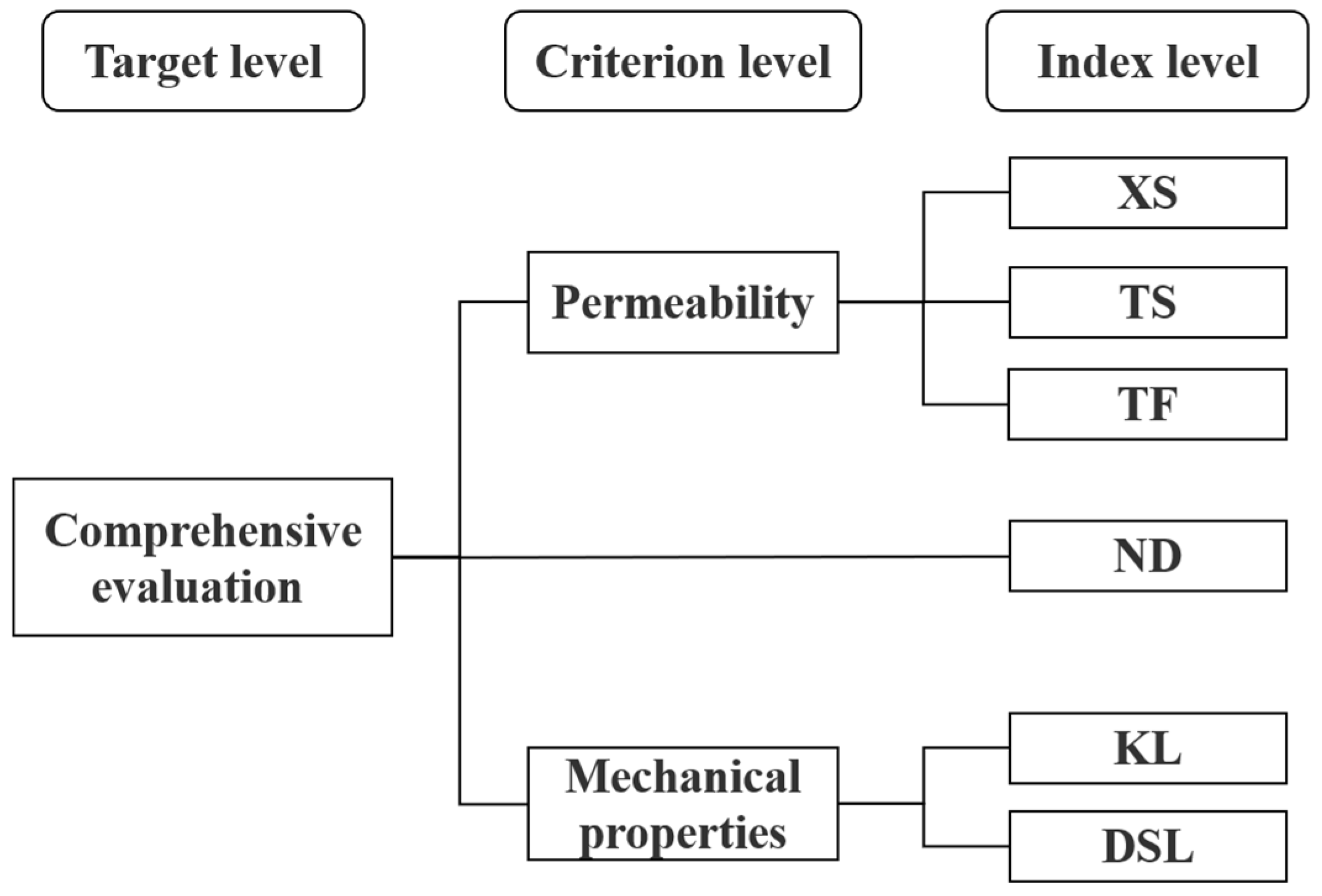
- Build a hierarchical model: A hierarchy diagram was constructed based on XS, TS, KL, DSL, TF, and ND.
- Construct the optimal judgment matrix: The degree of correlation among XS, TS, KL, DSL, TF, and ND was analyzed, and the paired comparison matrix was constructed by combining the evaluation criteria of the 1–9 scale method.
- Hierarchical ranking and consistency check: The consistency of the judgment matrix was checked by calculating the CR value.
- Calculate the comprehensive score of each index: The weight of each index was multiplied by the standardized value and then accumulated to obtain the comprehensive score of each treatment.
3. Results and Analysis
3.1. Statistical Analysis of Membrane Material Indices
3.2. Construction of the Model Hierarchy
3.3. Establishment of Judgment Matrix
3.4. Consistency Check of Judgment Matrix
3.5. Establishment of Index Weight
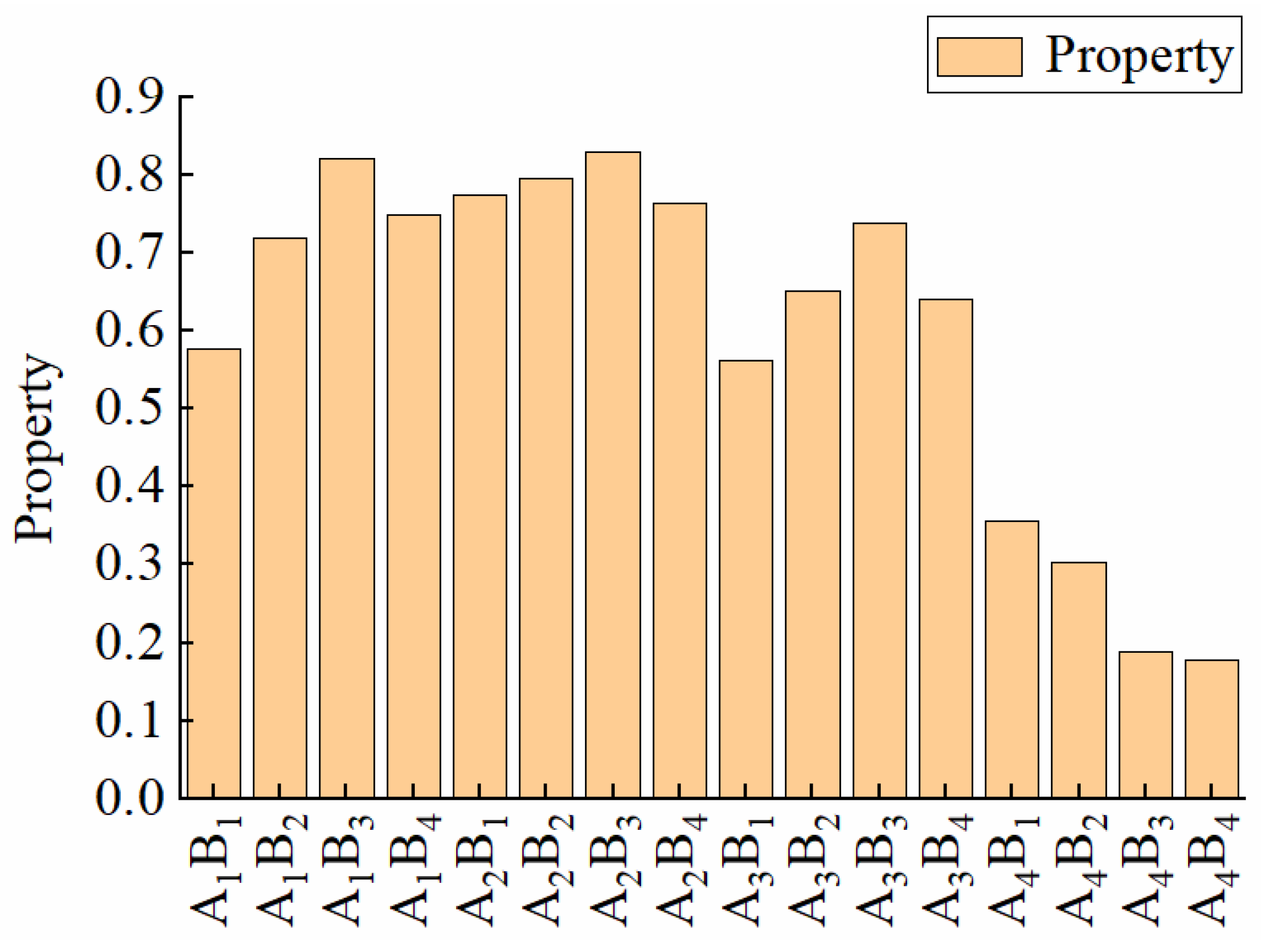
3.6. Comprehensive Evaluation of Membrane Materials
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ayoub, A.T. Fertilizers and the environment. Nutr. Cycl. Agroecosyst. 1999, 55, 117–121. [Google Scholar] [CrossRef]
- Tayoh, L.N.; Kiyo, L.M.I.; Nkemnyi, M.F. Chemical fertilizer application and farmers perception on food safety in Buea, Cameroon. Agric. Sci. Res. J. 2016, 6, 287–295. [Google Scholar]
- Savci, S. Investigation of effect of chemical fertilizers on environment. Apcbee Procedia 2012, 1, 287–292. [Google Scholar] [CrossRef]
- Fan, X.; Li, Y. Nitrogen release from slow-release fertilizers as affected by soil type and temperature. Soil Sci. Soc. Am. J. 2010, 74, 1635–1641. [Google Scholar] [CrossRef]
- Lateef, A.; Nazir, R.; Jamil, N.; Alam, S.; Shah, R.; Khan, M.N.; Saleem, M. Synthesis and characterization of zeolite based nano–composite: An environment friendly slow release fertilizer. Microporous Mesoporous Mater. 2016, 232, 174–183. [Google Scholar] [CrossRef]
- Ye, H.-M.; Li, H.-F.; Wang, C.-S.; Yang, J.; Huang, G.; Meng, X.; Zhou, Q. Degradable polyester/urea inclusion complex applied as a facile and environment-friendly strategy for slow-release fertilizer: Performance and mechanism. Chem. Eng. J. 2020, 381, 122704. [Google Scholar] [CrossRef]
- Lin, X.; Guo, L.; Shaghaleh, H.; Hamoud, Y.A.; Xu, X.; Liu, H. A TEMPO-oxidized cellulose nanofibers/MOFs hydrogel with temperature and pH responsiveness for fertilizers slow-release. Int. J. Biol. Macromol. 2021, 191, 483–491. [Google Scholar] [CrossRef]
- Ni, B.; Lu, S.; Liu, M. Novel multinutrient fertilizer and its effect on slow release, water holding, and soil amending. Ind. Eng. Chem. Res. 2012, 51, 12993–13000. [Google Scholar] [CrossRef]
- Azeem, B.; KuShaari, K.; Man, Z.B.; Basit, A.; Thanh, T.H. Review on materials & methods to produce controlled release coated urea fertilizer. J. Control. Release 2014, 181, 11–21. [Google Scholar]
- Nishida, A.; Yamada, M.; Kanazawa, T.; Takashima, Y.; Ouchi, K.; Okada, H. Use of silk protein, sericin, as a sustained-release material in the form of a gel, sponge and film. Chem. Pharm. Bull. 2010, 58, 1480–1486. [Google Scholar] [CrossRef]
- Maiti, J.; Kakati, N.; Lee, S.H.; Jee, S.H.; Yoon, Y.S. PVA nano composite membrane for DMFC application. Solid State Ion. 2011, 201, 21–26. [Google Scholar] [CrossRef]
- Subianto, S.; Pica, M.; Casciola, M.; Cojocaru, P.; Merlo, L.; Hards, G.; Jones, D.J. Physical and chemical modification routes leading to improved mechanical properties of perfluorosulfonic acid membranes for PEM fuel cells. J. Power Sources 2013, 233, 216–230. [Google Scholar] [CrossRef]
- Tang, Y.; Karlsson, A.M.; Santare, M.H.; Gilbert, M.; Cleghorn, S.; Johnson, W.B. An experimental investigation of humidity and temperature effects on the mechanical properties of perfluorosulfonic acid membrane. Mater. Sci. Eng. A 2006, 425, 297–304. [Google Scholar] [CrossRef]
- Li, K.; Hou, D.; Fu, C.; Wang, K.; Wang, J. Fabrication of PVDF nanofibrous hydrophobic composite membranes reinforced with fabric substrates via electrospinning for membrane distillation desalination. J. Environ. Sci. 2019, 75, 277–288. [Google Scholar] [CrossRef]
- Sari, M.; Tamrin; Kaban, J.; Alfian, Z. The effect of glutaraldehyde on the properties of Chi-Pec-PVA membrane. AIP Conf. Proc. 2020, 2267, 020049. [Google Scholar]
- Shaari, N.; Kamarudin, S.; Basri, S.; Shyuan, L.; Masdar, M.; Nordin, D. Enhanced mechanical flexibility and performance of sodium alginate polymer electrolyte bio-membrane for application in direct methanol fuel cell. J. Appl. Polym. Sci. 2018, 135, 46666. [Google Scholar] [CrossRef]
- Cu, L.N.; Ao, X.Q.; Chen, Q.L.; Guo, Y.; Cao, Y. Properties and characterization of coating materials for slow-release fertilizers by adding distillers’grains to modified poly (vinyl alcohol). Chem. Ind. Eng. Prog. 2020, 39, 627–663. (In Chinese) [Google Scholar]
- Gowriboy, N.; Kalaivizhi, R.; Kaleekkal, N.J.; Ganesh, M.R.; Aswathy, K.A. Fabrication and characterization of polymer nanocomposites membrane (Cu-MOF@CA/PES) for water treatment. J. Environ. Chem. Eng. 2022, 10, 108668. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhang, Z.Y.; Li, C.P.; Hu, Z.; Liang, Y.L.; Yang, Z.M.; Huang, D.J. Preparation and characterization of amphiphilic chitosan/iodine composite film as antimicrobial material. Int. J. Biol. Macromol. 2022, 222, 2426–2438. [Google Scholar] [CrossRef]
- Sun, H.; Lei, T.; Liu, J.; Guo, X.; Lv, J. Physicochemical Properties of Water-Based Copolymer and Zeolite Composite Sustained-Release Membrane Materials. Materials 2022, 15, 8553. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Fei, S.; Hassan, M.A.; Ma, Y.; Shu, M.; Cheng, Q.; Li, Z.; Xiao, Y. Entropy weight ensemble framework for yield prediction of winter wheat under different water stress treatments using unmanned aerial vehicle-based multispectral and thermal data. Front. Plant Sci. 2021, 12, 730181. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, Y.; Zhou, X.; Wei, Z. Selection of agricultural machinery based on improved CRITIC-entropy weight and GRA-TOPSIS method. Processes 2022, 10, 266. [Google Scholar] [CrossRef]
- Shen, Z.; Zhao, Q.; Fang, Q. Analysis of green traffic development in Zhoushan based on entropy weight TOPSIS. Sustainability 2021, 13, 8109. [Google Scholar] [CrossRef]
- Dong, D.L.; Li, X.; Lin, G.; Bian, J.L.; Cao, C.L.; Wu, H. Identification model of the independence right-fuzzy variable theory of water inrush source. Coal Geol. Explor. 2019, 47, 48–53. (In Chinese) [Google Scholar]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Kitworawut, P.; Rungreunganun, V. An application of analytical hierarchy process (AHP) for affect factor to corn price in Thailand market. J. Adv. Agric. Technol. 2017, 4, 280–284. [Google Scholar] [CrossRef]
- Rozman, Č.; Hühner, M.; Kolenko, M.; Tojnko, S.; Unuk, T.; Pažek, K. Apple variety assessment with analytical hierarchy process. Erwerbs Obstbau 2015, 57, 97–104. [Google Scholar] [CrossRef]
- Bureika, G.; Liudvinavičius, L.; Vaičiūnas, G.; Bekintis, G. Applying analytic hierarchy process to assess traffic safety risk of railway infrastructure. Eksploat. I Niezawodn. 2013, 15, 376–383. [Google Scholar]
- Farooq, D.; Moslem, S. Estimating Driver Behavior Measures Related to Traffic Safety by Investigating 2-Dimensional Uncertain Linguistic Data—A Pythagorean Fuzzy Analytic Hierarchy Process Approach. Sustainability 2022, 14, 1881. [Google Scholar] [CrossRef]
- Palcic, I.; Lalic, B. Analytical Hierarchy Process as a tool for selecting and evaluating projects. Int. J. Simul. Model. IJSIMM 2009, 8, 16–26. [Google Scholar] [CrossRef]
- Subramanian, N.; Ramanathan, R. A review of applications of Analytic Hierarchy Process in operations management. Int. J. Prod. Econ. 2012, 138, 215–241. [Google Scholar] [CrossRef]
- Singh, R.P.; Nachtnebel, H.P. Analytical hierarchy process (AHP) application for reinforcement of hydropower strategy in Nepal. Renew. Sustain. Energy Rev. 2016, 55, 43–58. [Google Scholar] [CrossRef]
- Zuo, Y.; Wang, Z. Subjective product evaluation system based on Kansei Engineering and analytic hierarchy process. Symmetry 2020, 12, 1340. [Google Scholar] [CrossRef]
- Cinelli, P.; Chiellini, E.; Gordon, S.H.; Imam, S.H. Characteristics and degradation of hybrid composite films prepared from PVA, starch and lignocellulosics. Macromol. Symp. 2003, 197, 143–156. [Google Scholar] [CrossRef]
- El Assimi, T.; Blažic, R.; Vidović, E.; Raihane, M.; El Meziane, A.; Baouab, M.H.V.; Lahcini, M. Polylactide/cellulose acetate biocomposites as potential coating membranes for controlled and slow nutrients release from water-soluble fertilizers. Prog. Org. Coat. 2021, 156, 106255. [Google Scholar] [CrossRef]
- Kim, D.H.; Na, S.K.; Park, J.S.; Yoon, K.J.; Ihm, D.W. Studies on the preparation of hydrolyzed starch-g-PAN (HSPAN)/PVA blend films––Effect of the reaction with epichlorohydrin. Eur. Polym. J. 2002, 38, 1199–1204. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Y.; Liu, L.; Liu, L.; Chen, M.; Zhang, C.; Lu, Q. Green coatings from renewable modified bentonite and vegetable oil based polyurethane for slow release fertilizers. Polym. Compos. 2018, 39, 4355–4363. [Google Scholar] [CrossRef]
- Li, M.L.; Ding, X.B.; Han, J.; Xu, G.P.; Yu, B. Study on the Thermal Stability and Surface Morphology of PVC Membrane Structure Materials. J. Zhejiang Sci-Tech Univ. Nat. Sci. Ed. 2011, 28, 700–704. [Google Scholar]
- Do Nascimento, D.M.; Nunes, Y.L.; Feitosa, J.P.; Dufresne, A.; Rosa, M.d.F. Cellulose nanocrystals-reinforced core-shell hydrogels for sustained release of fertilizer and water retention. Int. J. Biol. Macromol. 2022, 216, 24–31. [Google Scholar] [CrossRef]
- Niu, X.; Ma, Q.; Li, S.; Wang, W.; Ma, Y.; Zhao, H.; Wang, J. Preparation and characterization of biodegradable composited films based on potato starch/glycerol/gelatin. J. Food Qual. 2021, 2021, 6633711. [Google Scholar] [CrossRef]
- Tang, S.; Zou, P.; Xiong, H.; Tang, H. Effect of nano-SiO2 on the performance of starch/polyvinyl alcohol blend films. Carbohydr. Polym. 2008, 72, 521–526. [Google Scholar] [CrossRef]
- Kufel, A.; Kuciel, S. Hybrid composites based on polypropylene with basalt/hazelnut shell fillers: The influence of temperature, thermal aging, and water absorption on mechanical properties. Polymers 2019, 12, 18. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liu, X.; Yang, S. A Note on the 1–9 Scale and Index Scale in AHP. In Cutting-Edge Research Topics on Multiple Criteria Decision Making; Springer: Berlin/Heidelberg, Germany, 2009; pp. 630–634. [Google Scholar]
- An, T.; Cheng, H.; Qin, Y.; Su, W.; Deng, H.; Wu, J.; Guo, X. The dual mechanisms of composite biochar and biofilm towards sustainable nutrient release control of phosphate fertilizer: Effect on phosphorus utilization and crop growth. J. Clean. Prod. 2021, 311, 127329. [Google Scholar] [CrossRef]
- Gu, H.; Zhang, Y.; Li, X.; Li, W.; Huang, S. Lignin improves release behavior of slow-release fertilizers with high content of urea. J. Appl. Polym. Sci. 2019, 136, 48238. [Google Scholar] [CrossRef]
- You, S.Y.; Dai, R.Y.; Li, L.; Zhng, P.; Jin, Z.Y.; Le, J.F. Study on Preparation and Properties of Coating Materials for Slow-release Organosilicon Fertilizer. Acta Agric. Jiangxi 2018, 30, 66–70. (In Chinese) [Google Scholar]
- Wang, Z.; Kang, X.J.; Wang, C.P.; Xue, Z.H.; Sun, H.W.; Wang, J.G. Preparation and Sustained Release Properties of a New Type of Coating Reinforced Slow Release Oxidation Materia. Acta Sci. Nat. Univ. Nankaiensis 2021, 54, 84–91. (In Chinese) [Google Scholar]
- Liu, T.; Deng, Y.; Chan, F. Evidential supplier selection based on DEMATEL and game theory. Int. J. Fuzzy Syst. 2018, 20, 1321–1333. [Google Scholar] [CrossRef]
- Chen, S.; Yang, M.; Ba, C.; Yu, S.; Jiang, Y.; Zou, H.; Zhang, Y. Preparation and characterization of slow-release fertilizer encapsulated by biochar-based waterborne copolymers. Sci. Total Environ. 2018, 615, 431–437. [Google Scholar] [CrossRef]
- Pan, X.J.; Shen, L.; Ruan, J.; Dai, N.; Xu, C.Q. Evaluation and screening of water-soluble pellicular materials for pellicles. Chin. J. Hosp. Pharm. 2009, 29, 973–976. (In Chinese) [Google Scholar]
- Sun, H.; Gao, S.; Liu, J.; Liu, W. Research on comprehensive benefits and reasonable selection of marine resources development types. Open Geosci. 2022, 14, 141–150. [Google Scholar] [CrossRef]


| Index | XS | TS | ND | KL | DSL | TF |
|---|---|---|---|---|---|---|
| XS | 1 | 0.886 ** | −0.770 ** | −0.865 ** | −0.611 * | 0.913 ** |
| TS | 0.886 ** | 1 | −0.865 ** | −0.755 ** | −0.713 ** | 0.839 ** |
| ND | −0.770 ** | −0.865 ** | 1 | 0.571 * | 0.593 * | −0.783 ** |
| KL | −0.865 ** | −0.755 ** | 0.571 * | 1 | 0.720 ** | −0.757 ** |
| DSL | −0.611 ** | −0.713 ** | 0.593 * | 0.720 ** | 1 | −0.594 * |
| TF | 0.913 ** | 0.839 ** | −0.783 ** | −0.757 ** | −0.594 * | 1 |
| Scale | Implication |
|---|---|
| 1 | The two factors are of equal importance |
| 3 | The former is slightly more important than the latter |
| 5 | The former is more important than the latter |
| 7 | The former is strongly important compared to the latter |
| 9 | The former is extremely important compared to the latter |
| 2, 4, 6, 8 | The judgment is of intermediate value |
| Reciprocal | If the ratio of the importance of factor i to factor j is aij, then the ratio of factor j to the importance of factor i is aij = 1/aij |
| P1 | XS | TS | TF |
|---|---|---|---|
| XS | 1 | 3 | 1/3 |
| TS | 1/3 | 1 | 1/4 |
| TF | 3 | 4 | 1 |
| P2 | Mechanical Properties | Permeability | ND |
|---|---|---|---|
| Mechanical properties | 1 | 1/4 | 2 |
| Permeability | 4 | 1 | 4 |
| ND | 1/2 | 1/4 | 1 |
| P3 | KL | DSL |
|---|---|---|
| KL | 1 | 3 |
| DSL | 1/3 | 1 |
| Evaluation Criterion Level | Weight | Evaluation Index Level | Weight | Total Weight |
|---|---|---|---|---|
| Permeability | 0.661 | TF | 0.614 | 0.406 |
| TS | 0.117 | 0.078 | ||
| XS | 0.268 | 0.177 | ||
| Mechanical properties | 0.208 | KL | 0.750 | 0.156 |
| DSL | 0.250 | 0.052 | ||
| ND | 0.131 | ND | 0.131 | 0.131 |
| Index | KL | DSL | TF | TS | ND | XS |
|---|---|---|---|---|---|---|
| Entropy value | 0.912 | 0.892 | 0.946 | 0.931 | 0.929 | 0.936 |
| Weight | 0.193 | 0.238 | 0.119 | 0.153 | 0.156 | 0.141 |
| Index | KL | DSL | TF | TS | ND | XS |
|---|---|---|---|---|---|---|
| Multiple correlation coefficient | 0.925 | 0.827 | 0.924 | 0.945 | 0.891 | 0.969 |
| Weight | 0.1642 | 0.1836 | 0.1644 | 0.1608 | 0.1705 | 0.1566 |
| Evaluation Method | Optimal Analytic Hierarchy Process | Entropy Weight Method | Independence Weight Coefficient Method |
|---|---|---|---|
| Optimal analytic hierarchy process | 1 | ||
| Entropy weight method | 0.952 ** | 1 | |
| Independence weight coefficient method | 0.973 ** | 0.995 ** | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Lei, T.; Guo, X.; Liu, J.; Lv, J. Evaluation of Physicochemical Properties of Sustained-Release Membranes Based on Analytic Hierarchy. Membranes 2023, 13, 313. https://doi.org/10.3390/membranes13030313
Sun H, Lei T, Guo X, Liu J, Lv J. Evaluation of Physicochemical Properties of Sustained-Release Membranes Based on Analytic Hierarchy. Membranes. 2023; 13(3):313. https://doi.org/10.3390/membranes13030313
Chicago/Turabian StyleSun, Haonan, Tao Lei, Xianghong Guo, Jianxin Liu, and Jiangjian Lv. 2023. "Evaluation of Physicochemical Properties of Sustained-Release Membranes Based on Analytic Hierarchy" Membranes 13, no. 3: 313. https://doi.org/10.3390/membranes13030313
APA StyleSun, H., Lei, T., Guo, X., Liu, J., & Lv, J. (2023). Evaluation of Physicochemical Properties of Sustained-Release Membranes Based on Analytic Hierarchy. Membranes, 13(3), 313. https://doi.org/10.3390/membranes13030313






