Evaluation of a Novel Cuboid Hollow Fiber Hemodialyzer Design Using Computational Fluid Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Design Overview
2.2. Model Development
2.2.1. Assumptions
- (1)
- (2)
- The lumen of the membranes is always filled with liquid.
- (3)
- There is no clotting in the bloodstream.
- (4)
- Fully developed laminar flow is assumed within the lumen [49].
- (5)
- Since this work focuses on fluid flow characteristics in the headers and within the membrane lumen, the transport of species through the membrane wall is not considered. The hollow fiber is considered to be a cylindrical tube with impermeable wall. Blood is transported along the length of the hollow fiber without any change in composition [50].
- (6)
- No slip conditions exist at the wall [51].
- (7)
- Although the neighboring fibers in a real hemodialyzer are randomly spaced due to the nature of the manufacturing process, the fibers in the simulated devices are considered to be equally spaced according to a specific pattern.
2.2.2. Numerical Method
2.2.3. Limitations
3. Results and Discussion
3.1. Flow Distribution
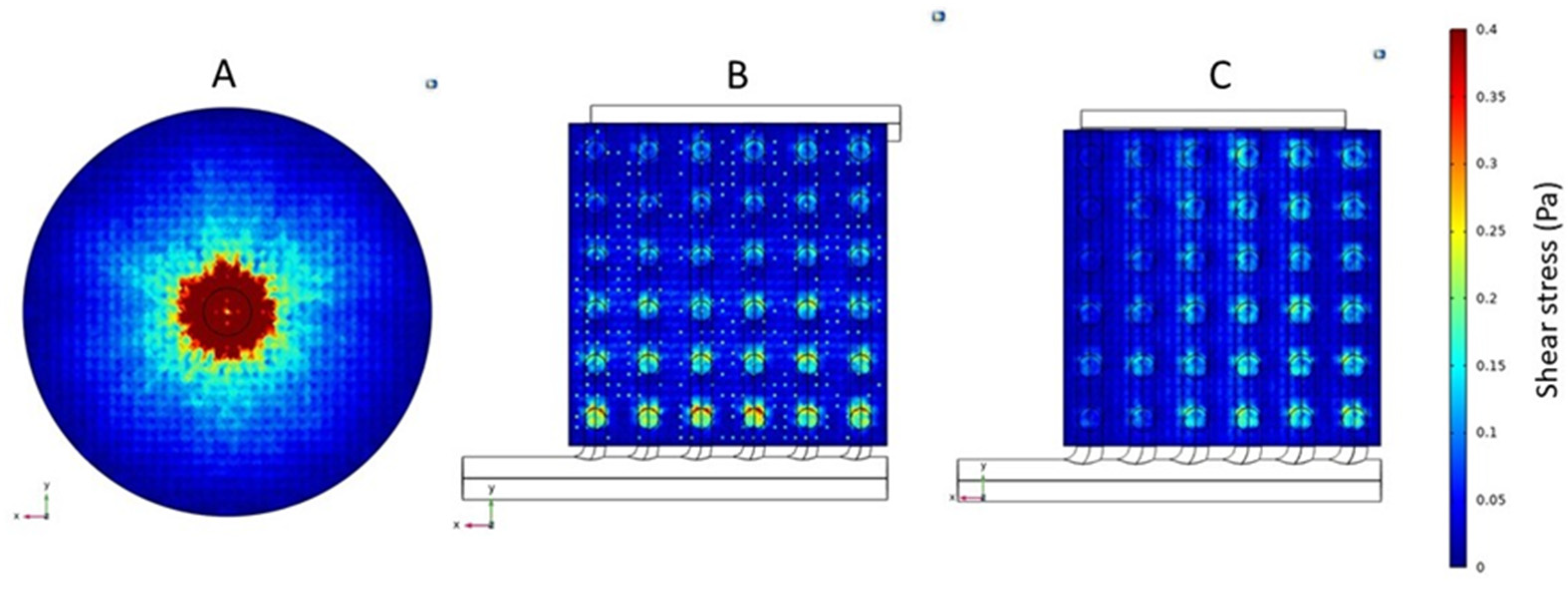
3.2. Shear Rate and Stress
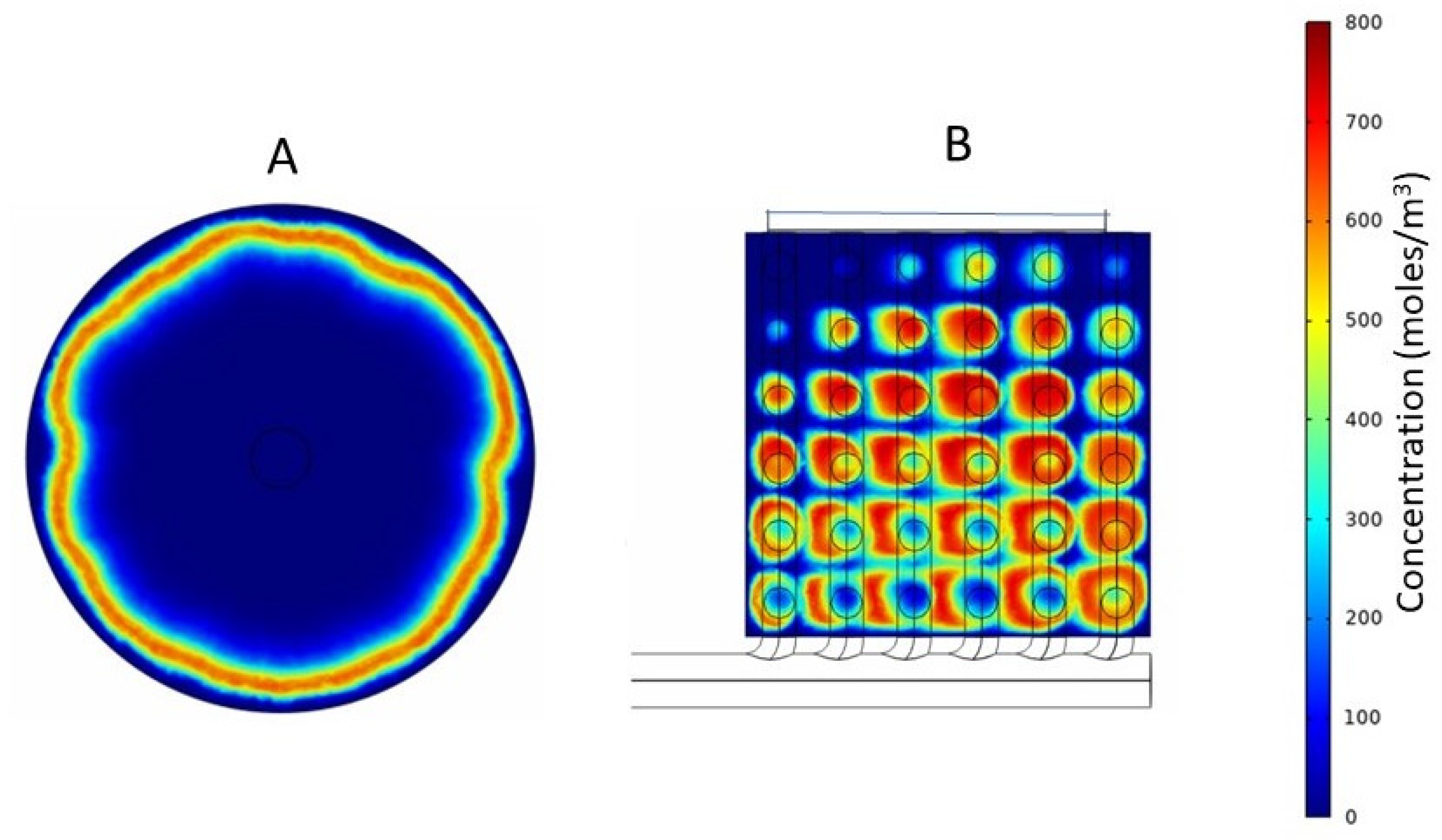
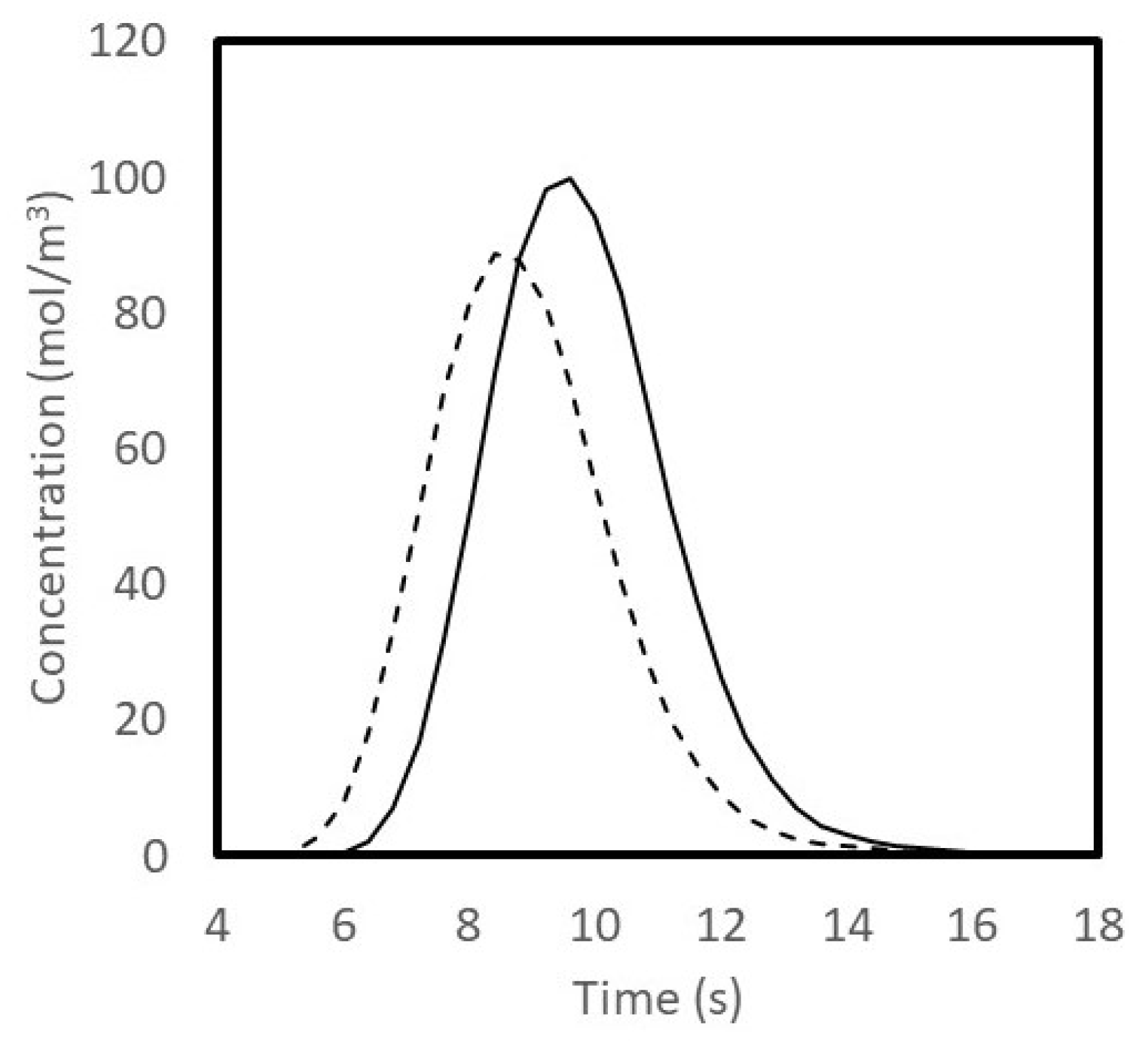
3.3. Tracer Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Parameter |
| ρ | Fluid density (kg/m3) |
| t | Time (s) |
| u | Fluid velocity field (m/s) |
| P | Pressure (Pa) |
| μ | Fluid dynamic viscosity (Pa s) |
| I | Identity matrix (-) |
| F | External forces (Pa) |
References
- Benjamin, O.; Lappin, S.L. End-Stage Renal Disease—Statpearls—NCBI Bookshelf. Available online: https://www.ncbi.nlm.nih.gov/books/NBK499861/ (accessed on 3 August 2022).
- Gentry, S.E.; Montgomery, R.A.; Segev, D.L. Kidney paired donation: Fundamentals, Limitations, and expansions. Am. J. Kidney Dis. 2011, 57, 144–151. [Google Scholar] [CrossRef] [PubMed]
- Aslam, S. Understanding Dialyzer Types, Fresenius Medical Care. 2019. Available online: https://fmcna.com/insights/articles/Understanding-Dialyzer-Types/#:~:text=A%20hollow%20fiber%20dialyzer%20bundle%20comprises%207%E2%80%9317%20x,microns%2C%20yielding%201.0%E2%80%932.5%20m%202%20of%20surface%20area/ (accessed on 3 August 2022).
- Sunohara, T.; Anbo, H.; Masuda, T. Dialyzer and Method for Manufacturing the Same. US Patent 7,524,417 B2, 28 April 2009. [Google Scholar]
- Park, J.K.; Chang, H.N. Flow distribution in the fiber lumen side of a hollow-fiber module. AIChE J. 1986, 32, 1937–1947. [Google Scholar] [CrossRef]
- Twardowski, Z.J. History of hemodialyzers’ designs. Hemodial. Int. 2008, 12, 173–210. [Google Scholar] [CrossRef] [PubMed]
- Mollahosseini, A.; Abdelrasoul, A.; Shoker, A. A critical review of recent advances in hemodialysis membranes hemocompatibility and guidelines for future development. Mater. Chem. Phys. 2020, 248, 122911. [Google Scholar] [CrossRef]
- Eduok, U.; Abdelrasoul, A.; Shoker, A.; Doan, H. Recent developments, current challenges and future perspectives on cellulosic hemodialysis membranes for highly efficient clearance of uremic toxins. Mater. Today Commun. 2021, 27, 102183. [Google Scholar] [CrossRef]
- Gao, A.; Liu, F.; Xue, L. Preparation and evaluation of heparin-immobilized poly (lactic acid) (PLA) membrane for Hemodialysis. J. Membr. Sci. 2014, 452, 390–399. [Google Scholar] [CrossRef]
- Wang, H.; Yang, L.; Zhao, X.; Yu, T.; Du, Q. Improvement of hydrophilicity and blood compatibility on polyethersulfone membrane by blending sulfonated polyethersulfone. Chin. J. Chem. Eng. 2009, 17, 324–329. [Google Scholar] [CrossRef]
- Barzin, J.; Madaeni, S.S.; Mirzadeh, H.; Mehrabzadeh, M. Effect of polyvinylpyrrolidone on morphology and performance of hemodialysis membranes prepared from polyether sulfone. J. Appl. Polym. Sci. 2004, 92, 3804–3813. [Google Scholar] [CrossRef]
- Idris, A.; Yet, L.K. The effect of different molecular weight peg additives on cellulose acetate asymmetric dialysis membrane performance. J. Membr. Sci. 2006, 280, 920–927. [Google Scholar] [CrossRef]
- Lemanski, J.; Lipscomb, G.G. Effect of shell-side flows on hollow-fiber membrane device performance. AIChE J. 1995, 41, 2322–2326. [Google Scholar] [CrossRef]
- Mat, N.C.; Lou, Y.; Lipscomb, G.G. Hollow fiber membrane modules. Curr. Opin. Chem. Eng. 2014, 4, 18–24. [Google Scholar] [CrossRef]
- Donato, D.; Storr, M.; Krause, B. Design optimization of hollow fiber dialyzers to enhance internal filtration based on a mathematical model. J. Membr. Sci. 2020, 598, 117690. [Google Scholar] [CrossRef]
- Donato, D.; Boschetti-de-Fierro, A.; Zweigart, C.; Kolb, M.; Eloot, S.; Storr, M.; Krause, B.; Leypoldt, K.; Segers, P. Optimization of dialyzer design to maximize solute removal with a two-dimensional transport model. J. Membr. Sci. 2017, 541, 519–528. [Google Scholar] [CrossRef]
- Günther, J.; Schmitz, P.; Albasi, C.; Lafforgue, C. A numerical approach to study the impact of packing density on fluid flow distribution in hollow fiber module. J. Membr. Sci. 2010, 348, 277–286. [Google Scholar] [CrossRef]
- Leverett, L.B.; Hellums, J.D.; Alfrey, C.P.; Lynch, E.C. Red blood cell damage by shear stress. Biophys. J. 1972, 12, 257–273. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, F.; Josipovic, I.; Boone, M.; Van Biesen, W.; Eloot, S. Impact of intradialytic fiber clotting on dialyzer extraction and solute removal: A randomized cross-over study. Sci. Rep. 2022, 12, 5717. [Google Scholar] [CrossRef]
- Li, X.; Mo, Y.; Li, J.; Guo, W.; Ngo, H.H. In-situ monitoring techniques for membrane fouling and local filtration characteristics in hollow fiber membrane processes: A critical review. J. Membr. Sci. 2017, 528, 187–200. [Google Scholar] [CrossRef]
- Vander Velde, C.; Leonard, E.F. Theoretical assessment of the effect of flow maldistributions on the mass transfer efficiency of artificial organs. Med. Biol. Eng. Comput. 1985, 23, 224–229. [Google Scholar] [CrossRef]
- Ronco, C.; Ghezzi, P.M.; Metry, G.; Spittle, M.; Brendolan, A.; Rodighiero, M.P.; Milan, M.; Zanella, M.; La Greca, G.; Levin, N.W. Effects of hematocrit and blood flow distribution on solute clearance in hollow-fiber Hemodialyzers. Nephron 2001, 89, 243–250. [Google Scholar] [CrossRef]
- Davenport, A. How can dialyzer designs improve solute clearances for hemodialysis patients? Hemodial. Int. 2014, 18, 43–47. [Google Scholar] [CrossRef]
- Cooney, D.O.; Kim, S.-S.; James Davis, E. Analyses of mass transfer in hemodialyzers for laminar blood flow and homogeneous dialysate. Chem. Eng. Sci. 1974, 29, 1731–1738. [Google Scholar] [CrossRef]
- Ronco, C.; Brendolan, A.; Crepaldi, C.; Rodighiero, M.; Scabardi, M. Blood and dialysate flow distributions in hollow-fiber hemodialyzers analyzed by computerized helical scanning technique. J. Am. Soc. Nephrol. 2002, 13, 53–61. [Google Scholar] [CrossRef]
- Mineshima, M. Optimal design of Dialyzers. Contrib. Nephrol. 2016, 204–209. [Google Scholar]
- Haroon, S.; Davenport, A. Choosing a dialyzer: What clinicians need to know. Hemodial. Int. 2018, 22, 65–74. [Google Scholar] [CrossRef]
- Ronco, C.; Clark, W. Factors affecting hemodialysis and peritoneal dialysis efficiency. Semin. Dial. 2008, 14, 257–262. [Google Scholar] [CrossRef]
- Heese, F.; Robson, P.; Hall, L.D. Quantification of fluid flow through a clinical blood filter and kidney dialyzer using magnetic resonance imaging. IEEE Sens. J. 2005, 5, 273–276. [Google Scholar] [CrossRef]
- Ronco, C.; Clark, W.R. Haemodialysis membranes. Nat. Rev. Nephrol. 2018, 14, 394–410. [Google Scholar] [CrossRef]
- Down, L.A.; Papavassiliou, D.V.; O’Rear, E.A. Significance of extensional stresses to red blood cell lysis in a shearing flow. Ann. Biomed. Eng. 2011, 39, 1632–1642. [Google Scholar] [CrossRef]
- Polaschegg, H.-D. Red blood cell damage from extracorporeal circulation in Hemodialysis. Semin. Dial. 2009, 22, 524–531. [Google Scholar] [CrossRef]
- Sargent, A. Dialysis in the 1960s and the First Hollow Fiber Dialyzer. Int. J. Artif. Organs 2007, 30, 953–963. [Google Scholar] [CrossRef]
- Mareels, G.; De Wachter, D.S.; Verdonck, P.R. Computational Fluid Dynamics-analysis of the Niagara Hemodialysis catheter in a right heart model. Artif. Organs 2004, 28, 639–648. [Google Scholar] [CrossRef] [PubMed]
- Casa, L.D.C.; Deaton, D.H.; Ku, D.N. Role of high shear rate in thrombosis. J. Vasc. Surg. 2015, 61, 1068–1080. [Google Scholar] [CrossRef] [PubMed]
- Ronco, C.; Bowry, S.K.; Brendolan, A.; Crepaldi, C.; Soffiati, G.; Fortunato, A.; Bordoni, V.; Granziero, A.; Torsello, G.; La Greca, G. Hemodialyzer: From macro-design to membrane nanostructure; the case of the fx-class of hemodialyzers. Kidney Int. 2002, 61, 126–142. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, N.; Sakai, K.; Yamamoto, K.; Iwasaki, H. Effects of hollow fiber packing fraction on blood flow pattern and gas transfer rate of an intravascular oxygenator (IVOX). J. Membr. Sci. 2000, 179, 231–241. [Google Scholar] [CrossRef]
- Kim, J.C.; Kim, J.H.; Sung, J.; Kim, H.-C.; Kang, E.; Lee, S.H.; Kim, J.K.; Kim, H.C.; Min, B.G.; Ronco, C. Effects of arterial port design on blood flow distribution in hemodialyzers. Blood Purif. 2009, 28, 260–267. [Google Scholar] [CrossRef]
- Ronco, C.; Ballestri, M.; Brendolan, A. New developments in hemodialyzers. Blood Purif. 2000, 18, 267–275. [Google Scholar] [CrossRef]
- Poh, C.K.; Hardy, P.A.; Liao, Z.; Huang, Z.; Clark, W.R.; Gao, D. Effect of Spacer Yarns on the Dialysate Flow Distribution of Hemodialyzers: A Magnetic Resonance Imaging Study. ASAIO J. 2003, 49, 440–448. [Google Scholar]
- Ronco, C.; Scabardi, M.; Goldoni, M.; Brendolan, A.; Crepaldi, C.; La Greca, G. Impact of spacing filaments external to hollow fibers on dialysate flow distribution and dialyzer performance. Int. J. Artif. Organs 1997, 20, 261–266. [Google Scholar] [CrossRef]
- Ghosh, R.; Chen, G.; Umatheva, U.; Gatt, P. A flow distribution and collection feature for ensuring scalable uniform flow in a chromatography device. J. Chromatogr. A 2020, 1618, 460892. [Google Scholar] [CrossRef]
- Chen, G.; Roshankhah, R.; Ghosh, R. A cuboid chromatography device having short bed-height gives better protein separation at a significantly lower pressure drop than a taller column having the same bed-volume. J. Chromatogr. A 2021, 1647, 462167. [Google Scholar] [CrossRef]
- Ghosh, R.; Hale, G.; Durocher, Y.; Gatt, P. Dry-compression packing of hydroxyapatite nanoparticles within a flat cuboid chromatography device and its use for fast protein separation. J. Chromatogr. A 2022, 1667, 462881. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Pagano, J.; Yu, D.; Ghose, S.; Li, Z.; Ghosh, R. Fast and high-resolution purification of a PEGylated protein using a z2 laterally-fed membrane chromatography device. J. Chromatogr. A 2021, 1652, 462375. [Google Scholar] [CrossRef] [PubMed]
- Food and Drug Administration. Available online: https://www.accessdata.fda.gov/CDRH510K/K030974.pdf (accessed on 3 August 2022).
- Peskin, C.S.; McQueen, D.M. A three-dimensional computational method for blood flow in the heart I. Immersed elastic fibers in a viscous incompressible fluid. J. Comput. Phys. 1989, 81, 372–405. [Google Scholar] [CrossRef]
- Canic, S.; Mikelic, A. Effective equations modeling the flow of a viscous incompressible fluid through a long elastic tube arising in the study of blood flow through small arteries. SIAM J. Appl. Dyn. Syst. 2003, 2, 431–463. [Google Scholar] [CrossRef]
- Islam, M.S.; Szpunar, J. Study of Dialyzer Membrane (polyflux 210h) and effects of different parameters on dialysis performance. Open J. Nephrol. 2013, 03, 161–167. [Google Scholar] [CrossRef]
- Swamee, P.K.; Aggarwal, N. Explicit equations for laminar flow of Bingham Plastic Fluids. J. Pet. Sci. Eng. 2011, 76, 178–184. [Google Scholar] [CrossRef]
- Tan, H.; Wong, K.Y.; Othman, M.H.; Kek, H.Y.; Tey, W.Y.; Nyakuma, B.B.; Mong, G.R.; Kuan, G.; Ho, W.S.; Kang, H.S.; et al. Controlling infectious airborne particle dispersion during surgical procedures: Why mobile air supply units matter? Build. Environ. 2022, 223, 109489. [Google Scholar] [CrossRef]
- Tan, H.; Wong, K.Y.; Lee, C.T.; Wong, S.L.; Nyakuma, B.B.; Wahab, R.A.; Lee, K.Q.; Chiong, M.C.; Ho, W.S.; Othman, M.H.; et al. Numerical assessment of ceiling-mounted air curtain on the particle distribution in surgical zone. J. Therm. Anal. Calorim. 2022, 23, 1–14. [Google Scholar] [CrossRef]
- Kamar, H.M.; Wong, K.Y.; Kamsah, N. The effects of medical staff turning movements on airflow distribution and particle concentration in an operating room. J. Build. Perform. Simul. 2020, 13, 684–706. [Google Scholar] [CrossRef]
- Fouad, E.A.; Bart, H.J. Emulsion liquid membrane extraction of zinc by a hollow-fiber contactor. J. Membr. Sci. 2008, 307, 156–168. [Google Scholar] [CrossRef]
- Edwie, F.; Chung, T.S. Development of hollow fiber membranes for water and salt recovery from highly concentrated brine via direct contact membrane distillation and crystallization. J. Membr. Sci. 2012, 421, 111–123. [Google Scholar] [CrossRef]
- Xu, Z.L.; Qusay, F.A. Polyethersulfone (PES) hollow fiber ultrafiltration membranes prepared by PES/non-solvent/NMP solution. J. Membr. Sci. 2004, 233, 101–111. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Cui, Z.; Yao, Y. Modeling of filtration characteristics during submerged hollow fiber membrane microfiltration of yeast suspension under aeration condition. J. Membr. Sci. 2016, 510, 455–465. [Google Scholar] [CrossRef]
- Kelsey, L.J.; Pillarella, M.R.; Zydney, A.L. Theoretical analysis of convective flow profiles in a hollow-fiber membrane bioreactor. Chem. Eng. Sci. 1990, 45, 3211–3220. [Google Scholar] [CrossRef]
- Cancilla, N.; Gurreri, L.; Marotta, G.; Ciofalo, M.; Cipollina, A.; Tamburini, A.; Micale, G. A porous media CFD model for the simulation of hemodialysis in hollow fiber membrane modules. J. Membr. Sci. 2022, 646, 120219. [Google Scholar] [CrossRef]
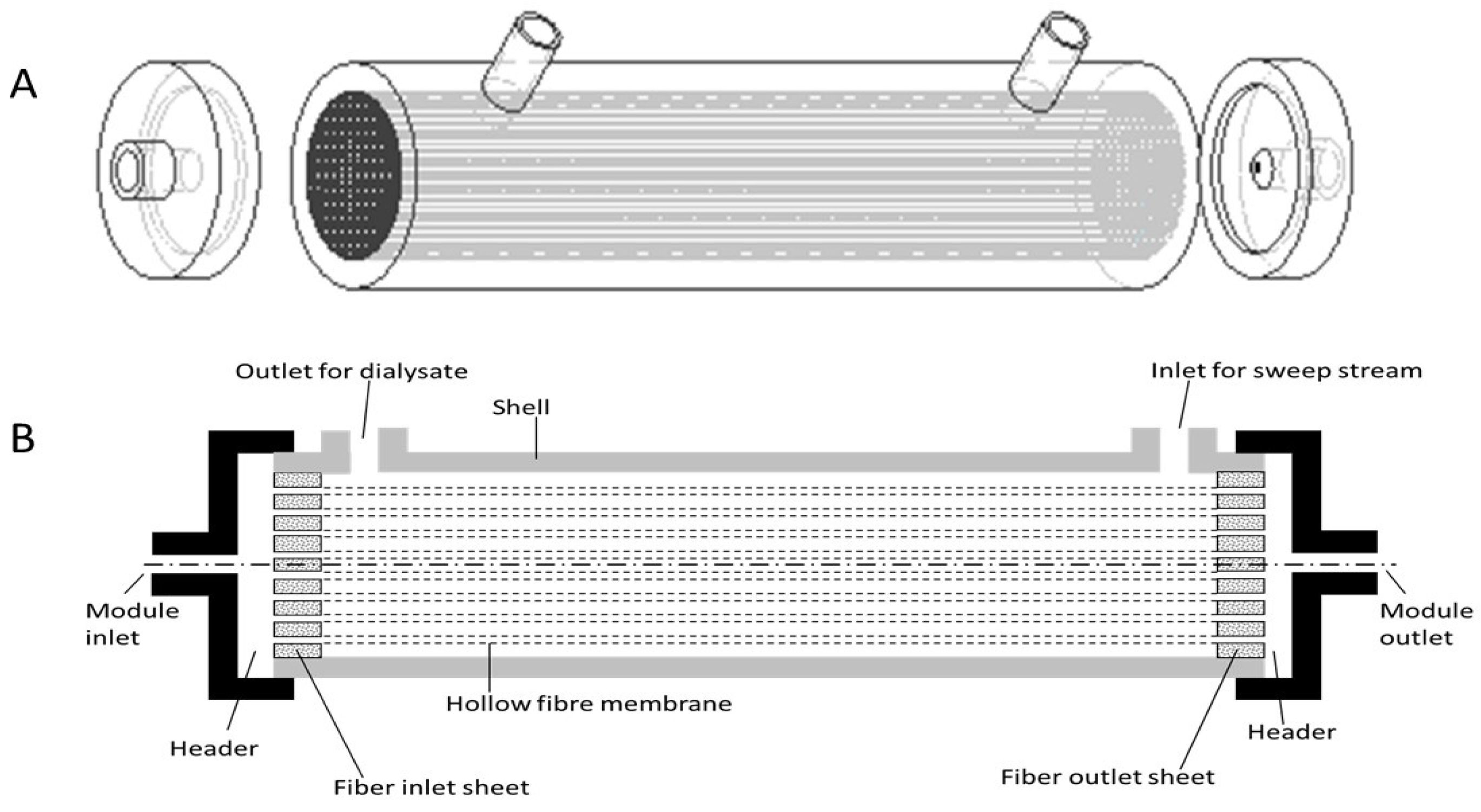
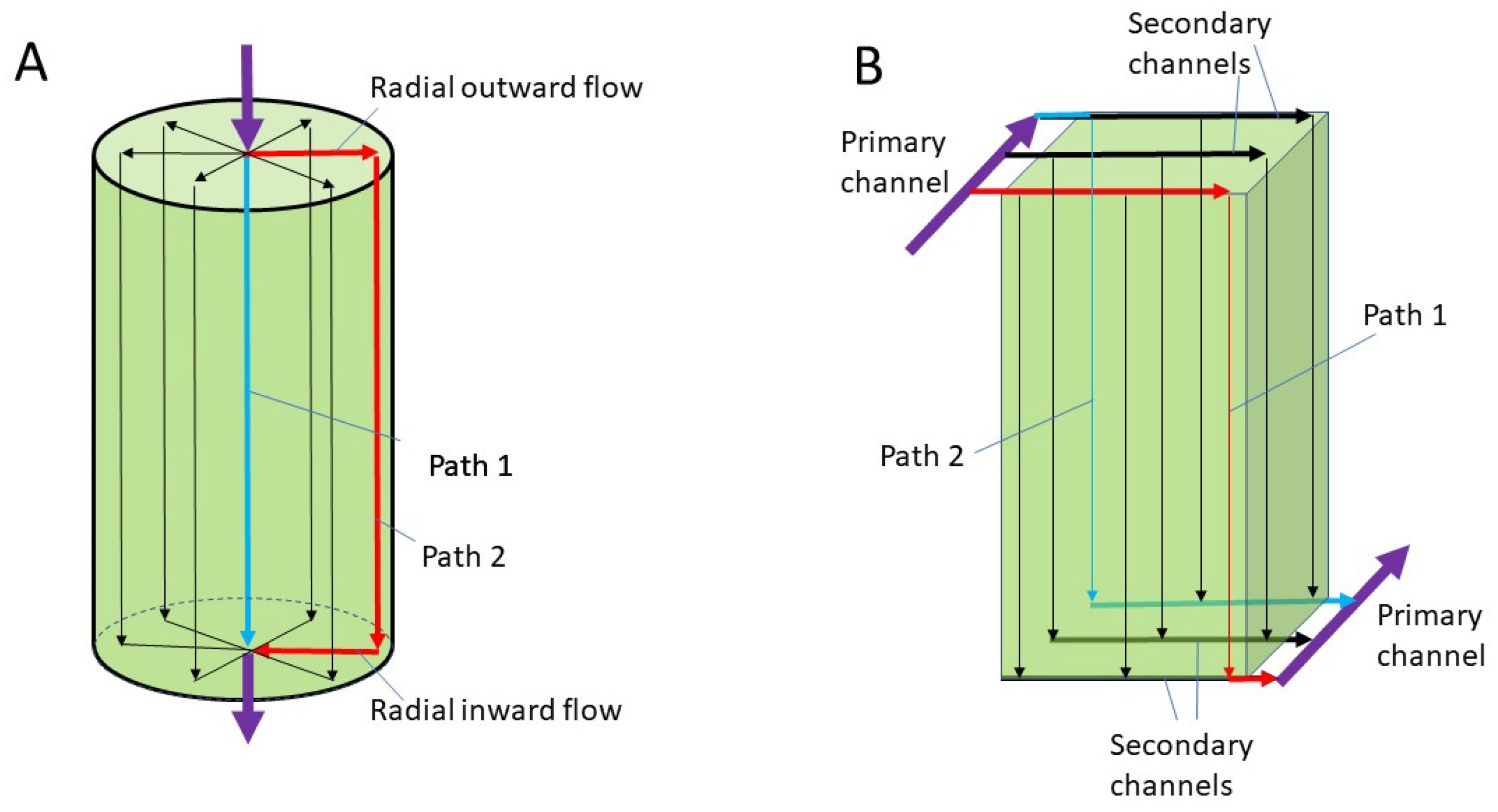
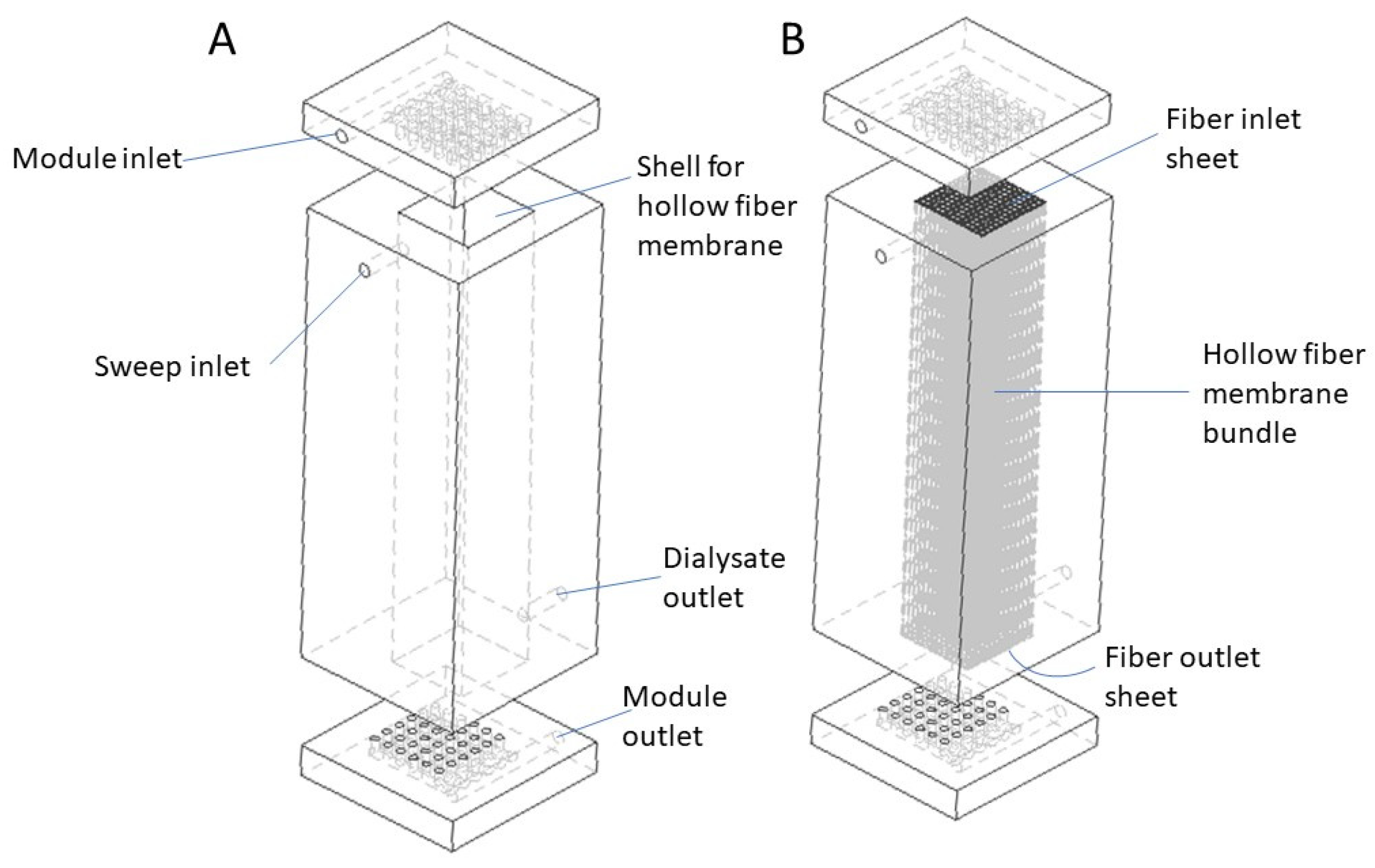
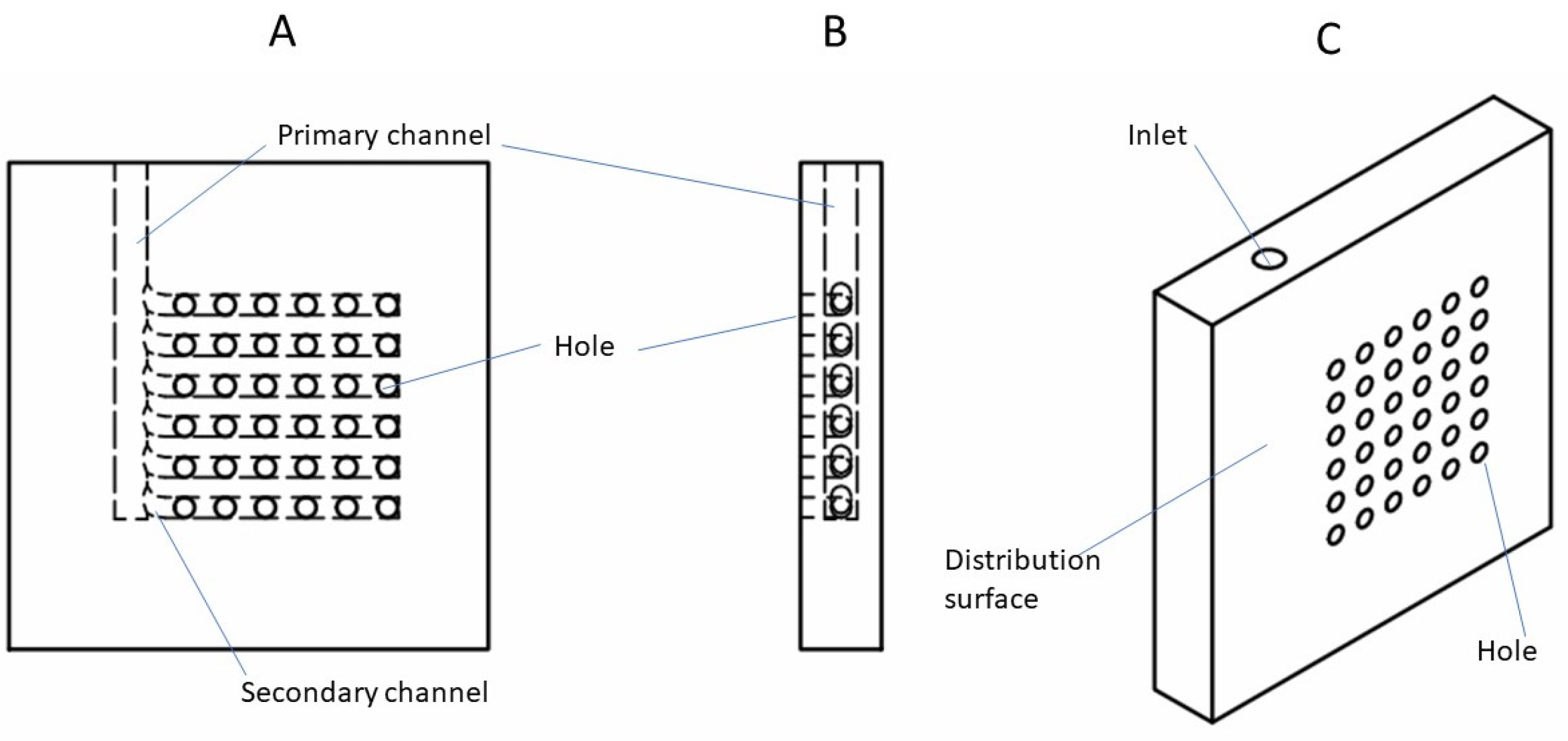



| Parameter | Value |
|---|---|
| Depth of the header (manifold) | 0.001 m |
| Length of hollow fiber membrane | 0.245 m |
| Effective length of membranes (excluding dimension lost in tube sheet) | 0.230 m |
| Inner radius of arterial/venous/dialysate port | 0.002 m |
| Inner radius of the membranes | 2.00 × 10−4 m |
| Outer radius of the membrane | 2.45 × 10−4 m |
| Number of hollow fiber membranes | 900 |
| Radius of header (manifold) in conventional | 0.017 m |
| Inner radius of shell of conventional | 0.017 m |
| Outer length of conventional | 0.030 m |
| Outer length of cuboid (both cuboids) | 0.030 m |
| Radius of primary channel (both cuboids) | 0.00200 m |
| Radius of secondary channels (cuboid 1) | 0.00100 m |
| Radius of hole (cuboid 1) | 0.00100 m |
| Radius of secondary channels (cuboid 2) | 0.00125 m |
| Radius of hole (cuboid 2) | 0.00125 m |
| Parameter | Value |
|---|---|
| Inlet volumetric flow rate | 2.5 × 10−6 (m3/s) |
| Temperature | 298.15 Kelvin |
| Concentration of the tracer solution (NaCl) | 0.8 (mol/L) |
| Diffusion coefficient of NaCl in water | 2.9 × 10−9 (m2/s) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Umatheva, U.; Ghosh, R. Evaluation of a Novel Cuboid Hollow Fiber Hemodialyzer Design Using Computational Fluid Dynamics. Membranes 2023, 13, 93. https://doi.org/10.3390/membranes13010093
Xu Y, Umatheva U, Ghosh R. Evaluation of a Novel Cuboid Hollow Fiber Hemodialyzer Design Using Computational Fluid Dynamics. Membranes. 2023; 13(1):93. https://doi.org/10.3390/membranes13010093
Chicago/Turabian StyleXu, Yating, Umatheny Umatheva, and Raja Ghosh. 2023. "Evaluation of a Novel Cuboid Hollow Fiber Hemodialyzer Design Using Computational Fluid Dynamics" Membranes 13, no. 1: 93. https://doi.org/10.3390/membranes13010093
APA StyleXu, Y., Umatheva, U., & Ghosh, R. (2023). Evaluation of a Novel Cuboid Hollow Fiber Hemodialyzer Design Using Computational Fluid Dynamics. Membranes, 13(1), 93. https://doi.org/10.3390/membranes13010093










