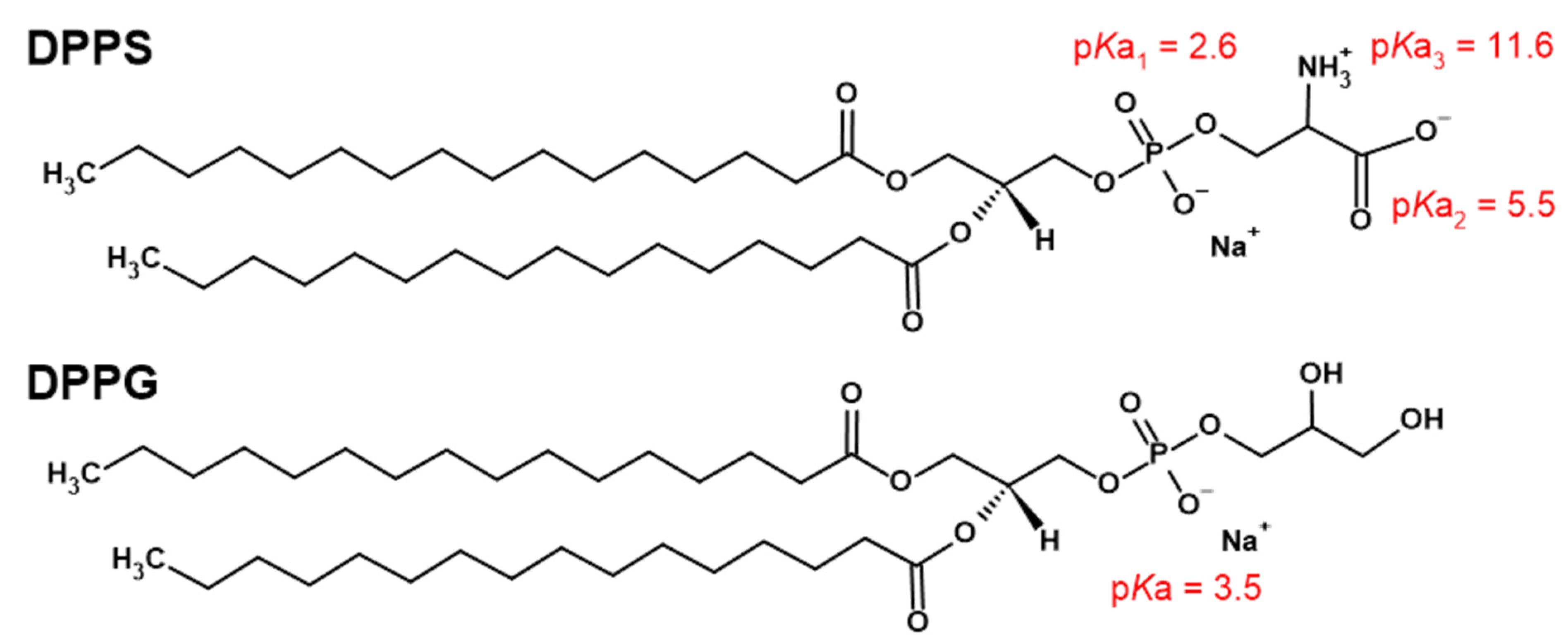
Lamellarity-Driven Differences in Surface Structural Features of DPPS Lipids: Spectroscopic, Calorimetric and Computational Study
Abstract
1. Introduction
2. Experimental
2.1. Chemicals and Liposome Preparation
2.2. Dynamic Light Scattering (DLS) and Confocal Microscopy: Measurements and Data Analysis
2.3. Differential Scanning Calorimetry (DSC): Data Acquisition and Curve Analysis
2.4. UV/Vis Spectroscopy: Data Acquisition and Spectral Analysis
2.5. FTIR ATR Spectroscopy: Data Acquisition and Spectral Analysis
3. Molecular Dynamics Simulations
4. Results
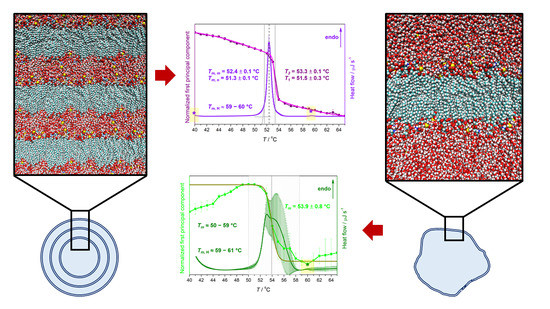
4.1. Thermotropic Properties of DPPS Lipids: UV/Vis and DSC Data
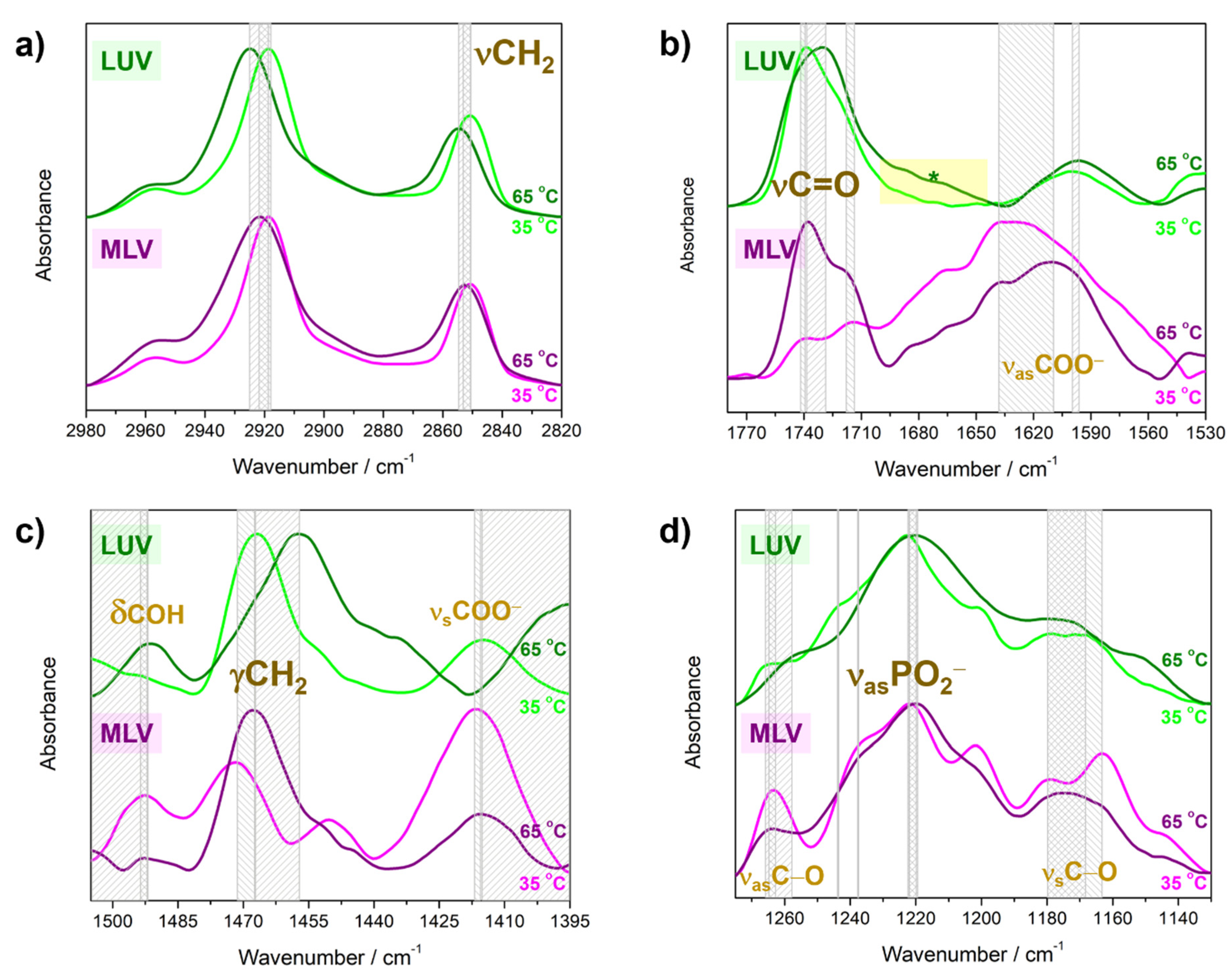
4.2. Molecular Properties of DPPS Lipids in Gel and Fluid Phase: FTIR Data
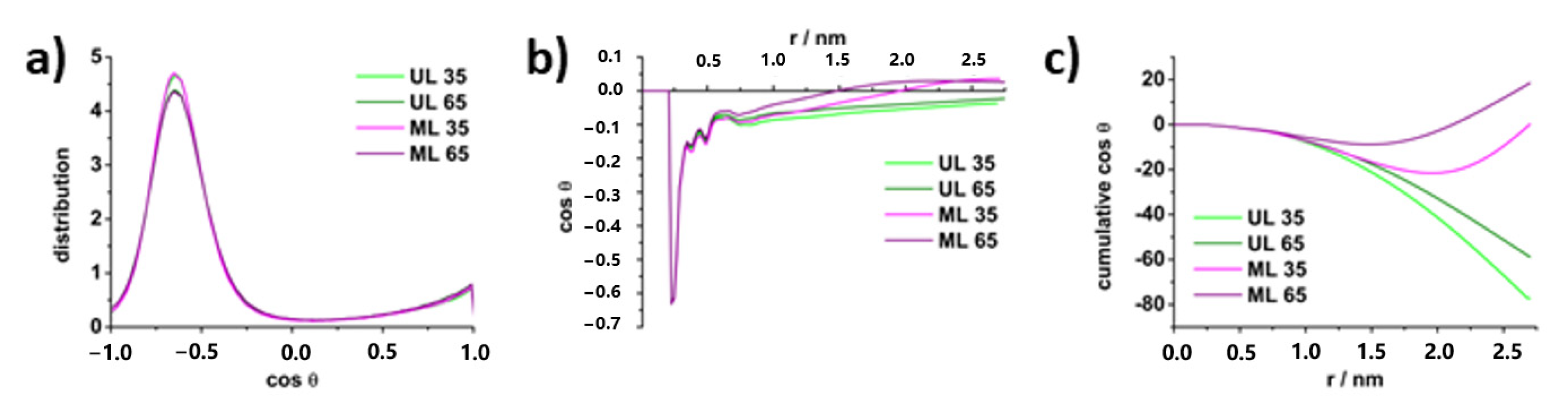
4.3. Molecular Properties of DPPS Lipids in Gel and Fluid Phase: Molecular Dynamics Data
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, S.; Davoudi, Z.; Wang, G.; Xu, Z.; Rehman, T.; Prominski, A.; Tian, B.; Bratlie, K.M.; Peng, H.; Wang, Q. Soft Materials as Biological and Artificial Membranes. Chem. Soc. Rev. 2021, 50, 12679–12701. [Google Scholar] [CrossRef] [PubMed]
- Hirama, T.; Lu, S.M.; Kay, J.G.; Maekawa, M.; Kozlov, M.M.; Grinstein, S.; Fairn, G.D. Membrane Curvature Induced by Proximity of Anionic Phospholipids Can Initiate Endocytosis. Nat. Commun. 2017, 8, 1393. [Google Scholar] [CrossRef] [PubMed]
- Fuller, N.L.; Benatti, C.R.; Rand, R.P. Curvature and Bending Constants for Phosphatidylserine-Containing Membranes. Biophys. J. 2003, 85, 1667–1674. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Korte, T.; Herrmann, A.; Wohland, T. Plasma Membrane Asymmetry of Lipid Organization: Fluorescence Lifetime Microscopy and Correlation Spectroscopy Analysis. J. Lipid Res. 2020, 61, 252–266. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Kim, J.; Huang, Z.; St Clair, J.R.; Brown, D.A.; London, E. Efficient Replacement of Plasma Membrane Outer Leaflet Phospholipids and Sphingolipids in Cells with Exogenous Lipids. Proc. Natl. Acad. Sci. USA 2016, 113, 14025–14030. [Google Scholar] [CrossRef]
- Vorobyov, I.; Allen, T.W. On the Role of Anionic Lipids in Charged Protein Interactions with Membranes. Biochim. Biophys. Acta Biomembr. 2011, 1808, 1673–1683. [Google Scholar] [CrossRef]
- Sinn, C.G.; Antonietti, M.; Dimova, R. Binding of Calcium to Phosphatidylcholine-Phosphatidylserine Membranes. Colloids Surf. A Physicochem. Eng. Asp. 2006, 282–283, 410–419. [Google Scholar] [CrossRef]
- Vernier, P.T.; Ziegler, M.J.; Dimova, R. Calcium Binding and Head Group Dipole Angle in Phosphatidylserine-Phosphatidylcholine Bilayers. Langmuir 2009, 25, 1020–1027. [Google Scholar] [CrossRef]
- Sahoo, A.; Matysiak, S. Microscopic Picture of Calcium-Assisted Lipid Demixing and Membrane Remodeling Using Multiscale Simulations. J. Phys. Chem. B 2020, 124, 7327–7335. [Google Scholar] [CrossRef]
- Martín-Molina, A.; Rodríguez-Beas, C.; Faraudo, J. Effect of Calcium and Magnesium on Phosphatidylserine Membranes: Experiments and All-Atomic Simulations. Biophys. J. 2012, 102, 2095–2103. [Google Scholar] [CrossRef]
- Poyton, M.F.; Pullanchery, S.; Sun, S.; Yang, T.; Cremer, P.S. Zn2+ binds to Phosphatidylserine and Induces Membrane Blebbing. J. Am. Chem. Soc. 2020, 142, 18679–18686. [Google Scholar] [CrossRef] [PubMed]
- Poojari, C.S.; Scherer, K.C.; Hub, J.S. Free Energies of Membrane Stalk Formation from a Lipidomics Perspective. Nat. Commun. 2021, 12, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Meng, X.W.; Flatten, K.S.; Loegering, D.A.; Kaufmann, S.H. Phosphatidylserine Exposure during Apoptosis Reflects Bidirectional Trafficking between Plasma Membrane and Cytoplasm. Cell Death Differ. 2013, 20, 64–76. [Google Scholar] [CrossRef] [PubMed]
- Wodlej, C.; Riedl, S.; Rinner, B.; Leber, R.; Drechsler, C.; Voelker, D.R.; Choi, J.Y.; Lohner, K.; Zweytick, D. Interaction of Two Antitumor Peptides with Membrane Lipids—Influence of Phosphatidylserine and Cholesterol on Specificity for Melanoma Cells. PLoS ONE 2019, 14, 1–37. [Google Scholar] [CrossRef]
- Beasley, M.; Groover, S.; Valentine, S.J.; Legleiter, J. Lipid Headgroups Alter Huntingtin Aggregation on Membranes. Biochim. Biophys. Acta Biomembr. 2021, 1863, 183497. [Google Scholar] [CrossRef] [PubMed]
- Darabi, M.; Lhomme, M.; Dahik, V.D.; Guillas, I.; Frisdal, E.; Tubeuf, E.; Poupel, L.; Patel, M.; Gautier, E.L.; Huby, T.; et al. Phosphatidylserine Enhances Anti-Inflammatory Effects of Reconstituted HDL in Macrophages via Distinct Intracellular Pathways. FASEB J. 2022, 36, 1–16. [Google Scholar] [CrossRef]
- Bach, D.; Miller, I.R. Hydration of Phospholipid Bilayers in the Presence and Absence of Cholesterol. Biochim. Biophys. Acta 1998, 1368, 216–224. [Google Scholar] [CrossRef]
- Cevc, G.; Watts, A.; Marsh, D. Titration of the Phase Transition of Phosphatidylserine Bilayer Membranes. Effects of pH, Surface Electrostatics, Ion Binding, and Head-Group Hydration. Biochemistry 1981, 20, 4955–4965. [Google Scholar] [CrossRef]
- Cevc, G.; Hauser, M.; Kornyshev, A.A. Effects of the Interfacial Structure on the Hydration Force between Laterally Nonuniform Surfaces. Langmuir 1995, 11, 3111–3118. [Google Scholar] [CrossRef]
- Ionization Constants of Phospholipids. Available online: https://avantilipids.com/tech-support/physical-properties/ionization-constants (accessed on 31 October 2022).
- Lewis, R.N.A.H.; McElhaney, R.N. Calorimetric and Spectroscopic Studies of the Thermotropic Phase Behavior of Lipid Bilayer Model Membranes Composed of a Homologous Series of Linear Saturated Phosphatidylserines. Biophys. J. 2000, 79, 2043–2055. [Google Scholar] [CrossRef]
- Koynova, R.; Caffrey, M. Phases and Phase Transitions of the Phosphatidylcholines. Biochim. Biophys. Acta 1998, 1376, 91–145. [Google Scholar] [CrossRef] [PubMed]
- Browning, J.L.; Seelig, J. Bilayers of Phosphatidylserine: A Deuterium and Phosphorus Nuclear Magnetic Resonance Study. Biochemistry 1980, 19, 1262–1270. [Google Scholar] [CrossRef] [PubMed]
- Galassi, V.V.; Wilke, N. On the Coupling between Mechanical Properties and Electrostatics in Biological Membranes. Membranes 2021, 11, 478. [Google Scholar] [CrossRef] [PubMed]
- May, S. Curvature Elasticity and Thermodynamic Stability of Electrically Charged Membranes. J. Chem. Phys. 1996, 105, 8314–8323. [Google Scholar] [CrossRef]
- Heimburg, T. Thermal Biophysics of Membranes, 1st ed.; Wiley-VCH Verlag GmbH, Ed.; Wiley-VCH: Weinheim, Germany, 2007; ISBN 9783527404711. [Google Scholar]
- Disalvo, E.A.; Rosa, A.S.; Cejas, J.P.; de los Frias, M.A. Water as a Link between Membrane and Colloidal Theories for Cells. Molecules 2022, 27, 4994. [Google Scholar] [CrossRef]
- Langner, M.; Kubica, K. The Electrostatics of Lipid Surfaces. Chem. Phys. Lipids 1999, 101, 3–35. [Google Scholar] [CrossRef]
- Chou, T.; Jarić, M.V.; Siggia, E.D. Electrostatics of Lipid Bilayer Bending. Biophys. J. 1997, 72, 2042–2055. [Google Scholar] [CrossRef][Green Version]
- Smirnova, Y.G.; Aeffner, S.; Risselada, H.J.; Salditt, T.; Marrink, S.J.; Müller, M.; Knecht, V. Interbilayer Repulsion Forces between Tension-Free Lipid Bilayers from Simulation. Soft Matter 2013, 9, 10705–10718. [Google Scholar] [CrossRef]
- Petrache, H.I.; Tristram-Nagle, S.; Harries, D.; Kuĉerka, N.; Nagle, J.F.; Parsegian, V.A. Swelling of Phospholipids by Monovalent Salt. J. Lipid Res. 2006, 47, 302–309. [Google Scholar] [CrossRef]
- Cowley, A.C.; Fuller, N.L.; Parsegian, V.A. Measurement of Repulsive Forces between Charged Phospholipid Bilayers. Biochemistry 1978, 17, 3163–3168. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Interactions of Biological Membranes and Structures; Intermolecular and Surface Forces; Academic Press: Burlington, MA, USA, 2011; ISBN 9780123751829. [Google Scholar]
- Ge, M.; Freed, J.H. Hydration, Structure, and Molecular Interactions in the Headgroup Region of Dioleoylphosphatidylcholine Bilayers: An Electron Spin Resonance Study. Biophys. J. 2003, 85, 4023–4040. [Google Scholar] [CrossRef] [PubMed]
- Petrache, H.I.; Tristram-Nagle, S.; Gawrisch, K.; Harries, D.; Parsegian, V.A.; Nagle, J.F. Structure and Fluctuations of Charged Phosphatidylserine Bilayers in the Absence of Salt. Biophys. J. 2004, 86, 1574–1586. [Google Scholar] [CrossRef] [PubMed]
- Binder, H.; Dietrich, U.; Schalke, M.; Pfeiffer, H. Hydration-Induced Deformation of Lipid Aggregates before and after Polymerization. Langmuir 1999, 15, 4857–4866. [Google Scholar] [CrossRef]
- Sciacca, M.F.M.; Carbone, V.; Pappalardo, M.; Milardi, D.; La Rosa, C.; Grasso, D.M. Interaction of Human Amylin with Phosphatidylcholine and Phosphatidylserine Membranes. Mol. Cryst. Liq. Cryst. 2009, 500, 73–81. [Google Scholar] [CrossRef]
- Marr, J.M.; Li, F.; Petlick, A.R.; Schafer, R.; Hwang, C.T.; Chabot, A.; Ruggiero, S.T.; Tanner, C.E.; Schultz, Z.D. The Role of Lateral Tension in Calcium-Induced DPPS Vesicle Rupture. Langmuir 2012, 28, 11874–11880. [Google Scholar] [CrossRef]
- Maleš, P.; Pem, B.; Petrov, D.; Domazet Jurašin, D.; Bakarić, D. Deciphering the Origin of the Melting Profile of Unilamellar Phosphatidylcholine Liposomes by Measuring the Turbidity of Its Suspensions. Soft Matter 2022, 18, 6703–6715. [Google Scholar] [CrossRef] [PubMed]
- Nele, V.; Holme, M.N.; Kauscher, U.; Thomas, M.R.; Doutch, J.J.; Stevens, M.M. Effect of Formulation Method, Lipid Composition, and PEGylation on Vesicle Lamellarity: A Small-Angle Neutron Scattering Study. Langmuir 2019, 35, 6064–6074. [Google Scholar] [CrossRef]
- Marquardt, D.; Heberle, F.A.; Miti, T.; Eicher, B.; London, E.; Katsaras, J.; Pabst, G. 1H NMR Shows Slow Phospholipid Flip-Flop in Gel and Fluid Bilayers. Langmuir 2017, 33, 3731–3741. [Google Scholar] [CrossRef]
- Höhne, G.W.H.; Cammenga, H.K.; Eysel, W.; Gmelin, E.; Hemminger, W. The Temperature Calibration of Scanning Calorimeters. Thermochim. Acta 1990, 160, 1–12. [Google Scholar] [CrossRef]
- Menges, F. “Spectragryph—Optical Spectroscopy Software”, Version 1.2.15. 2015. Available online: https://www.effemm2.de/spectragryph/ (accessed on 1 October 2022).
- Jaumot, J.; Gargallo, R.; De Juan, A.; Tauler, R. A Graphical User-Friendly Interface for MCR-ALS: A New Tool for Multivariate Curve Resolution in MATLAB. Chemom. Intell. Lab. Syst. 2005, 76, 101–110. [Google Scholar] [CrossRef]
- Maeder, M.; de Juan, A. Two-Way Data Analysis: Evolving Factor Analysis. Compr. Chemom. 2009, 2, 261–274. [Google Scholar] [CrossRef]
- De Juan, A.; Jaumot, J.; Tauler, R. Multivariate Curve Resolution (MCR). Solving the Mixture Analysis Problem. Anal. Methods 2014, 6, 4964–4976. [Google Scholar] [CrossRef]
- Keller, H.R.; Massart, D.L. Evolving Factor Analysis. Chemom. Intell. Lab. Syst. 1991, 12, 209–224. [Google Scholar] [CrossRef]
- Maleš, P.; Brkljača, Z.; Crnolatac, I.; Bakarić, D. Application of MCR-ALS with EFA on FT-IR Spectra of Lipid Bilayers in the Assessment of Phase Transition Temperatures: Potential for Discernment of Coupled Events. Colloids Surf. B Biointerfaces 2021, 201, 111645. [Google Scholar] [CrossRef]
- Wu, E.L.; Cheng, X.; Jo, S.; Rui, H.; Song, K.C.; Dávila-Contreras, E.M.; Qi, Y.; Lee, J.; Monje-Galvan, V.; Venable, R.M.; et al. CHARMM-GUI Membrane Builder toward Realistic Biological Membrane Simulations. J. Comput. Chem. 2014, 35, 1997–2004. [Google Scholar] [CrossRef]
- Tieleman, D.P.; Berendsen, H.J.C. Molecular Dynamics Simulations of a Fully Hydrated Dipalmitoylphosphatidylcholine Bilayer with Different Macroscopic Boundary Conditions and Parameters. J. Chem. Phys. 1996, 105, 4871–4880. [Google Scholar] [CrossRef]
- Pandit, S.A.; Berkowitz, M.L. Molecular Dynamics Simulation of Dipalmitoylphosphatidylserine Bilayer with Na+ Counterions. Biophys. J. 2002, 82, 1818–1827. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; De Groot, B.L.; Grubmüller, H.; MacKerell, A.D. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2016, 14, 71–73. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Arouri, A.; Dathe, M.; Blume, A. Peptide Induced Demixing in PG/PE Lipid Mixtures: A Mechanism for the Specificity of Antimicrobial Peptides towards Bacterial Membranes? Biochim. Biophys. Acta Biomembr. 2009, 1788, 650–659. [Google Scholar] [CrossRef] [PubMed]
- Biltonen, R.L.; Lichtenberg, D. The Use of Differential Scanning Calorimetry as a Tool to Characterize Liposome Preparations. Chem. Phys. Lipids 1993, 64, 129–142. [Google Scholar] [CrossRef]
- Maleš, P.; Brkljača, Z.; Domazet Jurašin, D.; Bakarić, D. New Spirit of an Old Technique: Characterization of Lipid Phase Transitions via UV/Vis Spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 272, 121013. [Google Scholar] [CrossRef]
- Hauser, H.; Paltauf, F.; Shipley, G.G. Structure and Thermotropic Behavior of Phosphatidylserine Bilayer Membranes. Biochemistry 1982, 21, 1061–1067. [Google Scholar] [CrossRef]
- Mitomo, H.; Kobayashi, S.; Iwayanagi, S.; Taktzawa, T.; Hayashi, K. Structural Changes in Phosphatidylserine Salts by Hydration and Addition of Calcium Ion. J. Phys. Soc. Jpn. 1993, 62, 2174–2179. [Google Scholar] [CrossRef]
- de Araújo Pimenta, L.; Duarte, E.L.; Muniz, G.S.V.; Pasqualoto, K.F.M.; de Mattos Fontes, M.R.; Lamy, M.T.; Sampaio, S.C. Correlating Biological Activity to Thermo-Structural Analysis of the Interaction of CTX with Synthetic Models of Macrophage Membranes. Sci. Rep. 2021, 11, 1–17. [Google Scholar] [CrossRef]
- Peters, J.; Marion, J.; Becher, F.J.; Trapp, M.; Gutberlet, T.; Bicout, D.J.; Heimburg, T. Thermodynamics of Lipid Multi-Lamellar Vesicles in Presence of Sterols at High Hydrostatic Pressure. Sci. Rep. 2017, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Bakarić, D.; Petrov, D.; Kunhi Mouvenchery, Y.; Heissler, S.; Oostenbrink, C.; Schaumann, G.E. Ion-Induced Modification of the Sucrose Network and Its Impact on Melting of Freeze-Dried Liposomes. DSC and Molecular Dynamics Study. Chem. Phys. Lipids 2018, 210, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Casal, H.L.; Martin, A.; Mantsch, H.H.; Paltauf, F.; Hauser, H. Infrared Studies of Fully Hydrated Unsaturated Phosphatidylserine Bilayers. Effect of Li+ and Ca2+. Biochemistry 1987, 26, 7395–7401. [Google Scholar] [CrossRef] [PubMed]
- Lewis, R.N.A.H.; McElhaney, R.N. Membrane Lipid Phase Transitions and Phase Organization Studied by Fourier Transform Infrared Spectroscopy. Biochim. Biophys. Acta Biomembr. 2013, 1828, 2347–2358. [Google Scholar] [CrossRef] [PubMed]
- López Cascales, J.J.; García de la Torre, J.; Marrink, S.J.; Berendsen, H.J.C. Molecular Dynamics Simulation of a Charged Biological Membrane. J. Chem. Phys. 1996, 104, 2713–2720. [Google Scholar] [CrossRef]
- Demel, R.A.; Paltauf, F.; Hauser, H. Monolayer Characteristics and Thermal Behavior of Natural and Synthetic Phosphatidylserines. Biochemistry 1987, 26, 8659–8665. [Google Scholar] [CrossRef]
- López Cascales, J.J.; Otero, T.F.; Smith, B.D.; González, C.; Márquez, M. Model of an Asymmetric DPPC/DPPS Membrane: Effect of Asymmetry on the Lipid Properties. A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2006, 110, 2358–2363. [Google Scholar] [CrossRef]
- Grossman, J.C.; Schwegler, E.; Galli, G. Quantum and Classical Molecular Dynamics Simulations of Hydrophobic Hydration Structure around Small Solutes. J. Phys. Chem. B 2004, 108, 15865–15872. [Google Scholar] [CrossRef]
- Choudhary, A.; Chandra, A. Spatial and Orientational Structure of the Hydration Shell of Benzene in Sub- and Supercritical Water. J. Phys. Chem. B 2015, 119, 8600–8612. [Google Scholar] [CrossRef]
- Patra, M.; Karttunen, M.; Hyvönen, M.T.; Falck, E.; Lindqvist, P.; Vattulainen, I. Molecular Dynamics Simulations of Lipid Bilayers: Major Artifacts Due to Truncating Electrostatic Interactions. Biophys. J. 2003, 84, 3636–3645. [Google Scholar] [CrossRef]
- Sachs, J.N.; Nanda, H.; Petrache, H.I.; Woolf, T.B. Changes in Phosphatidylcholine Headgroup Tilt and Water Order Induced by Monovalent Salts: Molecular Dynamics Simulations. Biophys. J. 2004, 86, 3772–3782. [Google Scholar] [CrossRef] [PubMed]
- Bostick, D.; Berkowitz, M.L. The Implementation of Slab Geometry for Membrane-Channel Molecular Dynamics Simulations. Biophys. J. 2003, 85, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Pimthon, J.; Willumeit, R.; Lendlein, A.; Hofmann, D. All-Atom Molecular Dynamics Simulation Studies of Fully Hydrated Gel Phase DPPG and DPPE Bilayers. J. Mol. Struct. 2009, 921, 38–50. [Google Scholar] [CrossRef]
- Lindahl, A.; van der Spoel, H. GROMACS 2020 Manual 2020, 623. Available online: https://manual.gromacs.org/documentation/2020/manual-2020.pdf (accessed on 31 October 2022).
- Kagawa, R.; Hirano, Y.; Taiji, M.; Yasuoka, K.; Yasui, M. Dynamic Interactions of Cations, Water and Lipids and Influence on Membrane Fluidity. J. Memb. Sci. 2013, 435, 130–136. [Google Scholar] [CrossRef]
- Woolf, L.A. Tracer Diffusion of Tritiated Heavy Water (DTO) in Heavy Water (D2O) under Pressure. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1976, 72, 1267. [Google Scholar] [CrossRef]
- Lichtenberg, D.; Menashe, M.; Donaldson, S.; Biltonen, R.L. Thermodynamic Characterization of the Pretrasition of Unilamellar Dipalmitoyl-Phosphatidylcholine Vesicles. Lipids 1984, 19, 395–400. [Google Scholar] [CrossRef]
- Ebel, H.; Grabitz, P.; Heimburg, T. Enthalpy and Volume Changes in Lipid Membranes. I: The Proportionality of Heat and Volume Changes in the Lipid Melting Transition and Its Implication for the Elastic Constants. J. Phys. Chem. B 2001, 105, 7353–7360. [Google Scholar] [CrossRef]
- Heimburg, T. Mechanical Aspects of Membrane Thermodynamics. Estimation of the Mechanical Properties of Lipid Membranes Close to the Chain Melting Transition from Calorimetry. Biochim. Biophys. Acta Biomembr. 1998, 1415, 147–162. [Google Scholar] [CrossRef]
- Maleš, P.; Butumović, M.; Erceg, I.; Brkljača, Z.; Bakarić, D. Influence of DPPE Surface Undulations on Melting Temperature Determination: UV/Vis Spectroscopic and MD Study. Biochim. Biophyica Acta Biomembr. 2023, 1865, 184072. [Google Scholar] [CrossRef]
- Vlahovska, P.M. Voltage-Morphology Coupling in Biomimetic Membranes: Dynamics of Giant Vesicles in Applied Electric Fields. Soft Matter 2015, 11, 7232–7236. [Google Scholar] [CrossRef]
- Cascales, J.J.L.; Costa, S.D.O.; Garro, A.; Enriz, R.D. Mechanical Properties of Binary DPPC/DPPS Bilayers. RSC Adv. 2012, 2, 11743. [Google Scholar] [CrossRef]
- Pan, J.; Cheng, X.; Monticelli, L.; Heberle, F.A.; Kučerka, N.; Tieleman, D.P.; Katsaras, J. The Molecular Structure of a Phosphatidylserine Bilayer Determined by Scattering and Molecular Dynamics Simulations. Soft Matter 2014, 10, 3716. [Google Scholar] [CrossRef] [PubMed]
- Angelova, M.I.; Bitbol, A.F.; Seigneuret, M.; Staneva, G.; Kodama, A.; Sakuma, Y.; Kawakatsu, T.; Imai, M.; Puff, N. PH Sensing by Lipids in Membranes: The Fundamentals of PH-Driven Migration, Polarization and Deformations of Lipid Bilayer Assemblies. Biochim. Biophys. Acta Biomembr. 2018, 1860, 2042–2063. [Google Scholar] [CrossRef] [PubMed]
- Ahmadpoor, F.; Sharma, P. Flexoelectricity in Two-Dimensional Crystalline and Biological Membranes. Nanoscale 2015, 7, 16555–16570. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, Y.; Majumder, R.; Das, S.; Ray, A.; Parui, P.P. Detection of Curvature-Radius-Dependent Interfacial pH/Polarity for Amphiphilic Self-Assemblies: Positive versus Negative Curvature. Langmuir 2018, 34, 6271–6284. [Google Scholar] [CrossRef]
- Qiao, B.; Olvera De La Cruz, M. Driving Force for Water Permeation across Lipid Membranes. J. Phys. Chem. Lett. 2013, 4, 3233–3237. [Google Scholar] [CrossRef]
- Brzustowicz, M.R.; Brunger, A.T. X-ray Scattering from Unilamellar Lipid Vesicles. J. Appl. Crystallogr. 2005, 38, 126–131. [Google Scholar] [CrossRef]
- Kučerka, N.; Pencer, J.; Sachs, J.N.; Nagle, J.F.; Katsaras, J. Curvature Effect on the Structure of Phospholipid Bilayers. Langmuir 2006, 22, 1292–1299. [Google Scholar] [CrossRef]
- De Los Angeles Frías, M.; Disalvo, E.A. Configuration of Carbonyl Groups at the Lipid Interphases of Different Topological Arrangements of Lipid Dispersions. Langmuir 2009, 25, 8187–8191. [Google Scholar] [CrossRef]
- Holloway, P.W.; Mantsch, H.H. Infrared Spectroscopic Analysis of Salt Bridge Formation between Cytochrome B5 and Cytochrome C. Biochemistry 1988, 27, 7991–7993. [Google Scholar] [CrossRef]
- Hack, J.; Grills, D.C.; Miller, J.R.; Mani, T.; Ahmadpoor, F.; Sharma, P.; Angelova, M.I.; Bitbol, A.F.; Seigneuret, M.; Staneva, G.; et al. Identification of Ion-Pair Structures in Solution by Vibrational Stark Effects. J. Phys. Chem. B 2016, 120, 1149–1157. [Google Scholar] [CrossRef] [PubMed]
- Donon, J.; Habka, S.; Very, T.; Charnay-Pouget, F.; Mons, M.; Aitken, D.J.; Brenner, V.; Gloaguen, E. Ion Pair Supramolecular Structure Identified by ATR-FTIR Spectroscopy and Simulations in Explicit Solvent**. ChemPhysChem 2021, 22, 2442–2455. [Google Scholar] [CrossRef] [PubMed]
- Habka, S.; Very, T.; Donon, J.; Vaquero-Vara, V.; Tardivel, B.; Charnay-Pouget, F.; Mons, M.; Aitken, D.J.; Brenner, V.; Gloaguen, E. Identification of Ion Pairs in Solution by IR Spectroscopy: Crucial Contributions of Gas Phase Data and Simulations. Phys. Chem. Chem. Phys. 2019, 21, 12798–12805. [Google Scholar] [CrossRef]
- Mendelsohn, R.; Flach, C.R.; Moore, D.J. Determination of Molecular Conformation and Permeation in Skin via IR Spectroscopy, Microscopy, and Imaging. Biochim. Biophys. Acta Biomembr. 2006, 1758, 923–933. [Google Scholar] [CrossRef] [PubMed]
- Arsov, Z.; Rappolt, M.; Grdadolnik, J. Weakened Hydrogen Bonds in Water Confined between Lipid Bilayers: The Existence of a Long-Range Attractive Hydration Force. ChemPhysChem 2009, 10, 1438–1441. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.-X.; Pautot, S.; Weitz, D.A.; Xie, X.S. Ordering of Water Molecules between Phospholipid Bilayers Visualized by Coherent Anti-Stokes Raman Scattering Microscopy. Proc. Natl. Acad. Sci. USA 2003, 100, 9826–9830. [Google Scholar] [CrossRef]
- Róg, T.; Murzyn, K.; Milhaud, J.; Karttunen, M.; Pasenkiewicz-Gierula, M. Water Isotope Effect on the Phosphatidylcholine Bilayer Properties: A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2009, 113, 2378–2387. [Google Scholar] [CrossRef]

| Suspension | Tma | ||||
|---|---|---|---|---|---|
| DSC | UV/Vis (MCA) | ||||
| Tm,o | Tm,m | Tm,H | T1 | T2 | |
| MLV | 51.3 ± 0.1 | 52.4 ± 0.1 | ≈60 | 51.5 ± 0.3 | 53.3 ± 0.1 |
| LUV | ≈50–59 | ≈59–61 | 53.9 ± 0.8 b | ||
| System | T a | APL b | Membrane Thickness c |
|---|---|---|---|
| UL | 35 | 0.458 ± 0.003 | 4.514 ± 0.006 |
| 65 | 0.578 ± 0.013 | 4.057 ± 0.032 | |
| ML | 35 | 0.462 ± 0.004 | 4.516 ± 0.007 |
| 65 | 0.563 ± 0.013 | 4.194 ± 0.003 |
| Hydrogen Bonds | UL 35 °C | UL 65 °C | ML 35 °C | ML 65 °C |
|---|---|---|---|---|
| Lipid-lipid total | 217 ± 8 | 183 ± 11 | 219 ± 7 | 190 ± 10 |
| Lipid-lipid per molecule | 1.70 ± 0.06 | 1.43 ± 0.09 | 1.71 ± 0.06 | 1.48 ± 0.08 |
| Water-water total | 9604 ± 45 | 9061 ± 54 | 3630 ± 31 | 3371 ± 35 |
| Water-water per molecule | 1.50 ± 0.01 | 1.42 ± 0.01 | 1.31 ± 0.01 | 1.21 ± 0.01 |
| Water-lipid | 1315 ± 24 | 1430 ± 37 | 1296 ± 23 | 1395 ± 33 |
| Water-PO2− | 346 ± 12 | 398 ± 16 | 348 ± 12 | 390 ± 15 |
| Water-C=O | 130 ± 9 | 179 ± 11 | 123 ± 9 | 175 ± 10 |
| Water-COO− | 552 ± 13 | 537 ± 17 | 544 ± 13 | 523 ± 16 |
| Water-glycerol | 147 ± 9 | 202 ± 11 | 139 ± 10 | 197 ± 11 |
| System | T a | D (Water) b | Dxy (Lipid) c |
|---|---|---|---|
| UL | 35 | 3.12 ± 0.04 × 10−5 | 0.91 ± 0.05 × 10−7 |
| 65 | 4.16 ± 0.06 × 10−5 | 4.24 ± 0.14 × 10−7 | |
| ML | 35 | 1.83 ± 0.09 × 10−5 | 0.25 ± 0.05 × 10−7 |
| 65 | 2.30 ± 0.03 × 10−5 | 3.94 ± 0.33 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pašalić, L.; Pem, B.; Bakarić, D. Lamellarity-Driven Differences in Surface Structural Features of DPPS Lipids: Spectroscopic, Calorimetric and Computational Study. Membranes 2023, 13, 83. https://doi.org/10.3390/membranes13010083
Pašalić L, Pem B, Bakarić D. Lamellarity-Driven Differences in Surface Structural Features of DPPS Lipids: Spectroscopic, Calorimetric and Computational Study. Membranes. 2023; 13(1):83. https://doi.org/10.3390/membranes13010083
Chicago/Turabian StylePašalić, Lea, Barbara Pem, and Danijela Bakarić. 2023. "Lamellarity-Driven Differences in Surface Structural Features of DPPS Lipids: Spectroscopic, Calorimetric and Computational Study" Membranes 13, no. 1: 83. https://doi.org/10.3390/membranes13010083
APA StylePašalić, L., Pem, B., & Bakarić, D. (2023). Lamellarity-Driven Differences in Surface Structural Features of DPPS Lipids: Spectroscopic, Calorimetric and Computational Study. Membranes, 13(1), 83. https://doi.org/10.3390/membranes13010083