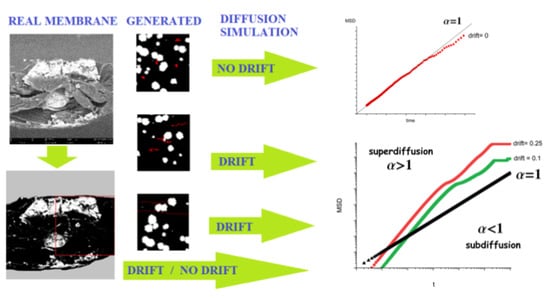
Numerical Study of Drift Influence on Diffusion Transport through the Hybrid Membrane
Abstract
:1. Introduction
2. Materials and Methods
2.1. Real Membrane Preparation
2.2. Binarisation and Morphology Analysis
- -
- The observed amount of polymer matrix , which is defined as the ratio of the polymer matrix area visible in the picture (black regions) to the total image area,
- -
- The fractal dimension of polymer matrix ,
- -
- The degree of multifractality .
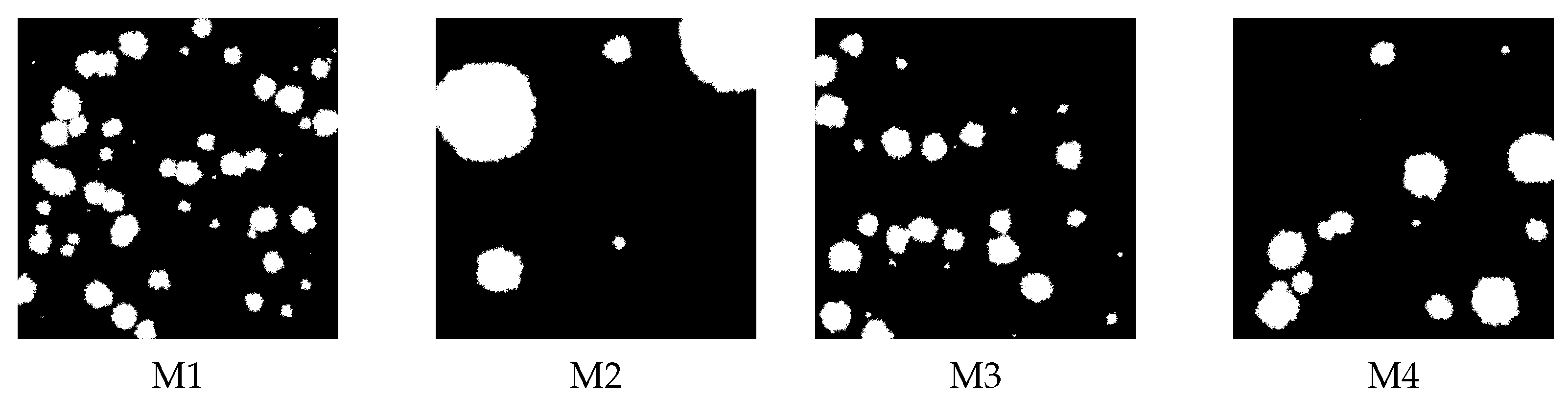
2.3. Artificial Membranes
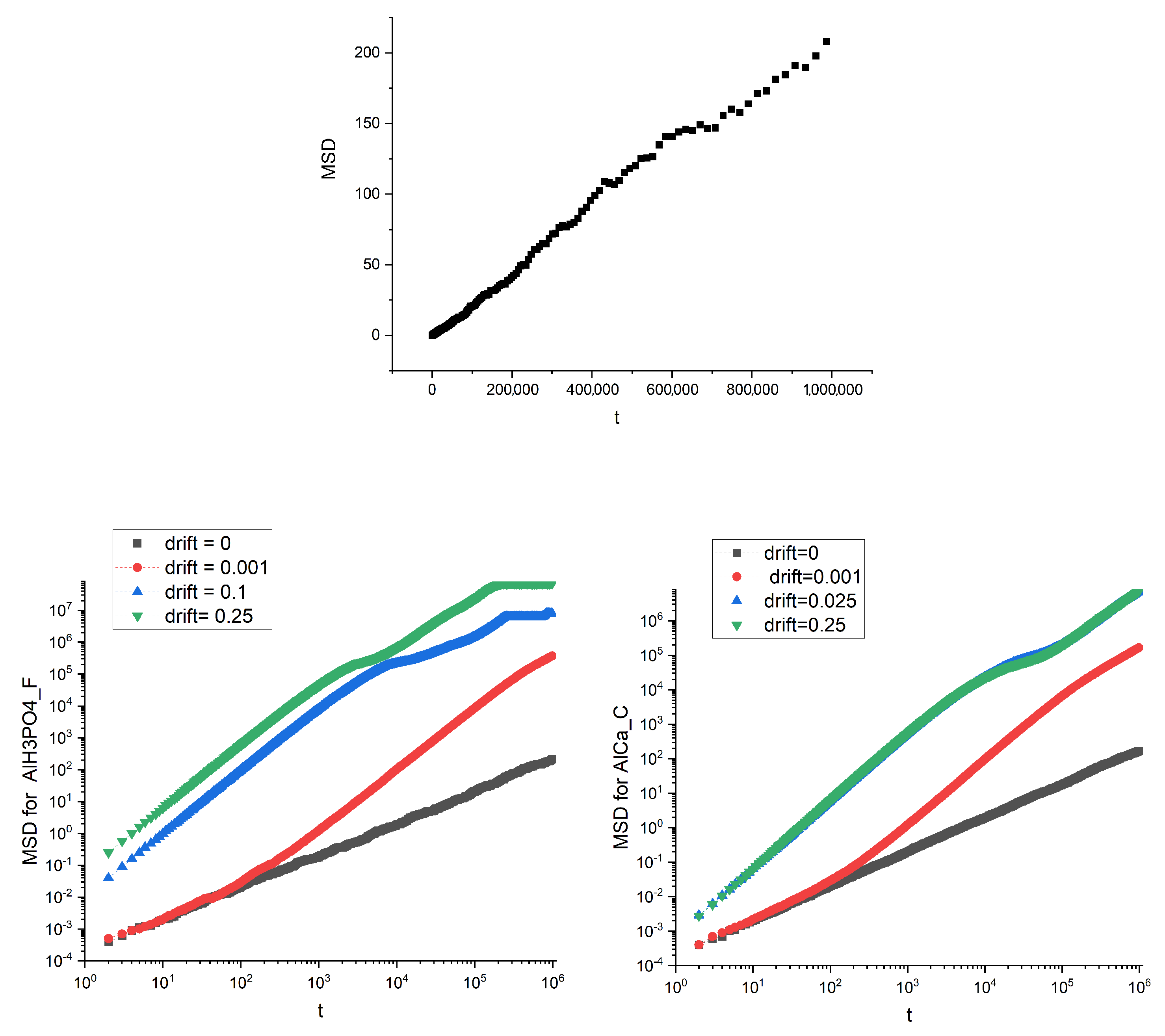
2.4. Diffusion Model
- The jump length is selected randomly according to Gaussian probability distribution of zero mean and variance;
- The direction of the above jump is selected randomly from the uniform probability distribution in the interval
- The constant term corresponding to the drift is added to the previously determined movement.
- The position of the particle is updated only if the movement does not end in or intersect an obstacle.
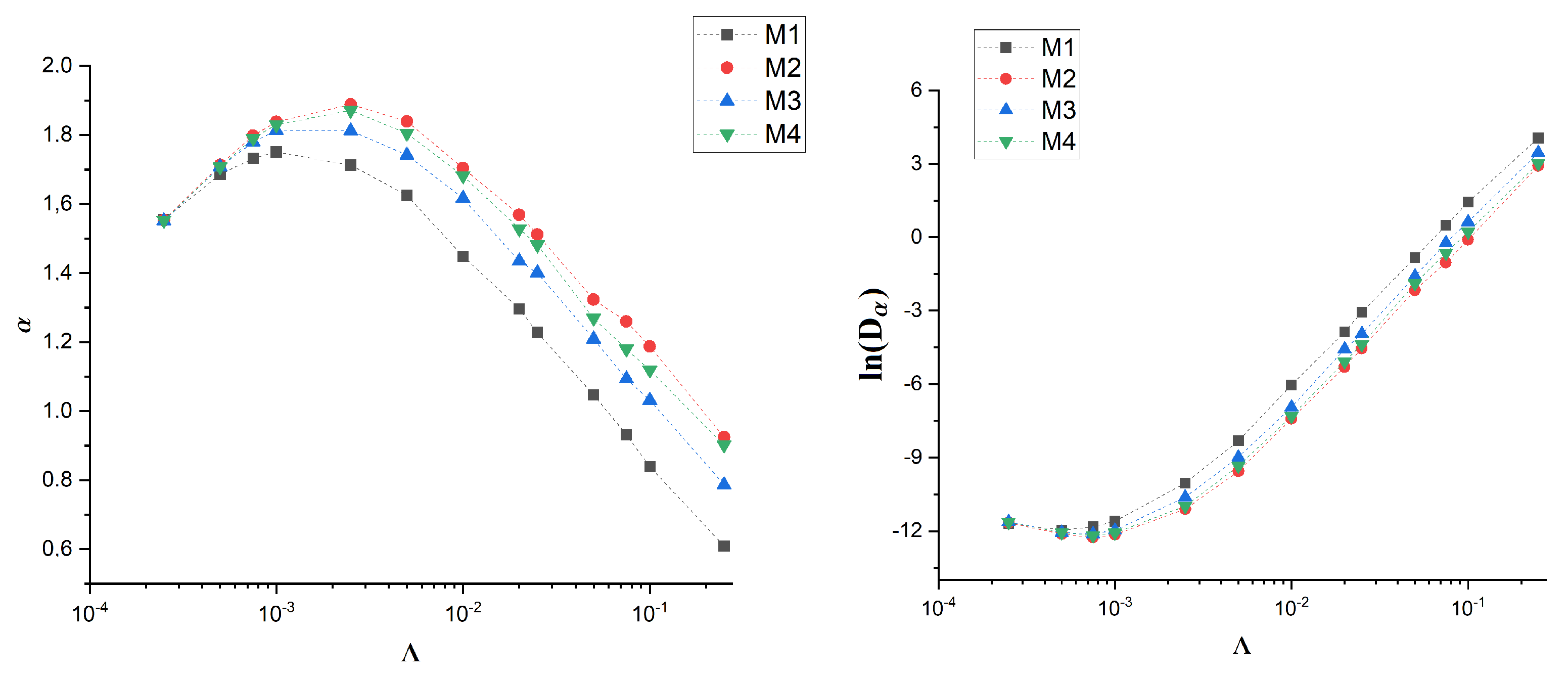
3. Results
3.1. Real Membranes
3.2. Artificial Membranes
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AlCa | Alginate membrane cross-linked by calcium chloride with 15 wt% of magnetite particles |
| AlHPO | Alginate membrane cross-linked by phosphoric acid with 15 wt% of magnetite particles |
| MSD | Mean square displacement |
Appendix A
| Membrane | |||
|---|---|---|---|
| 0.00000 | 1.0027 ± 0.0006 | −8.9173 ± 0.0057 | |
| 0.00025 | 1.5548 ± 0.0108 | −11.7190 ± 0.0965 | |
| 0.00050 | 1.6974 ± 0.0091 | −12.0403 ± 0.0813 | |
| 0.00075 | 1.7609 ± 0.0075 | −12.0175 ± 0.0671 | |
| 0.00100 | 1.7752 ± 0.0067 | −11.7494 ± 0.0601 | |
| 0.00250 | 1.7527 ± 0.0099 | −10.2851 ± 0.0879 | |
| 0.00500 | 1.6665 ± 0.0137 | −8.5712 ± 0.1222 | |
| 0.01000 | 1.4797 ± 0.0187 | −6.2336 ± 0.1662 | |
| 0.02000 | 1.2534 ± 0.0228 | −3.6803 ± 0.2029 | |
| 0.02500 | 1.1647 ± 0.0243 | −2.7738 ± 0.2161 | |
| 0.05000 | 0.9528 ± 0.0256 | −0.4219 ± 0.2276 | |
| 0.07500 | 0.8689 ± 0.0253 | 0.7349 ± 0.2251 | |
| 0.10000 | 0.8096 ± 0.0251 | 1.5445 ± 0.2234 | |
| 0.25000 | 0.5873 ± 0.0229 | 4.1089 ± 0.2040 | |
| 0.00000 | 1.0016 ± 0.0006 | −8.8763 ± 0.0058 | |
| 0.00025 | 1.5491 ± 0.0105 | −11.6427 ± 0.0938 | |
| 0.00050 | 1.6946 ± 0.0092 | −12.0225 ± 0.0820 | |
| 0.00075 | 1.7529 ± 0.0073 | −11.9371 ± 0.0655 | |
| 0.00100 | 1.7866 ± 0.0065 | −11.8214 ± 0.0583 | |
| 0.00250 | 1.7926 ± 0.0084 | −10.5556 ± 0.0746 | |
| 0.00500 | 1.6718 ± 0.0132 | −8.5978 ± 0.1176 | |
| 0.01000 | 1.4880 ± 0.0180 | −6.2783 ± 0.1606 | |
| 0.02000 | 1.2414 ± 0.0234 | −3.6113 ± 0.2080 | |
| 0.02500 | 1.1898 ± 0.0243 | −2.8969 ± 0.2161 | |
| 0.05000 | 0.9915 ± 0.0256 | −0.5834 ± 0.2274 | |
| 0.07500 | 0.8467 ± 0.0253 | 0.8250 ± 0.2249 | |
| 0.10000 | 0.8166 ± 0.0251 | 1.5149 ± 0.2233 | |
| 0.25000 | 0.5888 ± 0.0230 | 4.1083 ± 0.2046 | |
| 0.00000 | 0.9872 ± 0.0006 | −8.8056 ± 0.0061 | |
| 0.00025 | 1.5352 ± 0.0103 | −11.5435 ± 0.0918 | |
| 0.00050 | 1.6480 ± 0.0083 | −11.7404 ± 0.0740 | |
| 0.00075 | 1.6915 ± 0.0075 | −11.6050 ± 0.0665 | |
| 0.00100 | 1.6963 ± 0.0084 | −11.2913 ± 0.0745 | |
| 0.00250 | 1.6440 ± 0.0129 | −9.6653 ± 0.1145 | |
| 0.00500 | 1.5111 ± 0.0173 | −7.7364 ± 0.1541 | |
| 0.01000 | 1.3353 ± 0.0211 | −5.4783 ± 0.1882 | |
| 0.02000 | 1.0957 ± 0.0247 | −2.9066 ± 0.2198 | |
| 0.02500 | 1.0300 ± 0.0253 | −2.1543 ± 0.2248 | |
| 0.05000 | 0.8166 ± 0.0251 | 0.1305 ± 0.2234 | |
| 0.07500 | 0.7366 ± 0.0246 | 1.2344 ± 0.2188 | |
| 0.10000 | 0.6669 ± 0.0240 | 2.0422 ± 0.2131 | |
| 0.25000 | 0.4507 ± 0.0207 | 4.4201 ± 0.1838 |
| Membrane | |||
|---|---|---|---|
| 0.00000 | 1.0075 ± 0.0020 | −8.9991 ± 0.0186 | |
| 0.00025 | 1.5542 ± 0.0109 | −11.6921 ± 0.0971 | |
| 0.00030 | 1.5902 ± 0.0103 | −11.7740 ± 0.0917 | |
| 0.00040 | 1.6483 ± 0.0106 | −11.8981 ± 0.0947 | |
| 0.00050 | 1.6777 ± 0.0093 | −11.8377 ± 0.0833 | |
| 0.00075 | 1.7442 ± 0.0073 | −11.9039 ± 0.0651 | |
| 0.00100 | 1.7712 ± 0.0074 | −11.6999 ± 0.6572 | |
| 0.00250 | 1.7620 ± 0.0107 | −10.3687 ± 0.0953 | |
| 0.00500 | 1.6567 ± 0.0148 | −8.4944 ± 0.1316 | |
| 0.01000 | 1.4961 ± 0.0199 | −6.2902 ± 0.1770 | |
| 0.02000 | 1.3099 ± 0.0233 | −3.9347 ± 0.2070 | |
| 0.02500 | 1.2404 ± 0.0242 | −3.1323 ± 0.2155 | |
| 0.05000 | 0.9949 ± 0.0253 | −0.6088 ± 0.2250 | |
| 0.07500 | 0.9289 ± 0.0256 | 0.4937 ± 0.2273 | |
| 0.10000 | 0.8115 ± 0.0251 | 1.5388 ± 0.2235 | |
| 0.25000 | 0.6040 ± 0.0233 | 4.0647 ± 0.2066 | |
| 0.50000 | 0.4517 ± 0.0207 | 5.8110 ± 0.7370 | |
| 0.00000 | 1.0018 ± 0.0019 | −8.9305 ± 0.0177 | |
| 0.00025 | 1.5450 ± 0.0119 | −11.6071 ± 0.1061 | |
| 0.00030 | 1.6047 ± 0.0104 | −11.8923 ± 0.0926 | |
| 0.00040 | 1.6674 ± 0.0104 | −12.0907 ± 0.0926 | |
| 0.00050 | 1.7226 ± 0.0096 | −12.2484 ± 0.0855 | |
| 0.00075 | 1.7749 ± 0.0080 | −12.1502 ± 0.0718 | |
| 0.00100 | 1.8042 ± 0.0071 | −11.9647 ± 0.0638 | |
| 0.00250 | 1.8087 ± 0.0084 | −10.5423 ± 0.0748 | |
| 0.00500 | 1.7371 ± 0.0133 | −8.9492 ± 0.1186 | |
| 0.01000 | 1.5943 ± 0.0177 | −6.7806 ± 0.1574 | |
| 0.02000 | 1.3698 ± 0.0222 | −4.2374 ± 0.1979 | |
| 0.02500 | 1.2861 ± 0.0237 | −3.3489 ± 0.2107 | |
| 0.05000 | 1.1470 ± 0.0251 | −1.2961 ± 0.2234 | |
| 0.07500 | 1.0860 ± 0.0254 | −0.1959 ± 0.2257 | |
| 0.10000 | 0.9023 ± 0.0255 | 1.1783 ± 0.2268 | |
| 0.25000 | 0.7335 ± 0.0246 | 3.6554 ± 0.2188 | |
| 0.50000 | 0.5296 ± 0.0221 | 5.6490 ± 0.1969 | |
| 0.00000 | 1.0038 ± 0.0019 | −8.9172 ± 0.0174 | |
| 0.00025 | 1.5435 ± 0.0100 | −11.5307 ± 0.0892 | |
| 0.00030 | 1.5946 ± 0.0099 | −11.7422 ± 0.0882 | |
| 0.00040 | 1.6585 ± 0.0101 | −11.9446 ± 0.0901 | |
| 0.00045 | 1.6800 ± 0.0099 | −11.9983 ± 0.0881 | |
| 0.00050 | 1.7015 ± 0.0093 | −12.0099 ± 0.0827 | |
| 0.00075 | 1.7664 ± 0.0079 | −12.0747 ± 0.0701 | |
| 0.00100 | 1.8016 ± 0.0062 | −11.8638 ± 0.0552 | |
| 0.00250 | 1.7829 ± 0.0097 | −10.4806 ± 0.0862 | |
| 0.00500 | 1.7512 ± 0.0124 | −9.0391 ± 0.1109 | |
| 0.01000 | 1.4974 ± 0.0205 | −6.3091 ± 0.1824 | |
| 0.02000 | 1.4187 ± 0.0221 | −4.4949 ± 0.1967 | |
| 0.02500 | 1.3322 ± 0.0234 | −3.5878 ± 0.2079 | |
| 0.05000 | 1.1523 ± 0.0251 | −1.3182 ± 0.2230 | |
| 0.07500 | 1.0796 ± 0.0254 | −0.1681 ± 0.2261 | |
| 0.10000 | 1.0560 ± 0.0254 | 0.5146 ± 0.2259 | |
| 0.25000 | 0.7108 ± 0.0244 | 3.7301 ± 0.2170 | |
| 0.50000 | 0.5531 ± 0.0225 | 5.5903 ± 0.2000 |
| Membrane | |||
|---|---|---|---|
| M1 | 0.00000 | 0.9898 ± 0.0006 | −8.8089 ± 0.0054 |
| M1 | 0.00025 | 1.5547 ± 0.0108 | −11.7079 ± 0.0964 |
| M1 | 0.00050 | 1.6855 ± 0.0089 | −11.9618 ± 0.0798 |
| M1 | 0.00075 | 1.7323 ± 0.0079 | −11.8228 ± 0.0707 |
| M1 | 0.00100 | 1.7505 ± 0.0078 | −11.5999 ± 0.0699 |
| M1 | 0.00250 | 1.7128 ± 0.0126 | −10.0363 ± 0.1122 |
| M1 | 0.00500 | 1.6247 ± 0.0167 | −8.3096 ± 0.1489 |
| M1 | 0.01000 | 1.4487 ± 0.0208 | −6.0322 ± 0.1849 |
| M1 | 0.02000 | 1.2968 ± 0.0234 | −3.8709 ± 0.2085 |
| M1 | 0.02500 | 1.2275 ± 0.0243 | −3.0686 ± 0.2159 |
| M1 | 0.05000 | 1.0470 ± 0.0255 | −0.8288 ± 0.2268 |
| M1 | 0.07500 | 0.9315 ± 0.0256 | 0.4812 ± 0.2273 |
| M1 | 0.10000 | 0.8393 ± 0.0253 | 1.4301 ± 0.2248 |
| M1 | 0.25000 | 0.6090 ± 0.0233 | 4.0524 ± 0.2071 |
| M2 | 0.00000 | 1.0036 ± 0.0006 | −8.9092 ± 0.0060 |
| M2 | 0.00025 | 1.5535 ± 0.0108 | −11.6600 ± 0.0958 |
| M2 | 0.00050 | 1.7138 ± 0.0094 | −12.1198 ± 0.0843 |
| M2 | 0.00075 | 1.7980 ± 0.0082 | −12.2650 ± 0.0736 |
| M2 | 0.00100 | 1.8383 ± 0.0068 | −12.1455 ± 0.0611 |
| M2 | 0.00250 | 1.8882 ± 0.0059 | −11.0998 ± 0.0531 |
| M2 | 0.00500 | 1.8397 ± 0.0099 | −9.5582 ± 0.0879 |
| M2 | 0.01000 | 1.7040 ± 0.0155 | −7.4194 ± 0.1383 |
| M2 | 0.02000 | 1.5688 ± 0.0194 | −5.2968 ± 0.1724 |
| M2 | 0.02500 | 1.5120 ± 0.0206 | −4.5355 ± 0.1833 |
| M2 | 0.05000 | 1.3232 ± 0.0236 | −2.1600 ± 0.2100 |
| M2 | 0.07500 | 1.2594 ± 0.0243 | −1.0291 ± 0.2161 |
| M2 | 0.10000 | 1.1875 ± 0.0249 | −0.1003 ± 0.2213 |
| M2 | 0.25000 | 0.9250 ± 0.0256 | 2.9178 ± 0.2273 |
| Membrane | |||
|---|---|---|---|
| M3 | 0.00000 | 1.0008±0.0007 | −8.8996 ± 0.0068 |
| M3 | 0.00025 | 1.5509 ± 0.0107 | −11.6224 ± 0.0950 |
| M3 | 0.00050 | 1.7085 ± 0.0092 | −12.0638 ± 0.0824 |
| M3 | 0.00075 | 1.7791 ± 0.0079 | −12.1137 ± 0.0708 |
| M3 | 0.00100 | 1.8130 ± 0.0066 | −11.9707 ± 0.0593 |
| M3 | 0.00250 | 1.8119 ± 0.0090 | −10.6145 ± 0.0804 |
| M3 | 0.00500 | 1.7420 ± 0.0136 | −8.9810 ± 0.1210 |
| M3 | 0.01000 | 1.6163 ± 0.0177 | −6.9412 ± 0.1578 |
| M3 | 0.02000 | 1.4346 ± 0.0218 | −4.5740 ± 0.1938 |
| M3 | 0.02500 | 1.4006 ± 0.0223 | −3.9472 ± 0.1985 |
| M3 | 0.05000 | 1.2094 ± 0.0247 | −1.5942 ± 0.2199 |
| M3 | 0.07500 | 1.0931 ± 0.0254 | −0.2297 ± 0.2258 |
| M3 | 0.10000 | 1.0316 ± 0.0255 | 0.6248 ± 0.2272 |
| M3 | 0.25000 | 0.7872 ± 0.0250 | 3.4615 ± 0.2223 |
| M4 | 0.00000 | 1.0006 ± 0.0005 | −8.8927 ± 0.0050 |
| M4 | 0.00025 | 1.5524 ± 0.0107 | −11.6419 ± 0.0957 |
| M4 | 0.00050 | 1.7074 ± 0.0095 | −12.0586 ± 0.0845 |
| M4 | 0.00075 | 1.7903 ± 0.0082 | −12.1917 ± 0.0730 |
| M4 | 0.00100 | 1.8298 ± 0.0066 | −12.0739 ± 0.0594 |
| M4 | 0.00250 | 1.8712 ± 0.0064 | −10.9861 ± 0.0573 |
| M4 | 0.00500 | 1.8047 ± 0.0107 | −9.3423 ± 0.0952 |
| M4 | 0.01000 | 1.6816 ± 0.0158 | −7.3097 ± 0.1409 |
| M4 | 0.02000 | 1.5286 ± 0.0199 | −5.0806 ± 0.1771 |
| M4 | 0.02500 | 1.4812 ± 0.0210 | −4.3725 ± 0.1872 |
| M4 | 0.05000 | 1.2689 ± 0.0242 | −1.8885 ± 0.2152 |
| M4 | 0.07500 | 1.1801 ± 0.0249 | −0.6404 ± 0.2218 |
| M4 | 0.10000 | 1.1190 ± 0.0253 | 0.2243 ± 0.2249 |
| M4 | 0.25000 | 0.9015 ± 0.0255 | 3.0148 ± 0.2268 |
References
- Baker, R. Membrane Technology and Applications, 3rd ed.; Wiley: Chichester, UK, 2012. [Google Scholar]
- Das, C.; Gebru, K.A. Polymeric Membrane Synthesis, Modification, and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Hilal, N.; Khayet, M.; Wright, C. Membrane Modification: Technology and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Wu, H.; Zamanian, M.; Kruczek, B.; Thibault, J. Gas Permeation Model of Mixed-Matrix Membranes with Embedded Impermeable Cuboid Nanoparticles. Membranes 2020, 10, 422. [Google Scholar] [CrossRef] [PubMed]
- De Angelis, M.G.; Sarti, G.C. Gas Transport in Glassy Polymers. Membranes 2020, 10, 400. [Google Scholar] [CrossRef]
- Minelli, M.; Sarti, G.C. Gas Transport in Glassy Polymers: Prediction of Diffusional Time Lag. Membranes 2018, 8, 8. [Google Scholar] [CrossRef]
- Gałczyńska, K.; Rachuna, J.; Ciepluch, K.; Kowalska, M.; Wa̧sik, S.; Kosztołowicz, T.; Lewandowska, K.D.; Semaniak, J.; Kurdziel, K.; Arabski, M. Experimental and Theoretical Analysis of Metal Complex Diffusion through Cell Monolayer. Entropy 2021, 23, 360. [Google Scholar] [CrossRef] [PubMed]
- Rico-Martinez, S.; Alvarez, C.; Hernandez, A.; Miguel, J.A.; Lozano, A.E. Mixed Matrix Membranes Loaded with a Porous Organic Polymer Having Bipyridine Moieties. Membranes 2022, 12, 547. [Google Scholar] [CrossRef] [PubMed]
- Lau, H.S.; Lau, S.K.; Soh, L.S.; Hong, S.U.; Gok, X.Y.; Yi, S.; Yong, W.F. State-of-the-Art Organic- and Inorganic-Based Hollow Fiber Membranes in Liquid and Gas Applications: Looking Back and Beyond. Membranes 2022, 12, 539. [Google Scholar] [CrossRef] [PubMed]
- Kurihara, M. Current Status and Future Trend of Dominant Commercial Reverse Osmosis Membranes. Membranes 2021, 11, 906. [Google Scholar] [CrossRef]
- Friess, K.; Izák, P.; Kárászová, M.; Pasichnyk, M.; Lanč, M.; Nikolaeva, D.; Luis, P.; Jansen, J.C. A Review on Ionic Liquid Gas Separation Membranes. Membranes 2021, 11, 97. [Google Scholar] [CrossRef]
- Yang, G.; Xie, Z.; Cran, M.; Wu, C.; Gray, S. Dimensional Nanofillers in Mixed Matrix Membranes for Pervaporation Separations: A Review. Membranes 2020, 10, 193. [Google Scholar] [CrossRef]
- Liu, G.; Jin, W. Pervaporation membrane materials: Recent trends and perspectives. J. Membr. Sci. 2021, 636, 119557. [Google Scholar] [CrossRef]
- Siekierka, A.; Smolińska-Kempisty, K.; Wolska, J. Enhanced Specific Mechanism of Separation by Polymeric Membrane Modification; A Short Review. Membranes 2021, 11, 942. [Google Scholar] [CrossRef] [PubMed]
- Minelli, M.; Sarti, G.C. Thermodynamic Modeling of Gas Transport in Glassy Polymeric Membranes. Membranes 2017, 7, 46. [Google Scholar] [CrossRef] [PubMed]
- Bissadi, G.; Melo Santos, T.; Kruczek, B. Synthesis and Gas Transport Properties of Poly(2,6-dimethyl-1,4-phenylene oxide)—Silica Nanocomposite Membranes. Membranes 2018, 8, 125. [Google Scholar] [CrossRef] [PubMed]
- Krasowska, M.; Rybak, A.; Dudek, G.; Strzelewicz, A.; Pawełek, K.; Grzywna, Z.J. Structure morphology problems in the air separation by polymer membranes with magnetic particles. J. Membr. Sci. 2012, 415, 864–870. [Google Scholar] [CrossRef]
- Krasowska, M.; Strzelewicz, A.; Rybak, A.; Dudek, G.; Cieśla, M. Structure and transport properties of ethylcellulose membranes with different types and granulation of magnetic powder. Physica A 2016, 452, 241–250. [Google Scholar] [CrossRef]
- Krasowska, M.; Strzelewicz, A.; Dudek, G.; Cieśla, M. Structure-diffusion relationship of polymer membranes with different texture. Phys. Rev. E 2017, 95, 012155. [Google Scholar] [CrossRef]
- Dudek, G.; Gnus, M.; Strzelewicz, A.; Turczyn, R.; Krasowska, M. The influence of metal oxides on the separation properties of hybrid alginate membranes. Sep. Sci. Technol. 2018, 53, 1178–1190. [Google Scholar] [CrossRef]
- Dudek, G.; Krasowska, M.; Turczyn, R.; Gnus, M.; Strzelewicz, A. Structure, morphology and separation efficiency of hybrid Alg /Fe3O4 membranes in pervaporative dehydration of ethanol. Sep. Purif. Technol. 2017, 182, 101–109. [Google Scholar] [CrossRef]
- Krasowska, M.; Strzelewicz, A.; Dudek, G. Stereological—Fractal Analysis as a Tool for a Precise Description of the Morphology of Hybrid Alginate Membranes. Acta Phys. Polon. B 2019, 50, 1463–1478. [Google Scholar] [CrossRef]
- Dudek, G.; Borys, P.; Strzelewicz, A.; Krasowska, M. Characterization of the Structure and Transport Properties of Alginate/Chitosan Microparticle Membranes Utilized in the Pervaporative Dehydration of Ethanol. Polymers 2020, 12, 411. [Google Scholar] [CrossRef]
- Strzelewicz, A.; Krasowska, M.; Dudek, G.; Cieśla, M. Design of polymer membrane morphology with prescribed structure and diffusion properties. Chem. Phys. 2020, 531, 110662. [Google Scholar] [CrossRef]
- Strzelewicz, A.; Krasowska, M.; Dudek, G.; Cieśla, M. Optimal hybrid membrane structure based on experimental results and simulation analysis of diffusion process. J. Mater. Sci. 2022, 57, 11491–11504. [Google Scholar] [CrossRef]
- Dudek, G.; Turczyn, R.; Gnus, M.; Konieczny, K. Pervaporative dehydration of ethanol/water mixture through hybrid alginate membranes with ferroferic oxide nanoparticles. Sep. Purif. Technol. 2018, 193, 398–407. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Hänggi, P.; Luczka, J.; Talkner, P. Focus on Brownian Motion and Diffusion in the 21st Century. New J. Phys. 2005, 7, E01. [Google Scholar] [CrossRef]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E. Discriminating between normal and anomalous random walks. Phys. Rev. E 2009, 80, 061122. [Google Scholar] [CrossRef]
- Kubala, P.; Cieśla, M.; Dybiec, B. Diffusion in crowded environments: Trapped by the drift. Phys. Rev. E 2021, 104, 044127. [Google Scholar] [CrossRef]
- Ochab-Marcinek, A.; Hołyst, R. Scale-dependent diffusion of spheres in solutions of flexible and rigid polymers: Mean square displacement and autocorrelation function for FCS and DLS measurements. Soft Matter 2011, 7, 7366–7374. [Google Scholar] [CrossRef]
- Arango-Restrepo, A.; Rubi, J.M. Entropic transport in a crowded medium. J. Chem. Phys 2020, 153, 034108. [Google Scholar] [CrossRef]
- Malgaretti, P.; Pagonabarraga, I.; Rubi, J.M. Rectification and Non-Gaussian Diffusion in Heterogeneous Media. Entropy 2016, 18, 394. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Barkai, E.; Dubkov, A.A. Lévy flights versus Lévy walks in bounded domains. Phys. Rev. E 2017, 95, 052102. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krasowska, M.; Strzelewicz, A.; Dudek, G.; Cieśla, M. Numerical Study of Drift Influence on Diffusion Transport through the Hybrid Membrane. Membranes 2022, 12, 788. https://doi.org/10.3390/membranes12080788
Krasowska M, Strzelewicz A, Dudek G, Cieśla M. Numerical Study of Drift Influence on Diffusion Transport through the Hybrid Membrane. Membranes. 2022; 12(8):788. https://doi.org/10.3390/membranes12080788
Chicago/Turabian StyleKrasowska, Monika, Anna Strzelewicz, Gabriela Dudek, and Michał Cieśla. 2022. "Numerical Study of Drift Influence on Diffusion Transport through the Hybrid Membrane" Membranes 12, no. 8: 788. https://doi.org/10.3390/membranes12080788
APA StyleKrasowska, M., Strzelewicz, A., Dudek, G., & Cieśla, M. (2022). Numerical Study of Drift Influence on Diffusion Transport through the Hybrid Membrane. Membranes, 12(8), 788. https://doi.org/10.3390/membranes12080788