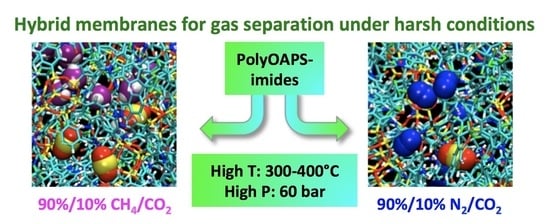
Molecular Characterization of Membrane Gas Separation under Very High Temperatures and Pressure: Single- and Mixed-Gas CO2/CH4 and CO2/N2 Permselectivities in Hybrid Networks
Abstract
:1. Introduction
2. Models and Methodologies
2.1. MD Simulation Parameters
2.2. Generation of the Hyper-Cross-Linked Networks
2.3. Modelling Single-Gas and Mixed-Gas Sorption in the Networks
2.4. Modelling Gas Diffusion, Permeability and Permselectivity in the Networks
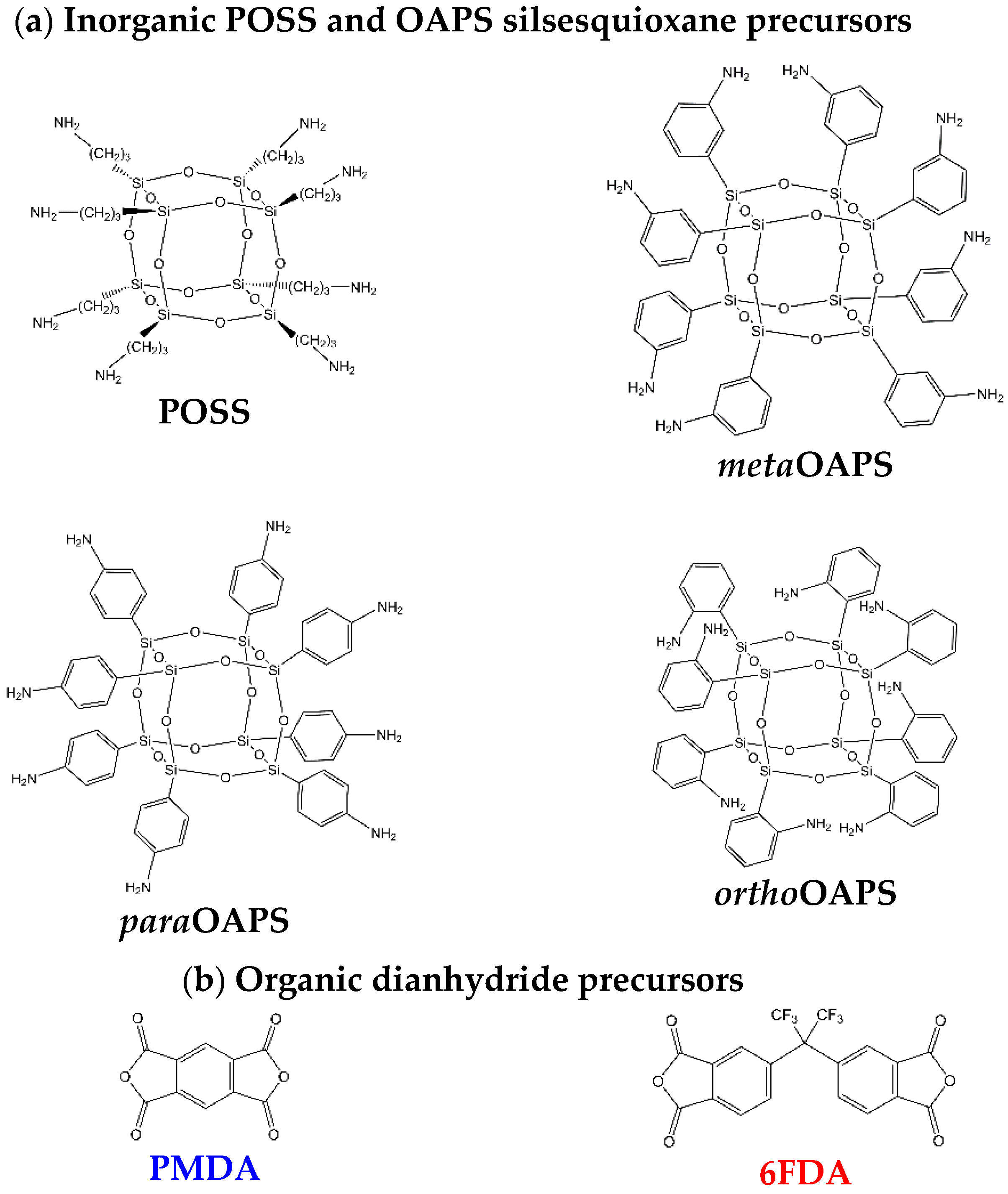
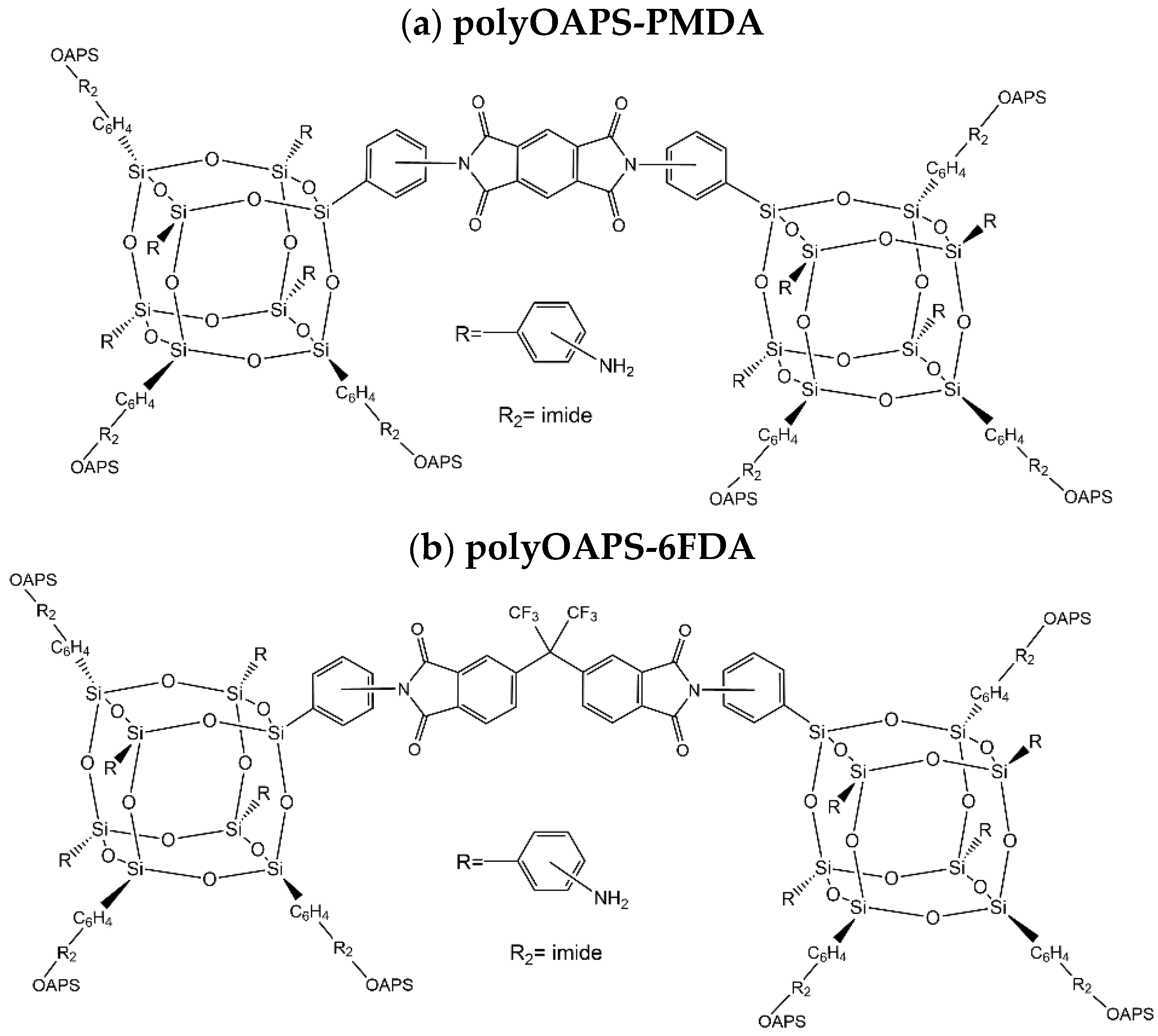
3. The PolyOAPS/POSS-Imide Hyper-Cross-Linked Networks
3.1. Molecular Connectivities
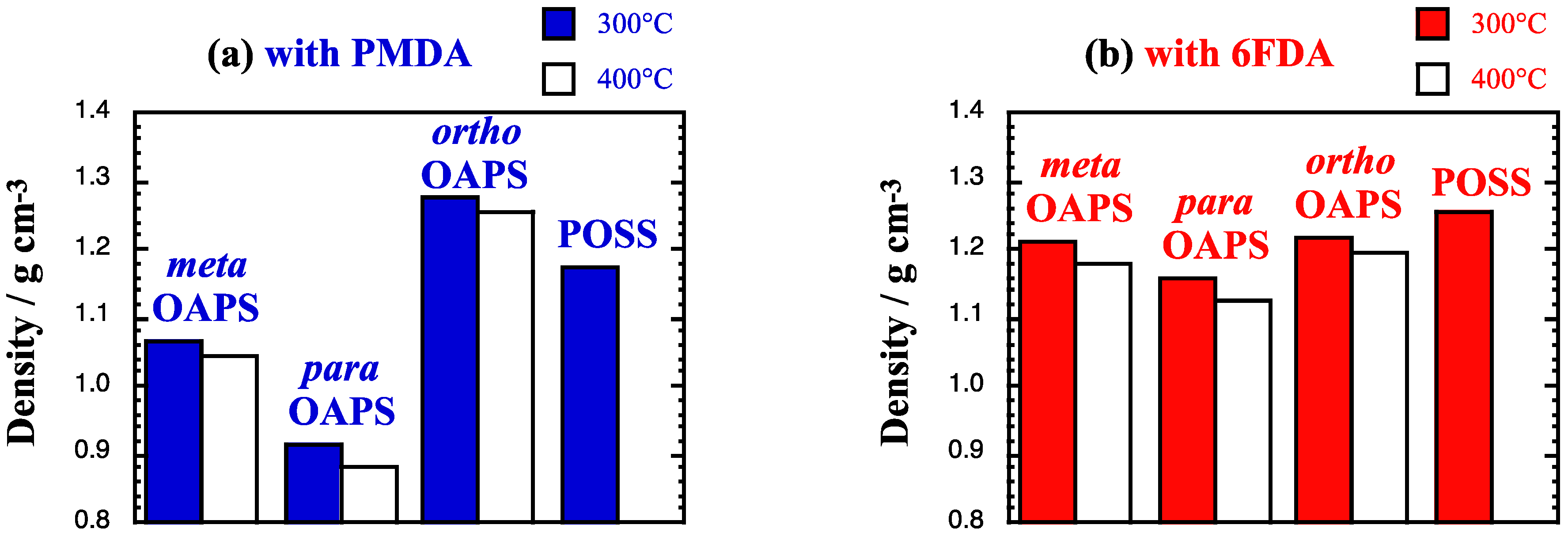
3.2. Densities
3.3. Free Volume Available for Gas Insertion
4. Ideal CO2/CH4 and CO2/N2 Permselectivities at 300 °C and 400 °C from Single-Gas N2, CH4 and CO2 Uptakes
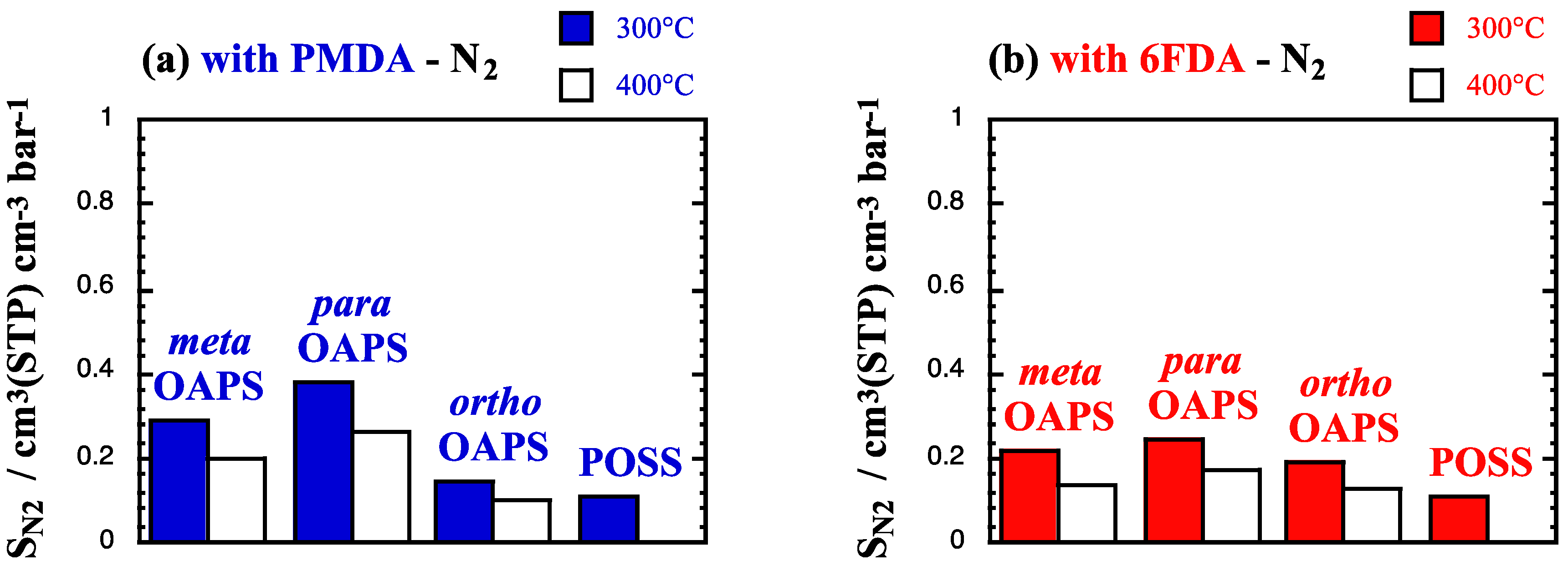
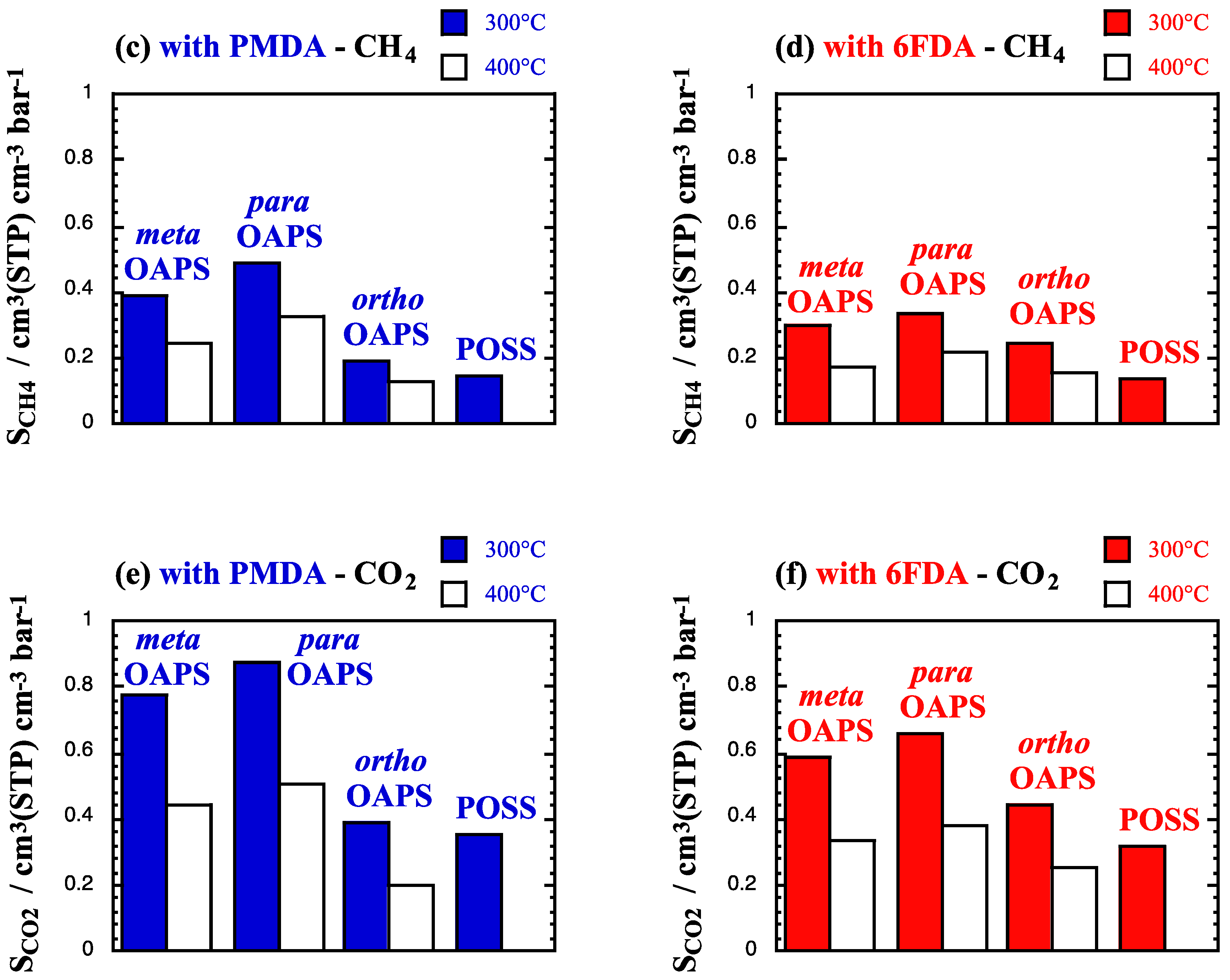
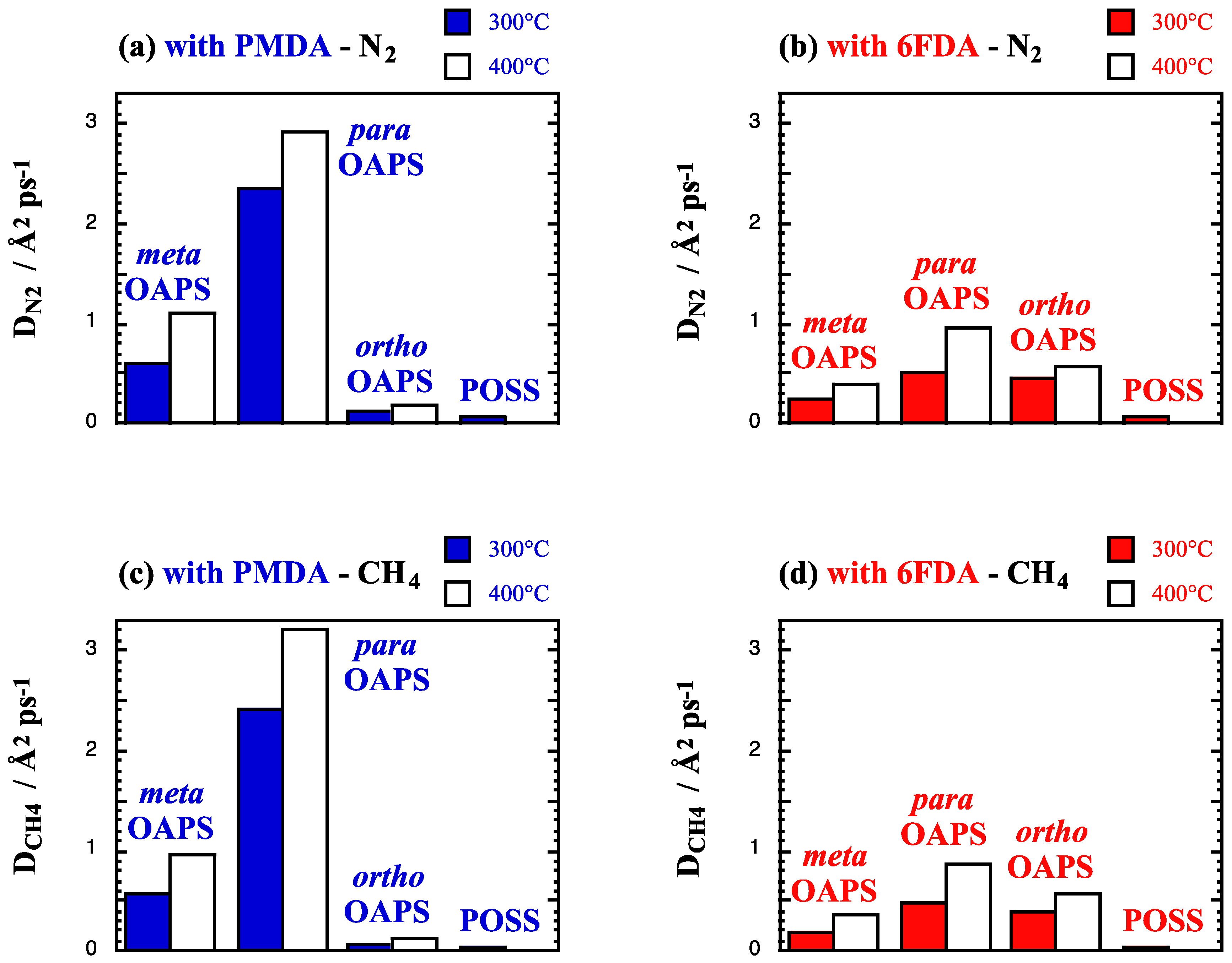
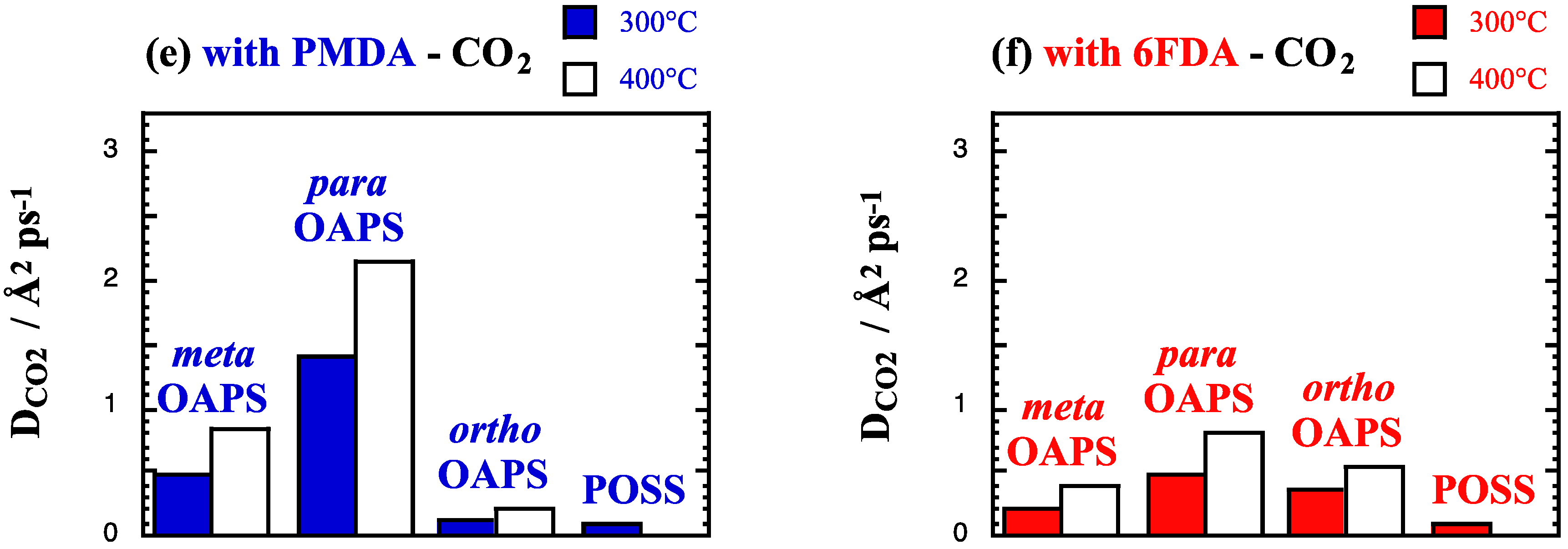
4.1. Single-Gas Solubilities and Diffusivities
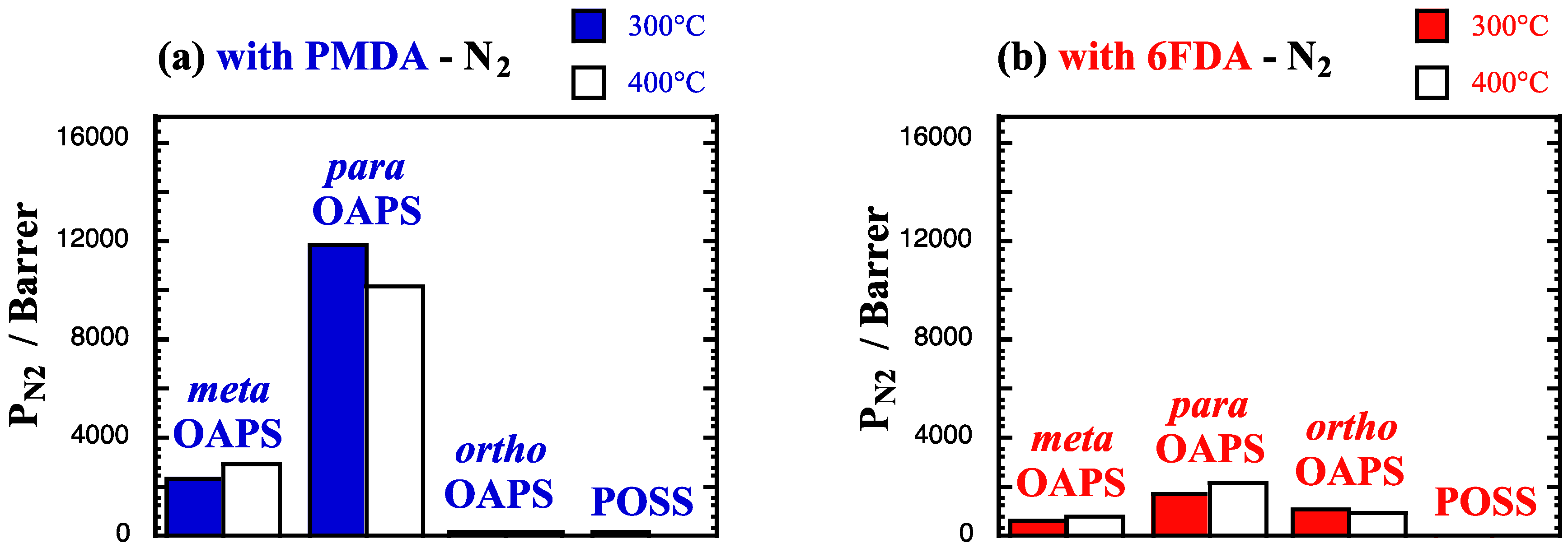
4.2. Single-Gas Permeabilities and Permselectivities
5. Mixed-Gas Separation Factors for Binary 90%/10% CH4/CO2 and N2/CO2 Mixtures at 300 °C and 400 °C
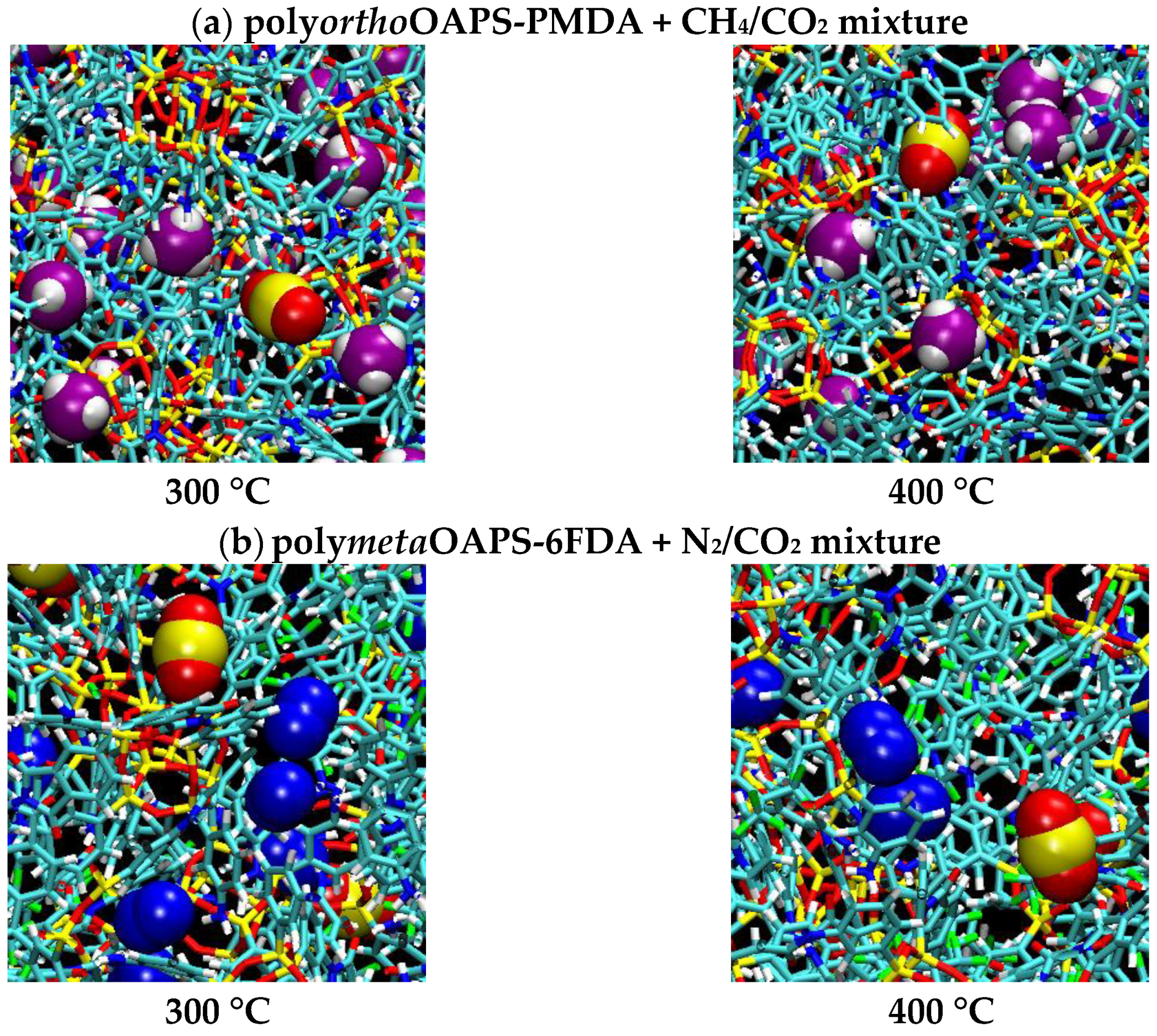
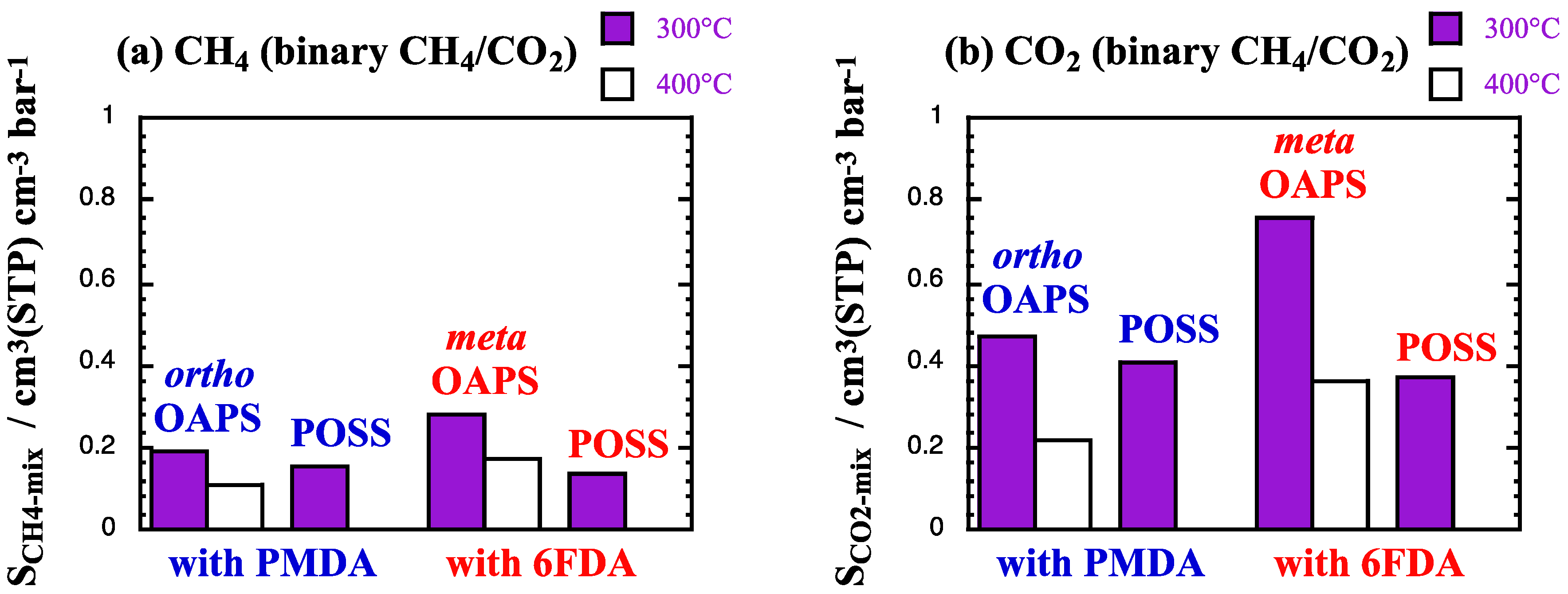
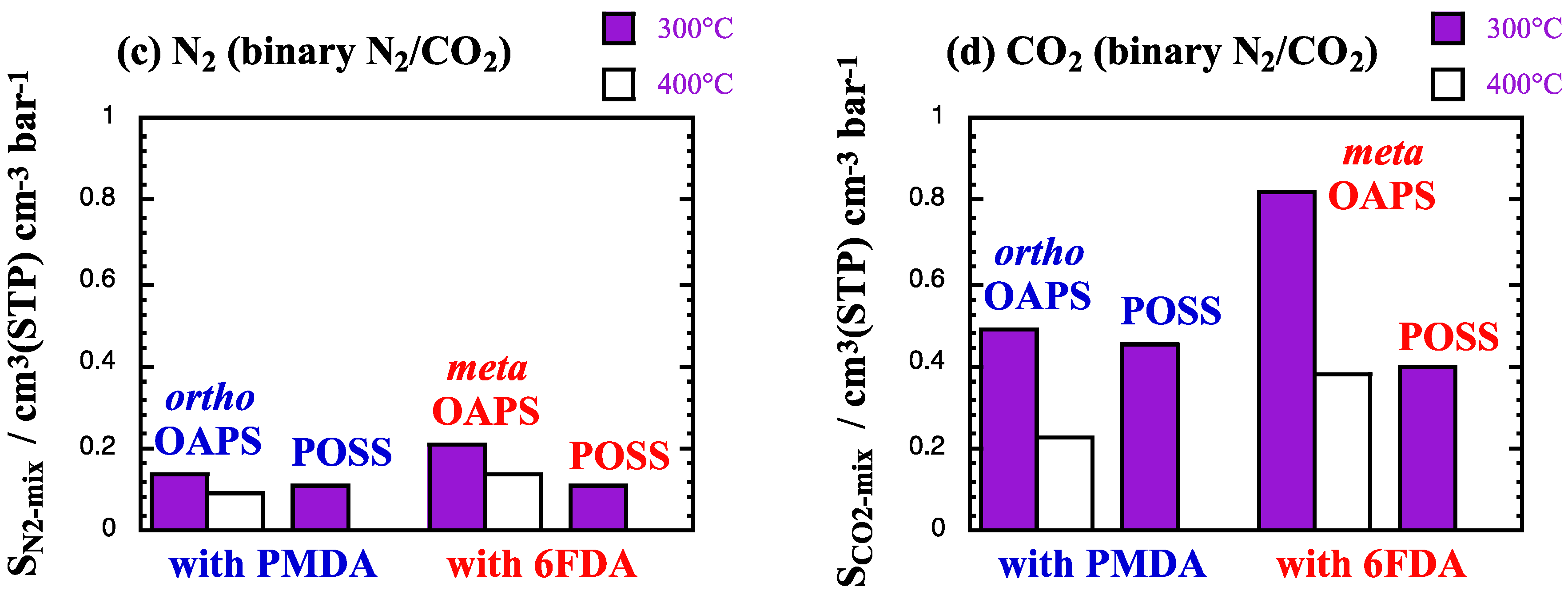
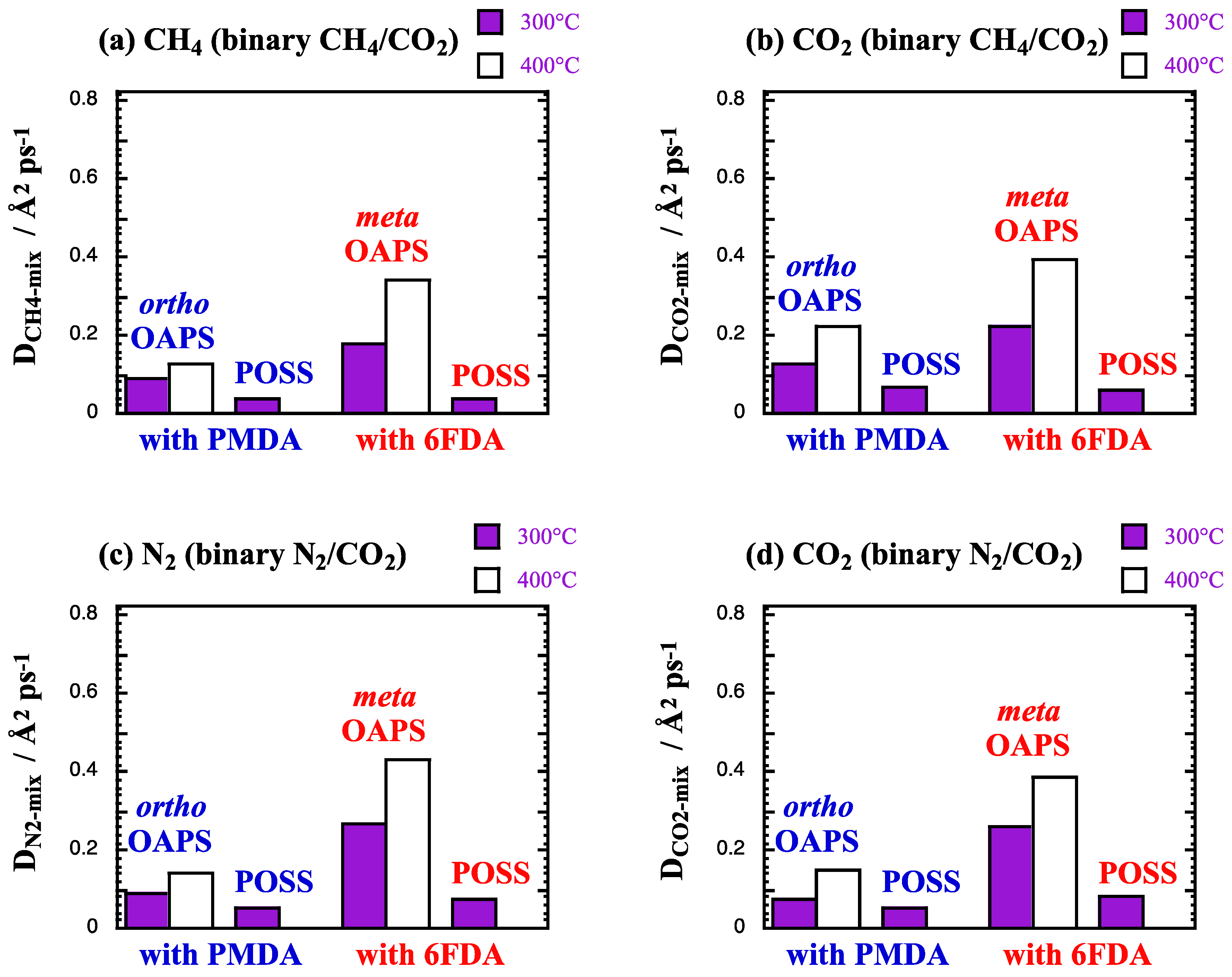
5.1. Mixed-Gas Solubilities and Diffusivities
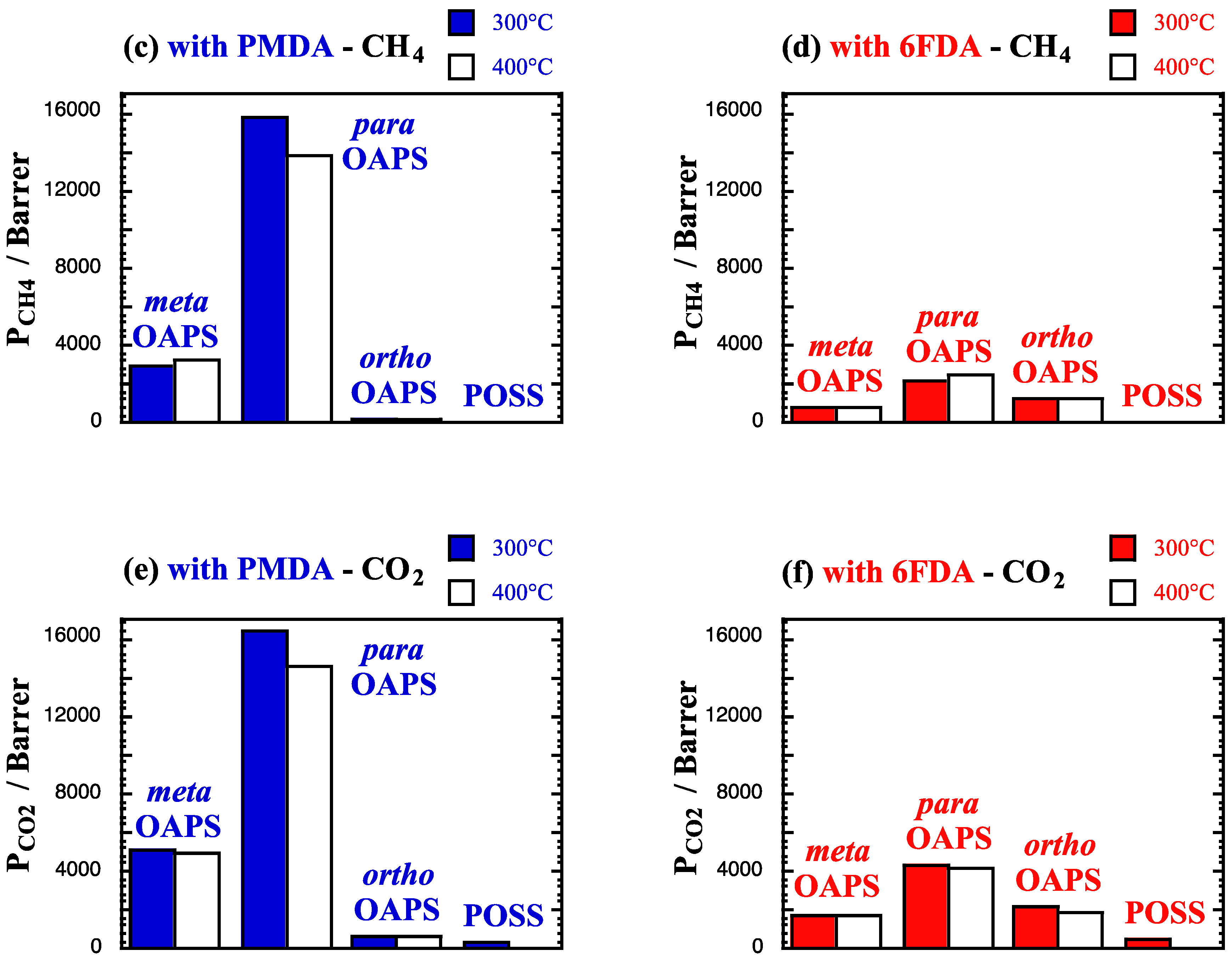
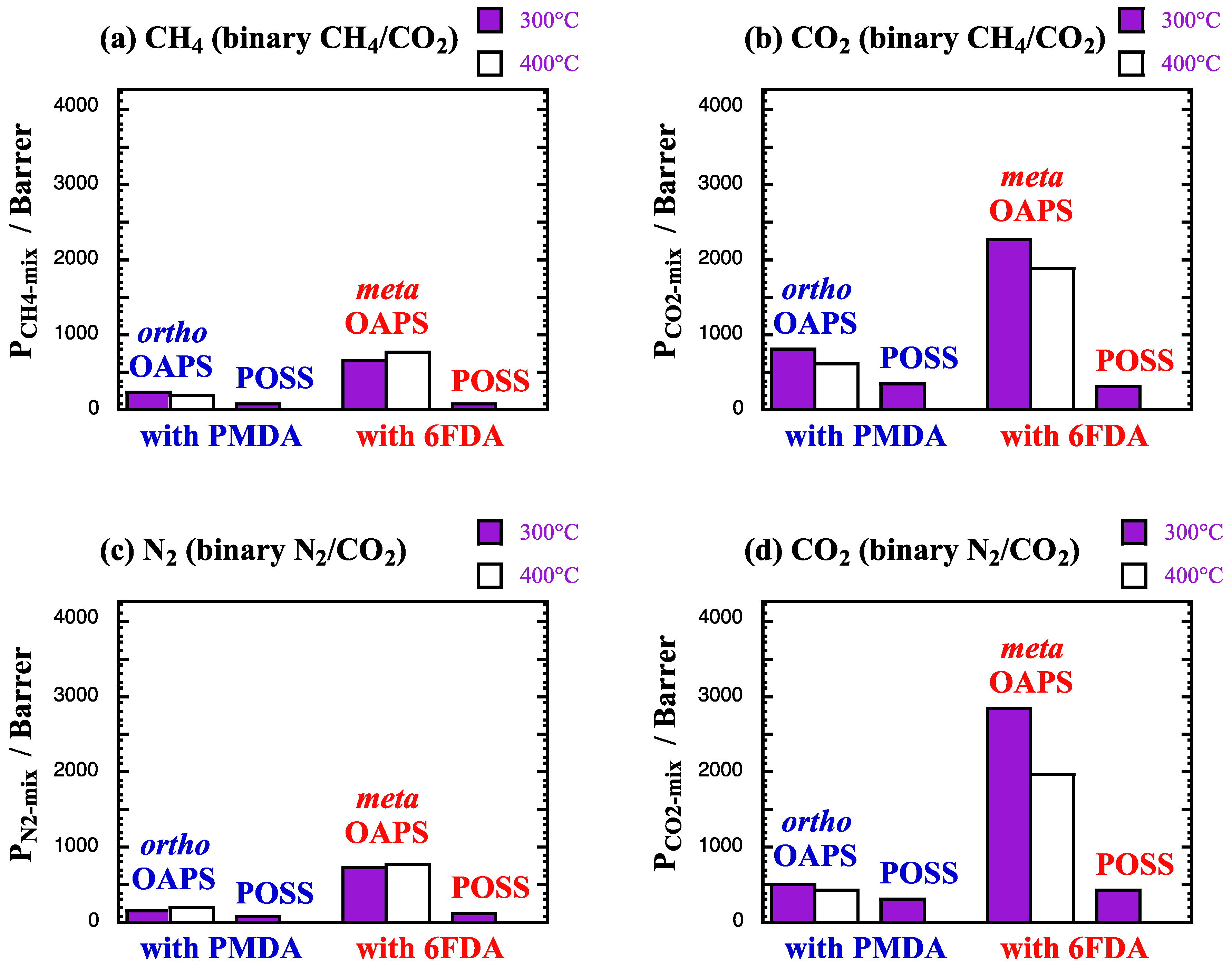
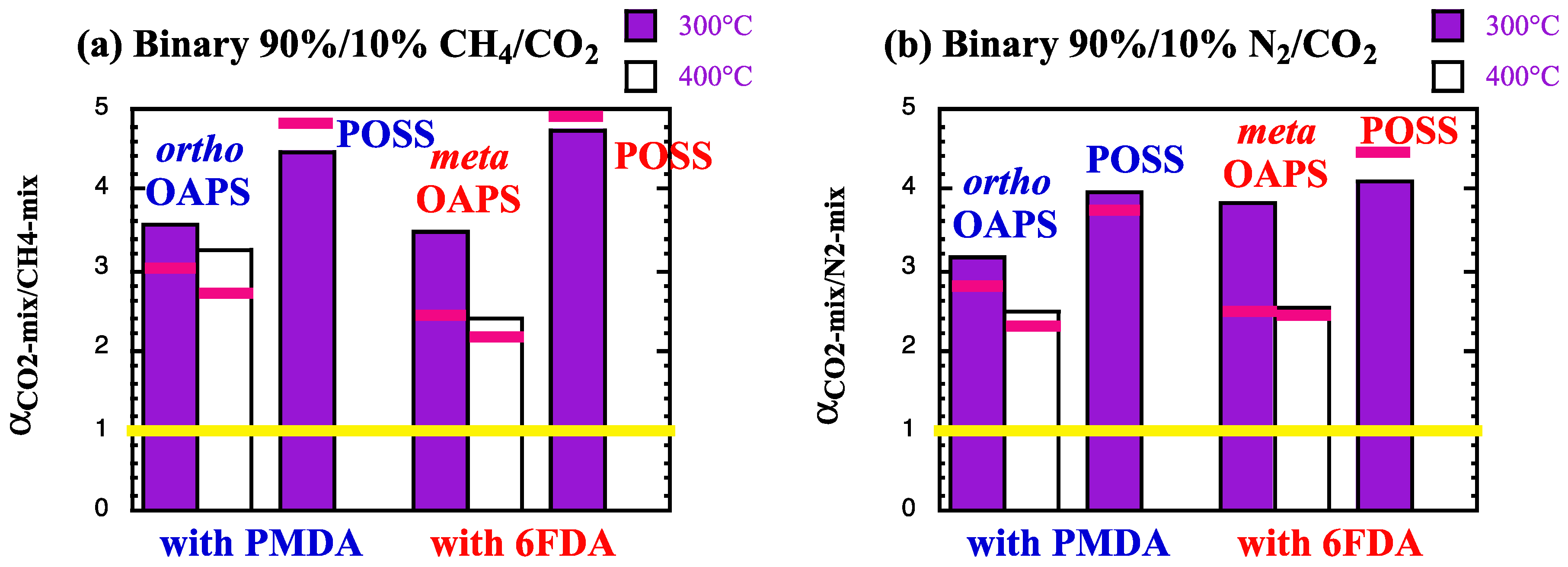
5.2. Mixed-Gas Permeabilities and Separation Factors
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sholl, D.S.; Lively, R.P. Exemplar Mixtures for Studying Complex Mixture Effects in Practical Chemical Separations. J. Am. Chem. Soc. Au 2022, 2, 322–327. [Google Scholar] [CrossRef] [PubMed]
- Sholl, D.S.; Lively, R.P. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef] [PubMed]
- Yampolskii, Y.; Pinnau, I.; Freeman, B.D. Materials Science of Membranes for Gas and Vapor Separation; John Wiley & Sons Ltd.: Chichester, UK, 2006. [Google Scholar]
- Arya, R.K.; Thapliyal, D.; Sharma, J.; Verros, G.D. Glassy Polymers—Diffusion, Sorption, Ageing and Applications. Coatings 2021, 11, 1049. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th anniversary perspective: Polymers and mixed matrix membranes for gas and vapor separation: A review and prospective opportunities. Macromolecules 2017, 50, 7809–7843. [Google Scholar] [CrossRef]
- Hennessy, J. Membranes from academia to industry. Nat. Mater. 2017, 16, 280–282. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Sadrzadeh, M.; Matsuura, T. Thermally stable polymers for advanced high-performance gas separation membranes. Prog. Ener. Combus. Sci. 2018, 66, 1–41. [Google Scholar] [CrossRef]
- Rowe, B.W.; Robeson, L.M.; Freeman, B.D.; Paul, D.R. Influence of temperature on the upper-bound: Theoretical considerations and comparison with experimental results. J. Membr. Sci. 2010, 360, 58–69. [Google Scholar] [CrossRef]
- Wessling, M.; Lidon Lopez, M.; Strathmann, H. Accelerated plasticization of thin-film composite membranes used in gas separation. Sep. Purif. Technol. 2001, 24, 223–233. [Google Scholar] [CrossRef]
- Heidenreich, S. Hot gas filtration—A review. Fuel 2013, 104, 83–94. [Google Scholar] [CrossRef]
- Lasseuguette, E.; Malpass-Evans, R.; Carta, M.; McKeown, N.B.; Ferrari, M.-C. Temperature and Pressure Dependence of Gas Permeation in a Microporous Tröger’s Base Polymer. Membranes 2018, 8, 132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ricci, E.; Benedetti, F.M.; Dose, M.E.; De Angelis, M.G.; Freeman, B.D.; Paul, D.R. Competitive sorption in CO2/CH4 separations: The case of HAB-6FDA polyimide and its TR derivative and a general analysis of its impact on the selectivity of glassy polymers at multicomponent conditions. J. Membr. Sci. 2020, 612, 118374. [Google Scholar] [CrossRef]
- Vanherck, K.; Koeckelberghs, G.; Vankelecom, I.F.J. Crosslinking polyimides for membrane applications: A review. Prog. Polym. Sci. 2013, 38, 874–896. [Google Scholar] [CrossRef]
- Reddy, B.S.R. Advances in Nanocomposites—Synthesis, Characterization and Industrial Applications; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Moore, T.; Koros, W.J. Non-ideal effects in organic-inorganic materials for gas separation membranes. J. Mol. Struct. 2005, 739, 87–98. [Google Scholar] [CrossRef]
- Peng, F.; Lu, L.; Sun, H.; Wang, Y.; Liu, J.; Jiang, Z. Hybrid organic-inorganic membrane: Solving the tradeoff between permeability and selectivity. Chem. Mater. 2005, 17, 6790–6796. [Google Scholar] [CrossRef]
- Cordes, D.B.; Lickiss, P.D.; Rataboul, F. Recent developments in the chemistry of cubic polyhedral oligosilsesquioxanes. Chem. Rev. 2010, 110, 2081–2173. [Google Scholar] [CrossRef]
- Laine, R.M.; Roll, M.F. Polyhedral phenylsilsesquioxanes. Macromolecules 2011, 44, 1073–1109. [Google Scholar] [CrossRef]
- Du, Y.; Liu, H. Cage-like silsesquioxanes-based hybrid materials. Dalton Trans. 2020, 49, 5396–5405. [Google Scholar] [CrossRef]
- Raftopoulos, K.N.; Pielichowski, K. Segmental dynamics in hybrid polymer/POSS nanomaterials. Prog. Polym. Sci. 2016, 52, 136–187. [Google Scholar] [CrossRef]
- Iyer, P.; Iyer, G.; Coleman, M. Gas transport properties of polyimide-POSS nanocomposites. J. Membr. Sci. 2010, 358, 26–32. [Google Scholar] [CrossRef]
- Pinson, D.M.; Yandek, G.R.; Haddad, T.S.; Horstman, E.M.; Mabry, J.M. Thermosetting poly(imide silsesquioxane)s featuring reduced moisture affinity and improved processability. Macromolecules 2013, 46, 7363–7377. [Google Scholar] [CrossRef]
- Mohamed, M.G.; Kuo, S.-W. Functional polyimide/polyhedral oligomeric silsesquioxane nanocomposites. Polymers 2019, 11, 26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lan, Z.; Chen, X.; Zhang, X.; Zhu, C.; Yu, Y.; Wei, J. Transparent, high glass-transition temperature, shape memory hybrid polyimides based on polyhedral oligomeric silsesquioxane. Polymers 2019, 11, 1058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, X.; Dumée, L.F. Polyhedral oligomeric silsesquioxane (POSS) nano-composite separation membranes—A review. Adv. Eng. Mater. 2019, 21, 1800667. [Google Scholar] [CrossRef]
- Raaijmakers, M.J.T.; Wessling, M.; Nijmeijer, A.; Benes, N.E. Hybrid polyhedral oligomeric silsesquioxanes-imides with tailored intercage spacing for sieving of hot gases. Chem. Mater. 2014, 26, 3660–3664. [Google Scholar] [CrossRef]
- Raaijmakers, M.J.T.; Hempenius, M.A.; Schön, P.M.; Vancso, G.J.; Nijmeijer, A.; Wessling, M.; Benes, N.E. Sieving of hot gases by hyper-cross-linked nanoscale-hybrid membranes. J. Am. Chem. Soc. 2014, 136, 330–335. [Google Scholar] [CrossRef] [Green Version]
- Raaijmakers, M.J.T.; Ogieglo, W.; Wiese, M.; Wessling, M.; Nijmeijer, A.; Benes, N.E. Sorption behavior of compressed CO2 and CH4 on ultrathin hybrid poly(POSS-imide) layers. ACS Appl. Mater. Interfaces 2015, 7, 26977–26988. [Google Scholar] [CrossRef]
- Raaijmakers, M.J.T.; Kappert, E.J.; Nijmeijer, A.; Benes, N.E. Thermal imidization kinetics of ultrathin films of hybrid poly(POSS-imide)s. Macromolecules 2015, 48, 3031–3039. [Google Scholar] [CrossRef]
- Ghosh, M.K.; Mittal, K.L. Polyimides: Fundamentals and Applications; Marcel Dekker, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Yampolskii, Y. Polymeric gas separation membranes. Macromolecules 2012, 45, 3298–3311. [Google Scholar] [CrossRef]
- Ansaloni, L.; Louradour, E.; Radmanesh, F.; van Veen, H.; Pilz, M.; Simon, C.; Benes, N.E.; Peters, T.A. Upscaling polyPOSS-imide membranes for high temperature H2 upgrading. J. Membr. Sci. 2021, 620, 118875. [Google Scholar] [CrossRef]
- Maaskant, E.; De Wit, P.; Benes, N.E. Direct interfacial polymerization onto thin ceramic hollow fibers. J. Membr. Sci. 2018, 550, 296–301. [Google Scholar] [CrossRef] [Green Version]
- Neyertz, S.; Brown, D.; Raaijmakers, M.J.T.; Benes, N.E. A molecular characterization of hyper-cross-linked hybrid polyPOSS-imide networks. Comp. Mater. Sci. 2016, 117, 338–353. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D.; Raaijmakers, M.J.T.; Benes, N.E. The influence of the dianhydride precursor in hyper-cross-linked hybrid polyPOSS-imide networks. Phys. Chem. Chem. Phys. 2016, 18, 28688–28703. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.; Neyertz, S.; Raaijmakers, M.J.T.; Benes, N.E. Sorption and permeation of gases in hyper-cross-linked hybrid poly(POSS-imide) networks: An in silico study. J. Membr. Sci. 2019, 577, 113–119. [Google Scholar] [CrossRef]
- Tamaki, R.; Tanaka, Y.; Asuncion, M.Z.; Choi, J.; Laine, R.M. Octa(aminophenyl)silsesquioxane as a nanoconstruction site. J. Am. Chem. Soc. 2001, 123, 12416–12417. [Google Scholar] [CrossRef]
- Nagendiran, S.; Chandramohan, A.; Dinakaran, K.; Alagar, M. Octahedral oligomeric silsesquioxane (OAPS and OG)—Polyimide hybrid nanocomposite films: Thermo-mechanical, dielectric and morphology properties. J. Macromol. Sci. Part A Pure Appl. Chem. 2019, 56, 1082–1096. [Google Scholar] [CrossRef]
- Yao, J.; Ma, S.; Zhang, J.; Wang, Y.; Wang, C.; Zhou, H.; Chen, C.; Liu, G. Multiple shape memory effects of polyimide nanocomposites based on octa(aminophenyl) silsequioxanes. EXPRESS Polym. Lett. 2021, 15, 433–444. [Google Scholar] [CrossRef]
- Huang, J.-C.; He, C.-B.; Xiao, Y.; Mya, K.Y.; Dai, J.; Siow, Y.P. Polyimide/POSS nanocomposites: Interfacial interaction, thermal properties and mechanical properties. Polymer 2003, 44, 4491–4499. [Google Scholar] [CrossRef]
- Krishnan, P.S.G.; He, C. Octa(maleimido phenyl) silsesquioxane copolymers. J. Polym. Sci. Part A Polym. Chem. 2005, 43, 2483–2494. [Google Scholar] [CrossRef]
- Govindaraj, B.; Sundararajan, P.; Sarojadevi, M. Synthesis and characterization of polyimide/polyhedral oligomeric silsesquioxane nanocomposites containing quinolyl moiety. Polym. Int. 2011, 61, 1344–1352. [Google Scholar] [CrossRef]
- Kim, S.G.; Choi, J.; Tamaki, R.; Laine, R.M. Synthesis of amino-containing oligophenylsilsesquioxanes. Polymer 2005, 46, 4514–4524. [Google Scholar] [CrossRef]
- Choi, J.; Tamaki, R.; Kim, S.G.; Laine, R.M. Organic/inorganic imide nanocomposites from aminophenylsilsesquioxanes. Chem. Mater. 2003, 15, 3365–3375. [Google Scholar] [CrossRef]
- Lo, M.Y.; Ueno, K.; Tanabe, H.; Sellinger, A. Silsesquioxane-based nanocomposite dendrimers with photo-luminescent and charge transport properties. Chem. Rec. 2006, 6, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lee, S.H.; Yoonessi, M.; Toghiani, H.; Pittman, C.U., Jr. Phenolic Resin/Octa(aminophenyl)-T8-Polyhedral Oligomeric Silsesquioxane (POSS) Hybrid Nanocomposites: Synthesis, Morphology, Thermal and Mechanical Properties. J. Inorg. Organomet. Polym. 2007, 17, 159–171. [Google Scholar] [CrossRef]
- Männle, F.; Tofteberg, T.; Skaugen, M.; Bu, H.; Peters, T.; Dietzel, P.D.C.; Pilz, M. Polymer nanocomposite coatings based on polyhedral oligosilsesquioxanes: Route for industrial manufacturing and barrier properties. J. Nanopart. Res. 2011, 13, 4691–4701. [Google Scholar] [CrossRef]
- Lee, A.; Haddad, T.S.; Schwab, J.J.; An, Y.Z. Molecular Structure Analysis of Aminophenyl Silsesquioxanes. 2006. Available online: https://www.researchgate.net/publication/277880144 (accessed on 8 January 2021).
- Koech, J.K.; Shao, Q.; Mutua, F.N.; Wang, Y. Application of hydrazine hydrate in the synthesis of octa(aminophenyl)silsesquioxane (OAPS) Poss. Adv. Chem. Eng. Sci. 2013, 3, 93–97. [Google Scholar] [CrossRef] [Green Version]
- Anstine, D.M.; Demidov, A.G.; Mendez, N.F.; Morgan, W.J.; Colina, C.M. Screening PIM-1 performance as a membrane for binary mixture separation of gaseous organic compounds. J. Membr. Sci. 2020, 599, 117798. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Single- and mixed-gas sorption in large-scale molecular models of glassy bulk polymers. Competitive sorption of a binary CH4/N2 and a ternary CH4/N2/CO2 mixture in a polyimide membrane. J. Membr. Sci. 2020, 614, 118478. [Google Scholar] [CrossRef]
- De Angelis, M.G.; Sarti, G.C. Gas Transport in Glassy Polymers. Membranes 2020, 10, 400. [Google Scholar] [CrossRef]
- Vergadou, N.; Theodorou, D.N. Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers. Membranes 2019, 9, 98. [Google Scholar] [CrossRef] [Green Version]
- Raaijmakers, M.J.T. Hyper-Cross-Linked, Hybrid Membranes via Interfacial Polymerization; University of Twente: Enschede, The Netherlands, 2015. [Google Scholar]
- Ricci, E.; Benedetti, F.M.; Noto, A.; Merkel, T.C.; Jin, J.; De Angelis, M.G. Enabling experimental characterization and prediction of ternary mixed-gas sorption in polymers: C2H6/CO2/CH4 in PIM-1. Chem. Eng. J. 2021, 426, 130715. [Google Scholar] [CrossRef]
- Walton, K.S. 110th Anniversary: Commentary: Perspectives on Adsorption of Complex Mixtures. Ind. Eng. Chem. Res. 2019, 58, 17100–17105. [Google Scholar] [CrossRef]
- Shade, D.; Mounfield, W.P.; Huang, Y.; Marszalek, B.; Walton, K.S. An automated multi-component gas adsorption system (MC GAS). Rev. Sci. Instrum. 2021, 92, 054102. [Google Scholar] [CrossRef] [PubMed]
- Neyertz, S.; Salimi, S.; Radmanesh, F.; Benes, N.E.; Brown, D. High-temperature molecular screening of hybrid polyOAPS-imide networks based on octa(aminophenyl)silsesquioxane for increased thermomechanical resistance. Phys. Chem. Chem. Phys. 2021, 23, 11438–11454. [Google Scholar] [CrossRef] [PubMed]
- Neyertz, S.; Brown, D.; Salimi, S.; Radmanesh, F.; Benes, N.E. Molecular characterization of polyOAPS-imide isomer hyper-cross-linked membranes: Free-volume morphologies and sorption isotherms for CH4 and CO2. J. Membr. Sci. 2021, 636, 119531. [Google Scholar] [CrossRef]
- Yang, Y.; Nair, A.K.N.; Sun, S. Sorption and Diffusion of Methane, Carbon Dioxide, and Their Mixture in Amorphous Polyethylene at High Pressures and Temperatures. Ind. Eng. Chem. Res. 2021, 60, 7729–7738. [Google Scholar] [CrossRef]
- Vopička, O.; De Angelis, M.G.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes: I. CO2/CH4 and n-C4/CH4 mixtures sorption in poly(1-trimethylsilyl-1-propyne) (PTMSP). J. Membr. Sci. 2014, 449, 97–108. [Google Scholar] [CrossRef]
- Vopička, O.; De Angelis, M.G.; Du, N.; Li, N.; Guiver, M.D.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes: II. CO2/CH4 mixtures in a polymer of intrinsic microporosity (PIM-1). J. Membr. Sci. 2014, 459, 264–276. [Google Scholar] [CrossRef] [Green Version]
- Gemeda, A.E.; De Angelis, M.G.; Du, N.; Li, N.; Guiver, M.D.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes. III. CO2/CH4 mixtures in a polymer of intrinsic microporosity (PIM-1): Effect of temperature. J. Membr. Sci. 2017, 524, 746–757. [Google Scholar] [CrossRef]
- Ricci, E.; Gemeda, A.E.; Du, N.; Li, N.; De Angelis, M.G.; Guiver, M.D.; Sarti, G.C. Sorption of CO2/CH4 mixtures in TZ-PIM, PIM-1 and PTMSP: Experimental data and NELF-model analysis of competitive sorption and selectivity in mixed gases. J. Membr. Sci. 2019, 585, 136–149. [Google Scholar] [CrossRef]
- Ricci, E.; De Angelis, M.G. Modelling mixed-gas sorption in glassy polymers for CO2 removal: A sensitivity analysis of the Dual Mode Sorption model. Membranes 2019, 9, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, D. The gmq User Manual Version 6. 2021. Available online: http://www.lmops.univ-savoie.fr/brown/gmq.html (accessed on 8 January 2021).
- Vrabec, J.; Stoll, J.; Hasse, H. A Set of Molecular Models for Symmetric Quadrupolar Fluids. J. Phys. Chem. B 2001, 105, 12126–12133. [Google Scholar] [CrossRef]
- Yin, D.; MacKerell, A.D., Jr. Combined ab initio/empirical approach for optimization of Lennard–Jones parameters. J. Comput. Chem. 1998, 19, 334–348. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, Z. An optimized molecular potential for carbon dioxide. J. Chem. Phys. 2005, 122, 214507. [Google Scholar] [CrossRef]
- Tildesley, D.J.; Madden, P. An effective pair potential for liquid carbon disulphide. Mol. Phys. 1981, 42, 1137–1156. [Google Scholar] [CrossRef]
- Ciccotti, G.; Ferrario, M.; Ryckaert, J.P. Molecular dynamics of rigid systems in cartesian coordinates. A general formulation. Mol. Phys. 1982, 47, 1253–1264. [Google Scholar] [CrossRef]
- Hammonds, K.D.; Ryckaert, J.-P. On the convergence of the SHAKE algorithm. Comput. Phys. Commun. 1991, 62, 336–351. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Brown, D.; Clarke, J.H.R. A loose-coupling constant pressure molecular dynamics algorithm for use in the modelling of polymer materials. Comput. Phys. Commun. 1991, 62, 360–369. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Wu, C.; Xu, W. Atomistic molecular modelling of crosslinked epoxy resin. Polymer 2006, 47, 6004–6009. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. A molecular dynamics study of epoxy-based networks: Cross-linking procedure and prediction of molecular and material properties. Macromolecules 2008, 41, 6837–6842. [Google Scholar] [CrossRef]
- Lacevic, N.; Gee, R.H.; Saab, A.; Maxwell, R. Computational exploration of polymer nanocomposite mechanical property modification via cross-linking topology. J. Chem. Phys. 2008, 129, 124903. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.-H.; Khare, R. Molecular simulation of cross-linked epoxy and epoxy-POSS nanocomposite. Macromolecules 2009, 42, 4319–4327. [Google Scholar] [CrossRef]
- Lin, P.-H.; Khare, R. Glass transition and structural properties of glycidyloxypropyl-heptaphenyl polyhedral oligomeric silsesquioxane-epoxy nanocomposites. A molecular simulation study. J. Therm. Anal. Calorim. 2010, 102, 461–467. [Google Scholar] [CrossRef]
- Shenogina, N.B.; Tsige, M.; Patnaik, S.S.; Mukhopadhyay, S.M. Molecular modeling approach to prediction of thermo-mechanical behavior of thermoset polymer networks. Macromolecules 2012, 45, 5307–5315. [Google Scholar] [CrossRef]
- Abbott, L.J.; Colina, C.M. Atomistic structure generation and gas adsorption simulations of microporous polymer networks. Macromolecules 2011, 44, 4511–4519. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Valavala, P.K.; Clancy, T.C.; Wise, K.E.; Odegard, G.M. Molecular modeling of crosslinked epoxy polymers: The effect of crosslink density on thermomechanical properties. Polymer 2011, 52, 2445–2452. [Google Scholar] [CrossRef]
- Moon, J.H.; Katha, A.R.; Pandian, S.; Kolake, S.M.; Han, S. Polyamide-POSS hybrid membranes for seawater desalination: Effect of POSS inclusion on membrane properties. J. Membr. Sci. 2014, 461, 89–95. [Google Scholar] [CrossRef]
- Jang, C.; Sirk, T.W.; Andzelm, J.W.; Abrams, C.F. Comparison of crosslinking algorithms in molecular dynamics simulation of thermosetting polymers. Macromol. Theory Simul. 2015, 24, 260–270. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, Y.; Yang, H. A molecular dynamics study of crosslinked epoxy networks: Construction of atomistic models. Mol. Simul. 2020, 46, 121–127. [Google Scholar] [CrossRef]
- Anstine, D.M.; Colina, C.M. Sorption-induced polymer rearrangement: Approaches from molecular modeling. Polym. Int. 2020, 70, 984–989. [Google Scholar] [CrossRef]
- Stubbs, J.M.; Chen, B.; Potoff, J.J.; Siepmann, J.I. Monte Carlo calculations for the phase equilibria of alkanes, alcohols, water and their mixtures. Fluid Phase Equilib. 2001, 183–184, 301–309. [Google Scholar] [CrossRef]
- Rizzuto, C.; Caravella, A.; Brunetti, A.; Park, C.H.; Lee, Y.M.; Drioli, E.; Barbieri, G.; Tocci, E. Sorption and diffusion of CO2/N2 in gas mixture in thermally-rearranged polymeric membranes: A molecular investigation. J. Membr. Sci. 2017, 528, 135–146. [Google Scholar] [CrossRef]
- Kupgan, G.; Demidov, A.G.; Colina, C.M. Plasticization behavior in polymers of intrinsic microporosity (PIM-1): A simulation study from combined Monte Carlo and molecular dynamics. J. Membr. Sci. 2018, 565, 95–103. [Google Scholar] [CrossRef]
- Brunetti, A.; Tocci, E.; Cersocimo, M.; Kim, J.S.; Lee, W.H.; Seong, J.G.; Lee, Y.M.; Drioli, E.; Barbieri, G. Mutual influence of mixed-gas permeation in thermally rearranged poly(benzoxazole-co-imide) polymer membranes. J. Membr. Sci. 2019, 580, 202–213. [Google Scholar] [CrossRef]
- Chatterjee, R.; Kumar, A.G.; Nikiforov, R.; Ryzhikh, V.; Belov, N.; Padmanabhan, V.; Yampolskii, Y.; Banerjee, S. Novel semi-fluorinated poly(ether imide)s with benzyl ether side groups: Synthesis, physicochemical characterization, gas transport properties and simulation. Eur. Polym. J. 2020, 135, 109879. [Google Scholar] [CrossRef]
- Amirkhani, F.; Harami, H.R.; Asghari, M. CO2/CH4 mixed gas separation using poly(ether-b-amide)-ZnO nanocomposite membranes: Experimental and molecular dynamics study. Polym. Testing 2020, 86, 106464. [Google Scholar] [CrossRef]
- Deitrick, G.L.; Scriven, L.E.; Davis, H.T. Efficient molecular simulation of chemical potentials. J. Chem. Phys. 1989, 90, 2370–2385. [Google Scholar] [CrossRef]
- Tamai, Y.; Tanaka, H.; Nakanishi, K. Molecular simulation of permeation of small penetrants through membranes. 2. Solubilities. Macromolecules 1995, 28, 2544–2554. [Google Scholar] [CrossRef]
- Dömötör, G.; Hentschke, R. Atomistically modeling the chemical potential of small molecules in dense systems. J. Phys. Chem. B 2004, 108, 2413–2417. [Google Scholar] [CrossRef]
- Van der Vegt, N.F.A.; Briels, W.J.; Wessling, M.; Strathmann, H. The sorption induced glass transition in amorphous glassy polymers. J. Chem. Phys. 1999, 110, 11061–11069. [Google Scholar] [CrossRef]
- Pandiyan, S.; Brown, D.; Neyertz, S.; Van der Vegt, N.F.A. Carbon dioxide solubility in three fluorinated polyimides studied by molecular dynamics simulations. Macromolecules 2010, 43, 2605–2621. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Permeation of polymers. A computational approach. Acta Polym. 1994, 45, 259–293. [Google Scholar] [CrossRef]
- Widom, B. Some topics in theory of fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Tanis, I.; Brown, D.; Neyertz, S.; Heck, R.; Mercier, R.; Vaidya, M.; Ballaguet, J.-P. A comparison of pure and mixed-gas permeation of nitrogen and methane in 6FDA-based polyimides as studied by molecular dynamics simulations. Comp. Mater. Sci. 2018, 141, 243–253. [Google Scholar] [CrossRef]
- Velioglu, S.; Ahunbay, M.G.; Tantekin-Ersolmaz, S.B. Investigation of CO2-induced plasticization in fluorinated polyimide membranes via molecular simulation. J. Membr. Sci. 2012, 417–418, 217–227. [Google Scholar] [CrossRef]
- Velioglu, S.; Ahunbay, M.G.; Tantekin-Ersolmaz, S.B. An atomistic insight on CO2 plasticization resistance of thermally rearranged 6FDA-bisAPAF. J. Membr. Sci. 2018, 556, 23–33. [Google Scholar] [CrossRef]
- Balçik, M.; Ahunbay, M.G. Prediction of CO2-induced plasticization pressure in polyimides via atomistic simulations. J. Membr. Sci. 2018, 547, 146–155. [Google Scholar] [CrossRef]
- Yang, Y.; Nair, A.K.N.; Sun, S. Adsorption and Diffusion of Methane and Carbon Dioxide in Amorphous Regions of Cross-Linked Polyethylene: A Molecular Simulation Study. Ind. Eng. Chem. Res. 2019, 58, 8426–8436. [Google Scholar] [CrossRef]
- Roy, P.K.; Kumar, K.; Thakkar, F.M.; Pathak, A.D.; Ayappa, K.G.; Maiti, P.K. Investigations on 6FDA/BPDA-DAM polymer melt properties and CO2 adsorption using molecular dynamics simulations. J. Membr. Sci. 2020, 613, 118377. [Google Scholar] [CrossRef]
- Balçik, M.; Tantekin-Ersolmaz, S.B.; Ahunbay, M.G. Interfacial analysis of mixed-matrix membranes under exposure to high-pressure CO2. J. Membr. Sci. 2020, 607, 118147. [Google Scholar] [CrossRef]
- Yang, Y.; Nair, A.K.N.; Sun, S. Sorption and Diffusion of Methane and Carbon Dioxide in Amorphous Poly(alkyl acrylates): A Molecular Simulation Study. J. Phys. Chem. B 2020, 124, 1301–1310. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, USA; London, UK, 2002. [Google Scholar]
- Ben-Naim, A.; Marcus, Y. Solvation thermodynamics of nonionic solutes. J. Chem. Phys. 1984, 81, 2016–2027. [Google Scholar] [CrossRef]
- Neyertz, S. Gas transport in dense polymeric membranes, molecular dynamics simulations. In Encyclopedia of Membrane Science and Technology; Hoek, E.M.V., Tarabara, V.V., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Neyertz, S.; Brown, D. A trajectory-extending kinetic Monte Carlo (TEKMC) method for estimating penetrant diffusion coefficients in molecular dynamics simulations of glassy polymers. Macromolecules 2010, 43, 9210–9214. [Google Scholar] [CrossRef]
- Maginn, E.J.; Bell, A.T.; Theodorou, D.N. Transport diffusivity of methane in silicalite from equilibrium and nonequilibrium simulations. J. Phys. Chem. 1993, 97, 4173–4181. [Google Scholar] [CrossRef]
- Tsige, M.; Grest, G.S. Molecular dynamics simulation of solvent-polymer interdiffusion: Fickian diffusion. J. Chem. Phys. 2004, 120, 2989–2995. [Google Scholar] [CrossRef] [Green Version]
- Tepper, H.L.; Briels, W.J. Comments on the use of the Einstein equation for transport diffusion: Application to argon in AlPO4-5. J. Chem. Phys. 2002, 116, 9464–9474. [Google Scholar] [CrossRef]
- Yahaya, G.O.; Qahtani, M.S.; Ammar, A.Y.; Bahamdan, A.A.; Ameen, A.W.; Alhajry, R.H.; Ben Sultan, M.M.; Hamad, F. Aromatic block co-polyimide membranes for sour gas feed separations. Chem. Eng. J. 2016, 304, 1020–1030. [Google Scholar] [CrossRef]
- Gleason, K.L.; Smith, Z.P.; Liu, Q.; Paul, D.R.; Freeman, B.D. Pure- and mixed-gas permeation of CO2 and CH4 in thermally rearranged polymers based on 3,3′-dihydroxy-4,4′-diamino-biphenyl (HAB) and 2,2′-bis-(3,4-dicarboxyphenyl) hexafluoropropane dianhydride (6FDA). J. Membr. Sci. 2015, 475, 204–214. [Google Scholar] [CrossRef] [Green Version]
- Genduso, G.; Ghanem, B.S.; Pinnau, I. Experimental Mixed-Gas Permeability, Sorption and Diffusion of CO2-CH4 Mixtures in 6FDA-mPDA Polyimide Membrane: Unveiling the Effect of Competitive Sorption on Permeability Selectivity. Membranes 2019, 9, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ricci, E.; Di Maio, E.; Degli Esposti, M.; Liu, L.; Mensitieri, G.; Fabbri, P.; Kentish, S.E.; De Angelis, M.G. Towards a systematic determination of multicomponent gas separation with membranes: The case of CO2/CH4 in cellulose acetates. J. Membr. Sci. 2021, 628, 119226. [Google Scholar] [CrossRef]
- Tsai, M.-H.; Chiang, P.-C.; Whang, W.-T.; Ko, C.-J.; Huang, S.-L. Synthesis and characteristics of polyimide/siloxane hybrid films for reliability adhesion. Surf. Coat. Technol. 2006, 200, 3297–3302. [Google Scholar] [CrossRef]
- Ahmad, Z.; Al Sagheer, F.; Al Arbash, A.; Ali, A.A.M. Synthesis and characterization of chemically cross-linked polyimide–siloxane hybrid films. J. Non-Cryst. Solids 2009, 355, 507–517. [Google Scholar] [CrossRef]
- Mazo, M.; Balabaev, N.; Alentiev, A.; Strelnikov, I.; Yampolskii, Y. Structure and properties of high and low free volume polymers studied by molecular dynamics simulation. Computation 2019, 7, 27. [Google Scholar] [CrossRef] [Green Version]
- Pant, P.V.K.; Boyd, R.H. Molecular dynamics simulation of diffusion of small penetrants in polymers. Macromolecules 1993, 26, 679–686. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Molecular dynamics study of carbon dioxide sorption and plasticization at the interface of a glassy polymer membrane. Macromolecules 2013, 46, 2433–2449. [Google Scholar] [CrossRef]
- Kirchheim, R. Sorption and partial molar volume of small molecules in glassy polymers. Macromolecules 1992, 25, 6952–6960. [Google Scholar] [CrossRef]
- Gotthardt, P.; Grüger, A.; Brion, H.G.; Plaetschke, R.; Kirchheim, R. Volume change of glassy polymers by sorption of small molecules and its relation to the intermolecular space. Macromolecules 1997, 30, 8058–8065. [Google Scholar] [CrossRef]
- Robeson, L.M.; Smith, Z.P.; Freeman, B.D.; Paul, D.R. Contributions of diffusion and solubility selectivity to the upper bound analysis for glassy gas separation membranes. J. Membr. Sci. 2014, 453, 71–83. [Google Scholar] [CrossRef]
- Böhning, M.; Springer, J. Sorptive dilation and relaxational processes in glassy polymer/gas systems—I. Poly(sulfone) and poly(ether sulfone). Polymer 1998, 39, 5183–5195. [Google Scholar] [CrossRef]
- Wessling, M.; Huisman, I.; Van der Boomgaard, T.; Smolders, C.A. Dilation kinetics of glassy, aromatic polyimides induced by carbon dioxide sorption. J. Polym. Sci. Part B Polym. Phys. 1995, 33, 1371–1384. [Google Scholar] [CrossRef]
- Wind, J.D.; Sirard, S.M.; Paul, D.R.; Green, P.F.; Johnston, K.P.; Koros, W.J. Carbon dioxide-induced plasticization of polyimide membranes: Pseudo-equilibrium relationships of diffusion, sorption, and swelling. Macromolecules 2003, 36, 6433–6441. [Google Scholar] [CrossRef]
- Ogieglo, W.; Wormeester, H.; Eichhorn, K.J.; Wessling, M.; Benes, N.E. In situ ellipsometry studies on swelling of thin polymer films: A review. Prog. Polym. Sci. 2015, 42, 42–78. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D.; Pandiyan, S.; Van der Vegt, N.F.A. Carbon dioxide diffusion and plasticization in fluorinated polyimides. Macromolecules 2010, 43, 7813–7827. [Google Scholar] [CrossRef]
- Bos, A.; Pünt, I.G.M.; Wessling, M.; Strathmann, H. CO2-induced plasticization phenomena in glassy polymers. J. Membr. Sci. 1999, 155, 67–78. [Google Scholar] [CrossRef]
- Robeson, L.M.; Freeman, B.D.; Paul, D.R.; Rowe, B.W. An empirical correlation of gas permeability and permselectivity in polymers and its theoretical basis. J. Membr. Sci. 2009, 341, 178–185. [Google Scholar] [CrossRef]
- Coleman, M.R.; Koros, W.J. Isomeric polyimides based on fluorinated dianhydrides and diamines for gas separation applications. J. Membr. Sci. 1990, 50, 285–297. [Google Scholar] [CrossRef]
- Coleman, M.R.; Koros, W.J. The transport properties of polyimide isomers containing hexafluoroisopropylidene in the diamine residue. J. Polym. Sci. Part B Polym. Phys. 1994, 32, 1915–1926. [Google Scholar] [CrossRef]
- Cornelius, C.J.; Marand, E. Hybrid silica-polyimide composite membranes: Gas transport properties. J. Membr. Sci. 2002, 202, 97–118. [Google Scholar] [CrossRef]
- Robeson, L.M.; Dose, M.E.; Freeman, B.D.; Paul, D.R. Analysis of the transport properties of thermally rearranged (TR) polymers and polymers of intrinsic microporosity (PIM) relative to upper bound performance. J. Membr. Sci. 2017, 525, 18–24. [Google Scholar] [CrossRef] [Green Version]
- Faramawy, S.; Zaki, T.; Sakr, A.A.-E. Natural gas origin, composition, and processing: A review. J. Nat. Gas Sci. Eng. 2016, 34, 34–54. [Google Scholar] [CrossRef]


| Connectivities | meta OAPS + PMDA | para OAPS + PMDA | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | para OAPS + 6FDA | ortho OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|---|---|---|---|
| Total no. of atoms | 33,672 | 33,828 | 33,492 | 31,644 | 43,183 | 43,245 | 41,974 | 41,362 |
| <No. of links per cage> | 5.3 | 5.4 | 5.2 | 5.1 | 4.9 | 4.9 | 4.5 | 4.9 |
| <No. of intercage links per cage> | 4.6 | 5.1 | 3.3 | 4.3 | 3.7 | 3.7 | 3.9 | 4.1 |
| <No. of intracage links per cage> | 0.7 | 0.3 | 1.9 | 0.8 | 1.2 | 1.2 | 0.6 | 0.8 |
| <No. of different cages linked to a cage> (=cross-linking density) | 4.2 | 4.7 | 3.0 | 4.0 | 3.4 | 3.5 | 3.6 | 3.7 |
| <%FSV> | meta OAPS + PMDA | para OAPS + PMDA | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | para OAPS + 6FDA | ortho OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|---|---|---|---|
| N2 at 300 °C | 10.5 | 19.9 | 5.2 | 3.2 | 6.4 | 8.9 | 8.9 | 2.9 |
| N2 at 400 °C | 11.6 | 22.0 | 5.8 | - | 7.3 | 10.2 | 9.6 | - |
| CH4 at 300 °C | 8.8 | 17.8 | 4.2 | 2.4 | 5.1 | 7.4 | 7.6 | 2.1 |
| CH4 at 400 °C | 9.8 | 19.8 | 4.7 | - | 5.9 | 8.5 | 8.2 | - |
| CO2 at 300 °C | 7.8 | 16.4 | 3.6 | 2.0 | 4.4 | 6.5 | 6.9 | 1.8 |
| CO2 at 400 °C | 8.8 | 18.5 | 4.2 | - | 5.1 | 7.6 | 7.5 | - |
| No. of Molecules | meta OAPS + PMDA | para OAPS + PMDA | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | para OAPS + 6FDA | ortho OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|---|---|---|---|
| N2 at 300 °C | 255 | 399 | 106 | 73 | 221 | 264 | 187 | 95 |
| N2 at 400 °C | 182 | 287 | 73 | - | 147 | 191 | 131 | - |
| CH4 at 300 °C | 346 | 524 | 140 | 97 | 306 | 370 | 246 | 122 |
| CH4 at 400 °C | 230 | 355 | 93 | - | 186 | 243 | 158 | - |
| CO2 at 300 °C | 704 | 943 | 287 | 234 | 610 | 727 | 442 | 281 |
| CO2 at 400 °C | 411 | 562 | 153 | - | 356 | 433 | 259 | - |
| % Volume Swelling | meta OAPS + PMDA | para OAPS + PMDA | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | para OAPS + 6FDA | ortho OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|---|---|---|---|
| N2 at 300 °C | 0 | 1.4 | 0.4 | 0.1 | 0.3 | 0.2 | 0.7 | −0.2 |
| N2 at 400 °C | 1.3 | 1.2 | 0.1 | - | −0.1 | 1.0 | 0.2 | - |
| CH4 at 300 °C | 0.7 | 2.6 | 0.5 | 0.4 | 1.1 | 1.4 | 0.6 | 0.3 |
| CH4 at 400 °C | 2.2 | 1.6 | 0.5 | - | 0 | 1.4 | 0.2 | - |
| CO2 at 300 °C | 2.3 | 3.8 | 0.9 | 1.5 | 1.7 | 2.6 | 1.2 | 1.7 |
| CO2 at 400 °C | 2.5 | 2.3 | 0.3 | - | 1.3 | 3.0 | 0.8 | - |
| αSA/B and αDA/B | meta OAPS + PMDA | para OAPS + PMDA | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | para OAPS + 6FDA | ortho OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|---|---|---|---|
| αSCO2/CH4 at 300 °C | 2 | 1.8 | 2 | 2.4 | 2 | 1.9 | 1.8 | 2.3 |
| αSCO2/CH4 at 400 °C | 1.8 | 1.6 | 1.6 | - | 1.9 | 1.8 | 1.6 | - |
| αDCO2/CH4 at 300 °C | 0.8 | 0.6 | 1.5 | 2 | 1.2 | 1 | 0.9 | 2.2 |
| αDCO2/CH4 at 400 °C | 0.9 | 0.7 | 1.6 | - | 1.1 | 0.9 | 0.9 | - |
| αSCO2/N2 at 300 °C | 2.7 | 2.3 | 2.7 | 3.2 | 2.7 | 2.7 | 2.4 | 2.9 |
| αSCO2/N2 at 400 °C | 2.2 | 1.9 | 2.1 | - | 2.4 | 2.2 | 2 | - |
| αDCO2/N2 at 300 °C | 0.8 | 0.6 | 1 | 1.2 | 0.9 | 0.9 | 0.8 | 1.5 |
| αDCO2/N2 at 400 °C | 0.7 | 0.7 | 1.1 | - | 1 | 0.8 | 0.9 | - |
| No. of Molecules | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|
| CH4/CO2 at 300 °C | 125/35 | 91/27 | 259/78 | 105/32 |
| CH4/CO2 at 400 °C | 77/16 | - | 166/38 | - |
| N2/CO2 at 300 °C | 93/36 | 68/30 | 193/85 | 82/34 |
| N2/CO2 at 400 °C | 63/17 | - | 128/40 | - |
| % Volume Swelling | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|
| CH4/CO2 at 300 °C | 0.6 | 0.2 | 0.6 | 0.1 |
| CH4/CO2 at 400 °C | 0.2 | - | 0.5 | - |
| N2/CO2 at 300 °C | 0.3 | 0.2 | 1.2 | −0.2 |
| N2/CO2 at 400 °C | 0 | - | −0.2 | - |
| αS*A/B and αD*A/B | ortho OAPS + PMDA | POSS + PMDA | meta OAPS + 6FDA | POSS + 6FDA |
|---|---|---|---|---|
| αS*CO2/CH4 at 300 °C | 2.5 | 2.7 | 2.7 | 2.7 |
| αS*CO2/CH4 at 400 °C | 1.9 | - | 2.1 | - |
| αD*CO2/CH4 at 300 °C | 1.4 | 1.7 | 1.3 | 1.7 |
| αD*CO2/CH4 at 400 °C | 1.7 | - | 1.2 | - |
| αS*CO2/N2 at 300 °C | 3.5 | 4 | 4 | 3.7 |
| αS*CO2/N2 at 400 °C | 2.4 | - | 2.8 | - |
| αD*CO2/N2 at 300 °C | 0.9 | 1 | 1 | 1.1 |
| αD*CO2/N2 at 400 °C | 1 | - | 0.9 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neyertz, S.; Brown, D.; Salimi, S.; Radmanesh, F.; Benes, N.E. Molecular Characterization of Membrane Gas Separation under Very High Temperatures and Pressure: Single- and Mixed-Gas CO2/CH4 and CO2/N2 Permselectivities in Hybrid Networks. Membranes 2022, 12, 526. https://doi.org/10.3390/membranes12050526
Neyertz S, Brown D, Salimi S, Radmanesh F, Benes NE. Molecular Characterization of Membrane Gas Separation under Very High Temperatures and Pressure: Single- and Mixed-Gas CO2/CH4 and CO2/N2 Permselectivities in Hybrid Networks. Membranes. 2022; 12(5):526. https://doi.org/10.3390/membranes12050526
Chicago/Turabian StyleNeyertz, Sylvie, David Brown, Saman Salimi, Farzaneh Radmanesh, and Nieck E. Benes. 2022. "Molecular Characterization of Membrane Gas Separation under Very High Temperatures and Pressure: Single- and Mixed-Gas CO2/CH4 and CO2/N2 Permselectivities in Hybrid Networks" Membranes 12, no. 5: 526. https://doi.org/10.3390/membranes12050526
APA StyleNeyertz, S., Brown, D., Salimi, S., Radmanesh, F., & Benes, N. E. (2022). Molecular Characterization of Membrane Gas Separation under Very High Temperatures and Pressure: Single- and Mixed-Gas CO2/CH4 and CO2/N2 Permselectivities in Hybrid Networks. Membranes, 12(5), 526. https://doi.org/10.3390/membranes12050526