Impact of Particle Shape and Surface Group on Membrane Fouling
Abstract
:1. Introduction
2. Theory
2.1. Shear-Induced Diffusion (SID) Model
2.2. DLVO and Extended DLVO (XDLVO) Models
2.2.1. Lifshitz–van der Waals (LW) Interaction
2.2.2. Electrostatic Double-Layer (EL) Interaction
2.2.3. Lewis Acid–Base (AB) Interaction
3. Materials and Methods
3.1. Chemicals and Reagents
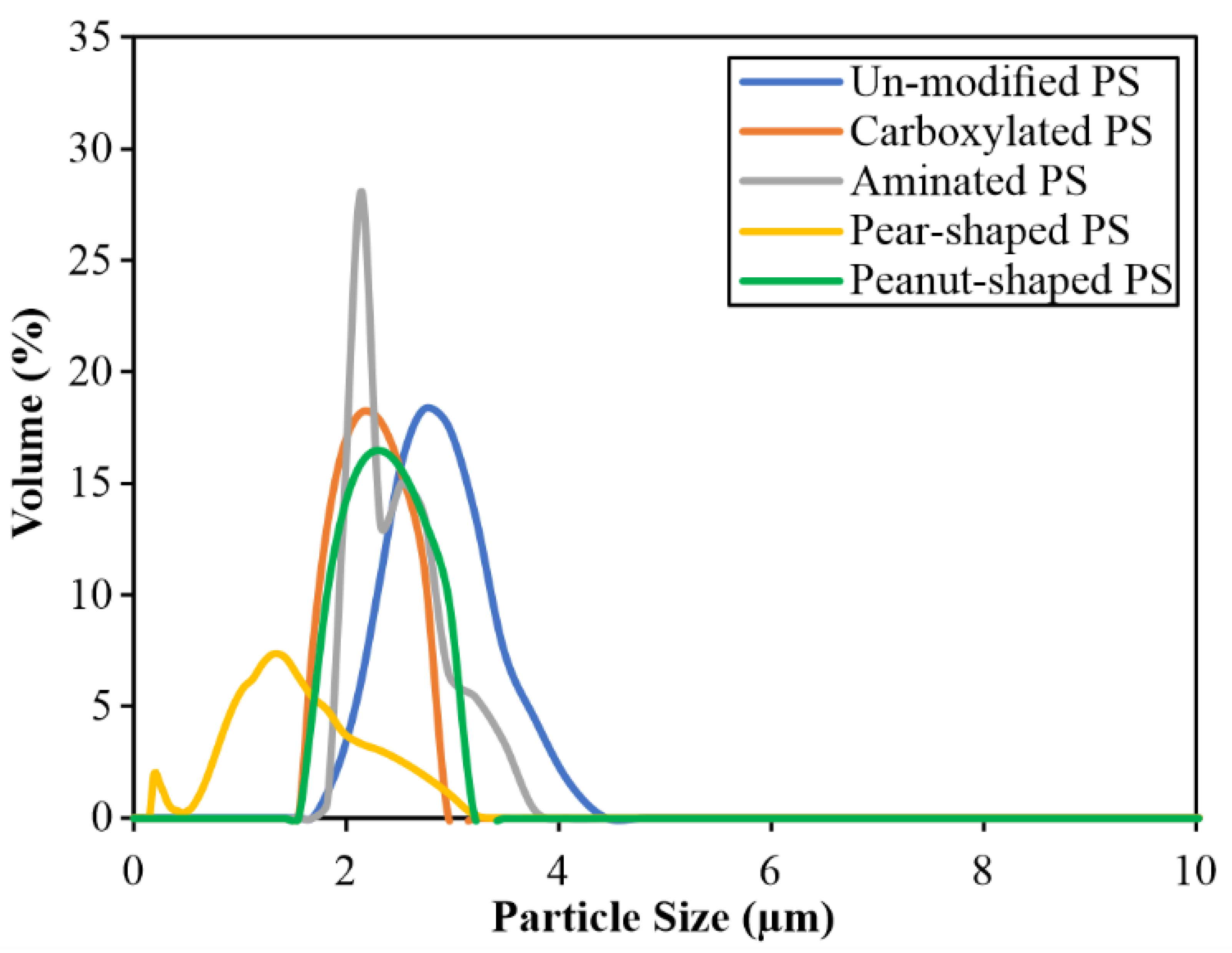
3.2. Determining Particle Sphericity
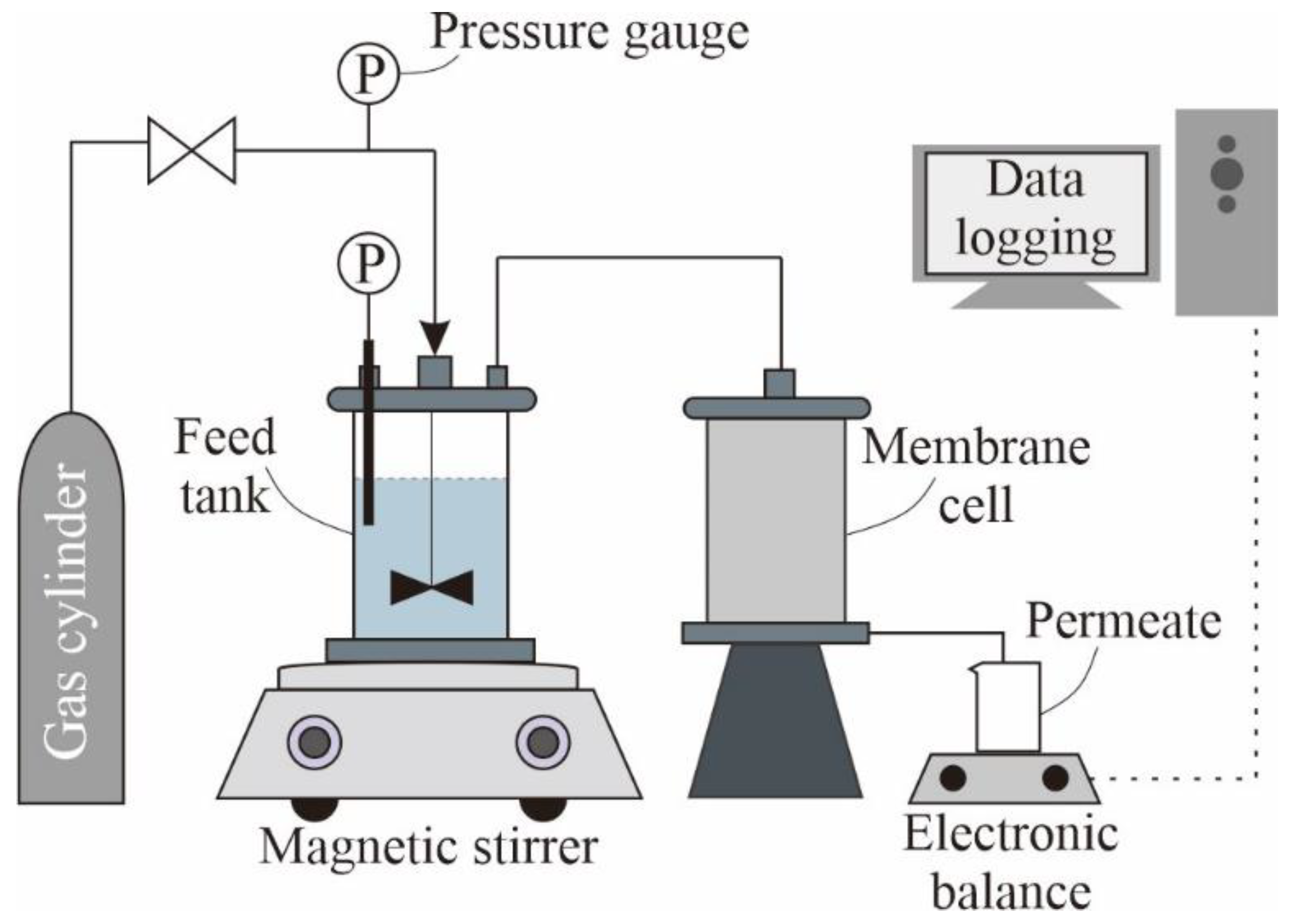
3.3. Experimental Setups
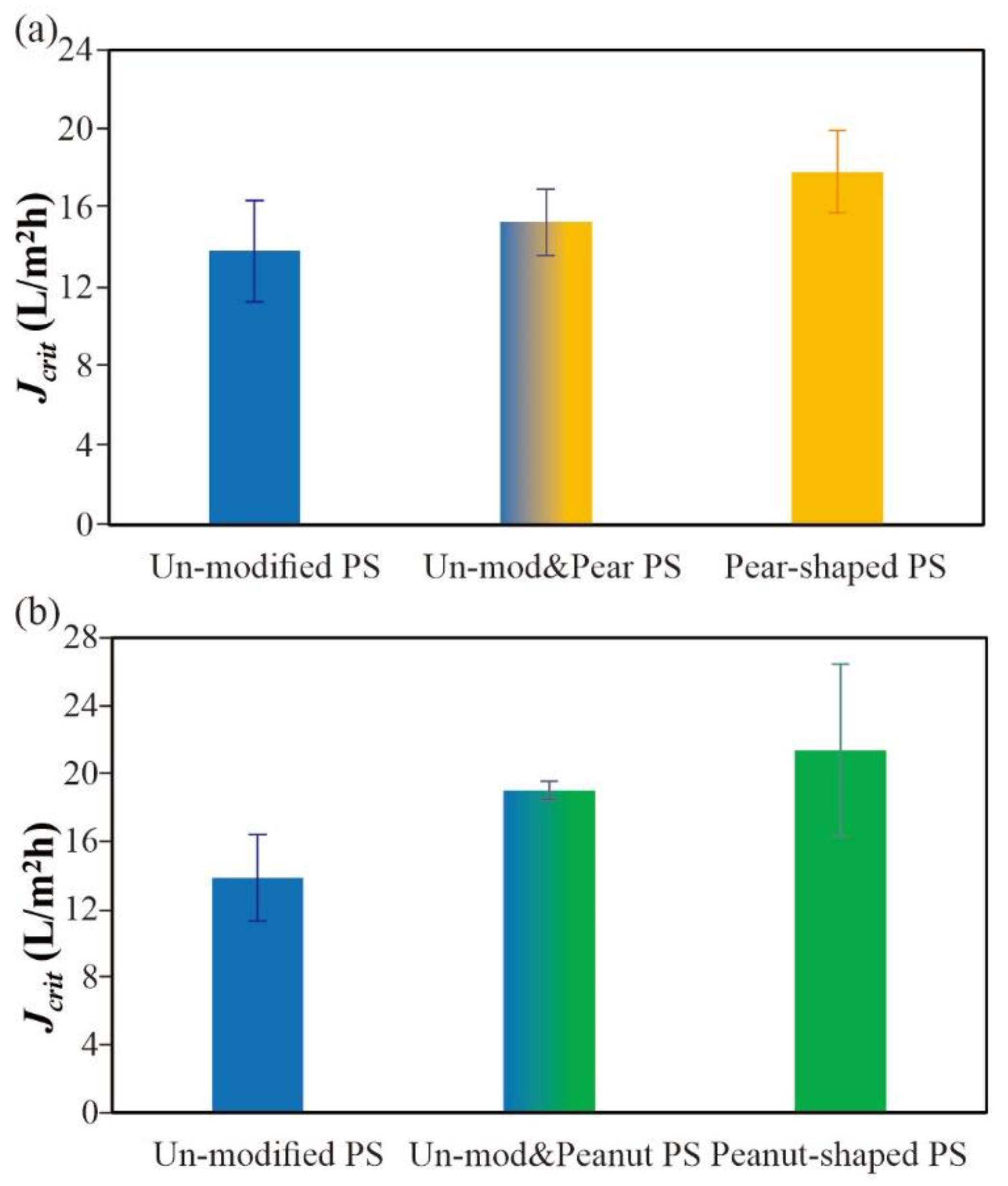
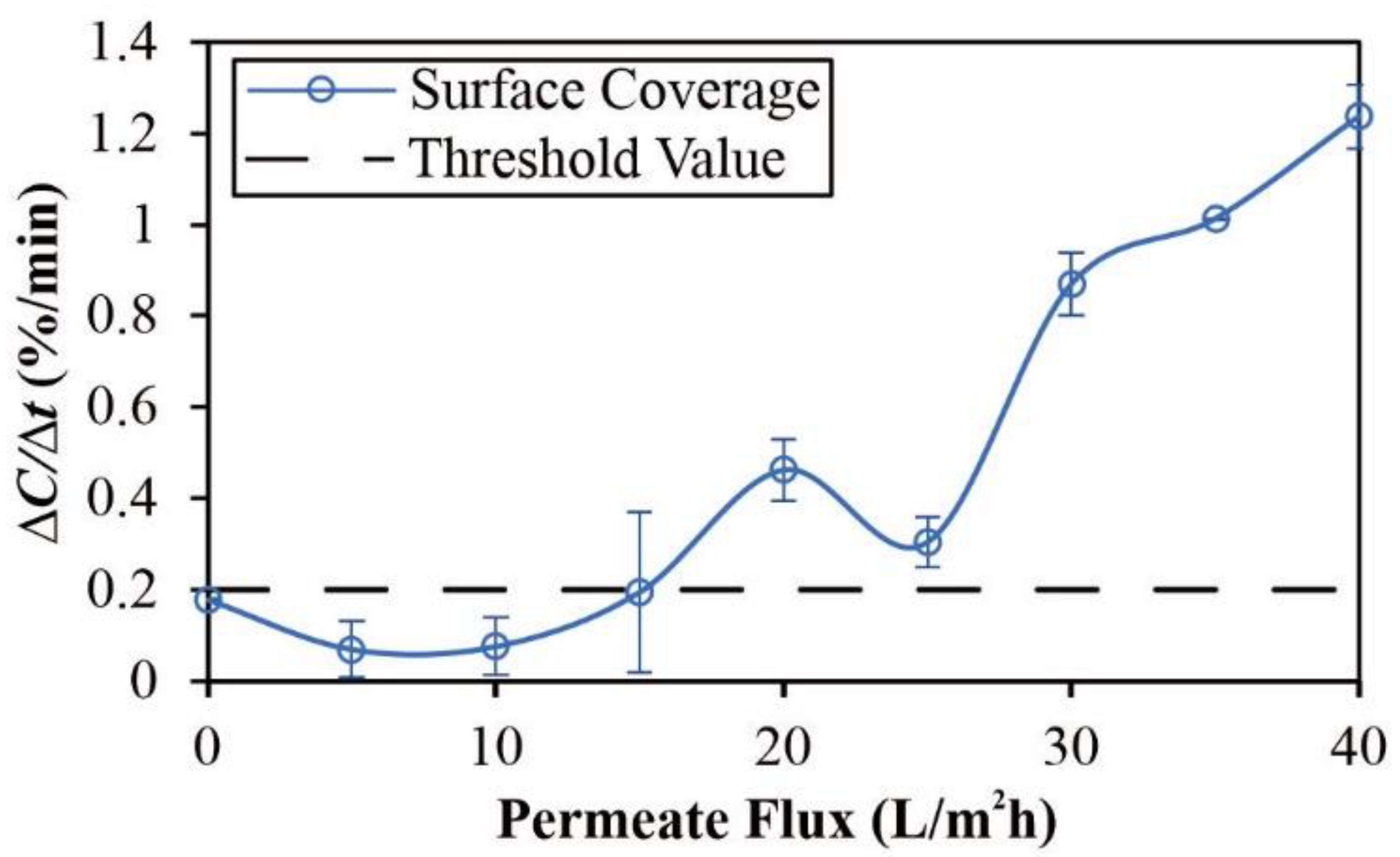
3.4. Critical Flux Determination
4. Results and Discussion
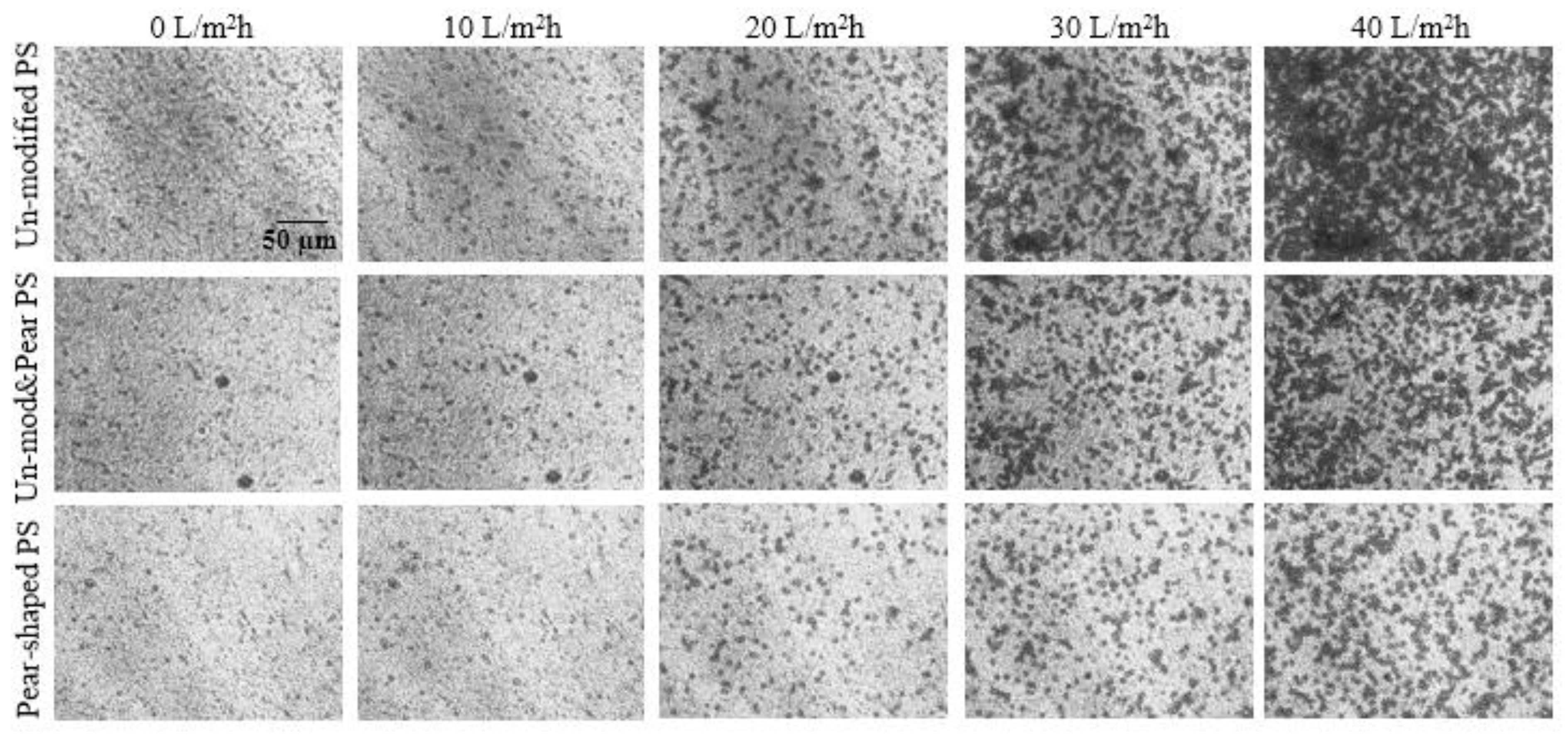
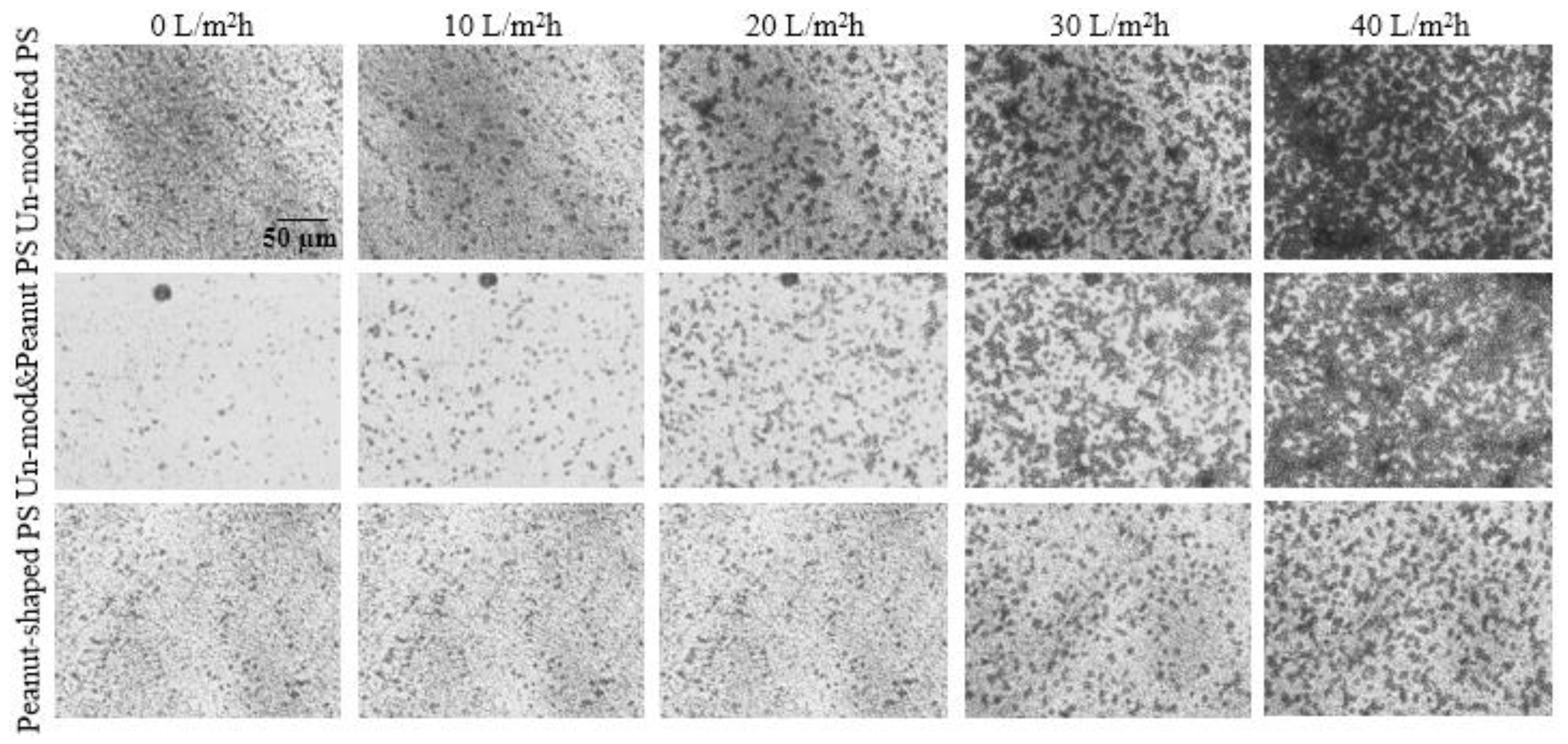
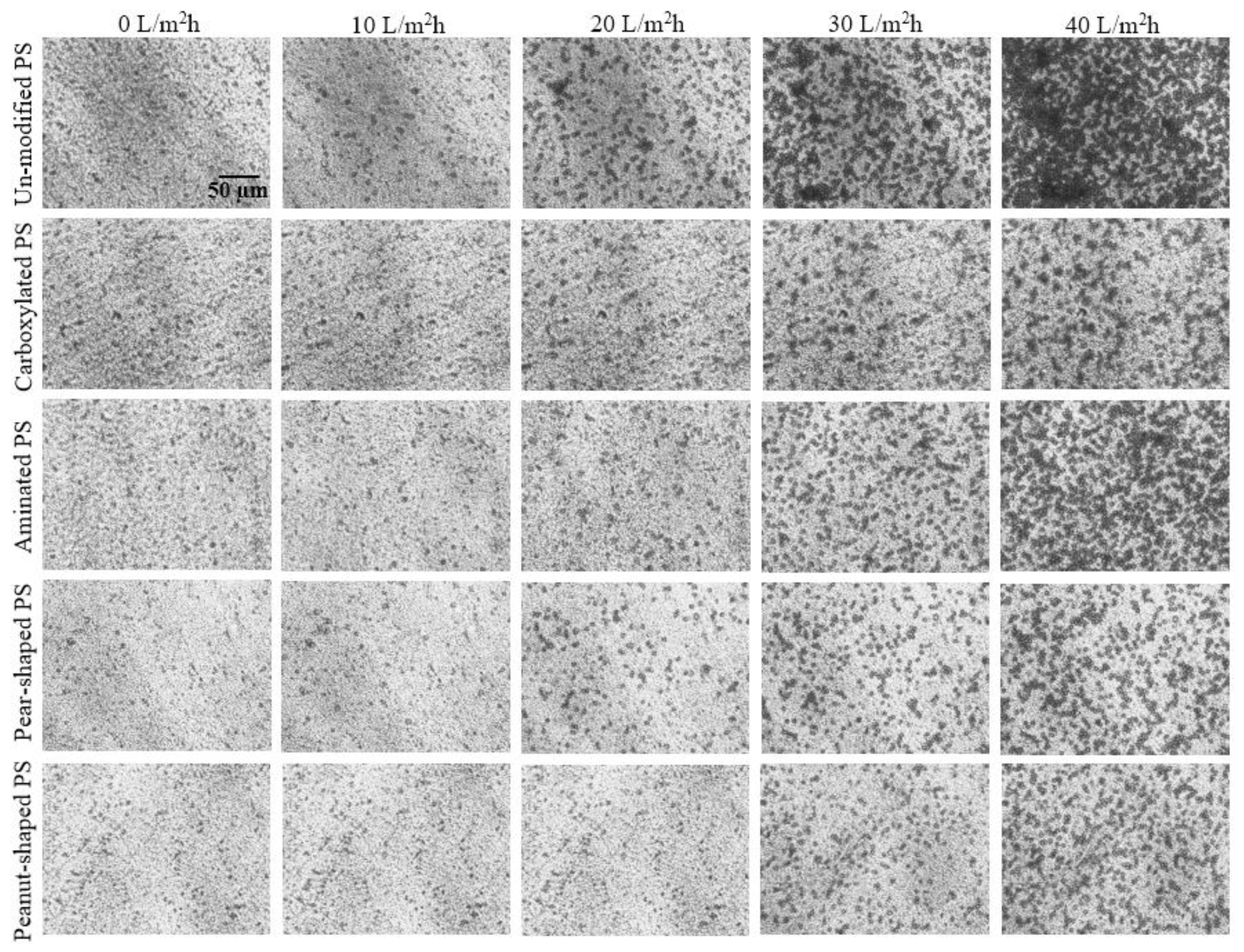
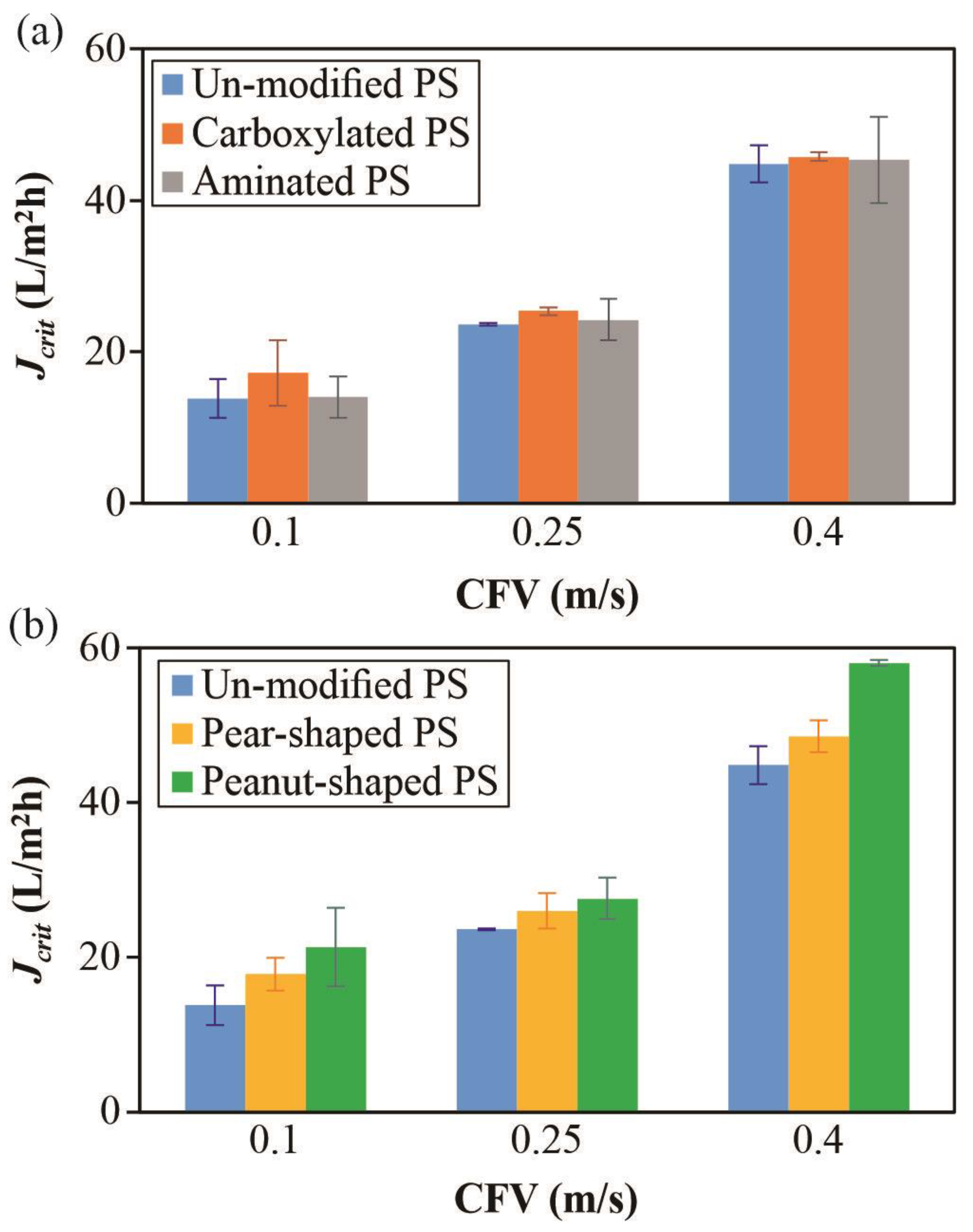
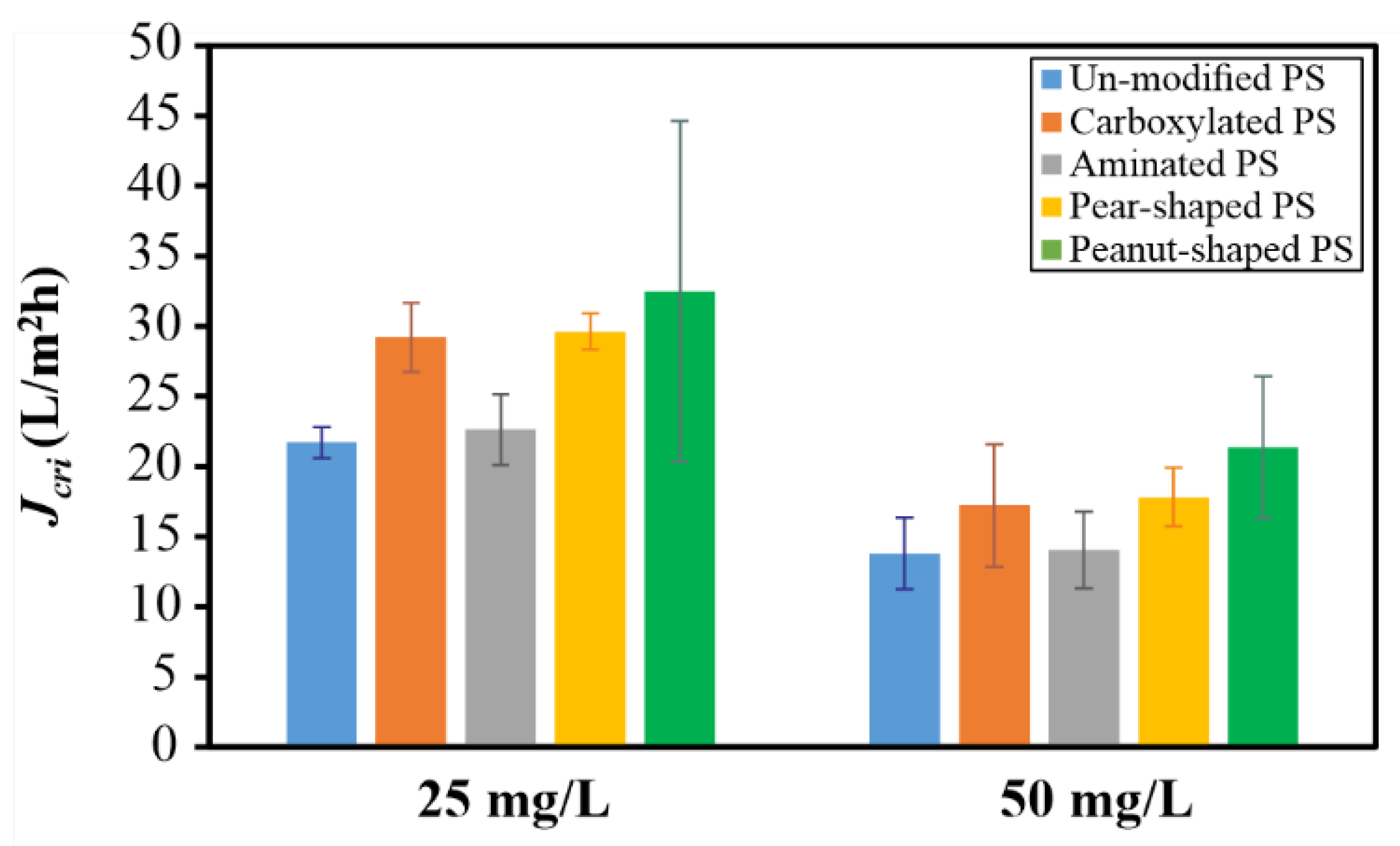
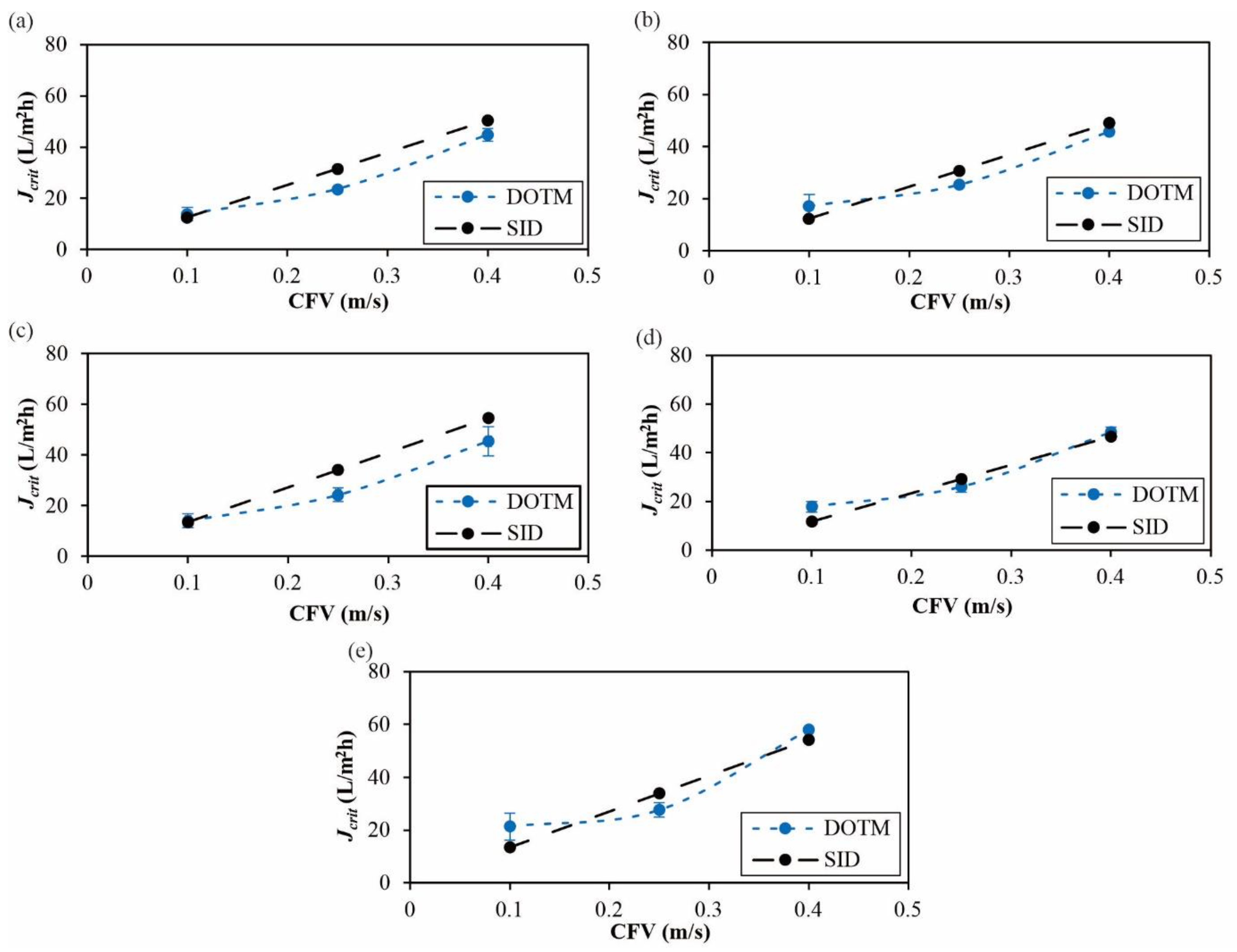
4.1. Crossflow Studies
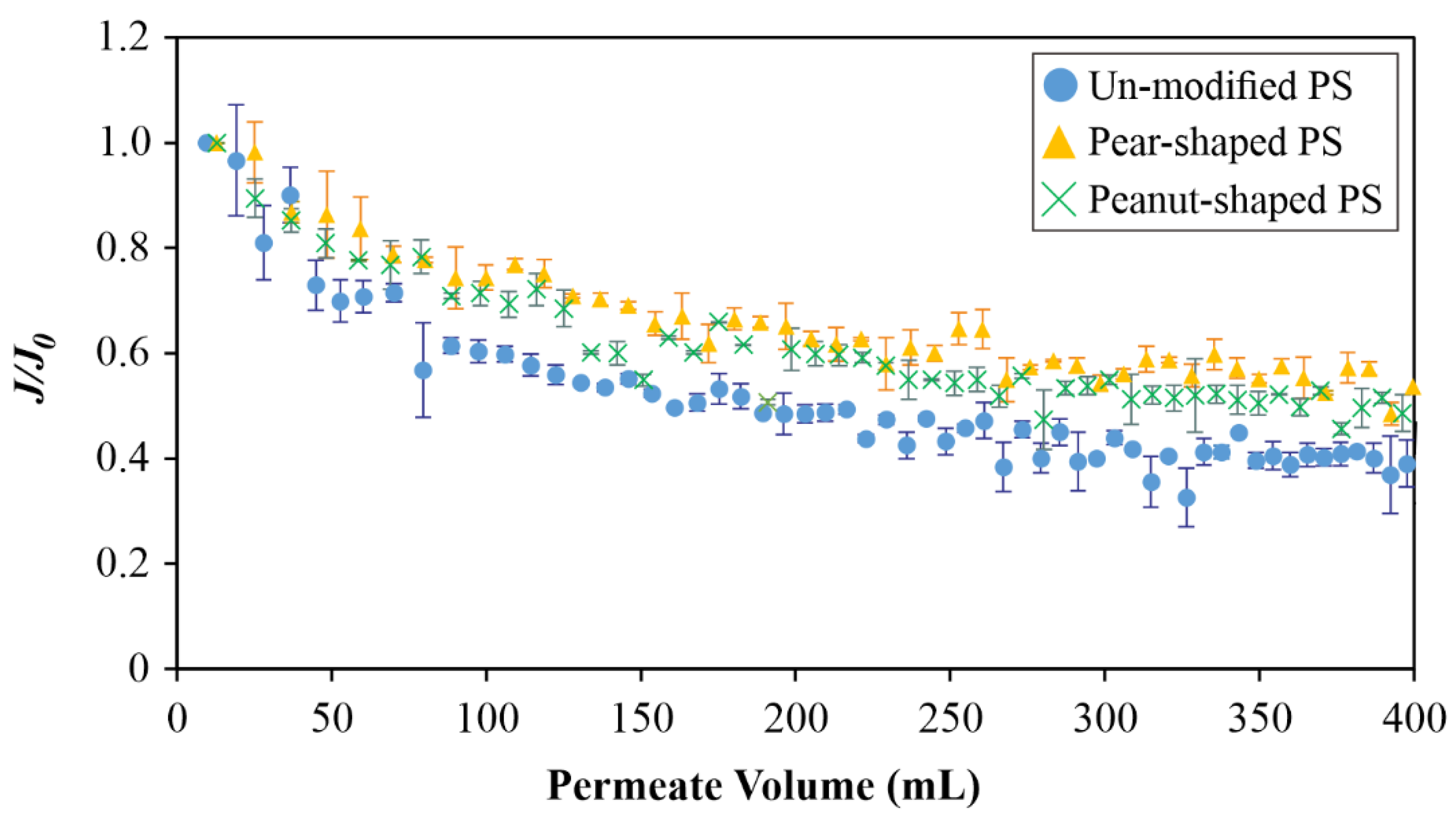
4.2. Dead-End Studies
4.3. Interaction Energy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Hao, S.; Jia, Z.; Wen, J.; Li, S.; Peng, W.; Huang, R.; Xu, X. Progress in adsorptive membranes for separation—A review. Sep. Purif. Technol. 2021, 255, 117772. [Google Scholar] [CrossRef]
- Rezende Moreira, V.; Abner Rocha Lebron, Y.; Cristina Santos Amaral, M. Enhancing industries exploitation: Integrated and hybrid membrane separation processes applied to industrial effluents beyond the treatment for disposal. Chem. Eng. J. 2022, 430, 133006. [Google Scholar] [CrossRef]
- Ahmad, T.; Guria, C. Progress in the modification of polyvinyl chloride (PVC) membranes: A performance review for wastewater treatment. J. Water Process Eng. 2022, 45, 102466. [Google Scholar] [CrossRef]
- Du, Y.; Pramanik, B.K.; Zhang, Y.; Dumée, L.; Jegatheesan, V. Recent Advances in the Theory and Application of Nanofiltration: A Review. Curr. Pollut. Rep. 2022, 8, 51–80. [Google Scholar] [CrossRef]
- Bai, R.; Leow, H.F. Mufiltration of polydispersed suspension by a membrane screen/hollow-fiber composite module. Desalination 2001, 140, 277–287. [Google Scholar] [CrossRef]
- Cui, Z.F.; Jiang, Y.; Field, R.W. Chapter 1—Fundamentals of Pressure-Driven Membrane Separation Processes. In Membrane Technology; Cui, Z.F., Muralidhara, H.S., Eds.; Butterworth-Heinemann: Oxford, UK, 2010; pp. 1–18. [Google Scholar]
- Frenkel, V.S. Chapter 8—Membrane Technologies for Food Processing Waste Treatment. In Membrane Technology; Cui, Z.F., Muralidhara, H.S., Eds.; Butterworth-Heinemann: Oxford, UK, 2010; pp. 155–177. [Google Scholar]
- Tanis-Kanbur, M.B.; Peinador, R.I.; Calvo, J.I.; Hernández, A.; Chew, J.W. Porosimetric membrane characterization techniques: A review. J. Membr. Sci. 2021, 619, 118750. [Google Scholar] [CrossRef]
- Fane, A.G.; Chong, T.H.; Le-Clech, P. Chapter 6—Fouling in Membrane Processes. In Membrane Operations: Innovative Separations and Transformations; Drioli, E., Giorno, L., Eds.; Wiley-VCH: Weinheim, Germany, 2009; pp. 121–138. [Google Scholar]
- Belfort, G.; Davis, R.H.; Zydney, A.L. The behavior of suspensions and macromolecular solutions in crossflow microfiltration. J. Membr. Sci. 1994, 96, 1–58. [Google Scholar] [CrossRef]
- Li, H.; Fane, A.G.; Coster, H.G.L.; Vigneswaran, S. Direct observation of particle deposition on the membrane surface during crossflow microfiltration. J. Membr. Sci. 1998, 149, 83–97. [Google Scholar] [CrossRef]
- Koo, C.H.; Mohammad, A.W.; Suja’, F.; Meor Talib, M.Z. Review of the effect of selected physicochemical factors on membrane fouling propensity based on fouling indices. Desalination 2012, 287, 167–177. [Google Scholar] [CrossRef]
- Tanis-Kanbur, M.B.; Velioğlu, S.; Tanudjaja, H.J.; Hu, X.; Chew, J.W. Understanding membrane fouling by oil-in-water emulsion via experiments and molecular dynamics simulations. J. Membr. Sci. 2018, 566, 140–150. [Google Scholar] [CrossRef]
- Tanudjaja, H.J.; Tanis-Kanbur, M.B.; Tarabara, V.V.; Fane, A.G.; Chew, J.W. Striping phenomenon during cross-flow microfiltration of oil-in-water emulsions. Sep. Purif. Technol. 2018, 207, 514–522. [Google Scholar] [CrossRef]
- Xue, S.; Lin, C.-W.; Ji, C.; Guo, Y.; Liu, L.; Yang, Z.; Zhao, S.; Cai, X.; Niu, Q.J.; Kaner, R.B. Thin-Film Composite Membranes with a Hybrid Dimensional Titania Interlayer for Ultrapermeable Nanofiltration. Nano Lett. 2022, 22, 1039–1046. [Google Scholar] [CrossRef] [PubMed]
- Connell, H.; Zhu, J.; Bassi, A. Effect of particle shape on crossflow filtration flux. J. Membr. Sci. 1999, 153, 121–139. [Google Scholar] [CrossRef]
- Šmídová, D.; Mikulášek, P.; Wakeman, R.J.; Velikovská, P. Influence of ionic strength and pH of dispersed systems on microfiltration. Desalination 2004, 163, 323–332. [Google Scholar] [CrossRef]
- Wang, J.; Fane, A.G.; Chew, J.W. Characteristics of non-spherical fluidized media in a fluidized bed–membrane reactor: Effect of particle sphericity on critical flux. Sep. Purif. Technol. 2018, 202, 185–199. [Google Scholar] [CrossRef]
- Abdelrasoul, A.; Doan, H.; Lohi, A.; Cheng, C.H. The effect of contaminated particle sphericity and size on membrane fouling in cross flow ultrafiltration. Environ. Technol. 2018, 39, 203–220. [Google Scholar] [CrossRef] [PubMed]
- Escudié, R.; Epstein, N.; Grace, J.R.; Bi, H.T. Effect of particle shape on liquid-fluidized beds of binary (and ternary) solids mixtures: Segregation vs. mixing. Chem. Eng. Sci. 2006, 61, 1528–1539. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Vollmari, K.; Jasevičius, R.; Kruggel-Emden, H. Experimental and numerical study of fluidization and pressure drop of spherical and non-spherical particles in a model scale fluidized bed. Powder Technol. 2016, 291, 506–521. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, X.; Wang, L.; Hong, H. Fluidization of non-spherical particles: Sphericity, Zingg factor and other fluidization parameters. Particuology 2008, 6, 125–129. [Google Scholar] [CrossRef]
- Nan, W.; Wang, Y.; Wang, J. Numerical analysis on the fluidization dynamics of rodlike particles. Adv. Powder Technol. 2016, 27, 2265–2276. [Google Scholar] [CrossRef]
- Wu, X.; Cen, K.; Luo, Z.; Wang, Q.; Fang, M. Measurement on particle rotation speed in gas–solid flow based on identification of particle rotation axis. Exp. Fluids 2008, 45, 1117–1128. [Google Scholar] [CrossRef]
- Eckstein, E.C.; Bailey, D.G. Self-diffusion of particles in shear flow of a suspension. J. Fluid Mech. 1977, 79, 191–208. [Google Scholar] [CrossRef]
- Li, H.; Fane, A.G.; Coster, H.G.L.; Vigneswaran, S. An assessment of depolarisation models of crossflow microfiltration by direct observation through the membrane. J. Membr. Sci. 2000, 172, 135–147. [Google Scholar] [CrossRef]
- Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Prog. Surf. Sci. 1993, 43, 30–59. [Google Scholar] [CrossRef]
- Verwey, E.J.W. Theory of the Stability of Lyophobic Colloids. J. Phys. Colloid Chem. 1947, 51, 631–636. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brant, J.A.; Childress, A.E. Assessing short-range membrane–colloid interactions using surface energetics. J. Membr. Sci. 2002, 203, 257–273. [Google Scholar] [CrossRef]
- Chew, J.W.; Kilduff, J.; Belfort, G. The behavior of suspensions and macromolecular solutions in crossflow microfiltration: An update. J. Membr. Sci. 2020, 601, 117865. [Google Scholar] [CrossRef]
- Van Oss, C.J. Chapter 5—Electrical Double Layer Interactions. In Interfacial Forces in Aqueous Media; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Yin, Z.; Ma, Y.; Tanis-Kanbur, B.; Chew, J.W. Fouling behavior of colloidal particles in organic solvent ultrafiltration. J. Membr. Sci. 2020, 599, 117836. [Google Scholar] [CrossRef]
- Subramani, A.; Hoek, E.M.V. Direct observation of initial microbial deposition onto reverse osmosis and nanofiltration membranes. J. Membr. Sci. 2008, 319, 111–125. [Google Scholar] [CrossRef]
- Giese, R.F.; Wu, W.; Oss, C.J.v. Surface and Electrokinetic Properties of Clays and Other Mineral Particles, Untreated and Treated with Organic or Inorganic Cations. J. Dispers. Sci. Technol. 1996, 17, 527–547. [Google Scholar] [CrossRef]
- Van Oss, C.J. Chapter 17—Surface Tension Components and Parameters of Liquids and Solids. In Interfacial Forces in Aqueous Media; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Wadell, H. Sphericity and Roundness of Rock Particles. J. Geol. 1933, 41, 310–331. [Google Scholar] [CrossRef]
- Ozturk, I.; Ercisli, S.; Kalkan, F.; Demir, B. Some chemical and physico-mechanical properties of pear cultivars. Afr. J. Biotechnol. 2009, 8, 687–693. [Google Scholar]
- Rotimi, D. Some Physical and Mechanical Properties of Pear Fruits and Seeds. Int. J. Res. Stud. Sci. Eng. Technol. 2018, 5, 51–57. [Google Scholar]
- Aydin, C. Some engineering properties of peanut and kernel. J. Food Eng. 2007, 79, 810–816. [Google Scholar] [CrossRef]
- Gojiya, D.; Dobariya, U.; Pandya, P.; Gojiya, K. Studies on Physical Properties of Peanut Seed. Acta Sci. Agric. 2020, 4, 01–05. [Google Scholar] [CrossRef]
- Li, H.; Fane, A.G.; Coster, H.G.L.; Vigneswaran, S. Observation of deposition and removal behaviour of submicron bacteria on the membrane surface during crossflow microfiltration. J. Membr. Sci. 2003, 217, 29–41. [Google Scholar] [CrossRef]
- Wicaksana, F.; Fane, A.G.; Pongpairoj, P.; Field, R. Microfiltration of algae (Chlorella sorokiniana): Critical flux, fouling and transmission. J. Membr. Sci. 2012, 387–388, 83–92. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Fane, A.G.; Law, A.W.K. Critical flux and particle deposition of fractal flocs during crossflow microfiltration. J. Membr. Sci. 2010, 353, 28–35. [Google Scholar] [CrossRef]
- Zamani, F.; Ullah, A.; Akhondi, E.; Tanudjaja, H.J.; Cornelissen, E.R.; Honciuc, A.; Fane, A.G.; Chew, J.W. Impact of the surface energy of particulate foulants on membrane fouling. J. Membr. Sci. 2016, 510, 101–111. [Google Scholar] [CrossRef]
- Lay, H.T.; Chew, J.W. Critical flux of colloidal foulant in microfiltration: Effect of organic solvent. J. Membr. Sci. 2020, 616, 118531. [Google Scholar] [CrossRef]
- Tanis-Kanbur, M.B.; Tamilselvam, N.R.; Chew, J.W. Membrane fouling mechanisms by BSA in aqueous-organic solvent mixtures. J. Ind. Eng. Chem. 2022, 108, 389–399. [Google Scholar] [CrossRef]
- Field, R.W.; Wu, D.; Howell, J.A.; Gupta, B.B. Critical flux concept for microfiltration fouling. J. Membr. Sci. 1995, 100, 259–272. [Google Scholar] [CrossRef]
- Espinasse, B.; Bacchin, P.; Aimar, P. On an experimental method to measure critical flux in ultrafiltration. Desalination 2002, 146, 91–96. [Google Scholar] [CrossRef]
- Gong, C.; Chen, D.; Jiao, X.; Wang, Q. Continuous hollow [small alpha]-Fe2O3 and [small alpha]-Fe fibers prepared by the sol-gel method. J. Mater. Chem. 2002, 12, 1844–1847. [Google Scholar] [CrossRef]
- Lay, H.T.; Wang, R.; Chew, J.W. Membrane fouling by mixtures of oppositely charged particles. J. Membr. Sci. 2021, 625, 119093. [Google Scholar] [CrossRef]
- Trinh, T.A.; Li, W.; Chew, J.W. Internal fouling during microfiltration with foulants of different surface charges. J. Membr. Sci. 2020, 602, 117983. [Google Scholar] [CrossRef]




| Ref. | ||||||
|---|---|---|---|---|---|---|
| Al2O3 (Membrane) | 39.6 | 31.6 | 8.0 | 0.6 | 27.2 | [35] |
| Water | 72.8 | 21.8 | 51.0 | 25.5 | 25.5 | [36] |
| Polystyrene (PS) | 42.0 | 42.0 | 0 | 0 | 1.1 | [35] |
| PS Type | Vendor-Given Particle Dimensions (µm) | Measured Particle Dimensions via FESEM (µm) | Measured Mean Particle Sizes via Particle Analyzer (µm) | Particle Sphericity | Surface Group | Surfactant | Zeta Potential (mV) |
|---|---|---|---|---|---|---|---|
| Unmodified | 5.1 ± 0.16 | 5.1 ± 0.10 | 2.8 ± 0.39 | 1.00 | Sulfate | Anionic | −53.23 ± 0.08 |
| Carboxylated | 5.2 ± 0.18 | 5.1 ± 0.06 | 2.2 ± 0.31 | 1.00 | Carboxyl | Anionic | −16.28 ± 0.45 |
| Aminated | 5.3 ± 0.16 | 5.3 ± 0.09 | 2.4 ± 0.23 | 1.00 | Amino | Cationic | 15.62 ± 4.65 |
| Pear-shaped | 3.8 by 5.1 | 3.9 by 5.4 | 1.4 ± 0.38 | 0.82 | Sulfate | Anionic | −41.41 ± 0.42 |
| Peanut-shaped= | 3.4 by 5.1 | 3.0 by 5.1 | 1.1 ± 0.18 | 0.52 | Sulfate | Anionic | −44.75 ± 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanis-Kanbur, M.B.; Tamilselvam, N.R.; Lai, H.Y.; Chew, J.W. Impact of Particle Shape and Surface Group on Membrane Fouling. Membranes 2022, 12, 403. https://doi.org/10.3390/membranes12040403
Tanis-Kanbur MB, Tamilselvam NR, Lai HY, Chew JW. Impact of Particle Shape and Surface Group on Membrane Fouling. Membranes. 2022; 12(4):403. https://doi.org/10.3390/membranes12040403
Chicago/Turabian StyleTanis-Kanbur, Melike Begum, Navin Raj Tamilselvam, Hsiao Yu Lai, and Jia Wei Chew. 2022. "Impact of Particle Shape and Surface Group on Membrane Fouling" Membranes 12, no. 4: 403. https://doi.org/10.3390/membranes12040403
APA StyleTanis-Kanbur, M. B., Tamilselvam, N. R., Lai, H. Y., & Chew, J. W. (2022). Impact of Particle Shape and Surface Group on Membrane Fouling. Membranes, 12(4), 403. https://doi.org/10.3390/membranes12040403







