Theoretical Analysis of Electroconvection in the Electrodialysis Desalination Channel under the Action of Direct Current
Abstract
1. Introduction
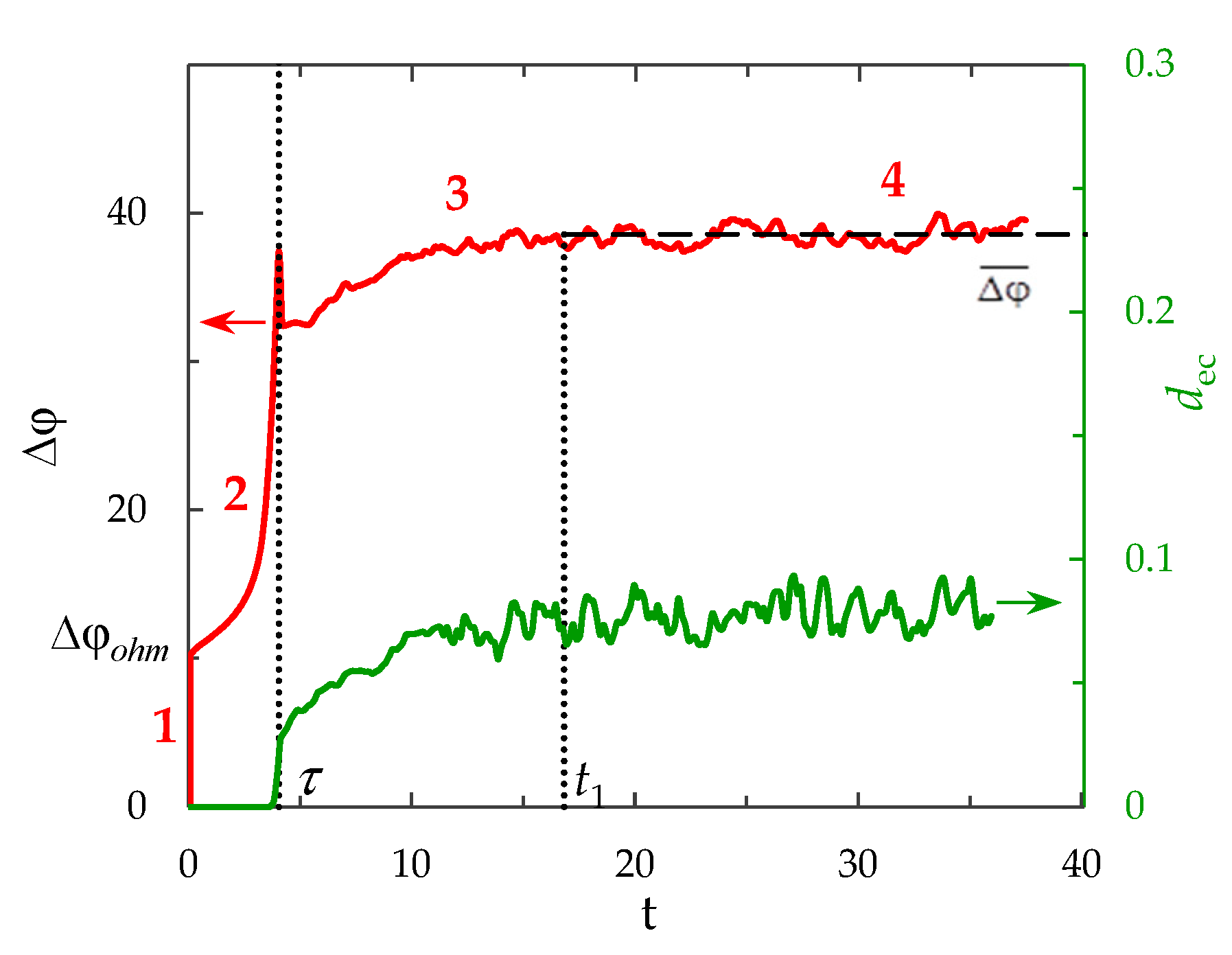
- An initial, almost vertical section, defined by the initial ohmic resistance of the solution;
- A region of slow growth of the potential jump, which is associated with a decrease in the concentration in the depleted solution near the membrane surface as a result of electrodiffusion processes;
- At overlimiting current densities, an inflection point of the ChP curve is noted, which is associated with the appearance of another ion transport mechanism [4]; thus, the third transition region of the ChP corresponds to the development of additional ion transport mechanisms;
- A section where the system is in a stationary or quasi-stationary state (when the potential jump oscillates about a certain fixed value).
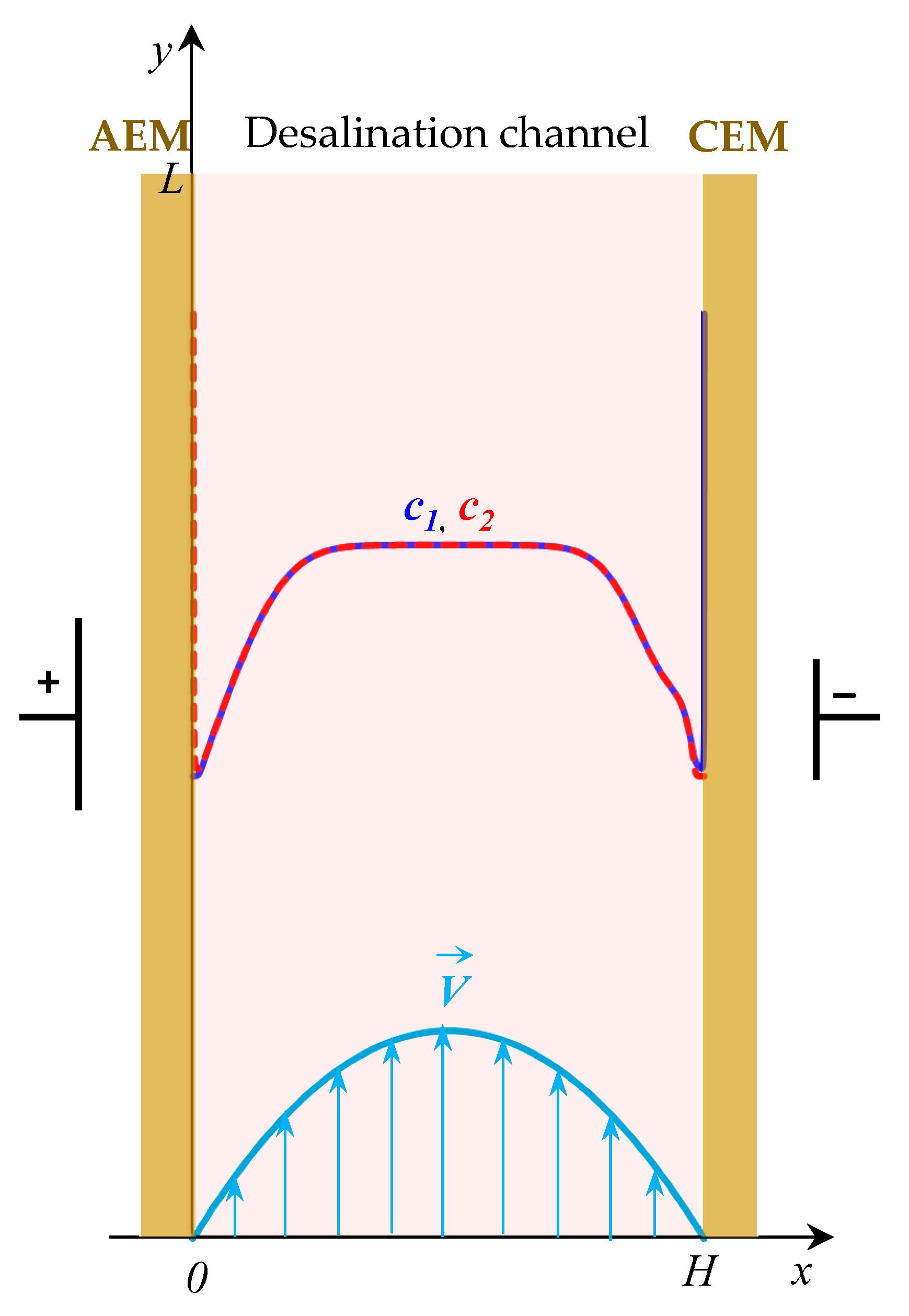
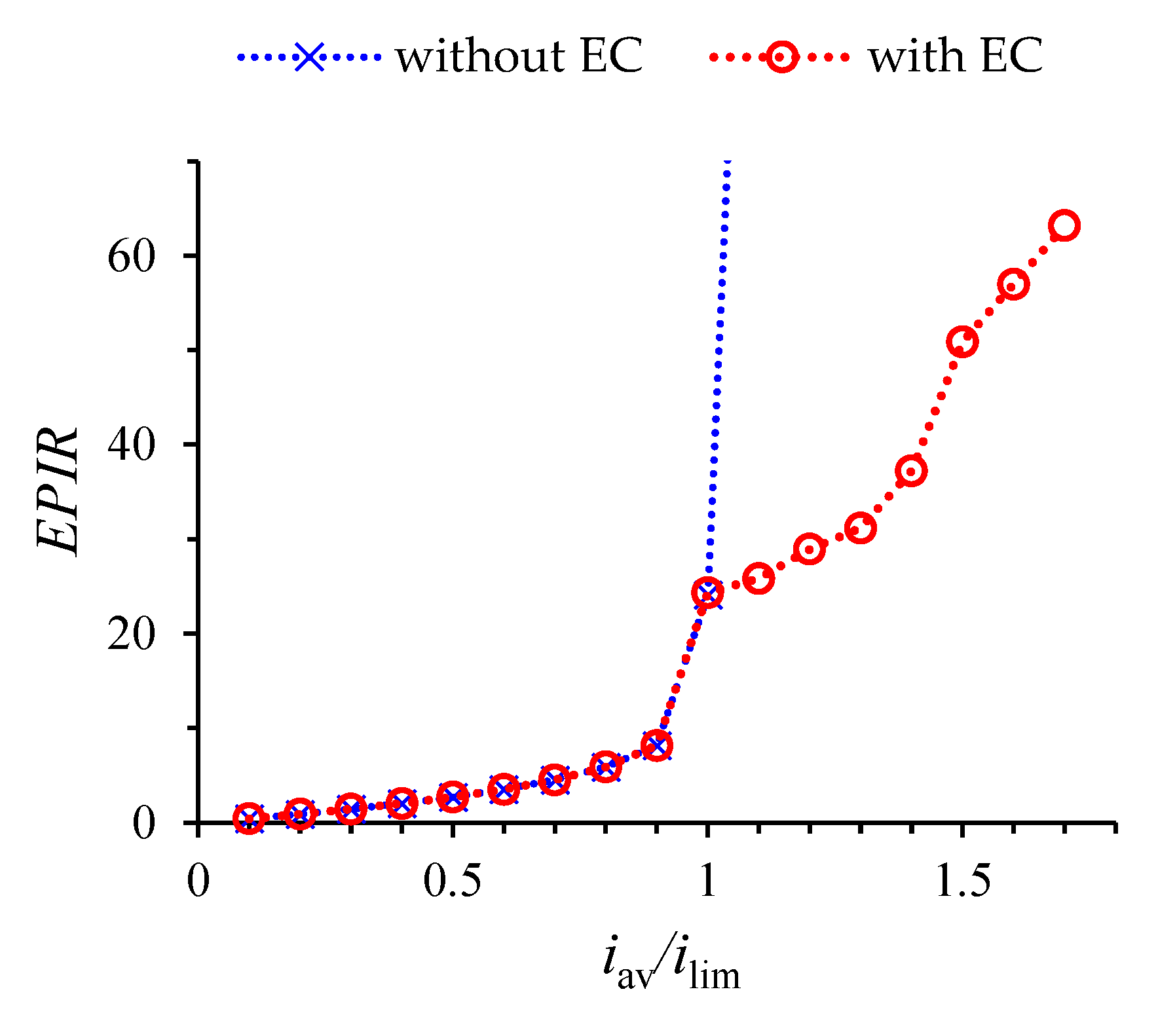
2. Mathematical Model
3. Results and Discussion
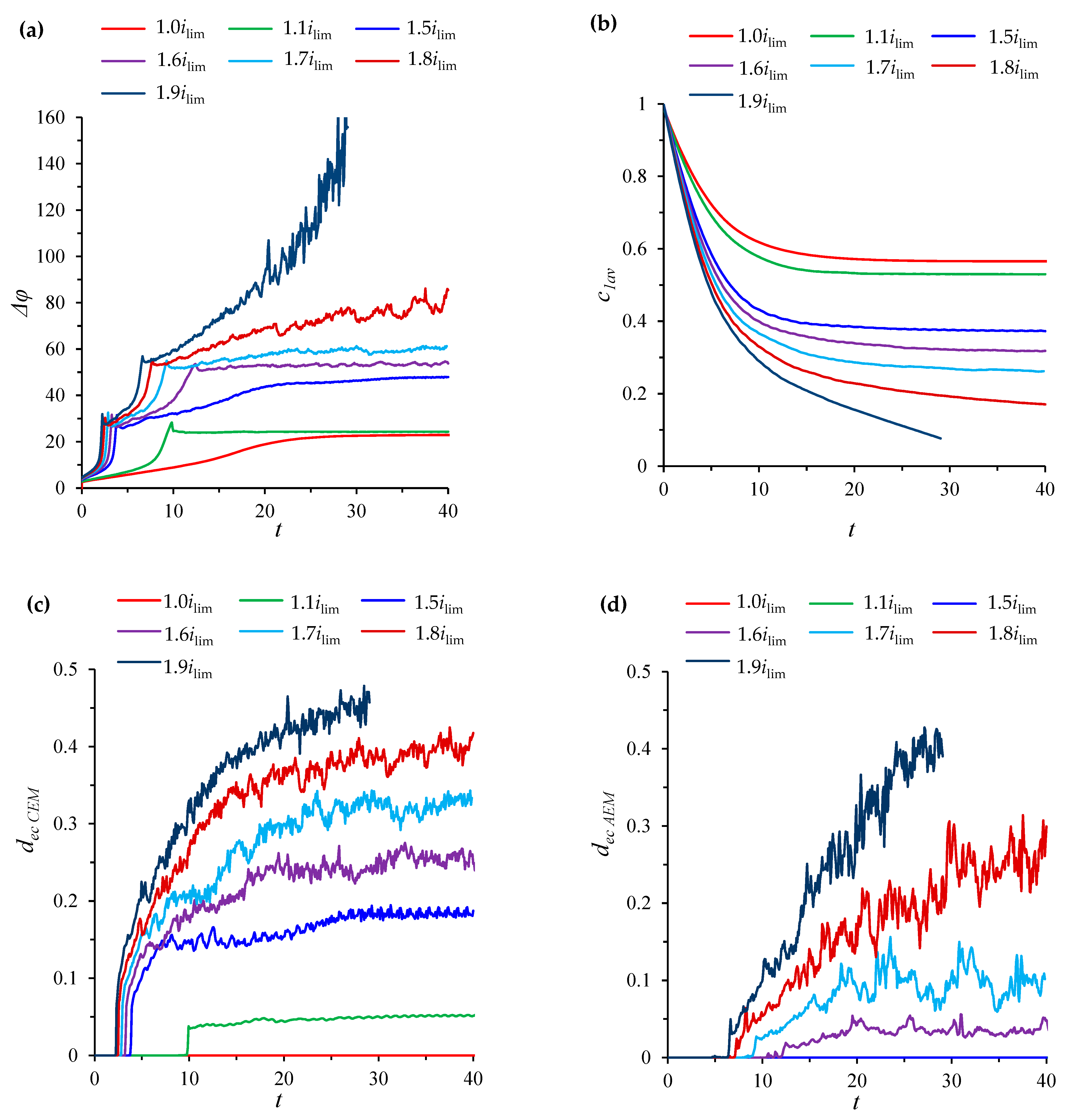
3.1. The Condition for the Transition of the System to a Quasi-Stationary State
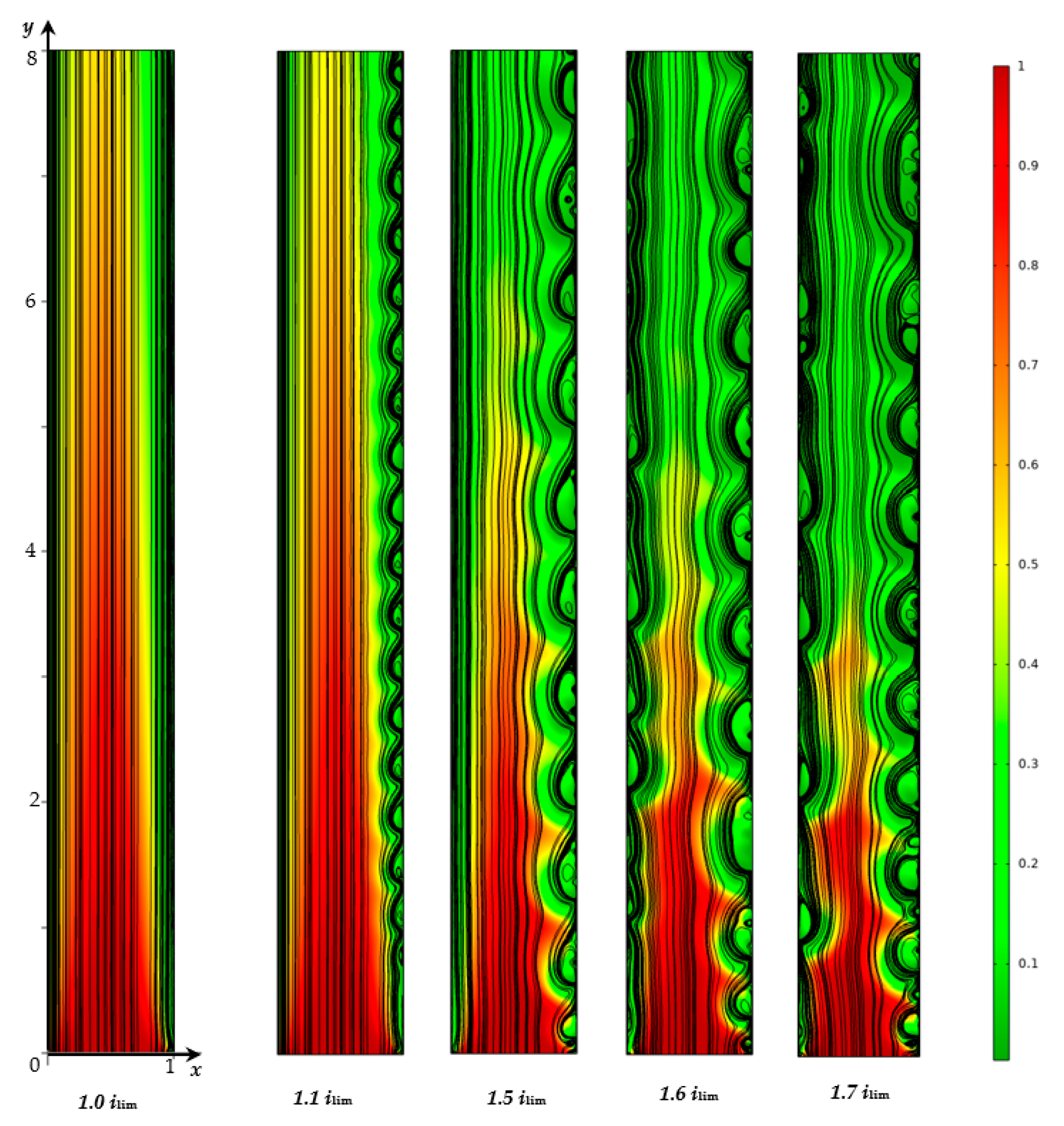
3.2. Numerical Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Strathmann, H. Ion-Exchange Membrane Processes in Water Treatment. In Sustainability Science and Engineering; Escobar, I.C., Schäfer, A.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; Volume 2, pp. 141–199. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G. Electrodialysis Applications in Wastewater Treatment for Environmental Protection and Resources Recovery: A Systematic Review on Progress and Perspectives. Membranes 2020, 10, 146. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.R. Demineralization by Electrodialysis; Butterworths Scientific Publications: London, UK, 1960. [Google Scholar]
- Pismenskaia, N.; Sistat, P.; Huguet, P.; Nikonenko, V.; Pourcelly, G. Chronopotentiometry applied to the study of ion transfer through anion exchange membranes. J. Membr. Sci. 2004, 228, 65–76. [Google Scholar] [CrossRef]
- Belova, E.I.; Lopatkova, G.Y.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. The effect of anion-exchange membrane surface properties on mechanisms of overlimiting mass transfer. J. Phys. Chem. B 2006, 110, 13458. [Google Scholar] [CrossRef] [PubMed]
- Martí-Calatayud, M.C.; Buzzi, D.C.; García-Gabaldón, M.; Bernardes, A.M.; Tenório, J.A.S.; Pérez-Herranz, V. Ion transport through homogeneous and heterogeneous ion-exchange membranes in single salt and multicomponent electrolyte solutions. J. Membr. Sci. 2014, 466, 45–57. [Google Scholar] [CrossRef]
- Gil, V.V.; Andreeva, M.A.; Jansezian, L.; Han, J.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Dammak, L. Impact of heterogeneous cation-exchange membrane surface modification on chronopotentiometric and current-voltage characteristics in NaCl, CaCl2 and MgCl2 solutions. Electrochim. Acta 2018, 281, 472–485. [Google Scholar] [CrossRef]
- Titorova, V.D.; Mareev, S.A.; Gorobchenko, A.D.; Gil, V.V.; Nikonenko, V.V.; Sabbatovskii, K.G.; Pismenskaya, N.D. Effect of current-induced coion transfer on the shape of chronopotentiograms of cation-exchange membranes. J. Membr. Sci. 2021, 624, 119036. [Google Scholar] [CrossRef]
- Dukhin, S.S. Electrokinetic phenomena of the second kind and their applications. Adv. Colloid Interface Sci. 1991, 35, 173–196. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Electro-osmosis of the second kind near the heterogeneous ion-exchange membrane. Colloids Surf. A Physicochem. Eng. Asp. 1998, 140, 75–89. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef]
- Zaltzman, B.; Rubinstein, I. Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 2007, 579, 173–226. [Google Scholar] [CrossRef]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Rubinshtein, I.; Zaltzman, B.; Pretz, J.; Linder, C. Experimental Verification of the Electroosmotic Mechanism of Overlimiting Conductance Through a Cation Exchange Electrodialysis Membrane. Russ. J. Electrochem. 2002, 38, 853–863. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nikonenko, V.V.; Belova, E.I.; Lopatkova, G.Y.; Sistat, P.; Pourcelly, G.; Larchet, C. Coupled convection of solution near the surface of ion-exchange membranes in intensive current regimes. Russ. J. Electrochem. 2007, 43, 307. [Google Scholar] [CrossRef]
- Kwak, R.; Guan, G.; Peng, W.K.; Han, J. Microscale electrodialysis: Concentration profiling and vortex visualization. Desalination 2013, 308, 138–146. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Nikitin, N.V.; Shelistov, V.S. Direct numerical simulation of electrokinetic instability and transition to chaotic motion. Phys. Fluids 2013, 25, 122001. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Uzdenova, A.M.; Kovalenko, A.V.; Nikonenko, V.V.; Pismenskaya, N.D.; Vasil’eva, V.I.; Sistat, P.; Pourcelly, G. Basic mathematical model of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells. J. Membr. Sci. 2013, 447, 190–202. [Google Scholar] [CrossRef]
- Pham, S.V.; Li, Z.; Lim, K.M.; White, J.K.; Han, J. Direct numerical simulation of electroconvective instability and hysteretic current-voltage response of a permselective membrane. Phys. Rev. E 2012, 86, 046310. [Google Scholar] [CrossRef]
- Uzdenova, A. 2D mathematical modelling of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells in galvanodynamic mode. Membranes 2019, 9, 39. [Google Scholar] [CrossRef]
- Kovalenko, A.V.; Vasil’eva, V.I.; Nikonenko, V.V.; Uzdenova, A.M.; Urtenov, M.K.; Sistat, P.; Belashova, E.D. Similarity theory of transport processes in electrodialysis desalination channel. Condens. Matter Interphases 2014, 16, 429–438. Available online: http://www.kcmf.vsu.ru/resources/t_16_4_2014_006.pdf (accessed on 1 September 2022).
- Cohen, H.; Cooley, J.W. The numerical solution of the time-dependent Nernst-Planck equations. Biophys. J. 1965, 5, 145. [Google Scholar] [CrossRef]
- Pismensky, A.V.; Urtenov, M.K.; Nikonenko, V.V.; Sistat, P.; Pismenskaya, N.D.; Kovalenko, A.V. Model and Experimental Studies of Gravitational Convection in an Electromembrane Cell. Russ. J. Electrochem. 2012, 48, 756–766. [Google Scholar] [CrossRef]
- Roache, P.J. Computational Fluid Dynamics; Hermosa Publishers: Albuquerque, NM, USA, 1976. [Google Scholar]
- Larchet, C.; Nouri, S.; Auclair, B.; Dammak, L.; Nikonenko, V. Application of chronopotentiometry to determine the thickness of diffusion layer adjacent to an ion-exchange membrane under natural convection. Adv. Colloid Interface Sci. 2008, 139, 45–61. [Google Scholar] [CrossRef] [PubMed]
- Uzdenova, A.; Kovalenko, A.; Urtenov, M.; Nikonenko, V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8, 84. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.; Kim, M.; Shin, J.; Yang, D.; Kim, M.; Kim, B. Experimental Study on Ion Transport in Microfluidic Electrodialysis Using Partially Masked Ion Exchange Membranes. Micromachines 2022, 13, 356. [Google Scholar] [CrossRef]
- Uzdenova, A.; Urtenov, M. Potentiodynamic and Galvanodynamic Regimes of Mass Transfer in Flow-Through Electrodialysis Membrane Systems: Numerical Simulation of Electroconvection and Current-Voltage Curve. Membranes 2020, 10, 49. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Vasil’eva, V.I.; Akberova, E.M.; Uzdenova, A.M.; Urtenov, M.K.; Kovalenko, A.V.; Pismenskaya, N.D.; Mareev, S.A.; Pourcelly, G. Competition between diffusion and electroconvection at an ion-selective surface in intensive current regimes. Adv. Colloid Interface Sci. 2016, 235, 233–246. [Google Scholar] [CrossRef]
- Gil, V.V.; Andreeva, M.A.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Dammak, L. Effect of counterion hydration numbers on the development of Electroconvection at the surface of heterogeneous cation-exchange membrane modified with an MF-4SK film. Pet. Chem. 2016, 56, 440–449. [Google Scholar] [CrossRef]
- Valenca, J.; Jogi, M.; Wagterveld, R.M.; Karatay, E.; Wood, J.A.; Lammertink, R.G.H. Confined electroconvective vortices at structured ion exchange membranes. Langmuir 2018, 34, 2455–2463. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, Y.; Shi, P. Shear electroconvective instability in electrodialysis channel under extreme depletion and its scaling laws. Phys. Rev. E 2020, 101, 043105. [Google Scholar] [CrossRef]
- Kovalenko, A.; Wessling, M.; Nikonenko, V.; Mareev, S.; Moroz, I.; Evdochenko, E.; Urtenov, M.K. Space-Charge breakdown phenomenon and spatio-temporal ion concentration and fluid flow patterns in overlimiting current electrodialysis. J. Membr. Sci. 2021, 636, 119583. [Google Scholar] [CrossRef]
- De Valença, J.C.; Wagterveld, R.M.; Lammertink, R.G.H.; Tsai, P.A. Dynamics of microvortices induced by ion concentration polarization. Phys. Rev. E 2015, 92, 031003. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzdenova, A.; Kovalenko, A.; Urtenov, M. Theoretical Analysis of Electroconvection in the Electrodialysis Desalination Channel under the Action of Direct Current. Membranes 2022, 12, 1125. https://doi.org/10.3390/membranes12111125
Uzdenova A, Kovalenko A, Urtenov M. Theoretical Analysis of Electroconvection in the Electrodialysis Desalination Channel under the Action of Direct Current. Membranes. 2022; 12(11):1125. https://doi.org/10.3390/membranes12111125
Chicago/Turabian StyleUzdenova, Aminat, Anna Kovalenko, and Makhamet Urtenov. 2022. "Theoretical Analysis of Electroconvection in the Electrodialysis Desalination Channel under the Action of Direct Current" Membranes 12, no. 11: 1125. https://doi.org/10.3390/membranes12111125
APA StyleUzdenova, A., Kovalenko, A., & Urtenov, M. (2022). Theoretical Analysis of Electroconvection in the Electrodialysis Desalination Channel under the Action of Direct Current. Membranes, 12(11), 1125. https://doi.org/10.3390/membranes12111125








