Can Hindered Transport Models for Rigid Spheres Predict the Rejection of Single Stranded DNA from Porous Membranes?
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiment
2.2. Modeling
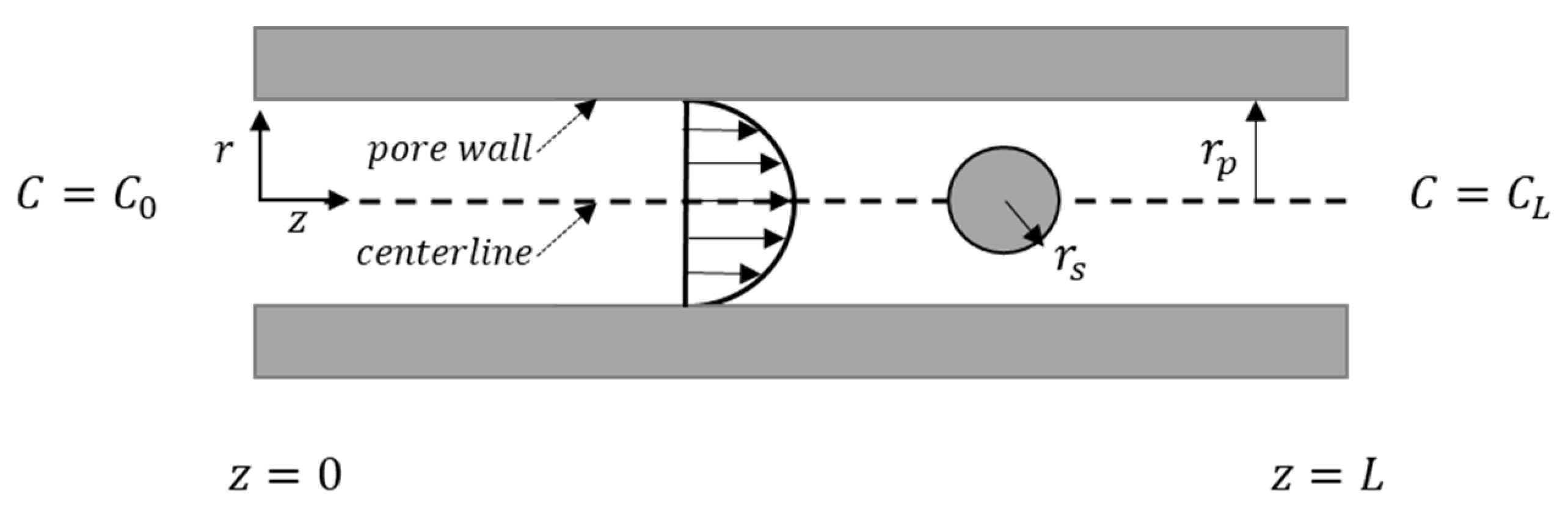
2.2.1. Solute and Pore Sizes
2.2.2. Hydrodynamic Interactions
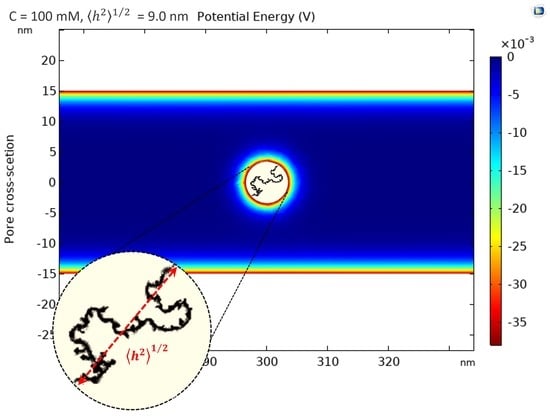
2.2.3. Electrostatic Interactions
3. Results and Discussion
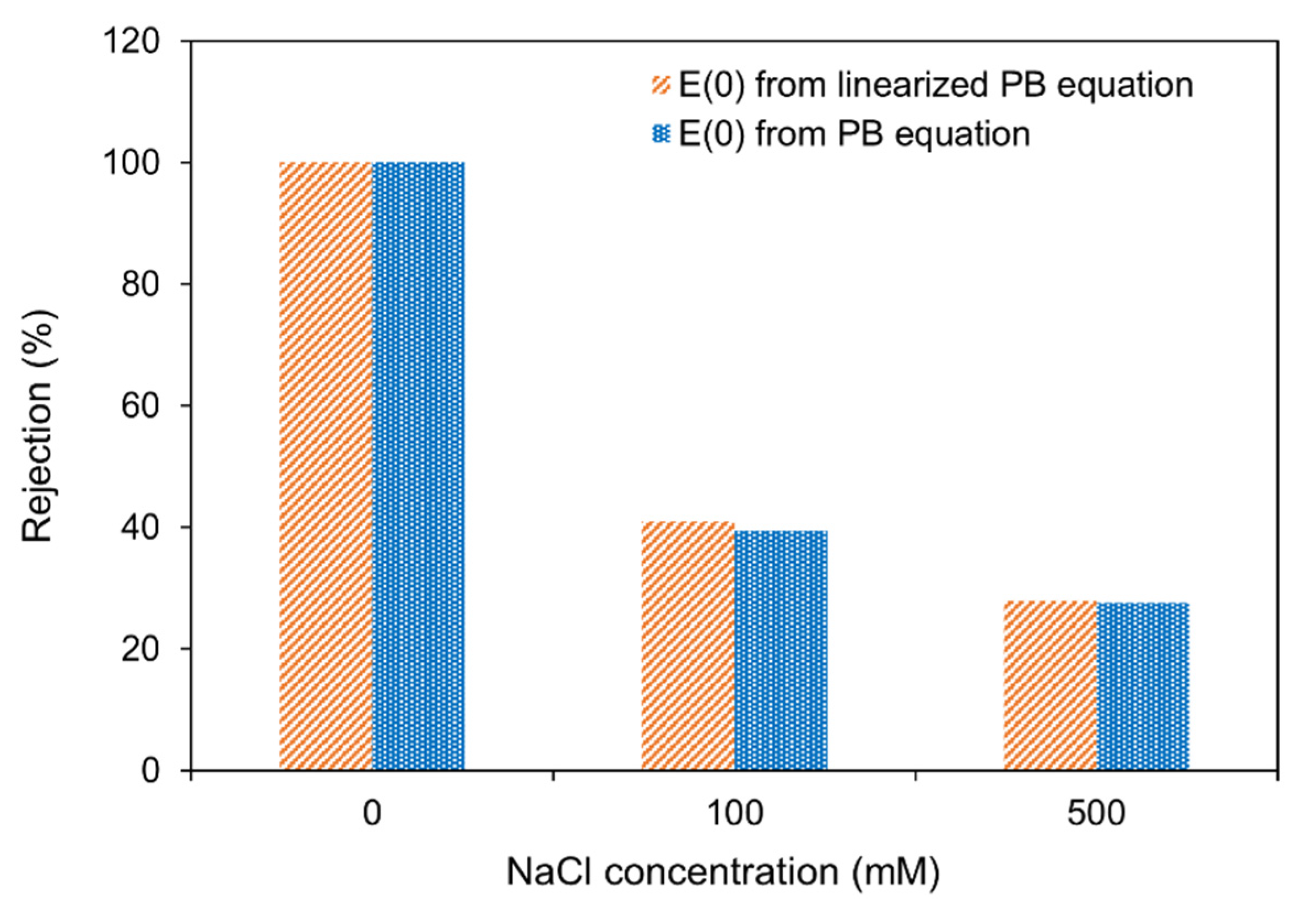
3.1. Linearized vs. Non-Linearized Poisson Boltzmann Equation
3.2. Hydrodynamic Interactions
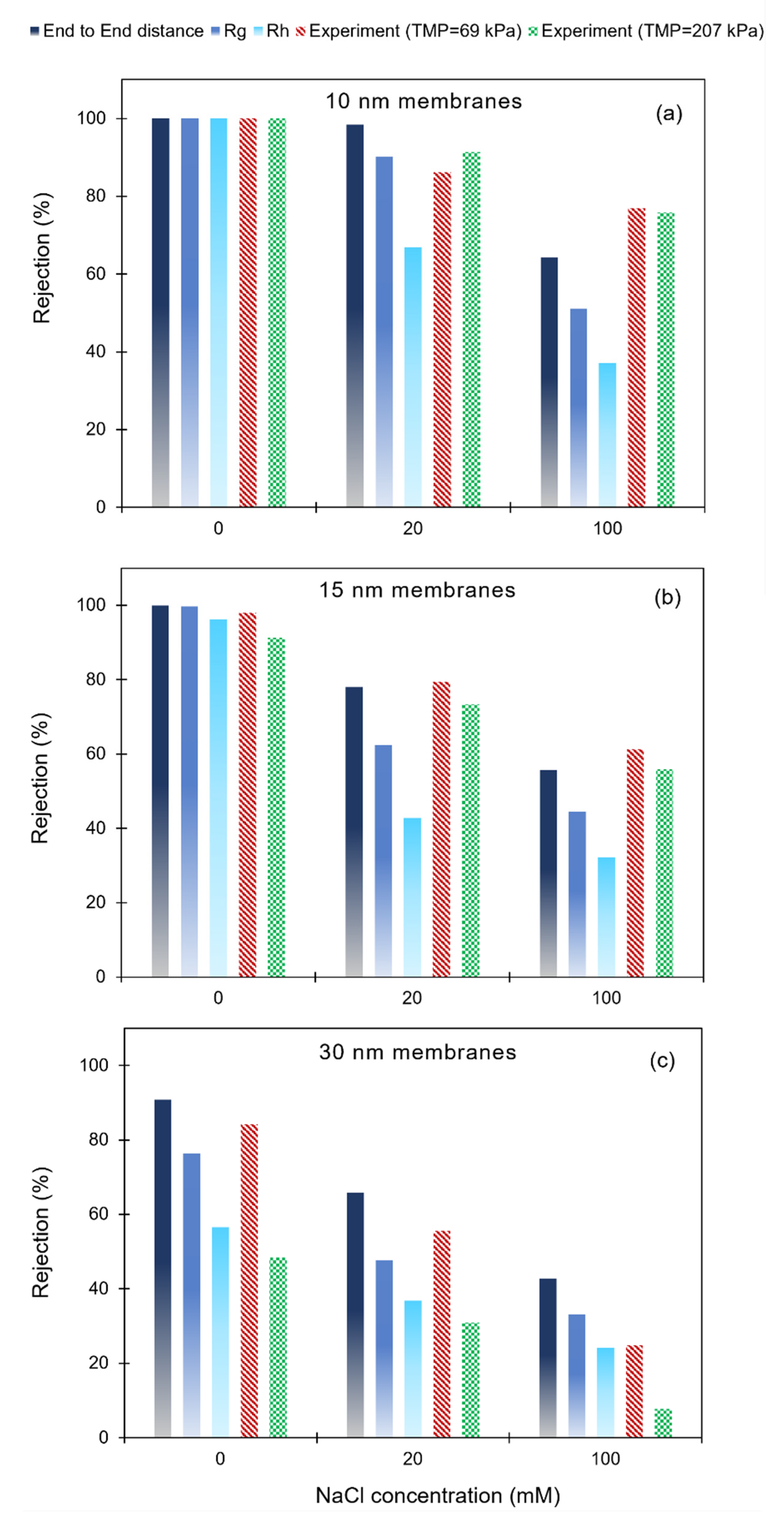
3.3. Poly(dT60) ssDNA Rejection: Model Predictions and Experimental Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Patil, S.D.; Rhodes, D.G.; Burgess, D.J. DNA-based therapeutics and DNA delivery systems: A comprehensive review. AAPS J. 2005, 7, E61–E77. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Zheng, M.; Tao, W.; Chung, R.; Jin, D.; Ghaffari, D.; Farokhzad, O.C. Challenges in DNA Delivery and Recent Advances in Multifunctional Polymeric DNA Delivery Systems. Biomacromolecules 2017, 18, 2231–2246. [Google Scholar] [CrossRef] [PubMed]
- Yurina, V. Live Bacterial Vectors—A Promising DNA Vaccine Delivery System. Med. Sci. 2018, 6, 27. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Gao, H.; Guo, C.; Liu, T.; Li, N.; Qian, Q. Therapeutic Mechanism of Nucleic Acid Drugs. ChemistrySelect 2021, 6, 903–916. [Google Scholar] [CrossRef]
- Latulippe, D.R.; Zydney, A.L. Separation of plasmid DNA isoforms by highly converging flow through small membrane pores. J. Colloid Interface Sci. 2011, 357, 548–553. [Google Scholar] [CrossRef]
- Morão, A.M.; Nunes, J.C.; Sousa, F.; Pessoa de Amorim, M.T.; Escobar, I.C.; Queiroz, J.A. Ultrafiltration of supercoiled plasmid DNA: Modeling and application. J. Membr. Sci. 2011, 378, 280–289. [Google Scholar] [CrossRef]
- Zydney, A.L. New developments in membranes for bioprocessing—A review. J. Membr. Sci. 2021, 620, 118804. [Google Scholar] [CrossRef]
- Quinn, J.A.; Anderson, J.L.; Ho, W.S.; Petzny, W.J. Model Pores of Molecular Dimension. Biophys. J. 1972, 12, 990–1007. [Google Scholar] [CrossRef]
- Anderson, J.L. Configurational effect on the reflection coefficient for rigid solutes in capillary pores. J. Theor. Biol. 1981, 90, 405–426. [Google Scholar] [CrossRef]
- Deen, W.M. Hindered transport of large molecules in liquid-filled pores. AIChE J. 1987, 33, 1409–1425. [Google Scholar] [CrossRef]
- Giddings, J.C.; Kucera, E.; Russell, C.P.; Myers, M.N. Statistical theory for the equilibrium distribution of rigid molecules in inert porous networks. Exclusion chromatography. J. Phys. Chem. 1968, 72, 4397–4408. [Google Scholar] [CrossRef]
- Brenner, H.; Gaydos, L.J. The constrained brownian movement of spherical particles in cylindrical pores of comparable radius: Models of the diffusive and convective transport of solute molecules in membranes and porous media. J. Colloid Interface Sci. 1977, 58, 312–356. [Google Scholar] [CrossRef]
- Dechadilok, P.; Deen, W.M. Hindrance Factors for Diffusion and Convection in Pores. Ind. Eng. Chem. Res. 2006, 45, 6953–6959. [Google Scholar] [CrossRef]
- Smith, F.G.; Deen, W.M. Electrostatic double-layer interactions for spherical colloids in cylindrical pores. J. Colloid Interface Sci. 1980, 78, 444–465. [Google Scholar] [CrossRef]
- Smith, F.G.; Deen, W.M. Electrostatic effects on the partitioning of spherical colloids between dilute bulk solution and cylindrical pores. J. Colloid Interface Sci. 1983, 91, 571–590. [Google Scholar] [CrossRef]
- Pujar, N.S.; Zydney, A.L. Electrostatic and Electrokinetic Interactions during Protein Transport through Narrow Pore Membranes. Ind. Eng. Chem. Res. 1994, 33, 2473–2482. [Google Scholar] [CrossRef]
- Burns, D.B.; Zydney, A.L. Contributions to electrostatic interactions on protein transport in membrane systems. AIChE J. 2001, 47, 1101–1114. [Google Scholar] [CrossRef]
- Agasanapura, B.; Baltus, R.E.; Tanneru, C.T.; Chellam, S. Effect of electrostatic interactions on rejection of capsular and spherical particles from porous membranes: Theory and experiment. J. Colloid Interface Sci. 2015, 448, 492–500. [Google Scholar] [CrossRef]
- Dechadilok, P.; Deen, W.M. Electrostatic and electrokinetic effects on hindered convection in pores. J. Colloid Interface Sci. 2009, 338, 135–144. [Google Scholar] [CrossRef]
- Delavari, A.; Breite, D.; Schulze, A.; Baltus, R.E. Latex particle rejections from virgin and mixed charged surface polycarbonate track etched membranes. J. Membr. Sci. 2019, 584, 110–119. [Google Scholar] [CrossRef]
- Rohani, M.M.; Zydney, A.L. Effect of surface charge distribution on protein transport through semipermeable ultrafiltration membranes. J. Membr. Sci. 2009, 337, 324–331. [Google Scholar] [CrossRef]
- Arunkumar, A.; Etzel, M.R. Negatively charged tangential flow ultrafiltration membranes for whey protein concentration. J. Membr. Sci. 2015, 475, 340–348. [Google Scholar] [CrossRef]
- Casassa, E.F.; Tagami, Y. An Equilibrium Theory for Exclusion Chromatography of Branched and Linear Polymer Chains. Macromolecules 1969, 2, 14–26. [Google Scholar] [CrossRef]
- Morão, A.; Nunes, J.C.; Sousa, F.; Amorim, M.T.P.; De Escobar, I.C.; Queiroz, J.A. Development of a model for membrane filtration of long and flexible macromolecules: Application to predict dextran and linear DNA rejections in ultrafiltration. J. Membr. Sci. 2009, 336, 61–70. [Google Scholar] [CrossRef]
- Davidson, M.G.; Suter, U.W.; Deen, W.M. Equilibrium partitioning of flexible macromolecules between bulk solution and cylindrical pores. Macromolecules 1987, 20, 1141–1146. [Google Scholar] [CrossRef]
- Bleha, T.; Cifra, P.; Karasz, F.E. The effects of concentration on partitioning of flexible chains into pores. Polymer 1990, 31, 1321–1327. [Google Scholar] [CrossRef]
- Davidson, M.G.; Deen, W.M. Hydrodynamic theory for the hindered transport of flexible macromolecules in porous membranes. J. Membr. Sci. 1988, 35, 167–192. [Google Scholar] [CrossRef]
- Latulippe, D.R.; Zydney, A.L. Elongational flow model for transmission of supercoiled plasmid DNA during membrane ultrafiltration. J. Membr. Sci. 2009, 329, 201–208. [Google Scholar] [CrossRef]
- Nouri Alavijeh, H.; Baltus, R. Transmission of Poly(dT60) Single-Stranded DNA through Polycarbonate Track-Etched Ultrafiltration Membranes. Biotechnol. Prog. 2022; submitted. [Google Scholar]
- Li, Y.; Currie, D.; Zydney, A.L. Enhanced purification of plasmid DNA isoforms by exploiting ionic strength effects during ultrafiltration. Biotechnol. Bioeng. 2016, 113, 783–789. [Google Scholar] [CrossRef]
- Latulippe, D.R.; Zydney, A.L. Salt-induced changes in plasmid DNA transmission through ultrafiltration membranes. Biotechnol. Bioeng. 2008, 99, 390–398. [Google Scholar] [CrossRef]
- Li, Y.; Butler, N.; Zydney, A.L. Size-based separation of supercoiled plasmid DNA using ultrafiltration. J. Colloid Interface Sci. 2016, 472, 195–201. [Google Scholar] [CrossRef]
- Manzano, I.; Zydney, A.L. Quantitative study of RNA transmission through ultrafiltration membranes. J. Membr. Sci. 2017, 544, 272–277. [Google Scholar] [CrossRef]
- Nouri Alavijeh, H. A Study on Membrane Filtration of Single-Stranded DNA. Ph.D. Thesis, Clarkson University, Potsdam, NY, USA, 2021. [Google Scholar]
- Laurence, T.A.; Kong, X.; Jäger, M.; Weiss, S. Probing structural heterogeneities and fluctuations of nucleic acids and denatured proteins. Proc. Natl. Acad. Sci. USA 2005, 102, 17348–17353. [Google Scholar] [CrossRef] [PubMed]
- Meisburger, S.P.; Sutton, J.L.; Chen, H.; Pabit, S.A.; Kirmizialtin, S.; Elber, R.; Pollack, L. Polyelectrolyte properties of single stranded DNA measured using SAXS and single molecule FRET: Beyond the wormlike chain model. Biopolymers 2013, 99, 1032–1045. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.C.; Rasnik, I.; Cheng, W.; Lohman, T.M.; Ha, T. Probing single-stranded DNA conformational flexibility using fluorescence spectroscopy. Biophys. J. 2004, 86, 2530–2537. [Google Scholar] [CrossRef]
- Mills, J.B.; Vacano, E.; Hagerman, P.J. Flexibility of single-stranded DNA: Use of gapped duplex helices to determine the persistence lengths of poly(dT) and poly(dA). J. Mol. Biol. 1999, 285, 245–257. [Google Scholar] [CrossRef]
- Kuznetsov, S.V.; Shen, Y.; Benight, A.S.; Ansari, A. A semiflexible polymer model applied to loop formation in DNA hairpins. Biophys. J. 2001, 81, 2864–2875. [Google Scholar] [CrossRef][Green Version]
- Sim, A.Y.L.; Lipfert, J.; Herschlag, D.; Doniach, S. Salt dependence of the radius of gyration and flexibility of single-stranded DNA in solution probed by small-angle X-ray scattering. Phys. Rev. E 2012, 86, 021901. [Google Scholar] [CrossRef]
- Doose, S.; Barsch, H.; Sauer, M. Polymer properties of polythymine as revealed by translational diffusion. Biophys. J. 2007, 93, 1224–1234. [Google Scholar] [CrossRef]
- Plumridge, A.; Meisburger, S.P.; Andresen, K.; Pollack, L. The impact of base stacking on the conformations and electrostatics of single-stranded DNA. Nucleic Acids Res. 2017, 45, 3932–3943. [Google Scholar] [CrossRef]
- Desruisseaux, C.; Long, D.; Drouin, G.; Slater, G.W. Electrophoresis of composite molecular objects. 1. Relation between friction, charge, and ionic strength in free solution. Macromolecules 2001, 34, 44–52. [Google Scholar] [CrossRef]
- Tinland, B.; Pluen, A.; Sturm, J.; Weill, G. Persistence Length of Single-Stranded DNA. Macromolecules 1997, 30, 5763–5765. [Google Scholar] [CrossRef]
- Chen, Z.; Graham, R.; Burns, M.A.; Larson, R.G. Modeling ssDNA electrophoretic migration with band broadening in an entangled or cross-linked network. Electrophoresis 2007, 28, 2783–2800. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Record, M.T.; Anderson, C.F.; Lohman, T.M. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: The roles of ion association or release, screening, and ion effects on water activity. Q. Rev. Biophys. 1978, 11, 103–178. [Google Scholar] [CrossRef] [PubMed]
- Huertas, M.L.; Navarro, S.; Lopez Martinez, M.C.; García de la Torre, J. Simulation of the conformation and dynamics of a double-helical model for DNA. Biophys. J. 1997, 73, 3142–3153. [Google Scholar] [CrossRef][Green Version]
- Kratky, O.; Porod, G. Röntgenuntersuchung gelöster Fadenmoleküle. Recl. Trav. Chim. Pays-Bas 1949, 68, 1106–1122. [Google Scholar] [CrossRef]
- Mehta, A.; Zydney, A.L. Effect of Membrane Charge on Flow and Protein Transport during Ultrafiltration. Biotechnol. Prog. 2006, 22, 484–492. [Google Scholar] [CrossRef]
- Higdon, J.J.L.; Muldowney, G.P. Resistance functions for spherical particles, droplets and bubbles in cylindrical tubes. J. Fluid Mech. 1995, 298, 193–210. [Google Scholar] [CrossRef]

| NaCl Concentration (mM) | Diffusion Coefficient (µm2/s) | (nm) | (nm) | (nm) | (nm) |
|---|---|---|---|---|---|
| 0 | 85 ± 5 | 2.8 ± 0.3 | 4.0 ± 0.5 | 10.5 | 2.2 |
| 100 | 96 ± 13 | 2.5 ± 0.4 | 3.5 ± 0.6 | 9.0 | 1.6 |
| 500 | 142 ± 16 | 1.6 ± 0.1 | 2.3 ± 0.2 | 5.6 | 0.6 |
| 1000 | 136 ± 10 | 1.6 ± 0.1 | 2.2 ± 0.2 | 5.6 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alavijeh, H.N.; Baltus, R.E. Can Hindered Transport Models for Rigid Spheres Predict the Rejection of Single Stranded DNA from Porous Membranes? Membranes 2022, 12, 1099. https://doi.org/10.3390/membranes12111099
Alavijeh HN, Baltus RE. Can Hindered Transport Models for Rigid Spheres Predict the Rejection of Single Stranded DNA from Porous Membranes? Membranes. 2022; 12(11):1099. https://doi.org/10.3390/membranes12111099
Chicago/Turabian StyleAlavijeh, Hossein Nouri, and Ruth E. Baltus. 2022. "Can Hindered Transport Models for Rigid Spheres Predict the Rejection of Single Stranded DNA from Porous Membranes?" Membranes 12, no. 11: 1099. https://doi.org/10.3390/membranes12111099
APA StyleAlavijeh, H. N., & Baltus, R. E. (2022). Can Hindered Transport Models for Rigid Spheres Predict the Rejection of Single Stranded DNA from Porous Membranes? Membranes, 12(11), 1099. https://doi.org/10.3390/membranes12111099