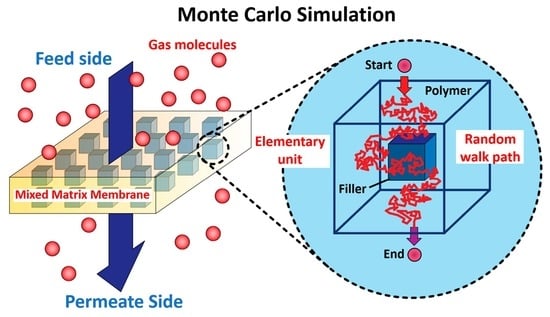
Monte Carlo Simulations for the Estimation of the Effective Permeability of Mixed-Matrix Membranes
Abstract
1. Introduction
2. Methodology
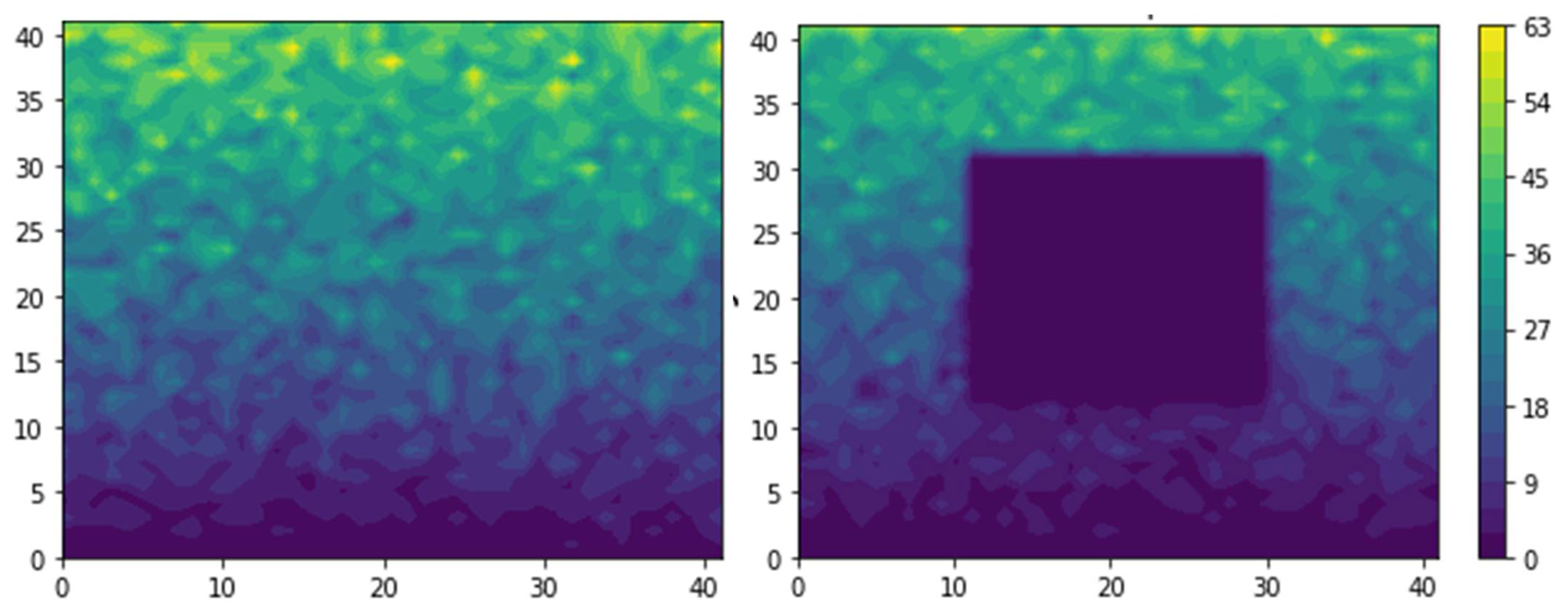
2.1. Definition of the Simulation Domain
2.2. Monte Carlo Algorithm
- (a)
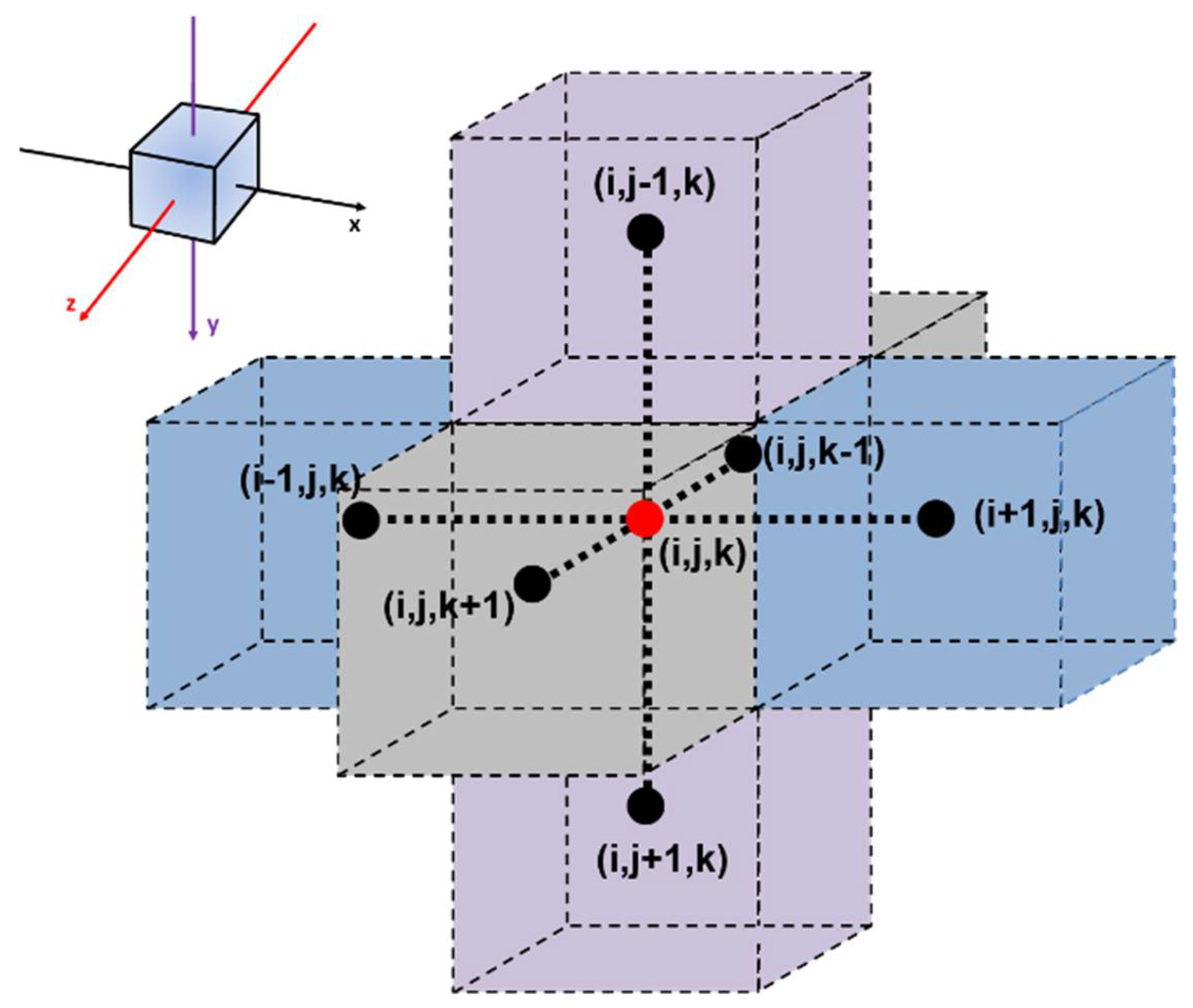
- All members of the current population are, in turn, subjected to a random move in one of the six adjoining meshes (Figure 2) such that a molecule will potentially move to an adjacent mesh. To consider the difference in the diffusivity coefficient between the two phases of the MMM, the probability of a molecule adopting the suggested move is made equal to the ratio of the diffusivity at the current mesh location and the maximum diffusivity value as expressed in Equation (5).If the random number (RN) is smaller than the diffusivity ratio, the move is considered. A move is always suggested but not necessarily realized depending on some additional considerations when the molecule under consideration is currently located within the phase having the lowest diffusivity. For instance, assuming a diffusivity ratio of 0.1, if the molecule is located in the phase with the lowest diffusivity, the probability of moving to a neighboring mesh slot is 0.1. If a molecule is currently located in the phase having the highest diffusivity, the move is always accepted provided few additional conditions are satisfied.
- (b)
- Indeed, when a move of a molecule is accepted, this particular move is subjected to two additional conditions to be realized.
- (i)
- If a molecule is currently located at one of the four lateral faces perpendicular to the x- and z-direction of the elementary unit and the move brings that molecule outside the elementary unit, then this molecule simply re-enters the elementary unit directly on the opposite face in order to satisfy the four symmetrical periodic conditions in the x- and z-directions [23].
- (ii)
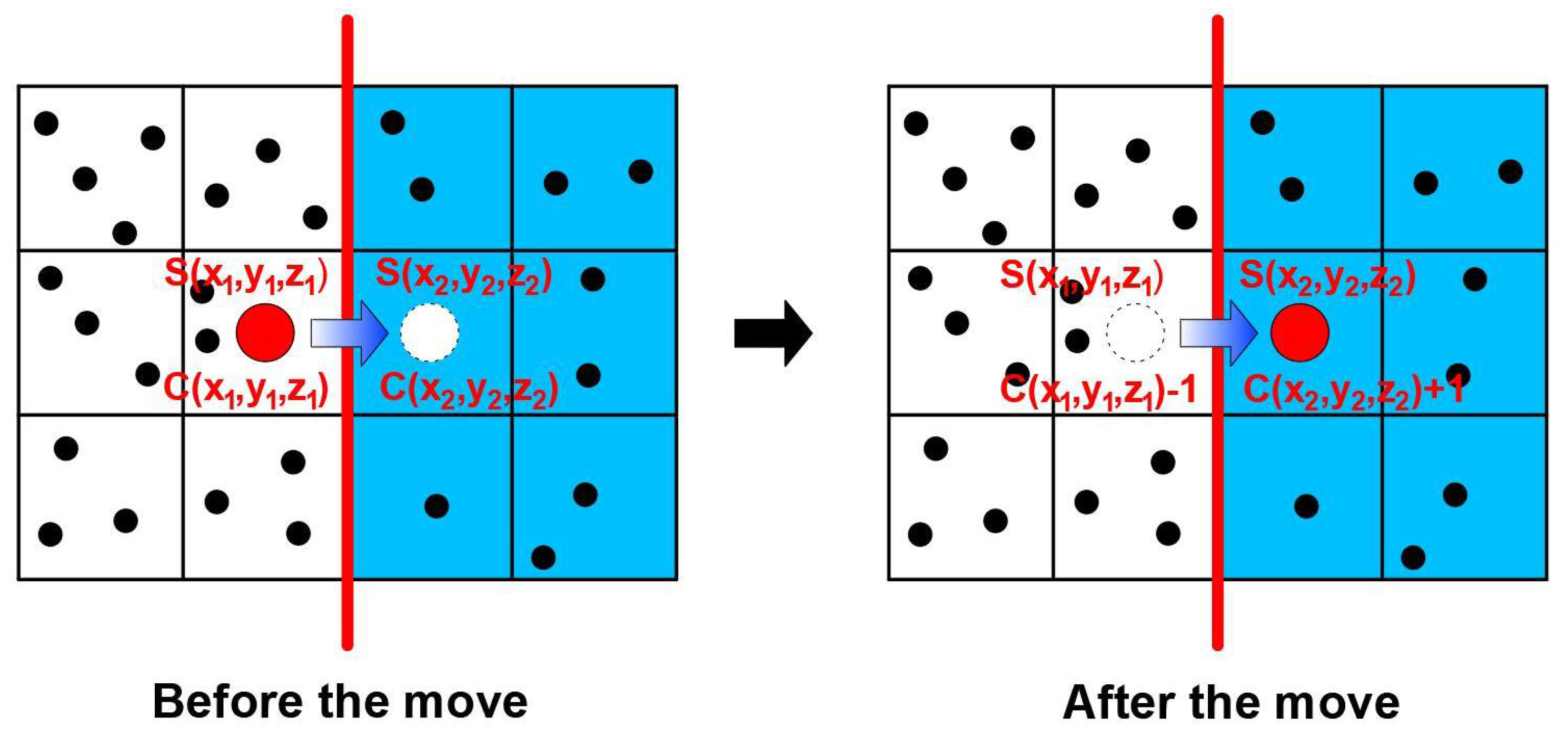
- Since it is assumed that equilibrium prevails at the polymer–solid interface, if the suggested random move is from phase 1 to phase 2 (Figure 4), the move will be accepted if it favors the attainment of the equilibrium between the two phases. If the two solubility coefficients differ, a discontinuity in concentration will prevail at the polymer–solid interface. If the current ratio of concentration C2/C1 already exceeds the solubility ratio S2/S1, the move is not performed (Equation (6)). If the ratio of concentration following the move remains smaller than the solubility ratio, the move is performed (Equation (7)). Finally, if the concentration ratio before the move is smaller than the solubility ratio whereas it becomes greater after the move, the probability of accepting the move is calculated as given in Equation (8). It is important to point out that the interface equilibrium cannot be specified directly, but must be attained progressively through molecule random walk. Equations (6)–(8) ensure that the system is always trying to achieve equilibrium.
- (c)
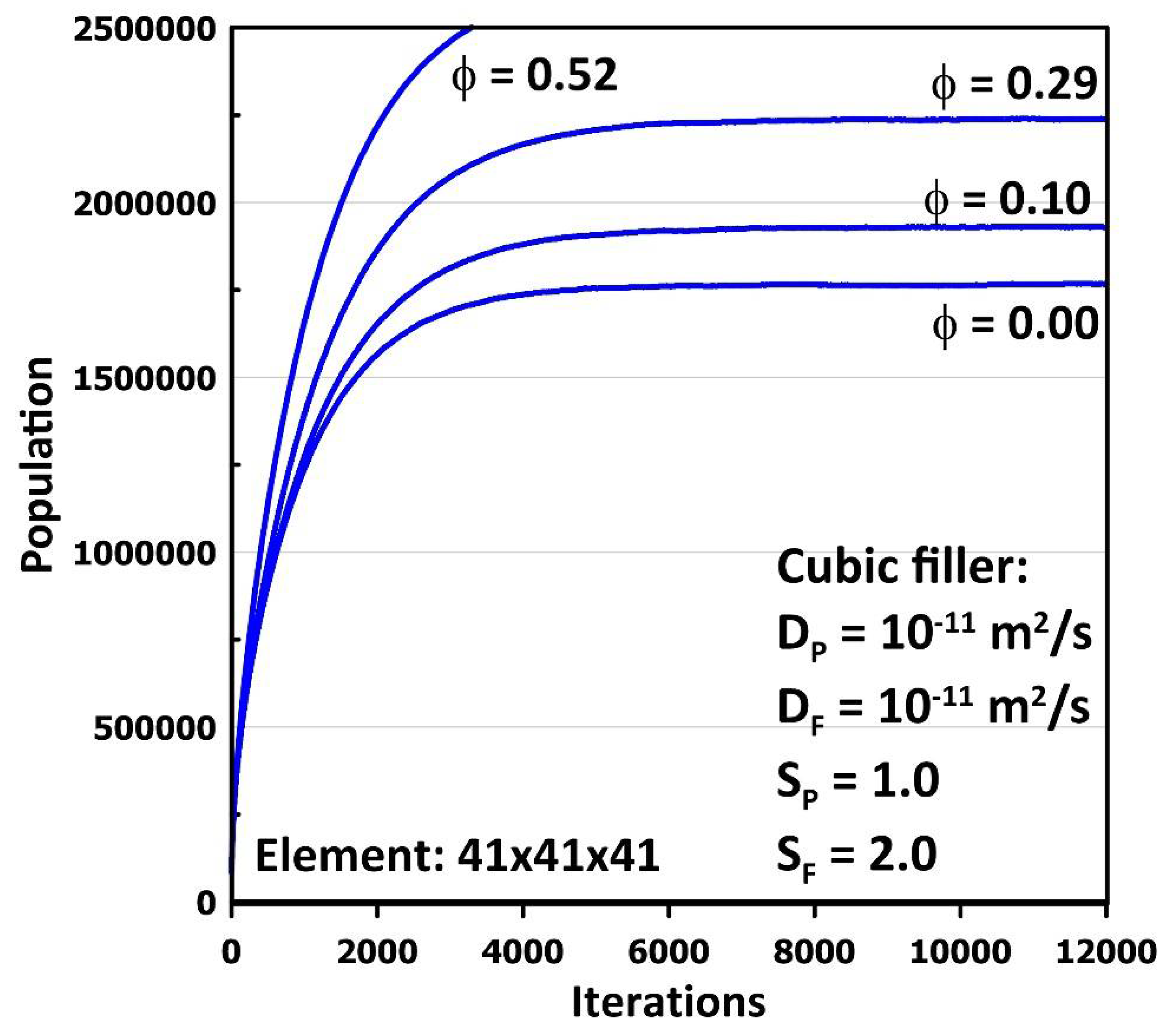
- When all the members of the current molecule population have been considered in one given iteration, the population is updated. First, the number of molecules in the upstream surface layer is reset to its original number to satisfy the equilibrium condition between the constant surrounding gas pressure and the polymer surface of the MMM. Resetting the original number of molecules automatically calculates the flux of molecules entering the membrane at each iteration. As the Brownian motion is purely a random process, it is possible to encounter a negative flux for some iterations. Secondly, all the molecules that exited the downstream side of the membrane allow the calculation of the instantaneous permeation flux of molecules leaving the membrane. At each iteration, the molecules added or removed from the upstream membrane surface layer and the molecules exiting the downstream side serve to update the current population of molecules.
- (d)
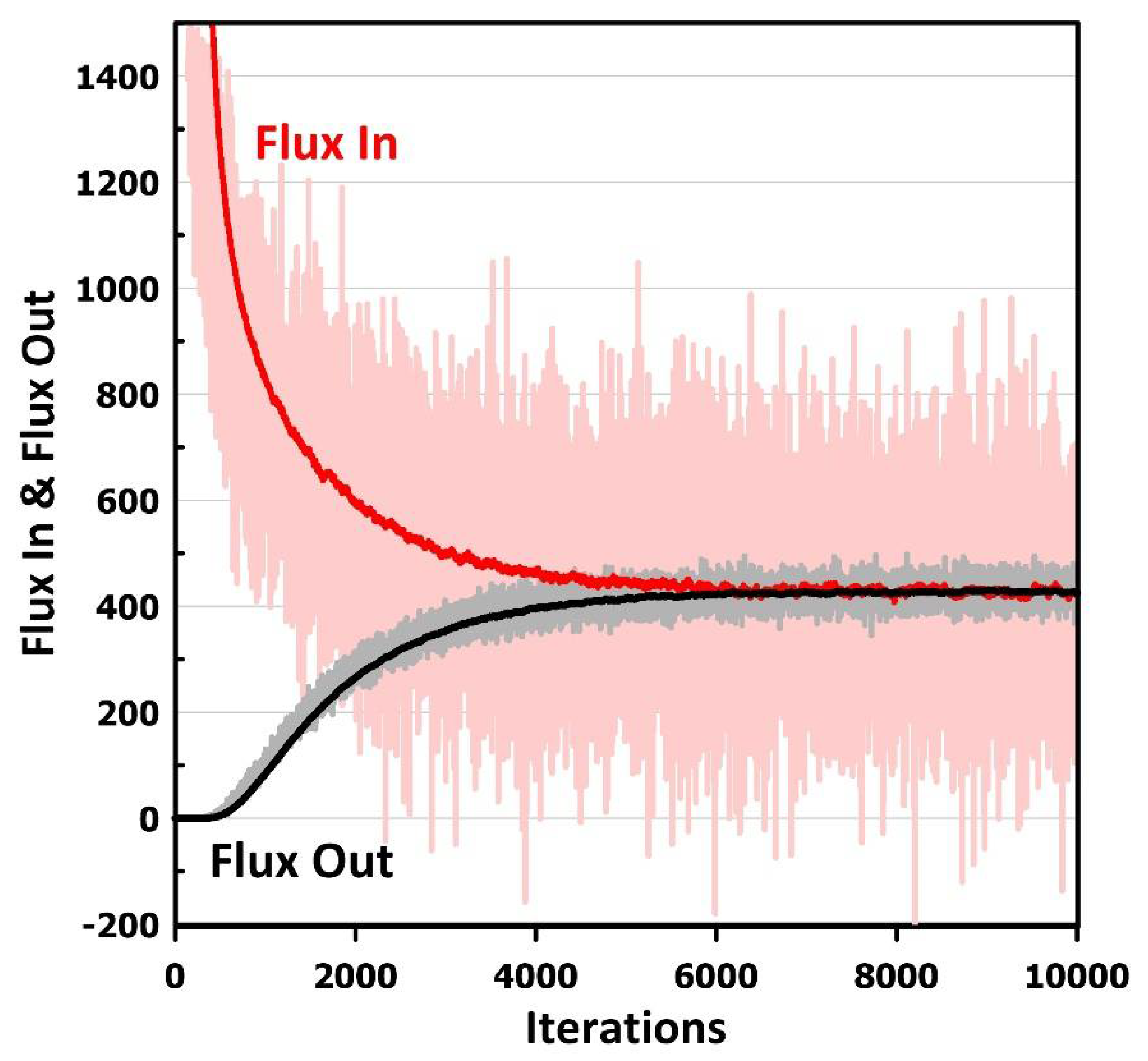
- The above procedure is followed for a given number of iterations or until molecules’ average inlet and outlet fluxes are the same, i.e., the steady-state permeation is attained. The final results are then printed. The relative permeability of the MMM is calculated by dividing the steady-state permeation flux obtained for the MMM by the permeation flux of the neat membrane under identical conditions, implying that the conditions of Equation (5) are considered in calculating the flux of the neat membrane even if a filler is absent.
- (e)
- The above procedure pertains to the lattice MC. In the case of the second method alluded to earlier (MC2), the only difference is in calculating the displacement of the molecules permeating through the membrane. In the lattice MC, the molecules can jump from the central cubic mesh to one of the six neighboring meshes. In the second method, the molecules can move in any direction by randomly choosing a displacement in the three directions and calculating the new coordinates of a given molecule. In this method, a move is always accepted, but the distance travelled by one molecule is adjusted via the diffusivity ratio of the two phases, similar to what was performed in the lattice MC. All the other considerations, such as the periodic symmetrical conditions and the polymer–solid equilibrium interface, remain the same. For the latter two considerations and the upstream surface population, the number of molecules in each cubic mesh of the MMM is calculated and used in the same way as in the lattice MC.
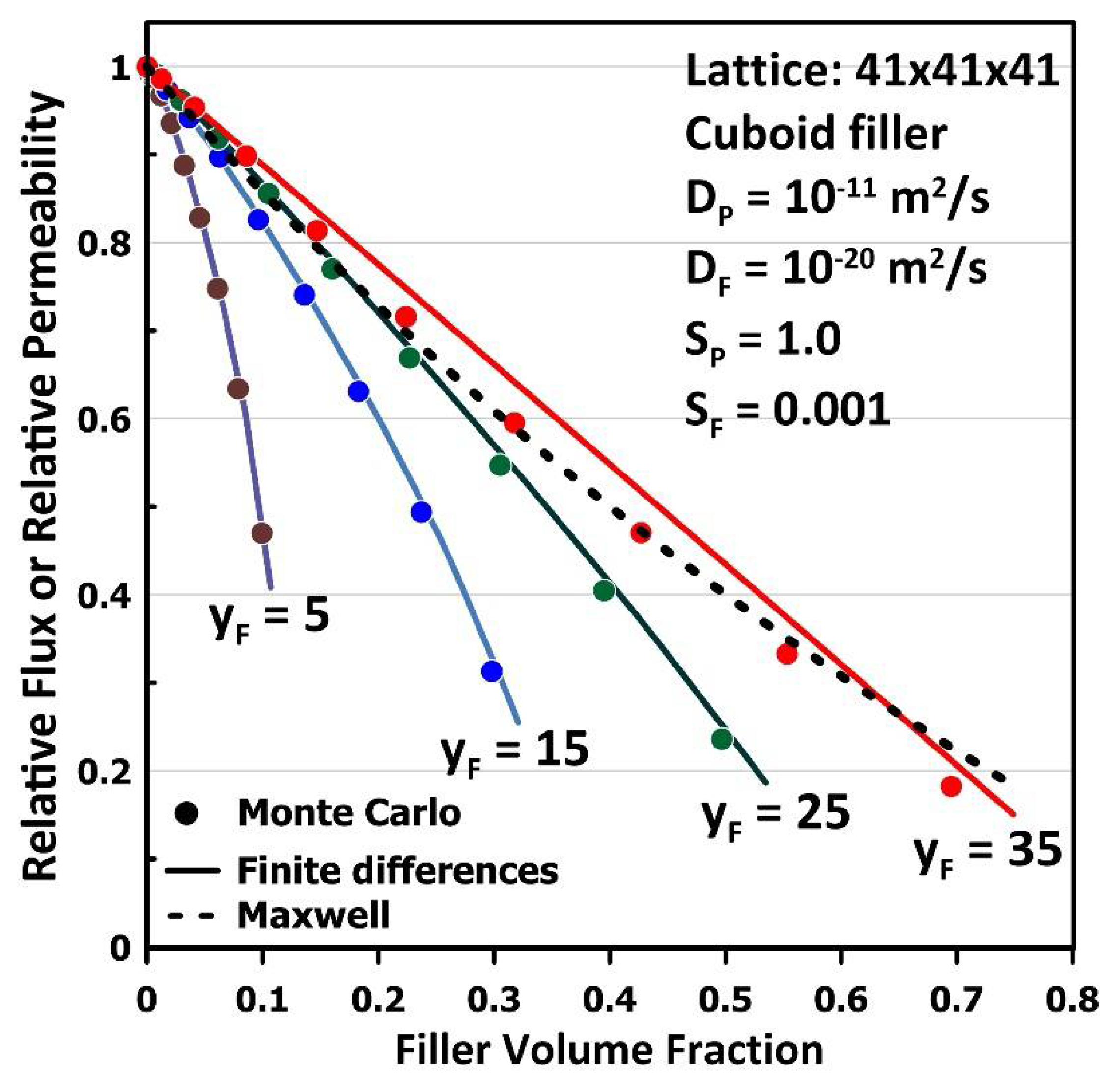
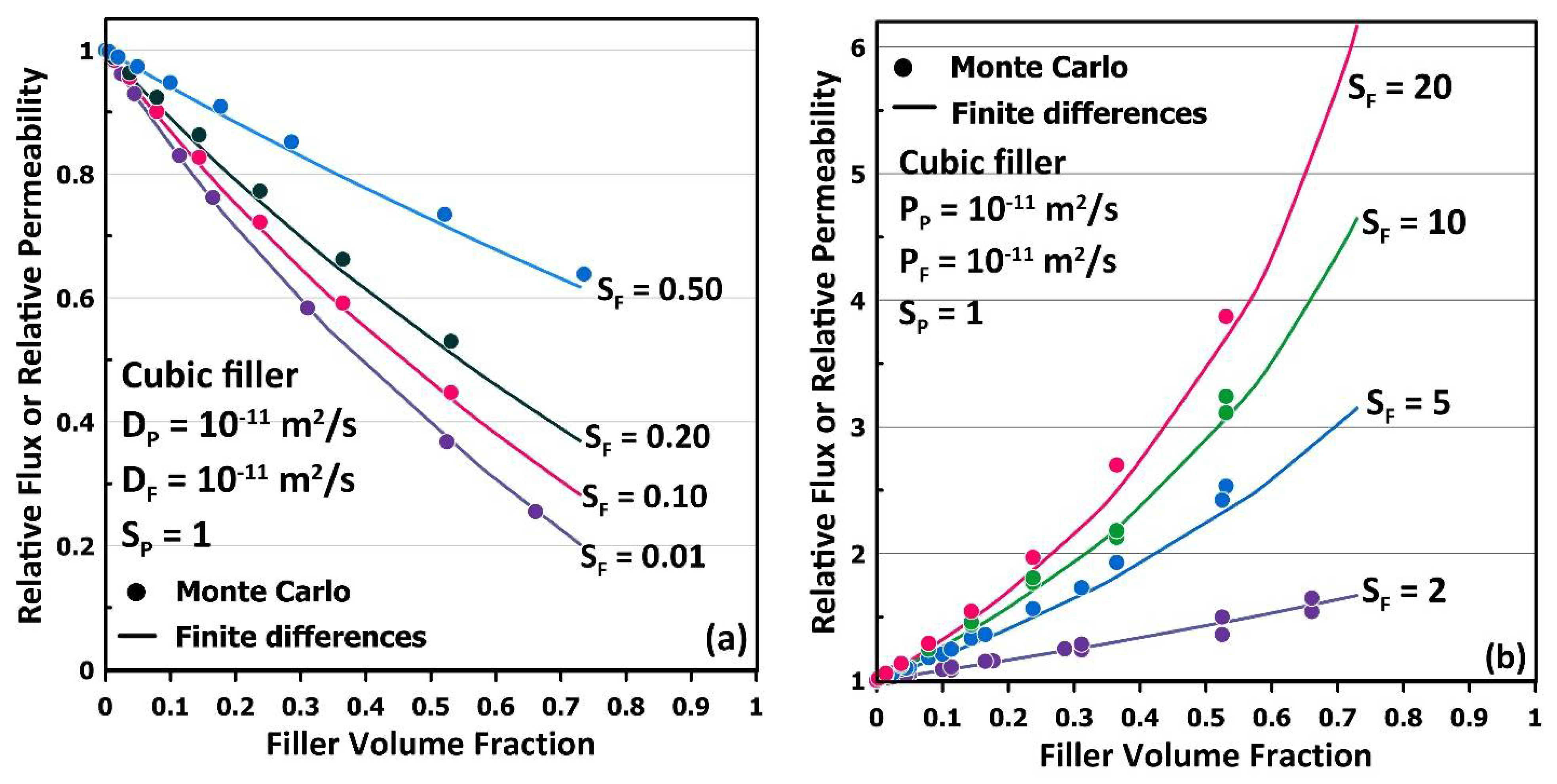
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | Concentration of the permeating gas surrounding of the MMM (mol/m3) |
| C | Concentration of the permeating gas inside the MMM (mol/m3) |
| D | Diffusivity coefficient (m2/s) |
| L | Dimension of one side of the elementary unit (m) |
| n | Number of divisions of the elementary unit along a particular axis |
| p | Pressure of the permeating gas in the surrounding of the MMM (Pa) |
| P | Permeability (m2/s) |
| R | Ideal gas constant (Pa m3/(mol K)) |
| S | Solubility coefficient ((mol/m3)/(mol/m3)) |
| t | Time (s) |
| T | Temperature (K) |
| xF | Length of the side of the cuboid filler along the x-axis (m) |
| yF | Length of the side of the cuboid filler along the y-axis (m) |
| zF | Length of the side of the cuboid filler along the z-axis (m) |
| Subscripts: | |
| e | Effective |
| F | Filler phase |
| i | Index for mesh point in the x-direction |
| j | Index for mesh point in the y-direction |
| k | Index for mesh point in the z-direction |
| P | Polymer phase |
| r | Relative |
| x | x-coordinate (m) |
| y | y-coordinate (m) |
| z | z-coordinate (m) |
| 0 | Initial |
| 1 | Phase 1 |
| 2 | Phase 2 |
| Abreviations: | |
| AE | Absolute value of the error |
| BC | Boundary condition |
| FD | Finite differences |
| IC | Initial condition |
| MC | Monte Carlo |
| RN | Random number |
References
- Salahshoori, I.; Seyfaee, A.; Babapoor, A. Recent advances in synthesis and applications of mixed matrix membranes. Synth. Sinter. 2021, 1, 1–27. [Google Scholar] [CrossRef]
- Decknik, J.; Sumby, C.J.; Janiak, C. Enhancing Mixed-Matrix Membrane Performance with Metal−Organic Framework Additives. Cryst. Growth Des. 2017, 17, 4467–4488. [Google Scholar] [CrossRef]
- Gnus, M.; Dudek, G.; Turczyn, R. The influence of filler type on the separation properties of mixed-matrix membranes. Chem. Pap. 2018, 72, 1095–1105. [Google Scholar] [CrossRef] [PubMed]
- Azimi, H.; Ebneyamini, A.; Tezel, F.H.; Thibault, J. Separation of Organic Compounds from ABE Model Solutions via Pervaporation Using Activated Carbon/PDMS Mixed Matrix Membranes. Membranes 2018, 8, 40. [Google Scholar] [CrossRef]
- Liu, W.; Ban, Y.; Liu, J.; Wang, Y.; Hu, Z.; Wang, Y.; Li, Q.; Yang, W. ZIF-L based mixed matrix membranes for acetone-butanol-ethanol (ABE) recovery from diluted aqueous solution. Sep. Purif. Technol. 2021, 276, 119085. [Google Scholar] [CrossRef]
- Liang, H.; Zou, C.; Tang, W. Development of novel polyether sulfone mixed matrix membranes to enhance antifouling and sustainability: Treatment of oil sands produced water (OSPW). J. Taiwan Inst. Chem. Eng. 2021, 118, 215–222. [Google Scholar] [CrossRef]
- Feng, B.; Xu, K.; Huang, A. Synthesis of graphene oxide/polyimide mixed matrix membranes for desalination. RSC Adv. 2017, 7, 2211–2217. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Q.; Wang, Q.; Ding, W.; Zhang, K. Organo-Functionalization: An Effective Method in Enhancing the Separation and Antifouling Performance of Thin-Film Nanocomposite Membranes by Improving the Uniform Dispersion of Palygorskite Nanoparticles. Membranes 2021, 11, 889. [Google Scholar] [CrossRef]
- Hamid, M.R.A.; Jeong, H.-K. Recent advances on mixed-matrix membranes for gas separation: Opportunities and engineering challenges. Korean J. Chem. Eng. 2018, 35, 1577–1600. [Google Scholar] [CrossRef]
- Ebneyamini, A.; Azimi, H.; Tezel, F.H.; Thibault, J. Modelling of mixed-matrix membranes: Validation of the resistance-based model. J. Memb. Sci. 2017, 543, 361–369. [Google Scholar] [CrossRef]
- Singh, T.; Kang, D.-Y.; Nair, S. Rigorous calculations of permeation in mixed-matrix membranes: Evaluation of interfacial equilibrium effects and permeability-based models. J. Membr. Sci. 2013, 448, 160–169. [Google Scholar] [CrossRef]
- Zamanian, M.; Sadrnia, H.; Khojastehpour, M.; Hosseini, F.; Kruczek, B.; Thibault, J. Barrier Properties of PVA/TiO2/MMT Mixed-Matrix Membranes for Food Packaging. J. Polym. Environ. 2021, 29, 1396–1411. [Google Scholar] [CrossRef]
- Monsalve-Bravo, G.M.; Bhatia, S.K. Extending effective medium theory to finite size systems: Theory and simulation for permeation in mixed-matrix membranes. J. Membr. Sci. 2017, 531, 148–159. [Google Scholar] [CrossRef]
- Wang, S.; Lu, L.; Wu, D.; Lu, X.; Cao, W.; Yang, T.; Zhu, Y. Molecular Simulation Study of the Adsorption and Diffusion of a Mixture of CO2/CH4 in Activated Carbon: Effect of Textural Properties and Surface Chemistry. J. Chem. Eng. Data 2016, 61, 4139–4147. [Google Scholar] [CrossRef]
- Dutta, R.C.; Bhatia, S.K. Transport Diffusion of Light Gases in Polyethylene Using Atomistic Simulations. Langmuir 2017, 33, 936–946. [Google Scholar] [CrossRef]
- Wei, W.; Liu, J.; Jiang, J. Atomistic Simulation Study of Polyarylate/Zeolitic-Imidazolate Framework Mixed-Matrix Membranes for Water Desalination. ACS Appl. Nano Mater. 2020, 3, 10022–10031. [Google Scholar] [CrossRef]
- Ebneyamini, A.; Azimi, H.; Tezel, F.H.; Thibault, J. Mixed-matrix membranes applications: Development of a resistance-based model. J. Memb. Sci. 2017, 543, 351–360. [Google Scholar] [CrossRef]
- Wu, H.; Zamanian, M.; Kruczek, B.; Thibault, J. Gas Permeation Model of Mixed-Matrix Membranes with Embedded Impermeable Cuboid Nanoparticles. Membranes 2020, 10, 422. [Google Scholar] [CrossRef]
- Wu, H.; Kruczek, B.; Thibault, J. A generalized model for the prediction of the permeability of mixed-matrix membranes using impermeable fillers of diverse geometry. J. Membr. Sci. 2022, 641, 119951. [Google Scholar] [CrossRef]
- Brandimarte, P. Handbook in Monte Carlo Simulation: Applications in Financial Engineering, Risk Management, and Economics; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-1-118-59451-3. [Google Scholar]
- Mode, C.J. Applications of Monte Carlo Methods in Biology, Medicine and Other Fields of Science; IntechOpen: London, UK, 2011; pp. 1–440. Available online: https://www.intechopen.com/books/105 (accessed on 15 July 2022).
- Sin, G.; Espuna, A. Editorial: Applications of Monte Carlo Method in Chemical, Biochemical and Environmental Engineering. Front. Energy Res. 2020, 8, 68. [Google Scholar] [CrossRef]
- Belova, I.V.; Murch, G.E.; Fiedler, T.; Ochsner, A. The Lattice Monte Carlo Method for Solving Phenomenological Mass and Heat Transport Problems. Diffus. Fundam. 2017, 4, 13–22. [Google Scholar]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 1st ed.; Clarendon Press: London, UK, 1873. [Google Scholar]
- Lewis, T.B.; Nielsen, L.E. Dynamic Mechanical Properties of Particulate-Filled Composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Pal, R. New Models for Thermal Conductivity of Particulate Composites. J. Reinf. Plast. Compos. 2007, 26, 643–651. [Google Scholar] [CrossRef]
- Wolf, C.; Angellier-Coussy, H.; Gontard, N.; Doghieri, F.; Guillard, V. How the shape of fillers affects the barrier properties of polymer/non-porous particles nanocomposites: A review. J. Membr. Sci. 2018, 556, 393–418. [Google Scholar] [CrossRef]
- Ahn, J.; Chung, W.-J.; Pinnau, I.; Guiver, M.D. Polysulfone/silica nanoparticle mixed-matrix membranes for gas separation. J. Membr. Sci. 2008, 314, 123–133. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Kruczek, B.; Thibault, J. Monte Carlo Simulations for the Estimation of the Effective Permeability of Mixed-Matrix Membranes. Membranes 2022, 12, 1053. https://doi.org/10.3390/membranes12111053
Cao Z, Kruczek B, Thibault J. Monte Carlo Simulations for the Estimation of the Effective Permeability of Mixed-Matrix Membranes. Membranes. 2022; 12(11):1053. https://doi.org/10.3390/membranes12111053
Chicago/Turabian StyleCao, Zheng, Boguslaw Kruczek, and Jules Thibault. 2022. "Monte Carlo Simulations for the Estimation of the Effective Permeability of Mixed-Matrix Membranes" Membranes 12, no. 11: 1053. https://doi.org/10.3390/membranes12111053
APA StyleCao, Z., Kruczek, B., & Thibault, J. (2022). Monte Carlo Simulations for the Estimation of the Effective Permeability of Mixed-Matrix Membranes. Membranes, 12(11), 1053. https://doi.org/10.3390/membranes12111053