Theoretical Investigation of the Phenomenon of Space Charge Breakdown in Electromembrane Systems
Abstract
1. Introduction
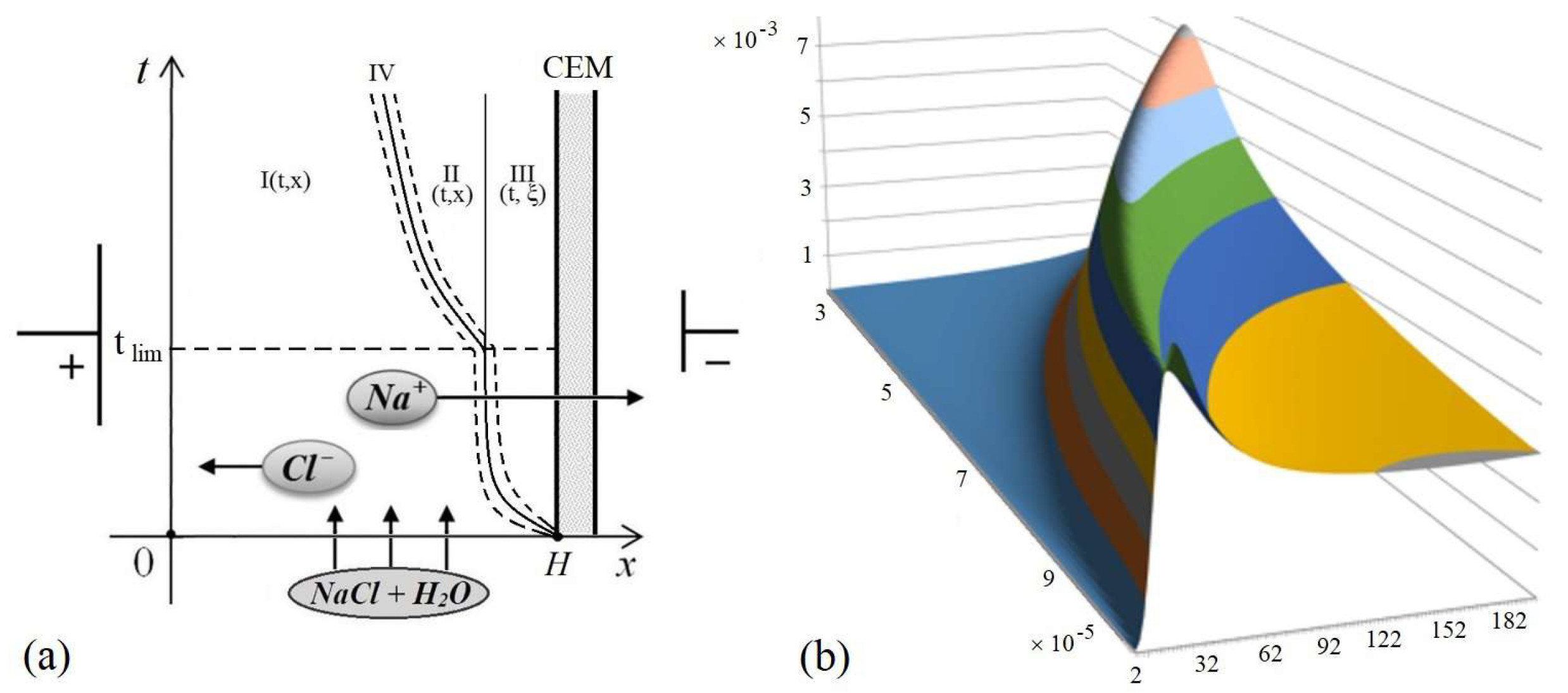
2. Formation and Properties of a Quasi-Equilibrium Layer (QEL)
3. Formation of an Extended Space Charge Region and Local Extrema of the Space Charge
4. Analytical Solution of the Boundary Value Problem in Quasi-Equilibrium Layers in the Section of the Desalination Channel
5. Model Formulation wQEL (without Quasi-Equilibrium Boundary Layer)
6. A New Numerical-Analytical Method for Solving Boundary Value Problems for the System of Nernst-Planck and Poisson Equations
6.1. Algorithm of the Numerical-Analytical Method of Solution
- We numerically solve the boundary value problem (A15)–(A24) of the wQEL model, and find, among other things, ;
- We find the potential jump for the base model. For this, we use the ratioTaking into account that , we obtainHere, the first term is the potential jump in the quasi-equilibrium layers of the anion-exchange and cation-exchange membranes, and the second potential jump is , calculated using the wQEL model. Let us estimate the potential jump , assuming that the minimum value of the concentration has decreased by 100 and times.Then, in the first case, we obtain , and in the second .Then, the dimensionless jumps will be and .Taking into account that V, we obtain that in dimensional form the total potential jump in quasi-equilibrium layers is approximately equal to V and V.Taking into account the fact that the potential jump in the desalination chamber can reach 1 V–3 V, the potential jump in quasi-equilibrium layers can make a significant contribution with an increase in the degree of desalination.
6.2. Verification of Calculations
6.3. Comparison of the Results of Calculations of the Base Model and the wQEL Model
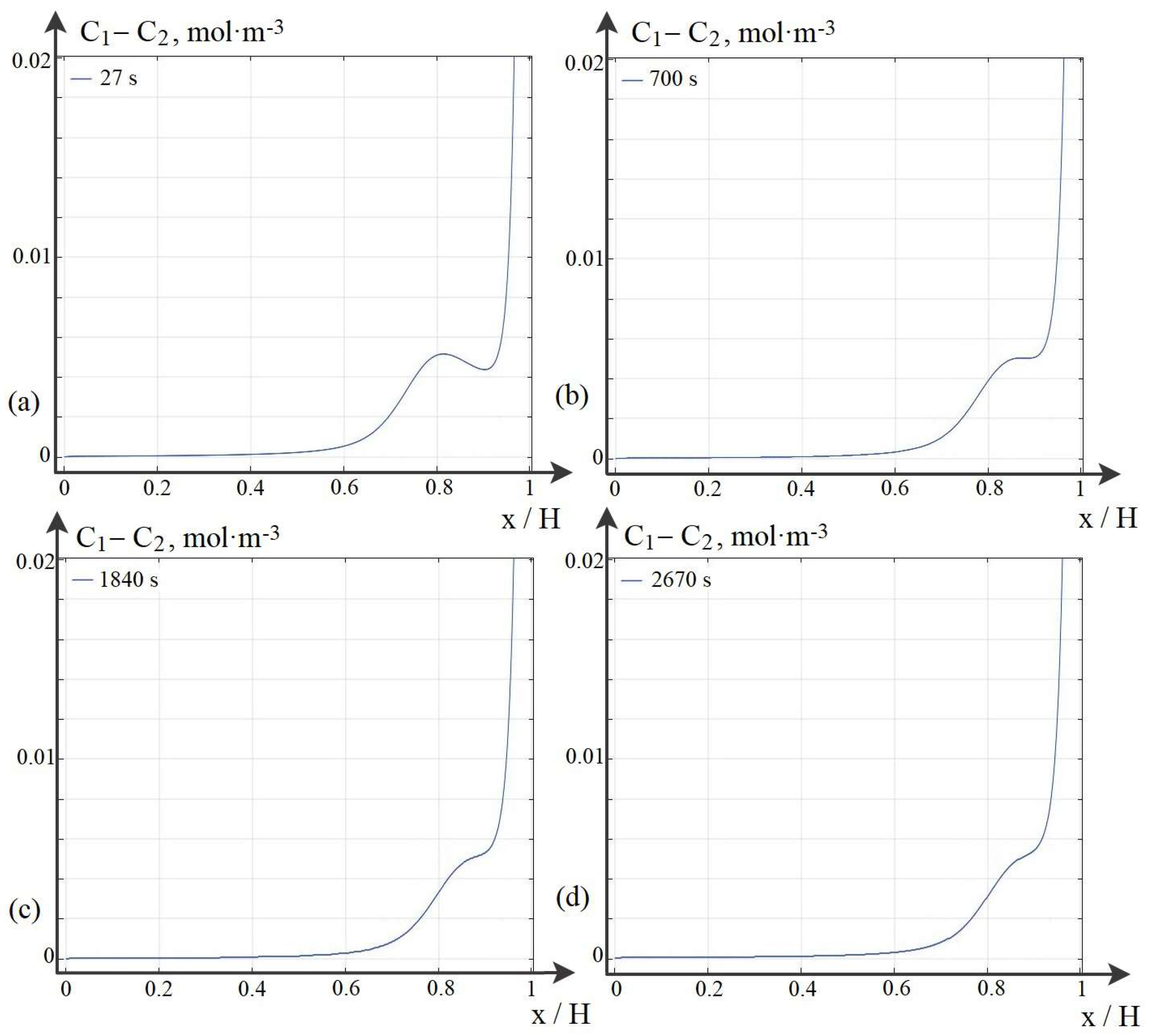
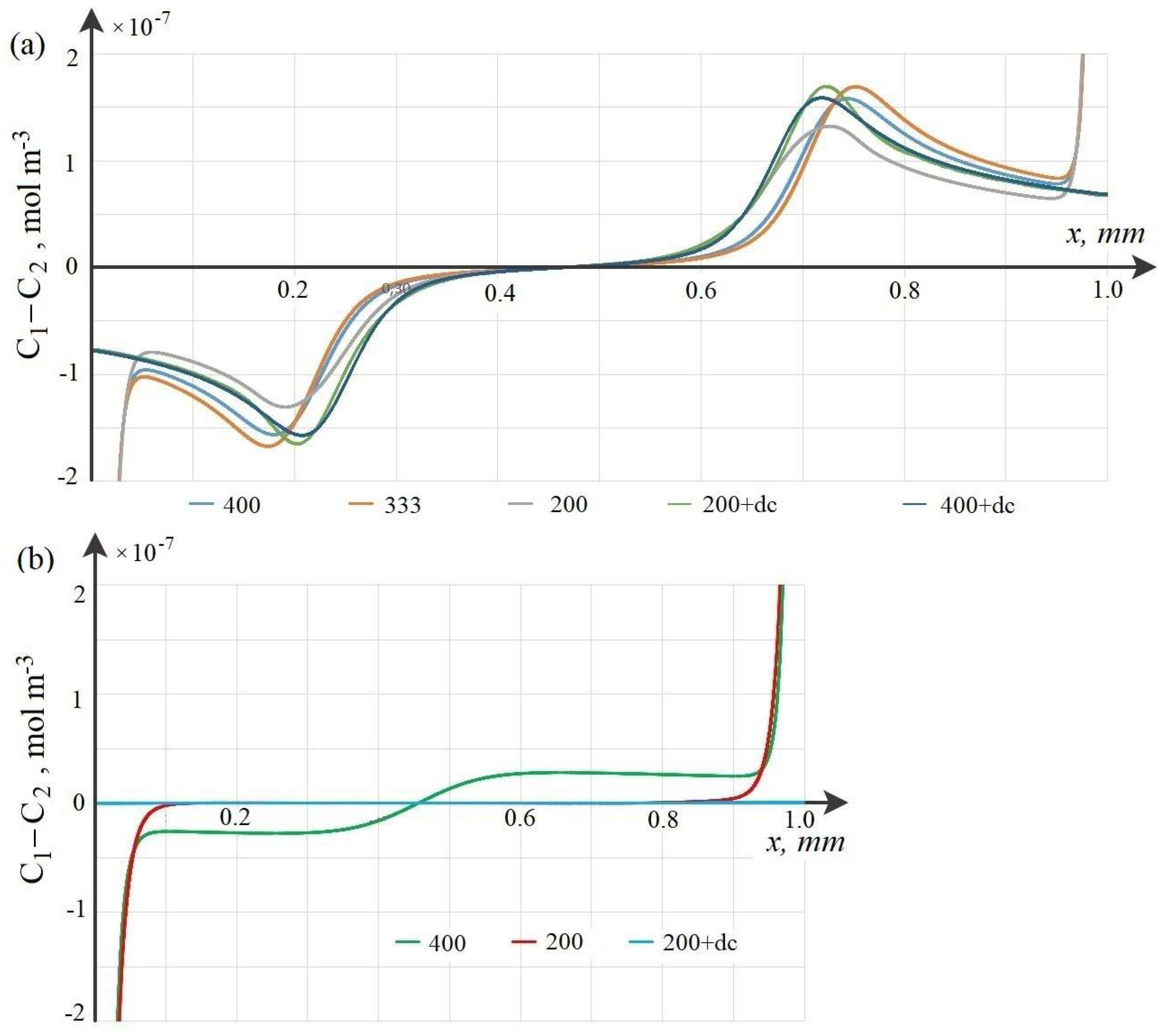
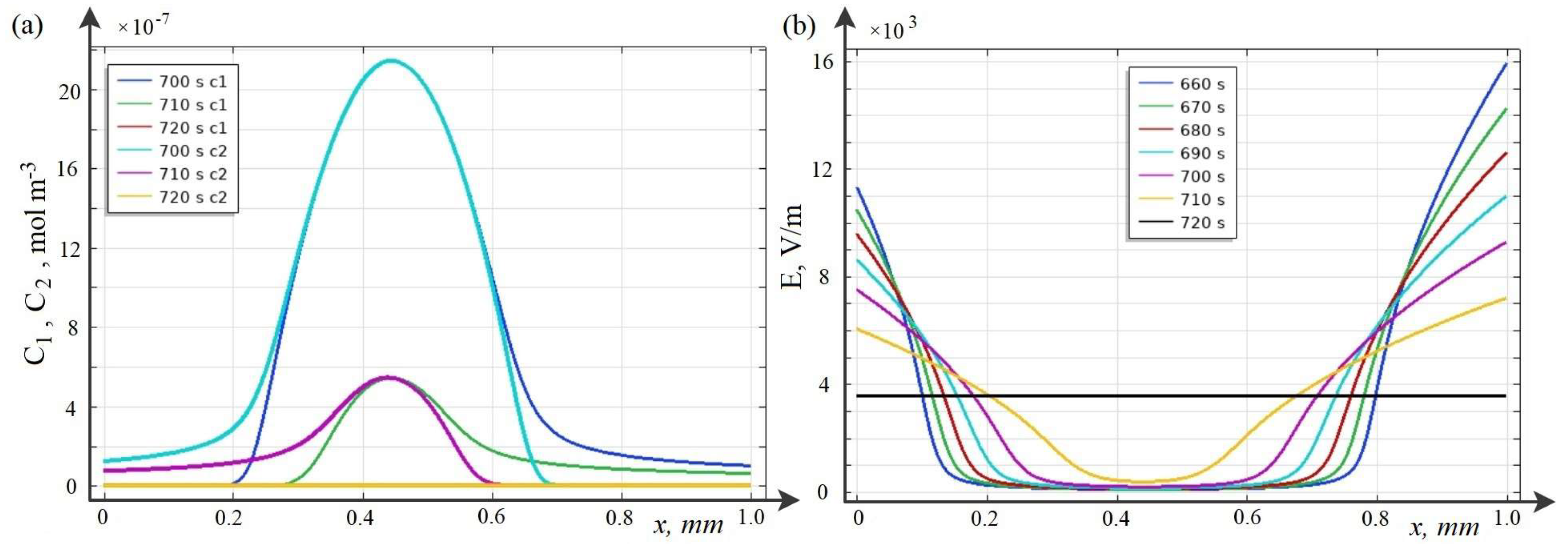
7. Patterns of Space Charge Breakdown at High Initial Concentrations
8. Dependence of the Time (Potential Jump) of the Onset of Breakdown on the Initial Concentration of the Solution
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPP | Nernst-Planck and Poisson |
| SCB | Space charge breakdown |
| QEL | Quasi-equilibrium layer |
| CEM | Cation-exchange membrane |
| AEM | Anion exchange membrane |
| REN | Region of electrical neutrality |
| SCR | Space charge region |
| wQEL | Without Quasi-equilibrium boundary layer |
| QCD | Quasi-uniform charge distribution |
List of Symbols
| The initial concentration of the solution | |
| The concentration of cations | |
| The concentration of anions | |
| H | The distance between membranes (Channel width) |
| The flux of cations | |
| The flux of anions | |
| The duffusion of cations | |
| The duffusion of anions | |
| The electric field potential (Potential jump) | |
| The initial value of the potential | |
| The speed of the potential sweep | |
| The absolute permittivity of the solution | |
| F | The Faraday constant |
| R | The gas constant |
| T | The absolute temperature |
| t | The time |
| The space charge breakdown start time | |
| The space charge breakdown start potential jump |
Appendix A
Appendix A.1. Basic Mathematical Model
Appendix A.1.1. System of Equations
Appendix A.1.2. Boundary Conditions
Appendix A.2. Characteristic Quantities and Transition to Dimensionless Form
Appendix A.2.1. Characteristic Quantities, Their Physical Meaning
Appendix A.2.2. Estimation of Characteristic Quantities
Appendix A.2.3. Trivial Similarity Criteria, Their Physical Meaning and Estimation of Values
| mol/m | 0.01 | 0.1 | 1 | 10 | 100 |
|---|---|---|---|---|---|
| 0.003865 | 0.03865 | 0.3865 | 3.865 | 38.65 | |
Appendix A.3. Basic Mathematical Model in Dimensionless Form
Appendix A.3.1. System of Equations in Dimensionless Form
Appendix A.3.2. Boundary Conditions
References
- Deng, D.C.; Dydek, E.V.; Han, J.; Schlumpberger, S.; Mani, A.; Zaltzman, B.; Bazant, M.Z. Overlimiting current and shock electrodialysis in porous media. Langmuir ACS J. Surf. Colloids 2013, 29, 16167–16177. [Google Scholar] [CrossRef] [PubMed]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G. Electrodialysis Applications in Wastewater Treatment for Environmental Protection and Resources Recovery: A Systematic Review on Progress and Perspectives. Membranes 2020, 10, 146. [Google Scholar] [CrossRef]
- Campione, A.; Gurreri, L.; Ciofalo, M.; Micale, G.; Tamburini, A.; Cipollina, A. Electrodialysis for water desalination: A critical assessment of recent developments on process fundamentals, models and applications. Desalination 2018, 434, 121–160. [Google Scholar] [CrossRef]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Haiyang, X.; Ji, X.; Wang, L.; Huang, J.; Han, J.; Yue, W. Performance study on a small-scale photovoltaic electrodialysis system for desalination. Renew. Energy 2020, 154, 1008–1013. [Google Scholar]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 10, 85–106. [Google Scholar] [CrossRef]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion exchange membranes: New developments and applications. J. Membr. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Shelistov, V.S.; Polyanskikh, S.V. Linear and nonlinear evolution and diffusion layer selection in electrokinetic instability. Phys. Rev. E 2011, 84, 036318. [Google Scholar] [CrossRef]
- Urtenov, M.; Chubyr, N.; Gudza, V. Reasons for the Formation and Properties of Soliton-like Charge Waves in Membrane Systems When Using Overlimiting Current Modes. Membranes 2020, 10, 189. [Google Scholar] [CrossRef]
- Kovalenko, A.V.; Urtenov, M.K.; Chubyr, N.; Uzdenova, A.; Gudza, V. Mathematical modeling of the influence of the main temperature effects in stationary transport of ions of salt in the diffusion layer. Ecol. Bull. Res. Cent. Black Sea Econ. Coop. 2018, 15, 78–86. [Google Scholar]
- Urtenov, M.; Gudza, V.; Chubyr, N.; Shkorkina, I. Theoretical Analysis of the Stationary Transport of 1:1 Salt Ions in a Cross-Section of a Desalination Channel, Taking into Account the Non-Catalytic Dissociation/Recombination Reaction of Water Molecules. Membranes 2020, 10, 342. [Google Scholar] [CrossRef] [PubMed]
- Uzdenova, A.; Kovalenko, A.; Urtenov, M.; Nikonenko, V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8, 84. [Google Scholar] [CrossRef] [PubMed]
- Gudza, V.A.; Chubyr, N.O.; Kirillova, E.V.; Urtenov, M.K. Numerical and Asymptotic Study of Non-Stationary Mass Transport of Binary Salt Ions in the Diffusion Layer near the Cation Exchange Membrane at Prelimiting Currents. Appl. Math. Inf. Sci. 2021, 15, 411–422. [Google Scholar]
- Vendin, S.V. To the solution of issues of nonstationary diffusion in layered environments. Bull. Belgorod State Technol. Univ. Named V. G. Shukhov 2019, 3, 100–105. [Google Scholar]
- Mishchuk, N.A. Concentration polarization of interface and non-linear electrokinetic phenomena. Adv. Colloid Interface Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Urtenov, M.K. Analysis of electrodiffusion equations in the decomposition form. Russ. J. Electrochem. 1996, 32, 187–194. [Google Scholar]
- Nikonenko, V.V.; Urtenov, M.K. On a generalization of the electroneutrality condition. Russ. J. Electrochem. 1996, 32, 195–198. [Google Scholar]
- Kovalenko, A.V. Solving boundary value problem for system of equations Nernst–Plank and Poisson in the space charge. Fundam. Res. 2015, 9, 28–32. [Google Scholar]
- Uzdenova, A.M. Simulation of electroconvection in membrane systems: Analysis of boundary conditions at the surface. Fundam. Res. 2016, 12, 1010–1017. [Google Scholar] [CrossRef][Green Version]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Theoretical analysis of the effect of ion concentration in solution bulk and at membrane surface on the mass transfer at overlimiting currents. Russ. J. Electrochem. 2017, 53, 1254–1265. [Google Scholar] [CrossRef]
- Uzdenova, A.; Urtenov, M. Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel. Membranes 2021, 11, 873. [Google Scholar] [CrossRef] [PubMed]
- Chubyr, N.O.; Kovalenko, A.V.; Urtenov, M.K.; Gudza, I.V. Mathematical model of salt ion stationary transport in the cross section of the channel at equilibrium. Model. Optim. Inf. Technol. 2022, 10, 1–10. [Google Scholar]
- Kovalenko, A.V.; Gudza, V.A.; Chubyr, N.O.; Khromykh, A.A.; Urtenov, M.K. Study of current chronograms, structure of dissociation, recombination and equilibrium regions in problems of nonstationary 1:1 electrolyte transfer in membrane systems using a mathematical model. Model. Optim. Inf. Technol. 2022, 10, 1–18. [Google Scholar]
- Kovalenko, A.V.; Wessling, M.; Nikonenko, V.V.; Mareev, S.A.; Moroz, I.A.; Evdochenko, E.; Urtenov, M.K. Space-Charge breakdown phenomenon and spatio-temporal ion concentration and fluid flow patterns in overlimiting current electrodialysis. J. Membr. Sci. 2021, 636, 119583. [Google Scholar] [CrossRef]
- Gudza, V.A. One-dimensional mathematical models of salt ion transport in electromembrane systems. Laplage Rev. 2021, 7, 253–267. [Google Scholar] [CrossRef]
- Chubyr, N.O.; Gudza, V.A.; Urtenov, M.K.; Shkorkina, I.V. Analysis of nonstationary transfer of 1:1 electrolyte in intensive current regimes. Int. J. Emerg. Trends Eng. Res. 2020, 8, 4337–4345. [Google Scholar]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; JohnWiley & Sons: Hoboken, NJ, USA, 2004; p. 647. [Google Scholar]
- Rubinstein, I.; Maletzki, F. Electroconvection at an electrically inhomoheneous permselective membrane surface. Trans. Faraday Soc. 1991, 87, 2079–2087. [Google Scholar] [CrossRef]


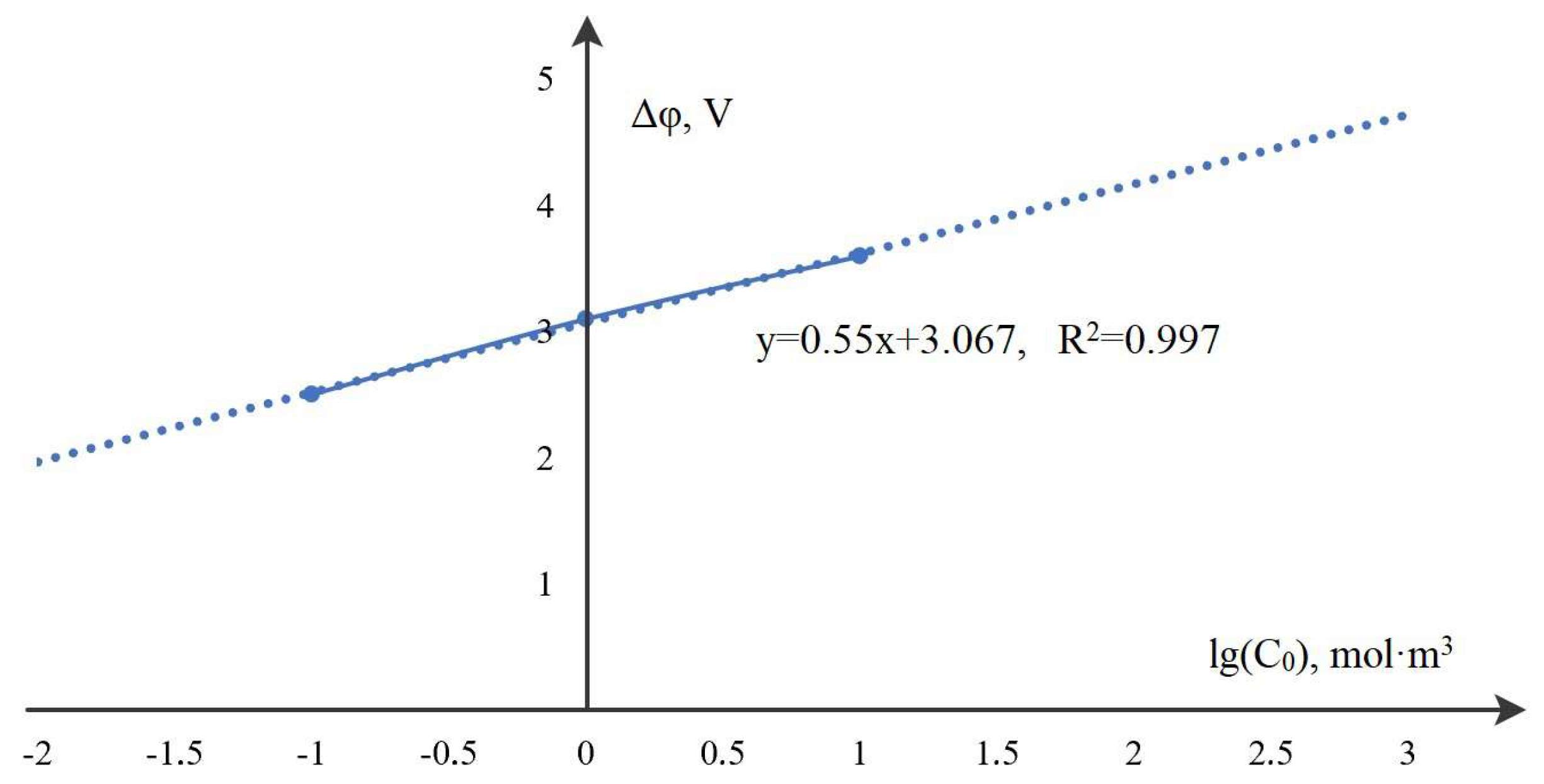
| mol/m | 0.01 | 0.1 | 1 | 10 | 100 |
|---|---|---|---|---|---|
| 400 | 500 | 620 | 720 | 820 | |
| 2 | 2.5 | 3.1 | 3.6 | 4.1 | |
| 2 | 2.5 | 3 | 3.5 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalenko, A.; Chubyr, N.; Uzdenova, A.; Urtenov, M. Theoretical Investigation of the Phenomenon of Space Charge Breakdown in Electromembrane Systems. Membranes 2022, 12, 1047. https://doi.org/10.3390/membranes12111047
Kovalenko A, Chubyr N, Uzdenova A, Urtenov M. Theoretical Investigation of the Phenomenon of Space Charge Breakdown in Electromembrane Systems. Membranes. 2022; 12(11):1047. https://doi.org/10.3390/membranes12111047
Chicago/Turabian StyleKovalenko, Anna, Natalia Chubyr, Aminat Uzdenova, and Makhamet Urtenov. 2022. "Theoretical Investigation of the Phenomenon of Space Charge Breakdown in Electromembrane Systems" Membranes 12, no. 11: 1047. https://doi.org/10.3390/membranes12111047
APA StyleKovalenko, A., Chubyr, N., Uzdenova, A., & Urtenov, M. (2022). Theoretical Investigation of the Phenomenon of Space Charge Breakdown in Electromembrane Systems. Membranes, 12(11), 1047. https://doi.org/10.3390/membranes12111047









